ART, THE 4TH DIMENSION & NON-PERIODIC TILING
MATHEMATICS & THE ART OF M.C.ESCHER
MIXING MATHEMATICS & ART OF ABRECHT DÜRER
The most beautiful thing we can experience is the mysterious. It is the source of all true art and science.
—Albert Einstein
Linking mathematics and art may seem alien to many people. But mathematical worlds of geometries, algebra, dimensions, computers have provided tools for artists to explore, enhance, simplify, and perfect their work. Over the centuries, artists and their works have been influenced by the knowledge and use of mathematics. The ancient Greek sculptor, Phidias, is said to have used the golden mean in the proportions of many of his works. Albrecht Dürer employed concepts from projective geometry to achieve perspective, and geometric constructions played a vital role in his typography of Roman letters. Since religious doctrine prohibited the use of animate objects in Moslem art, Moslem artists had to rely on mathematics as an avenue for their artistic expression, thus leading them to create a wealth of tessellation designs. Leonardo da Vinci felt “…no human inquiry can be called science unless it pursues its path through mathematical exposition and demonstration.” Leonardo’s sculptures and paintings illustrate his study of the golden rectangle, proportions, and projective geometry, while his architectural designs show his work in geometric structures and knowledge of symmetry. The topics in this section are a few examples illustrating the connection between mathematics and art.

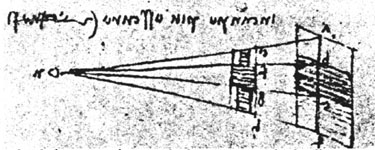
A sketch from one of Leonardo da Vinci’s notebooks illustrating lines converging to a vanishing point.
Mathematics takes us into the region of absolute necessity, to which not only the actual world, but every possible world, must conform. —Albert Einstein
On a canvas, the artist is restricted to two-dimensions to communicate the feeling of other dimensions. Icon artists of the Byzantine period depicted three-dimensional religious scenes in only two-dimensions, giving the subject matter a mystical appearance. During the Renaissance, artists using the concepts of projective geometry transformed their flat canvas into the three-dimensional world they wanted to convey. Today, mathematics plays an active role in providing inspiration and tools for the creation and communication of an artist’s ideas. Artists use mathematical ideas to escape into higher dimensions. The hypercube1, for example, has been used by artists to take a step into the fourth-dimension. In the early 1900’s architect Claude Bragdon adapted the hypercube along with other four-dimensional designs in his work2. Intrigued by the hypercube, Salvador Dali3 delved into mathematics for his model of an unfolded hypercube which is the focal point in his painting The Crucifixion 4 (1954).
Today, there are a number of artists pursuing art in connection with mathematical ideas — in particular, mathematics of non-periodic tiling, multi-dimensions and computer renditions. In fact, computer renditions of the hypercube, created by mathematician Thomas Banchoff and computer scientist Charles Strauss of Brown University, produce visualization of the hyper-cube moving in and out of a 3-D space. Various images of the hypercube in the 3-D world are thereby captured on the computer monitor. Introduced to this part of mathematics, artist Tony Robbin has created 3-D canvas representations of the hypercube with the canvas acting as a plane intersecting the hypercube. Non-periodic tilings, Penrose tiles, quasicrystal geometry and fivefold symmetry5, have aided Robbin in creating fascinating structures, which change dramatically according to the perspective of the viewer. One moment one views a series of triangles while in the next position interlaced pentagonal stars appear. The combination of non-periodic tiling of both 2 and 3-D forms intertwined in an unusual type of symmetry create an almost contradictory image.

The unfolded hypercube was the inspiration for Salvador Dali’s The Crucifixion (1954).
Metropolitan Museum of Art, Gift of the Chester Dale Collection, 1955. (55.5)
1 Also known as the tesseract — a 4-dimensional representation of a cube.
2 At the same time Bragdon used magic lines in architectural ornaments and graphic designs of books and textiles.
3 Dali contacted the mathematics department at Brown University for further information.
4 Jesus Christ is nailed to a cross represented by the unfolded fourth-dimensional hypercube.
5 Non-periodic tiling is tessellating with tiles or shapes which create designs which have no pattern.
n-fold symmetry: If a pattern is preserved when rotated 360°/n, it is said to have n-fold symmetry. Therefore, a pattern has fivefold symmetry if a rotation of 72° retains the pattern.
Quasicrystals are a newly discovered state of solid matter. Solid matter was thought to exist only in two states, amorphorous or crystalline. In amorphorous the atoms (or molecules) are arranged randomly, while in crystalline the arrangement is the periodic repetition of a unit cell building block. The discovery of quasicrystals revealed a new state in which the arrangement of units is non-periodic and with an unusual symmetry, e.g. fivefold, not present in amorphorous or crystalline matter.

The Discobolus (circa 450 B.C.) by Myron, cast in bronze, captures a moment in motion.
Dimensions, space, center of gravity, symmetry, geometric objects, and complementary sets are all mathematical ideas which come into play when a sculptor creates. Space plays a prominent role in a sculptor’s works. Some works simply occupy space in the same way we and other living things do. In these works the center of gravity1 is a point within the sculpture. These are objects that are anchored to the ground and occupy space in a manner with which we are comfortable or accustomed. For example Michelangelo’s David, the Discobolus by the ancient Greek artist, Myron, or Beniamino Bufano’s St. Francis on Horseback all have their center of gravity within the mass of their sculpture. Some modern art sculptures play with space and its three dimensions in unconventional ways. These use space as an integral part of the work. Consequently the center of gravity can be a point of space rather than a point of the mass, as illustrated by such works as Red Cube by Isamu Noguchi, the Eclipse by Charles Perry, and the Vaillancourt Fountain by Louis Vaillancourt. Other sculptures depend on their interaction with space. Here the space around the artwork (the complementary set of points of the mass) is as, or equally, important as the sculpture. Consid-er Zinc Zinc Plain by Carl Andre. This sculpture is staged in a room devoid of any other works or objects. The plane is created by 36 small squares forming a square which lies flat on the floor. The room represents space, the set of all points, and he describes his work as “a cut of space”.2 Some works seem to defy gravity. These include such sculptures as the mobiles of Alexander Calder with their exquisite balance and symmetry and Isamu’s Noguchi’s Red Cube balancing mysteriously on its vertex. There are even sculptures which use the Earth itself as an integral part of the art and its statement, e.g. The Running Fence by Cristo, Carl Andre’s Secant, and the mysterious geometric grass theorems appearing in England.

San Francisco’s controversial Vaillancourt Fountain has as its center of gravity a point of space.
Often the physical nature of an artist’s conceptional work requires mathematical understanding and knowledge to make the work possible. Leonardo da Vinci mathematically analyzed most of his creations before undertaking a work. If M.C. Escher had not mathematically dissected the ideas of tessellation and optical illusions, his works would not have evolved with the ease with which he was able to undertake them once he understood the mathematics of these ideas. Today there are many examples of sculptors looking at mathematical ideas to expand their art. Tony Robbin uses the study of quasicrystal geometry, 4th dimensional geometry, and computer science to develop and expand his art. In his Easter egg giant sculpture Ronald Dale Resch had to use intuition, ingenuity, mathematics, and the computer as well as his hands to complete his creation. And artist-mathematician Helaman R.P. Ferguson uses traditional sculpting, the computer and mathematical equations to create such works as Wide Sphere and Klein Bottle with Cross-cap & Vector. Consequently it is not surprising to find mathematical models doubling as artistic models. Among these we find the cube, the polycube, the sphere, the torus, the trefoil knot, the Möbius strip, polyhedrons, the hemisphere, knots, squares, circles, triangles, pyramids, prisms,…. Mathematical objects from Euclidean geometry and topology have played important roles in the sculptures of such artists as Isamu Noguchi, David Smith, Henry Moore, Sol LeWitt.
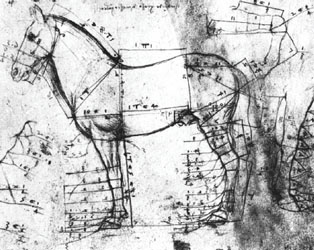
This sketch by Leonardo shows his analysis of the horse’s anatomy.

Author in front of Continuum by Charles Perry. National Air & Space Museum, Washington D.C.
Regardless of the sculpture, mathematics is inherent in it. It may have been conceived and created without a mathematical thought, nevertheless mathematics exists in that work, just as it exists in natural creations.

An Alexander Calder mobile. East Building of the National Gallery of Art, Washington, D.C..
1The center of gravity is the point on which an object can be balanced. For example, the center of gravity or centroid of a triangle can be determined by drawing that triangle’s medians. The point where the three medians intersect happens to be the center of gravity.
2Art & Physics, Leonard Shlain, William Morrow & Co. NY, 1981.
Trefoil knots — torus — spheres — vectors — flow — movement — these are some of the mathematical ideas inherent in the sculptures of Helaman Ferguson.
We have often heard of artists using mathematical ideas to enhance their work. Mathematician- artist Helaman R.P. Ferguson conveys the beauty of mathematics in his phenomenal sculptures. As he states “Mathematics is both an art form and a science…I believe it is feasible to communicate mathematics along aesthetic channels to the general audience.”1
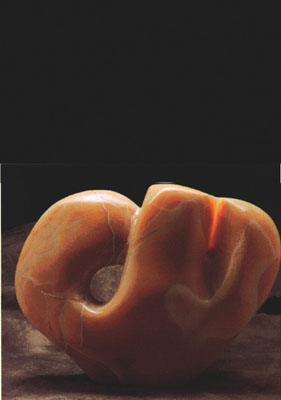
Eine Kleine Rock Musik III
Photography by Ed Bernik. From Helaman Ferguson: Mathematics in Stone and Bronze by Claire Ferguson. Meridian Creative Group, Copyright © 1994.
To create his exquisite forms, Ferguson utilizes methods from traditional sculpting, the computer, and mathematical equations. His works bear such names as Wild Sphere; Klein Bottle With Cross-cap And Vector Field, Torus, Umbilical Torus With Vector Field., Whaledream II (horned sphere).
1 Ivars Peterson. Equations in Stone, Science News Vol. 138 September 8, 1990.

When Ronald Dale Resch accepted the commission to design a gigantic Easter egg sculpture for Vegreville, Alberta, he soon discovered he would have to develop the mathematics for the task virtually from scratch.
Over the years Resch has refined the art of manipulating 2-D objects into 3-D forms. His work and the problems he has solved point to mathematics, yet he has had little formal mathematical training. Working with sheets of various materials such as paper or aluminum, he transforms them into works of art by folding techniques he has developed. He solves geometric problems using intuition, ingenuity, mathematics, the computer and his hands.
His initial instincts about the design of the egg were that he could make two ellipsoids for the ends and a bulging cylinder for the center. He quickly realized this would not work. Discovering that available mathematics for the egg was limited 1, he realized he would have to go it alone. His resulting design for the magnificent Easter egg required 2,208 identical equilateral triangular tiles and 524 three-pointed stars tiles, which were equilateral and whose width varied according to their location on the egg. He found that by varying the angle of placement of the tiles ever so slightly (from less than 1° to 7°), the flat tiles gave the impression of curving and the contour of the egg resulted. The final structure is 25.7 feet long and 18.3 feet wide, and weighs 5000 pounds.
1 Algebraic equations for egg-shaped curves were developed by French mathematician René Descartes (1596-1650). In 1842, as a youth, Scottish mathematician James Clerk Maxwell (1831-1879) devised a method for constructing an egg using a pencil, string and tacks.
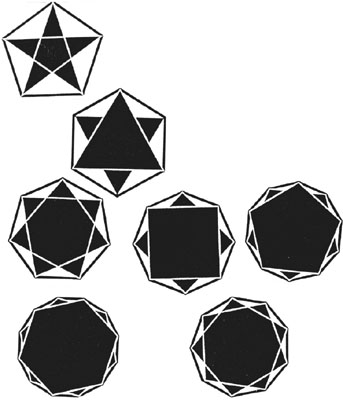
The following figures can and have been used to create artistic and graphic designs. Their bases are mathematical, but that does not take away from their beauty and simple elegance.
The illustrations show how to generate stars by using regular polygons. For odd sided polygons simply join every other vertex of the polygon, and you will arrive back at the starting point. For even pointed stars, note that the star is made up of two rotated polygons. These will have half the number of sides as the generating polygon.
Math enthusiasts have been “embroidering” mathematical curves over the centuries. It is always fascinating to discover a curve formed from a series of straight line segments. The “stitches” (line segments) end up being tangents for the curve they form. One can mathematically “embroider” a circle, an ellipse, a parabola, a hyperbola, a cardioid, a limaçon, a deltoid, etc. In the process of embroidering these curves, one discovers some of their special characteristics. Here is how an astroid can be made.
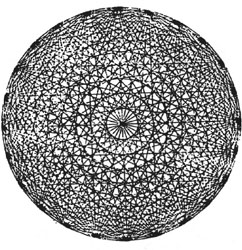
Concentric circles appear when the diagonals of a 24-sided polygon are stitched.
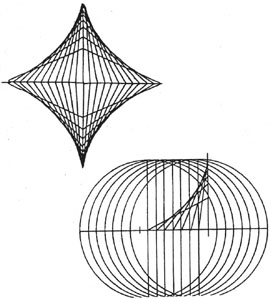
One way to make an astroid is to think of it as a sliding ladder. Circles, the radius of the ladder, are used to mark the base of the ladder’s new location.
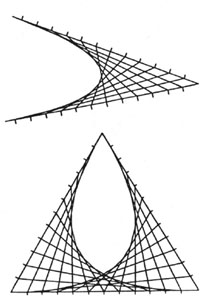
Variations of parabolas.
Spirals are mathematical objects that seem to convey motion. They encompass a family of curves from two-dimensional spirals — equiangular (logarithmic) and Archimedean spirals for examples — to three-dimensional spirals such as the conchoid and helix spirals. Spirals touch many areas in our lives and many living objects. A few examples are — antlers of certain goats, seedheads of flowers, many sea shells, the growth of certain vines, DNA, architecture, art, graphic designs.
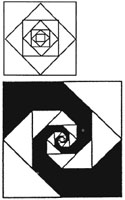
This nest of squares is the first step in making the spiral below.
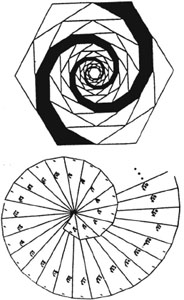
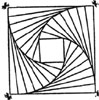
Straight line spirals are formed by making a nest of regular polygons in which each reduced polygon is formed by connecting the midpoints of its sides. Looking at a nest of polygons, the spiral is hard to see until it is shaded. Here are some exciting designs these straight line spirals produce.
This spiral is formed from square root numbers using the Pythagorean theorem.
There are many variations of these spirals. Some of these variations have been connected to pursuit problems, such as the four spiders problem.
Another famous straight line spiral is the one produced by constructing square roots numbers using the Pythagorean theorem.
Four spiders start crawling from the four corners of a square. Each spider is crawling toward the one on its right, moving toward the center at a constant rate. Thus, the spiders are always located at four corners of a square. The curves formed by the spiders’ path are equiangular spirals. The size of the initial square and speed of spiders determines how long it will take for the spiders to meet.
The Platonic solids — convex polyhedra with faces that are regular convex polygons — are only five in number. It is interesting to discover the connection between the Platonic and their duals.
a tetrahedron & its dual
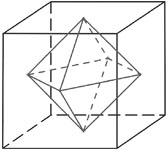
a cube & its dual
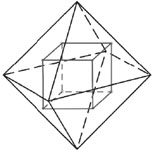
an octahedron & its dual
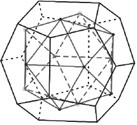
a dodecahedron & its dual

an icosahedron & its dual
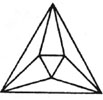
To make the dual of a polyhedron, one first finds the center of each face and then joins the centers of faces that share a common edge. The illustrations reveal that the dual for a tetrahedron is a tetrahedron, the dual for a cube (hexahedron) is an octahedron, while an octahedron’s dual is a cube. The dodecahedron’s dual is an icosahedron, and an icosahedron’s is a dodecahedron. None of the five Platonic solids’ duals is anything but a Platonic solid!
Each of these diagrams represents one of the five Platonic solids. They are called Schlegel diagrams, after the German mathematician Viktor Schlegel, who invented these particular diagrams in 1883. They remind one of 3-D objects which have been deflated. In essence, however, the polyhedron is inscribed in a sphere and projected through a point that is along the line of the north pole of the sphere. Its projection can change according to the polyhedron’s position in the sphere. These Schlegel diagrams have the special property that one face of the polyhedron contains all the images of all the other vertices. In addition, the diagrams show all the polyhedron’s vertices, edges and faces, even though their size and shape are distorted.
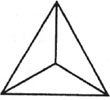
tetrahedron
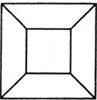
hexahedron (cube)
octahedron
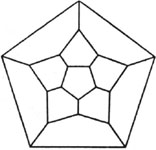
dodecahedron
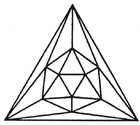
icosahedron
The laws of mathematics are not merely human inventions or creations. They simply “are”; they exist quite independently of the human intellect. The most that any man with a keen intellect can do is to find out that they are there and to take cognizance of them. —M.C. Escher
And M.C. Escher certainly did take cognizance of mathematics. It is exciting to view many of his works through mathematical eyes.

A section from Escher’s work Metamorphosis III.
© 1994 M.C. Escher/Cordon Art-Baarn-Holland.
All rights reserved.
Most of us are familiar with Escher’s magical creations of the tessellations of a plane. His works far surpassed the traditional tessellations of a plane. He gives motion and life to the objects he tessellates, as illustrated in such famous works as Metamorphosis, Sky and Water, Day and Night, Fish and Scales, and Encounter. Besides transforming the plane, the tessellated objects undergo a transformation themselves. In addition, one sees his mastery of the concepts of translations, rotations, and reflections in periodic tiling.
Escher also used objects and ideas from the field of topology. The Möbius strip plays a key role in his woodcuts Möbius Strip I and II and Horseman. He exquisitely produces trefoil knots in his work Knots. And even though Escher probably did not intend it, his Snakes is a perfect piece of art to introduce a topic on knot theory. Print Gallery and Balcony are wonderful examples of topological distortion. These lithographs almost seem to be printed on rubber sheets which are magically distorted via topology.

Escher signed his name in the circle above. Page 156 of MATHEMATICS SNIPPETS explains what mathematically could exisit there. M.C. Esher’s Print Gallery illustrates a topological distortion. © 1994 M.C. Escher/Cordon Art-Baarn-Holland. All rights reserved.
Manipulation and mixing dimensions are other mathematical themes found in many of Escher’s works. In Reptiles, Escher has 2-dimensional lizards eerily come to life in realistic crawling 3-dimensional forms. Similar transformations take place in Magic Mirror and Cycle. His use of concepts from projective geometry—perspective, traditional vanishing points, his own curved vanishing points—are responsible for the feeling of depth and dimension in St. Peter’s Rome, Tower of Babel and High and Low.
Reptiles illustrates Escher’s use of tessellations as well as his mastery of moving between the worlds of the 2nd and 3rd dimensions. © 1994 M.C. Escher/Cordon Art-Baarn-Holland. All rights reserved.
Circles, ellipses, spirals, polyhedra and other solids are some of the geometric objects one finds in Escher’s work. For example, Three Spheres creates a 3-dimensional illusion of spheres, although it is composed entirely of circles and ellipses. In Stars we find a variety of solids, including the Platonic solids, while a tetrahedron is the focus in Tetrahedral Planetoid. And in Gravity the stellated dodecahedron is present.
Escher makes the concepts of infinity come to life. No words are needed to define it, his work portrays its meaning. In Whirpools the spirals lead one’s eyes on an endless journey. In Square Limit the feeling of infinite sequence approaching its boundary is projected. And Circle Limit would be an ideal model for Henri Poincaré’s finite yet infinite non-Euclidean geometry. We get both the concepts of infinity and space tessellating in Cubic Space Division.
Lastly, in the field of optical illusion, Escher is phenomenal. His use of such impossible geometric figures as the Penrose tribar, help trick our eyes and confuse our minds. His Waterfall has us believing water is going upstream in an endless loop, while in Ascending and Descending there are two sets of people — one endlessly climbing a staircase and the other descending a staircase all in a loop. Impossible figures are also his means for creating illusions in Belvedere and Relativity. In Concave and Convex, Escher is a master of oscillation illusion. Our eyes and mind are taken back and forth in the interior and exterior of an incredible structure and cast of characters. For example, one moment the vaulted dome is a roof and then within seconds it is a ceiling.
It is satisfying to explore Escher’s work on many different levels. This introduction is but a glimpse of the wealth of mathematical ideas found in the work of M.C. Escher.
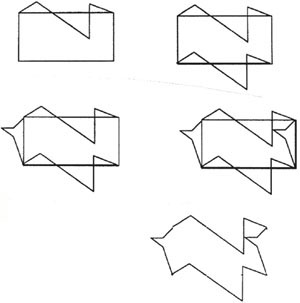
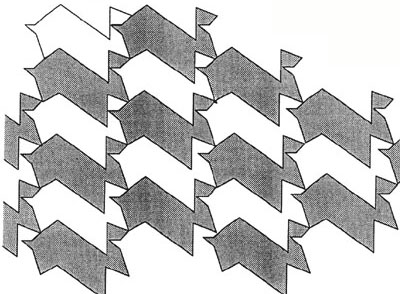
M.C. Escher mastered the art of tessellations. He also envisioned a tessellation stamp. The six faces of the cube have a design in six different positions. So as the stamp is rolled on a piece of paper, the design is tessellated. The design reproduced here was not done with a stamp. Instead, a computer was used to rotate and flip the design so that it could be tessellated.
Starting by modifying one of its lengths, translate that modification to the other length’s position.
Now modify one of its widths, and translate the modification to the other width also.
Now take the resulting shape, and tessellate a plane.
From nature’s tessellation of the honeycomb, to Roman mosaics, to the tiles of ancient Greece, to the marvelous designs by Moslem artists at The Alhambra, to M.C. Escher’s phenomenal tessellations, to the simplicity of the Penrose tiles—tessellations cross centuries and cultures.
Here we have a tessellation design using pentagons and rhombi created by artist Albrecht Dürer. It dates back to the 15th century.

Roman mosaic floors have a variety of designs. This simple yet elegant pattern appears at the baths of Caracalla in Rome.
Projective geometry is a field of mathematics that deals with properties and spatial relations of figures as they are projected — and therefore with problems of perspective. Many artists of the 15th century often worked in a number of different disciplines. Some of these artists, such as Giotto di Bondone (1266?-1337), Leon Battista Alberti (1404-1472), Piero della Francesca (1410?-1492), Leonardo da Vinci and Albrecht Dürer, studied engineering, mathematics, science and architecture, while pursuing their art. As a result Renainssance artists connected mathematical concepts, such as projective geometry, to the creation of their works. These artists developed techniques for painting realistic three dimensional scenes on two dimensional canvases. They analyzed how things changed when viewed from different distances and positions and developed ideas of perspective. They reasoned that if they perceived a scene outside through a window, it would be possible to project what they saw onto a window as a collection of points of vision if they kept their eye at a single focal point. The window would act as their canvas. The scene would naturally be affected by the position of the artist’s eye and the position of the canvas. Some artists actually invented mechanical devices to aid drawing in perspective, as illustrated by the two diagrams.

An Albrecht Dürer perspective instrument.
Leonardo da Vinci’s spectograph.

This study of The Adoration of the Magic by Leonardo illustrates his use of linear perspective and a vanishing point.
Artists’ works on perspective influenced the development of projective geometry. Just as topology studies the properties of objects that remain unchanged after they have undergone a transformation, projective geometry studies properties of plane figures that do not change when they undergo projections. For example, when a circle is viewed from the side, it appears as an ellipse. Similarly a square would become a different shaped quadrilateral. Having been influenced by perspective in the art of the Renaissance and desiring to help artists, 17th century architect/engineer/mathematician Girard Desargues initiated the study of projective geometry. He wrote a number of theorems (Desargues’ Theorem) which are still essential in the study of projective geometry. His work influenced later mathematicians in this field, especially Blaise Pascal (1623-1662) and Jean Victor Poncelet (1788-1867). To create realistic three dimensional paintings Renaissance artists used concepts from projective geometry, namely— point of projection, parallel converging lines, and vanishing points.

This work by Jesuit monk Andrea del Pozzo (circa 1685), was painted on the hemi-cylindrical ceiling of St. Ignasio Church in Rome. His mural is an excellent example of perspective which illustrates the concepts of projective geometry of a single vanishing point. In fact, it may be considered to be too exact. A mark is located on the floor of the church, indicating where the viewer should stand to get the full effect the artist intended. At this location one actually feels the ceiling is infinite and the reality of St. Ignatius Carried into Paradise. Viewing the painting from any other point creates a distorted and uncomfortable effect.
…geometry is the foundation of all painting. —Albrecht Dürer
Albrecht Dürer (1471-1528) was an artist of many talents. Of his 18 children, Dürer’s father hoped it would be Albrecht who would follow him in his work as a goldsmith. As a result, Dürer was apprenticed to Michael Wohlgemut, who also happened to be an artist. After a three year apprentice, Dürer traveled and worked throughout Europe, where he learned painting, engraving, printing, and making woodcuts, all of which influenced his life’s work. He felt the study of mathematics enhanced art, in particular geometry, perspective and ideas of projective geometry. He also did extensive work on the proportion of the human body. In addition, he wrote books on the mathematics he used. Some of his work in mathematics was original and exact1, while other work and geometric constructions were approximate and served his artistic needs. Along this line he developed mechanical devices to aid artists drawing in perspective.

A woodcut from Dürer’s Treatise on Geometry.
The following sections illustrate how the work he pursued had a mathematical overtone, which helped him immeasurably in his art and other creations.
In Dürer’s woodcut Melancolia we find a magic square in the background, geometric solids and the sun’s rays acting as lines of projection in this perspective drawing.
1 Dürer generated an epicycloid by following a fixed point of a circle as it rolled along the circumference of another circle, but lacking an algebraic foundation he did not analyze the curve. Likewise, he produced spirals from the projection of helical space curves, but did not pursue them mathematically.
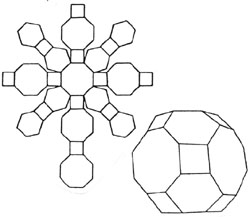
In addition to the many innovative techniques he developed, Dürer is credited with describing solids on a plane in unassembled form. Here is Dürer’s description of one such solid, which, when cut and assembled, forms a cuboctahedron truncum.
This illustration by Albrecht Dürer shows his interpretation of a conic section. His ellipse is somewhat egg-shaped, which implies he either believed the inclination of the plane cutting the cone made the ellipse narrower at the top or he made a slight error in calculation. Regardless, it is interesting to see his study of an ellipse.
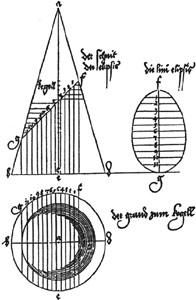
From Underqweysung der Messung mit dem Zircklelund Richtscheyt (a treatise on geometric constructions) by Albrecht Dürer.
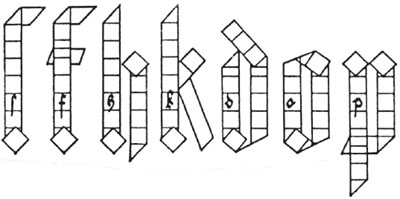
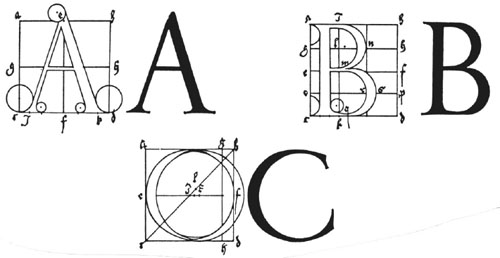
Dürer can be credited with launching the concept of topography. In one of his books he illustrates the geometric construction of Roman letters. Dürer devised his own mathematical methods for Gothic letters, by constructing each letter from a combination of squares, triangles, trapezoids and/or parallelograms. He systematized the structure of Gothic letters by using these little building blocks — somewhat similar to how letters are formed on a computer’s monitor using the pixel1 as the building block.
These geometric construction were devise a diring the Renaissance, although the ideas we’re not published at that time.
1 Pixel is the abbreviation for picture element. It is the visual representation of a bit on the computer’s monitor. A bit stands for binary digit, which is the smallest unit of information that a computer can hold. The bit’s value corresponds to the numbers 0 or 1, representing electrical flow as “off” or “on” which translates to a white or black square on the screen.
Over the centuries the tools of an artist have ranged from a stick to a paint brush, to such devices as the camera obscura and the perspective window. Today artists are exploring a new form or medium of art that is linked to mathematics — the computer. Until recently computer art was produced by mathematicians, scientists, engineers, and just about everyone but artists. Initially, we were flooded with a great deal of art that resembled curve stitching, line work and optical illusions.
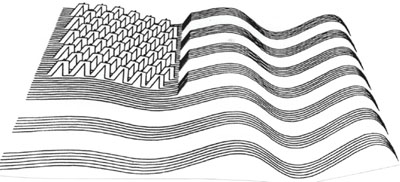
Computer generated art. Reproduced from Computer Graphics by Melvin L. Prueitt. Courtesy of Dover Publications.
Today, computers play a major role in commercial art. A computer skilled artist with advanced software can transform graphic art ideas for advertisements to multiple variations by changing type-styles, introducing various colors, scaling sizes of objects, rotating or flipping objects, duplicating various parts of an object in minutes. In the past, all of these changes would have taken the graphic artist hours if not days.
This watercolor painting effect was achieved by scanning a photograph and altering using a Photoshop filter on the computer.
Engineers, architects and other designers have not hesitated to embrace the computer in their creations. With just a few clicks of a mouse a building could easily be modified, a plane could be rotated to show all possible perspectives, cross-sections could be added, parts added or removed effortlessly. In the past this work was slow and painstaking.
With today’s advanced computers and software, Leonardo da Vinci might have rendered this sketch on a computer via an electronic sketch pad.
Artists over the centuries have used different mediums to create their works—watercolor, oils, acrylic, chalk, etc. There are some artists who feel the computer is an artificial means that lacks freedom of spontaneous expression. They prefer the direct contact of their hands with the medium of their choice, rather than working by means of electricity on a keyboard and screen or with stylus and electronic tablet and screen. Others view the computer as a challenge.
With improved software and hardware, colors can be mixed on the screen. Rigid computer lines can be easily softened with any shaped curve. Changes can be made from an oil painting effect to a watercolor, and brush shapes can be changed at whim. Minute areas can be magnified and reworked more easily. Parts can be erased or cut out and pasted elsewhere in the work. The artist is definitely in charge of his or her creative work. The result can be either printed or entered on video, paper or film. Film leaves the option of enlarging it to any size. Perhaps a printer will be designed capable of capturing the texture of the work the artists create. Or perhaps we should consider this a new form of texture in itself.
Esteemed artists have displayed art created with a computer in well known international galleries, but it is still labeled computer art. Such works have yet to be simply labeled art.
What would Leonardo da Vinci think of the use of computers in art? Given his fondness for innovation1, we can assume he would not have snubbed the use of the computer. He said “…no human inquiry can be called science unless it pursues its path through mathematical exposition and demonstration.” His works reflect that he extended this to his art– for example, the predominant use of the golden rectangle in many of his works and the concepts of projective geometry in his masterpiece, The Last Supper.
One form of art should not be considered better than another, just different. Artists should be free to choose any means or medium.
1 His notes and various innovations were used by artists to enhance and facilitate their artwork. Leonardo’s mathematical inclinations led him to invent various types of special compasses capable of producing parabolas, ellipses and proportional figures. He is also credited with the invention of the perspectograph, used by artists to help draw objects in perspective.