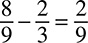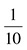CHAPTER 8
Mathematical Ability
You are probably not planning to become a nurse because you live for simplifying equations or calculating hypotenuses. However, there is math involved in the job, and that is why it is tested on nursing school entrance exams. If you are like many nursing school candidates, it has been a while since you were in math class. If you are like most people, you have not necessarily used those skills a whole lot since leaving.
Do not worry. The math on nursing school entrance exams does not have to be scary. It is not as advanced as the math you studied in your high school classes, and we will make it as easy as possible to relearn the basics you need. If you have taken the math diagnostic test in Chapter 5 of this book, you can use your results to identify any weak areas and focus your attention on them. You should work through this whole chapter to be fully prepared for your nursing school entrance exam. While reading, it is a good idea to have index cards and a notebook nearby so that you can record topics to study later and make flash cards; there are many shortcuts you will be able to take on your exams if you do some memorization beforehand.
Each section of this chapter has practice problems. You will find the solutions at the end of the chapter. Once you are finished with the chapter, build your test-taking confidence by taking the two Mathematical Ability Practice Tests in Chapter 10 of this book. Before you take those or any other math tests, here are some test-taking tips to keep in mind:
• Show your work. No, you will not get partial credit if you get something wrong, but writing everything down helps you keep track of what you are doing and makes it easier to catch your mistakes.
• Do the easy stuff first. Do the things that are least challenging to you first so that the stress of working harder problems will not make you mess up on the easier problems. Some exams are arranged in a rough order of difficulty, but what really matters is what is easy or hard to you, so do not be afraid to skip around. Just be sure to mark any problems you skip so that you come back to them at the end.
• Estimate. Sometimes you can get a problem right—or at least make an educated guess if you are running out of time—just by estimating, ballparking, or eyeballing (whatever you want to call it). For example, if you are asked to subtract 7,348 − 5,492, you can estimate that the correct answer will be just less than 2,000. How much will this help on the actual test? That depends on the answer choices. If the numbers in the choices vary widely, then estimating is an easy to way eliminate wrong answers. If the choices are closer together, there is still a good chance that you can eliminate one or more of them. This builds you a little bit of a “safety net” when you are doing the math, because you have already eliminated answers that simply cannot be correct.
• Neatness counts! No one is going to see your test paper, but you will do yourself a big favor if you keep everything organized as you work. We will show you examples as we approach the different problem types.
Ready to begin your review? Good! Let’s get started.
COMPUTATION
No matter which entrance exam you take, you will definitely be tested on your basic computation skills (addition, subtraction, multiplication, and division), and some tests will not allow the use of a calculator. That sounds like bad news, but it is not entirely; it means that there is a very definite cap on the difficulty level of the math you will be required to do. It is time to brush off those grade school basics such as “borrowing ten” and “carrying the one.”
Addition
Many addition problems simply line up two numbers and ask you to add them, like this:
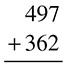
Other addition problems may present information in a word problem, which we will get to later, but word problems are really the same thing; you just need to write down the numbers yourself so that they look like the above problem. Remember—neatness counts!
How do you solve this problem? In bite-sized pieces. Make sure the numbers are lined up in neat columns, and start on the right:
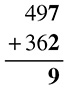
Now on to the middle column.
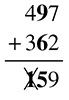
Well, unfortunately you cannot fit both the 1 and the 5 in the same column, so you leave the 5 there and carry the 1 over to the left column. Now your left column looks like this:
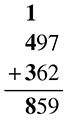
The total is 859.
Ready for another one? Try this one first, and the explanation will follow.
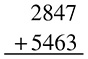
Okay, here is how to do it, starting with the first column on the right. Adding up the far right column you get 10; leave the 0 there and carry the 1.
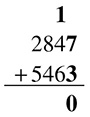
Adding up the second column you get 11; leave a 1 there and carry a 1.
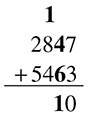
Adding up the third column you get 13; leave a 3 there and carry a 1.
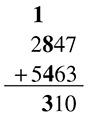
Adding up the fourth column you get 8, so your answer is 8,310.
Subtraction
Subtraction is very similar; you still line up the numbers in columns and deal with them one column at a time, starting with the right, even if the test writers do not line up the numbers for you. There is no carrying in subtraction; however, if the number you are subtracting in a column is larger than the number you are subtracting from, you may have to borrow from the column to the left.
For example:
Starting with the first column on the right, you can simply subtract 7 − 5.
In the next column over, you cannot really subtract 2 − 3, so you borrow from the column to the left. Borrowing lets you add 10 to the current number you are subtracting from, so now you can subtract 12 − 3 instead:
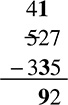
Now all you have left is the last column, the hundreds.
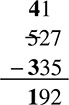
The answer is 192.
Multiplication
In multiplication problems, you still want to be very aware of lining your numbers up properly. Multiplying several-digit numbers is always a matter of multiplying smaller numbers several times.
For example:
Because there are two digits in the number on the second line, you actually work two smaller multiplication problems. First, multiply everything in the first line by 1 (because you are starting from the right).
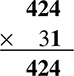
Then move one column to the left and multiply everything in the top line by the 3. Notice how you shift over when writing your answer. Also, if you end up with a two-digit number, you can carry to the next column to the left, just like in addition. Then just add that carried number after you multiply the original first and second line.
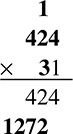
Now you have two numbers, 424 and 1,272. Keeping them in their current columns, you add to get the final result:
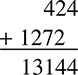
The final answer is 13,144.
Division
Division is a bit different. Division problems may be presented like this:
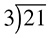
. . . or like this:
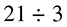
. . . or even like this:
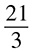
All of these mean the same thing. You would say “21 divided by 3” or, as a question, “How many times does 3 go into 21?” We will talk about fractions later, but for now, let’s focus on long division, which means if you are given a problem such as 21 ÷ 3, you will write it out as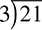 
.
Unlike in addition, subtraction, and multiplication, you are going to start division problems on the left inside the division sign. Just as you did with the other operations, you are still going to keep things in neat columns.
Let’s take 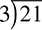. Starting at the left, ask: Is 2 divisible by 3? No, because 2 is smaller than 3. Then you include the next column to the right, as well: Is 21 divisible by 3? Yes, and the result is 7, so you put the 7 above the 1:
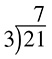
. . . and that is your answer.
What if the problem were 
instead? You just keep going; 21 is divisible by 3, and the result is 7, then 0 is divisible by 3, and the result is 0.
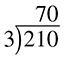
Not all numbers divide evenly, however. Sometimes the dividend (the number inside the division sign) will have something left over when you divide it by the divisor (the number to the left of the division sign). Then you have a quotient (the result), and you also have a remainder. The remainder is the integer that is left over when you have divided out as many digits of the divisor as you can.
What if you are asked to divide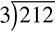 
? The first 2 is not divisible by 3, so you move on to 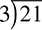. That gives you 7. The last 2 is not divisible by 3 either, so you put a 0 above the 2:
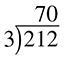
However, that is not the whole story. You still have that 2 that is not represented in the answer, so it becomes your remainder, and you write that as 70r2. To check your math, you can multiply the quotient by the divisor, then add the remainder, and you should come up with the dividend: 70 × 3 + 2 = 212. The math works, so 70r2 is the correct answer.
Of course, remainders are often expressed as decimals after the whole number quotient. This is called “long division.” If you have a remainder, add a decimal point and a zero to the quotient and divide again. Keep dividing until there is no remainder or the decimal part of the quotient begins repeating. Here is an example.
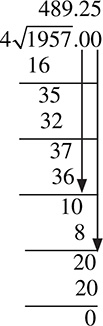
Time for some practice on computation. Use scratch paper and remember to work carefully. Solutions are at the end of the chapter.
DRILL: ADDITION, SUBTRACTION, MULTIPLICATION, AND DIVISION
1. 1473 + 582 =
2. 5391 + 6729 =
3. 12,843 + 5928 =
4. 3609 − 1727 =
5. 2381 − 963 =
6. 768 − 529 =
7. 408 × 52 =
8. 823 × 7 =
9. 521 × 47 =
10. 709 ÷ 4 =
11. 341 ÷ 3 =
12. 672 ÷ 16 =
NUMBER PROPERTIES
Most of the numbers you will deal with on your entrance exams are integers, which are undoubtedly the ones that you are most used to dealing with day to day. Integers are divisible by one, so they do not have anything after the decimal. You may round things to the nearest integer at the grocery store to keep track of how much you are spending without having to do a lot of mental math. They are the numbers you use to count things that are not divisible, such as cars, marbles, and children.
The Number Line, Positive Numbers, Negative Numbers, and Zero
There may be questions on the test that deal with the concept of a number line, which is basically just a line with numbers on it, like this:
Generally number lines are divided up in increments of 1, so they show you the integers close to and including 0. All numbers to the right of 0 are positive and all numbers to the left of 0 are negative. This means that anything greater than 0—even the fractions and decimals between 0 and 1—is positive. The same is true for anything less than 0: even between 0 and −1, it is all negative.
What does that make 0? It is neither positive nor negative, but it is an integer, and it does have a place on the number line.
Absolute Value
Whenever you see a number with vertical lines on either side of it, such as |−3|, you are being asked to figure out the absolute value of that number. Absolute values are positive numbers only, so the absolute value of −3 is 3. To put it in math terms, |−3| = 3.
If there is a positive number inside the symbols, such as |2|, then the absolute value is just equal to that same number: |2| = 2. When you see the absolute value signs, remember that everything goes on the right, or positive, side of the number line. (Yes, it really is that easy. We are going to trust that mathematicians had a very good reason for giving this simple concept a fancy name and unfamiliar symbols, but whatever that reason is, you are not going to need to know it for your entrance exams. You are going to be tested only on the basics.)
Another way to think of absolute value is distance from 0, and distances are always positive. For example, −5 is five tick marks from 0 on the number line, so |−5| = 5.
Place Value
It’s good to brush up on this terminology for your tests, and it will also help keep things straight when we review computation. The digit farthest to the right (unless there are digits after a decimal, but we will get to that later) is called the ones or units digit. Moving further to the left, you have the tens, hundreds, thousands, and ten thousands digits in order. The number 36,827 has a 7 in the ones place, a 2 in the tens place, an 8 in the hundreds place, a 6 in the thousands place, and a 3 in the ten thousands place.
Factors
Factors are the sets of numbers that other numbers can be divided by. In the division problems you just did, the quotient and divisor are factors of the dividend. Some problems may require you to find factor pairs of numbers, and the process is pretty simple. For example, if you are asked to find the factors of 12, you just draw a factor T, like this:
At first you will not know how many factor pairs the number will have, so leave some room for your factor T to grow downward.
The first pair of factors in the factor T should be 1 and the number itself:
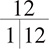
Then continue counting and fill in a pair every time you find a number that the original number is divisible by. (By the way, if this is new or challenging, we’re about to review how you can tell if a number is divisible by another number.) The number 12 is also divisible by 2, so you add 2 to the list along with the result of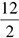 
, or 6.
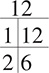
The number 12 is also divisible by 3, so you can add 3 and the result of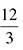 
, or 4.
Now you could go on to add the next number that 12 is divisible by, which is 4, but 4 is already in the list, meaning that all of 12’s factors are in the factor T and you are done. The factors of 12 are 1, 2, 3, 4, 6, and 12.
Now it is your turn to find all the factors of the following numbers. Solutions are at the end of the chapter.
DRILL: FACTORS
1. 18
2. 27
3. 30
4. 36
5. 42
6. 45
Divisibility
When finding factors, dividing, reducing fractions, solving equations, and doing many other tasks, it’s good to be able to tell quickly and easily if one number is divisible by another. To do this, memorize the rules of divisibility below. Do you have your flashcards ready?
A few other notes on divisibility:
• Numbers that are divisible by other numbers are called multiples. For instance, 36 is a multiple of 3. It is also a multiple of 1, 2, 4, 6, 9, 12, 18, and 36.
• If you noticed that the numbers listed above are the factors of 36, you are right. Any number has many multiples, but probably only a few factors.
• Negatives that meet the divisibility requirements are also divisible. For example, −5,256 is also divisible by 8.
• Zero is divisible by any number; the result is 0. No number is divisible by zero; the result is undefined.
• There are no easy divisibility rules for 7. If you need to determine whether a number is divisible by 7 or a number larger than 10 (or if you forget the divisibility rules for any of the above numbers), just divide it out. If there is a remainder, the number is not evenly divisible.
Order of Operations
When solving any equation or making any calculation that has more than one operation to perform, the order in which you perform the operations has an effect on what answer you will get. For example, in the expression 5 + 4 × 2, if you perform the addition first and then the multiplication, you get a result of 18. If you perform the multiplication first and then the addition, you get 13. Which is correct? Many people just perform the operations from left to right and often get the wrong answer! There is an order of operations that must be followed to get the math right. The order can be remembered with the acronym PEMDAS, which stands for:
• Parentheses
• Exponents
• Multiplication and Division (from left to right)
• Addition and Subtraction (from left to right)
Anything that is in parentheses takes precedence and is calculated first, then exponents, and so on. That means that in the problem above, the multiplication should be done first and then the addition, giving you 13. Try the order of operations on the following drill; solutions are at the end of the chapter.
DRILL: ORDER OF OPERATIONS
1. 3 + 2 × 4 =
2. (10 − 4) ÷ 3 =
3. 4 × 3 − 5 =
4. 15 − 8 ÷ 2 =
5. (9 + 2) × 2 =
6. 3 × 4 ÷ 2 + 5 =
Prime Numbers
A prime number is a number that has exactly two different factors: itself and one. Prime numbers cannot be negative numbers, 0, or 1; none of those fits the definition. It is a good idea to memorize the first six or so prime numbers so that you do not have to spend time figuring these out on the test. Any primes after the first six generally do not appear, even on tests that test much harder math, so these are your safest bet. Do you have some index cards ready to make flash cards? The six smallest six prime numbers are 2, 3, 5, 7, 11, and 13.
If you forget these and have to figure out whether a number is prime on the test, follow these steps:
1. Remember that negative numbers, 0, and 1 are not prime.
2. Check whether the number is even (divisible by 2). No prime numbers except 2 are even, so if the number is greater than 2 and even, it is not prime.
3. Check whether the number is divisible by 3. Remember, all numbers that are divisible by 3 have numerals that add up to something that is divisible by 3.
4. It is not really necessary to check divisibility by 4 because anything divisible by 4 is also divisible by 2 (which you took care of in step 2), so check whether the number is divisible by 5. Do you remember the rule to find numbers that are divisible by 5?
5. Keep checking divisibility with higher numbers until you reach half the value of the number in question. If it is not divisible by a number half its size, it is not going to be divisible by anything larger. If you have not found factors other than the number and one by this point, you have found a prime number.
Let’s try this out a few times. If a number is prime, circle Prime. If it is not, circle Not Prime and list which factors it has other than itself and 1. Solutions are at the end of the chapter.
DRILL: PRIME NUMBERS
1. 17 Prime Not Prime: __________
2. 23 Prime Not Prime: __________
3. 39 Prime Not Prime: __________
4. 45 Prime Not Prime: __________
5. 54 Prime Not Prime: __________
6. 67 Prime Not Prime: __________
Prime Factors
Sometimes you will need to calculate the prime factors of a number, which are all of the prime numbers that are multiplied together to create that number. Each number only has one prime factorization, or way that it can be divided into prime factors. You may be asked specifically to find prime factors, or you may have to find them as part of another problem, such as finding square roots or calculating the diagonal of a rectangle.
To find prime factors, it helps to make what is called a factor tree. Let’s use 60 as an example. Start by writing down the number.
Then you need to determine whether it is divisible by the first prime number, which is 2. If it is, draw two branches leading from the number, one for 2 and one for the result of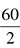 
, or 30. It should look something like this:
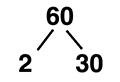
The 2 is prime, so it cannot be factored further. Factor 30. It is divisible by 2, so you draw a branch for 2 and branch for 
, or 15.
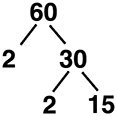
15 is not divisible by 2, so move on to the next prime number, which is 3. 15 is divisible by 3, so draw a branch for 3 and a branch for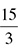 
, or 5.
Now you are done, because the tips of the branches are all prime numbers: 2, 2, 3, and 5. The prime factors of 60 are 2, 2, 3, and 5, and therefore, 2 × 2 × 3 × 5 = 60.
This is called the prime factorization and may also be written as 22 × 3 × 5. (Exponents will be explained in a later section). The distinct – different – prime factors of 60 are 2, 3, and 5.
Ready to try some on your own? Solutions to the drill are at the end of the chapter.
DRILL: PRIME FACTORS
1. 36
2. 42
3. 45
4. 92
5. 81
6. 75
EXPONENTS
Exponents are very easy to recognize: Whenever you see a superscript number (like this: 32), you are working with exponents. Just for the sake of simplicity in this section, we are going to give some terminology; exponents themselves are the numbers in superscript, whereas the number being raised to an exponent is called a base. In 52, 5 is the base and 2 is the exponent. Exponents are sort of shorthand for multiplication; they tell you how many times the same number is being multiplied together. For example, if you see 24, that is the same as 2 × 2 × 2 × 2, or 2 multiplied four times.
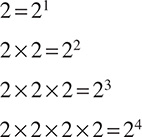
. . . and so on.
Just to solidify your familiarity with exponents, let’s do a short drill. If you see the exponent (with a superscript number, such as 24), write out the multiplication (such as 2 × 2 × 2 × 2). If you see the multiplication, write the exponent. Solutions are at the end of the chapter.
DRILL: EXPONENTS 1
1. 35 =
2. 43 =
3. 23 =
4. 6 × 6 × 6 × 6 =
5. 3 × 3 =
6. 8 × 8 × 8 × 8 =
Now that you have refamiliarized yourself with the concept of exponents, let’s review how to work with them. Whenever you have exponents that are being multiplied, divided, or raised to other exponents, there are a few rules to follow. Let’s look at some examples.
• Multiplication: If a problem has exponents of the same base being multiplied, such as 32 × 35, you combine or add the exponents to get 37.
• Division: If a problem has exponents of the same base being divided, such as 47 ÷ 45, you subtract the exponents to get 42.
• Exponents: If an exponent is raised to another exponent, such as (32)4, you multiply the exponents to get 38.
Warning: It is really easy to confuse multiplication of exponents and raising exponents to exponents, so be careful! Also, you need to be aware that if you are dealing with two different bases, you cannot combine the exponents in any way—by adding, subtracting, multiplying, or dividing. For example, 43 and 32 cannot be combined, because their bases (4 and 3) are not the same. Technically there is an exception to this, and that is when one base can be raised to an exponent to equal the other base, but you are extremely unlikely to see that situation on nursing school entrance exams, so we are not going to spend time on it here.
Now it is time for some more practice. In each of the following, combine the exponents using the above rules, or write “cannot be combined” if the bases are unequal. You do not need to actually calculate the result. Solutions are at the end of the chapter.
DRILL: EXPONENTS 2
1. 32 × 33 =
2. 45 × 55 =
3. 27 ÷ 23 =
4. x8 ÷ x3 =
5. (25)4 =
6. (y2)3 =
Squares
You may have also heard the phrase “two squared” or “five squared”; squared means that you raise the base to an exponent of 2. There are a few squares that you really need to memorize to save yourself a lot of math during the exams. Flash card time!
12 = 1
22 = 4
32 = 9
42 = 16
52 = 25
62 = 36
72 = 49
82 = 64
92 = 81
102 = 100
112 = 121
122 = 144
132 = 169
142 = 196
152 = 225
202 = 400
252 = 625
ROOTS
Roots are the opposite of exponents; they generally ask you which number has been multiplied by itself to get a number. For the purposes of nursing school entrance exams, we will only deal with calculating square roots, which means finding which numbers have been raised to an exponent of 2. For example, if you need to calculate the square root of 25, it will look something like this:
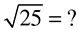
One huge help when dealing with square roots is to know your squares from the Exponents section above. If you have those memorized, you know that 52 = 25, and therefore 
We call 25 a perfect square, because it is the result of squaring a single integer. If you are not dealing with a perfect square or you forget one of the squares you memorized, you can still calculate the square root. For example:
Remember calculating prime factors? Those skills are going to come in handy now. To calculate the square root of 12, find its prime factors.
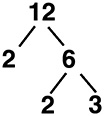
Notice how the prime factor tree has two 2s and one 3. Circle the 2s. For any pair of prime factors, you are going to bring just one factor outside of the root sign.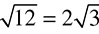 
. The 3 has to stay inside, because it is not part of a pair.
Let’s try another:
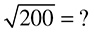
The prime factor tree looks like this:
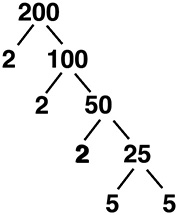
Now you have two 5s and three 2s. The pair of 5s can go outside of the root sign and so can a pair of 2s, but one 2 has to stay inside because it has no partner. When you find more than one pair of factors, you multiply the factors that come outside. In this case, you would multiply 5 and 2 (remember, just one from each pair), which gives 10 on the outside; a 2 stays on the inside.
Ready to try some on your own? Just simplify the roots as much as possible; you do not need to do any calculation past what we have done above. Solutions are at the end of the chapter.
DRILL: CALCULATING ROOTS
1. 
2. 
3. 
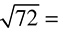
4. 
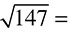
5. 
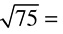
6. 
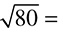
DECIMALS
Decimals are one way to express parts of numbers. You have seen decimals all over the place—in price tags, paychecks, and digital scales. Everything after the decimal point is smaller than 1, and the place values have their own names: tenths, hundredths, thousandths, ten thousandths, and so on. In the number 123.456, 4 is in the tenths place, 5 is in the hundredths place, and 6 is in the thousandths place.
Addition with decimals is exactly the same as it is with whole numbers; you just have to be sure to line up the decimals (remember—neatness counts!). If a problem asks you to add 123.456 and 789.8099, you would line up the decimals with each other and get:
Adding each column, you get 913.2659.
Subtracting with decimals is also exactly the same; just line up the decimals and subtract, borrowing as you need to.
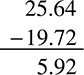
You only get into new rules when you start multiplying and dividing with decimals. With multiplication, you do not really have to deal with the decimals and the multiplication at the same time—you just have to remember to add an extra step on the end. For example, if a problem asks you to multiply 14.6 and 2.1, you can ignore the decimals and treat it as a regular multiplication problem:
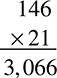
Now it is time for the extra step. Go back to your original numbers, 14.6 and 2.1, and count the number of digits after the decimal. There is one in each number, or two total. That means your answer has to have two digits after the decimal, so 3,066 becomes 30.66. That is it. Having said that, you must be sure to include that last step, or you will definitely get the problem wrong (and the test writers may even include 3,066 in the answer choices so that you do not know you have made a mistake and therefore will not correct yourself). Tricky, but that is what the test creators like to do.
Let’s try another one: 3.49 × 6.8. First, ignore the decimals and line the numbers up like a regular multiplication problem:
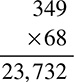
Then count the digits after the decimals: There are two in 3.49 and one in 6.8, giving you three total, so your answer also must have three digits after the decimal: 23.732. Done!
With division, the rules change a little bit, which is both good news and bad news. The good news is that you do not have to worry about remainders; remainders and decimals just do not mix. The better news is that dividing with decimals is usually kept pretty straightforward on these tests. Really, the only (kind of) bad news is that sometimes, you have to pay a little extra attention to what you are doing.
When dividing with decimals, you can ignore the decimals again, just like with multiplication. If the problem says 4.8 ÷ 1.6, you would put those numbers into our regular long division format: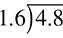 
When you divide, you get 3. Here is the part where you have to pay attention to what you are doing: To determine how many digits are behind the decimal, you take the number of digits behind the decimal in the dividend (4.8) and subtract the number of digits behind the decimal in the divisor (1.6). Because there is one digit behind the decimal in each of these numbers, you have 1 − 1, which equals 0. That means there are zero digits after the decimal in the answer (or we move the decimal zero places), so the answer remains 3.
Now try some problems with decimals. Solutions are at the end of the chapter.
DRILL: DECIMALS
1. 4.2 + 1.83 =
2. 0.95 + 1.28 =
3. 82.4 − 7.93 =
4. 2.4 − 1.99 =
5. 0.12 × 0.27 =
6. 6.23 × 0.4 =
7. 1.45 ÷ 0.5 =
8. 2.06 ÷ 0.4 =
FRACTIONS
Fractions express the same kind of idea as decimals—basically, you are dealing with some parts smaller than one. The top of the fraction is called the numerator and the bottom is the denominator. The denominator tells you how many pieces the whole is being divided into, and the numerator tells you how many of those pieces you are dealing with. For example, if Scott has 
of a candy bar, the candy bar has been divided up into three pieces, and he has two of them. If Joanne counts 10 marbles in a bag and 7 of them are blue,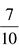 
of the marbles in the bag are blue.
Of course, sometimes fractions represent larger numbers than they seem to. Perhaps Heather tells you that 
of the employees in her office manage at least one other person. You know that Heather works in a large office, so she is probably talking about more than literally two people out of five in the whole office. The fraction is one way to present “two in every five.” How did she come up with that number? Perhaps there are 1,000 people who work in her office, and 400 of them are managers. That means the fraction was originally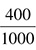 
. Those are pretty big numbers to manipulate, so we reduce fractions to make them more manageable. Also, on exams, you generally will have to reduce any fractions you work with because the correct answers are reduced as much as they can be, which means they have had as much as possible divided out of both the numerator and denominator—whatever you divide out of one of them, you must do with the other, as well. (By the way, you probably learned in school to reduce by finding the greatest common factor, but we are going to do it a different way. Sometimes it takes a few more steps, but each step is much less stressful and therefore better for your test scores overall.)
Let’s reduce 
. The first thing you should look for to reduce is whether there are 0s at the end of both the numerator and the denominator. In this case, there are two 0s in the numerator and three 0s in the denominator. Remember, you cannot do something to one part that you could not do to the other part, so in this case you can remove just two 0s from both parts. (It is actually not just removing 0s, of course; it is dividing by 100. This applies only to 0s; you could not just remove 3s on the end of both the numerator and denominator!)
Now your fraction is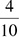 
. After removing 0s (i.e., a dividing by 10 or 100 or 1,000), you look for other numbers to divide by. Remember the divisibility rules you reviewed in the Integers section? Those really come in handy here. Two is always a good factor to check toward the beginning of the process; if both the numerator and the denominator are even, divide them both by 2 as many times as you can.
In this case, the numerator and the denominator are divisible by 2, so your fraction is now 
. You cannot divide by 2 again because 5 is odd. You cannot divide by 3 either, because neither 2 nor 5 is divisible by 3. This is kind of similar to checking possible factors and trying to determine whether a number is prime; once you have reached halfway to the larger number, you can stop. The fraction is reduced as much as it can be. (One other way to tell that it is reduced is that both numbers are prime. Not all reduced fractions have two primes, but if you do have two primes, you know the fraction is reduced.) Let’s try some more reducing:
What is the most reduced form of 
? This problem does not let you divide by 10 or 100 because there are no 0s at the end, so let’s go straight to 2. Both the numerator and the denominator are divisible by 2, giving you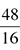 
. Again, you can divide by 2, giving you 
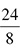. Divide again by 2 to get 
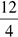. Dividing again by 2 gives you 
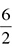. Divide again and you have or 
just 3. One more:
What is the most reduced form of 
? Again, you do not have 0s at the end, but this time you do not have two even numbers either. Checking divisibility for 3, you see that 15 is divisible but 130 is not. There is no reason to check for 4, because 15 is not even (and all numbers divisible by 4 are definitely even). Both are divisible by 5, so divide. Your new numerator is 15 ÷ 5 = 3. Your new denominator is 130 ÷ 5 = 26. The fraction must be reduced now because you know you cannot divide by 3 or anything smaller than 3, so your answer is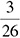 
.
It is your turn to reduce some fractions. Solutions are at the end of the chapter.
DRILL: REDUCING FRACTIONS
1. 
2. 
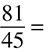
3. 
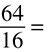
4. 
5. 
6. 
Adding and Subtracting Fractions
You may have learned in school that to add and subtract fractions, you need to find the least common multiple of the denominators or something to that effect. That is a good method, but we are going to use a shortcut method called the bowtie for our purposes. This method has three steps and it can be used on any two fractions, no matter whether you are adding or subtracting.
Let’s try an example:
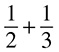
The first step of the bowtie is to multiply following the arrows below:
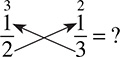
Now you have 3 × 1 = 3 and 2 × 1 = 2. The second step is to add or subtract your new numbers, based on the operator in the problem. Here you have an addition sign, so you add: 3 + 2 = 5. The result, 5, is the numerator of your answer. The third step is to multiply the denominators to get the denominator of your answer.
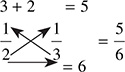In this case, 2 × 3 = 6, so your answer is 
.
Let’s try another:
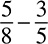
Step 1 involves multiplying across in the direction of the arrows.
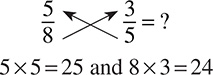
Step 2 involves adding or subtracting, according to the operation sign, to get the numerator of the correct answer.
25 − 24 = 1
Step 3 involves multiplying denominators to get the denominator of the correct answer.
8 × 5 = 40
The correct answer is 
.
Now it is time to try a few on your own. The solutions to the drill are at the end of the chapter.
DRILL: ADDING AND SUBTRACTING FRACTIONS
1. 
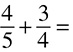
2. 
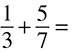
3. 
4. 
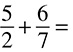
5. 
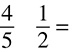
6. 
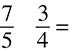
7. 
8. 
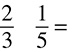
Multiplying and Dividing Fractions
Multiplying fractions, by comparison, is pretty easy. All you have to do is multiply the numerators, then multiply the denominators. For example:
The calculation 3 × 2 = 6 makes 6 the numerator of the fraction. The calculation 2 × 5 = 10 makes 10 the denominator. Your new fraction is 
, but that needs to be reduced to be a correct answer on most tests; you can reduce it to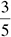 
.
Dividing fractions is almost the same, but there is one step to add at the beginning: You must flip the second fraction first, and then you can just multiply straight across as you did for multiplying fractions. For example, if you start with this problem:
You would just flip the second fraction so that your new problem looks like this:
Multiply straight across and you get 3 × 4 = 12 for the numerator and 10 × 5 = 50 for the denominator.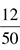 
reduces to 
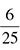, so that is your answer. One thing to note: Sometimes you may see fraction division problems expressed this way:
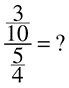
A line separating a numerator from a denominator is essentially a division sign, so this is really the same as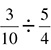 
. Feel free to rewrite it that way first if it makes things easier to work!
Now it is your turn. Solutions are at the end of the chapter.
DRILL: MULTIPLYING AND DIVIDING FRACTIONS
1. 
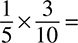
2. 
3. 
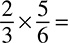
4. 
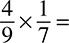
5. 
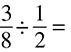
6. 
7. 
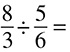
8. 
Comparing Fractions
You can use the bowtie method to compare two fractions as well, and the process is even shorter than for adding and subtracting. Given two fractions side-by-side, just multiply in the direction of the arrows again.
In this example, you end up with 12 on the left and 8 on the right, which means that the fraction on the left is larger than the fraction on the right.
Mixed Numbers
Occasionally, you will see numbers such as 
or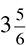 
. These are called mixed numbers—numbers that are fractions but larger than 1. To add, subtract, or otherwise manipulate them, you must convert them to improper fractions, which are fractions that have a larger numerator than denominator. To convert a mixed number to an improper fraction requires two steps.
Let’s take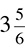 
as an example. Step 1 is to multiply the integer (in this case, 3) by the denominator (in this case, 6), which works out to 3 × 6 = 18. Step 2 is to add the result to the numerator, which is 5. That looks like 
, which solves as 
. Done!
How about 
? Multiply the integer in front by the denominator (1 × 4 = 4), then add it to the numerator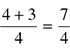 
, and you are done; 
.
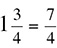Once a mixed number is converted to an improper fraction, you can treat it exactly the same as a regular fraction; follow the same rules for adding, subtracting, multiplying, dividing, reducing, and anything else you can think of to do to a fraction.
Ready to try a few more? Solutions are at the end of the chapter.
DRILL: CONVERTING MIXED NUMBERS TO IMPROPER FRACTIONS
1. 
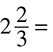
2. 
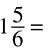
3. 
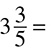
4. 
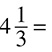
5. 
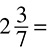
6. 
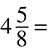
One final note on fractions: Any integer can be converted into a fraction by making it the numerator with 1 as the denominator, so if you need to subtract a fraction from an integer, it is a good idea to take that quick step first.
PERCENTAGES
You almost certainly deal with (or at least see) percentages every single day. If you think about it, there is a good chance that you have seen one or all of the following examples on a regular basis:
• Sales tax of 7% on your purchase
• Clearance sales offering 75% off the lowest marked price
• A 3% increase in inflation
• Annual interest of 19.99% on a credit card balance
• A 15% gratuity at a restaurant
Even if percentages were not a frequent topic on nursing school entrance exams (which they are), it would make your everyday life easier to know how to deal with them well.
First, you need to know that percent means out of one hundred. If you are paying a 15 percent gratuity, you are paying 15 cents for every 100 cents (or one dollar) you have already paid. Have you ever heard the expression “pennies on the dollar”? Well, it is the same as saying percent—if you are paying only a few pennies on the dollar, you are paying only a few percent of the original price. (Of course, ads that say you are paying pennies on the dollar could well mean you will pay 80 pennies on the dollar, but the impression they want to give is that you are paying only a few percent.)
CONVERTING FRACTIONS, DECIMALS, AND PERCENTS
One of the most important things to know about percentages is how to convert fractions, decimals, and percents. In fact, some exams have sections dedicated to these conversions, but the lucky thing is that you can memorize the most common conversions and learn a basic formula to calculate the rest. Ready with your index cards?
Should you come across a problem that is unfamiliar on one of your exams (or you blank out, as even the best test-takers do from time to time), remember that you can always follow these steps to convert from one system to another:
• From percents to decimals. Take off the percent sign and move the decimal two places to the left.
75% becomes 0.75
500% becomes 5.0
• From decimals to percents. Do the opposite; move the decimal two places to the right and add a percent sign.
0.345 becomes 34.5%
0.6 becomes 60%
2.6 becomes 260%
• From fractions to percents. Treat the fraction as a division problem; actually move the numbers into a division sign and work the math. Then move the decimal two places to the right and add a percent sign at the end.
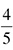becomes 0.8, or 80%
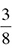becomes 0.375, or 37.5%
• From percents to fractions. Remove the percent sign and make the number the numerator of a fraction, with 100 on the bottom. Reduce, and you are done. (If you need to brush up on reducing, see the section on fractions.)
65% becomes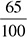 
, which reduces to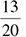 
120% becomes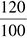 
, which reduces to 
• From fractions to decimals. Treat the fraction as a division problem; actually move the numbers into a division sign and work the math. This time you do not have to convert to percents, so you are done!
becomes 0.25
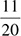becomes 0.55
• From decimals to fractions. Move the decimal two places to the right and make the number the numerator of a fraction, with 100 on the bottom. Reduce and you are done.
0.75 becomes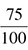 
, which reduces to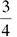 
0.60 becomes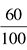 
, which reduces to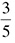 
Changing a percent or decimal to a fraction is less common than the other four types of conversions, but should you need to do it in the context of any problem type, there is your guide. One note on converting from fractions: If a problem asks you to convert from a ratio to a decimal or percent, it is the exact same as converting from a fraction; just take the ratio and change it into a fraction (for example, 3:2 becomes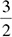 
).
Ready for some practice on your own? Solutions are at the end of the chapter.
DRILL: CONVERTING FRACTIONS, DECIMALS, AND PERCENTS
1. What is 27.5% as a decimal?
2. What is 33% as a decimal?
3. What is 0.425 as a percent?
4. What is 3.9 as a percent?
5. What is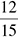 
as a decimal?
6. What is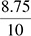 
as a percent?
Calculating Percentages Using Fractions or Decimals
As you may have noticed from the examples at the beginning of this section, you really never deal with percentages alone; a percent is only significant when it is a percent of something else. That means that you are always multiplying the percent times another number. If you are calculating 7 percent sales tax on a $20 purchase, you multiply 7% × 20. You do that by converting the percentage to either a fraction or a decimal, whichever you prefer, and multiplying out:
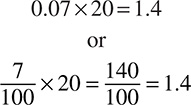
Either way, you end up with 1.4, or $1.40 in sales tax.
Let’s take another example. You find a shirt on clearance and it is marked at 75% off the original price of $40. How do you find 75% of $40? With decimals, that is 0.75 × 40 = 30. With fractions, that is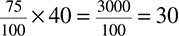 
.
75% of $40 is $30, but remember what you are calculating; the item is 75% off, which is the same as saying $30 off. The clearance price of the item is $40 − $30, or $10. A little ballparking will take you a long way toward the correct answer on these problems; if an item is 75% off, that is more than half off, so the final price should be less than half of the original.
One more: The bill at a restaurant is $80 and you want to leave a 15 percent gratuity. What is 15% of 80? With decimals, that is 0.15 × 80 = 12. With fractions, that is 
. Either way, you are leaving a $12 tip.
By the way, what if the problem asked you to calculate the entire bill, including gratuity? You would just add $12 to the $80 you already had, giving you a $92 total.
Okay, now it is your turn for some practice. Solutions are at the end of the chapter.
DRILL: CALCULATING PERCENTAGES
1. What is 75% of 120?
2. What is 40% of 75?
3. What is 80% of 90?
4. What is 45% of 80?
5. What is 25% of 30?
6. What is 65% of 160?
Translating Word Problems Involving Percents
Some problems are set up as word problems and they appear as if you have to make up an equation to solve them. Actually, you do not have to make up that equation yourself. In fact, all it takes is some translation to take the problem directly from English into equation form. That is great news, because setting up the equation correctly is at least half the battle toward getting that question right.
For example, take the following question:
The number 5 is what percent of 4?
This type of question is extremely common, but do not worry—each word in the question has a direct correlation in math-speak (and the numbers stay the same). Here is the same sentence, translated into a mathematical equation:
5 = x% × 4
You know from your experience with percentages that percent means out of one hundred or over one hundred, so you can do a little bit of manipulating and get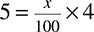 
, which is the same as 
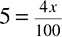. Now you can just solve the equation 
.
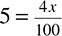Multiply each side by 100, which gives 500 = 4x. Then divide each side by 4, which gives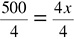 
, or 125 = x.
If you do not remember how to manipulate the equation, do not worry. We will take it step by step and go into all of the “whys” in the algebra section.
Let’s try another translation question:
80 percent of what number is 4?
First, you translate: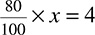 
. That is the same as 
. Multiply each side by 100 to get 80x = 400. Divide each side by 80 to get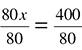 
. Solve: x = 5.
Ready to put these skills to the test? Translate and calculate percentages on the following drill. The solutions are at the end of the chapter.
DRILL: TRANSLATING WORD PROBLEMS INVOLVING PERCENTS
1. 49 is what percent of 140?
2. 21 is what percent of 70?
3. 36 is what percent of 45?
4. 15% of what number is 12?
5. 80% of what number is 40?
6. 20% of what number is 12?
Other Shortcuts
Now that you have learned how to approach most percent problems on your entrance exams, here are some other shortcuts to help out in a pinch (on tests and in real life). If you do not like multiplying by 15 or 12.5, you can use the hints to “brute force” your way through percentage problems when your math muscles just are not in shape.
• You can calculate 10% of anything. Calculating 10% is just moving the decimal one place to the left, so 10% of 50 is 5, 10% of 0.3 is 0.03, and 10% of 873 is 87.3. This alone can help you ballpark if, say, you are asked to take 12% of a number; just find 10% and pick the one that is a little bit more.
• You can calculate 1% of anything. Calculating 1% is just moving the decimal two places to the left, so 1% of 400 is 4, 1% of 62 is 0.62, and 1% of 0.4 is 0.004. Again, helpful for ballparking on its own, but when you combine it with your ability to take 10%, you are able to add or subtract 1% and zoom in on the correct answer with ease.
• You can calculate 5% of anything. Remember how you can calculate 10% of anything? Well, calculating 5% of that number is the same as calculating 10% of the same number, then dividing it by two. Between now and your test, practice calculating tips such as this: Take 10% of the bill (and write it down if you wish), then take half of that and add it to the 10% you wrote down. Voila—you have just calculated a 15% gratuity.
MEAN, MEDIAN, AND MODE
Mean, median, and mode are ways of interpreting (or finding the significance of) a set of related numbers. On exams, you may be asked to calculate them based simply on some given numbers, or based on data that are presented in a chart or graph. Before calculating them, be sure you know which one the problem is asking for. It is important to know the difference between mean, median, and mode, based on what each one measures.
Mean
Mean is basically another word for average. When you are calculating a grade based on several tests or a batting average based on many at-bats, you are calculating a mean. Calculating a mean involves adding and dividing. You are generally given a list of numbers—such as 8, 11, 4, 17, and 5—and asked to find their mean.
To do this, add up the list of numbers: 8 + 11 + 4 + 17 + 5 = 45. Then divide by the number of numbers in the original list, which in this case is 5. The expression 
, and you are done! The average of 8, 11, 4, 17, and 5 is 9.
Now it is your turn to find the means of the following number sets. Solutions are at the end of the chapter.
DRILL: MEAN
1. 2, 6, 9, 4, 14
2. 9, 2, 5, 11, 18
3. 7, 21, − 5, 8, 4
4. −2, 9, −5, 6
Median
A median is simply the number in the middle in an ordered list. Calculating a median involves less math—it is really just putting numbers in order and finding the middle value.
For example, if you are asked to find the median of the list 8, 11, 4, 17, and 5, you would start by putting them in numerical order: 4, 5, 8, 11, 17. Then choose the number in the middle.
For a short list such as this one, you can probably see that 8 is in the middle; however, to check yourself or to find the middle of a longer list, start eliminating one number from each end of the list. That means the 4 and the 17 are first—just cross them out. Then the 5 and 11. When you are left with one only number, that is your median (in this case, 8). Another good reason to eliminate end pairs is to make sure that you do not actually have two numbers left in the middle. If that happens, you just take the mean of those two numbers, and that is your median.
Ready to try finding medians by yourself? Solutions are at the end of the chapter.
DRILL: MEDIAN
1. 3, 5, 2, 7, −2
2. 4, 8, 2, 7, 3
3. −3, 5, 1, 9
4. −5, 3, 2, 10, 2
Mode
The mode is the number that appears most frequently in the list. As with medians, it is a good idea to put the list of numbers in order first, because that makes the repeated numbers tend to stand out.
Let’s take this list: 11, 8, −4, 11, 4, 17, and 5. First, you would carefully put the numbers in order. (It is a good idea to cross out numbers as you go, and remember, a negative number never has the same value as a positive—so it is not the same number!) Your ordered list looks like this: −4, 4, 5, 8, 11, 11, 17.
If you want, feel free to cross off numbers that only appear once after you have made your list. Here you would cross off−4, 4 (remember, they are not the same), 5, 8, and 17. That just leaves two 11s, so 11 is the mode.
You are unlikely to run into this scenario, but in case you do find two different values that appear the most, both of them are modes. You do not “average” them by finding their mean; they stay as they are. For example, in the list −4, 4, 5, 5, 8, 11, 11, and 17, 5 and 11 are the modes. If you encounter a list in which each value appears only once, there is no mode.
It is your turn to find the modes. Solutions are at the end of this chapter.
DRILL: MODE
1. 2, 10, −2, 3, 8, 2
2. 3, 5, 3, −5, 0
3. 4, −2, 2, −3, 5, −3
4. 5, 12, 11, 11, 9, 12, 11
ALGEBRA
Algebra is usually one of the most intimidating topics for people who have not been to math class for a long time. It is easy to freeze up when you see letters instead of the numbers that you are used to working with. Before you resolve to just skip all of the algebra questions, remember these things:
1. Nursing school entrance exams only test basic algebra at most, so a little review goes a long way.
2. If x and y make you freeze up, you can rewrite any algebra problem so that it uses blanks or symbols that are more friendly.
Let’s look at a traditional math problem:
2 + 4 = ____
In this problem, there is an unknown. It is represented by a ____. What is the value of the ____? If you answered 6, you are correct.
Algebra problems are just a little different. Algebra problems essentially say this instead:
2 + ____ = 6.
What is the value of the blank now? If you said 4, you are correct, but how did you know that? You probably have this sum memorized, or you may not have even noticed that you quickly and automatically performed an operation in your head. If you did not get it, that is okay, too. To figure out the value of the blank, you need to figure out how many are between 2 and 6, which is just another way to say the difference between 2 and 6. You would subtract 2 from 6 to get 4.
Solving for x
Luckily though, you really do not have to go through this process of figuring that stuff out. Most algebra test questions have to do with solving for the unknown, usually called x, and there are very straightforward rules to follow to do this. Basically, they go like this:
1. Get x alone. The main goal is to get x on one side of the equal sign and everything else on the other. That’s because you want to end up with a statement that says, x equals this. When you get that, you have solved for x.
2. Do not play favorites. In the process of getting x alone, whatever you do to one side of the equation, you have to do the same thing to the other side. Think of it this way: When you see an equation, it is like seeing this:
The scales are perfectly balanced right now, because the two sides are equal. If you were to add something to one side but not the other, the scales would tip and you would no longer have an equation, and that is not good.
Let’s see how those rules work out in the above example, 2 + ____ = 6, which can be rewritten as 2 + x = 6. The x is the variable (also called an unknown), which could also be represented as a blank space, question mark, smiley face, or whichever other symbol you want to use. According to rule 1, you need to get x alone, which means you need to get rid of that 2 that is being added to it. The rules for this are also very straightforward:
1. If a variable has a number added to it, subtract to get rid of the number.
2. If a variable is being multiplied by a number, divide to get rid of the number.
The other two rules are exactly the same, just reversed:
3. If a variable has a number subtracted from it, add to get rid of the number.
4. If a variable is being divided by a number, multiply to get rid of the number.
In 2 + x = 6, the variable has a 2 added to it, so you would subtract the 2 to get the x alone. You cannot just subtract it from the right side of the equation; that would be playing favorites. You must also subtract it from the left side. Your equation should look like this:
2 − 2 + x = 6 − 2
Now you have 0 + x = 4, or just x = 4. You have solved for x.
Let’s solve another problem together, and then you can solve a few problems on your own.
4x = 12
In case you do not remember from algebra class, 4x is another way of saying 4 times x. You could also see it written as 4(x), but it all means the same thing: 4 multiplied by x. When a number is multiplied by a variable, you divide by that number to get the variable alone. Dividing by 4 on both sides gives you: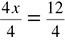 
, so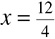 
, which means x = 3.
Ready to try some on your own? Here’s a short drill. Solutions can be found at the end of the chapter.
DRILL: SOLVING FOR X
1. 3 + 2x = 7
2. 3x − 10 = 5
3. 
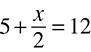
4. 4x + 3 = 15
5. 2x + 8 = 4
6. 
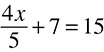
Combining Terms
Some algebra problems will not ask you to solve for x at all; in fact, solving for x will not even be possible. These problems just ask you to simplify as much as possible. For example, you could see a problem that asks
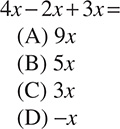
See how all of the answer choices include x? That is a giveaway that the correct answer includes x (makes sense, right?), so you will not actually solve for x and get rid of it. All you have to do is combine terms that are alike. The 4x, 2x, and 3x are alike, because they all include the x. That means you can add and subtract them just as if they were regular numbers. 4x − 2x + 3x = 5x, just like 4 − 2 + 3 = 5. Remember, though, that if the test-makers had thrown in a term that was not multiplied by x, you could not have combined that term with the others. 4x − 2x + 3x + 6, for example, would equal 5x + 6.
Even when a problem requires solving for x, you may still need to combine terms to do it. For example:
If 2x + 3x = 15, what is the value of x?
(A)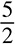 
(B) 3
(C) 5
(D)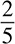 
Clearly, you are going to be solving for x because the problem asks for the value of x, but you cannot get x alone on one side until the terms have been combined. Both terms are alike, so you can simply add 2x and 3x to get 5x. Now you have 5x = 15. What else do you need to do to get x alone? Because it is multiplied by 5, you need to divide each side by 5:
Once you reduce, x = 3 (choice B).
Translating Algebra Word Problems
Some algebra problems really just involve translating from English into math, as you did with percentages. For example: If 10x is equal to 42 more than 28x, what is the value of x?
Although you are unlikely to see percents in algebra translation, you still have a few translations that you have seen before:
• “Of” translates to × (multiplication).
• “Is” (as well as has, have, do, does, equals, and some other words) translates to = (equal sign).
• “Number” translates to x or any variable of your choosing.
You are also more likely to see these words:
• “More than” means you need to add.
• “Less than” means you need to subtract the number before the “less than.”
• “Divided by” or “multiplied by” means you need to divide or multiply.
Let’s try a couple together, shall we?
If 8 more than a certain number is the same as three times that number, what is the number?
Translation:
8 + x = 3x
Then solve. The most direct way to get x alone is to remove the x from the left side.
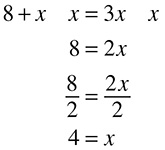
Try another:
If 2 less than 3 times a certain number is 13, what is the value of that number?
Translation: 3x − 2 = 13. Then solve:
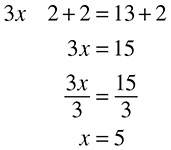
Done!
Ready to try a few on your own? Solutions are at the end of the chapter.
DRILL: TRANSLATING ALGEBRA WORD PROBLEMS
1. If 10 more than a certain number is the same as 3 times that number, what is the number?
2. When a certain number is multiplied by 5, that’s the same as increasing its value by 8. What is the value of that number?
3. A certain number is 4 less than 5 multiplied by 10. What is the value of that number?
4. A certain number divided by 
is equal to 40. What is the value of that number?
Last Notes on Translating Algebra Problems
You could also see questions that cannot be solved completely, where the point is just to translate from English to math. These can be identified pretty easily by looking at the answer choices, because the answer choices have full equations instead of single numbers. Typically, these equations also have more than one variable (which is why you cannot solve them completely; it takes more than one equation to solve for more than one variable). Here are some example phrasings for these problems:
• Sandra has 3 less than 4 times the number of marbles that Marla has.
• Mr. Geary is 5 years more than twice his daughter Kelly’s age.
• As of today, Abbey has worked at the hospital half as long as Lauren has.
Remember, all you have to do on problems such as these is translate, and maybe do a little bit of rearranging to make the equation look like one of the answer choices (and as long as you do the same thing on each side of the equation, that is fine).
Systems of Equations
Occasionally, you will run into problems that ask you to “solve for a system of equations” or “make both of these mathematical statements true.” Although the terminology sounds fancy, these problems really are not hard to do. You will be presented with two equations, and each answer choice will contain a pair of values for the variables in the equations. All you have to do is select the answer choice that satisfies both equations, and you can tell just by substituting the answers into the equations. Be careful to check both equations! Here’s an example:
Solve this system of equations:
2x + 3y = 19
3x + 2y = 21
(A) x = 3, y = 5
(B) x = 5, y = 3
(C) x = 3, y = 2
(D) x = 2, y = 3
There are more complex mathematical ways to solve, but why not just use the values given in the answer choices instead? Let’s start with answer choice A and substitute the value into the first equation:
2(3) + 3(5) = 19
That gives you 6 + 15 = 19, so choice A is clearly incorrect. Move on to choice B.
2(5) + 3(3) = 19
10 + 9 = 19 . . . that works! Before you pick it, you also have to make sure it works for the second equation.
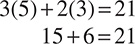
Again, that works, so you do not even have to look at the remaining answers; B is correct.
Factoring
You may see a question or two on your exams that ask you to factor an algebraic expression. Basically, this means “divide out as much as you can” from the expression. For instance, if you are asked to factor 2x2 + x3, it is your job to find the common numbers and exponents in each term being added. The only thing these terms have in common is x, and you want to divide out as many of them as you can from each term. You can only divide out x2 from the first term, so that’s your limit from the second term, as well. The factored expression looks like this: x2(2 + x).
CHARTS, GRAPHS, AND TABLES
Charts, graphs, and tables appear in some way on almost every exam you could take for nursing school admission. Luckily, they tend to be fairly straightforward as long as you know what to look for. They also tend to fall into very predictable types, so let’s review each type of chart or graph that you are likely to see.
Column Charts
A column chart generally compares categories of information, such as a car model’s sales revenue in different regions, numbers of adoptions of different dog breeds, or the number of people who went to see a particular movie by age range. The “columns” in column charts make it easy to compare amounts, because the taller the column, the larger the amount. Here’s an example:
Notice the lines on the bottom and left of the chart. Those are called axes. Each axis contains a different kind of information. Generally in a column chart, the x-axis (or the line across the bottom) is labeled according to the categories of information (regions where a car was sold, breeds of dog that were adopted, age ranges of people going to see a movie). The axis on the left side of the columns generally displays numbers that represent how many cars were sold, dogs were adopted, or people went to see the movie. This is called the y-axis. Sometimes, the y-axis displays very large numbers, so to save space, the makers of the chart tell you that every unit or “1” on the chart actually represents tens, hundreds, thousands, or even millions. The above chart does that, using the label (in thousands).
Occasionally, you could see a column chart that looks like this:
It is really the same chart, just on its side. The numbers are going to run along the length of the columns to show you “how many” each column represents, so do not be thrown off by the chart being on its side.
Line Graphs
Line graphs are very similar to column charts, but they tend to be used to track progress over time. For example, a line chart may track the closing value of a stock day by day, a patient’s temperature hour by hour, or a country’s gross domestic product from year to year. Again, the labels across the bottom tell you which categories or units of time you are viewing, and the numbers on the left tell you the values at each point, which may be expressed in larger units. Line graphs look like this:
Pie Charts
Pie charts are different from column charts and line graphs in two major ways: First, they have no axes. Second, they do not necessarily have any real values. Instead, pie charts make it easy for you to see percents of a whole. For example, you may see a pie chart that shows the percentage of males versus females in a certain nursing program, the percentage of students who make As, Bs, Cs, Ds, and Fs in a freshman-level class, or the percentage of cars sold that are economy, mid-size, or luxury. For example, take this pie chart:
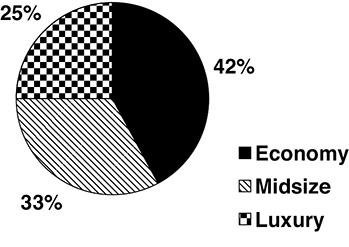
You can easily tell that more economy cars were sold than mid-size, and more mid-size than luxury, but you cannot tell the actual numbers of cars sold in any particular category or in total.
Pie charts are usually labeled with the percentage that each “slice” represents, and the category that is being measured by each slice may be labeled on the pie as well, or the labels might be in a legend (also called a key) near the chart.
Tables
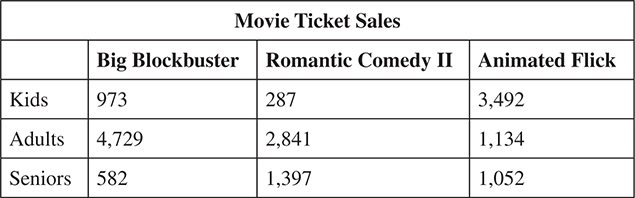
Finally, there are tables, which are just ways to organize numeric data. They are not as visual as charts and graphs, but they can make it easier to display large amounts of data in a small amount of space. They also make it possible to see exact numbers for calculations, whereas using charts and graphs often just allows you to ballpark and compare. Tables look like this:
Stem-and-Leaf Plots
Stem-and-leaf plots are just a kind of table that, again, makes it easier to display larger amounts of data in limited space. In this case, they replace a list of numbers and make it easier to see patterns in the list. These will probably be the least familiar type of chart, graph, or table of all that you will see in this lesson. Here is an example of a stem-and-leaf plot:
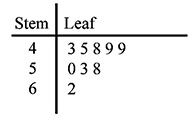
Remember your place values? The numbers in the “stem” category (on the left) represent the tens place (and sometimes hundreds or more, but that is rare on these exams). The “leaves” on the right represent the units digits for each stem. The list of values represented by this stem-and-leaf plot is:
43, 45, 48, 49, 49, 50, 53, 58, 62
Answering Questions with Charts, Graphs, and Tables
When you see any of these on your test, be sure to check for a few things before you get started with the problem:
1. How many questions refer to it? Usually there are two, sometimes even three questions that refer to one chart, graph, or table, so noting how many questions are involved before you get started can save you some time and confusion. Typically, if there are two questions or more, there is a note above the chart, graph, or table that looks something like this: Use the chart below to answer questions 9 and 10.
2. Read the labels. It may sound obvious, but most chart, graph, and table problems become a lot easier when you go into the problem already knowing what information you’re given. Be sure to read the title, the category, and value labels on the axes, the legend (if there is one), and any other notes that have been added. Also, note the units on the y-axis!
3. Note any trends. Is one column significantly taller than all the other ones? Does the line in a line graph generally point up or down? Is there one tiny slice in a pie chart? Are there more leaves for one stem than any of the others? Do not do any math here; just take a second to notice the data being presented.
Now you are ready to look at some questions.
Use the chart below to answer the following two questions.
What is the best approximation of the number of dachshunds adopted in both months combined?
(A) 18
(B) 23
(C) 40
(D) 46
Approximately how many more boxers than pugs were adopted in January?
(A) 5
(B) 9
(C) 12
(D) 14
Start with the first question, What is the best approximation of the number of dachshunds adopted in both months combined? In January, the column for dachshunds is in the middle, either 22 or 23. In February, it is also in the middle, either 17 or 18. The number of dachshunds adopted is between 39 and 41, making choice C the clear winner.
Then answer the second question, Approximately how many more boxers than pugs were adopted in January? This time you are focusing on just the January numbers, in black. It looks like the boxers column is almost all the way to the 15 line, so call it 14. The pugs column is almost all the way to the 10 line, so call it 9, giving you a difference of about 5, which is choice A; no other answer comes close.
Are you ready to try some on your own? The solutions to this drill are at the end of the chapter.
DRILL: CHARTS, GRAPHS, AND TABLES
Use the following graph for questions 1–2.
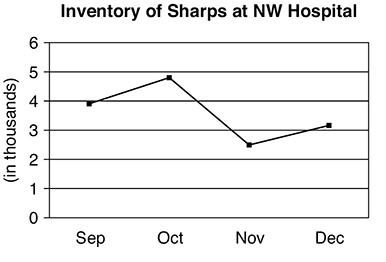
1. Which of the following is the best approximation of the percent decrease in sharps inventory from October to November?
(A) 25
(B) 50
(C) 75
(D) 100
2. If 500 sharps were used between the inventory counts in September and October, approximately how many were purchased in the same time period?
(A) 500
(B) 1,000
(C) 1,500
(D) 2,500
Use the following table for questions 3–4.
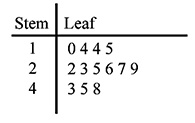
3. What is the mode of the numbers in the above stem-and-leaf plot?
(A) 10
(B) 14
(C) 25
(D) 26
4. What is the difference between the largest and smallest numbers represented?
(A) 10
(B) 25
(C) 38
(D) 48
PROPORTIONS AND RATIOS
Proportion and ratio problems both deal with conversions. They are essentially the same kind of problem and they are set up similarly, but they have a little different terminology.
Proportions
Proportions compare two parts, such as miles and gallons or cents and oranges. They are usually presented like this:
If Ben can type 5 pages in 12 minutes, how long will it take him to type 15 pages?
If apples cost 50 cents for 3, how many apples can you buy with $2?
If it takes 2 cans of paint to cover a wall, how many walls can be covered with 8 cans of paint?
Essentially, proportions ask you to convert one pair of numbers. They are easy to miss if you are not being careful or if you are making up a method on the spot, but there are very predictable ways to set them up properly. Once you realize you are working with a proportion problem, draw two blank fractions, like this:
Be sure to remember the equal sign, because they will actually be equal fractions. Now it is time to fill in the information that you know.
For example, let’s take the first problem above:
If Ben can type 5 pages in 12 minutes, how long will it take him to type 15 pages?
The first part of the problem tells you that Ben can type 5 pages in 12 minutes. Fill that information in to your first blank fraction, making sure that you label both the numerator and the denominator.
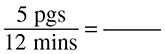
The second part of the problem asks how long it will take to type 15 pages. Because “pages” is in the numerator of the first fraction, you are going to put it in the numerator of the second fraction—that is why it is important to label. You do not know what the time is in the second fraction—that is what you are trying to figure out—so you can put an x there.
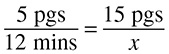
Now there are two ways to solve. First, you can cross-multiply, which will work in any situation. Cross-multiplication is a lot like comparing fractions using the bowtie method; just multiply diagonally and upward. Cross-multiply here:
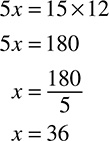
The answer is: it takes Ben 36 minutes to type 15 pages.
Sometimes you may notice a shortcut that can save you some calculation. Starting from filling in the fractions:
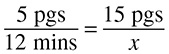
If you happen to notice that a number in one fraction is easily divisible by a number directly across from it, for example, 15 and 5, you can use that as a shortcut. The number 5 multiplied by 3 is 15, so you would also multiply 12 by 3 to get the value of x. It is just like finding the multiplier in a ratio problem. Because 12 × 3 = 36, again, Ben can type 15 pages in 36 minutes.
Try another:
If apples cost 50 cents for 3, how many apples can you buy with $2?
First, fill in your fractions:
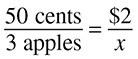
Now, you may notice that when you fill in 50 cents and $2, they are not in the same units and therefore, the math really is not going to be accurate. The easiest way to deal with this is to convert dollars to cents, or change the $2 to 200 cents.
That’s better. Now you can either cross-multiply or find the multiplier. If you cross-multiply:
You can buy 12 apples for $2. If you recognize the multiplier, you can see that 50 × 4 = 200. Therefore, you can multiply 3 by 4 to get 12, the number of apples that can be bought for $2.
One more:
If it takes 2 cans of paint to cover a wall, how many walls can be covered with 8 cans of paint?
The only trick in this problem is that it does not appear to give you two numbers to put into the first fraction, but it does: 2 cans of paint and 1 wall. You may see the same situation if the problem tells you something can be done per minute, per gallon, or per mile. Just think of that as per 1 minute, 1 gallon, 1 mile, and so on. Your fractions should look like this:
Cross-multiplying, you get:
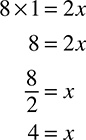
It takes 4 cans of paint to cover 8 walls. If you see that 2 and 8 have a multiplier of 4, then you can say 4 × 1 = 4 cans of paint.
Ratios
Ratios are also comparisons of numbers. If you have ever doubled or halved a recipe, you have worked with ratios. Probably the best news about ratios is that they are pretty easy to spot; they usually have the word “ratio” right there in the problem. Ratio problems do not tend to be very complex; you will usually have two parts to deal with. For example:
The ratio of minivans to sedans in the parking lot is 3:2. If there are 69 minivans in the parking lot, how many sedans are there?
Time for the good news: You can deal with these problems in exactly the same way as you dealt with proportions. Start by setting up two equal fractions, this time with the parts of the ratio (3 and 2) making up one fraction:
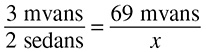
Then cross-multiply:
3x = 2 × 69
Solve:
Another way ratios can be expressed is even closer to proportions.
The ratio of the base to height of two triangles is equal. If one triangle has a base of 4 and a height of 7, and the second triangle has a base of 6, what is the height of the second triangle?
Set up fractions:
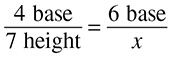
Cross-multiply:
4x = 42
Solve:
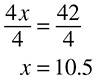
Now it is time for you to attack a few ratio and proportion problems on your own. Solutions are at the end of the chapter.
DRILL: PROPORTIONS AND RATIOS
1. If long-distance telephone calls are billed at a rate of $0.13 per minute, how many minutes can Jorge talk for $6.50?
2. Sally’s lemonade stand charges $0.15 for a glass of lemonade. How many glasses can Charlie buy for $1.80?
3. Ferdinand paid $0.25 for 3 marbles. How much would it cost him to buy 15 marbles?
4. If the ratio of women to men in the debate club is 5:4 and there are 40 women in the club, how many men are in the club?
CONVERTING U.S. AND METRIC UNITS
Remember how proportions and ratios really just deal with conversions? Well, you can use the same setup to handle unit conversions for fluid, mass/weight, and length. Sometimes you will be asked to convert from U.S. unit to U.S. unit (such as pounds to ounces), or metric unit to metric unit (such as meters to centimeters), or you may even be asked to approximate between U.S. and metric units. Memorizing the following values will help with these conversions.
U.S. Measurements
FLUID
8 ounces = 1 cup
2 cups = 1 pint
2 pints = 1 quart
4 quarts = 1 gallon
WEIGHT
16 ounces = 1 pound
2000 pounds = 1 ton
LENGTH
12 inches = 1 foot
3 feet = 1 yard
5280 feet = 1 mile
Metric Measurements
MASS
1 gram =
• 1,000 milligrams
• 100 centigrams
• 10 decigrams
• 
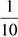decagrams (1 decagram = 10 grams)
• 
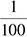hectograms (1 hectogram = 100 grams)
• 
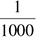kilograms (1 kilogram = 1,000 grams)
LENGTH
The scale for length is the same as for mass, except the base unit is the meter instead of the gram. A meter is equal to 1,000 millimeters or 100 centimeters, and a kilometer is equal to 1,000 meters.
FLUID
The scale for fluid is the same, except the base unit is the liter.
Roman Numerals
You may see a question that requires you to translate between Arabic and Roman numerals. Here are the most common Roman numerals and their Arabic equivalents:
In the Roman numeral system, the numerals for 4 and 9 are usually shown as IV (one less than 5) and IX (one less than 10). For example, here are the numbers from 1 – 10:
A larger number, such as 2,348, would be translated as MM (2,000) CCC (300) XL (40) VIII (8) and written MMCCCXLVIII.
Military Time
You may also need to read “military time,” which is based on a 24-hour clock. Here are the equivalent times for each hour of the day:
Metric/U.S. Conversions
Here are some approximate conversions between the U.S. and metric systems. Remember to use your ballparking skills; although you may or may not be given conversions on the test, it will usually be enough to know that a yard is slightly bigger than a meter, a quart is slightly bigger than a liter, and so on.
Now that you have conversion rates, you can use them to set up a proportion to do any conversion. For example, if a problem asks you to approximate how many kilograms are in 11 pounds, you would set up two fractions just as if you were doing a proportion problem, then cross-multiply and solve.
Cross-multiplication gives 11 × 1 = 2.2x. Once you divide by 2.2 on both sides, you get 5 = x.
Fahrenheit/Celsius Conversions
These conversion rates are normally given to you within a problem, but it is good to be prepared for them ahead of time, because they require a slightly different process than the proportional conversions you have been doing.
• To convert degrees Fahrenheit to degrees Celsius: subtract 32, then multiply by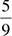 
.
• To convert degrees Celsius to degrees Fahrenheit: multiply by 
, then add 32.
To convert 100 degrees Fahrenheit to degrees Celsius:
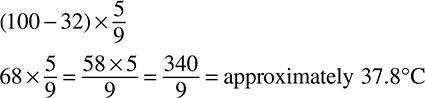
To convert 20 degrees Celsius to degrees Fahrenheit:
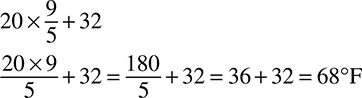
Ready to try some conversions on your own? The answers are at the end of the chapter.
DRILL: UNIT CONVERSIONS
1. Convert 77°F to degrees Celsius.
2. How many millimeters is 32 meters?
3. If Kara is carrying an empty one-gallon container, approximately how many liters of fluid could she pour into it?
4. A five-pound brick weighs how many ounces?
5. What is 48 in Roman numerals?
6. What is 6:25 PM in military time?
APPLIED MATH
Most of this chapter is about specific mathematical skills, such as multiplying decimals or calculating percentages. This section is about a skill that is probably tested more than any other, which is your ability to interpret a word problem and decide which of those other mathematical skills to use on any problem. For example, you already know how to subtract fractions such as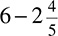 
. Many problems on your entrance exams may test the same math, but in a context that looks like this:
A certain beaker can hold 6 ounces of fluid without running over. If there is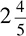 
ounces already in the beaker, how much can be added without overflowing the beaker?
This kind of problem adds an extra step: You have to decide which operations to perform. The translation skills you have learned in the Percentages and Algebra sections will be helpful in this process, and this section will add a few helpful hints and lots of practice.
One of the best things you can do if you do not know where to begin on a word problem is to start drawing. If your mind is freezing up, it may be because it cannot deal concretely with the information it is given. Particularly if you are a visual learner, drawing a picture can help you start to deal with the information. Do not worry; you do not have to be an expert artist. Even the most basic shapes can represent the information you are given.
For example, for the beaker problem above, you might draw something that looks like this:
From there, you can even write out questions or emphasize areas that represent the amount you are trying to find. For example:
You can see that to find the missing quantity, you would have to subtract 
from the whole. Set up the problem:
Multiplying across gives you 30−14 for the numerator and 5 for the denominator, so that is a complete fraction of 
or, if the question has mixed numbers in the answers, 
.
Try another one.
Labels will be cut from a sheet of paper that measures 9 inches by 12 inches. If each label needs to be 
inches by 
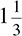inches, how many labels can be cut from that sheet of paper?
This is another good one to draw, just so that you do not have to deal with all of this in your head.
A problem like this does not require you to arrange each label; you just need to decide which side of the paper divides most neatly into sections of the size you need. Is 9 divisible by 
? Yes, but 12 is not, so it is a good bet that you are going to be dividing up the 9-inch side into 
-inch sections; 
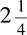divides into 9 four times:
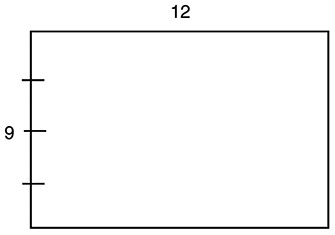
Now how many times does 
go into 12? Some quick calculation tells you 9, so you will have 4 × 9 labels on the sheet of paper, which multiplies out to 36. Again, draw out as much as you need to help with the problem, label as much as you can, be neat, and do not waste time trying to make it perfect.
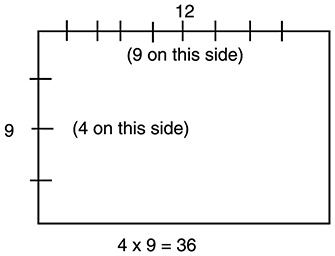
On the other hand, sometimes you will not have much to draw, but you still will have words in the problem that will give you clues of what to do.
Here is another example:
Mrs. Aziz walks two miles per day at the beginning of a fitness program. Exactly five months later, she is walking four miles per day. On average, how much per month has she increased her daily walk?
You can tell by the word “average” that this is an average/mean problem. Normally, you would be given a list of numbers to add up and divide, but does this problem have another way of telling you the total that you need to divide by? Well, you know that Mrs. Aziz’s walk went from two to four miles, so that is an increase of two; that is your total. Because the increase happened over five months and you are being asked for a monthly average, you would divide by five. She increased her daily walk an average of 
of a mile per month.
Try one more.
A certain hospital has 24 beds in the emergency room. If 25 percent of the beds are currently occupied, how many more patients can the emergency room accept before all beds are full?
Whether you draw this one is up to you; it might be a good idea just to remind you of what you’re looking for.
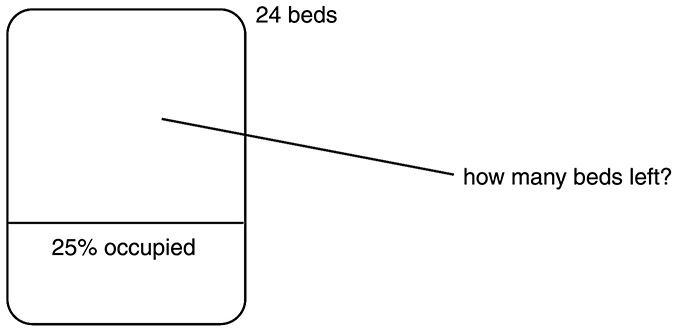
Now you need to do the math; 25% of 24 = 6. That means 6 beds are occupied, and 24−6 = 18 beds are available in the emergency room.
Be careful on problems like these to focus on what the problem is asking (how many beds are available) instead of the first calculation you need to do (how many beds are occupied). Drawing a quick picture can help keep you focused on the correct part of the problem.
Now it is your turn to try a few. Solutions are at the end of the chapter.
DRILL: APPLIED MATH
1. A patient is taking 150mg of a certain prescription every day. How much of the prescription will the patient take during one week?
2. Marci is planning to sell all her shares of a certain stock if their value falls to $30 per share. If the value of the stock is now $45 per share, by what percent would they have to fall for Marci to sell?
3. A banquet room that measures 100 feet by 200 feet is being arranged for a party. If a space measuring 20 feet by 20 feet is needed for each table, what is the maximum number of tables that can be arranged in the room?
4. A certain barrel can hold 50 gallons of liquid. If Tom has to fill it using a one-quart container and he fills the container up completely each time, how many times will he have to pour the container into the barrel?
5. If Sara’s current salary is $25,000 per year and she is due to get a 3 percent raise this year in addition to a 2 percent cost of living increase, how much will her salary be after these increases take effect?
6. If a family’s total income is spent on the following expenses: one-fourth for the mortgage, one-eighth for car payments, one-eighth for groceries, two-fifths on other expenses, and the rest to savings, what fraction of the family’s total income goes toward savings?
GEOMETRY
Geometry is probably one of the more dreaded topics for people who have not been in a math class for a long time, but there is good news. First, there are very few geometry problems on nursing school entrance exams. Second, there are no proofs or theorems, as you might remember from math classes. Third, you are going to be tested only on basic concepts and application. Fourth, geometry is a very concrete topic; most of it deals with shapes and measurements that you can easily see, rather than letters that stand in for numbers. (Okay, there are a few letters that stand for numbers in the geometry we are going to cover, but it is still far less abstract than algebra.) We will start with a basic review of the geometric shapes you are likely to see on the exams.
Angles
Okay, angles are not shapes, but they are important. Any time two lines or line segments connect, they form an angle, and that angle can be measured in degrees. Some of the important degree measurements to know are:
• 180 degrees: This is really a straight line.
• 90 degrees: This is probably the most common angle measurement that you will see. Lines that cross each other at a 90-degree angle are perpendicular lines. You will see 90-degree angles in right triangles and rectangles (including squares). When you see an angle with a little box where the lines meet, that means it is a 90-degree angle.
That’s pretty much it for angles for right now.
Rectangles
Rectangles are four-sided figures and by definition, they have to have four right angles. In fact, “rectangle” is Latin for right angle. (Go ahead, look it up, we’ll wait.) Because all four of the angles are “right” angles (meaning they are 90 degrees each), the total degree measure is 360 degrees.
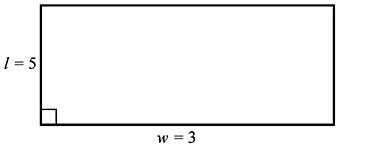
To obtain the perimeter of a rectangle (which is the measurement around the outside), you add up the lengths of all of the sides. Hint: There are always two pairs of sides, so if you know the length of one side, you know the length of the side directly opposite. To obtain the area of a rectangle, you multiply one side by another side that is adjacent to (or right beside) it. The sides are known as l and w for length and width, but it really does not matter which is which. Here are the formulas:
Perimeter: P = 2l + 2w
Area: A = lw
What is the perimeter of the rectangle above? _______ (all answers to the questions in this section are at the end of the shapes review, before the drill.)
What is the area of the rectangle above? _______
The word rectangle is usually used to mean the kind of shape shown above, where the height is different from the length, but technically, rectangles include squares.
Squares
Squares follow all the same rules that rectangles do, but they have one additional requirement: All sides have to be the same length. A square is just a rectangle (a four-sided, 360-degree, all–right-angle shape) with all sides the same length.
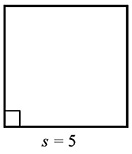
Because all sides are the same length, squares have some shortcuts once you know one of the sides (abbreviated as s): You can multiply by four to get the perimeter or square one side (raise it to an exponent of two) to get the area. Here are the formulas:
Perimeter: P = 4s
Area: A = s2
What is the perimeter of the square above? _______
What is the area of the square above? _______
Triangles
Triangles are three-sided figures with angles that add up to 180 degrees. That does not necessarily mean that each angle is 60 degrees; the angles can have any combination of measurements. The triangles that you will deal with most on your entrance exams are right triangles, which are triangles that have one right angle. Right triangles look like this:
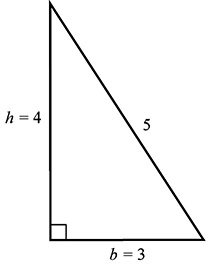
It is good news that you will see mostly right triangles on your exams, because you can figure out the perimeter and area of these triangles much more easily than with other kinds of triangles. Here are the formulas for area and perimeter of a triangle:
Perimeter: P = s1 + s2 + s3 (just add up all the sides)
Area: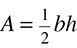 
What is the perimeter of the triangle above? _______
What is the area of the triangle above? _______
(In a later section, we will review a couple ways to calculate the third side of a triangle, because you will usually need to calculate it—it will not be given to you.)
Circles
Circles have no sides, but they do have some measurements you need to review. First, they have 360 degrees total, just like a rectangle or square. They have a center, and the measurement from the center to any part of the outside edge is called the radius. Any radius within one circle is equal to all others. The radius is the most important measurement because if you have it, you can find many other measurements. Double the radius and you get the diameter, the longest measurement across the circle. Multiply the radius by 2π and you get the circumference, which is kind of like a perimeter; it is the measurement around the outside of the circle. Square the radius and multiply it by π (pi), and you get the area of the circle.
Here are the formulas for diameter, circumference, and area of a circle.
Diameter of a circle: d = 2r
Circumference of a circle: C = 2πr
Area of a circle: A = πr2
What is π again? It is a Greek letter that stands in for 22/7, or 3.14. It just turns out that this measurement figures in to both the circumference and the area of circles, no matter how big or small the circle is. Do not worry, you will not have to deal with π much. You can think of it like any other variable because it follows the same rules.
What is the diameter of this circle? _______
What is the circumference of this circle? _______
What is the area of this circle? _______
Basic Geometric Shapes Quick-Fact Sheet
Before going on to the drill, take a few moments to review this quick-fact sheet about basic geometric shapes. If you’re having trouble remembering any of this information, it’s time to make flash cards, because you don’t want to waste time trying to recall it during the test. Also, if you had trouble figuring out any of the above measurements, the solutions to the drill are more step-by-step.
• Angle measure of a straight line: 180 degrees
• Angle measure of a right angle: 90 degrees
• A word that describes two lines that meet at a right angle: perpendicular
• A word that describes two lines on the same plane that never touch: parallel
• Total degree measure in a rectangle: 360 degrees
• Formula for perimeter of a rectangle: P = 2l + 2w
• Formula for area of a rectangle: A = lw
• Total degree measure in a square: 360 degrees
• Formula for perimeter of a square: P = 4s
• Formula for area of a square: A = s2
• Only difference between rectangles and squares: All sides are equal in a square.
• Total degree measure in a triangle: 180 degrees
• Formula for perimeter of a triangle: P = s1 + s2 + s3
• Formula for area of a triangle: A =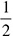 
bh
• Total degree measure in a circle: 360 degrees
• Formula for diameter of a circle: d = 2r
• Formula for circumference of a circle: C = 2πr
• Formula for area of a circle: A = πr2
Ready for the answers to the questions in this section? Here they are:
Now it is time for some practice. Solutions are at the end of the chapter.
DRILL: RECTANGLES, SQUARES, TRIANGLES, AND CIRCLES
1. What is the circumference of the above circle?
(A) 8 in
(B) 16 in
(C) 8π in
(D) 16π in
2. What is the perimeter of the previous rectangle?
(A) 9 ft
(B) 18 ft
(C) 20 ft
(D) 22 ft
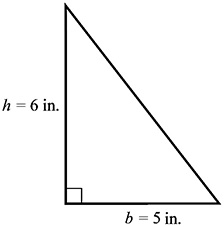
3. What is the area of the above triangle?
(A) 11 in2
(B) 15 in2
(C) 17 in2
(D) 30 in2
4. What is the area of the above square?
(A) 7cm2
(B) 14cm2
(C) 28cm2
(D) 49cm2
Now that you have covered the basic geometric shapes, let’s review a few other geometry topics that tend to come up on nursing school entrance exams.
Calculating Hypotenuse and Diagonals
These questions tend to be phrased two different ways: Either you are asked to calculate the diagonal of a rectangle (which is the line from one corner to the opposite corner), or you are asked to calculate the hypotenuse of a right triangle (which is the longest line in a right triangle—the one across from the 90-degree angle). The trick is, they are actually the same thing. See?
By the way, there are two diagonals in a rectangle, one connecting each pair of opposite angles, but they always have the same length, so it does not matter which one you calculate.
There are two ways to calculate the diagonal/hypotenuse. One is called the Pythagorean theorem, which is a fancy term you may have heard of in school before but probably do not remember. Not to worry; the Pythagorean theorem says that the two legs of the triangle (or the two sides of the rectangle) are a and b, and the diagonal/hypotenuse is c. The formula is:
a2 + b2 = c2
If you know your squares from the Exponents section and you are comfortable working with roots, this gets quite a bit easier than it would be otherwise.
Let’s try some examples.
What is the length of a diagonal of a rectangle with sides 4 and 6?
The problem tells you that a = 4 and b = 6, so it is good to write that out or even draw a rectangle and label the sides. That serves as a quick resource in case you need to go back and rework the problem. (It does not really matter whether you draw things to scale, as long as you are using a somewhat realistic figure.) Now let’s plug your numbers into the Pythagorean theorem:
42 + 62 = c2
Now it’s just a matter of solving for c.
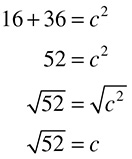
Now simplify the root.
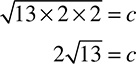
Try another one:
What is the length of the hypotenuse of a right triangle with sides of length 3 and 5?
Remember to draw your triangle and jot down your measurements:
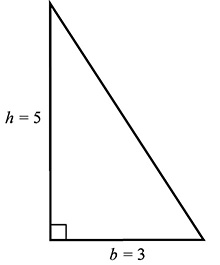
Now you plug the numbers into the Pythagorean theorem and solve:
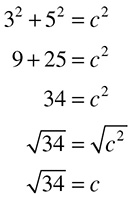
In this case, that is as far as you can go; the prime factors of 34 are 2 and 17, neither of which has a partner.
Now here is a twist: The problem could give you the length of one side and the hypotenuse/diagonal, and ask you to figure out the length of the other side. Take a moment to think about how that would make the equation look.
Okay, try it:
Find the length of the base of a triangle that has a height of 4 and hypotenuse of 5.
This time the problem gives you a (or b; it really doesn’t matter which one you choose as the base and which one you choose as the height) and c, the hypotenuse. You would draw:
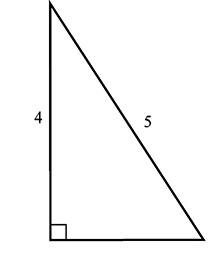
Your equation looks like this:
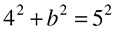
Solve!
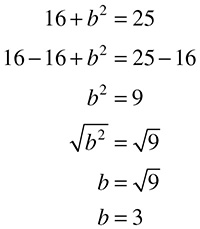
The following drill has two of the three measurements filled in for you; your job is to find the third. Remember to draw the appropriate shape, label it, and fill the numbers you know into the equation.
DRILL: CALCULATING HYPOTENUSE AND DIAGONALS
1. a = 6, b = 3, c = ?
2. a = 4, b = 7, c = ?
3. a = 4, b = ?, c = 8
4. a = ?, b = 5, c = 6
Pythagorean Shortcuts
If you did not love doing all that math, it is time to pull out your flash cards again. Did you notice how, when you found a diagonal/hypotenuse, it ended up as a noninteger? Well, there are a few sets of sides that show up often on standardized tests, probably because they are all integers and therefore easier to calculate. If you memorize them, you will often save yourself from having to use any math at all! Here are the sides to memorize:
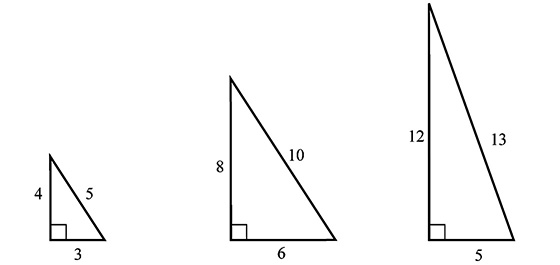
Notice that it matters which lengths are designated as a and b (the sides), and which one is c (the diagonal/hypotenuse). If you are given two sides of length 3 and 5, the hypotenuse is not going to be 4 (it is going to be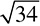 
, as you saw in an earlier problem). A good way to check yourself on this is once you have done the math, make sure that your hypotenuse is always longer than the other two sides.
By the way, did you notice that 3, 4, and 5 is really the same as 6, 8, and 10? You just multiply each side by 2 to get the second triangle. That is the way it works with Pythagorean shortcuts; any multiple of one of these triangles is another Pythagorean shortcut, so 60, 80, and 100 is also a Pythagorean shortcut; so is 50, 120, and 130.
More about Circles
You may need to use your knowledge of circles to solve questions about pie charts. Pie charts are circles, and like all circles, they have 360 degrees. They are usually divided into “slices,” with the size of each slice dependent on what percent of the whole the slice represents. Each slice has a certain degree measure, based on that percentage. Some questions ask you to calculate how many degrees a certain slice encompasses (although the questions may refer to a slice as a “central angle” instead). For example:
If a family’s monthly expenses are shown in a pie chart and their mortgage encompasses 40 percent of their monthly expenses, how many degrees is the central angle representing their mortgage payment?
To solve this question, just take the percentage that the slice represents and multiply it by 360.
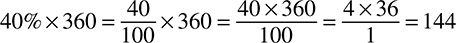
As a quick point of reference, if you want to be able quickly to estimate the answer, here is a guide to memorize:
5% of 360 = 18
10% of 360 = 36
25% of 360 = 90
50% of 360 = 180
75% of 360 = 270
DRILL: MORE ABOUT CIRCLES
1. What is the measure of a central angle encompassing 90 percent of a pie chart?
2. What is the measure of a central angle encompassing 15 percent of a pie chart?
Coordinate Geometry
To give yourself an extra edge, you need to be familiar with at least the basics of coordinate geometry. First, you should learn to plot points on the coordinate plane.
POINTS
Each point on the coordinate plane has two coordinates: one that tells how far up or down the point is, and one that tells how far left or right the point is. The two coordinates are known as x and y, after the axes they relate to. (See how each axis is labeled on the coordinate plane diagram?) The x-coordinate tells you how far the point is to the left or right, and the y-coordinate tells you how far the point is up or down. The two coordinates are always written in this order: (x, y).
The x-axis has positive numbers on the right and negative numbers on the left, just like a number line. The y-axis is like a number line turned on its side, with positive numbers going up and negative numbers going down. To plot the point (2, −3), you would start where the axes cross; this is also known as the origin, or (0, 0), and count two units to the right, then three units down—like this:
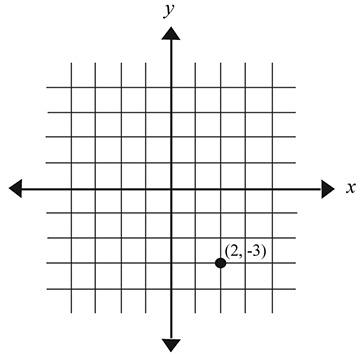
Now you try. Using the above coordinate plane, plot each of the following points. Solutions are at the end of the chapter.
DRILL: PLOTTING POINTS
1. (1, −4)
2. (4, 2)
3. (−3, −2)
4. (0, −3)
5. (2, 4)
6. (−3, 3)
Of course, points are not the only things that can be plotted on a coordinate plane. Lots of other shapes and figures can be plotted, including circles, rectangles, ellipses, parabolas, and so on. For nursing school admission exams, we are only going to discuss points and lines.
LINES
Lines are basically what you would think of when you think of the word “line”; they are straight and connect any two points on the plane, and they go on forever in either direction. To be able to draw a line on the coordinate plane, you basically need to know two things: where it is and what direction it is pointed. “What direction it is pointed” is known more formally as slope.
There are several ways to figure out slope. The first is called the rise-over-run method. This method is helpful if there is a picture on which you can see the coordinates for two points. Starting at one point, you just count how many units up or down to the other point (the rise) and write it down as the top of your fraction. (Remember: up means positive, and down means negative.) Then count how many units left or right to get to the other point (again: left is negative, and right is positive). Write that down as the bottom of your fraction. Now you have 
.
Step 1: Picture a right triangle forming part of the line. Measure the base and height.
Step 2: Set the rise (height) over the run (base). If the line is going down from left to right, the slope is negative. In other words, it falls rather than rises.
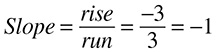
SLOPE FORMULA
If you know any two points on the line, you can figure out the slope even without a picture. The formula to use is:
Now, do not let the subscripts throw you off; the only reason they are important is to remind you that the first number in both the numerator and the denominator belong to one point, whereas the second number in both the numerator and the denominator belong to the other point. Make sure you do not get them mixed up when filling in the formula with the numbers you know.
Try this a couple of times. Let’s say you have two points on a line, (2, 4) and (0, 5), and you want to find the slope. Take one point and plug it in to the formula in its appropriate place:
Then take the other point and plug it in:
Then solve:
The slope is 
.
Try one more: The points are (4, 6) and (−2, −3). Plug in one point:
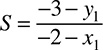
Then another:
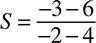
Solve:
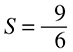
The slope is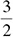 
.
Here are a few for practice on your own. Solutions are at the end of the chapter.
DRILL: SLOPE FORMULA
1. (0, 1) and (2, 3)
2. (3, 2) and (−4, −2)
3. (4, 5) and (2, −1)
4. (−2, 3) and (4, 0)
SLOPE-INTERCEPT FORMULA
Another formula you may see on some exams is the slope-intercept formula. It follows this format:
y = mx + b
Luckily, you will not have to do a lot of manipulation, but you do need to know what the parts stand for. The m in the formula stands for the slope, like the ones you just found in the last drill. The b stands for the point at which the line crosses the y-axis. Of course, you just learned that all points have two coordinates, an x and a y. How come this point only has b? Because b is the y-coordinate and the x-coordinate is always 0; you know that because it is directly on the y-axis.
That leaves x and y, which are the coordinates of any other point on the line. Here is a sample problem:
Which of the following equations represents the line drawn in the coordinate plane on the previous page?
(A) y = 2x + 3
(B)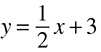 
(C) y = −2x + 2
(D)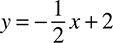 
One of the easiest things in the equation to determine just by looking at the chart is the y-intercept, or where the line crosses the y-axis. In this case, the line crosses at 2, so you can eliminate answer choices A and B without even looking at them further.
A quick 
on any two points on the line shows that the slope is−2, so the correct answer must be choice C.
BALLPARKING
Want to be even faster at estimating slope? It is also handy to know a bit about ballparking so that you can check yourself and make sure you did not forget a negative sign or something when you calculated slope. Here are the ballparking basics:
• A positive slope will always point up and to the right.
• A negative slope will always point down and to the right.
• A slope of 0 runs parallel to the x-axis.
To become even more advanced:
• A slope of 1 makes a 45-degree angle, pointing up.
• The greater the slope, the more the line points up.
• A line that is parallel to the y-axis has no slope, and it will not be tested on the exams.
Do you want to become a ballparking whiz? Here are some good ranges to know:
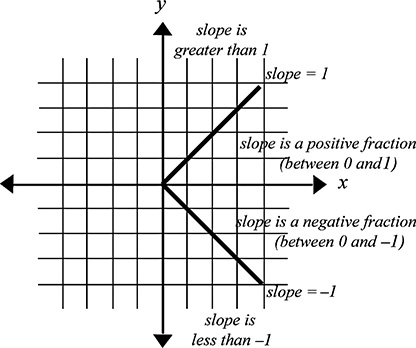
SPATIAL RELATIONS
This final section is for questions that are not quite geometry but do deal with shapes. Spatial relations questions ask you to draw a relationship between two shapes. Given a third shape, you are to choose a fourth shape that best completes the same relationship. Sometimes, the correct answer does not complete the relationship in entirely the same way; however, your job is to choose the one that fits better than the rest.
Here is an example:
On spatial relation questions, start by describing what happened to turn the first shape into the second shape. In this case, it might be, “The shape got smaller.” Then go to the third shape and apply the same to it. In this case, when the third shape gets smaller, the closest fit for it is answer choice A. It is not a perfect completion of the relationship, but clearly choices B, C, and D are worse.
Try another one:
In this problem, the shape stays pretty much the same but a circle is added inside it. Choice D is pretty much the same thing; there is not much room for interpretation on this one.
Now try a couple on your own. Answers are at the end of the chapter.
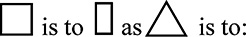
Congratulations, you have worked through the math you need to prepare for your nursing school entrance exams! The fun is not over yet; there are two Mathematical Ability practice tests in Chapter 10 of this book to provide further practice. We recommend taking one, then going back and studying any area that you need to brush up on further before taking the second one.
Good luck!
SOLUTIONS
Addition, Subtraction, Multiplication, and Division
1. 1,473 + 582 = 2,055
2. 5,391 + 6,729 = 12,120
3. 12,843 + 5,928 = 18,771
4. 3,609 − 1,727 = 1,882
5. 2,381 − 963 = 1,418
6. 768 − 529 = 239
7. 408 × 52 = 21,216
8. 823 × 7 = 5,761
9. 521 × 47 = 24,487
10. 709 ÷ 4 = 177 r1 or 177.25
11. 341 ÷ 3 = 113 r2 or 113.67
12. 672 ÷ 16 = 42
Factors
1. 18: 1, 2, 3, 6, 9, 18
2. 27: 1, 3, 9, 27
3. 30: 1, 2, 3, 5, 6, 10, 15, 30
4. 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
5. 42: 1, 2, 3, 6, 7, 14, 21, 42
6. 45: 1, 3, 5, 9, 15, 45
Order of Operations
1. 3 + 2 × 4 = 11. Multiply 2 and 4, and then add 3.
2. (10 − 4) ÷ 3 = 2. Subtract 4 from 10 first because these numbers are inside parentheses, and then divide by 3.
3. 4 × 3 − 5 = 7. Multiply 4 and 3, and then subtract 5.
4. 15 − 8 ÷ 2 = 11. Divide 8 by 2, and then subtract the result from 15.
5. (9 + 2) × 2 = 22. Add 9 and 2 first because these numbers are inside parentheses, and then multiply the result by 2.
6. 3 × 4 ÷ 2 + 5 = 11. Multiply 3 and 4, then divide by 2, and then add 5.
Prime Numbers
1. 17: Prime
2. 23: Prime
3. 39: Not prime—3, 13
4. 45: Not prime—3, 5, 9, 15
5. 54: Not prime—2, 3, 6, 9, 18, 27
6. 67: Prime
Prime Factors
1. 36: 2, 2, 3, 3
2. 42: 2, 3, 7
3. 45: 3, 3, 5
4. 92: 2, 2, 23
5. 81: 3, 3, 3, 3
6. 75: 3, 5, 5
Exponents 1
1. 35 = 3 × 3 × 3 × 3 × 3
2. 43 = 4 × 4 × 4
3. 23 = 2 × 2 × 2
4. 6 × 6 × 6 × 6 = 64
5. 3 × 3 = 32
6. 8 × 8 × 8 × 8 = 84
Exponents 2
1. 32 × 33 = 35
2. 45 × 55 cannot be combined.
3. 27 ÷ 23 = 24
4. x8 ÷ x3 = x5
5. (25)4 = 220
6. (y2)3 = y6
Calculating Roots
1. 
. The prime factors of 125 are 5, 5, and 5.
2. 
. The prime factors of 64 are 2, 2, 2, 2, 2, and 2.
3. 
. The prime factors or 72 are 2, 2, 2, 3, and 3.
4. 
. The prime factors of 147 are 3, 7, and 7.
5. 
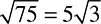. The prime factors of 75 are 3, 5, and 5.
6. 
. The prime factors of 80 are 2, 2, 2, 2, and 5.
Decimals
1. 4.2 + 1.83 = 6.03
2. 0.95 + 1.28 = 2.23
3. 82.4 − 7.93 = 74.47
4. 2.4 − 1.99 = 0.41
5. 0.12 × 0.27 = 0.0324
6. 6.23 × 0.4 = 2.492
7. 1.45 ÷ 0.5 = 2.9
8. 2.06 ÷ 0.4 = 5.15
Reducing Fractions
1. 
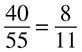
2. 
3. 
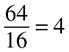
4. 
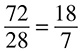
5. 
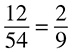
6. 
Adding and Subtracting Fractions
1. 
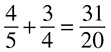
16 + 15 = 31 for the numerator and 5 × 4 = 20 for the denominator makes 
.
2. 
7 + 15 for the numerator and 3 × 7 for the denominator makes 
.
3. 
10 + 27 for the numerator and 9 × 5 for the denominator makes 
.
4. 
35 + 12 for the numerator and 2 × 7 for the denominator makes 
.
5. 
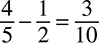
8 − 5 for the numerator and 5 × 2 for the denominator makes 
.
6. 
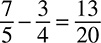
28 − 15 for the numerator and 5 × 4 for the denominator makes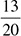 
.
24 − 18 for the numerator and 9 × 3 for the denominator makes 
, which reduces to 
.
8. 
10 − 3 for the numerator and 5 × 3 for the denominator makes 
.
Multiplying and Dividing Fractions
1. 
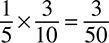
2. 
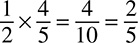
3. 
4. 
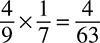
5. 
6. 
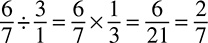
7. 
8. 
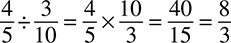
Converting Mixed Numbers to Improper Fractions
1. 
2. 
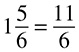
3. 
4. 
5. 
6. 
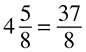
Converting Fractions, Decimals, and Percents
1. 27.5% as a decimal = 0.275
2. 33% as a decimal = 0.33
3. 0.425 as a percent = 42.5%
4. 3.9 as a percent = 390%
5. 
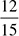as a decimal = 0.8
6. 
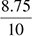as a percent = 87.5%
Calculating Percentages
1. 90
0.75 × 120
75 × 120 = 9,000, then move the decimal two places to the left.
2. 30
0.40 × 75
40 × 75 = 3,000, then move the decimal two places to the left.
3. 72
0.80 × 90
80 × 90 = 7,200, then move the decimal two places to the left. (If you prefer, you can start with 0.8 × 90, calculate 8 × 90 = 720, and move the decimal 1 place to the left. You end up in the same place, and the same is true for question 2 above.)
4. 36
0.45 × 80
45 × 80 = 3,600, then move the decimal two places to the left.
5. 7.5
0.25 × 30
25 × 30 = 750, then move the decimal two places to the left.
6. 104
0.65 × 160
65 × 160 = 10,400, then move the decimal two places to the left.
Translating Word Problems Involving Percents
1. 35
Translation: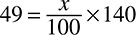 
2. 30
Translation: 
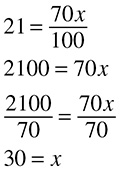
3. 80
Translation: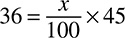 
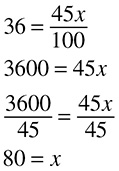
4. 80
Translation: 
5. 50
Translation: 
6. 60
Translation: 
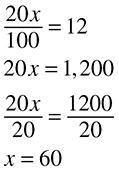
Mean
1. (2 + 6 + 9 + 4 + 14) ÷ 5 = 7
2. (9 + 2 + 5 + 11 + 18) ÷ 5 = 9
3. (7 + 21 + − 5 + 8 + 4) ÷ 5 = 7
4. ( − 2 + 9 + − 5 + 6) ÷ 4 = 2
Median
1. The median of ordered list −2, 2, 3, 5, and 7 is 3.
2. The median of ordered list 2, 3, 4, 7, and 8 is 4.
3. The median of ordered list −3, 1, 5, and 9 is 3 (the mean of 1 and 5).
4. The median of ordered list −5, 2, 2, 3, and 10 is 2.
Mode
1. The mode of ordered list −2, 2, 2, 3, 8, and 10 is 2.
2. The mode of ordered list −5, 0, 3, 3, and 5 is 3.
3. The mode of ordered list −3, −3, −2, 2, 4, and 5 is −3.
4. The mode of ordered list 5, 11, 11, 11, 12, and 12 is 11.
Solving for x
1. x = 2
Translation: 3 + 2x = 7
3 − 3 + 2x = 7 − 3
2x = 4
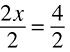
x = 2
2. x = 5
Translation: 3x − 10 = 5
3x − 10 + 10 = 5 + 10
3x = 15
x = 5
3. x = 14
Translation: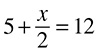 
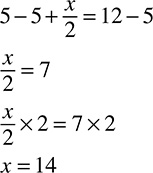
4. x = 3
Translation: 4x + 3 = 15
4x + 3 − 3 = 15 − 3
4x = 12
x = 3
5. x = − 2
Translation: 2x + 8 = 4
2x + 8 − 8 = 4 − 8
2x = − 4
x = − 2
6. x = 10
Translation: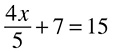 
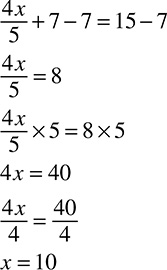
Translating Algebra Word Problems
1. x = 5
Translation: 10 + x = 3x
10 + x − x = 3x − x
10 = 2x
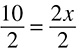
5 = x
2. x = 2
Translation: 5x = x + 8
5x − x = x − x + 8
4x = 8
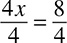
x = 2
3. x = 46
Translation: x = 5 × 10 − 4
x = 50 − 4
x = 46
4. x = 30
Translation: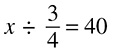 
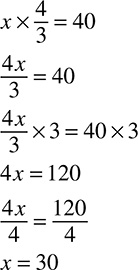
Charts, Graphs, and Tables
1. B If you are starting from about 5,000 and going to about 2,500, that is a decrease of about 2,500, which is a percent decrease of about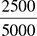 
, or 50%.
2. C The inventory of sharps increased from about 4,000 to about 5,000 during that period, so if 500 were discarded, a total of 1,500 must have been added to replace them and increase the inventory by 1,000.
3. B The list of numbers represented by the diagram is 10, 14, 14, 15, 22, 23, 25, 26, 27, 29, 43, 45, and 48. The number 14 is the only one that appears more than once; therefore, it must be the mode.
4. C The number 10 is the smallest number represented and 48 is the largest; 48 − 10 = 38.
Proportions and Ratios
1. 50.
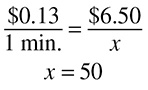
2. 12.
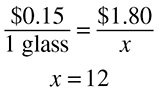
3. $1.25.
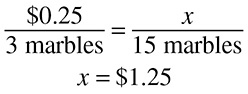
4. 32.
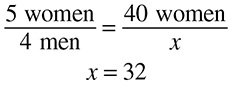
Unit Conversions
1. 25°C
The process for converting to Celsius is to subtract 32, then multiply by 
.
77 − 32 = 45, and 
.
2. 32,000
There are 1,000 millimeters in one meter, so 32 meters would have 32,000 millimeters.
3. About 4
Because a liter is a little less than a quart and there are 4 quarts in a gallon, 4 will probably be a close enough answer. If there are two answer choices that are close, you would want to pick the one that is more than 4, because a liter is smaller than a quart and therefore more of them can fit in a gallon.
4. 80
There are 16 ounces in a pound; therefore, there are 80 ounces in 5 pounds.
5. XLVIII
48 in Roman numerals becomes XL (50 – 10) + VIII (8).
6. 1825
6:25 PM is 1825 in military time.
Applied Math
1. 1,050
The patient is taking 150mg per day over 7 days, so you need to multiply to get the total amount taken during that period; 150 × 7 = 1,050.
2. 
.
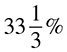Because the problem asks “by what percent” a change is made, you are dealing with percent change. The original is 45, and a drop to 30 would represent a difference of 15; this would make the fraction
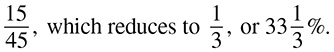
3. 50
It may help to draw this one out if you are having trouble visualizing it. Twenty can fit into the 100-ft side five times and into the 200-ft side ten times. When you multiply 5 × 10, you get 50.
4. 200
This is essentially a proportions problem. There are four quarts in a gallon, and the question is asking how many quarts there are in 50 gallons.
. Cross-multiply and solve, and you get 200.
5. $26,250
This problem is asking you to calculate a certain percentage of 25,000. The two percentages total up to 5%, and 5% of 25,000 is 1,250. Add this to 25,000 and you get 26,250.
To complete this problem, you need to add up the fractions. You can do this by using the bowtie method on individual fractions or by combining fractions using any shortcuts you can find. For example,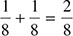 
, which reduces to 
. Then, 
, which equals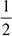 
. You can bowtie with 
to get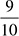 
. If 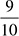is spent on other expenses and the rest is saved, then 
is saved.
Rectangles, Squares, Triangles, and Circles
1. C The radius of the circle is 4 in. When you plug that into the formula for circumference, you get C = 2π (4) or C = 8(π).
2. B The formula for perimeter of a rectangle is P = 2l + 2w. When you plug in the values from the picture, you get P = (2 × 4) + (2 × 5), which equals 18. Be careful to calculate perimeter, not area!
3. B The formula for area of a triangle is 
, and when you plug in the base of 5, and the height of 6, you get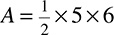 
, which equals 15.
4. D Each side of the square is 7cm, so you just need to square that to get a value of 49cm2.
Calculating Hypotenuse and Diagonals
1. 
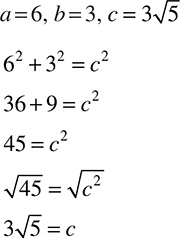
2. 
3. 
4. 
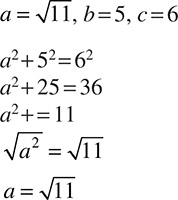
More about Circles
1. 324
90% of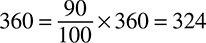 
2. 54
15% of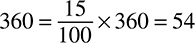 
Plotting Points
Slope Formula
1. (0, 1) and (2, 3) create a line with a slope of 1.
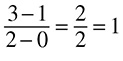
2. (3, 2) and ( − 4, − 2) create a line with a slope of 
.
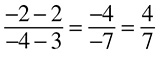
3. (4, 5) and (2, − 1) create a line with a slope of 3.
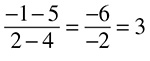
4. ( − 2, 3) and (4, 0) create a line with a slope of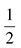 
.
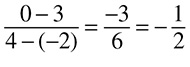
Spatial Relations
1. In the first pair, one of the shapes grows larger and encompasses one of the other shapes, which turns black. Choice B shows the same relationship. Choice D is incorrect because the parallelogram is not part of the second group.
2. Choice C is the correct answer; in the first pair, the shape halves and choice C is the only answer choice that reproduces this. It may look as if the initial square gets narrower, but because none of the answers correspond to that, you must consider the possibility that it is cut in half instead.