Anhang F. Funktionale Programmierung
Praxistipp
Wie die funktionale Denkweise hilft
Der eine oder andere mag sich vielleicht wundern, was eine solch lange Abhandlung über das funktionale Programmieren in einem Buch über C++11 zu suchen hat. Der Grund ist ganz einfach. Die funktionale Denkweise erlaubt es, die Standard Template Library besser zu nutzen. Der Schlüssel zu diesem Umgang mit C++ auf höherer Ebene sind die funktionalen Ideen, für die nicht nur die C++-Community sehr empfangsbereit ist. Insofern verfolgt dieses Unterkapitel zwei Ziele: zum einen die funktionale Denkweise und zum anderen, den effizienten Umgang mit der STL vorzustellen.
C++11 ist eine Multiparadigmen-Programmiersprache. Neben der objektorientierten, der strukturierten, der generischen und der generativen (Template-Metaprogramming) Programmierung tritt ein Paradigma immer mehr in den Vordergrund: die funktionale Programmierung. Zwar ist C++11 keine funktionale Programmiersprache im engeren Sinn, doch sie unterstützt das Programmieren im funktionalen Stil. Diese Aussage trifft nur auf das klassische C++ zu. Template-Metaprogramming, bei dem zur Übersetzungszeit der resultierende Code erzeugt wird, ist eine eingebettete, rein funktionale Subsprache in der imperativen Programmiersprache C++. Der Begriff der funktionalen Programmierung ist erfahrungsgemäß schwierig zu fassen, daher werde ich die Charakteristiken funktionaler Programmierung vorstellen und mit Leben füllen. Es wird spannend, denn für einige Beispiele muss ich Anleihen aus der rein funktionalen Programmiersprachen Haskell verwenden.
Programmieren mit mathematischen Funktionen
Funktionale Programmierung lässt sich in einem Satz kurz und bündig definieren.
Diese so unscheinbar wirkende Aussage besitzt mächtige Implikationen. Zuallererst sind mathematische Funktionen Funktionen, die bei gleichen Argumenten immer das gleiche Ergebnis liefern. Das ist ein gefundenes Fressen für den Optimierer, da er für den Funktionsaufruf sein Ergebnis verwenden kann. Natürlich ist er auch frei, die Reihenfolge der Funktionsaufrufe umzustellen oder in einen anderen Thread zu verschieben, denn es gibt keinen gemeinsamen Zustand zu respektieren. Der Programmfluss in der funktionalen Programmierung wird nicht wie in der imperativen Programmierung durch die Sequenz der Anweisungen, sondern durch deren Datenabhängigkeiten vorgegeben. Ein Funktionsaufruf verhält sich wie eine Abfrage in einer unendlich großen Tabelle. Die Eigenschaft mathematischer Funktionen, einen Ausdruck durch seinen Wert zu ersetzen, ist unter dem Begriff »Referenzielle Transparenz« (Referenzielle_Transparenz, 2011) bekannt. Die Definition der funktionalen Programmierung über mathematische Funktionen ist zwar leicht einzuprägen, sie hilft aber nicht wirklich weiter. Das wird sich gleich ändern.
Charakteristiken funktionaler Programmierung
Bevor die Charakteristiken der funktionalen Programmierung im Detail besprochen werden, will ich sie kurz nennen:
First-class functions
First-class functions sind Daten sehr ähnlich. Diese Funktionen können zur Laufzeit erzeugt, in Variablen gespeichert oder als Ein- oder Rückgabewert einer Funktion verwendet werden. Ein bekanntes Beispiel für die Mächtigkeit von first-class functions sind Dispatch Tables. Eine Dispatch Table ist eine beliebte Technik, eine aufrufbare Einheit hinter einem Schlüssel zu verstecken. Diese aufrufbaren Einheiten können Funktionszeiger, Funktionsobjekte oder auch Lambda-Funktionen sein. In Listing F.1 wird mithilfe einer Dispatch Table eine einfache Rechenmaschine implementiert.
dispatchTable.cpp
01 #include <cmath>
02 #include <functional>
03 #include <iostream>
04 #include <map>
05
06 int main(){
07
08 std::cout << std::endl;
09
10 // dispatch table
11 std::map< const char ,
std::function<double(double,double)>> dispTable;
12 dispTable.insert( std::make_pair('+',
[](double a, double b, { return a + b;}));
13 dispTable.insert( std::make_pair('-',
[](double a, double b){ return a - b;}));
14 dispTable.insert( std::make_pair('*',
[](double a, double b){ return a * b;}));
15 dispTable.insert( std::make_pair('/',
[](double a, double b){ return a / b;}));
16
17 // do the math
18 std::cout << "3.5+4.5= " << dispTable['+'](3.5,4.5)
<< std::endl;
19 std::cout << "3.5-4.5= " << dispTable['-'](3.5,4.5)
<< std::endl;
20 std::cout << "3.5*4.5= " << dispTable['*'](3.5,4.5)
<< std::endl;
21 std::cout << "3.5/4.5= " << dispTable['/'](3.5,4.5)
<< std::endl;
22
23 // add a new operation
24 dispTable.insert( std::make_pair('^',
[](double a, double b){ return std::pow(a,b);}));
25 std::cout << "3.5^4.5= " << dispTable['^'](3.5,4.5)
<< std::endl;
26
27 std::cout << std::endl;
28
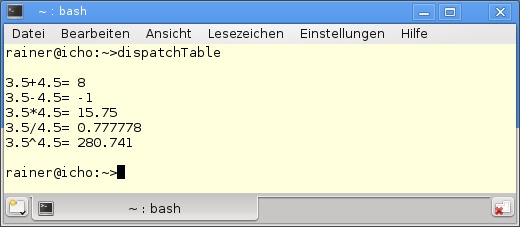
29 };Beeindruckt? Abbildung F.1 zeigt das Ergebnis des Programms dispatchTable.cpp in Listing F.1. Die zentrale Datenstruktur für die Dispatch Table ist die std::map dispTable in Zeile 11. Als Schlüssel wird ein const char, als Wert ein Funktionsobjekt std::function<double(double,double)> verwendet. Dieses Funktionsobjekt nimmt die Lambda-Funktionen, die in den Zeilen 12 bis 15 folgen, an. Um std::function zu verwenden, muss der Header functional in Zeile 2 eingebunden werden. Die Anwendung der Arithmetik ist denkbar einfach. Als Schlüssel wird in den Zeilen 18 bis 21 das arithmetische Zeichen verwendet. Die std::map gibt das Funktionsobjekt zurück, in das die Argumente 3.5 und 4.5 eingesetzt werden. Natürlich lässt sich auch nachträglich eine weitere Lambda-Funktion registrieren. Dabei kommt die Funktion std::pow in Zeile 25 zum Einsatz. Die Direktheit einer Interpreter-Sprache kombiniert mit der statischen Typsicherheit von C++: das erlaubt std::function in Zusammenarbeit mit Lambda-Funktionen.
Funktionen höherer Ordnung
Funktionen, die entweder Funktionen als Argument annehmen oder als Ergebnis zurückgeben können, werden Funktionen höherer Ordnung genannt. Die Klassiker aus der funktionalen Programmierung sind die drei Funktionen map, filter und fold. Diese drei Funktionen höherer Ordnung werden über eine Funktion parametrisiert und wenden diese sukzessive auf die Elemente einer Liste an. Für diese Funktionen kommen gern Lambda-Funktionen zum Einsatz, da sie die Funktionalität an Ort und Stelle anbieten.
map: Wendet eine Funktion auf jedes Element einer Liste an.
filter: Filtert Elemente aus einer Liste heraus.
fold: Reduziert sukzessive eine Liste auf einen Ausgabewert, indem eine binäre Operation auf ein Element der Liste und das vorherige Ergebnis der Operation auf die Liste angewandt wird.
Die Strategie der Funktion fold ist erfahrungsgemäß am schwierigsten zu verstehen. Exemplarisch ist std::accumulate(vec.begin(), vec.end(),0) in Abbildung F.2 dargestellt, das sukzessive Paare des Vektors vec zusammenaddiert, bis der Vektor auf ein Ergebnis reduziert ist. std::accumulate ist die C++-Implementierung des fold-Algorithmus und wendet im Standardfall (+) als Operation an. Der Einfachheit halber werde ich den Vektor std::vector<int> myVec{1,2,3,4,5} durch <1,2,3,4,5> darstellen.
Wird nun in std:::accumulate als viertes optionales Template-Argument eine andere Operation verwendet, findet diese anstelle von (+) statt.
Dabei beziehen sich die drei Funktionsnamen auf die funktionale Programmiersprache Haskell.
Diese drei Operationen repräsentieren die Verarbeitung von Listen in so typischer Weise, dass eine Programmiersprache sie anbieten wird, die das Programmieren im funktionalen Stil unterstützt. Die Namen können natürlich variieren. In der Tabelle F.1 sind die Varianten der drei Funktionen map, filter und fold* in Haskell, Python und C++ gegenübergestellt.
Haskell | Python | C++ |
|
|
|
|
|
|
|
|
|
Die Algorithmen aus Tabelle F.1 können auf die Container der Standard Template Library angewandt werden. Kombiniert mit den neuen Lambda-Funktionen, lässt sich beeindruckend kompakt in C++11 programmieren (Listing F.2).
higherOrder.cpp
01 #include <algorithm>
02 #include <cassert>
03 #include <iostream>
04 #include <list>
05 #include <string>
06 #include <vector>
07
08 template<typename InputIter>
09 std::string join(InputIter begin, InputIter end,
std::string sep) {
10
11 // Container must be not empty
12 assert( begin != end);
13 return std::accumulate(++begin,end,
*begin,
[sep](std::string a, std::string b)
{ return a + sep + b;});
14
15 }
16
17 int main(){
18
19 std::cout << std::endl;
20
21 std::list<std::string> myList
{"Programming","in","C++11","in","a",
"functional","style."};
22
23 // starting with 10
24 std::vector<int> myVec(20);
25 std::iota(myVec.begin(),myVec.end(),10);
26
27 std::cout << "myVec: ";
28 for (auto i: myVec) std::cout << i << " ";
29 std::cout << std::endl;
30 std::cout << "myList: ";
31 for (auto i: myList) std::cout << i << " ";
32
33 std::cout << "\n\n" << "std::transform" << std::endl;
34
35 // i -> i*i
36 std::transform(myVec.begin(),myVec.end(),
myVec.begin(),[](int i){ return i*i; });
37 std::cout << " myVec: ";
38 for (auto i: myVec) std::cout << i << " ";
39
40
41 // string -> (string,string.length())
42 std::vector<std::pair<std::string,int>> listLength;
43 std::transform(myList.begin(),myList.end(),
std::back_inserter(listLength),
[](std::string s){return std::make_pair(s,s.length());});
44 std::cout << std::endl << " ";
45 for (auto i: listLength) std::cout << "(" << i.first
<< "," << i.second << ") ";
46
47 std::cout << "\n\n"
<< "std::remove_if and std::remove_copy_if"
<< std::endl;
48
49 auto it= std::remove_if(myVec.begin(),
myVec.end(),
[](int i){ return (i < 200) or( i > 500); });
50 myVec.erase(it,myVec.end());
51 std::cout << " myVec: ";
52 for (auto i: myVec) std::cout << i << " ";
53 std::cout << std::endl;
54
55 std::string myString
{"Programming in C++11 in a functional style."};
56 std::string lowerChars;
57
58 // lower -> lowerChars
59 std::remove_copy_if(myString.begin(),myString.end(),
std::back_inserter(lowerChars),
[](char c){ return std::isupper(c);});
60
61 std::cout << " lowerChars: " << lowerChars
<< std::endl;
62
63 std::cout << "\n" << "std::accumulate" << std::endl;
64
65 // mean of myVec
66 double sum= static_cast<double>(std::accumulate(myVec.begin(),myVec.end(),
0,
[](int a, int b){ return a+b;}));
67 std::cout << " mean of myVec: " << sum/myVec.size()
<< std::endl;
68
69 // join the strings with ":"
70 std::string myListJoin=
std::accumulate(myList.begin(),myList.end(),
std::string(""),
[](std::string a, std::string b){ return a + ":" + b;});
71
72 std::cout << " joined myList:" << myListJoin
<< std::endl;
73
74 std::cout << std::endl;
75
76 std::cout << join(myList.begin(),myList.end(),"#");
77
78 std::cout << std::endl;
79
80 std::cout << join(myList.begin(),myList.end()," => ");
81
82 std::vector<std::string>
myVec2(myList.begin(),myList.end());
83
84 std::cout << std::endl;
85
86 std::cout << join(myVec2.rbegin(),myVec2.rend()," <= ");
87
88 std::cout << std::endl << std::endl;
89
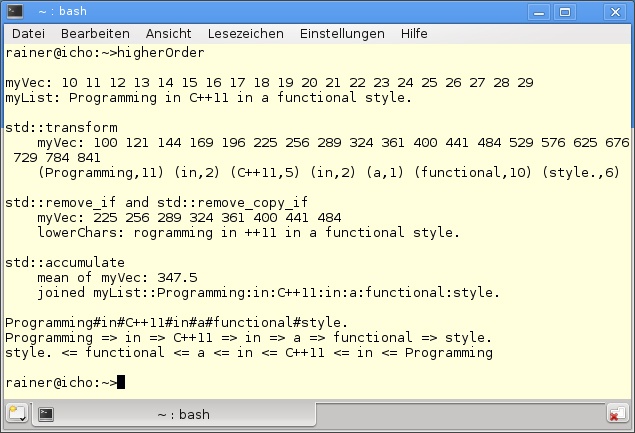
90 }Das Verhalten lässt sich am leichtesten in Abbildung F.3 nachvollziehen. Zuerst werden die Container vorbereitet. In Zeile 21 wird eine Liste über Strings, in Zeile 25 ein Vektor über natürliche Zahlen initialisiert und ausgegeben. Das Spiel kann beginnen. Der Aufruf von std::transform in Zeile 36 überschreibt jeden Wert des Vektors mit seinem Quadrat. Dabei wird durch das dritte Argument des Algorithmus (std::vector<int>begin()) der Ausgabe-Iterator und durch das letzte Argument ([](int i){ return i*i;}) die verarbeitende Funktion angegeben. Wird, wie in Zeile 43, als Ausgabe-Iterator ein Iterator auf einen anderen Container spezifiziert, bleibt der ursprüngliche Container unverändert. In der Lambda-Funktion wird der std::string s auf ein Paar (s,s.length()) und anschließend auf listLength geschoben. Das Paar (s,s.length()) ist in Abbildung F.3 dargestellt. Auf die Transformation folgt das Filtern. std::remove_if in Zeile 49 filtert alle Elemente aus myVec heraus, die kleiner als 200 oder größer als 500 sind. Da dieser Algorithmus als Ergebnis einen Iterator auf das neue logische Ende von myVec zurückgibt, werden die überflüssigen Elemente mit der erase-Funktion entfernt. Dieses bekannte C++-Idiom, zuerst das logische Ende mit std::remove_if zu bestimmen und im zweiten Schritt die Elemente tatsächlich zu löschen, wird gern in einem Ausdruck geschrieben:
myVec.erase(std::remove_if(... ,myVec.end())
std::string ist auch ein Container. Daher lässt sich std::remove_copy_if in Zeile 59 anwenden, um alle kleinen Buchstaben auf den std::string lowerChars zu schieben und auszugeben. Entspricht std::transform der map-, std::remove der filter-Funktion, gilt es noch, die fold-Funktion in C++ darzustellen. Dies ist die Aufgabe von std::accumulate. Zeile 66 sieht auf den ersten Blick recht komplex aus. In ihr wird die Summe der verbleibenden Zahlen aus myVec berechnet und in der nächsten Zeile, durch dessen Länge geteilt, als Mittelwert ausgegeben. std::accumulate iteriert durch den ganzen Eingabebereich (myVec.begin,myVec.end()) und addiert die Paare ([](int a, int b){ return a+b;}). Dabei ist das dritte Argument 0 der Initialwert der Anhäufung. Um das Fließkommaergebnis nicht irrtümlich als Ganzzahl auszugeben, wird die Summe nach double konvertiert. Die gleiche Verarbeitungslogik, auf myList in Zeile 70 angewandt, verbindet die Elemente der Liste mit einem Doppelpunkt (:). Der Algorithmus besitzt aber noch einen Bug. Nicht nur zwischen den Strings, sondern vor dem ersten String wird der Trenner (:) ausgegeben.
Eine kleine Funktion verpackt, und schon steht die generische Funktion join in Zeile 8 für Container von Strings zur Verfügung. Die Zusicherung an den Algorithmus ist, dass der Container nicht leer sein darf. Dies wird durch assert (begin != end) sichergestellt. Diese Bedingung muss erfüllt sein, denn der erste String *begin in Zeile 13 wird als Startwert von std::accumulate verwendet. Erst die folgenden Elemente werden durch das Trennzeichen sep verbunden. Dieser kleine Trick bewirkt, dass das Trennzeichen tatsächlich nur als Verbindungsglied der Strings verwendet wird. In den Zeilen 76, 80 und 86 wird join angewendet.
map und filter werden in vielen Programmiersprachen als List Comprehension angeboten. Obwohl genau genommen nur syntactic sugar, vereinfachen sie den Umgang mit Funktionen höherer Ordnung. Als syntactic sugar wird eine alternative Ausdrucksweise bezeichnet, die einfacher zu lesen und zu schreiben ist. C++11 unterstützt kein List Comprehension, sodass ein kleines Beispiel in Python ausreichen muss. Dabei ist List Comprehension so idiomatisch in Python, dass deren funktionale Wurzeln fast vergessen werden.
01 [ i for i in range(1,11) ] 02 [ i*i for i in range(1,11) ] 03 [ i*i for i in range(1,11) if (i%2 != 0) ]
In Zeile 1 werden auf sehr umständliche Weise die Zahlen von 1 bis 10 erzeugt. Dabei wird jede Zahl aus range(1,11) auf i abgebildet und ist somit Element der resultierenden Liste. Interessanter ist da schon Zeile 2, denn hier tritt die map-Funktionalität von List Comprehension in Aktion. Jede Zahl aus range(1,11) wird auf i*i abgebildet. Die gleiche Abbildungsvorschrift wird ebenso im letzten Ausdruck verwendet. Der Unterschied zur vorherigen List Comprehension besteht darin, dass lediglich die Elemente aus range(1,11) verwendet werden, für die gilt: i%2 != 0. Der Filter lässt nur die Elemente passieren, die ungerade sind. Die drei Zeilen lassen sich schnell in der Python Interpreter Shell (Abbildung F.4) ausführen.
Reine Funktionen
Reine Funktionen sind mathematische Funktionen, die noch ein paar weitere Eigenschaften aufweisen. Reine funktionale Programmiersprachen wie Haskell besitzen nur reine Funktionen. Bryan O’Sullivan, Don Stewart und John Goerzen stellen in ihrem online verfügbaren Buch Real World Haskell (O’Sullivan, Stewart, & Goerzen, 2008) reine den unreinen Funktionen gegenüber.
Unreine Funktionen | |
Erzeugen bei gleichen Argumenten immer das gleiche Ergebnis. | Können verschiedene Ergebnisse bei gleichen Argumenten erzeugen. |
Besitzen keine Seiteneffekte. | Können Seiteneffekte besitzen. |
Können den Zustand des Programms nicht verändern. | Können den Zustand des Programms verändern. |
Eine Funktion, die bei gleichen Eingabewerten immer das gleiche Ergebnis produziert, wird auch als mathematische Funktion bezeichnet. Als Seiteneffekt einer Funktion wird ein Effekt bezeichnet, der außerhalb der Funktion zu Veränderungen führt.
Der Vorteil von reinen Funktionen liegt auf der Hand. Das Programmverhalten wird deutlich transparenter und vorhersagbarer. Folgende Vorteile ergeben sich für Programmierer und für Optimierer.
Programmierer:
Funktionen sind in sich abgeschlossen, da sie von keinem globalen Zustand abhängen.
Korrektheitsbeweise sind einfacher durchzuführen.
Refactoring und Testen ist einfacher möglich.
Optimierer:
Zwischenergebnisse von Funktionsaufrufen können gespeichert werden (referenzielle Transparenz).
Die Ausführungsreihenfolge der Funktion kann umgeordnet werden.
Funktionen können in andere Threads oder Prozesse verlagert werden.
Umgang mit Seiteneffekten
Will eine rein funktionale Sprache mit der Außenwelt kommunizieren, muss sie sich für Seiteneffekte öffnen. Die Eingabe von Daten, das Auslesen einer Datei, die zufällige Wahl einer Zahl, all das kann nicht in reinen Funktionen angeboten werden. Haskell beschreitet hier einen besonderen Weg, denn es bindet die imperative Welt der Seiteneffekte in die reine funktionale Sprache in den Monaden ein. Monaden zeichnen sich durch zwei Eigenschaften aus: In ihnen gilt das sequenzielle Ausführen von Anweisungen. Operationen in ihnen sind in sich abgeschlossen und können die Monade nicht verlassen.
Rekursion
Die Kontrollstruktur in der funktionalen Programmierung ist die Rekursion. Der Grund ist ganz einfach. Rein funktionale Programmiersprachen kennen keine Variablen. Schleifen setzen aber Variablen voraus. So wird in for (int i=0; i <=10, ++i) die Variable i verwendet.
Exemplarisch steht in Listing F.4 die Berechnung der Fakultät mit einer Schleife der durch Rekursion gegenüber. Dies ist auch eine Gegenüberstellung der imperativen und der funktionalen Denkweise.
factorial.cpp
01 #include <iostream>
02
03 int factorialLoop(int n){
04 int fac=1;
05 for (int i= 2; i <= n; ++i) fac *= i;
06 return fac;
07 }
08
09 template <int N>
10 struct FactorialRec{
11 static int const value= N * FactorialRec<N-1>::value;
12 };
13
14 template <>
15 struct FactorialRec<1>{
16 static int const value = 1;
17 };
18
19 template <>
20 struct FactorialRec<0>{
21 static int const value = 1;
22 };
23
24 int main(){
25
26 std::cout << std::endl;
27
28 // check at compile time the value
29 static_assert(FactorialRec<5>::value == 120,
"Is not available at compile time.");
30 std::cout << "FactorialRec<5>::value: "
<< FactorialRec<5>::value << std::endl;
31
32 std::cout << "factorialLoop(5): "
<< factorialLoop(5) << std::endl;
33
34 std::cout << std::endl;
35
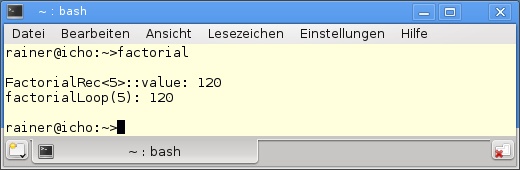
36 }factorialLoop in Listing F.4, Zeile 3 sollte eigentlich vertraut sein. Die Fakultät einer Zahl n wird dadurch berechnet, dass sukzessive die Zahlen von 1 bis n zu der Variablen fac hinzumultipliziert werden. Für das imperative Auge ist die funktionale Variante deutlich schwieriger zu erfassen. Zuerst wird das primäre oder auch allgemeine Template in Zeile 9 definiert. Der Wert der Fakultät N wird auch durch N * Factorial<N-1>::value in Zeile 11 bestimmt. Diese Rekursion benötigt natürlich eine Endbedingung. Hier tritt die Template-Spezialisierung für N == 1 in Zeile 14 in Aktion. Der Wert für die Fakultät von 1 ist per definitionem 1. Für den Spezialfall N == 0 steht die weitere Template-Spezialisierung in Zeile 19 zur Verfügung. Wird nun in Zeile 29 der Wert FactorialRec<5>::value angefordert, wird der Ausdruck in Zeile 11 instanziiert, bis die Endbedingung N == 1 zutrifft. Zur Laufzeit reduziert sich der Ausdruck auf die Konstante 120. Das ist der feine Unterschied zu factorialLoop(5) in Zeile 32. Dieser Wert wird zur Laufzeit evaluiert.
Kritiker mögen entgegenhalten, dass der entscheidende Nachteil der rekursiven Berechnung deren enormer Speicherbedarf ist, da jede Iteration ihren stack frame anlegt. Listing F.4 diente aber nur der Illustration. Funktionale Programmiersprachen sind für die Rekursion optimiert. Ist die letzte Berechnung einer Funktion deren rekursiver Aufruf, kann der Compiler diese Rekursion so optimieren, dass sie konstante Speicherplatzanforderungen besitzt. Rekursive Funktionen, die dieser besonderen Struktur genügen, werden tail recursive (Tail Recursion, 2011) genannt.
Dies ist ein Buch über C++11, daher kann ich eine weitere Variante, die Fakultät einer Zahl zur Übersetzungszeit zu berechnen, nicht unterschlagen. Dies alles ist mit dem neuen und mittlerweile bekannten Feature constexpr (siehe Kapitel 10, Abschnitt „Konstante Ausdrücke“) möglich. In Listing F.5 wird die Fakultät einer Zahl rekursiv mit einer als constexpr deklarierten Funktion berechnet.
01 #include <iostream>
02
03 constexpr long long factorial( long long i ){
04 return (i > 0) ? i * factorial(i - 1) : 1;
05 }
06
07 int main(){
08
09 std::cout << std::endl;
10
11 std::cout << "factorial(10): " << factorial(10)
<< std::endl;
12 std::cout << "factorial(20): " << factorial(20)
<< std::endl;
13
14 static_assert( factorial(5) == 120,
"Not available at compile time.");
15
16 std::cout << std::endl;
17
18 }Abbildung F.6 zeigt das Ergebnis des Programms. Beeindruckt? Die Werte der Fakultät 5, 10 und 20 stehen zur Laufzeit als Konstanten zur Verfügung.
Verarbeitung von Listen
LISt Processing abgekürzt ergibt LISP. Aber nicht nur für die funktionale Programmiersprache LISP, sondern für funktionale Programmiersprachen im Allgemeinen ist das Verarbeiten von Listen ein wichtiges Charakteristikum. Das trifft auf das Transformieren einer Liste in eine neue Liste oder auf die Komposition von Listenoperationen zu (Grimm, Haskell - Kurz und bündig, 2011). Hier soll, der Ästhetik halber, ein einfaches Haskell-Beispiel folgen. Zwar lassen sich mit Template-Metaprogramming und Variadic Templates Algorithmen formulieren, die die Verarbeitungslogik der funktionalen Verarbeitung von Listen mit Containern der STL simulieren, das ist aber nicht idiomatisch in C++11. Für den interessierten Leser ist in einem Artikel im Linux Magazin Template Metaprogramming 01/11 (Grimm, Template Metaprogramming, 2010) eine map-Funktion implementiert, die zur Übersetzungszeit ausgeführt wird.
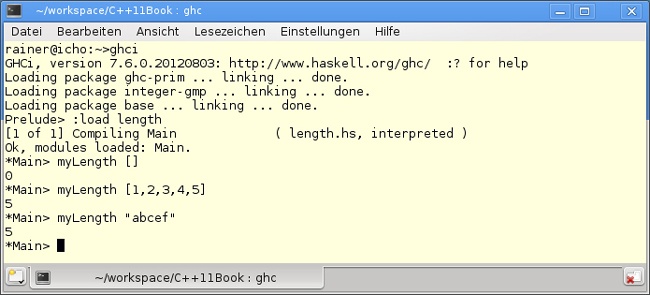
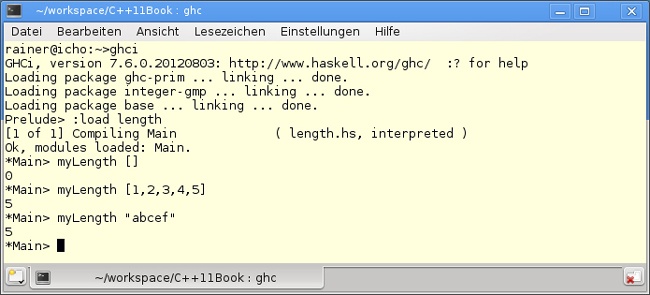
In Listing F.6 wird die Länge einer Liste in Haskell berechnet. Natürlich gibt es für diese einfache Funktion auch Build-in-Funktionen.
length.hs
Die Länge der leeren Liste in Zeile 1 ist per definitionem 0. Die Länge der Liste, die mindestens ein Element besitzt, wird in Zeile 2 rekursiv bestimmt. Sie ist 1 + die Länge der Liste ohne das erste Element. Per Konvention bezeichnet in dem Ausdruck (x:xs) x den Kopf und xs den Rest der Liste. Die Rekursion myLength(xs) wird durch den Spezialfall der leeren Zeile terminiert. Ähnlichkeiten mit der Berechnung der Fakultät in Listing F.4 durch Rekursion sind nicht zufällig. In Abbildung F.7 ist die Anwendung der Funktion in der Haskell-Interpreter-Shell zu sehen. Dabei wird durch den Aufruf :load length der Quellcode geladen und kompiliert.
Bedarfsauswertung
Bedarfsauswertung ist in den meisten Programmiersprachen wohl besser unter dem Begriff Lazy Evaluation bekannt. Der Gegenbegriff zur Lazy Evaluation ist die Eager Evaluation. Während die Bedarfsauswertung den Ausdruck erst bei Nachfrage evaluiert, wertet die strikte Auswertung (Eager Evaluation) den Ausdruck sofort aus. Imperative Programmiersprachen wie Java oder auch C++ kennen nur die strikte Auswertung, sieht man von der Kurzschlussauswertung ab. Funktionale Sprachen wie Haskell verwenden per Default eine Bedarfsauswertung, lassen aber auch die strikte Auswertung zu. Die Vorteile der Bedarfsauswertung liegen auf der Hand:
Ausdrücke werden nur dann evaluiert, wenn sie wirklich benötigt werden. Das spart Zeit und Speicher.
Unendliche Datenstrukturen können formuliert werden, von denen zur Laufzeit nur endlich viele Elemente angefordert werden.
Als Beispiel soll wieder Haskell dienen. Die Funktion successor in Listing F.7 gibt alle Nachfolger des Arguments i aus.
succ.hs
In Abbildung F.8 ist das Listing F.7 in der Anwendung zu sehen. Durch take 5 (successor 10 ) werden die 5 Nachfolger der Zahl 10 angefordert. Dabei ist successor i als die Liste bestehend aus i und dem Nachfolger von i definiert.
Durch den Aufruf successor i wird die ganze, unendliche Liste angefordert. Dieser Prozess lässt sich nur durch (Strg+C) unterbrechen (Abbildung F.9).
In imperativen Programmiersprachen ist die Kurzschlussauswertung (Short Circuit Evaluation) bekannt. Sie ist ein Spezialfall der Bedarfsauswertung. Durch sie werden logische Ausdrücke nur so weit ausgewertet, bis das Ergebnis des Gesamtausdrucks feststeht. Das lässt sich schnell in C++ zeigen.
shortCircuitEvaluation.cpp
01 #include <iostream>
02
03 int main(){
04
05 std::cout << std::endl;
06
07 if ( 1/0 ) std::cout << "(1/0)" << std::endl;
08 if ( true or (1/0) ) std::cout << "(true or 1/0)"
<< std::endl;
09
10 std::cout << std::endl;
11
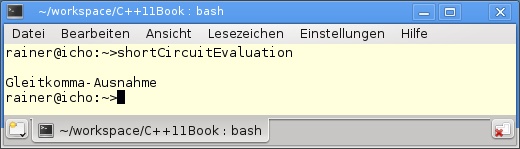
12 }Wird das kleine Programm übersetzt und ausgeführt, führt das zu dem Laufzeitfehler aus Abbildung F.10.
Der Schuldige ist schnell entlarvt. In Zeile 7 wird 1 durch 0 geteilt. Wird die Zeile auskommentiert, ist das Programm syntaktisch richtig, denn der logische Ausdruck ( true or (1/0) ), in Zeile 8 wird nur so weit ausgewertet, bis das Ergebnis des Gesamtausdrucks feststeht. Das Ergebnis des logischen Ausdrucks steht bereits durch true fest (Abbildung F.11).
