accélération: contrairement à l’usage courant, en physique, l’accélération désigne tout changement de vitesse (la « décélération » n’étant qu’une accélération négative). Comme l’accélération représente la variation de la vitesse d’un mouvement en fonction du temps, quand un objet change de direction tout en maintenant une vitesse constante, il subit toujours une accélération. En termes quantitatifs, l’accélération est la mesure de la fréquence de variation d’une vitesse.
calcul différentiel: nom donné par Leibniz à ce que Newton appelait la « méthode des fluxions ». Le calcul différentiel permet de déterminer le taux de variation d’une valeur en fonction d’une autre valeur, en étudiant l’effet de variations infiniment petites et en permettant à ces variations de tendre vers zéro.
calcul fluxionnel: la version de Newton du calcul infinitésimal, dans laquelle le taux de variation des quantités fluentes était mesuré en termes de fluxions dans ce que l’on appelle aujourd’hui le « calcul différentiel », et s’inversait pour déterminer les fluentes dans ce que l’on appelle aujourd’hui le « calcul intégral ».
calcul intégral: terme utilisé par Leibniz, toujours en vigueur aujourd’hui. Le calcul intégral est le processus inverse du calcul différentiel. On l’utilise, par exemple, pour déterminer l’aire sous une courbe en faisant la somme de termes correspondant aux surfaces de fines bandelettes dont la largeur finit par tendre vers zéro.
Cauchy, Augustin-Louis: mathématicien du xixe siècle qui affina les versions newtonienne et leibnizienne du calcul infinitésimal en remplaçant l’infini et le zéro par des valeurs variables tendant vers l’infini ou le zéro.
fluxions: dans la version newtonienne du calcul différentiel, la fluxion était le taux de variation d’une quantité. On la nota quelques années plus tard par un point au-dessus de la lettre représentant la valeur, le point suscrit. Un x avec un point au-dessus ( . x) désignait donc le taux de variation de x avec le temps, que l’on écrirait aujourd’hui dx/dt.
L’Analyste: doté du sous-titre frappant de Discours adressé à un mathématicien infidèle, ce petit livre écrit par l’évêque George Berkeley critique les bases de la méthode des fluxions et du calcul infinitésimal. Bien que son intention semble avoir été principalement de répondre à une offense religieuse de l’admirateur de Newton, Edmond Halley, Berkeley y soulève une importante question mathématique: la méthode originale comportait des équations dans lesquelles zéro était divisé par zéro, ce qui est mathématiquement impossible.
loch à bateau: corde à nœuds munie d’un flotteur que l’on jetait d’un navire pour mesurer la vitesse de celui-ci grâce au déroulement de la ligne. De là vient le nom de l’unité nautique: le nœud.
mouvement fluide continu: Newton était conscient du problème de l’« évanouissement » des quantités infinitésimales dans sa méthode des fluxions. Il tenta de contourner le problème en disant qu’il s’occupait d’un mouvement fluide continu, et que c’était de là que provenait son usage des termes « fluente » et « fluxion », mais ce n’était qu’un rideau de fumée. Le problème était réel et ne serait résolu que plusieurs centaines d’années plus tard.
points maxima et minima: points situés sur une courbe, qui possèdent les plus grandes (maxima) et les plus petites (minima) valeurs.
quantités infinitésimales: parts trop petites pour que l’on puisse les mesurer. Le calcul infinitésimal s’intéresse à la division de valeurs en quantités infinitésimales. Quand elles deviennent si petites qu’elles s’évanouissent littéralement, on obtient le résultat recherché.
summa: en latin, summa veut dire « somme », mais Leibniz se servit de ce terme pour désigner la limite de la somme d’une série de portions de l’aire sous une courbe, la largeur de ces portions se réduisant de plus en plus. Il représenta cette somme par un S allongé, que l’on appelle aujourd’hui « signe somme », « signe intégral » ou « signe intégrateur » (∫).
Du premier coup d’œil que l’on jette au réveille-matin au trajet que l’on effectue jusqu’à son travail, on utilise constamment des outils pour mesurer le temps et l’espace. Mais, dans l’Angleterre de Newton, les horloges mécaniques étaient encore rares, et l’unité de mesure de la vitesse commençait seulement à se répandre. Le terme « nœud » vient de la technique marine consistant à jeter une ligne à nœuds dans l’eau pour évaluer la vitesse du navire en fonction du rapport entre longueur de corde et temps écoulé. On peut représenter cela graphiquement: une distance exprimée en temps ressemble à une ligne droite dont la pente est la vitesse. Mais que se passe-t-il si la vitesse change et que le mouvement est représenté par une courbe ? Dans une société qui venait juste d’adopter une terminologie pour la vitesse et qui manquait d’outils pour la mesurer précisément, ce phénomène était difficile à comprendre. Newton étudia et développa les mathématiques des ellipses et des courbes exposées par Descartes et les appliqua au mouvement pour déterminer la pente d’une courbe, c’est-à-dire le taux de variation ou d’accélération. Les orbites des planètes échappaient encore aux mathématiciens, mais la méthode de Newton allait lui permettre d’en décrire le mouvement avec précision.
Les mathématiciens n’avaient pas d’outil pour décrire le mouvement en termes de taux de variation – ou d’accélération. Newton fit de cette limitation un problème de géométrie.
Le loch à bateau fut le premier compteur de vitesse – on y faisait des nœuds à intervalles de 14,40 mètres ou 8 brasses. Les marins comptaient le nombre de nœuds qui leur passaient entre les doigts en l’espace de 28 secondes (mesurées avec un sablier). Le nombre de nœuds durant ce laps de temps représentait la vitesse en nœuds ou en miles nautiques par heure.
RENÉ DESCARTES
1596–1650
Mathématicien français qui traduisit en équations algébriques les questions de géométrie.
ISAAC BARROW
1630–1677
Mathématicien anglais qui enseigna la géométrie et l’optique à l’université de Cambridge.
Sophie Hebden
Quand la vitesse ne varie pas de façon régulière, il en résulte une accélération sous forme de courbe.
L’université de Cambridge ayant fermé en raison d’une épidémie de peste entre 1665 et 1667, Newton, en séjour forcé à Woolsthorpe, commença à réfléchir à la nature de l’accélération et aux approches mathématiques pour la décrire. Mais il serait exagéré de dire que c’est à ce moment-là qu’il élabora sa méthode des fluxions. Aujourd’hui, c’est ce qu’on appelle le « calcul différentiel », le calcul intégral étant alors appelé « calcul des fluentes ». Il lui faudra plusieurs années pour établir fermement la méthode, et son ouvrage, La Méthode des fluxions, publié après sa mort en 1736, fut d’abord esquissé au début des années 1670. Conscient des périls qu’il y avait à considérer des nombres infiniment petits (ce que ne manqua pas de pointer l’évêque Berkeley dans L’Analyste), Newton basa son approche sur le concept de mouvement fluide continu et baptisa « fluxion » le taux de variation, et « fluente », la variation résultante. La fluxion qu’il écrivit x– à présent notée dx/dt dans le calcul infinitésimal – représentait le taux de variation de x au cours du temps.
Entre 1666 et le début des années 1670, Newton élabora sa méthode des fluxions – aujourd’hui appelée « calcul différentiel » – qui traitait du rapport de deux variations infinitésimales.
Newton espérait qu’en considérant des rapports de taux de variations – le x pointé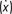 
étant indissociable d’un rapport – plutôt que de petites valeurs individuelles évanescentes, il pourrait éviter l’écueil des infiniment petits. Cette approche aboutit à un « taux ultime de variation », soit le taux de minuscules variations, de distance ou de temps, au moment où elles s’évanouissent. Sa fluxion était la valeur « à laquelle le corps se meut… à l’instant même où il arrive » sur un point donné.
GEORGE BERKELEY
1685–1753
Évêque philosophe angloirlandais.
Brian Clegg
Newton réfléchissait au mouvement fluide ininterrompu, celui d’un torrent par exemple. Il inventa sa « notation pointée » pour représenter le taux de variation.
S’il ne fait aucun doute que Newton a bien élaboré sa méthode des fluxions indépendamment de Leibniz, et que celle-ci fut largement utilisée en Angleterre durant un siècle, la convergence de ces deux théories n’en reste pas moins déconcertante pour quiconque étudie le calcul infinitésimal. Leibniz avait baptisé sa version « calcul infinitésimal », nom qui lui est resté, et s’était servi d’une notation tout à fait différente. C’est également sa notation qui a été conservée, et pour une bonne raison: elle était meilleure. Conscient du danger de travailler sur des valeurs infinitésimales, Newton avait fait de ses fluxions des rapports et les avait notées d’un x pointé. On utiliserait par la suite deux points pour représenter ce que l’on appelle aujourd’hui la « seconde dérivée », le taux de variation d’un taux de variation. Dans la notation de Leibniz, celles-ci s’écrivent respectivement dx/dt et d2x/d2t, ce qui introduit explicitement les variations infinitésimales dans la valeur de x et du temps. Il utilisa ensuite dx/dy pour considérer la manière dont x varie avec y, là où Newton dut se servir d’un taux de taux représenté par un x au-dessus d’un y.
Newton et Leibniz élaborèrent tous deux une notation pour représenter les fonctions du calcul infinitésimal, mais celle de Leibniz étant plus pratique, la notation de Newton fut graduellement écartée.
L’un des avantages de la notation de Leibniz était l’usage du symbole ∫ pour représenter ce qu’il appelait l’« intégration », soit le processus inverse de la différenciation, utilisé pour calculer les variations. L’intégration, qui s’occupe de combiner des nombres ou des formes infinitésimales pour calculer par exemple une aire sous une courbe, est représentée par un ∫, le symbole de la somme. Newton l’appelait la « méthode des fluentes » et la représentait par une barre verticale au-dessus de la valeur à intégrer.
LA GRANDE DISPUTE D’ANTÉRIORITÉ
GOTTFRIED WILHELM LEIBNIZ
1646–1716
Mathématicien allemand, grand adversaire de Newton.
Brian Clegg
Malgré quelques échanges, Leibniz et Newton semblent avoir élaboré séparément leurs versions du calcul infinitésimal. Mais Newton pensait qu’il avait été plagié.
C’est peut-être avec la question suivante : un arbre existe-t-il quand il est caché au milieu de la forêt et que personne ne le voit ?, que l’évêque George Berkeley se fit connaître. Il argumenta que Dieu étant partout et sachant tout, Il était au courant de la présence de l’arbre, et que celui-ci existait donc vraiment. Cependant, George Berkeley est plus connu dans l’histoire du xviie siècle pour avoir rédigé une attaque cinglante contre la méthode des fluxions et le calcul infinitésimal.
Fils d’un gentleman-farmer, Berkeley naquit à Dysart Castle, près de Thomastown, en Irlande. Sa famille avait quitté l’Angleterre après la restauration de la monarchie en 1660. Il fut éduqué au Trinity College de Dublin, puis ordonné prêtre au sein de l’Église anglicane d’Irlande. Toutefois, il n’était pas un curé ennuyeux et détaché de ce monde. Il était déjà bien connu (voire controversé) dans les cercles philosophiques avant son ordination, et il avait publié quelques textes originaux sur sa vision de la nature de la matière.
Berkeley partit ensuite pour Newport, dans l’état de Rhode Island, où il passa trois ans à travailler sur un projet de collège aux Bermudes. Ce projet ne vit jamais le jour mais favorisa son ascension sociale à son retour. En effet, les récits qu’il fit de son séjour lui valurent les faveurs de la reine, qui demanda qu’on lui propose le poste influent de doyen de la ville de Down, en Irlande. Cependant, de crainte que le vice-roi d’Irlande ne s’offusque de cette influence, la hiérarchie de l’Église ignora cette requête. À cela, la reine répondit que si l’on ne voulait pas laisser Berkeley « être doyen en Irlande, il devait alors être évêque » (bien qu’il fût déjà doyen d’une autre ville). Berkeley fut donc fait évêque de Cloyne.
C’est à cette époque qu’il se lança dans le débat concernant le calcul infinitésimal. Ayant une dent particulière contre Edmond Halley, il réagit aux publications de celui-ci sur les travaux de Newton par une attaque cinglante, L’Analyste. Un discours adressé à un mathématicien infidèle. Malgré sa hargne religieuse envers l’athée qu’était Halley, Berkeley était un mathématicien honorable, et sa critique du traitement cavalier que le premier calculus réservait aux quantités infiniment petites était fondée. Si sa philosophie eut peu d’influence à long terme, il ne fait aucun doute que sa contribution au débat sur le calcul infinitésimal eut un impact sur le développement des mathématiques durant les décennies suivantes.
Brian Clegg
1707
Obtient un master du Trinity College de Dublin.
1707
Publie deux études mathématiques: Arithmetica et Miscellanea mathematica.
1709
Publie Essai sur une nouvelle théorie de la vision.
1710
Publie Traité des principes de la connaissance humaine.
1721
Est ordonné prêtre au sein de l’Église d’Irlande.
1722
Devient doyen de Dromore.
1724
Devient doyen de Derry.
1725
Commence à travailler sur un projet de collège aux Bermudes.
1728
Épouse Anne Forster.
1729
Part pour l’Amérique et achète une plantation dans l’État de Rhode Island.
1732
Retourne à Londres.
Années 1730
Participe à la fondation d’un asile pour les enfants abandonnés, le Foundling Hospital, dont il devient l’un des premiers administrateurs.
1734
Est ordonné évêque de Cloyne.
1734
Publie L’Analyste.
1752
Prend sa retraite et s’installe à Oxford, où réside son fils.
14 janvier 1753
S’éteint subitement à Oxford.
Newton élabora son calcul fluxionnel au milieu des années 1660, mais ne le dévoila que des décennies plus tard. Gottfried Leibniz, qui étudiait sous la direction de Christian Huygens à Paris, fit un séjour de deux mois en Angleterre en 1673. À la Royal Society, il rencontra certains des amis de Newton, dont Henry Oldenburg, et continua à correspondre avec eux après son départ. Huygens n’avait pas encore rencontré Newton, qui n’avait rien publié à l’époque, mais il retira de ses échanges l’impression que c’était un expert des suites infinies – une technique mathématique permettant d’additionner des séquences de nombres. En 1675, Leibniz avait élaboré son calcul différentiel, et, en juin 1676, Oldenburg lui fit passer une lettre de Newton exposant son travail sur les suites. Elle ne faisait aucune allusion au calcul infinitésimal. Leibniz écrivit immédiatement à Newton par l’intermédiaire d’Oldenburg, demandant des clarifications et décrivant son propre travail sur les suites. Newton répondit en octobre 1676 qu’il avait développé une méthode générale pour tracer les tangentes des courbes et déterminer leurs points minima et maxima, mais qu’il ne souhaitait pas en dévoiler les détails. Il dissimula ses fluxions et ses fluentes dans une formule codée: « 5accdae10effhlli4l3m9n6oqqr8sllt9v3x:l lab3cddloeaegloillrm7n6o3p3q6r5sllt8vx, 3acae4 egh5i4l4m5n8oq4r3s6t4vaaddaeeeeeeiijmmnnooprrssssttuu », et en nota la signification dans ses carnets.
Newton retarda la publication de sa méthode des fluxions pendant des décennies et n’y fit allusion qu’en langage codé dans sa correspondance avec le mathématicien allemand Gottfried Leibniz.
Au xviie siècle, une réputation scientifique ne se gagnait pas en publiant des articles, mais en recherchant la faveur royale. Aussi étrange que puisse paraître aujourd’hui le comportement de Newton, il n’était pas inhabituel à l’époque de dissimuler une découverte intellectuelle en l’écrivant à l’aide d’un code.
LA GRANDE DISPUTE D’ANTÉRIORITÉ
HENRY OLDENBURG
1619–1677
Théologien et scientifique allemand, premier secrétaire de la Royal Society.
CHRISTIAN HUYGENS
1629–1695
Physicien hollandais qui eut de nombreuses controverses avec Newton.
GOTTFRIED WILHELM LEIBNIZ
1646–1716
Mathématicien allemand qui fit éditer ses travaux sur le calcul infinitésimal avant Newton.
Sophie Hebden
Leibniz publia ses premiers articles sur le calcul infinitésimal en 1684 et 1686, sans faire allusion aux méthodes de Newton, basées sur les suites. Quand ce dernier publia quelques articles mathématiques exposant sa méthode des fluxions en 1704, il revendiqua l’antériorité de sa découverte. Ses techniques correspondaient effectivement au calcul différentiel de Leibniz, mais avec une notation différente, ce qui déclencha l’une des plus féroces disputes de l’histoire scientifique. Newton avait plusieurs motifs de plainte contre Leibniz, mais le plus important concernait une lettre qu’il avait envoyée à John Collins, de la Royal Society, en 1672, dans laquelle il décrivait en détail les fluxions, et que Leibniz avait lue lors de son séjour à Londres en 1676. Cependant, Leibniz avait déjà inventé le calcul infinitésimal à cette époque, et l’analyse historique montre que ce sont d’autres détails de cette lettre qui l’ont intéressé. Prenant conscience de l’importance de la découverte du calcul infinitésimal, d’autres savants se lancèrent dans la controverse. La Royal Society ouvrit une enquête, mais ce fut Newton en personne qui écrivit et révisa le rapport. Leibniz mourut en 1716, alors que rien n’avait encore été décidé. La dispute se poursuivit de nombreuses années, entravant le progrès des mathématiques en Angleterre, où la loyauté envers la notation de Newton était devenue une affaire de fierté nationale.
De nos jours, on accorde aussi bien à Leibniz qu’à Newton le crédit de l’invention du calcul infinitésimal, mais, en leur temps, aucun d’eux ne voulait admettre qu’ils avaient pu l’élaborer de façon indépendante. Chacun accusait l’autre de plagiat.
C’est le goût du secret de Newton qui fut à l’origine de la controverse: eût-il rendu public son calcul fluxionnel dès le début que la dispute n’aurait pas eu lieu. Mais il garda secrète sa méthode, et convertit les fluxions de ses Principia en une approche géométrique bien moins évidente. Quand Leibniz eut publié à son tour, il n’était bien sûr plus possible de revenir en arrière.
DISCOURS ADRESSÉ À UN MATHÉMATICIEN INFIDÈLE
JOHN COLLINS
1625–1683
Mathématicien anglais, membre de la Royal Society.
GOTTFRIED WILHELM LEIBNIZ
1646–1716
Philosophe et mathématicien allemand, membre de l’Académie des sciences de Berlin.
Sophie Hebden
Newton gagna la partie à l’époque, mais la querelle entre les deux scientifiques freina les progrès en mathématiques.
Dans son pamphlet L’Analyste. Un discours adressé à un mathématicien infidèle, l’évêque-philosophe George Berkeley attaquait les fondements des fluxions de Newton (et du calcul infinitésimal de Leibniz). L’infidèle en question était sans doute Edmond Halley, l’astronome royal, farouche partisan de Newton depuis des années. Fait surprenant pour l’époque, Halley était athée et il avait persuadé un ami de Berkeley de renier sa foi sur son lit de mort. Berkeley se vengea en démontant le cœur de la méthode des fluxions, chef-d’œuvre du protégé de Halley. L’évêque souligna ainsi que la méthode requérait que l’on prenne en considération des quantités inconcevablement petites – qu’on pouvait utiliser en mathématiques, mais qui devenaient si petites qu’elles disparaissaient –, qu’il qualifia avec ironie de « fantômes de quantités défuntes ». Le calcul infinitésimal semblait n’avoir aucun sens, et pourtant il fonctionnait: tout ce que pouvaient faire les utilisateurs de la méthode était d’y accorder foi. Berkeley ne manqua pas de relever l’hypocrisie qu’il y avait à croire à une méthode douteuse tout en dénigrant le rôle de la foi dans la religion, comme le faisait Halley.
L’évêque Berkeley soutint que les fluxions étaient erronées parce qu’elles supposaient des opérations arithmétiques sur des valeurs non existantes.
L’attaque de Berkeley ne relevait pas uniquement du dénigrement religieux. Si la méthode des fluxions fournissait des résultats corrects, son fonctionnement était douteux. Quand ces « fantômes de quantités défuntes » étaient ramenés à zéro, il en résultait une équation dans laquelle on divisait zéro par zéro, une catastrophe mathématique. Dans une fraction, un zéro au-dessus donne un résultat égal à zéro, et un zéro en dessous donne un résultat égal à l’infini. Divisez zéro par zéro et le résultat devient impossible à déterminer.
LA GRANDE DISPUTE D’ANTÉRIORITÉ
CLARIFICATION DU CALCUL INFINITÉSIMAL
EDMUND HALLEY
1656–1742
Second astronome royal.
GEORGE BERKELEY
1685–1753
Évêque-philosophe angloirlandais qui critiqua les fondements des fluxions et du calcul infinitésimal.
Brian Clegg
Aux yeux de Berkeley, la méthode du calcul infinitésimal était aussi étayée par la foi que sa propre vie religieuse.
Newton tenta de se servir de taux pour dissimuler des opérations mathématiques risquées, comme la division de quantités infinitésimales. Mais sa méthode des fluxions n’était pas mathématiquement sûre, parce qu’en laissant des quantités infinitésimales devenir égales à zéro, elle aboutissait à diviser zéro par zéro. George Berkeley avait raison en soulignant ce point. Newton ne semble pas s’en être véritablement soucié, car sa méthode produisait des résultats exacts, lui permettant de poursuivre son travail sur les forces et la gravité. Plus tard, d’autres mathématiciens comprirent d’une part qu’il s’agissait là d’une position intenable, et d’autre part que la tentative de Newton pointait dans la bonne direction. Plutôt que de laisser sa fluxion, représentée par o, devenir égale à zéro, Newton attendait d’elle qu’elle « tende vers zéro ». Ainsi, dans la fonction 2x + o, il n’attribua pas zéro à o pour obtenir le résultat 2x, mais affirma que le résultat « tend vers 2x comme o tend vers O ». Ce tour de passe-passe fut formalisé dans les années 1820 par Augustin-Louis Cauchy, qui proposa que l’infini et les quantités infinitésimales soient variables: elles ne correspondaient pas à un nombre fixe, mais à quelque chose qui approchait de l’infini ou du zéro sans jamais vraiment l’atteindre.
Malgré son efficacité, le calcul infinitésimal était mathématiquement erroné, car il laissait des quantités infinitésimales devenir égales à zéro. Plus tard, d’autres mathématiciens réhabilitèrent cette théorie en y introduisant le concept de « limite », qui permettait d’éviter d’atteindre le zéro.
Si l’approche de Cauchy était suffisante à des fins pratiques, dans les années 1850, Karl Weierstrass l’améliora en introduisant le concept de « limite ». Dans les faits, il supprima l’infini du calcul (bien que son symbole apparaisse toujours dans l’intégration) en proposant d’affirmer qu’un résultat tend vers une limite s’il approche cette limite plus vite que le minimum requis.
DISCOURS ADRESSÉ À UN MATHÉMATICIEN INFIDÈLE
AUGUSTIN-LOUIS CAUCHY
1789–1857
Mathématicien français qui donna forme à l’idée de Newton de « tendre vers » une valeur.
KARL WEIERSTRASS
1815–1897
Mathématicien allemand qui introduisit le concept de « limite » pour supprimer l’infini du calcul infinitésimal.
Brian Clegg
Newton et ses successeurs définirent des quantités importantes ou minuscules en tendant vers l’infini ou le zéro, mais sans jamais l’atteindre.