
Any pattern in space and time can be thought of as a superposition of sinusoidal patterns with different frequencies.
The component frequencies can be used to analyse the patterns, create them to order, extract important features, and remove random noise.
Fourier’s technique is very widely used, for example in image processing and quantum mechanics. It is used to find the structure of large biological molecules like DNA, to compress image data in digital photography, to clean up old or damaged audio recordings, and to analyse earthquakes. Modern variants are used to store fingerprint data efficiently and to improve medical scanners.
Newton’s Principia opened the door to the mathematical study of nature, but his fellow countrymen were too obsessed with the priority dispute over calculus to find out what lay beyond. While England’s finest were seething over what they perceived to be disgraceful allegations about the country’s greatest living mathematician – much of it probably his own fault for listening to well-intentioned but foolish friends – their continental colleagues were extending Newton’s ideas about laws of nature to most of the physical sciences. The wave equation was quickly followed by remarkably similar equations for gravitation, electrostatics, elasticity, and heat flow. Many bore the names of their inventors: Laplace’s equation, Poisson’s equation. The equation for heat does not; it bears the unimaginative and not entirely accurate name ‘heat equation’. It was introduced by Joseph Fourier, and his ideas led to the creation of a new area of mathematics whose ramifications were to spread far beyond its original source. Those ideas could have been triggered by the wave equation, where similar methods were floating around in the collective mathematical consciousness, but history plumped for heat.
The new method had a promising beginning: in 1807 Fourier submitted an article on heat flow to the French Academy of Sciences, based on a new partial differential equation. Although that prestigious body declined to publish the work, it encouraged Fourier to develop his ideas further and try again. At that time the Academy offered an annual prize for research on whatever topic they felt was sufficiently interesting, and they made heat the topic of the 1812 prize. Fourier duly submitted his revised and extended article, and won. His heat equation looks like this:
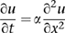
Here u(x, t) is the temperature of a metal rod at position x and time t, considering the rod to be infinitely thin, and a is a constant, the thermal diffusivity. So it really ought to be called the temperature equation. He also developed a higher-dimensional version,
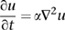
valid on any specified region of the plane or space.
The heat equation bears an uncanny resemblance to the wave equation, with one crucial difference. The wave equation uses the second time derivative ∂2u/∂t2, but in the heat equation this is replaced by the first derivative ∂u/∂t. This change may seem small, but its physical meaning is huge. Heat does not persist indefinitely, in the way that a vibrating violin string continues to vibrate forever (according to the wave equation, which assumes no friction or other damping). Instead, heat dissipates, dies away, as time passes, unless there is some heat source that can top it up. So a typical problem might be: heat one end of a rod to keep its temperature steady, cool the other end to do the same, and find out how the temperature varies along the rod when it settles to a steady state. The answer is that it falls off exponentially. Another typical problem is to specify the initial temperature profile along the rod, and then ask how it changes as time passes. Perhaps the left half starts at a high temperature and the right half at a cooler one; the equation then tells us how the heat from the hot part diffuses into the cooler part.
The most intriguing aspect of Fourier’s prizewinning memoir was not the equation, but how he solved it. When the initial profile is a trigonometric function, such as sin x, it is easy (to those with experience in such matters) to solve the equation, and the answer is e−αt sin x. This resembles the fundamental mode of the wave equation, but there the formula was sin ct sin x. The eternal oscillation of a violin string, corresponding to the sin ct factor, has been replaced by an exponential, and the minus sign in the exponent −αt tells us that the entire temperature profile dies away at the same rate, all along the rod. (The physical difference here is that waves conserve energy, but heat flow does not.) Similarly, for a profile sin 5x, say, the solution is e−25αt sin 5x, which also dies out, but at a much faster rate. The 25 is 52, and this is an example of a general pattern, applicable to initial profiles of the form sin nx or cos nx.1 To solve the heat equation, just multiply by e−n2αt.
Now the story follows the same general outline as the wave equation. The heat equation is linear, so we can superpose solutions. If the initial profile is
u(x; 0) = sin x + sin 5x
then the solution is
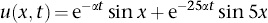
and each mode dies way at a different rate. But initial profiles like this are a bit artificial. To solve the problem I mentioned earlier, we want an initial profile where u(x, 0) = 1 for half the rod but −1 for the other half. This profile is discontinuous, a square wave in engineering terminology. But sine and cosine curves are continuous. So no superposition of sine and cosine curves can represent a square wave.
No finite superposition, certainly. But, again, what if we allowed infinitely many terms? Then we can try to express the initial profile as an infinite series, of the form
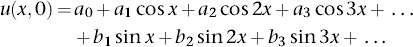
for suitable constants a0, a1, a2, a3,…, b1, b2, b3, …. (There is no b0because sin 0x = 0.) Now it does seem possible to get a square wave (see Figure 40). In fact, most coefficients can be set to zero. Only the bn for n odd are needed, and then bn = 8/nπ.
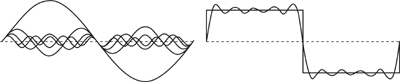
Fig 40 How to get a square wave from sines and cosines. Left: The component sinusoidal waves. Right: Their sum and a square wave. Here we show the first few terms of the Fourier series. Additional terms make the approximation to a square wave ever better.
Fourier even had general formulas for the coefficients an and bn for a general profile f(x), in terms of integrals:
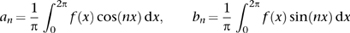
After a lengthy trek through power series expansions of trigonometric functions, he realised that there was a much simpler way to derive these formulas. If you take two different trigonometric functions, say cos 2x and sin 5x, multiply them together, and integrate from 0 to 2π, you get zero. This is even the case when they look like cos 5x and sin 5x. But if they are the same – say both equal to sin 5x – the integral of their product is not zero. In fact, it is π. If you start by assuming that f(x) is the sum of a trigonometric series, multiply everything by sin 5x, and integrate, all of the terms disappear except for the one corresponding to sin 5x, namely b5 sin 5x. Here the integral is π. Divide by that, and you have Fourier’s formula for b5. The same goes for all the other coefficients.
Although it won the academy’s prize, Fourier’s memoir was roundly criticised for being insufficiently rigorous, and the academy declined to publish it. This was highly unusual and it greatly irritated Fourier, but the academy held its ground. Fourier was incensed. Physical intuition told him he was right, and if you plugged his series into this equation it was clearly a solution. It worked. The real problem was that unwittingly he had reopened an old wound. As we saw in Chapter 8, Euler and Bernoulli had been arguing for ages about a similar issue for the wave equation, where Fourier’s exponential dissipation over time was replaced by an unending sinusoidal oscillation in the wave amplitude. The underlying mathematical issues were identical. In fact, Euler had already published the integral formulas for the coefficients in the context of the wave equation.
However, Euler had never claimed that the formula worked for discontinuous functions f(x), the most controversial feature of Fourier’s work. The violin-string model didn’t involve discontinuous initial conditions anyway – those would model a broken string, which would not vibrate at all. But for heat, it was natural to consider holding one region of a rod at one temperature and an adjacent region at a different one. In practice the transition would be smooth and very steep, but a discontinuous model was reasonable and more convenient for calculations. In fact, the solution to the heat equation explained why the transition would rapidly become smooth and very steep, as the heat diffused sideways. So an issue that Euler hadn’t needed to worry about was becoming unavoidable, and Fourier suffered from the fallout.
Mathematicians were starting to realise that infinite series were dangerous beasts. They didn’t always behave like nice finite sums. Eventually, these tangled complexities got sorted out, but it took a new view of mathematics and a hundred years of hard work to do that. In Fourier’s day, everyone thought they already knew what integrals, functions, and infinite series were, but in reality it was all rather vague – ‘I know one when I see one.’ So when Fourier submitted his epoch-making paper, there were good reasons for the academy officials to be wary. They refused to budge, so in 1822 Fourier got round their objections by publishing his work as a book, Théorie analytique de la chaleur (‘Analytic Theory of Heat’). In 1824 he got himself appointed secretary of the academy, thumbed his nose at all the critics, and published his original 1811 memoir, unchanged, in the academy’s prestigious journal.
We now know that although Fourier was right in spirit, his critics had good reasons for worrying about rigour. The problems are subtle and the answers are not terribly intuitive. Fourier analysis, as we now call it, works very well, but it has hidden depths of which Fourier was unaware.
The question seemed to be: when does the Fourier series converge to the function it allegedly represents? That is, if you take more and more terms, does the approximation to the function get ever better? Even Fourier knew that the answer was not ‘always’. It seemed to be ‘usually, but with possible problems at discontinuities’. For instance at its midpoint, where the temperature jumps, the square wave’s Fourier series converges – but to the wrong number. The sum is 0, but the square wave takes value 1.
For most physical purposes, it doesn’t greatly matter if you change the value of a function at one isolated point. The square wave, thus modified, still looks square. It just does something slightly different at the discontinuity. To Fourier, this kind of issue didn’t really matter. He was modelling the flow of heat, and he didn’t mind if the model was a bit artificial, or needed technical changes that had no important effect on the end result. But the convergence issue could not be dismissed so lightly, because functions can have far more complicated discontinuities than a square wave.
However, Fourier was claiming that his method worked for any function, so it ought to apply even to functions such as: f(x) = 0 when x is rational, 1 when x is irrational. This function is discontinuous everywhere. For such functions, at that time, it wasn’t even clear what the integral meant. And that turned out to be the real cause of the controversy. No one had defined what an integral was, not for strange functions like this one. Worse, no one had defined what a function was. And even if you could tidy up those omissions, it wasn’t just a matter of whether the Fourier series converged. The real difficulty was to sort out in what sense it converged.
Resolving these issues was tricky. It required a new theory of integration, supplied by Henri Lebesgue, a reformulation of the foundations of mathematics in terms of set theory, started by Georg Cantor and opening up several entirely new cans of worms, major insights from such towering figures as Riemann, and a dose of twentieth–century abstraction to sort out the convergence issues. The final verdict was that, with the right interpretations, Fourier’s idea could be made rigorous. It worked for a very broad, though not universal, class of functions. Whether the series converged to f(x) for every value of x wasn’t quite the right question; everything was fine provided the exceptional values of x where it didn’t converge were sufficiently rare, in a precise but technical sense. If the function was continuous, the series converged for any x. At a jump discontinuity, like the change from 1 to –1 in the square wave, the series converged very democratically to the average of the values immediately to either side of the jump. But the series always converged to the function with the right interpretation of ‘converge’. It converged as a whole, rather than point by point. Stating this rigorously depended on finding the right way to measure the distance between two functions. With all this in place, Fourier series did indeed solve the heat equation. But their real significance was much broader, and the main beneficiary outside pure mathematics was not the physics of heat but engineering. Especially electronic engineering.
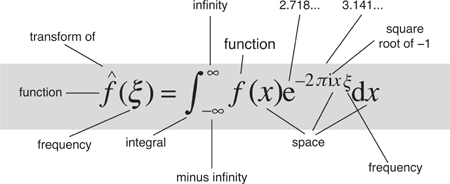
In its most general form Fourier’s method represents a signal, determined by a function f, as a combination of waves of all possible frequencies. This is called the Fourier transform of the wave. It replaces the original signal by its spectrum: a list of amplitudes and frequencies for the component sines and cosines, encoding the same information in a different way – engineers talk of transforming from the time domain to the frequency domain. When data are represented in different ways, operations that are difficult or impossible in one representation may become easy in the other. For example, you can start with a telephone conversation, form its Fourier transform, and strip out all parts of the signal whose Fourier components have frequencies too high or too low for the human ear to hear. This makes it possible to send more conversations over the same communication channels, and it’s one reason why today’s phone bills are, relatively speaking, so small. You can’t play this game on the original, untransformed signal, because that doesn’t have ‘frequency’ as an obvious characteristic. You don’t know what to strip out.
One application of this technique is to design buildings that will survive earthquakes. The Fourier transform of the vibrations produced by a typical earthquake reveals, among other things, the frequencies at which the energy imparted by the shaking ground is greatest. A building has its own natural modes of vibration, where it will resonate with the earthquake, that is, respond unusually strongly. So the first sensible step towards earthquake-proofing a building is to make sure that the building’s preferred frequencies are different from the earthquake’s. The earthquake’s frequencies can be obtained from observations; those of the building can be calculated using a computer model.
This is just one of many ways in which, tucked away behind the scenes, the Fourier transform affects our lives. People who live or work in buildings in earthquake zones don’t need to know how to calculate a Fourier transform, but their chance of surviving an earthquake is considerably improved because some people do. The Fourier transform has become a routine tool in science and engineering; its applications include removing noise from old sound recordings, such as clicks caused by scratches on vinyl records, finding the structure of large biochemical molecules such as DNA using X-ray diffraction, improving radio reception, tidying up photographs taken from the air, sonar systems such as those used by submarines, and preventing unwanted vibrations in cars at the design stage. I’ll focus here on just one of the thousands of everyday uses of Fourier’s magnificent insight, one that most of us unwittingly take advantage of every time we go on holiday: digital photography.
On a recent trip to Cambodia I took about 1400 photographs, using a digital camera, and they all went on a 2 GB memory card with room for about 400 more. Now, I don’t take particularly high-resolution photographs, so each photo file is about 1.1 MB. But the pictures are full colour, and they don’t show any noticeable pixellation on a 27-inch computer screen, so the loss in quality isn’t obvious. Somehow, my camera manages to cram into a single 2 GB card about ten times as much data as the card can possibly hold. It’s like pouring a litre of milk into an eggcup. Yet it all fits in. The question is: how?
The answer is data compression. The information that specifies the image is processed to reduce its quantity. Some of this processing is ‘lossless’, meaning that the original raw information can if necessary be retrieved from the compressed version. This is possible because most real-world images contain redundant information. Big blocks of sky, for instance, are often the same shade of blue (well, they are where we tend to go). Instead of repeating the colour and brightness information for a blue pixel over and over again, you could store the coordinates of two opposite corners of a rectangle and a short code that means ‘colour this entire region blue’. That’s not quite how it’s done, of course, but it shows why lossless compression is sometimes possible. When it’s not, ‘lossy’ compression is often acceptable. The human eye is not especially sensitive to certain features of images, and these features can be recorded on a coarser scale without most of us noticing, especially if we don’t have the original image to compare with. Compressing information this way is like scrambling an egg: it’s easy in one direction, and does the required job, but it’s not possible to reverse it. Non-redundant information is lost. It was just information that didn’t do a lot to begin with, given how human vision works.
My camera, like most point-and-click ones, saves its images in files with labels like P1020339.JPG. The suffix refers to JPEG, the Joint Photographic Experts Group, and it indicates that a particular system of data compression has been used. Software for manipulating and printing photos, such as Photoshop or iPhoto, is written so that it can decode the JPEG format and turn the data back into a picture. Millions of us use JPEG files regularly, fewer are aware that they’re compressed, and fewer still wonder how it’s done. This is not a criticism: you don’t have to know how it works to use it, that’s the point. The camera and software handle it all for you. But it’s often sensible to have a rough idea of what software does, and how, if only to discover how cunning some of it is. You can skip the details here if you wish: I’d like you to appreciate just how much mathematics goes into each image on your camera’s memory card, but exactly what mathematics is less important.
The JPEG format2 combines five different compression steps. The first converts the colour and brightness information, which starts out as three intensities for red, green, and blue, into three different mathematically equivalent ones that are more suited to the way the human brain perceives images. One (luminance) represents the overall brightness – what you would see with a black-and-white or ‘greyscale’ version of the same image. The other two (chrominance) are the differences between this and the amounts of blue and red light, respectively.
Next, the chrominance data are coarsened: reduced to a smaller range of numerical values. This step alone halves the amount of data. It does no perceptible harm because the human visual system is much less sensitive to colour differences than the camera is.
The third step uses a variant of the Fourier transform. This works not with a signal that changes over time, but with a pattern in two dimensions of space. The mathematics is virtually identical. The space concerned is an 8 × 8 sub-block of pixels from the image. For simplicity think just of the luminance component: the same idea applies to the colour information as well. We start with a block of 64 pixels, and for each of them we need to store one number, the luminance value for that pixel. The discrete cosine transform, a special case of the Fourier transform, decomposes the image into a superposition of standard ‘striped’ images instead. In half of them the stripes run horizontally; in the other half they are vertical. They are spaced at different intervals, like the various harmonics in the usual Fourier transform, and their greyscale values are a close approximation to a cosine curve. In coordinates on the block they are discrete versions of cos mx cos ny for various integers m and n, see Figure 41.

Fig 41 The 64 basic patterns from which any block of 8×8 pixels can be obtained.
This step paves the way to step four, a second exploitation of the deficiencies of human vision. We are more sensitive to variations in brightness (or colour) over large regions than we are to closely spaced variations. So the patterns in the figure can be recorded less accurately as the spacing of the stripes becomes finer. This compresses the data further. The fifth and final step uses a ‘Huffman code’ to express the list of strengths of the 64 basic patterns in a more efficient manner.
Every time you take a digital image using JPEG, the electronics in your camera does all of these things, except perhaps step one. (Professionals are now moving over to RAW files, which record the actual data without compression, together with the usual ‘metadata’ such as date, time, exposure, and so on. Files in this format take up more memory, but memory gets bigger and cheaper by the month, so that no longer matters.) A trained eye can spot the loss of image quality created by JPEG compression when the quantity of data is reduced to about 10% of the original, and an untrained eye can see it clearly by the time the file size is down to 2–3%. So your camera can record about ten times as many images on a memory card, compared with the raw image data, before anyone other than an expert would notice.
Because of applications like these, Fourier analysis has become a reflex among engineers and scientists, but for some purposes the technique has one major fault: sines and cosines go on forever. Fourier’s method runs into problems when it tries to represent a compact signal. It takes huge numbers of sines and cosines to mimic a localised blip. The problem is not getting the basic shape of the blip right, but making everything outside the blip equal to zero. You have to kill off the infinitely long rippling tails of all those sines and cosines, which you do by adding on even more high-frequency sines and cosines in a desperate effort to cancel out the unwanted junk. So the Fourier transform is hopeless for blip-like signals: the transformed version is more complicated, and needs more data to describe it, than the original.
What saves the day is the generality of Fourier’s method. Sines and cosines work because they satisfy one simple condition: they are mathematically independent. Formally, this means that they are orthogonal: in an abstract but meaningful sense, they are at right angles to each other. This is where Euler’s trick, eventually rediscovered by Fourier, comes in. Multiplying two of the basic sinusoidal waveforms together and integrating over one period is a way to measure how closely related they are. If this number is large, they are very similar; if it is zero (the condition for orthogonality), they are independent. Fourier analysis works because its basic waveforms are both orthogonal and complete: they are independent and there are enough of them to represent any signal if they are suitably superposed. In effect, they provide a coordinate system on the space of all signals, just like the usual three axes of ordinary space. The main new feature is that we now have infinitely many axes: one for each basic waveform. But this doesn’t cause many difficulties mathematically, once you get used to it. It just means you have to work with infinite series instead of finite sums, and worry a little about when the series converge.
Even in finite-dimensional spaces, there are many different coordinate systems; the axes can be rotated to point in new directions, for example. It’s not surprising to find that in an infinite-dimensional space of signals, there are alternative coordinate systems that differ wildly from Fourier’s. One of the most important discoveries in the whole area, in recent years, is a new coordinate system in which the basic waveforms are confined to a limited region of space. They are called wavelets, and they can represent blips very efficiently because they are blips.
Only recently did anyone realise that blip-like Fourier analysis was possible. Getting started is straightforward: choose a particular shape of blip, the mother wavelet (Figure 42). Then generate daughter wavelets (and granddaughters, great-granddaughters, whatever) by sliding the mother wavelet sideways into various positions, and expanding her or compressing her by a change of scale. In the same way, Fourier’s basic sine and cosine curves are ‘mother sinelets’, and the higher-frequency sines and cosines are daughters. Being periodic, these curves cannot be blip-like.
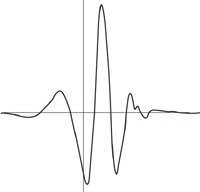
Wavelets are designed to describe bliplike data efficiently. Moreover, because the daughter and granddaughter wavelets are just rescaled versions of mother, it is possible to focus on particular levels of detail. If you don’t want to see small-scale structure, you just remove all the great-granddaughter wavelets from the wavelet transform. To represent a leopard by wavelets, you need a few big ones to get the body right, smaller ones for the eyes, nose, and of course the spots, and very tiny ones for individual hairs. To compress the data representing the leopard, you might decide that the individual hairs don’t matter, so you just remove those particular component wavelets. The great thing is, the image still looks like a leopard, and it still has spots. If you try to do this with the Fourier transform of a leopard then the list of components is huge, it’s not clear which items you should remove, and you probably won’t recognise the result as a leopard.
All very well and good, but what shape should the mother wavelet be? For a long time nobody could work that out, or even show that a good shape exists. But in the early 1980s geophysicist Jean Morlet and mathematical physicist Alexander Grossmann found the first suitable mother wavelet. In 1985 Yves Meyer found a better mother wavelet, and in 1987 Ingrid Daubechies, a mathematician at Bell Laboratories, blew the whole field wide open. Although the previous mother wavelets looked suitably bliplike, they all had a very tiny mathematical tail that wiggled off to infinity. Daubechies found a mother wavelet with no tail at all: outside some interval, mother was always exactly zero – a genuine blip, confined entirely to a finite region of space.
The bliplike features of wavelets make them especially good for compressing images. One of their first large-scale practical uses was to store fingerprints, and the customer was the Federal Bureau of Investigation. The FBI’s fingerprint database contains 300 million records, each of eight fingerprints and two thumbprints, which were originally stored as inked impressions on paper cards. This is not a convenient storage medium, so the records have been modernised by digitising the images and storing the results on a computer. Obvious advantages include being able to mount a rapid automated search for prints that match those found at the scene of a crime.
The computer file for each fingerprint card is 10 megabytes long: 80 million binary digits. So the entire archive occupies 3000 terabytes of memory: 24 quadrillion binary digits. To make matters worse, the number of new sets of fingerprints grows by 30,000 every day, so the storage requirement would grow by 2.4 trillion binary digits every day. The FBI sensibly decided that they needed some method for data compression. JPEG wasn’t suitable, for various reasons, so in 2002 the FBI decided to develop a new system of compression using wavelets, the wavelet/scalar quantization (WSQ) method. WSQ reduces the data to 5% of its size by removing fine detail throughout the image. This is irrelevant to the eye’s ability, as well as a computer’s, to recognise the fingerprint.
There are also many recent applications of wavelets to medical imaging. Hospitals now employ several different kinds of scanner, which assemble two-dimensional cross-sections of the human body or important organs such as the brain. The techniques include CT (computerised tomography), PET (positron emission tomography), and MRI (magnetic resonance imaging). In tomography, the machine observes the total tissue density, or a similar quantity, in a single direction through the body, rather like what you would see from a fixed position if all the tissue were to become slightly transparent. A two-dimensional picture can be reconstructed by applying some clever mathematics to a whole series of such ‘projections’, taken at many different angles. In CT, each projection requires an X-ray exposure, so there are good reasons to limit the amount of data acquired. In all such scanning methods, less data takes less time to acquire, so more patients can use the same amount of equipment. On the other hand, good images need more data so that the reconstruction method can work more effectively. Wavelets provide a compromise, in which reducing the amount of data leads to equally acceptable images. By taking a wavelet transform, removing unwanted components, and ‘detransforming’ back to an image again, a poor image can be smoothed and cleaned up. Wavelets also improve the strategies by which the scanners acquire their data in the first place.
In fact, wavelets are turning up almost everywhere. Researchers in areas as wide apart as geophysics and electrical engineering are taking them on board and putting them to work in their own fields. Ronald Coifman and Victor Wickerhauser have used them to remove unwanted noise from recordings: a recent triumph was a performance of Brahms playing one of his own Hungarian Dances. It was originally recorded on a wax cylinder in 1889, which partially melted; it was re-recorded on to a 78 rpm disc. Coifman started from a radio broadcast of the disc, by which time the music was virtually inaudible amid the surrounding noise. After wavelet cleansing, you could hear what Brahms was playing – not perfectly, but at least it was audible. It’s an impressive track record for an idea that first arose in the physics of heat flow 200 years ago, and was rejected for publication.