
The acceleration of a small segment of a violin string is proportional to the average displacement of neighbouring segments.
It predicts that the string will move in waves, and it generalises naturally to other physical systems in which waves occur.
Big advances in our understanding of water waves, sound waves, light waves, elastic vibrations… Seismologists use modified versions of it to deduce the structure of the interior of the Earth from how it vibrates. Oil companies use similar methods to find oil. In Chapter 11 we will see how it predicted the existence of electromagnetic waves, leading to radio, television, radar, and modern communications.
We live in a world of waves. Our ears detect waves of compression in the air: we call this ‘hearing’. Our eyes detect waves of electromagnetic radiation: we call this ‘seeing’. When an earthquake hits a town or a city, the destruction is caused by waves in the solid body of the Earth. When a ship bobs up and down on the ocean, it is reacting to waves in the water. Surfers use ocean waves for recreation; radio, television, and large parts of the mobile telephone network use waves of electromagnetic radiation, similar to those that we see by, but of differing wavelengths. Microwave ovens … well, the name gives it away, doesn’t it?
With so many practical instances of waves impinging on daily life, even centuries ago, the mathematicians who decided to follow up Newton’s epic discovery that nature has laws could hardly fail to start thinking about waves. What got them started, though, came from the arts: specifically, music. How does a violin string create sound? What does it do?
There was a reason for starting with violins, the kind of reason that appeals to mathematicians, though not to governments or businessmen considering investing in mathematicians and expecting a quick payback. A violin string can sensibly be modelled as an infinitely thin line, and its motion – which is clearly the cause of the sound that the instrument makes – can be assumed to take place in a plane. This makes the problem ‘low-dimensional’, which means you have a chance of solving it. Once you have understood this simple example of waves, there’s a good chance that the understanding can be transferred, often in small stages, to more realistic and more practical instances of waves.
The alternative, to plough headlong into highly complex problems, may appear attractive to politicians and captains of industry, but it usually gets bogged down in complexities. Mathematics thrives on simplicities, and if necessary mathematicians will invent them artificially to provide an entry route into more complex problems. They deprecatingly refer to such models as ‘toys’, but these are toys with a serious purpose. Toy models of waves led to today’s world of electronics and high-speed global communications, wide-bodied passenger jets and artificial satellites, radio, television, tsunami warning systems… but we’d never have achieved any of those if a few mathematicians hadn’t started to puzzle out how a violin works, using a model that wasn’t realistic, even for a violin.
The Pythagoreans believed that the world was based on numbers, by which they meant whole numbers or ratios between whole numbers. Some of their beliefs tended towards the mystical, investing specific numbers with human attributes: 2 was male, 3 female, 5 symbolised marriage, and so on. The number 10 was very important to the Pythagoreans because it was 1 + 2 + 3 + 4 and they believed there were four elements: earth, air, fire, water. This kind of speculation strikes the modern mind as slightly crazy – well, my mind, at least – but it was reasonable in an age when humans were only just starting to investigate the world around them, seeking crucial patterns. It just took a while to work out which patterns were significant and which were dross.
One of the great triumphs of the Pythagorean world view came from music. Various stories circulate: according to one, Pythagoras was passing a blacksmith’s shop and he noticed that hammers of different sizes made noises of different pitch, and that hammers related by simple numbers – one twice the size of the other, for instance – made noises that harmonised. Charming though this tale is, anyone who actually tries it out with real hammers will discover that a blacksmith’s operations are not especially musical, and hammers are too complicated a shape to vibrate in harmony. But there’s a grain of truth: on the whole, small objects make higher-pitched noises than large ones.
The stories are on stronger ground when they refer to a series of experiments that the Pythagoreans performed using a stretched string, a rudimentary musical instrument known as a canon. We know about these experiments because Ptolemy reported them in his Harmonics around 150 AD. By moving a support to various positions along the string, the Pythagoreans found that when two strings of equal tension had lengths in a simple ratio, such as 2 : 1 or 3 : 2, they produced unusually harmonious notes. More complex ratios were discordant and unpleasant to the ear. Later scientists pushed these ideas much further, probably a bit too far: what seems pleasant to us depends on the physics of the ear, which is more complicated than that of a single string, and it also has a cultural dimension because the ears of growing children are trained by being exposed to the sounds that are common in their society. I predict that today’s children will be unusually sensitive to differences in mobile phone ringtones. However, there is a solid scientific story behind these complexities, and a lot of it confirms and explains the early Pythagorean discoveries with their single-stringed experimental instrument.
Musicians describe pairs of notes in terms of the interval between them, a measure of how many steps separate them in some musical scale. The most fundamental interval is the octave, eight white notes on a piano. Notes an octave apart sound remarkably similar, except that one note is higher than the other, and they are extremely harmonious. So much so, in fact, that harmonies based on the octave can seem a bit bland. On a violin, the way to play the note one octave above an open string is to press the middle of that string against the fingerboard. A string half as long plays a note one octave higher. So the octave is associated with a simple numerical ratio of 2:1.
Other harmonious intervals are also associated with simple numerical ratios. The most important for Western music are the fourth, a ratio of 4:3, and the fifth, a ratio of 3:2. The names make sense if you consider a musical scale of whole notes C D E F G A B C. With C as base, the note corresponding to a fourth is F, the fifth is G, and the octave C. If we number the notes consecutively with the base as 1, these are respectively the 4th, 5th, and 8th notes along the scale. The geometry is especially clear on an instrument like a guitar, which has segments of wire, ‘frets’, inserted at the relevant positions. The fret for the fourth is one-quarter of the way along the string, that for a fifth is one-third of the way along, and the octave is halfway along. You can check this with a tape measure.
These ratios provide a theoretical basis for a musical scale and led to the scale(s) now used in most Western music. The story is complex, so I’ll give a simplified version. For later convenience I’ll rewrite a ratio like 3:2 as a fraction 3/2 from now on. Start at a base note and ascend in fifths, to get strings of lengths
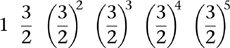
Multiplied out, these fractions become
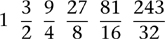
All of these notes, except the first two, are too high-pitched to remain within an octave, but we can lower them by one or more octaves, repeatedly dividing the fractions by 2 until the result lies between 1 and 2. This yields the fractions
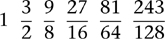
Finally, arrange these in ascending numerical order, obtaining
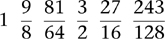
These correspond fairly closely to the notes C D E G A B on a piano. Notice that F is missing. In fact, to the ear, the gap between 81/64 and 3/2 sounds wider than the others. To fill that gap, we insert 4/3, the ratio for the fourth, which is very close to F on the piano. It is also useful to complete the scale with a second C, one octave up, a ratio of 2. Now we obtain a musical scale based entirely on fourths, fifths, and octaves, with pitches in the ratios
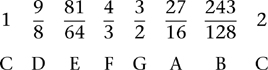
The length is inversely proportional to the pitch, so we would have to invert the fractions to get the corresponding lengths.
We have now accounted for all the white notes on the piano, but there are also black notes. These appear because successive numbers in the scale bear two different ratios to each other: 9/8 (called a tone) and 256/243 (semitone). For example the ratio of 81/64 to 9/8 is 9/8, but that of 4/3 to 81/64 is 256/243. The names ‘tone’ and ‘semitone’ indicate an approximate comparison of the intervals. Numerically they are 1.125 and 1.05. The first is larger, so a tone corresponds to a bigger change in pitch than a semitone. Two semitones give a ratio 1.052, which is about 1.11; not far from 1.25. So two semitones are close to a tone. Not very close, I admit.
Continuing in this vein we can divide each tone into two intervals, each close to a semitone, to get a 12-note scale. This can be done in several different ways, yielding slightly different results. However it is done, there can be subtle but audible problems when changing the key of a piece of music: the intervals change slightly if, say, we move every note up a semitone. This effect could have been avoided if we had chosen a specific ratio for a semitone and arranged for its twelfth power to equal 2. Then two tones would make an exact semitone, 12 semitones would make an octave, and you could change scale by shifting all notes up or down by a fixed amount.
There is such a number, namely the twelfth root of 2, which is about 1.059, and it leads to the so-called ‘equitempered scale’. It’s a compromise; for example on the equitempered scale the 4/3 ratio for a fourth is 1.0595 = 1.335, instead of 4/3 = 1.333. A highly trained musician can detect the difference, but it’s easy to get used to it and most of us never notice.
The Pythagorean theory of harmony in nature, then, is actually built into the basis of Western music. To explain why simple ratios go hand in hand with musical harmony, we have to look at the physics of a vibrating string. The psychology of human perception also comes into the tale, but not yet.
The key is Newton’s second law of motion, relating acceleration to force. You also need to know how the force exerted by a string under tension changes as the string moves, stretching or contracting slightly. For this, we use something that Newton’s unwilling sparring partner Hooke discovered in 1660, called Hooke’s law: the change in length of a spring is proportional to the force exerted on it. (This is not a misprint for string – a violin string is effectively a kind of spring, so the same law applies.) One obstacle remains. We can apply Newton’s laws to a system composed of a finite number of masses: we get one equation per mass, and then do our best to solve the resulting system. But a violin string is a continuum, a line composed of infinitely many points. So the mathematicians of the period thought of the string as a large number of closely spaced point masses, linked together by Hooke’s-law springs. They wrote down the equations, slightly simplified to make them soluble; solved them; finally they let the number of masses become arbitrarily large, and worked out what happened to the solution.
John Bernoulli carried out this programme in 1727, and the outcome was extraordinarily pretty, considering what difficulties were being swept under the carpet. To avoid confusion in the descriptions that follow, imagine that the violin is lying on its back with the string horizontal. If you pluck the string it vibrates up and down at right angles to the violin. This is the image to bear in mind. Using the bow causes the string to vibrate sideways, and the presence of the bow is confusing. In the mathematical model, all we have is one string, fixed at its ends, and no violin; the string vibrates up and down in a plane. In this set-up Bernoulli found that the shape of the vibrating string, at any instant of time, was a sine curve. The amplitude of the vibration – the maximum height of this curve – also followed a sine curve, in time rather than space. In symbols, his solution looked like sin ct sin x, where c is a constant, Figure 35. The spatial part sin x tells us the shape, but this is scaled by a factor sin ct at time t. The formula says that the string vibrates up and down, repeating the same motion over and over again. The period of oscillation, the time between successive repeats, is 2π/c.
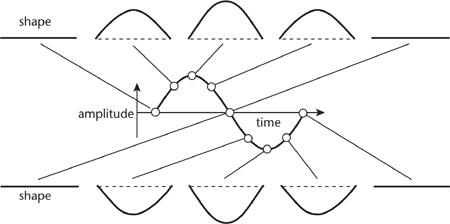
Fig 35 Successive snapshots of a vibrating string. The shape is a sine curve at each instant. The amplitude also varies sinusoidally with time.
This was the simplest solution that Bernoulli obtained, but there were others; all of them sine curves, different ‘modes’ of vibration, with 1, 2, 3, or more waves along the length of the string, Figure 36. Again, the sine curve was a snapshot of the shape at any instant, and its amplitude was multiplied by a time-dependent factor, which also varied sinusoidally. The formulas were sin 2ct sin 2x, sin 3ct sin 3x, and so on. The vibrational periods were 2π/2c, 2π/3c, and so on; so the more waves there were, the faster the string vibrated.

Fig 36 Snapshots of modes 1, 2, 3 of a vibrating string. In each case, the string vibrates up and down, and its amplitude varies sinusoidally with time. The more waves there are, the faster the vibration.
The string is always at rest at its ends, by the construction of the instrument and the assumptions of the mathematical model. In all modes except the first, there are additional points where the string is not vibrating; these occur where the curve crosses the horizontal axis. These ‘nodes’ are the mathematical reason for the occurrence of simple numerical ratios in the Pythagorean experiments. For example, since vibrational modes 2 and 3 occur in the same string, the gap between successive nodes in the mode-2 curve is 3/2 times the corresponding gap in the mode-3 curve. This explains why ratios like 3 : 2 arise naturally from the dynamics of the vibrating spring, but not why these ratios are harmonious while others are not. Before tackling this question, we introduce the main topic of this chapter: the wave equation.
The wave equation emerges from Newton’s second law of motion if we apply Bernoulli’s approach at the level of equations rather than solutions. In 1746 Jean Le Rond d’Alembert followed standard procedure, treating a vibrating violin string as a collection of point masses, but instead of solving the equations and looking for a pattern when the number of masses tended to infinity, he worked out what happened to the equations themselves. He derived an equation that described how the shape of the string changes over time. But before I show you what it looks like, we need a new idea, called a ‘partial derivative’.
Imagine yourself in the middle of the ocean, watching waves of various shapes and sizes pass by. As they do so, you bob up and down. Physically, you can describe how your surroundings are changing in several different ways. In particular, you can focus on changes in time or changes in space. As time passes at your location, the rate at which your height changes, with respect to time, is the derivative (in the sense of calculus, Chapter 3) of your height, also with respect to time. But this doesn’t describe the shape of the ocean near you, just how high the waves are as they pass you. To describe the shape, you can freeze time (conceptually) and work out how high the waves are: not just at your location, but at nearby ones. Then you can use calculus to work out how steeply the wave slopes at your location. Are you at a peak or trough? If so, the slope is zero. Are you halfway down the side of a wave? If so, the slope is quite large. In terms of calculus, you can put a number to that slope by working out the derivative of the wave’s height with respect to space.
If a function u depends on just one variable, call it x, we write the derivative as du/dx: ‘small change in u divided by small change in x’. But in the context of ocean waves the function u, the wave height, depends not just on space x but also on time t. At any fixed instant of time, we can still work out du/dx; it tells us the local slope of the wave. But instead of fixing time and letting space vary, we can also fix space and let time vary; this tells us the rate at which we are bobbing up and down. We could use the notation du/dt for this ‘time derivative’ and interpret it as ‘small change in u divided by small change in t’. But this notation hides an ambiguity: the small change in height, du, may be, and usually is, different in the two cases. If you forget that, you are likely to get your sums wrong. When we are differentiating with respect to space, we let the space variable change a little bit and see how the height changes; when we are differentiating with respect to time, we let the time variable change a little bit and see how the height changes. There is no reason why changes over time should equal changes over space.
So mathematicians decided to remind themselves of this ambiguity by changing the symbol d to something that did not (directly) make them think ‘small change’. They settled on a very cute curly d, written ∂. Then they wrote the two derivatives as ∂u/∂x and ∂u/∂t. You could argue that this isn’t a big advance, because it’s just as easy to confuse two different meanings of ∂u. There are two answers to this criticism. One is that in this context you are not supposed to think of ∂u as a specific small change in u. The other is that using a fancy new symbol reminds you not to get confused. The second answer definitely works: as soon as you see ∂, it tells you that you will be looking at rates of change with respect to several different variables. These rates of change are called partial derivatives, because conceptually you change only part of the set of variables, keeping the rest fixed.
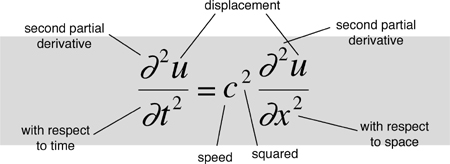
When d’Alembert worked out his equation for the vibrating string, he faced just this situation. The shape of the string depends on space – how far along the string you look – and on time. Newton’s second law of motion told him that the acceleration of a small segment of string is proportional to the force that acts on it. Acceleration is a (second) time derivative. But the force is caused by neighbouring segments of the string pulling on the one we’re interested in, and ‘neighbouring’ means small changes in space. When he calculated those forces, he was led to the equation
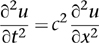
where u(x, t) is the vertical position at location x on the string at time t, and c is a constant related to the tension in the string and how springy it is. The calculations were actually easier than Bernoulli’s, because they avoided introducing special features of particular solutions.1
D’Alembert’s elegant formula is the wave equation. Like Newton’s second law, it is a differential equation – it involves (second) derivatives of u. Since these are partial derivatives, it is a partial differential equation. The second space derivative represents the net force acting on the string, and the second time derivative is the acceleration. The wave equation set a precedent: most of the key equations of classical mathematical physics, and a lot of the modern ones for that matter, are partial differential equations.
Once d’Alembert had written down his wave equation, he was in a position to solve it. This task was made much easier because it turned out to be a linear equation. Partial differential equations have many solutions, typically infinitely many, because each initial state leads to a distinct solution. For example, the violin string can in principle be bent into any shape you like before it is released and the wave equation takes over. ‘Linear’ means that if u(x, t) and v(x, t) are solutions, then so is any linear combination au(x, t) + bv(x, t), where a and b are constants. Another term is ‘superposition’. The linearity of the wave equation stems from the approximation that Bernoulli and d’Alembert had to make to get something they could solve: all disturbances are assumed to be small. Now the force exerted by the string can be closely approximated by a linear combination of the displacements of the individual masses. A better approximation would lead to a nonlinear partial differential equation, and life would be far more complicated. In the long run, these complications have to be tackled head-on, but the pioneers had enough to contend with already, so they worked with an approximate but very elegant equation and confined their attention to small-amplitude waves. It worked very well. In fact, it often worked pretty well for waves of larger amplitude too, a lucky bonus.
D’Alembert knew he was on the right track because he found solutions in which a fixed shape travelled along the string, just like a wave.2 The speed of the wave turned out to be the constant c in the equation. The wave could travel either to the left or to the right, and here the superposition principle came into play. D’Alembert proved that every solution is a superposition of two waves, one travelling leftwards and the other rightwards. Moreover, each separate wave could have any shape whatsoever.3 The standing waves found in the violin string, with fixed ends, turn out to be a combination of two waves of the same shape, one being upside down compared to the other, with one travelling to the left and the other (upside down) travelling to the right. At the ends, the two waves exactly cancel each other out: peaks of one coincide with troughs of the other. So they comply with the physical boundary conditions.
Mathematicians now had an embarrassment of riches. There were two ways to solve the wave equation: Bernoulli’s, which led to sines and cosines, and d’Alembert’s, which led to waves with any shape whatsoever. At first it looked as though d’Alembert’s solution must be more general: sines and cosines are functions, but most functions are not sines and cosines. However, the wave equation is linear, so you could combine Bernoulli’s solutions by adding constant multiples of them together. To keep it simple consider just a snapshot at a fixed time, getting rid of the time-dependence. Figure 37 shows 5 sin x + 4 sin 2x − 2 cos 6x, for example. It has a fairly irregular shape, and it wiggles a lot, but it’s still smooth and wavy.
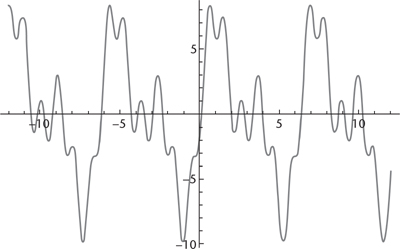
Fig 37 Typical combination of sines and cosines with various amplitudes and frequencies.
What bothered the more thoughtful mathematicians was that some functions are very rough and jagged, and you can’t get those as a linear combination of sines and cosines. Well, not if you use finitely many terms – and that suggested a way out. A convergent infinite series of sines and cosines (one whose sum to infinity makes sense) also satisfies the wave equation. Does it allow jagged functions as well as smooth ones? The leading mathematicians argued about this question, which finally came to a head when the same issue turned up in the theory of heat. Problems about heat flow naturally involved discontinuous functions, with sudden jumps, which was even worse than jagged ones. I’ll tell that story in Chapter 9, but the upshot is that most ‘reasonable’ wave shapes can be represented by an infinite series of sines and cosines, so they can be approximated as closely as you wish by finite combinations of sines and cosines.
Sines and cosines explain the harmonious ratios that so impressed the Pythagoreans. These special shapes of waves are important in the theory of sound because they represent ‘pure’ tones – single notes on an ideal instrument, so to speak. Any real instrument produces mixtures of pure notes. If you pluck a violin string, the main note you hear is the sin x wave, but superposed on that is a bit of sin 2x, maybe some sin 3x, and so on. The main note is called the fundamental and the others are its harmonics. The number in front of x is called the wave number. Bernoulli’s calculations tell us that the wave number is proportional to the frequency: how many times the string vibrates, for that particular sine wave, during a single oscillation of the fundamental.
In particular, sin 2x has twice the frequency of sin x. What does it sound like? It is the note one octave higher. This is the note that sounds most harmonious when played alongside the fundamental. If you look at the shape of the string for the second mode (sin 2x) in Figure 36, you’ll notice that it crosses the axis at its midpoint as well as the two ends. At that point, a so-called node, it remains fixed. If you placed your finger at that point, the two halves of the string would still be able to vibrate in the sin 2x pattern, but not in the sin x one. This explains the Pythagorean discovery that a string half as long produced a note one octave higher. A similar explanation deals with the other simple ratios that they discovered: they are all associated with sine curves whose frequencies have that ratio, and such curves fit together neatly on a string of fixed length whose ends are not allowed to move.
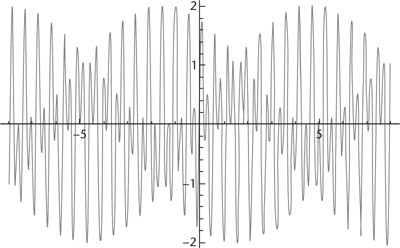
Why do these ratios sound harmonious? Part of the explanation is that sine waves with frequencies that are not in simple ratios produce an effect called ‘beats’ when they are superposed. For instance, a ratio like 11:23 corresponds to sin 11x + sin 23x, which looks like Figure 38, with lots of sudden changes in shape. Another part is that the ear responds to incoming sounds in roughly the same way as the violin string. The ear, too, vibrates. When two notes beat, the corresponding sound is like a buzzing noise that repeatedly gets louder and softer. So it doesn’t sound harmonious. However, there is a third part of the explanation: the ears of babies become attuned to the sounds that they hear most often. There are more nerve connections from the brain to the ear than there are in the other direction. So the brain adjusts the ear’s response to incoming sounds. In other words, what we consider to be harmonious has a cultural dimension. But the simplest ratios are naturally harmonious, so most cultures use them.
Mathematicians first derived the wave equation in the simplest setting they could think of: a vibrating line, a one-dimensional system. Realistic applications required a more general theory, modelling waves in two and three dimensions. Even staying within music, a drum requires two dimensions to model the patterns in which the drumskin vibrates. The same goes for water waves on the surface of the ocean. When an earthquake strikes, the whole Earth rings like a bell, and our planet is three-dimensional. Many other areas of physics involve models with two or three dimensions. Extending the wave equation to higher dimensions turned out to be straightforward; all you had to do was repeat the same kinds of calculation that had worked for the violin string. Having learned to play the game in this simple setting, it wasn’t hard to play it for real.
In three dimensions, for example, we use three space coordinates (x, y, z) and time t. The wave is described by a function u that depends on these four coordinates. For instance, this might describe the pressure in a body of air as sound waves pass through it. Making the same assumptions as d’Alembert, in particular that the amplitude of the disturbance is small, the same approach leads to an equally pretty equation:
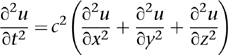
The formula inside the brackets is called the Laplacian, and it corresponds to the average difference between the value of u at the point in question, and its value nearby. This expression arises so often in mathematical physics that it has its own special symbol: ∇2u. To get the Laplacian in two dimensions, we just omit the term involving z, leading to the wave equation in that setting.
The main novelty in higher dimensions is that the shape within which the waves arise, called the domain of the equation, can be complicated. In one dimension the only connected shape is an interval, a segment of the line. In two dimensions, however, it can be any shape you can draw in the plane, and in three dimensions, any shape in space. You can model a square drum, a rectangular drum, a circular drum,4 or a drum shaped like the silhouette of a cat. For earthquakes, you might employ a spherical domain, or for greater accuracy, an ellipsoid squashed slightly at the poles. If you are designing a car and want to eliminate unwanted vibrations, your domain should be car-shaped – or whatever part of the car the engineers want to focus on.
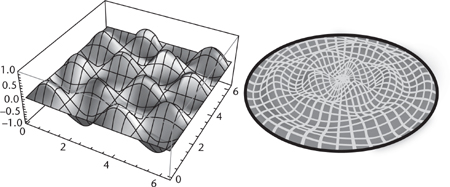
Fig 39 Left: Snapshot of one mode of a vibrating rectangular drum, with wave numbers 2 and 3. Right: Snapshot of one mode of a vibrating circular drum.
For any chosen shape of domain, there are functions analogous to Bernoulli’s sines and cosines: the simplest patterns of vibration. These patterns are called modes, or normal modes if you want to make it absolutely clear what you’re talking about. All other waves can be obtained by superposing normal modes, again using an infinite series if necessary. The frequencies of the normal modes represent the natural vibrational frequencies of the domain. If the domain is a rectangle, these are trigonometric functions of the form sin mx cos ny, for integers m and n, producing waves shaped like Figure 39 (left). If it is a circle, they are determined by new functions, called Bessel functions, with more interesting shapes, Figure 39 (right). The resulting mathematics applies not only to drums, but to water waves, sound waves, electromagnetic waves such as light (Chapter 11), even quantum waves (Chapter 14). It is fundamental to all of these areas. The Laplacian also turns up in equations for other physical phenomena; in particular, electric, magnetic, and gravitational fields. The mathematician’s favourite trick of starting with a toy problem, one so simple that it cannot possibly be realistic, pays off big time for waves.
This is one reason why it is unwise to judge a mathematical idea by the context in which it first arises. Modelling a violin string may seem pointless when what you want to understand is earthquakes. But if you jump in at the deep end, and try to cope with all of the complexities of real earthquakes, you’ll drown. You should start out paddling in the shallow end and gain confidence to swim a few lengths of the pool. Then you’ll be ready for the high diving board.
The wave equation was a spectacular success, and in some areas of physics it describes reality very closely. However, its derivation requires several simplifying assumptions. When those assumptions are unrealistic, the same physical ideas can be modified to suit the context, leading to different versions of the wave equation.
Earthquakes are a typical example. Here the main problem is not d’Alembert’s assumption that the amplitude of the wave is small, but changes in the physical properties of the domain. These properties can have a strong effect on seismic waves, vibrations that travel through the Earth. By understanding those effects, we can look deep inside our planet and find out what it is made of.
There are two main kinds of seismic wave: pressure waves and shear waves, usually abbreviated to P-waves and S-waves. (There are many others: this is a simplified account, covering some of the basics.) Both can occur in a solid medium, but S-waves don’t occur in fluids. P-waves are waves of pressure, analogous to sound waves in air, and the changes in pressure point in the direction along which the wave propagates. Such waves are said to be longitudinal. S-waves are transverse waves, changing at right angles to the direction of travel, like the waves on a violin string. They cause solids to shear, that is, deform like a pack of cards pushed sideways, so that the cards slide along one another. Fluids don’t behave like packs of cards.
When an earthquake happens, it sends out both kinds of wave. The P-waves travel faster, so a seismologist somewhere else on the Earth’s surface observes those first. Then the slower S-waves arrive. In 1906 the English geologist Richard Oldham exploited this difference to make a major discovery about our planet’s interior. Roughly speaking, the Earth has an iron core, surrounded by a rocky mantle, and the continents float on top of the mantle. Oldham suggested that the outer layers of the core must be liquid. If so, S-waves can’t pass through those regions, but P-waves can. So there is a kind of S-wave shadow, and you can work out where it is by observing signals from earthquakes. The English mathematician Harold Jeffreys sorted out the details in 1926 and confirmed that Oldham was right.
If the earthquake is big enough, it can cause the entire planet to vibrate in one of its normal modes – the analogues for the Earth of sines and cosines for a violin. The whole planet rings like a bell, in a sense that would be literal if only we could hear the very low frequencies involved. Instruments sensitive enough to record these modes appeared in the 1960s, and they were used to observe the two most powerful earthquakes yet recorded scientifically. These were the Chilean earthquake of 1960 (magnitude 9.5) and the Alaskan earthquake of 1964 (magnitude 9.2). The first killed around 5000 people; the second killed about 130 thanks to its remote location. Both caused tsunamis and did a huge amount of damage. Both offered an unprecedented view of the Earth’s deep interior, by exciting the Earth’s basic vibrational modes.
Sophisticated versions of the wave equation have given seismologists the ability to see what’s happening hundreds of kilometres beneath our feet. They can map the Earth’s tectonic plates as one slides beneath another, known as subduction. Subduction causes earthquakes, especially so-called megathrust earthquakes like the two just mentioned. It also gives rise to mountain chains along the edges of continents, such as the Andes, and volcanoes, where the plate gets so deep that it starts to melt and magma rises to the surface. A recent discovery is that the plates need not subduct as a whole, but can break up into gigantic slabs, sinking back into the mantle at different depths.
The biggest prize in this area would be a reliable way to predict earthquakes and volcanic eruptions. This is proving elusive, because the conditions that trigger such events are complex combinations of many factors in many locations. However, some progress is being made, and the seismologists’ version of the wave equation underpins many of the methods being investigated.
The same equations have more commercial applications. Oil companies prospect for liquid gold, a few kilometres underground, by setting off explosions at the surface and using returning echoes from the seismic waves they generate to map out the underlying geology. The main mathematical problem here is to reconstruct the geology from the signals received, which is a bit like using the wave equation backwards. Instead of solving the equation in a known domain to work out what the waves do, mathematicians use the observed wave patterns to reconstruct the geological features of the domain. As is often the case, working backwards like this – solving the inverse problem, in the jargon – is harder than going the other way. But practical methods exist. One of the major oil companies performs such calculations a quarter of a million times every day.
Drilling for oil has its own problems, as the blowout at the Deepwater Horizon oil rig in 2010 made clear. But at the moment, human society is heavily dependent on oil, and it would take decades to reduce this significantly, even if everyone wanted to. Next time you fill up your tank, give a thought to the mathematical pioneers who wanted to know how a violin produces its sounds. It wasn’t a practical problem then, and it still isn’t today. But without their discoveries, your car would take you nowhere.