
The equation models matter not as a particle, but as a wave, and describes how such a wave propagates.
Schrödinger’s equation is fundamental to quantum mechanics, which together with general relativity constitute today’s most effective theories of the physical universe.
A radical revision of the physics of the world at very small scales, in which every object has a ‘wave function’ that describes a probability cloud of possible states. At this level the world is inherently uncertain. Attempts to relate the microscopic quantum world to our macroscopic classical world led to philosophical issues that still reverberate. But experimentally, quantum theory works beautifully, and today’s computer chips and lasers wouldn’t work without it.
In 1900 the great physicist Lord Kelvin declared that the then current theory of heat and light, considered to be an almost complete description of nature, was ‘obscured by two clouds. The first involves the question: How could the Earth move through an elastic solid, such as is essentially the luminiferous ether? The second is the Maxwell–Boltzmann doctrine regarding the partition of energy.’ Kelvin’s nose for an important problem was spot on. In Chapter 13 we saw how the first question led to, and was resolved by, relativity. Now we will see how the second led to the other great pillar of present-day physics, quantum theory.
The quantum world is notoriously weird. Many physicists feel that if you don’t appreciate just how weird it is, you don’t appreciate it at all. There is a lot to be said for that opinion, because the quantum world is so different from our comfortable human-scale one that even the simplest concepts change out of all recognition. It is, for example, a world in which light is both a particle and a wave. It is a world where a cat in a box can be both alive and dead at the same time … until you open the box, that is, when suddenly the unfortunate animal’s wave function ‘collapses’ to one state or the other. In the quantum multiverse, there exists one copy of our universe in which Hitler lost World War II, and another in which he won it. We just happen to live in – that is, exist as quantum wave functions in – the first one. Other versions of us, just as real but inaccessible to our senses, live in the other one.
Quantum mechanics is definitely weird. Whether it is quite that weird, though, is another matter altogether.
It all began with light bulbs. This was appropriate, because those were one of the most spectacular applications to emerge from the burgeoning subjects of electricity and magnetism, which Maxwell so brilliantly unified. In 1894 a German physicist named Max Planck was hired by an electrical company to design the most efficient light bulb possible, one giving the most light while consuming the least electrical energy. He saw that the key to this question was a fundamental issue in physics, raised in 1859 by another German physicist, Gustav Kirchhoff. It concerned a theoretical construct known as a black body, which absorbs all electromagnetic radiation that falls on it. The big question was: how does such a body emit radiation? It can’t store it all; some has to come back out again. In particular, how does the intensity of the emitted radiation depend on its frequency and the body’s temperature?
There was already an answer from thermodynamics, in which a black body can be modelled as a box whose walls are perfect mirrors. Electromagnetic radiation bounces to and fro, reflected by the mirrors. How is the energy in the box distributed among the various frequencies when the system has settled to an equilibrium state? In 1876 Boltzmann proved the ‘equipartition theorem’: the energy is apportioned equally to each independent component of the motion. These components are just like the basic waves in a violin string: normal modes.
There was only one problem with this answer: it couldn’t possibly be correct. It implied that the total power radiated over all frequencies must be infinite. This paradoxical conclusion became known as the ultraviolet catastrophe: ultraviolet because that was the beginning of the high-frequency range, and catastrophe because it was. No real body can emit an infinite amount of power.
Although Planck was aware of this problem, it didn’t bother him, because he didn’t believe the equipartition theorem anyway. Ironically, his work resolved the paradox and did away with the ultraviolet catastrophe, but he noticed this only later. He used experimental observations of how energy depended on frequency, and fitted a mathematical formula to the data. His formula, derived early in 1900, did not initially have any physical basis. It was just a formula that worked. But later the same year he tried to reconcile his formula with the classical thermodynamic one, and decided that the energy levels of the black body’s vibrational modes could not form a continuum, as thermodynamics assumed. Instead, these levels had to be discrete – separated by tiny gaps. In fact, for any given frequency, the energy had to be an integer multiple of that frequency, multiplied by a very tiny constant. We now call this number Planck’s constant and denote it by h. Its value, in units of joule seconds, is 6.62606957(29) × 10−34, where the figures in brackets may be inaccurate. This value is deduced from theoretical relationships between Planck’s constant and other quantities that are easier to measure. The first such measurement was made by Robert Millikan using the photoelectric effect, described below. The tiny packets of energy are now called quanta (plural of quantum), from the Latin quantus, ‘how much.’
Planck’s constant may be tiny, but if the set of energy levels for a given frequency is discrete, the total energy turns out to be finite. So the ultraviolet catastrophe was a sign that a continuum model failed to reflect nature. And that implied that nature, on very small scales, must be discrete. Initially this didn’t occur to Planck: he thought of his discrete energy levels as a mathematical trick to get a sensible formula. In fact, Boltzmann had entertained a similar idea in 1877, but didn’t get anywhere with it. Everything changed when Einstein brought his fertile imagination to bear, and physics entered a new realm. In 1905, the same year as his work on special relativity, he investigated the photoelectric effect, in which light hitting a suitable metal causes it to emit electrons. Three years earlier Philipp Lenard had noticed that when the light has a higher frequency, the electrons have higher energies. But the wave theory of light, amply confirmed by Maxwell, implies that the energy of the electrons should depend on the intensity of the light, not on its frequency. Einstein realised that Planck’s quanta would explain the discrepancy. He suggested that light, rather than being a wave, was composed of tiny particles, now called photons. The energy in a single photon, of a given frequency, should be the frequency times Planck’s constant – just like one of Planck’s quanta. A photon was a quantum of light.
There’s an obvious problem with Einstein’s theory of the photoelectric effect: it assumes light is a particle. But there was abundant evidence that light was a wave. On the other hand, the photoelectric effect was incompatible with light being a wave. So was light a wave, or a particle?
Yes.
It was – or had aspects that manifested themselves as – either. In some experiments, light seemed to behave like a wave. In others, it behaved like a particle. As physicists came to grips with very small scales of the universe, they decided that light wasn’t the only thing to have this strange dual nature, sometimes particle, sometimes wave. All matter did. They called it wave–particle duality. The first person to grasp this dual nature of matter was Louis-Victor de Broglie, in 1924. He rephrased Planck’s law in terms not of energy, but of momentum, and suggested that the momentum of the particle aspect and the frequency of the wave aspect should be related: multiply them together and you get Planck’s constant. Three years later he was proved right, at least for electrons. One the one hand, electrons are particles, and can be observed behaving that way. On the other hand, they diffract like waves. In 1988 atoms of sodium were also spotted behaving like a wave.
Matter was neither particle nor wave, but a bit of both – a wavicle.
Several more or less intuitive images of this dual nature of matter were devised. In one, a particle is a localised clump of waves, known as a wave packet, Figure 54. The packet as a whole can behave like a particle, but some experiments can probe its internal wavelike structure. Attention shifted from providing images for wavicles to sorting out how they behaved. The quest quickly attained its goal, and the central equation of quantum theory emerged.
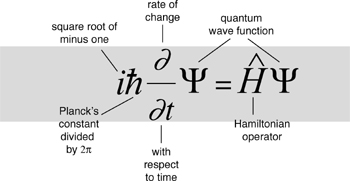
The equation bears the name of Erwin Schrödinger. In 1927, building on the work of several other physicists, notably Werner Heisenberg, he wrote down a differential equation for any quantum wave function. It looked like this:
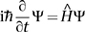
Here Ψ (Greek capital psi) is the form of the wave, t is time (so ∂/∂t applied to Ψ gives its rate of change with respect to time), Ĥ is an expression called the Hamiltonian operator, and ħ is h/2π, where h is Planck’s constant. And i? That was the weirdest feature of all. It’s the square root of minus one (Chapter 5). Schrödinger’s equation applies to waves defined over the complex numbers, not just the real numbers as in the familiar wave equation.
Waves in what? The classical wave equation (Chapter 8) defines waves in space, and its solution is a numerical function of space and time. The same goes for Schrödinger’s equation, but now the wave function Ψ takes complex values, not just real ones. It’s a bit like an ocean wave whose height is 2 + 3i. The appearance of i is in many ways the most mysterious and profound feature of quantum mechanics. Previously i had turned up in solutions of equations, and in methods for finding those solutions, but here it was part of the equation, an explicit feature of the physical law.
One way to interpret this is that quantum waves are linked pairs of real waves, as if my complex ocean wave were really two waves, one of height 2 and the other of height 3, with the two directions of height at right angles to each other. But it’s not quite that straightforward, because the two waves don’t have a fixed shape. As time passes, they cycle through a whole series of shapes, and each is mysteriously linked to the other. It’s a bit like the electric and magnetic components of a light wave, but now electricity can and does ‘rotate’ into magnetism, and conversely. The two waves are two facets of a single shape, which spins steadily around the unit circle in the complex plane. Both the real and the imaginary parts of this rotating shape change in a very specific way: they are combined in sinusoidally varying amounts. Mathematically this leads to the idea that a quantum wave function has a special kind of phase. The physical interpretation of that phase is similar to, but different from, the role of phase in the classical wave equation.
Remember how Fourier’s trick solves both the heat equation and the wave equation? Some special solutions, Fourier’s sines and cosines, have especially pleasant mathematical properties. All other solutions, however complicated, are superpositions of these normal modes. We can solve Schrödinger’s equation using a similar idea, but now the basic patterns are more complicated than sines and cosines. They are called eigenfunctions, and they can be distinguished from all other solutions. Instead of being some general function of both space and time, an eigenfunction is a function defined only on space, multiplied by one depending only on time. The space and time variables, in the jargon, are separable. The eigenfunctions depend on the Hamiltonian operator, which is a mathematical description of the physical system concerned. Different systems – an electron in a potential well, a pair of colliding photons, whatever – have different Hamiltonian operators, hence different eigenfunctions.
For simplicity, consider a standing wave for the classical wave equation – a vibrating violin string, whose ends are pinned down. At all instants of time, the shape of the string is almost the same, but the amplitude is modulated: multiplied by a factor that varies sinusoidally with time, as in Figure 35 (page 138). The complex phase of a quantum wave function is similar, but harder to visualise. For any individual eigenfunction, the effect of the quantum phase is just a shift of the time coordinate. For a superposition of several eigenfunctions, you split the wave function into these components, factor each into a purely spatial part times a purely temporal one, spin the temporal part round the unit circle in the complex plane at the appropriate speed, and add the pieces back together. Each separate eigenfunction has a complex amplitude, and this modulates at its own particular frequency.
It may sound complicated, but it would be completely baffling if you didn’t split the wave function into eigenfunctions. At least then you’ve got a chance.
Despite these complexities, quantum mechanics would be just a fancy version of the classical wave equation, resulting in two waves rather than one, were it not for a puzzling twist. You can observe classical waves, and see what shape they are, even if they are superpositions of several Fourier modes. But in quantum mechanics, you can never observe the entire wave function. All you can observe on any given occasion is a single component eigenfunction. Roughly speaking, if you attempt to measure two of these components at the same time, the measurement process on one of them disturbs the other one.
This immediately raises a difficult philosophical issue. If you can’t observe the entire wave function, does it actually exist? Is it a genuine physical object, or just a convenient mathematical fiction? Is an unobservable quantity scientifically meaningful? It is here that Schrödinger’s celebrated feline enters the story. It arises because of a standard way to interpret what a quantum measurement is, called the Copenhagen interpretation.1
Imagine a quantum system in some superposed state: say, an electron whose state is a mixture of spin-up and spin-down, which are pure states defined by eigenfunctions. (It doesn’t matter what spin-up and spin-down mean.) When you observe the state, however, you either get spin-up, or you get spin-down. You can’t observe a superposition. Moreover, once you’ve observed one of these – say spin-up – that becomes the actual state of the electron. Somehow your measurement seems to have forced the superposition to change into a specific component eigenfunction. This Copenhagen interpretation takes this statement literally: your measurement process has collapsed the original wave function into a single pure eigenfunction.
If you observe a lot of electrons, sometimes you get spin-up, sometimes spin-down. You can infer the probability that the electron is in one of those states. So the wave function itself can be interpreted as a kind of probability cloud. It doesn’t show the actual state of the electron: it shows how probable it is that when you measure it, you get a particular result. But that makes it a statistical pattern, not a real thing. It no more proves the wave function is real than Quetelet’s measurements of human height prove that a developing embryo possesses some sort of bell curve.
The Copenhagen interpretation is straightforward, reflects what happens in experiments, and makes no detailed assumptions about what happens when you observe a quantum system. For these reasons, most working physicists are very happy to use it. But some were not, in the early days when they theory was still being thrashed out, and some still are not. And one of the dissenters was Schrödinger himself.
In 1935, Schrödinger was worrying about the Copenhagen interpretation. He could see that it worked, on a pragmatic level, for quantum systems like electrons and photons. But the world around him, even though deep down inside it was just a seething mass of quantum particles, seemed different. Seeking a way to make the difference as glaring as he could, Schrödinger came up with a thought experiment in which a quantum particle had a dramatic and obvious effect on a cat.
Imagine a box, which when shut is impervious to all quantum interactions. Inside it, place an atom of radioactive matter, a radiation detector, a flask of poison, and a live cat. Now shut the box, and wait. At some point the radioactive atom will decay, and emit a particle of radiation. The detector will spot it, and is rigged so that when it does so, it causes the flask to break and release the poison inside. This kills the cat.
In quantum mechanics, the decay of a radioactive atom is a random event. From outside, no observer can tell whether the atom has decayed or not. If it has, the cat is dead; if not, it’s alive. According to the Copenhagen interpretation, until someone observes the atom, it is in a superposition of two quantum states: decayed and not decayed. The same goes for the states of the detector, the flask, and the cat. So the cat is in a superposition of two states: dead and alive.
Since the box is impervious to all quantum interactions, the only way to find out whether the atom has decayed and killed the cat is to open the box. The Copenhagen interpretation tells us that the instant we do this, the wave functions collapse and the cat suddenly switches to a pure state: either dead, or alive. However, the inside of the box is no different from the external world, where we never observe a cat that is in a superposed alive/dead state. So before we open the box and observe its contents, there must either be a dead cat inside, or a live one.
Schrödinger intended this thought experiment as a criticism of the Copenhagen interpretation. Microscopic quantum systems obey the superposition principle and can exist in mixed states; macroscopic ones can’t. By linking a microscopic system, the atom, to a macroscopic one, the cat, Schrödinger was pointing out what he believed to be a flaw in the Copenhagen interpretation: it gave nonsense when applied to a cat. He must have been startled when the majority of physicists responded, in effect: ‘Yes, Erwin, you’re absolutely right: until someone opens the box, the cat really is simultaneously dead and alive.’ Especially when it dawned on him that he couldn’t find out who was right, even if he opened the box. He would observe either a live cat or a dead one. He might infer that the cat had been in that state before he opened the box, but he couldn’t be sure. The observable result was consistent with the Copenhagen interpretation.
Very well: add a film camera to the contents of the box, and film what actually happens. That will decide the matter. ‘Ah, no,’ the physicists replied. ‘You can only see what the camera has filmed after you open the box. Before that, the film is in a superposed state: containing a movie of a live cat, and containing a movie of a dead one.’
The Copenhagen interpretation freed up physicists to do their calculations and sort out what quantum mechanics predicted, without facing up to the difficult, if not impossible, issue of how the classical world emerged from a quantum substrate – how a macroscopic device, unimaginably complex on a quantum scale, somehow made a measurement of a quantum state. Since the Copenhagen interpretation did the job, they weren’t really interested in philosophical questions. So generations of physicists were taught that Schrödinger had invented his cat to show that quantum superposition extended into the macroscopic world too: the exact opposite of what Schrödinger had been trying to tell them.
It’s not really a great surprise that matter behaves strangely on the level of electrons and atoms. We may initially rebel at the thought, out of unfamiliarity, but if an electron is really a tiny clump of waves rather than a tiny clump of stuff, we can learn to live with it. If that means that the state of the electron is itself a bit weird, spinning not just about an up axis or a down axis but a bit of both, we can live with that too. And if the limitations of our measuring devices imply that we can never catch the electron doing that kind of thing – that any measurement we make necessarily settles for some pure state, up or down – then that’s how it is. If the same applies to a radioactive atom, and the states are ‘decayed’ or ‘not decayed’, because its component particles have states as elusive as those of the electron, we can even accept that the atom itself, in its entirety, may be in a superposition of those states until we make a measurement. But a cat is a cat, and it seems to be a very big stretch of the imagination to imagine that the animal can be both alive and dead at the same time, only to miraculously collapse into one or the other when we open the box that contains it. If quantum reality requires a superposed alive/dead cat, why is it so shy that it won’t let us observe such a state?
There are sound reasons in the formalism of quantum theory that (until very recently) require any measurement, any ‘observable’, to be an eigenfunction. There are even sounder reasons why the state of a quantum system should be a wave, obeying Schrödinger’s equation. How can you get from one to the other? The Copenhagen interpretation declares that somehow (don’t ask how) the measurement process collapses the complex, superposed wave function down to a single component eigenfunction. Having been provided with this form of words, your task as a physicist is to get on with making measurements and calculating eigenfunctions and so on, and stop asking awkward questions. It works amazingly well, if you measure success by getting answers that agree with experiment. And everything would have been fine if Schrödinger’s equation permitted the wave function to behave in this manner, but it doesn’t. In The Hidden Reality Brian Greene puts it this way: ‘Even polite prodding reveals an uncomfortable feature … The instantaneous collapse of a wave … can’t possible emerge from Schrödinger’s math.’ Instead, the Copenhagen interpretation was a pragmatic bolt-on to the theory, a way to handle measurements without understanding or facing up to what they really were.
This is all very well, but it’s not what Schrödinger was trying to point out. He introduced a cat, rather than an electron or an atom, because it put what he considered to be the main issue in sharp relief. A cat belongs to the macroscopic world in which we live, in which matter does not behave the way quantum mechanics demands. We do not see superposed cats.2 Schrödinger was asking why our familiar ‘classical’ universe fails to resemble the underlying quantum reality. If everything from which the world is built can exist in superposed states, why does the universe look classical? Many physicists have performed wonderful experiments showing that electrons and atoms really do behave the way quantum and Copenhagen say they should. But this misses the point: you have to do it with a cat. Theorists wondered whether the cat could observe its own state, or whether someone else could secretly open the box and write down what was inside. They concluded, following the same logic as Schrödinger, that if the cat observed its state then the box contained a superposition of a dead cat that had committed suicide by observing itself, and a live cat that had observed itself to be alive, until the legitimate observer (a physicist) opened the box. Then the whole shebang collapsed to one or the other. Similarly the friend became a superposition of two friends: one of whom had seen a dead cat while the other had seen a live one, until a physicist opened the box, causing the friend’s state to collapse. You could proceed in this way until the state of the entire universe was a superposition of a universe with a dead cat and a universe with a live one, and then the state of the universe collapsed when a physicist opened the box.
It was all a bit embarrassing. Physicists could get on with their work without sorting it out, they could even deny there was anything to be sorted out, but something was missing. For example, what happens to us if an alien physicist on the planet Apellobetnees III opens a box? Do we suddenly discover we actually blew ourselves up in a nuclear war when the Cuban missile crisis of 1962 escalated, and have been living on borrowed time ever since?
The measurement process is not the neat, tidy mathematical operation that the Copenhagen interpretation assumes. When asked to describe how the apparatus comes to its decision, the Copenhagen interpretation replies ‘it just does’. The image of the wave function collapsing to a single eigenfunction describes the input and the output of the measurement process, but not how to get from one to the other. But when you make a real measurement you don’t just wave a magic wand and cause the wave function to disobey Schrödinger’s equation and collapse. Instead, you do something so enormously complicated, from a quantum viewpoint, that it is obviously hopeless to model it realistically. To measure an electron’s spin, for example, you make it interact with a suitable piece of apparatus, which has a pointer that either moves to the ‘up’ position or the ‘down’ one. Or a numerical display, or a signal sent to a computer … This device yields one state, and one state only. You don’t see the pointer in a superposition of up and down.
We are used to this, because that’s how the classical world works. But underneath it’s supposed to be a quantum world. Replace the cat with the spin apparatus, and it should indeed exist in a superposed state. The apparatus, viewed as a quantum system, is extraordinarily complicated. It contains gazillions of particles – between 1025 and 1030, at a rough estimate. The measurement emerges somehow from the interaction of that single electron with these gazillion particles. Admiration for the expertise of the company that manufactures the instrument must be boundless; to extract anything sensible from something so messy is almost beyond belief. It’s like trying to work out someone’s shoe size by making them pass through a city. But if you’re clever (arrange for them to encounter a shoe shop) you can get a sensible result, and a clever instrument designer can produce meaningful measurements of electron spin. But there’s no realistic prospect of modelling in detail how such a device works as a bona fide quantum system. There’s too much detail, the biggest computer in the world would flounder. That makes it difficult to analyse a real measurement process using Schrödinger’s equation.
Even so, we do have some understanding of how our classical world emerges from an underlying quantum one. Let’s start with a simple version, a ray of light hitting a mirror. The classical answer, Snell’s law, states that the reflected ray bounces off at the same angle as the one that hit. In his book QED on quantum electrodynamics, the physicist Richard Feynman explained that this is not what happens in the quantum world. The ray is really a stream of photons, and each photon can bounce all over the place. However, if you superpose all the possible things the photon could do, then you get Snell’s law. The overwhelming proportion of photons bounce back at angles very close to the one at which they hit. Feynman even managed to show why without using any complicated mathematics, but behind this calculation is a general mathematical idea: the principle of stationary phase. If you superpose all quantum states for an optical system, you get the classical outcome in which light rays follow the shortest path, measured by time taken. You can even add bells and whistles to decorate the ray paths with classical wave-optical diffraction fringes.
This example shows, very explicitly, that the superposition of all possible worlds – in this optical framework – yields the classical world. The most important feature is not so much the detailed geometry of the light ray, but the fact that it yields only one world at the classical level. Down in the quantum details of individual photons, you can observe all the paraphernalia of superposition, eigenfunctions, and so on. But up at the human scale, all that cancels out – well, adds together – to produce a clean, classical world.
The other part of the explanation is called decoherence. We’ve seen that quantum waves have a phase as well as an amplitude. It’s a very funny phase, a complex number, but it’s a phase nonetheless. The phase is absolutely crucial to any superposition. If you take two superposed states, change the phase of one, and add them back together, what you get is nothing like the original. If you do the same with a lot of components, the reassembled wave can be almost anything. Loss of phase information wrecks any Schrödinger’s cat-like superposition. You don’t just lose track of whether it’s alive or dead: you can’t tell it was a cat. When quantum waves cease to have nice phase relations, they decohere – they start to behave more like classical physics, and superpositions lose any meaning. What causes them to decohere is interactions with surrounding particles. This is presumably how apparatus can measure electron spin and get a specific, unique result.
Both of these approaches lead to the same conclusion: classical physics is what you observe if you take a human-scale view of a very complicated quantum system with gazillions of particles. Special experimental methods, special devices, might preserve some of the quantum effects, making them poke up into our comfortable classical existence, but generic quantum systems quickly cease to appear quantum as we move to larger scales of behaviour.
That’s one way to resolve the fate of the poor cat. Only if the box is totally impervious to quantum decoherence can the experiment produce the superposed cat, and no such box exists. What would you make it from?
But there’s another way, one that goes to the opposite extreme. Earlier I said that ‘You could proceed in this way until the state of the entire universe was a superposition.’ In 1957 Hugh Everett Jr. pointed out that in a sense, you have to. The only way to provide an accurate quantum model of a system is to consider its wave function. Everyone was happy to do so when the system was an electron, or an atom, or (more controversially) a cat. Everett took the system to be the entire universe.
He argued that you had no choice if that’s what you wanted to model. Nothing less than the universe can be truly isolated. Everything interacts with everything else. And he discovered that if you took that step, then the problem of the cat, and the paradoxical relation between quantum and classical reality, is easily resolved. The quantum wave function of the universe is not a pure eigenmode, but a superposition of all possible eigenmodes. Although we can’t calculate such things (we can’t for a cat, and a universe is a tad more complicated) we can reason about them. In effect, we are representing the universe, quantum-mechanically, as a combination of all the possible things that a universe can do.
The upshot was that the wave function of the cat does not have to collapse to give a single classical observation. It can remain completely unchanged, with no violation of Schrödinger’s equation. Instead, there are two coexisting universes. In one, the cat died; in the other, it didn’t. When you open the box, there are correspondingly two yous and two boxes. One of them is part of the wave function of a universe with a dead cat; the other is part of a different wave function with a live cat. In place of a unique classical world that somehow emerges from the superposition of quantum possibilities, we have a vast range of classical worlds, each corresponding to one quantum possibility.
Everett’s original version, which he called the relative state formulation, came to popular attention in the 1970s through Bryce DeWitt, who gave it a more catchy name: the many-worlds interpretation of quantum mechanics. It is often dramatised in historical terms: for example, that there is a universe in which Adolf Hitler won World War II, and another one in which he didn’t. The one in which I am writing this book is the latter, but somewhere alongside it in the quantum realm another Ian Stewart is writing a book very similar to this one, but in German, reminding his readers that they are in the universe where Hitler won. Mathematically, Everett’s interpretation can be viewed as a logical equivalent of conventional quantum mechanics, and it leads – in more limited interpretations – to efficient ways to solve physics problems. His formalism will therefore survive any experimental test that conventional quantum mechanics survives. So does that imply that these parallel universes, ‘alternate worlds’ in transatlantic parlance, really exist? Is another me typing away happily on a computer keyboard in a world where Hitler won? Or is the set-up a convenient mathematical fiction?
There is an obvious problem: how can we be sure that in a world dominated by Hitler’s dream, the Thousand Year Reich, computers like the one I’m using would exist? Clearly there must be many more universes than two, and events in them must follow sensible classical patterns. So maybe Stewart-2 doesn’t exist but Hitler-2 does. A common description of the formation and evolution of parallel universes involves them ‘splitting off’ whenever there is a choice of quantum state. Greene points out that this image is wrong: nothing splits. The universe’s wave function has been, and always will be, split. Its component eigenfunctions are there:we imagine a split when we select one of them, but the whole point of Everett’s explanation is that nothing in the wave function actually changes.
With that as a caveat, a surprising number of quantum physicists accept the many-worlds interpretation. Schrödinger’s cat really is alive and dead. Hitler really did win and lose. One version of us lives in one of those universes, others do not. That’s what the mathematics says. It’s not an interpretation, a convenient way to arrange the calculations. It’s as real as you and I. It is you and I.
I’m not convinced. It’s not the superposition that bothers me, though. I don’t find the existence of a parallel Nazi world unthinkable, or impossible.3 But I do object, strenuously, to the idea that you can separate a quantum wave function according to human-scale historical narratives. The mathematical separation occurs at the level of quantum states of constituent particles. Most combinations of particle states make no sense whatsoever as a human narrative. A simple alternative to a dead cat is not a live cat. It is a dead cat with one electron in a different state. Complex alternatives are far more numerous than a live cat. They include a cat that suddenly explodes for no apparent reason, one that turns into a flower vase, one that gets elected president of the United States, and one that survived even though the radioactive atom released the poison. Those alternative cats are rhetorically useful but unrepresentative. Most alternatives are not cats at all; in fact, they are indescribable in classical terms. If so, most of the alternative Stewarts aren’t recognisable as people – indeed as anything – and almost all of those that exist do so within a world that makes absolutely no sense in human terms. So the chance that another version of little old me happens to live in another world that makes narrative sense to a human being is negligible.
The universe may well be an incredibly complex superposition of alternative states. If you think quantum mechanics is basically right, it has to be. In 1983 the physicist Stephen Hawking said that the many-worlds interpretation was ‘self-evidently correct’ in this sense. But it doesn’t follow that there exists a superposition of universes in which a cat is alive or dead, and Hitler did or did not win. There is no reason to suppose that the mathematical components can be separated into sets that fit together to create human narratives. Hawking dismissed narrative interpretations of the many-worlds formalism, saying ‘All that one does, really, is to calculate conditional probabilities – in other words, the probability of A happening, given B. I think that that’s all the many-worlds interpretation is. Some people overlay it with a lot of mysticism about the wave function splitting into different parts. But all that you’re calculating is conditional probabilities.’
It’s worth comparing the Hitler tale with Feynman’s story of the light ray. In the style of alternative Hitlers, Feynman would be telling us that there is one classical world where the light ray bounces off the mirror at the same angle at which it hit, another classical world in which it bounces at an angle that’s one degree wrong, another where it’s two degrees wrong, and so on. But he didn’t. He told us that there is one classical world, emerging from the superposition of the quantum alternatives. There may be innumerable parallel worlds at the quantum level, but these do not correspond in any meaningful way to parallel worlds that are describable at the classical level. Snell’s law is valid in any classical world. If it weren’t, the world couldn’t be classical. As Feynman explained for light rays, the classical world emerges when you superpose all of the quantum alternatives. There is only one such superposition, so there is only one classical universe. Ours.
Quantum mechanics isn’t confined to the laboratory. The whole of modern electronics depends on it. Semiconductor technology, the basis of all integrated circuits – silicon chips – is quantum-mechanical. Without the physics of the quantum, no one would have dreamed that such devices could work. Computers, mobile phones, CD players, games consoles, cars, refrigerators, ovens, virtually all modern household gadgets, contain memory chips, to contain the instructions that make these devices do what we want. Many contain more complex circuitry, such as microprocessors, an entire computer on a chip. Most memory chips are variations on the first true semiconductor device: the transistor.
In the 1930s, American physicists Eugene Wigner and Frederick Seitz analysed how electrons move though a crystal, a problem that requires quantum mechanics. They discovered some of the basic features of semiconductors. Some materials are conductors of electricity: electrons can flow through them with ease. Metals are good conductors, and in everyday use copper wire is commonplace for this purpose. Insulators do not permit electrons to flow, so they stop the flow of electricity: the plastics that sheathe electrical wires, to prevent us electrocuting ourselves on the TV power lead, are insulators. Semiconductors are a bit of both, depending on circumstances. Silicon is the best known, and currently the most widely used, but several other elements such as antimony, arsenic, boron, carbon, germanium, and selenium are also semiconductors. Because semiconductors can be switched from one state to the other, they can be used to manipulate electrical currents, and this is the basis of all electronic circuits.
Wigner and Seitz discovered that the properties of semiconductors depend on the energy levels of the electrons within them, and these levels can be controlled by ‘doping’ the basic semiconductor material by adding small quantities of specific impurities. Two important types are p-type semiconductors, which carry current as a flow of electrons, and n-type semiconductors, in which current flows in the opposite direction to the electrons, carried by ‘holes’ – places where there are fewer electrons than normal. In 1947 John Bardeen and Walter Brattain at Bell Laboratories discovered that a crystal of germanium could act as an amplifier. If an electrical current was fed into it, the output current was higher. William Shockley, leader of the Solid State Physics Group, realised how important this could be, and initiated a project to investigate semiconductors. Out of this came the transistor – short for ‘transfer resistor’. There were some earlier patents but no working devices or published papers. Technically the Bell Labs’ device was a JFET (junction gate field-effect transistor, Figure 55). Since this initial breakthrough, many other kinds of transistor have been invented. Texas Instruments manufactured the first silicon transistor in 1954. The same year saw a transistor-based computer, TRIDAC, built by the US military. It was three cubic feet in size and its power requirement was the same as one light bulb. This was an early step in a huge American military programme to develop alternatives to vacuum tube electronics, which was too cumbersome, fragile, and unreliable for military use.
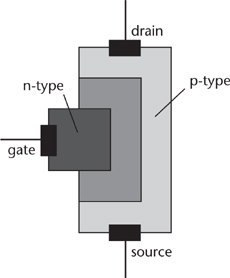
Fig 55 Structure of a JFET. The source and drain are at the ends, in a p-type layer, while the gate is an n-type layer that controls the flow. If you think of the flow of electrons from source to drain as a hose, the gate in effect squeezes the hose, increasing the pressure (voltage) at the drain.
Because semiconductor technology is based on doping silicon or similar substances with impurities, it lent itself to miniaturisation. Circuits can be built up in layers on a silicon substrate, by bombarding the surface with the desired impurity, and etching away unwanted regions with acid. The areas affected are determined by photographically produced masks, and these can be shrunk to very small size using optical lenses. Out of all this emerged today’s electronics, including memory chips that can hold billions of bytes of information and very fast microprocessors that orchestrate the activity of computers.
Another ubiquitous application of quantum mechanics is the laser. This is a device that emits a strong beam of coherent light: one in which the light waves are all in phase with each other. It consists of an optical cavity with mirrors at each end, filled with something that reacts to light of a specific wavelength by producing more light of the same wavelength – a light amplifier. Pump in energy to start the process rolling, let the light bounce to and fro along the cavity, amplifying all the time, and when it reaches a sufficiently high intensity, let it out. The gain medium can be a fluid, a gas, a crystal, or a semiconductor. Different materials work at different wavelengths. The amplification process depends on the quantum mechanics of atoms. The electrons in the atoms can exist in different energy states, and they can be switched between them by absorbing or emitting photons.
LASER means light amplification by stimulated emission of radiation. When the first laser was invented, it was widely derided as an answer looking for a problem. This was unimaginative: a whole host of suitable problems quickly appeared, once there was a solution. Producing a coherent beam of light is basic technology, and it was always bound to have uses, just as an improved hammer would automatically find many uses. When inventing generic technology, you don’t have to have a specific application in mind. Today we use lasers for so many purposes that it’s impossible to list them all. There are prosaic uses like laser pointers for lectures and laser beams for DIY. CD players, DVD players, and Blu-ray all use lasers to read information from tiny pits or marks on discs. Surveyors use lasers to measure distances and angles. Astronomers use lasers to measure the distance from the Earth to the Moon. Surgeons use lasers for fine cutting of delicate tissues. Laser treatment of eyes is routine, for repairing detached retinas and remoulding the surface of the cornea to correct vision instead of using glasses or contact lenses. The ‘Star Wars’ antimissile system was intended to use powerful lasers to shoot down enemy missiles, and although it was never built, some of the lasers were. Military uses of lasers, akin to the pulp science-fiction ray-gun, are being investigated right now. And it may even be possible to launch space vehicles from Earth by making them ride a powerful laser beam.
New uses of quantum mechanics arrive almost by the week. One of the latest is quantum dots, tiny pieces of semiconductor whose electronic properties, including the light that they emit, vary according to their size and shape. They can therefore be tailored to have many desirable features. They already have a variety of applications, including biological imaging, where they can replace traditional (and often toxic) dyes. They also perform much better, emitting brighter light.
Further down the line, some engineers and physicists are working on the basic components of a quantum computer. In such a device, the binary states of 0 and 1 can be superposed in any combination, in effect allowing computations to assume both values at the same time. This would allow many different calculations to be performed in parallel, speeding them up enormously. Theoretical algorithms have been devised, carrying out such tasks as splitting a number into its prime factors. Conventional computers run into trouble when the numbers have more than a hundred digits or so, but a quantum computer should be able to factorise much bigger numbers with ease. The main obstacle to quantum computing is decoherence, which destroys superposed states. Schrödinger’s cat is exacting revenge for its inhumane treatment.