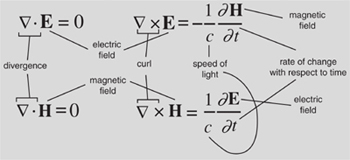

Electricity and magnetism can’t just leak away. A spinning region of electric field creates a magnetic field at right angles to the spin. A spinning region of magnetic field creates an electric field at right angles to the spin, but in the opposite direction.
It was the first major unification of physical forces, showing that electricity and magnetism are intimately interrelated.
The prediction that electromagnetic waves exist, travelling at the speed of light, so light itself is such a wave. This motivated the invention of radio, radar, television, wireless connections for computer equipment, and most modern communications.
At the start of the nineteenth century most people lit their houses using candles and lanterns. Gas lighting, which dates from 1790, was occasionally used in homes and business premises, mainly by inventors and entrepreneurs. Gas street lighting came into use in Paris in 1820. At that time, the standard way to send messages was to write a letter and send it by horse-drawn carriage; for urgent messages, keep the horse but omit the carriage. The main alternative, mostly restricted to military and official communications, was the optical telegraph. This used semaphore: mechanical devices placed on towers, which could represent letters or words in code by arranging rigid arms at various angles. These configurations could be seen through a telescope and relayed to the next tower in line. The first extensive system of this kind dates from 1792, when the French engineer Claude Chappe built 556 towers to create a 4800 kilometre network across most of France. It remained in use for sixty years.
Within a hundred years, homes and streets had electric lighting, electric telegraphy had come and gone, and people could talk to each other by telephone. Physicists had demonstrated radio communications in their laboratories, and one entrepreneur had already set up a factory selling ‘wirelesses’ – radio sets – to the public. Two scientists made the main discoveries that triggered this social and technological revolution. One was the Englishman Michael Faraday, who established the basic physics of electromagnetism – a tightly-knit combination of the previously separate phenomena of electricity and magnetism. The other was a Scotsman, James Clerk Maxwell, who turned Faraday’s mechanical theories into mathematical equations and used them to predict the existence of radio waves travelling at the speed of light.
The Royal Institution in London is an imposing building, fronted by classical columns, tucked away on a side street near Piccadilly Circus. Today its main activity is to host popular science events for the public, but when it was founded in 1799 its brief also included ‘diffusing the knowledge, and facilitating the general introduction, of useful mechanical inventions’. When John ‘Mad Jack’ Fuller established a Chair in Chemistry at the Royal Institution, its first incumbent was not an academic. He was the son of a would-be blacksmith, and he had trained as a bookseller’s apprentice. The position allowed him to read voraciously, despite his family’s lack of cash, and Jane Marcet’s Conversations on Chemistry and Isaac Watts’s The Improvement of the Mind inspired a deep interest in science in general and electricity in particular.
The young man was Michael Faraday. He had attended lectures at the Royal Institution given by the eminent chemist Humphry Davy, and he sent the lecturer 300 pages of notes. Shortly afterwards Davy had an accident that damaged his eyesight, and asked Faraday to become his secretary. Then an assistant at the Royal Institution got the sack, and Davy suggested Faraday as a replacement, setting him to work on the chemistry of chlorine.
The Royal Institution allowed Faraday to pursue his own scientific interests as well, and he carried out innumerable experiments on the newly discovered topic of electricity. In 1821 he learned of the work of the Danish scientist Hans Christian Ørsted, linking electricity to the much older phenomenon of magnetism. Faraday exploited this link to invent an electric motor, but Davy got upset when he didn’t get any credit, and told Faraday to work on other things. Davy died in 1831, and two years later Faraday began a series of experiments on electricity and magnetism that sealed his reputation as one of the greatest scientists ever to have lived. His extensive investigations were partly motivated by the need to come up with large numbers of novel experiments to edify the man in the street and entertain the great and the good, as part of the Royal Institution’s brief to encourage the public understanding of science.
Among Faraday’s inventions were methods for turning electricity into magnetism and both into motion (a motor) and for turning motion into electricity (a generator). These exploited his greatest discovery, electromagnetic induction. If material that can conduct electricity moves through a magnetic field, an electrical current will flow through it. Faraday discovered this in 1831. Francesco Zantedeschi had already noticed the effect in 1829, and Joseph Henry also spotted it a little later. But Henry delayed publishing his discovery, and Faraday took the idea much further than Zantedeschi had done. Faraday’s work went far beyond the Royal Institution’s brief to facilitate useful mechanical inventions, by creating innovative machines that exploited frontier physics. This led, fairly directly, to electric power, lighting, and a thousand other gadgets. When others took up the baton, the whole panoply of modern electrical and electronic equipment burst upon the scene, starting with radio, moving on to television, radar, and long-distance communications. It was Faraday, more than any other single individual, who created the modern technological world, with the help of vital new ideas from hundreds of gifted engineers, scientists, and businessmen.
Being working class and lacking the normal education of a gentleman, Faraday taught himself science but not mathematics. He developed his own theories to explain and guide his experiments, but they rested on mechanical analogies and conceptual machines, not on formulas and equations. His work took its deserved place in basic physics through the intervention of one of Scotland’s greatest scientific intellects, James Clerk Maxwell.
Maxwell was born the same year that Faraday announced the discovery of electromagnetic induction. One application, the electromagnetic telegraph, quickly followed, thanks to Gauss and his assistant Wilhelm Weber. Gauss wanted to use wires to carry electrical signals between Göttingen Observatory, where he hung out, to the Institute of Physics a kilometre away, where Weber worked. Presciently, Gauss simplified the previous technique for distinguishing letters of the alphabet – one wire per letter – by introducing a binary code using positive and negative current, see Chapter 15. By 1839 the Great Western Railway company was sending messages by telegraph from Paddington to West Drayton, a distance of 21 kilometres. In the same year Samuel Morse independently invented his own electric telegraph in the USA, employing Morse code (invented by his assistant Alfred Vail) and sending its first message in 1838.
In 1876, three years before Maxwell died, Alexander Graham Bell took out the first patent on a new gadget, the acoustic telegraph. It was a device that turned sound, especially speech, into electrical impulses, and transmitted them along a wire to a receiver, which turned them back into sound. We now know it as the telephone. He wasn’t the first person to conceive of such a thing, or even to build one, but he held the master patent. Thomas Edison improved the design with his carbon microphone of 1878. A year later, Edison developed the carbon filament electric light bulb, and cemented himself in the popular mind as the inventor of electric lighting. In point of fact, he was preceded by at least 23 inventors, the best known being Joseph Swan, who had patented his version in 1878. In 1880, one year after Maxwell’s death, the city of Wabash, Illinois became the first to use electric lighting for its streets.
These revolutions in communication and lighting owed a lot to Faraday; electrical power generation also owed a lot to Maxwell. But Maxwell’s most far-reaching legacy was to make the telephone seem like a child’s toy. And it stemmed, directly and inevitably, from his equations for electromagnetism.
Maxwell was born into a talented but eccentric Edinburgh family, which included lawyers, judges, musicians, politicians, poets, mining speculators, and businessmen. As a teenager he began to succumb to the charms of mathematics, winning a school competition with an essay on how to construct oval curves using pins and thread. At 16 he went to Edinburgh University, where he studied mathematics and experimented in chemistry, magnetism, and optics. He published papers in pure and applied mathematics in the Royal Society of Edinburgh’s journal. In 1850 his mathematical career took a more serious turn and he moved to Cambridge University, where he was privately coached for the mathematical tripos examination by William Hopkins. The tripos in those days consisted of solving complicated problems, often involving clever tricks and extensive calculations, against the clock. Later Godfrey Harold Hardy, one of England’s best mathematicians and a Cambridge professor, would have strong views about how to do creative mathematics, and cramming for a tricky examination wasn’t it. In 1926 he remarked that his aim was ‘not… to reform the tripos, but to destroy it’. But Maxwell crammed, and thrived, in the competitive atmosphere, probably because he had that sort of mind.
He also continued his weird experiments, among other things trying to work out how a cat always lands on its feet, even when it is held upside down only a few centimetres above a bed. The difficulty is that this appears to violate Newtonian mechanics; the cat has to rotate through 180 degrees, but has nothing to push against. The precise mechanism eluded him, and was not worked out until the French doctor Jules Marey made a series of photographs of a falling cat in 1894. The secret is that the cat is not rigid: it twists its front and back in opposite directions and back again, while extending and retracting its paws to stop these motions cancelling out.1
Maxwell got his mathematics degree, and continued as a postgraduate at Trinity College. There he read Faraday’s Experimental Researches and worked on electricity and magnetism. He took up a chair of Natural Philosophy in Aberdeen, investigating Saturn’s rings and the dynamics of the molecules in gases. In 1860 he moved to King’s College London, and here he could sometimes meet with Faraday. Now Maxwell embarked on his most influential quest: to formulate a mathematical basis for Faraday’s experiments and theories.
At the time, most physicists working on electricity and magnetism were looking for analogies with gravity. It seemed sensible: opposite electrical charges attract each other with a force which, like gravity, is proportional to the inverse square of the distance separating them. Like charges repel each other with a similarly varying force, and the same goes for magnetism, where charges are replaced by magnetic poles. The standard way of thinking was that gravity was a force whereby one body mysteriously acted on another distant body, without anything passing between the two; electricity and magnetism were assumed to act in the same manner. Faraday had a different idea: they are both ‘fields’, phenomena that pervade space and can be detected by the forces they produce.
What is a field? Maxwell could make little progress until he could describe the concept mathematically. But Faraday, lacking mathematical training, had posed his theories in terms of geometric structures, such as ‘lines of force’ along which the fields pulled and pushed. Maxwell’s first great breakthrough was to reformulate these ideas by analogy with the mathematics of fluid flow, where the field in effect is the fluid. Lines of force were then analogous to the paths followed by the molecules of the fluid; the strength of the electric or magnetic field was analogous to the velocity of the fluid. Informally, a field was an invisible fluid; mathematically, it behaved exactly like that, whatever it really was. Maxwell borrowed ideas from the mathematics of fluids and modified them to describe magnetism. His model accounted for the main properties observed in electricity.
Not content with this initial attempt, he went on to include not just magnetism, but its relation to electricity. As the electrical fluid flowed, it affected the magnetic one, and vice versa. For magnetic fields Maxwell used the mental image of tiny vortices spinning in space. Electric fields were similarly composed of tiny charged spheres. Following this analogy and the resulting mathematics, Maxwell began to understand how a change in the electric force could create a magnetic field. As the spheres of electricity move, they cause the magnetic vortices to spin, like a football fan passing through a turnstile. The fan moves without spinning; the turnstile spins without moving.
Maxwell was slightly dissatisfied with this analogy, saying ‘I do not bring it forward… as a mode of connection existing in nature… It is, however… mechanically conceivable and easily investigated, and it serves to bring out the actual mechanical connections between the known electromagnetic phenomena.’ To show what he meant, he used the model to explain why parallel wires carrying opposite electrical currents repel each other, and he also explained Faraday’s crucial discovery of electromagnetic induction.
The next step was to retain the mathematics while getting rid of the mechanical gadgetry that propelled the analogy. This amounted to writing down equations for the basic interactions between the electrical and magnetic fields, derived from the mechanical model, but divorced from this origin. Maxwell achieved this goal in 1864 in his famous paper ‘A dynamical theory of the electromagnetic field’.
We now interpret his equations using vectors, which are quantities that possess not just a size, but a direction. The most familiar is velocity: the size is the speed, how fast the object is moving; the direction is the one along which it moves. The direction really does matter: a body moving vertically upwards at 10 kps behaves very differently from one moving vertically downwards at 10 kps. Mathematically, a vector is represented by its three components: its effect along three axes at right angles to each other, such as north/south, east/west, and up/down. The bare bones are thus that a vector is a triple (x, y, z) composed of three numbers, Figure 44. The velocity of a fluid at a given point, for instance, is a vector. In contrast, the pressure at a given point is a single number: the fancy term used to distinguish this from a vector is ‘scalar’.
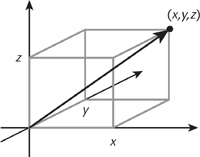
Fig 44 A three-dimensional vector.
In these terms, what is the electric field? From Faraday’s perspective it is determined by lines of electrical force. In Maxwell’s analogy, these are flow-lines of the electrical fluid. A flow-line tells us in which direction the fluid is flowing, and as a molecule moves along the flow-line, we can also observe its speed. For each point in space, the flow-line passing through that point therefore determines a vector, which describes the speed and direction of the electric fluid, that is, the strength and direction of the electric field at that point. Conversely, if we know these speeds and directions, for every point in space, we can deduce what the flow-lines look like, so in principle we know the electric field.
In short: the electric field is a system of vectors, one for each point in space. Each vector prescribes the strength and direction of the electrical force (exerted on a tiny charged test particle) at that point. Mathematicians call such a quantity a vector field: it is a function that assigns to each point in space the corresponding vector. Similarly, the magnetic field is determined by the magnetic lines of force; it is the vector field corresponding to the forces that would be exerted on a tiny magnetic test particle.
Having sorted out what electric and magnetic fields were, Maxwell could write down equations describing what they did. We now express these equations using two vector operators, known as divergence and curl. Maxwell used specific formulas involving the three components of the electric and magnetic fields. In the special case in which there are no conducting wires or metal plates, no magnets, and everything happens in a vacuum, the equations take a slightly simpler form, and I will restrict the discussion to this case.
Two of the equations tell us that the electric and magnetic fluids are incompressible – that is, electricity and magnetism cannot just leak away, they have to go somewhere. This translates as ‘the divergence is zero’, leading to the equations
∇. E = 0 ∇. H = 0
where the upside-down triangle and the dot are the notation for the divergence. Two more equations tell us that when a region of electric field spins in a small circle, it creates a magnetic field at right angles to the plane of that circle, and similarly a spinning region of magnetic field creates an electric field at right angles to the plane of that circle. There is a curious twist: the electric and magnetic fields point in opposite directions for a given direction of spin. The equations are
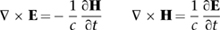
where now the upside-down triangle and the cross are the notation for the curl. The symbol t stands for time, and ∂/∂t is the rate of change with respect to time. Notice that the first equation has a minus sign, but the second does not: this represents the opposite orientations that I mentioned.
What is c? It is a constant, the ratio of electromagnetic to electrostatic units. Experimentally this ratio is just under 300,000, in units of kilometres divided by seconds. Maxwell immediately recognised this number: it is the speed of light in a vacuum. Why did that quantity appear? He decided to find out. One clue, dating back to Newton, and developed by others, was the discovery that light was some kind of wave. But no one knew what the wave consisted of.
A simple calculation provided the answer. Once you know the equations for electromagnetism, you can solve them to predict how the electric and magnetic fields behave in different circumstances. You can also derive general mathematical consequences. For instance, the second pair of equations relates E to H; any mathematician will immediately try to derive equations that contain only E and only H, because that lets us concentrate on each field separately. Considering its epic consequences, this task turns out to be absurdly simple – if you have some familiarity with vector calculus. I’ve put the detailed working in the Notes,2 but here’s a quick summary. Following our noses, we start with the third equation, which relates the curl of E to the time-derivative of H. We don’t have any other equations involving the time-derivative of H, but we do have one that involves the curl of H, namely, the fourth equation. This suggests that we should take the third equation and form the curl of both sides. Then we apply the fourth equation, simplify, and emerge with
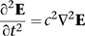
which is the wave equation!
The same trick applied to the curl of H produces the same equation with H in place of E. (The minus sign is applied twice, so it disappears.) So both the electric and magnetic fields, in a vacuum, obey the wave equation. Since the same constant c occurs in each wave equation, they both travel at the same speed, namely c. So this little calculation predicts that both the electric field and the magnetic field can simultaneously support a wave – making it an electromagnetic wave, in which both fields vary in concert with each other. And the speed of that wave is … the speed of light.
It’s another of those trick questions. What travels at the speed of light? This time the answer is what you’d expect: light. But there is a momentous implication: light is an electromagnetic wave.
This was stupendous news. There was no reason, prior to Maxwell’s derivation of his equations, to imagine such a fundamental link between light, electricity, and magnetism. But there was more. Light comes in many different colours, and once you know that light is a wave, you can work out that these correspond to waves with different wavelengths – distance betweens successive peaks. The wave equation imposes no conditions on the wavelength, so it can be anything. The wavelengths of visible light are restricted to a small range, because of the chemistry of the eye’s light-detecting pigments. Physicists already knew of ‘invisible light’, ultraviolet and infrared. Those, of course, had wavelengths just outside the visible range. Now Maxwell’s equations led to a dramatic prediction: electromagnetic waves with other wavelengths should also exist. Conceivably, any wavelength – long or short – could occur, Figure 45.
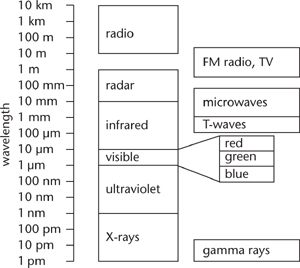
Fig 45 The electromagnetic spectrum.
No one had expected this, but as soon as theory said it ought to happen, experimentalists could go and look for it. One of them was a German, Heinrich Hertz. In 1886 he constructed a device that could generate radio waves and another that could receive them. The transmitter was little more than a machine that could produce a high-voltage spark; theory indicated that such a spark would emit radio waves. The receiver was a circular loop of copper wire, whose size was chosen to resonate with the incoming waves. A small gap in the loop, a few hundredths of a millimetre across, would reveal those waves by producing tiny sparks. In 1887 Hertz did the experiment, and it was a success. He went on to investigate many different features of radio waves. He also measured their speed, getting an answer close to the speed of light, which confirmed Maxwell’s prediction and confirmed that his apparatus really was detecting electromagnetic waves.
Hertz knew that his work was important as physics, and he published it in Electric Waves: being researches on the propagation of electric action with finite velocity through space. But it never occurred to him that the idea might have practical uses. When asked, he replied ‘It’s of no use whatsoever … just an experiment that proves Maestro Maxwell was right – we just have these mysterious electromagnetic waves that we cannot see with the naked eye. But they are there.’ Pressed for his view of the implications, he said ‘Nothing, I guess.’
Was it a failure of imagination, or just a lack of interest? It’s hard to tell. But Hertz’s ‘useless’ experiment, confirming Maxwell’s prediction of electromagnetic radiation, would quickly lead to an invention that made the telephone look like a children’s toy.
Radio.
Radio makes use of an especially intriguing range of the spectrum: waves with wavelengths much longer than light. Such waves would be likely to retain their structure over long distances. The key idea, the one that Hertz missed, is simple: if you could somehow impress a signal on a wave of that kind, you could talk to the world.
Other physicists, engineers, and entrepreneurs were more imaginative, and quickly spotted radio’s potential. To realise that potential, however, they had to solve a number of technical problems. They needed a transmitter that could produce a sufficiently powerful signal, and something to receive it. Hertz’s apparatus was restricted to a distance of a few feet; you can understand why he didn’t suggest communication as a possible application. Another problem was how to impose a signal. A third was how far the signal could be sent, which might well be limited by the curvature of the Earth. If a straight line between transmitter and receiver hits the ground, this would presumably block the signal. Later it turned out that nature has been kind to us, and the Earth’s ionosphere reflects radio waves in a wide range of wavelengths, but before this was discovered there were obvious ways round the potential problem anyway. You could build tall towers and put the transmitters and receivers on those. By relaying signals from one tower to another, you could send messages round the globe, very fast.
There are two relatively obvious ways to impress a signal on a radio wave. You can make the amplitude vary or you can make the frequency vary. These methods are called amplitude-modulation and frequency-modulation: AM and FM. Both were used and both still exist. That was one problem solved. By 1893 the Serbian engineer Nikola Tesla had invented and built all of the main devices needed for radio transmission, and he had demonstrated his methods to the public. In 1894 Oliver Lodge and Alexander Muirhead sent a radio signal from the Clarendon laboratory in Oxford to a nearby lecture theatre. A year later the Italian inventor Guglielmo Marconi transmitted signals over a distance of 1.5 kilometres using new apparatus he had invented. The Italian government declined to finance further work, so Marconi moved to England. With the support of the British Post Office he soon improved the range to 16 kilometres. Further experiments led to Marconi’s law: the distance over which signals can be sent is roughly proportional to the square of the height of the transmitting antenna. Make the tower twice as tall and the signal goes four times as far. This, too, was good news: it suggested that long-range transmission should be practical. Marconi set up a transmitting station on the Isle of Wight in the UK in 1897, and opened a factory the next year, making what he called ‘wirelesses’. We still called them that in 1952, when I listened to the Goon Show and Dan Dare on the wireless in my bedroom, but even then we also referred to the device as ‘the radio’. The word ‘wireless’ has of course come back into vogue, but now it is the links between your computer and its keyboard, mouse, modem, and Internet router that are wireless, rather than the link from your receiver to a distant transmitter. It’s still done by radio.
Initially Marconi owned the main patents to radio, but he lost them to Tesla in 1943 in a court battle. Technological advances quickly made those patents obsolete. From 1906 to the 1950s, the vital electronic component of a radio was the vacuum tube, like a smallish light bulb, so radios had to be big and bulky. The transistor, a much smaller and more robust device, was invented in 1947 at Bell Laboratories by an engineering team that included William Shockley, Walter Brattain, and John Bardeen (see Chapter 14). By 1954 transistor radios were on the market, but radio was already losing its primacy as an entertainment medium.
By 1953, I’d already seen the future. It was the coronation of Queen Elizabeth II, and my aunt in Tonbridge had … a television set! So we piled into my father’s rickety car and drove 40 miles to watch the event. I was more impressed by Bill and Ben the Flowerpot Men than by the coronation, to be honest, but from that moment radio was no longer the epitome of modern household entertainment. Soon we, too, possessed a television set. Anyone who has grown up with 48-inch flatscreen colour TVs with high definition and a thousand channels will be appalled to hear that in those days the picture was black-and-white, about 12 inches across, and (in the UK) there was exactly one channel, the BBC. When we watched ‘the television’ it really meant the television.
Entertainment was just one application of radio waves. They were also vital to the military, for communications and other purposes. The invention of radar (radio detection and ranging) may well have won World War II for the Allies. This top-secret device made it possible to detect aircraft, especially enemy aircraft, by bouncing radio signals off them and observing the reflected waves. The urban myth that carrots are good for your eyesight originated in wartime disinformation, intended to stop the Nazis wondering why the British were getting so good at spotting raiding bombers. Radar has peacetime uses as well. It is how air traffic controllers keep tabs on where all the planes are, to prevent collisions; it guides passenger jets to the runway in fog; it warns pilots of imminent turbulence. Archaeologists use ground-penetrating radar to locate likely sites for the remains of tombs and ancient structures.
X-rays, first studied systematically by Wilhelm Röntgen in 1875, have much shorter wavelengths than light. This makes them more energetic, so they can pass through opaque objects, notably the human body. Doctors could use X-rays to detect broken bones and other physiological problems, and still do, although modern methods are more sophisticated and subject the patient to far less damaging radiation. X-ray scanners can now create three-dimensional images of a human body, or some part of it, in a computer. Other kinds of scanner can do the same thing using different physics.
Microwaves are efficient ways to send telephone signals, and they also turn up in the kitchen in microwave ovens, quick ways to heat food. One of the latest applications to emerge is in airport security. Terahertz radiation, otherwise known as T-waves, can penetrate clothing and even body cavities. Customs officials can use them to spot drug smugglers and terrorists. Their use is a little controversial, since they amount to an electronic strip-search, but most of us seem to think that’s a small price to pay if it stops a plane being blown up or cocaine hitting the streets. T-waves are also useful to art historians, because they can reveal murals covered in layers of plaster. Manufacturers and commercial carriers can use T-waves to inspect products without taking them out of their boxes.
The electromagnetic spectrum is so versatile, and so effective, that its influence is now felt in virtually all spheres of human activity. It makes things possible that to any previous generation would appear miraculous. It took a vast number of people, from every profession, to turn the possibilities inherent in the mathematical equations into real gadgets and commercial systems. But none of this was possible until someone realised that electricity and magnetism can join forces to create a wave. The whole panoply of modern communications, from radio and television to radar and microwave links for mobile phones, was then inevitable. And it all stemmed from four equations and a couple of lines of basic vector calculus.
Maxwell’s equations didn’t just change the world. They opened up a new one.