CHAPTER 7
Capital Structure Decisions (Marriott Corporation and Gary Wilson)

This chapter illustrates how firms should think about their financial policies, in particular their capital structure. Our setting is the Marriott Corporation in 1980 and its exceptional CFO, Gary Wilson.

The Marriott Corporation began as an A&W Root Beer stand in 1927, two years before the Great Depression. In 1937, the firm began providing in-flight catering at Hoover Field, an airfield in Arlington, VA, which is now the site of the Pentagon. Marriott went public with a share price of $10.53 in 1953 and opened its first “motor lodge” hotel in 1957. By the late 1950s, the Marriott Corporation was at the forefront of both airline food and the motel industry. By 1979, the firm had grown substantially and was diversified into Hotels (35% of sales), Contract Food Services (32% of sales), Restaurants (25% of sales), and Theme Parks and Cruise Ships (8% of sales); the firm's total sales topped $1.5 billion. The firm remained family controlled (holding 6.5 million of the approximately 36.2 million shares outstanding), and family members occupied four of the eight seats on the board of directors. At a time when there were few women or minorities on boards, the firm was also proud to be one of the few Fortune 500 firms with a woman on its board—Mom.

In the late 1970s, Marriott implemented a major policy change in its product market operations. Marriott went from owning its hotel properties to managing them. That is, Marriott formerly had built, owned, and operated its hotels. Now, Marriott built its hotels and then sold them to investors, while maintaining a contract to operate the facility as a Marriott hotel. As explained in Marriott's 1980 Annual Report: “This enables Marriott's hotel business to expand 25% annually without commensurate capital requirements thereby releasing investment capacity to fund additional corporate growth.” (page 18)

CAPITAL STRUCTURE

Around the same time, Gary Wilson, Marriott's CFO, was considering changing the firm's capital structure by issuing debt and using the proceeds to retire equity. The first question we want to ask is: What are the implications of changing a firm's capital structure?

To answer the question, we first have to understand what capital structure is. At its simplest, capital structure is how a firm finances its assets. For example, Marriott uses straight debt, mortgages, convertible debt, leases, and equity to finance its assets (see Appendix 7A, Marriott's Financial Information, and Appendix 7B for selected ratios).

Let us begin, however, by keeping it simple and just focusing on the two largest categories: debt and equity. Does it make a difference whether a firm is financed with debt or equity? A major factor in that decision is the relative cost to the firm of using debt versus equity financing. There is typically a large difference in cost between debt and equity. In 1979, Marriott's after-tax cost of debt (K_d) was about 5% compared to its return on equity (ROE) of about 18%.¹ However, these are not the correct comparisons: we want to compare the “market” costs of debt and equity. Our cost of debt is already market-based: Marriott's before-tax cost of debt was about 10%, and its marginal tax rate was approximately 46%.² Since interest payments on debt are tax deductible, the effective after-tax cost of debt is the interest rate on debt times one minus the tax rate, or approximately 5%. We can write this as:

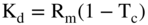
where:

• R_m is the firm's before tax market cost of debt, and
• T_c is the firm's corporate tax rate.

The cost of equity is not as easy to observe in the market. ROE is an accounting-based number and is not a correct estimate of the market cost of capital. Corporate finance professionals usually compute the cost of equity using the Capital Asset Pricing Model (CAPM). That model says:

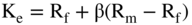
where:

• R_f is the risk-free rate in the market
• R_m is the market's rate of return
• β (Beta) is a measure of risk.³

We typically use the rate on U.S. government bonds as the risk-free rate (R_f). At the time of the decision, this was 10.4%.⁴ In using the CAPM formula, R_m is not used alone. Instead, an estimate of R_m – R_f, which is called the market risk premium, is used instead. This estimate is usually taken from the historical average of R_m − R_f. At the time of the case, Marriott's beta was 1.25, and a good estimate of the market risk premium was 8%. Using the CAPM, Marriott's cost of equity is therefore estimated as 20.4%, which is significantly above the 18% ROE.

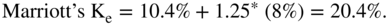
Now, if equity is so much more expensive than debt, why don't firms use all debt? The reason firms don't use 100% debt is that, while debt is safer to the investor, it is riskier to the firm. Debt is safer (to an investor) than equity because debt holders have priority claim to the firm's assets in bankruptcy (i.e., debt holders get paid first, before shareholders, in bankruptcy). Debt holders also have the right to force a firm into bankruptcy if their repayment terms are not honored. By contrast, firms are not contractually required to make any payments to equity holders. Consider what happens if a firm can't make any payments to equity: the owners' (i.e., the stockholders) principal recourse is to sell their shares to someone else. However, if a firm can't make its debt payments, the debt holders have the right to force the firm into bankruptcy.

To briefly summarize, firms choose to finance their assets with some combination of debt and equity. While debt is cheaper to the firm than equity, it is also riskier since it increases the chance of bankruptcy.

What Happens If the Capital Structure Changes?

Now, the costs of debt and equity do not stay constant. If a firm adds more debt to its capital structure, the cost of debt increases because the risk of default increases, and the debt holders will require a greater return to compensate for the increased risk. That is, if the current before-tax cost of debt is 10%, as a firm adds more debt, the additional debt becomes more expensive. The rate of increase in the cost of debt (or interest rate) is not constant for all debt levels. When a firm already has a high level of debt, the same percentage increase in debt will cause a greater increase in interest rates than it would at low levels of debt. That is, as we add debt to a firm's capital structure, the same incremental increases in debt become riskier and riskier, and thus more expensive.

As the percentage of debt increases, the cost of debt continues to rise. So, can the cost of debt ever go above the cost of equity? Modigliani and Miller⁵ (M&M) showed that as you add debt, while the cost of debt goes up, so does the cost of equity. The increases in the cost of equity, like debt, will increase by greater amounts as the percentage of debt in the firm's capital structure increases. This means that (in almost all cases) at any given level of debt, the cost of debt remains less than the cost of equity.

For example, let's look at a firm in bankruptcy. Due to the risk of not being paid, the cost of debt for a bankrupt firm is potentially as high as 20–30%. The question now is: If a firm's cost of debt is 25%, then what return does the market require on the firm's equity? The answer is something greater than 25%. Why? Because the equity holders are paid after the debt holders and, therefore, bear more risk and demand a higher return. There are very few instances in the world where this is not true. Thus, we usually state that the cost of debt is less than the cost of equity at all levels of debt.

To review, as we increase the percentage of debt, the cost of debt goes up and the cost of equity goes up, but the cost of debt remains below the cost of equity.

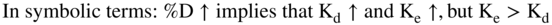
Let's next ask what happens to other financial measures if a firm substitutes debt for equity in its capital structure, as Wilson wants Marriott to do. First, let's look at earnings per share (EPS), where

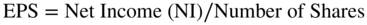
As a firm substitutes cheaper debt for expensive equity, NI goes down due to the increased interest expense, but the number of shares also goes down. As long as K_d is less than K_e, the number of shares will go down by a greater percentage than net income. As a consequence, the net impact will be a rise in EPS.

Next, if EPS goes up, what happens to the stock price? It goes up and then down. The price of the stock can be thought of as a function of the discount rate, K_e, and EPS.⁶

If a firm increases its EPS, the stock price should go up provided the discount rate stays constant. However, we know that as we increase debt in the capital structure, the discount rate rises. Thus, substituting debt for equity increases EPS and increases K_e. At first, the percentage increase in EPS is larger than the increase in the discount rate K_e. In that case, the price of the stock will rise. Eventually, as we add more and more debt, the discount rate rises faster than EPS. In that case, the price of the stock will decrease.

Thus, %D↑ implies that K_d↑ and K_e↑, but K_e > K_d, EPS↑ and the price of the stock↑ and then the price of the stock ↓.

The Marriott example provides an excellent illustration of the impact of changing the amounts of debt and equity, because the firm is not issuing debt to fund a new project. In this case, Wilson is considering having Marriott swap debt for equity with no other changes to the firm. The assets are the same, the business is the same, the management is the same—the only change the firm has made is in how it finances its assets. In other words, the only change is in the firm's capital structure and how much debt versus equity it uses.

So now we know that as we substitute debt for equity in the capital structure, the cost of debt goes up, the cost of equity goes up, but as we have already discussed, the cost of debt remains below the cost of equity. In addition, EPS goes up, the stock price at first increases and then decreases.

Our next question is: What happens to the Price/Earnings (P/E) ratio? It goes down. Suppose the discount rate is constant. If a firm increases its EPS by a certain percentage with a constant discount rate, the stock price will then increase by the same percentage. For example, if a firm increased earnings by 10% (assuming no other cash flow for now), it would increase cash flow by 10%. If the cost of capital is constant and the cash flow increases by 10%, then the stock price increases by 10%. However, as we know from above, as the firm adds more debt, the equity discount rate is not constant but goes up instead. Thus, if earnings increase by 10%, and K_e also increases, then the stock price will go up by less than 10%.

To summarize, if EPS goes up by 10% and the stock price goes up by less than 10%, the ratio of the two, which is P/E, will go down. Furthermore, (as we know from above) the cost of equity (K_e) will rise slowly at first and then more quickly. We may eventually reach a point where the cost of capital will rise more than the increase in EPS, but again the effect is that P/E goes down.

Another explanation of the same point: consider the P/E ratio as the price someone will pay for $1 of earnings. For example, earnings of $1 with a P/E of 10 gives a stock price of $10. As you add risk to the firm, the P/E will fall because the price someone will pay for riskier earnings is less than someone will pay for safer earnings. Now, as you add debt, you are adding risk, and as you add risk, the P/E goes down. Thus, the P/E goes down, and only down, when the percentage of debt is increased.

To summarize again: If the debt/equity ratio goes up, then the cost of both debt and equity goes up, and the cost of equity is always greater than the cost of debt. Also, if debt/equity rises, EPS goes up, the stock price goes up and then down, and the P/E goes down and only down.

A new question: What happens to beta as the firm adds debt? It goes up since there is more risk. The concept of asset beta is useful in understanding why beta rises as the firm adds debt. An asset beta, often called an unlevered beta, is the beta on assets for a firm financed entirely by equity (i.e., with no debt).⁷ If the asset beta is 1, this means that if the market return goes up by 10%, asset returns will also go up by 10%. Since the firm is all equity financed, the return on equity goes up by 10%. If the market goes down by 10%, then the return on the assets goes down by 10%, and the return on equity will fall by 10%.

Imagine a firm that typically gets a $100 return and has no debt or interest costs. The firm's equity receives the entire $100 because none of the return must be used to service debt. If the market goes up 10% and the asset beta is 1, the return on assets goes up 10% to $110. Equity will also now receive $110. This is a 10% increase for equity. If the market goes down 10%, the return on assets goes down 10% to $90. Equity now receives $90, and this is a decrease of 10%.

Now let's add leverage to the mix (i.e., the firm will now have debt financing in addition to equity financing). Assume interest costs are $50. This firm, which typically received a $100 return on assets, now pays interest of $50, which leaves equity with $50. If the market goes up 10%, the return on assets goes up 10% to $110 because the asset beta is 1 and has not changed. Debt must still get $50, but equity will now receive the remainder of $60. This is a 20%, not a 10%, increase for equity. If the market goes down 10%, the return on assets goes down 10% to $90. Debt still receives $50, leaving only $40 for equity. This is a decrease of 20%. Thus, the more leverage the firm has, the more volatile the return on equity. Since the firm's equity beta depends on the volatility of the return to the equity holders, the more leverage you have, the higher the equity beta.

To review, if the firm has no debt, the equity beta equals the asset beta. As you add leverage, the asset beta remains the same, but the return on equity becomes more volatile, which increases the equity beta. Interestingly, this is something you already know intuitively. If a firm subtracts a fixed cost to a varying income stream, the profitability becomes more volatile. This is shown in Table 7.1.

TABLE 7.1 Impact of Change on Beta

Assume the unlevered beta is 1. This is the asset beta.
Assume the normal cash flow to assets is $100.
Case 1 has no debt, so the cash flow to debt is $0. Equity gets the entire asset cash flow.
Case 2 has debt with a cash flow to debt of $50. Equity gets the asset cash flow minus $50.
Case 1: Cash Flow to Debt of 0	Cash Flow to Assets	Cash Flow to Debt	Cash Flow to Equity
Base case	$100	$0	$100
Market return increases by 10%	$110	$0	$110
Market return decreases by 10%	$ 90	$0	$ 90
Return to the assets goes up or down 10%, and the return to equity goes up or down 10%. Thus, the equity beta = the asset beta = 1.
Case 2: Cash Flow to Debt of 50	Cash Flow to Assets	Cash Flow to Debt	Cash Flow to Equity
Base case	$100	$50	$50
Market return increases by 10%	$110	$50	$60
Market return decreases by 10%	$ 90	$50	$40

Return to assets goes up or down 10%, and the return to equity goes up 20%. Thus, the equity beta = 2, the asset beta = 1.

Returning to our CAPM equation, K_e = R_f + β(R_m – R_f), where the β here is the equity β. Increasing debt increases the equity β, which increases K_e. This is consistent with what we said above: as we increase debt, K_d increases and K_e also increases because it is always higher than K_d.

To summarize yet again: What happens if a firm changes its debt/equity ratio? As the firm adds debt, the cost of debt goes up, the cost of equity goes up, the cost of equity remains above the cost of debt, EPS goes up, the stock price goes up and then down, the P/E goes down, and the beta goes up. Beta going up causes the cost of equity to go up. This is consistent with K_e increasing as debt/equity rises and with K_e remaining above K_d.

Next, let's plot the cost of debt and equity with changes in leverage. We do this in Figure 7.1. Start with K_d at the zero debt level. This is what lenders will charge for debt when we borrow the first dollar. It is shown as a point on the y-axis. Now, we know that as we add debt, the cost of debt goes up due to increased risk. In addition, the rate of increase also goes up as we add more debt. That is, the rate of cost increase is smaller at low levels of debt and larger as the level of debt increases. To state it yet another way, the cost of debt increases slowly at first, as lenders are willing to increase debt without increasing the interest rates much. However, as the firm's debt level increases, the risk of default (i.e., the risk that lenders will not be repaid) increases, making the additional debt riskier. Lenders demand an increasing rise in interest rates to compensate for the increasing rise in risk. This means that the interest rate not only rises, but it does so at an increasing rate. This is plotted in Figure 7.1 with the line labeled K_d.

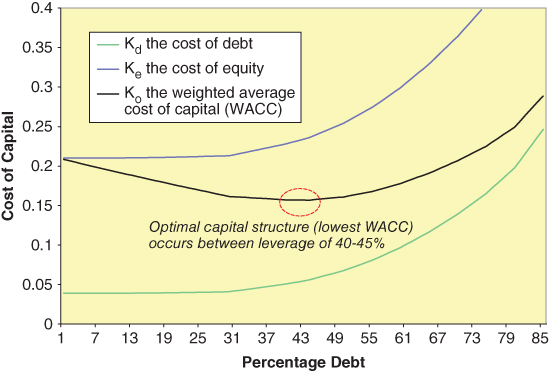
FIGURE 7.1 Capital Structure Costs

Next, let's plot K_e. We will start with K_e at the zero debt level. This is the return that equity investors expect with no debt. Note that the K_e at the zero debt level is above the K_d at the zero debt level because the cost of equity is greater than the cost of debt. This is because equity is riskier than debt to investors, as noted above. As we add debt, the cost of equity behaves similarly to the cost of debt: it rises. K_e also rises slowly at first and then faster, remaining above the cost of debt for any level of debt.

THE COST OF CAPITAL

Our primary concern as CFO, however, is not with the individual cost of debt or equity, but rather with the overall cost of capital. Our objective is not to minimize the cost of debt or equity alone—we can do that simply by having no debt (as seen in Figure 7.1). Our objective is to minimize the overall cost of capital (K_o). So now let's plot the overall cost of capital, which is the weighted average of the cost of debt and the cost of equity. With no debt, the overall cost of capital is K_e, the cost of equity alone (since the firm is 100% equity). As we change the debt/equity level, the percentage of debt goes up, and the percentage of equity decreases. Conceptually, we are substituting debt (which is less expensive) for equity (which is more expensive). This causes the overall cost of capital to initially go down. However, as we increase the debt/equity ratio, both the cost of debt and the cost of equity rise. While debt remains less expensive than equity at any given point, the overall cost of capital (after its initial decline) will also eventually rise because both its components are rising. This is seen graphically in Figure 7.1's plot of K_o. Note the overall cost of capital, while equal to K_e at zero debt, afterwards lies between K_d and K_e.⁸

We have just added one more element to our understanding of capital structure and the impact of changes in the debt/equity ratio. We previously explained that as we increase the debt/equity ratio, the cost of debt increases, the cost of equity increases, the cost of equity remains above the cost of debt, EPS goes up, the stock price goes up and then down, the P/E goes down, and the beta goes up. We can now add that when the debt/equity ratio rises, the overall cost of capital goes down and then up.

As noted above, the CFO is interested in minimizing the cost of capital for the firm. However, there is not necessarily a single debt/equity ratio that minimizes the cost of capital for a firm. And it is definitely true that there is no single debt/equity ratio that minimizes the cost of capital across different firms.

For an individual firm, in practice a CFO does not try to find a single optimal point. Rather, they try to find a debt/equity range that is optimal. As seen in Figure 7.1, the cost of capital for a firm declines and then flattens out over a range before increasing again. Since it is not possible to precisely measure the cost of capital for each debt/equity level in a firm, a target range is the best a CFO can achieve.

Optimal target debt/equity ranges differ by industry. For example: What happens to the cost of debt as a utility (with stable cash flows) adds more debt? Because the cash flows are stable, the risk of adding additional debt is lower than for many other firms, and thus lenders will not increase the cost of debt very much at first (i.e., K_d rises more slowly for a utility than for a firm in an industry with riskier cash flows). The cost of equity for a utility also rises more slowly. (Remember, the costs of debt and equity are related to the risk of investors receiving their returns. With stable cash flows, this risk is reduced at every level of debt.) This means that for a utility, the cost of capital goes down for a longer period of time or over a longer range before it begins to rise.

A firm in an industry with more volatile cash flows will have its cost of debt rise sooner and more quickly than that of utilities. As a consequence, K_e will also rise sooner and more quickly, and K_o will not go down as far or over as long a range. This means that not only will the overall cost of capital be higher for these firms but also that the optimal capital structure will occur at lower debt/equity levels than for utilities. As an example, a company like Wham-O⁹ (with a product line prone to consumer fads) will have more cyclical/volatile cash flows and consequently will have a higher cost of capital and achieve its minimum at a lower debt/equity ratio.

Figure 7.2 plots K_o for two hypothetical firms: one a utility with stable cash flows and the other a toy company with volatile cash flows. As seen, the K_o of the utility is not only below that of the toy company, but also has an optimal debt/equity ratio at a higher percentage of debt. The effects of higher debt levels will be the same for the two companies (i.e., as debt goes up, the cost of debt goes up, the cost of equity goes up, the price of the stock goes up and then down, etc.), but these effects will occur at different points and at different debt/equity ratios.

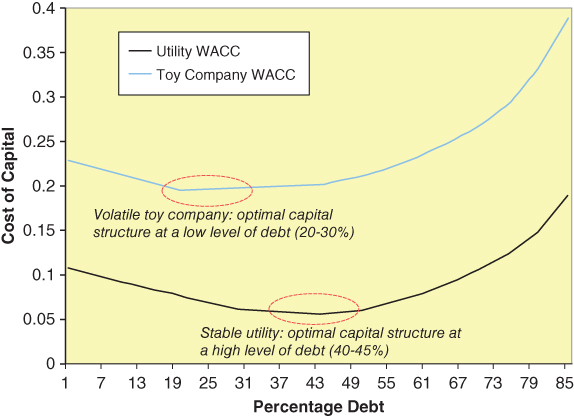
FIGURE 7.2 Capital Structure Costs

Next, in Figure 7.3, we plot the stock price against the debt/equity ratio on one graph, and against the cost of capital on another graph. If we examine the point (or range) at which the stock price is maximized, we notice it is the same point (or range) at which the cost of capital, K_o, is minimized. Thus, minimizing the cost of capital maximizes the stock price. This is not surprising once you think about it. Holding all else constant, you get the maximum stock price when you minimize the cost. This is true for any cost: for instance, if you minimize the cost of labor, all else equal, you maximize stock price, or if you minimize the cost of materials, all else equal, you maximize stock price. Logically, if you minimize the cost of capital, holding all else constant, then you maximize the stock price.

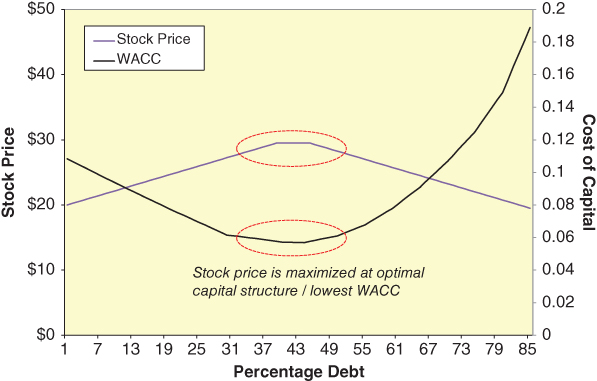
FIGURE 7.3 Capital Structure Impact on Stock Price

Industrial revenue bonds provide an example of how important this concept of cost of capital is. These bonds create strong competitive advantages for firms issuing them. The interest from these bonds is tax-free in the same way that interest on municipal bonds is tax-free, but the bonds are issued by a corporation instead of a municipality. As a consequence of this tax advantage, the interest rates paid on these bonds are lower than those paid on corporate bonds of similar risk.

Industrial revenue bonds were created to encourage economic development. Municipalities trying to get companies to locate in their town, build plants, and expand local employment authorized firms to issue the bonds. As the interest payments on these bonds are not subject to income tax for the people buying the bonds, the interest rates on the bonds are often lower than U.S. Treasury bonds. This greatly reduces the cost of capital to the issuing firm. These industrial revenue bonds were initially issued without size limits, but the U.S. government eventually capped the amount a municipality could authorize (with caps tied to the local population figures). Retail chains have been major issuers of these bonds. The use of these bonds provides these large chains with a competitive advantage over local businesses.¹⁰

As a hypothetical example, assume a small clothing store in Springfield (MA or MO or IL or OR) finances its inventory from the local bank at a cost of the bank prime rate plus 2%.¹¹ Next assume a Kmart or Walmart enters the local market by building a store next to the highway. The mega-store should have significant purchasing power economies, as well as economies of scale in advertising and so forth, over the local clothing store. Suppose that the mega-store also issues industrial revenue bonds to finance inventory. This means the mega-store is financing inventory at 2% to 3% below the U.S. government's rate, while the local merchant is paying prime + 2% (or about the U.S. government's rate + 5% today). The mega-store effectively has a total cost advantage of at least 6% on inventory financing. All things equal, even without the mega-store's other cost advantages, having a lower cost of capital than your competitors allows you either to charge lower prices, get higher profits, or both. Similarly, changing a firm's capital structure changes its cost of capital, thereby affecting the firm's competitive ability, its profitability, and its stock price compared to its competitors.

HOW FIRMS SET CAPITAL STRUCTURE IN PRACTICE

Now, let's take a step back. We have just outlined the theory of why capital structure and debt ratios matter. While this is all nice in theory, how do firms actually think about the right level of debt in practice? Few, if any, CFOs draw the graphs in Figures 7.1, 7.2, and 7.3. Instead, they determine their optimal cost of capital by considering three factors:

1. Internal: Determining how much debt the firm can afford in a downturn. This is done by projecting future cash flows and running pro formas under various negative scenarios to see at what point the firm would begin to experience difficulties with its debt payments.
2. External: Examining the impact of the firm's debt ratios on its relationships with bankers, investment bankers, analysts, and rating agencies. That is, will the rating agencies downgrade the firm, will the analysts issue alerts and warnings, and/or will the bankers treat the firm differently?
3. Cross-sectional: Looking at what the firm's competitors are doing. As we saw in Chapter 5 with Massey Ferguson: Would the firm really want to have a debt ratio of 47% if the industry average or that of its closest competitor was 30%? If the CFO does what its competitors are doing, then even if the CFO is wrong, they are all in it together. If the CFO chooses a capital structure that is radically different from the rest of the firms in the industry and she is wrong, the CFO has put the firm, and certainly her job, at risk.

So let us ask two questions. First: Can a firm have too much debt? Absolutely! Alarms go off, covenants are violated, debt ratings are downgraded, the firm potentially suffers the costs of financial distress, and the firm is open to competitive attack. Essentially, the firm becomes a Massey Ferguson waiting to happen.¹² The CFO does not want to do this. CFOs want to sleep at night rather than worry, which gives them an incentive to keep debt levels low.

Second: Can a firm have too little debt? Absolutely! Too little debt means the cost of capital is not minimized (i.e., at no debt, the firm's cost of capital would be the cost of equity, which is always above the cost of debt) and therefore the stock price is not maximized. Too little debt also means the firm is not using its maximum tax shield and is making extra tax payments to the government instead of creating value for the shareholders. A low stock price means the firm is vulnerable to a different kind of attack: it becomes a takeover target.¹³

Thus, as a CFO, you can't ignore capital structure. You have to get it right. Too much debt is not good, as you become a Massey Ferguson and have a John Deere come after you in the marketplace. Too little debt is also not good, as you have to worry about someone coming after the firm to buy it. It is important to get it right—to minimize the cost of capital and maximize the value of the firm.

CORPORATE FINANCIAL POLICIES

When Gary Wilson took over as CFO of Marriott, he proposed a series of financial policies for the firm that the Board of Directors approved. These policies stated that:¹⁴

1. Debt should be maintained between 40% and 45% (or debt + leases at 50–55%) of financing.
2. The Moody's commercial paper rating should be at P-1 or better (this is roughly equivalent to a bond rating of A or above).¹⁵
3. The principal source of financing should be domestic, unsecured, long-term, fixed-rate bonds.
4. No new convertible debt or straight preferred stock should be issued.
5. In addition, although not formally a guideline, Marriott started paying a cash dividend in January 1978 (they had previously paid a stock dividend).

Let's now discuss why these policies made sense for Marriott.

1. The 40–45% debt capital structure (a target announced in Marriott's annual report) is where CFO Gary Wilson believed the cost of capital was minimized, thus maximizing the firm's value. That is, if we drew Figure 7.3 for Marriott, the minimum cost of capital will be reached in the 40–45% debt range.
2. The P-1 Moody's commercial paper (A equivalent) rating allows continued access to capital markets.¹⁶ Marriott was borrowing money to build new hotels. Since there has never been a time when A-rated bonds could not be issued, this gave Marriott an effective guarantee that it would be able to raise debt in the public capital markets.
3. Issuing domestic debt was a policy based on the nature of the bond markets. There are two major bond/debt markets in the world: the U.S. and the Eurobond markets.¹⁷ The rationale for issuing in the United States was not due to a currency preference, as many Eurobonds are issued in U.S. dollars. The rationale was based, rather, on the different nature of the two markets at the time. The Eurobond market was a “name” market—one where individual investors play a larger role than institutional investors. This is characterized as a market where the investors' familiarity with the issuer's name is more important than credit ratings and other external measures. As such, in the Eurobond market, investments were based less on credit ratings than on the issuer's name and reputation.

   The reverse is true for the U.S. debt market, which is primarily a ratings market. In a ratings market, insurance companies, mutual funds, and retirement plans buy bonds based on their ratings. At the time, Marriott was not well known in Europe (as opposed to, say, Exxon) and would have had trouble raising a large issue in Europe to “name” investors. Marriott therefore chose to issue debt in the U.S. market.

   The rationale for issuing unsecured debt was based on Marriott's operational decision, announced in its 1978 annual report, to switch from owning and operating its hotels to only operating the hotels. Marriott's new strategy was to buy and/or build hotels and then sell the properties to outside investors but continue to operate them. Marriott could have issued secured debt¹⁸ to initially finance the hotels, which would have been less expensive. Instead, Marriott chose to issue unsecured debt because this provided it with the flexibility to sell off the properties without retiring the bonds.

   A typical answer for why a firm issues long-term debt is to match the maturity of the assets with the maturity of the liabilities.¹⁹ In this case, however, the maturity of the assets (since Marriott is selling the hotels after building them) is shorter than the maturity of the debt. Gary Wilson wanted to issue long-term, fixed-rate debt because of his belief that inflation and interest rates would rise. Did the capital market agree? At the time of the decision, there was an inverted yield curve (short-term rates are higher than long-term rates), which means that the market forecasts lower future inflation and hence interest rates will fall. If a CFO has the same expectations as the market, it makes little difference if the firm goes short or long term. The yield curve prices-in the market's expectations of the future. If Wilson believes interest rates will rise in the future, while the market believes they will fall, this means he will want to borrow long term at fixed rates. If he is correct, this will yield a major savings in financing costs. If he is incorrect, as long as the debt is callable,²⁰ the firm can refinance in the future (although at a cost).

   Finally, Marriott's policy of using the public market rather than the banks was due to banks only lending at variable rates.

4. The exclusion of convertibles²¹ and straight preferred²² can be explained by Marriott's expectations of its future cash flow and by the nature of its business. Convertibles are usually issued by firms like start-ups, which often have high growth potential, high option value, and high risk for lenders. Why? Because such firms can issue convertible debt at a lower rate than straight debt. Straight debt for these firms would require a very high interest rate. Convertible debt, where the holder can, at their option, convert into equity, provides firms with a lower interest rate if there is a reasonable probability that the price of equity will increase in the future. This option value is why the convertible debt holders accept a lower interest rate than the straight debt holders.²³ Since Marriott was viewed as a stable company with little growth potential, the market felt the firm had little if any option value, and therefore, Marriott would receive no benefit by issuing convertibles (i.e., there would be little or no reduction in interest rates below the rates on straight debt).

   Why did Marriott choose not to issue straight preferred stock? Most straight preferred stock is issued by banks and utilities, due to their regulated capital structures. That is, regulators require banks and utilities to maintain certain minimal levels of equity in their capital structure (for banks, this level is currently 8%). From a bank or utility's perspective, since there is usually an implicit or explicit government guarantee preventing the firm from going into bankruptcy, these firms have an incentive to lever up as much as possible. To limit this leverage, the government requires minimum equity levels. From a regulatory standpoint, preferred stock counts as equity capital. However, preferred stock has a fixed dividend and acts more like debt than common stock. Thus, if a firm prefers more leverage in its capital structure than is allowed by regulation, the firm will try to issue the type of equity that acts most like debt—which is straight preferred stock.

   The bottom line is that banks and utilities want to be more levered than they are allowed to be by regulators and hence choose straight preferred stock to satisfy their equity requirements when possible. Since Marriott did not have a regulated capital structure, it had no reason to issue straight preferred stock. Additionally, straight preferred stock has a fixed dividend rate, yet the dividend payments are not tax deductible, unlike interest payments, which are fixed but tax deductible. Thus, for most corporations, if the probability of default is low, issuing straight debt is preferable to issuing straight preferred, since the tax deduction on the interest lowers the effective after-tax cost of capital.

5. Marriott's decision to start paying cash dividends was welcomed by some shareholders. However, at the time, dividends were taxed at the personal income tax rate, making capital gains far more attractive because they were taxed at a lower rate. So why pay cash dividends if they are taxed at a higher rate? We will discuss dividend policy in detail in Chapter 11.

SUSTAINABLE GROWTH AND EXCESS CASH FLOW

Marriott's decision to establish a 45% limit on senior debt and capital lease obligations was announced in its December 31, 1978, annual report. Just two years later Marriott decides to issue $235 million of debt and buy back 10 million shares. How will this impact the 45% guideline? The repurchase will clearly violate the guidelines. So why do the repurchase? What has happened in the last two years to persuade management to violate the guidelines?

The answer is that Marriott believes it is now generating excess cash. If the firm does not change its policies, it believes its debt ratio will decrease. This is a result of a change in Marriott's sustainable growth rate. Sustainable growth is the rate a firm can grow internally without utilizing outside financing.

If a firm's ROE is greater than the sum of its internal growth rate and its dividend payout, and the firm does nothing else, leverage will fall. In 1976, Marriott's ROE was 9.8%, while assets were growing at 14.6%. Can a firm grow faster than its ROE? YES! We discussed this earlier in the Chapter 2 PIPES example. How does a firm grow faster than its ROE? It finances the growth with debt or equity. If a firm grows faster than its sustainable growth rate, it needs to issue debt or equity. Can a firm grow slower than ROE? Yes, but the result is the inverse: the firm must either pay out the excess cash or repurchase debt or equity.

Marriott's sustainable growth rate has recently risen. Why? For one thing, the sales/assets ratio rose (from 1.05 in 1976 to 1.51 in 1979). That is, Marriott is generating more sales per dollar of assets. This is largely because Marriott has been selling assets. As previously mentioned, Marriott made a policy change in its product strategy to no longer own and operate all of its hotel properties. Management decided to develop the hotel properties and then sell them to outside investors while continuing to operate the hotels. Because of this shift, the amount of assets needed to generate the same revenue stream fell dramatically. Thus, the sales/assets ratio, often called capital intensity, skyrocketed.

In addition, Marriott's profits/asset ratio, or profitability ratio, also increased (from 3.5% in 1976 to 4.7% in 1979). The firm not only changed its business strategy, it also exited unprofitable businesses, thereby increasing profits/assets.

At this point, let us reintroduce the DuPont formula, which is defined as follows:

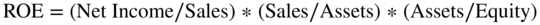
The DuPont formula says that a firm's return on equity (ROE) is the product of its profitability, its capital intensity, and its leverage. These are measured by NI/sales, sales/assets, and assets/equity, respectively. That is, there are three levers by which a firm can increase ROE: you can increase profitability, capital intensity, or leverage. In the above equation, if you do the cross products, sales cancel with sales, assets cancel with assets, and you are left with ROE = NI/equity.

Note that leverage is measured in many ways. Debt/equity or debt/assets are the common, more intuitive measures of leverage, with an increase in debt increasing the measure. Assets/equity (the measure used in the DuPont formula) is also a measure of leverage. As equity/assets increases, leverage decreases. Inversely, as assets/equity increases, leverage increases.

In the DuPont formula, the first two terms (NI/sales and sales/assets) when multiplied equal NI/assets. This is also called Return on Assets (ROA).²⁴ For Marriott, both its profit margin (NI/sales) and Asset Turnover (sales/assets) increased from 1976 to 1979. This caused Marriott's ROA (NI/assets) to increase from 3.7% in 1976 to 7.1% in 1979—or by 92%. Going back to the DuPont formula, if ROA goes up by 92% while leverage stays the same, then ROE goes up by 92%. However, Marriott's leverage did not stay the same. Over the entire period (1976 to 1979), the Leverage Ratio (TA/equity) fell by 17% (from 2.9 to 2.4). The net effect was that Marriott's ROE increased 76% going from 10.6% to 17.2%.

Let us work through the change in the levers of Marriott's ROE. In 1976, Marriott's ROA was 3.7%. By 1979, Marriott's ROA had increased to 7.1%. Marriott's interest coverage (i.e., EBIT/interest payment) in 1976 was 3.5 times (see Appendix 7B). In 1979 it was 5.4 times. Therefore, Marriott has become more profitable and less capital intensive than when the guidelines were passed. As a consequence, Marriott is generating excess cash, which, if nothing else changes, lowers Marriott's leverage.

DuPont	12/30/1976	12/30/1977	12/29/1978	12/28/1979
Profit margin (NI/Sales)	3.5%	3.6%	4.3%	4.7%
Asset turnover (Sales/TA)	1.05	1.29	1.32	1.51
ROA = PM Asset turnover	3.7%	4.6%	5.7%	7.1%
Leverage (TA/Equity)	2.90	2.68	2.60	2.39
ROE = PM AT Leverage	10.7%	12.4%	14.8%	17.0%

WHAT TO DO WITH EXCESS CASH?

In the case of Marriott or any firm, there are only five possibilities for what a firm can do with excess cash.²⁵ They are:

1. Pay down debt
2. Pay a higher dividend
3. Invest more in the current businesses
4. Acquire other firms
5. Buy back stock

What else can a firm do with excess cash? That's it. Those are the five things a firm can do. Note that possibilities one, two, and five are financial market solutions, while three and four are product market solutions. It is the exact inverse of a firm needing excess cash flow to grow. If a firm does not have enough cash, management can borrow money, cut the dividend, slow down business growth, sell off assets, or issue new stock. These are the same five decisions in inverse.

Of the five possibilities, what should Marriott do? How about paying down debt? In Marriott's 1980 Annual Report we find the following quote:

Maintaining excess debt capacity is inconsistent with the goal of maximizing shareholder wealth: Unused debt capacity is comparable to unused plant capacity because the existing equity base can support additional productive assets. Fully utilizing this capacity maximizes shareholders' returns. . . . Debt is less expensive than equity because it is tax deductible. High portions of debt therefore reduce the company's weighted cost of capital and real returns. (page 20)

Marriott is implicitly saying that it believes in an optimal capital structure and that a debt ratio below the optimal range does not minimize the cost of capital nor maximize the share price.

Should Marriott increase its dividends? Again, from the firm's 1980 Annual Report:

Marriott could pay out large dividends if investments yielding returns in excess of the company's cost of capital were unobtainable. However, dividends would be taxed at ordinary income tax rates. (page 20)

This can be interpreted as saying that it is unlikely Marriott will decide to distribute funds in a manner that, from a tax point of view, is disadvantageous to its largest stockholders, the Marriott family.

Should Marriott increase its investment in its current lines of business? Again, from the 1980 Annual Report:

Since Marriott already was growing its business rapidly, further acceleration could outpace the company's ability to develop sufficient operating management. (page 20)

Here, Marriott is saying it is growing as fast as it can with the current management.

Should Marriott acquire other firms? The 1980 Annual Report says:

Senior management's attention was focused on an aggressive hotel expansion program. The risk of diluting these energies in a concurrent diversification effort seemed imprudent. Further, many other firms were attempting to solve their excess liquidity problems by acquisition—resulting in unattractive prices for quality opportunities. (page 20)

Marriott is saying that new lines of business do not make sense due to management limitations and high acquisition prices.

Should Marriott buy back their shares? According to the 1980 Annual Report:

If the company's shares were undervalued, share repurchase could yield high financial returns. Further, the company also could utilize its debt capacity without straining operating management or assuming the risks associated with diversification. After a thorough study of the company's business prospects and projected cash flows, management concluded that the shares were undervalued. (page 20)

This speaks directly to Marriott's view on its current policy decision to issue debt and buy back equity.

Should Marriott issue new debt and repurchase shares? Gary Wilson believes Marriott is profitable and will continue to be so. Furthermore, he believes the level of cash flow is greater than Marriott's sustainable growth rate. As a consequence, if Marriott does nothing, its leverage ratio will decrease (either by increasing cash balances or paying down debt). Marriott then properly identifies the five things a firm can do with excess cash and eliminates four of them.²⁶

This leaves us with our original question: Should Marriott change its capital structure?

SUMMARY

Thus far, we have discussed capital structure and whether Marriott was near its optimal level. This is a financing decision. Given that repurchasing shares is the financing solution Marriott came to, we must now ask a second question, an investment question. How much should Marriott pay to repurchase its shares?

Thus, there are really two decisions that have to be made simultaneously. Is this a good financing decision, and is this a good investment decision? The answer does not have to be the same for both decisions. The firm could have a suboptimal capital structure, but its stock price could be too high to make repurchasing stock an attractive investment. The firm could have an optimal capital structure, but the stock price could be so low that repurchasing stock is a good investment. Note that there is always a price that will make an investment look bad, and there is usually a price that will make an investment look good. In other words, any project's cash flows combined with a high enough price will have a negative NPV. If you understand this last point, you understand 50% of all merger and acquisition (M&A) decisions. What is the right price to pay for something? The wisdom of any investment, whether good or bad, depends a whole lot on what price you pay.

Coming Attractions

The next chapter begins with Marriott considering a tender offer for 10 million of its shares at $23.50 a share. We begin by asking whether offering $23.50 to repurchase the stock is a good investment decision. Note, Marriott's book value at the time is $12.90, and the stock market price is 19⅝.²⁷ We will not do a full-blown valuation of Marriott's stock in the next chapter (we will do valuation later in the book), but we will start on the topic of the second job of the CFO: how to make good investment decisions.

APPENDIX 7A: MARRIOTT CORPORATION INCOME STATEMENTS AND BALANCE SHEETS

($000s)	1976	1977	1978	1979
Sales	890,403	1,090,313	1,249,595	1,509,957
Operating expenses	817,884	990,984	1,130,608	1,358,972
Operating profit	72,519	99,329	118,987	150,985
Interest expense, net	20,755	30,206	23,688	27,840
Income before income taxes	51,764	69,123	95,299	123,145
Provision for income taxes	20,919	30,073	40,999	52,145
Net income	30,845	39,050	54,300	71,000
Fully diluted earnings per share	0.86	1.04	1.43	1.95
Year-end market share price	13.54	11.75	12.13	17.38
Year-end shares outstanding (000's)	36,464.7	36,507.0	36,714.6	36,224.5
Market capitalization (price * shares)	493,732	428,957	445,348	629,582
Cash and marketable securities	20,753	16,990	53,257	21,270
Accounts receivable	50,293	61,484	76,774	99,955
Inventory	35,504	41,498	41,108	46,629
Prepaid expenses	7,580	9,444	9,571	9,868
Current assets	114,130	129,416	180,710	177,722
Property and equipment, at cost	836,611	956,072	957,474	1,066,338
Depreciation and amortization	155,218	204,152	212,430	241,160
Property and equipment, net	681,393	751,920	745,044	825,178
Other assets	48,703	68,174	74,501	77,465
Total assets	844,226	949,510	1,000,255	1,080,365
Short-term loans	2,989	3,976	3,473	4,054
Current portion of debt and leases	10,119	10,813	11,758	10,497
Accounts payable	41,503	46,666	66,960	71,528
Other liabilities	43,653	64,410	91,181	102,420
Current liabilities	98,264	125,865	173,372	188,499
Construction financing	16,000	—	—	—
Mortgage notes	219,906	214,090	175,565	163,520
Unsecured notes	115,022	107,332	110,457	178,075
Capital lease obligations	—	48,092	23,877	23,684
Convertible subordinated debt	31,340	29,515	28,165	26,918
Other liabilities	48,350	58,820	70,163	86,166
Total liabilities	528,882	583,714	581,599	666,862
Shareholders' equity	315,344	365,796	418,656	413,503
Total liabilities and owners' equity	844,226	949,510	1,000,255	1,080,365

APPENDIX 7B: MARRIOTT CORPORATION SELECTED RATIOS

	1976	1977	1978	1979
Sales growth	21.6%	22.5%	14.6%	20.8%
Gross profit margin (GP/sales)	8.1%	9.1%	9.5%	10.0%
Net profit margin (NI/sales)	3.5%	3.6%	4.3%	4.7%
ROA (NI/TAopen)	3.7%	4.6%	5.7%	7.1%
ROE (NI/equityopen)	10.7%	12.4%	14.8%	17.0%
Days receivable (A/R/(sales/365))	20.62	20.58	22.43	24.16
Days payable (A/P/(OpExp/365))	18.52	17.19	21.62	19.21
Asset turnover (sales/TAopen)	1.05	1.29	1.32	1.51
Current ratio (CA/CL)	1.16	1.03	1.04	0.94
Leverage (TAopen/equityopen)	2.90	2.68	2.60	2.39
Debt ratio (debt/(debt + equity))	55.6%	53.1%	45.8%	49.6%
Debt ratio (debt/(debt + market cap))	44.5%	49.1%	44.2%	39.2%
Times interest (EBIT/interest)	3.49	3.29	5.02	5.42

NOTES

  1 Net income for 1979 of $71 million ÷ beginning-of-year shareholder equity of $397 million = 17.9% (dividing by year-end shareholder equity of $414 million gives an ROE of 17.2%). As noted before (Chapter 2), ROE should be calculated as net income ÷ beginning-of-year shareholder equity.

  2 While Marriott's average tax rate is 42% (income tax of $52 million/profit before tax of $123 million), the marginal U.S. corporate tax rate at the time was 46% for amounts over $100,000.

  3 Beta is a measure of how a firm's stock return moves in relation to the market's return. Beta is defined as the coefficient in the regression R_stock = α + βR_market.

  4 There is some disagreement over whether to use the 5- or 10-year rate. We will discuss this, and other issues related to the risk-free rate, later in the book.

  5 There are two major papers by Franco Modigliani and Merton Miller on the cost of capital as discussed in Chapter 6. The first paper demonstrates the irrelevance of capital structure under certain conditions (which do not hold in reality). The next demonstrates the impact of corporate taxes on capital structure. See F. Modigliani and M. Miller, “The Cost of Capital, Corporation Finance and the Theory of Investment,” American Economic Review 48 (June 1958): 261–297; and F. Modigliani and M. Miller, “Taxes and the Cost of Capital: A Correction,” American Economic Review 53 (June 1963): 433–443.

  6 As discussed in an earlier chapter, the price of any asset should be equal to the present value of its cash flows discounted by its cost of capital. For stock, these are the equity cash flows discounted by K_e, but earnings are a major component of equity cash flows. We use the simplified statement above until we fully discuss cash flows later in the book.

  7 The equity betas that are typically ascribed to a firm are actually levered betas; that is, they are the beta of the equity given the firm's capital structure (or leverage). An asset beta is the beta of the assets alone without regard to capital structure. With no debt, the asset beta is the “unlevered” equity beta.

  8 Modigliani and Miller (1958) assume that in a no-tax world, the changes in K_d and K_e would balance each other so that K_o stays constant at all levels of debt.

  9 The Wham-O Toy Co. invented the Hula-Hoop, the Frisbee, and the Boogie Board, among other toys.

10 For a more detailed discussion on Industrial Revenue Bonds, see Alan Hall, “Industrial Bond Basics,” www.rodey.com/downloads/rodey_industrial_revenue_bond_basics.pdf, accessed December 20, 2014.

11 It would be typical for a small business to pay a rate of 2 to 3% above prime.

12 We discussed Massey Ferguson in Chapter 5.

13 The acquiring firm might even use the target firm's own (unused) debt capacity to help finance the takeover.

14 This list of financial policies was obtained from three sources: Marriott Corporation's annual reports (1978–1980), Marriott Corporation (1986) 9-282-042 Harvard Business School Publishing, Boston, and a conversation with a former Marriott board member.

15 As noted in the prior chapter, the three major rating agencies are S&P, Moody's, and Fitch. Each has a slightly different rating mechanism, but basically the safest rating for bonds is AAA, followed by AA+, and so on. The lowest rating is D, which means the firm is in default or not currently paying its interest and principal as per the debt contract. For commercial paper the safest rating is P-1.

16 Prior to the 1980s and the rise of the junk bond market (which was due to Michael Milken and his firm, Drexel Burnham Lambert), there were times when firms with ratings below A could not obtain funding in the debt market. Even after Drexel changed the market, in times of tight credit investors seek higher-rated (or government) debt.

17 Eurobonds are bonds denominated in any currency and sold to investors outside the United States. They are not subject to SEC regulation and registration.

18 Secured debt has specific collateral, like a hotel, which a lender can seize in the event of nonpayment. This contrasts with unsecured debt, where the lender can't seize any particular asset but must make a claim against the general assets of the firm after the secured creditors have been paid.

19 This rule is actually not correct since what you really want is to match the maturity of the product market and financing strategies. We will discuss this in more detail later.

20 Callable bonds can be redeemed (called) by the issuing firm prior to the bonds' maturity date. Thus, if interest rates fall, the issuing firm can call the old bonds and issue new bonds at a lower rate. To protect bondholders from this, corporate bonds are often noncallable for some period and/or have a call premium, which means that the effective interest rate is above that for a bond held until maturity.

21 Convertible bonds can be converted into equity at a contractually specified exchange rate.

22 Preferred stock gives the holder certain rights that common stock does not have. Usually this is a right to receive dividends prior to common stock and priority rights in bankruptcy.

23 For example, in 1981 MCI was paying about 14% for straight debt and 10% for convertible debt.

24 This definition is dependent on the firm's current capital structure because NI is after interest and taxes. To compute the return on assets independently of the effects of financing, the formula would be (NI + (interest expense) (1 – tax rate))/TA.

25 Excess cash is cash a firm does not need to fund operations. As noted in Chapter 6, in relation to a firm's capital structure, it can be thought of as negative debt.

26 To be clear, Marriott chose to eliminate four of the five options. A firm could do several options simultaneously. Importantly, there are only five things a firm can do with excess cash flow or, vice versa, only five things a firm can do when it has a shortage of cash flow.

27 Before decimalization in 1991, all NYSE stock prices were listed in 1/8ths.