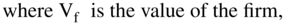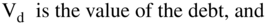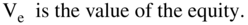CHAPTER 6
An Introduction to Capital Structure Theory
We started this book by stating that our approach to corporate finance would be from the CFO's point of view. We also stated that the three main tasks of the CFO are:
- Valuation: How to distinguish a good investment from a bad investment.
- Financing: How to finance the investment projects a firm chooses to undertake.
- Cash management: How to make sure the firm does not run out of cash while doing the first two tasks.
This chapter is all about task number two: financing. A firm's investment decisions dictate its funding needs. For the purposes of this unit, we will take the firm's investment decisions as given. If we know the firm's investment decisions, we can use the tools from our prior section on cash management to forecast the firm's funding needs. This is huge. If we know what projects the firm wants to undertake, we can then determine how much funding the firm needs.
Now, if a firm knows what its funding needs are, what is the best source of funds? Should it be from internal cash flows, should it be from debt, should it be from external equity, should it be from convertibles, and so forth? Once a firm decides on the sources of funds it will use, it still has many different options. Should internal cash flow funding come from excess cash or by cutting dividends? Should debt financing be obtained from banks or from issuing bonds in the capital markets? Should equity be raised from venture capital firms or from the capital markets, and should the equity be in the form of preferred or common stock?
These two decisions—the sources and forms of funding—determine capital structure.
An important point: In the practice of corporate finance a firm does not determine its funding requirements or its capital structure in isolation. The starting point is always to determine the firm's investment policies. What will the firm invest in? What is a good project? Next, the firm computes how much funding is required for its investment policies. After that, the firm decides what types of financing and where to obtain it. The four steps are:
- What investments?
- How much funding is required?
- What types of financing?
- Where to obtain the financing?
OPTIMAL CAPITAL STRUCTURE
A firm's capital structure is defined by how a firm's assets are financed. It represents the mix of claims against the firm's assets and cash flows. Three key questions are:
- Is there an optimal capital structure (i.e., an optimal mix between sources of financing, in particular between debt and equity)? Yes, there is—this section of the book would add little value otherwise.
- Is this optimal capital structure different across firms and time? Yes, optimal capital structure differs across different firms because it is dependent on a firm's operations and risk.
- Can a CFO add value on the right-hand side of the Balance Sheet with a good financing policy? Probably, but they can definitely destroy value with a bad financing policy.
The Empirical Evidence on Issuing Debt versus Equity
Let's begin with an overview of the empirical literature on two types of financing: debt versus equity.
Figure 6.1 graphs the ratio of debt over total funding (where total funding equals debt plus equity) for NYSE-listed corporations during the time period 1986–2017. We show both the market value and book value of equity because capital structure is often computed in two different ways. First, capital structure is computed using the accounting or book values for debt and equity. This is called book leverage. Second, it is computed using the accounting value for debt with the market value of equity (the market price per share times the number of shares outstanding, also called the market capitalization or market cap). This is called market leverage.
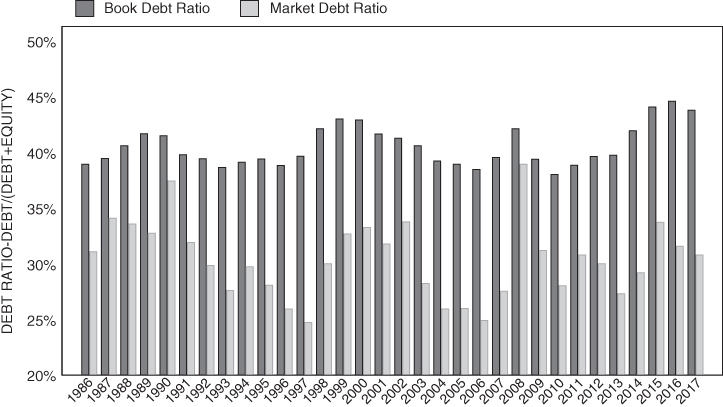
FIGURE 6.1 Capital Structure of NYSE Corporations 1986–2017
Source: Compustat.
As evidenced by Figure 6.1, the average amount of debt financing for NYSE corporations over 1986–2017 was about 40% if we use the accounting values for debt and equity and about 30% if we use the accounting values for debt and the market values for equity. Thus, the average firm listed on the NYSE is funded primarily by equity, not debt. Also, note that equity values vary substantially over time and that market leverage is less than book leverage because the equity value for most firms is above the book value (above the historical accounting value). (We are really much more interested in market ratios. When we start doing valuations, we will worry more about market caps and not the book equity.) We mentioned above that a firm's capital structure depends on its operations and risk. A firm faces both basic business risk (BBR)1 as well as financial risk. A firm's equity beta2 depends on both types of risk—that is, both a firm's operations and its finances. Later in the book we will try to remove the financial risk from the beta by unlevering the beta (i.e., removing debt from the evaluation of beta), which leaves only the operating risk. This unlevered beta is called an asset beta (as opposed to an equity beta).
Figure 6.2 shows that the primary source of funds for NYSE corporations over the period 1986–2017 was internally generated (cash from operations). This is why the issue of sustainable growth is so important. (There are other reasons as well that we will discuss later in the book.) Sustainable growth is when firms obtain most of their financing from their own operations. If a firm can't generate enough funds internally, the next largest source of funds is the debt markets (net cash flow from debt issue). Finally, if a firm can't fund its operations and investments with internally generated funds and debt, only then will a firm issue equity (net cash flow from equity issue). In a randomly selected sample of 360 NYSE and AMEX (American Stock Exchange) firms over the period 1972–1982, it was shown that the average number of equity offerings per year was 7.3 (or about 2% of the firms per year). In contrast, the average number of straight debt issues and private debt borrowing was 15.6 and 26.9 respectively (or about 5% and 7%). In total, 44% of the firms never engaged in any form of external financing.3 Thus, sustainable growth is very important, and firms choose not to issue equity very often. We will discuss the reasons for this later in the book.
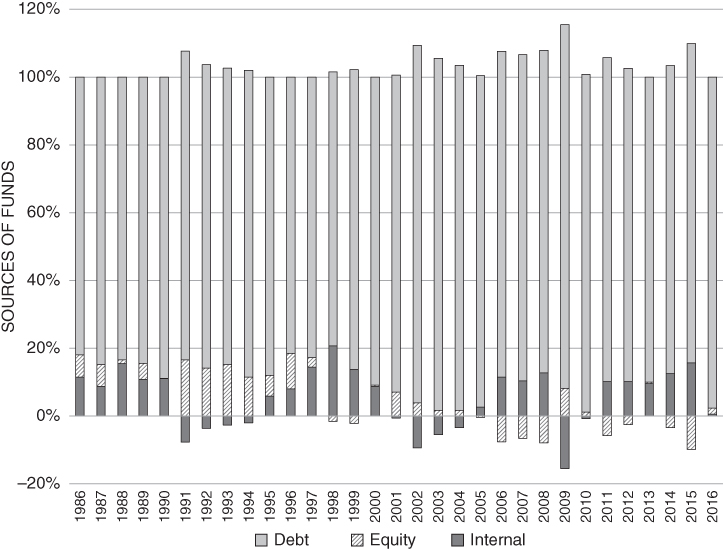
FIGURE 6.2 Source of Funds of NYSE Corporations 1986–2017
Source: Compustat.
Looking closely at Figure 6.2, in some years the amount of debt or equity issued is negative. How can the amount of debt or equity issued be negative? Because of debt repayments and stock buybacks. In many years, firms in aggregate repurchased more debt or equity than they issued. Obviously, it is not the same firms issuing and repurchasing.
Furthermore, as shown in Table 6.1, capital structure varies substantially across industries. The market debt ratio (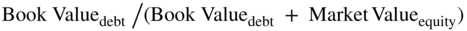
) for the electric and gas industry, which is primarily utilities, averages 39%. Food production averages 30%. For paper, rubber, and plastic equipment, it is 26%, while for computer software it is only 5% (Microsoft, Intel, and Dell have very low debt ratios). Computer firms have very little debt in their capital structures. By contrast, utilities have a very high level of debt in their capital structures.
TABLE 6.1 Debt Ratios of NYSE Firms by Industry in 2017
| Industry | BVdebt/(BVdebt + BVequity) | BVdebt/(BVdebt + MVequity) |
| Computer software | 26.0% | 5.0% |
| Airlines | 42.8% | 22.9% |
| Pharmaceuticals | 44.3% | 22.4% |
| Chemicals | 48.3% | 23.8% |
| Retailers | 53.0% | 30.7% |
| Electric, gas, and sanitary services | 54.4% | 38.7% |
| Food production | 58.1% | 29.8% |
| Paper, rubber, and plastics | 64.7% | 25.5% |
| All | 46.2% | 28.9% |
Source: Compustat.
M&M AND CORPORATE FINANCE
Modern corporate capital market theory is based on the work of two Nobel laureates, Franco Modigliani and Merton Miller (M&M).4 M&M (1958) shows that under certain key assumptions, capital structure is irrelevant to (does not alter) firm value. That is, in an M&M world, the value of the firm does not change with changes in the firm's capital structure (meaning changes in the percentage of debt versus equity).
M&M (1958) makes several strong assumptions:
- First, they assume a complete market. A complete market is one where any asset an individual or firm wants can be obtained. In other words, any possible payoff pattern can be currently purchased from the set of financial instruments available to investors and firms.
- Second, M&M assume the markets are efficient. This means there is no asymmetric information; everyone knows what everyone else knows.
- Third, they assume that any individual can arbitrage costlessly in the market.
- Additionally, they assume there are no taxes, no costs of financial distress, and no transaction costs.
If all these assumptions are true, then M&M (1958) shows that financing decisions are irrelevant for firm value and therefore that a firm's capital structure, in particular, does not matter.
One way to explain the reasoning behind this theory is that firm value is determined by the value of the cash flows generated from the operating assets (represented by the left-hand side of the Balance Sheet). These cash flows are then allocated to the suppliers of capital, who are the debt holders and the equity holders (represented by the right-hand side of the Balance Sheet). Thus, the cash flows from the assets (the left-hand side of the Balance Sheet) go to the suppliers of capital (the right-hand side of the Balance Sheet).
How the assets are financed (i.e., who supplies the capital) does not change the cash flows available from the operating assets. This is the reason why in an M&M world the value of the firm is independent of how the firm is financed. How the claims on the firm's asset cash flows are divided does not change the total cash flows or their value.
The mechanism that makes assets with identical cash flows have the same value is arbitrage or the possibility of arbitrage. What is arbitrage? Buying something at one price and selling it at a different price, without risk, when the cost of doing the transaction is less than the difference in price. (The concept of arbitrage is discussed in the box below.) As a consequence, two firms, Firm A and Firm B, that have identical cash flows but different capital structures have the same price (value):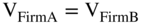 
. This also means that purely financial transactions, such as substituting debt for equity, can neither increase nor decrease firm value.
Let's do an example. Consider two firms, A and B. According to M&M (1958), if both firms have the same cash flows, they have the same value regardless of their capital structures. Let Firm A be financed entirely by equity while Firm B is financed with both debt and equity. The cash flows to the equity holders in Firm A equal the cash flows to the debt plus the equity holders in Firm B. This means that the value of equity in Firm A has to equal the value of the debt plus the equity in Firm B.
Note: Instead of two separate firms, A and B, the paragraph above could apply to one firm with two alternative capital structures. That is, call it Firm A if it is all equity financed and called it Firm B if it is financed with debt and equity.
Summary point: For M&M (1958), it is all about cash flows. If two firms have the same cash flows, they must have the same value.
To review: A firm's cash flows from the asset (left) side of the Balance Sheet (the firm's earnings, depreciation, CAPEX, etc.) equal the firm's cash flows to the financing (right) side of the Balance Sheet. If the value of two firms with the same cash flows is not equal, then we have the possibility of arbitrage, which will make them equal.
If the transaction cost of buying and selling shares (i.e., shares of both equity and debt) of Firm A and B is zero (or very low), then arbitrage will drive the price of Firm A to equal the price of Firm B. Investors are ultimately interested in the cash flows from the investment. If the price of Firm A is above the price of Firm B, then an arbitrage opportunity exists to sell shares of Firm A and buy shares of Firm B. As already stated, in our example the cash flows to shareowners of Firm A are identical to those for shareowners of Firm B. Arbitrage therefore allows you to buy an identical cash flow at a lower price. As the arbitrage is exercised and market participants keep selling Firm A and buying Firm B, the price of Firm A will go down and the price of Firm B will go up until the prices of the two firms equate.
Thus arbitrage, with zero transaction costs, will result in the M&M solution where firms with the same cash flows have the same value regardless of their capital structure. It does not matter if the firms are financed with debt or equity or a combination of debt and equity: both firms will have the same value because they have the same cash flows; the cash flows are just divided up in different ways.
In other words, the total cash flow is not dependent on the capital structure because it is generated by the firm's operating assets (the left-hand side of the Balance Sheet). That is, the cash flows received by the debt holders (principal + interest payments) plus the cash flows received by the equity holders (dividends + retained earnings) equal the cash flows generated by the assets (which do not change with the amount of debt or equity).
Furthermore, in the M&M world, arbitrage, or its possibility, keeps the value of Firms A and B equal regardless of capital structure. You sell whichever is of higher value and buy whichever is of lower value until the prices equate. That is one argument supporting M&M.
A second argument supporting M&M (1958) is that investors will not pay a premium to undertake financial transactions they can undertake themselves. For example, assume Firm A, which has identical cash flows to Firm B, is priced higher than Firm B. Further assume that Firm A has no debt, whereas Firm B is financed with debt and equity. An investor in Firm A can duplicate Firm B's capital structure by borrowing money to buy Firm A's stock. (Firm A's effective capital structure to the investor will be comprised of equity and the debt used to finance the purchase of equity.) Vice versa, an investor can buy Firm B and remove the leverage by borrowing stock and selling it short.5 Thus, if transaction costs are zero, an investor could take any firm and duplicate another firm's capital structure themselves. This is another reason why the prices of the two firms have to be equal in the M&M world with zero transaction costs.
The third argument that makes M&M (1958) valid is that financial transactions are zero net present values (NPVs). Net present value is how finance professionals, finance professors, and even finance students measure investment value. It considers the benefits and costs of an investment and measures them all at a single point in time, the present. We will discuss this concept in more detail and explicitly explain how it is calculated in its own chapter (Chapter 14), which is placed at the beginning of the third section of this book, where we analyze how a firm makes good investment decisions. Although it is not necessary, if the reader would like to jump ahead, that chapter is largely self-contained.
If a firm issues $100 million of debt and receives $100 million in proceeds, what is the NPV of the debt issuance? The NPV of the bond issue at the date of issue is zero. The firm sold $100 million worth of claims and received $100 million in cash. This is a zero NPV. Discounting the cash flows to the bondholders (i.e., interest and principal) at the current discount rate yields $100 million, which is the value of the bonds and results in an NPV of zero. The same is true for equity. If a firm issues equity for $100 million, it means the market believes the present value of the future cash flows to equity is $100 million, again yielding a zero NPV. Both issuances are zero NPVs. If all purely financial transactions are zero NPVs, they neither increase nor decrease firm value. Selling debt therefore does not increase firm value; it is a zero NPV. Selling equity also does not increase firm value; it is also a zero NPV. Hence, in an M&M world, changing capital structure by issuing new debt or equity doesn't change the value of the firm because it is a zero-NPV transaction.
To Review
M&M (1958) shows that capital structure, under certain key assumptions, is irrelevant to (does not alter) firm value. That is, in an M&M world, the value of the firm does not change with changes in the firm's capital structure (capital structure is often characterized as the percentage of debt versus equity).
The logic behind this theory comes from the fact that it is the value of the cash flows generated by the operating assets (the left-hand side of the Balance Sheet) that impacts firm value and not how those assets are financed. The size (or value) of the pizza is independent of how many slices there are or who gets them, since this does not change the size of the pizza (the total cash flows). Arbitrage, or the possibility of arbitrage, means that all assets that have identical cash flows have the same price. Likewise, two firms that have identical cash flows but different capital structure must have the same price (i.e.,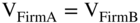 
).
M&M's theory on the irrelevance of capital structure is proven by three key elements of financial intuition:
- First, under the M&M assumptions, if Firm A were to adopt Firm B's capital structure, its total value would not be affected (and vice versa).
- Second, investors will not pay a premium for firms that undertake financial transactions that they can undertake themselves at the same cost in perfect markets. For instance, they will not pay a premium for Firm A over Firm B simply because A has less debt, or vice versa. Indeed, by combining Firm B's debt and equity in the right proportions, any investor can in effect unlever Firm B and reproduce the capital structure of Firm A.
- Third, all purely financial transactions are zero net present value (NPV) transactions. These transactions neither increase nor decrease firm value. Thus, it makes no difference if a firm raises $100 million by issuing only debt, only equity, or any combination thereof.
The M&M (1958) irrelevance theory was initially applied only to capital structure. However, it can be applied to a number of different financial policies. Using the same logic and assumptions, if capital structure is irrelevant, then so is a firm's term structure of debt (i.e., long term or short term). By using the same arguments, it is also irrelevant whether the debt is fixed or floating rate, how much the firm pays out in dividends, how the firm manages its risk (e.g., hedging), and so on. If a financial policy does not change a firm's cash flow, M&M (1958) implies that the financial policy is irrelevant. Indeed, M&M's proof can be applied to all purely financial transactions and concludes they are all zero-NPV transactions.
M&M's idea that financial policies do not matter was controversial and was not accepted by finance practitioners or by many finance academics in 1958. It is clearly not literally true in practice because their assumptions are not true (i.e., our world is not an M&M world; it has taxes, positive transaction costs, etc.). Still, M&M's theory eventually caused finance academics to ask the right question: Does financing change the size of the pie?
Why this discussion is so important is that before M&M (1958), there was no theory of corporate finance. Before M&M, finance professionals used ratio analysis, pro forma Balance Sheets, Income Statements, and Sources and Uses of Funds to ensure firms did not run out of funds. However, there was no analytical guidance on how a firm should choose to finance itself.
M&M is a starting point for modern finance. It started the academic examination of capital structure by asking: Does capital structure matter? This eventually led academics to ask the same question of many other corporate finance decisions. However, the M&M (1958) paper did not provide finance professionals with analytical guidance because in the M&M world, where markets are efficient, corporate finance does not matter. What the paper did was establish a framework that finance professionals and academics could use to analyze financial decisions.
When the elder of your two authors was doing his PhD, there was no separate doctoral corporate finance course at the University of Chicago. The doctoral two-course sequence in finance allocated two weeks to corporate finance. Those two weeks covered M&M (1958), M&M (1961),6 M&M (1963),7 and only a little more. It taught that nothing mattered in corporate finance and thus corporate finance did not matter. With efficient markets in an M&M world, there is no corporate finance. Capital structure does not matter without taxes or transaction costs, and dividend policy does not matter either. Efficient markets also imply that all securities are properly priced, maturities don't matter, the use of fixed versus floating (variable) rates is irrelevant, and so on. Today we have separate courses in corporate finance because M&M assumptions have been shown not to hold in reality—and corporate finance matters.
M&M's Assumptions
In the first part of this chapter, we listed the five assumptions necessary to define what we called an “M&M world.” Now, it is time to relax those assumptions and make our discussion more realistic. It is also time to consider whether our conclusion that capital structure does not matter holds in a more realistic setting.
Five key assumptions that M&M made in 19588 that we will relax are:
- Taxes are zero. In this chapter we will relax this assumption and examine the impact of positive corporate and personal taxes.
- There are no costs of financial distress. This assumption is clearly incorrect (see the prior chapter on Massey Ferguson). In this chapter we reject it and assume there are costs of financial distress.
- Transaction costs are zero. We will relax this assumption in Chapter 12.
- There is no asymmetric information; that is, no one knows more than anyone else about the true firm value. We will discuss this assumption in the next few chapters and relax it in Chapter 12.
- Capital structure does not affect investment decisions (i.e., investment policy is given no matter what a firm's capital structure is). This will be relaxed in Chapter 12 as well.
Relaxing the first two assumptions defined corporate finance until 1980. Since most early textbooks covered the impact of relaxing the two assumptions regarding taxes and the costs of financial distress, a theory of capital structure that uses M&M without these two assumptions is often called “textbook” capital structure. In a perfect M&M (1958) world, capital structure does not matter. Once taxes and the costs of financial distress are included, however, capital structure does matter, as we show below.
TAXES
M&M themselves relaxed the assumption of no taxes in M&M (1963) and found that in a world with corporate income taxes, capital structure does matter. Their analysis of taxes recognizes that different sources of financing are taxed differently. The key difference is that interest payments are deductible for corporate tax purposes, while dividend payments are not.9 Tax deductibility means that interest is treated like other corporate expenses and is a deduction from revenue before computing taxable profits. In contrast, dividends are paid to shareholders from after-tax funds.10 Interest payments therefore have a tax advantage to a firm over dividends payments because interest costs are paid before taxes, while dividends are paid after taxes.
Let's provide an example. Imagine that ABC Corporation generates a safe $100 million-a-year annual perpetuity and its risk-free rate of return is 10%. The perpetuity formula is:11
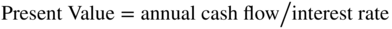
The formula above calculates that the value for our ABC Corporation is $1 billion. As M&M showed, when taxes are absent, this value is independent of how the firm is financed.
Now, assume there are corporate taxes of 21% but no personal taxes (we will add personal taxes shortly). The presence of taxes means the government has a claim on part of the $1 billion value. The value remaining after taxes will go to the debt and equity holders. This is often stated as the value of the firm being equal to the value of the debt plus the value of the equity.
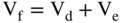
Capital structure—how the firm is financed with debt and equity—now matters because the interest payments reduce the firm's tax bill. As a result, more debt increases a firm's value because it reduces the firm's tax burden.
Returning to our example of two firms: the value of a firm financed with debt and equity and the value of an identical firm financed with only equity will now differ. This can be seen in Table 6.2. In the example, both firms start with earnings before interest, taxes, depreciation, and amortization (EBITDA) of $100 million.12 For simplicity we assume depreciation and amortization are zero for both firms. This means that earnings before interest and taxes (EBIT) is also $100 million for both firms. We also assume a riskless discount rate of 10% for the cash flows for both firms.
TABLE 6.2 Firm Value with Corporate Taxes
| Firm with Debt of $300 million | 100% Equity Firm | |
| Earnings before interest, taxes & depreciation | $100.0 million | $100.0 million |
| Depreciation and amortization | $0.0 million | $0.0 million |
| Earnings before interest and taxes | $100.0 million | $100.0 million |
| Interest expense (at 10%) | $30.0 million | $0.0 million |
| Profit before tax | $70.0 million | $100.0 million |
| Corporate tax (rate 21%) | $14.7 million | $21.0 million |
| Net income (income after tax) | $55.3 million | $79.0 million |
| Value of equity (perpetuity with r = 10%) | $553.0 million | $790.0 million |
| Value of debt | $300.0 million | $0.0 million |
| Firm value (value of debt + equity) | $853.0 million | $790.0 million |
In column one we assume one firm has a loan of $300 million at a rate of 10% and annual interest payments of $30 million (which is 30% of EBITDA and EBIT, corresponding to the maximum allowed under the 2018 U.S. corporate tax law). The taxable income is $70 million, and the tax is $14.7 million (21% times $70 million). The net income is $55.3 million ($70.0 – $14.7), which when discounted as a perpetuity at 10% gives an equity value of $553.0 million. To this we add the $300 million value of the debt to get a firm value of $853.0 million.13
The second column of Table 6.2 shows the all-equity firm. The EBITDA and EBIT are the same $100 million as the firm financed with debt and equity. However, since there is no debt, the second firm has no interest expense. This means the profit before tax is $100 million. Multiplying the profit before tax of $100 million by the corporate tax rate of 21% yields a tax amount of $21 million to be paid to the government. This means the $100 million in profit before tax is split, with $21 million going to the government and $79 million left for the equity holders. The value of the equity is thus $79 million a year in perpetuity discounted at 10% for a total of $790 million. The total firm value (value of debt + value of equity) is now also $790 million because there is no debt.
Therefore, if the firm is partly debt financed, it is worth $853 million, while if it is 100% equity financed, it is worth $790 million.13 The debt-financed firm is worth $63 million more than the all-equity-financed firm because of the way the government treats interest payments. This value is called a tax shield. The perpetuity value of the tax payments—the amount going to the government—is $147 million for the debt-financed firm and $210 million for the all-equity firm. These are the perpetuity values of the $14.7 million and $21 million in taxes discounted at 10% ($14.7 million/0.10 = $147 million; and $21 million/0.10 = $210 million, respectively). By using debt instead of equity, the firm “saves” $63 million worth of payments to the government.
Note: M&M still holds because the size of the total pie does not change—it is still $1 billion. The size of the pie is determined by the before-tax cash flow. What is the difference in the two firms? The difference is in who gets the slices of the pie. In the debt-financed firm, the debt and equity holders get $853 million and the government gets $147 million. In the all-equity-financed firm, the equity holders get $790 million (there are no debt holders) and the government gets $210 million. With the introduction of taxes, there is now a slice going to the government. Going forward, we should think of every firm as having an additional claim holder: the government.
As we noted earlier in this chapter, a key benefit of M&M theory is getting us to ask the right questions. The question that M&M causes us to ask, once we've added corporate taxes, is: How does a firm's financing choice affect the IRS's slice of the pie? A standard answer, in some textbooks, is that using debt generates a tax shield equal to:
where Tc is the corporate tax rate and D is the value of the debt outstanding.
However, remember how we arrived at the $147 million and $210 million above. We began with perpetual debt, and we discounted the debt at Kd. (The authors prefer to use Kd instead of Rd to represent the discount rate on debt. Kd is usually the same as the interest rate on the debt. There are some exceptions that we will ignore for now and discuss much later in the book, such as when the interest rate charged is a subsidized market rate.)
The present value of the perpetuity tax shield is the tax shield per year (the tax rate Tc times Kd times D, where the tax rate is 21%, the interest rate is 10%, and the amount of debt is $300 million) discounted using the discount rate Kd. The Kd's in the numerator and denominator cancel out, leaving Tc times D, which is equal to $63 million (21% times $300 million).
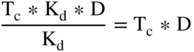
Unfortunately, it is not that simple. The formula above is only a first pass in understanding the value of the tax shields; it is not a complete picture. Moreover, the formula assumes the debt is perpetual, the interest is always below the 30% limit (i.e., all the interest can be deducted), and that there are no personal taxes. In fact, Tc * D is not complete until we add personal taxes.
Caveats: Marginal Tax Rates
Before adding personal taxes, let's take a small detour for some caveats to the above analysis. The first caveat is that not all firms pay taxes, or if they do, not all firms pay 21%. One way not to pay taxes is to have no taxable income. No taxable income can occur because, as seen above, the firm has high interest expense. Other ways a firm can have little or no taxable income is because earnings are low or because tax deductions are high. For example, historically, railroads paid no corporate income tax because their large infrastructure investments generated tax deductions from depreciation, causing their taxable income to be close to zero. For railroads, therefore, there is no interest tax shield from debt since they have already used a tax shield from depreciation. There is no additional benefit from the tax deductibility of interest costs because they generally don't pay taxes.14 Thus, any firm that does not pay taxes without debt financing will not obtain any tax shield from debt.
The second caveat is that issuing debt does not create value by itself. If a firm issues debt and then keeps the excess cash in the bank, the debt issue will not create a tax shield or value. This is an important point: In corporate finance, excess cash is the same as negative debt. Later in the book, it will be important to consider both levered and unlevered betas (beta is a measure of risk), and, when doing so, excess cash is treated as negative debt. For example, if a firm borrows $100 million at 10% and puts the $100 million in the bank earning 10%, there is no tax shield or value created. The firm pays $10 million a year in interest expense while earning $10 million a year in interest income, so the cash flow impact of the debt is zero and no value is added.
To repeat, borrowing money does not add value. Value from tax shields is only created when the firm uses borrowed money rather than equity to finance assets. It is the substitution of debt for equity that creates the tax shield. This can occur if a firm finances an investment with debt rather than equity or if the firm undertakes a recapitalization (buys back some of the firm's equity with borrowed money). Just borrowing money and sitting on the cash does not create a tax shield.
The third caveat is that taxes are not the only reason to issue debt! It is stunning how often MBAs (never any of the authors' former students, of course) make statements like, “Oh, the firm only took on debt because of the tax shield.” The tax shield makes debt less expensive (and thus more attractive), but it is not the only reason to issue debt. If taxes went to zero, would firms still issue debt? Many MBA students would answer, “No, because there is no tax shield.” However, this is not true. U.S. corporate taxes were not instituted until 1914, yet firms still used debt before 1914. The railroads that were built in the 1870s and 1880s used lots of debt (and railroads continue to use debt without interest tax shields). The tax shield makes debt more attractive, and firms will perhaps issue more debt than in a world without corporate taxes, but the shield is not the only reason for debt. We will discuss the other reasons to issue debt in more detail later in the book. At this time, it is important for the reader to understand that the tax shield is not the only reason why firms issue debt.
Personal Taxes
Let's now move on to the addition of personal taxes. Corporate taxes make it advantageous for firms to use debt instead of equity for financing. Personal taxes usually make it advantageous for firms to use equity instead of debt for financing. The net effect of the two is that debt is usually tax advantageous for a firm; however, the advantage is less than when we consider corporate taxes alone.
For corporate taxes we can use a single corporate tax rate—currently 21%.15 However, investors face two different forms of taxes on equity payments and one on debt payments. Equity payments to stockholders can take the form of either dividends or capital gains, both of which are taxed but often at different rates. Debt payments to debt holders take the form of interest, which is usually taxed at the personal income tax rate.
Prior to 2003 and for most of the twentieth century, interest income and dividend income were taxed at the same rate, equal to the rate on ordinary income, while capital gains were taxed at a lower rate. Today, capital gains and dividends are usually taxed at the same lower rate. By contrast, interest income (the payments received by debt holders) is still taxed at the higher rate equal to that on ordinary income.16
Capital gains are received by selling a share of stock for more than the initial investment. Furthermore, the taxes on capital gains were (and still are) deferred until realized. This is unlike dividends and interest, which are taxed in the year received. For example, if an investor bought a share of Goldman Sachs for $160 and over the year the stock increased in value to $180, the investor would not have to pay any taxes on the $20 gain until it was realized. When the share is sold, the investor “realizes” the gain and has to pay taxes. This means that the effective tax rate for capital gains is not just the capital gains rate, but rather the capital gains rate discounted back from the time when it will be realized.17
By contrast, the tax system for individuals in many countries (e.g., Europe and Canada) provides investors with a tax credit for dividends. The rationale is that the corporation has already paid tax on the earnings now being paid out as a dividend and this avoids double taxation. In the United States, a corporation pays the tax on its earnings and then the stockholder pays tax on the dividend received with no credit for the corporate tax already paid.18
From the corporation's viewpoint (ignoring the impact to its investors), there is a large advantage to financing with debt because the firm deducts the interest before calculating profit before taxes. This reduces the amount of corporate taxes. With equity financing, there is no tax deduction for dividends or retained earnings and thus no reduction in taxes.
From the individual investors' point of view, personal taxes favor equity payments. This is because of the relative personal tax rates on interest income, dividends, and capital gains. The personal tax rate on dividends is at most equal to and sometimes (e.g., currently) less than the personal tax rate on interest payments. Dividend income has never been taxed at a higher rate than interest income. Realized capital gains are usually taxed at a lower rate than both interest income and dividend income.19
So from the corporation's point of view, there is a tax advantage to debt over equity. By contrast, for investors choosing which financial security to buy, there is an advantage to receiving equity returns. Ultimately, what matters is the after-tax cash flow to investors, net of both corporate and personal taxes. One way to think about this is that if the firm uses debt financing, it pays less of its cash flows to the government and thus has more cash flow left for investors. However, given equal levels of post-corporate tax cash flows, investors have a preference for equity cash flows rather than debt. Combining the two, a firm financed with debt (equity) will have more (less) cash to return to investors, but the cash then received by those investors will be taxed at a higher (lower) rate. When combined, the net advantage is still for the firm to finance with debt, but this advantage is reduced from the section above that did not consider personal investor tax rates.20
Let's do an example illustrated in Table 6.3. There are three alternatives. In the first case, the firm is financed partly with equity and partly with $300 million of debt. The earnings to equity are paid out as dividends. In the second case, the firm is financed entirely with equity and pays out all its earnings as dividends. In the third case, the firm is financed entirely with equity and pays no dividends, so the investor realizes their returns from capital gains. As above, assume EBIT and EBITDA are both $100 million for all three cases (i.e., depreciation and amortization are zero).
TABLE 6.3 Relative Advantage of Debt
| Firm with Debt | 100% Equity All Dividends | 100% Equity All Capital Gains | |
| Corporate level: | |||
| EBIT | $100 million | $100 million | $100 million |
| Interest expense | $ 30 million | $0 | $0 |
| Profit before tax | $ 70 million | $100 million | $100 million |
| Corporate tax @ 21% | $14.7 million | $21.0 million | $21.0 million |
| Net corporate profit | $55.3 million | $79.0 million | $79.0 million |
| Personal level: | |||
| Gross to debt holder | $30.0 million | $0 | $0 |
| Personal tax at 37% | $11.1 million | $0 | $0 |
| Net to debt holder | $18.9 million | $0 | $0 |
| Gross to equity holder | $55.3 million | $ 79.0 million | $ 79.0 million |
| Dividend tax at 20% | $11.1 million | $15.8 million | $0 |
| Capital gain tax at 20% | $0 | $0 | $15.8 million |
| Net to equity holder | $44.2 million | $63.2 million | $63.2 million |
| Net to investors | $63.1 million | $63.2 million | $63.2 million |
| Total taxes | $36.9 million | $36.8 million | $36.8 million |
In the first case, the firm is partly financed with $300 million of debt and pays out interest of $30 million (i.e., $300 million * the interest rate of 10%) and dividends (after corporate tax) of $55.3 million. Now let's consider personal taxes. The debt holders, assuming the maximum personal tax rate of 37%, pay $11.1 million of taxes on their interest income. The equity holders, assuming a maximum dividend tax rate of 20%, also pay $11.1 million on the dividends. The net after tax to investors is $63.1 million ($18.9 million to debt holders and $44.2 million to equity holders). The total taxes, both corporate and personal, sum to $36.9 million. This is all shown in Table 6.3, column one.
In the second case, the firm is financed with 100% equity and pays out all of its net income as dividends. EBIT is again $100 million. However, in this case there is no interest expense, so the profit before tax is $100 million, and the firm will pay $21 million in taxes at a corporate income tax rate of 21%. This means the dividends paid to individuals, net of the corporate taxes, is $79 million (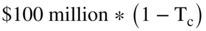
, where Tc is the corporate tax rate). After the stockholders receive the dividend payments of $79 million, they must now pay personal taxes on this amount. If the tax paid on dividends is 20%, the stockholders pay taxes of $15.8 million and receive an after-tax income of $63.2 million.
In the third case, the firm is again 100% equity financed and pays no dividends. The after-tax profits of $79 million go into retained earnings, which is not taxed until realized. Stockholders realize a capital gain when they sell their shares. Assuming the stock value rises by the amount of retained earnings and shareholders sell the stock to realize the gains immediately, stockholders will pay tax on the $79 million gain at the personal capital gains tax rate. If we assume the capital gains tax rate is 20%, the stockholders pay taxes of $15.8 million ($79 * 20%) and receive an after-tax income of $63.2 million ($79 – $15.8). Since, in our example, the tax rate on dividends and capital gains are identical, investors are indifferent between how they receive equity income (if they receive their capital gains immediately).
Note, however, that the tax advantage to debt has been reduced when we also consider personal taxes. With only corporate taxes, $300 million of debt financing means there is an additional $6.3 million per year paid to the investors of the firm (or to say it another way, investors get $6.3 million per year less because it goes to the government in taxes). When personal taxes are included, investors in the debt-financed firm receive $63.1 million net after both corporate and personal taxes. With a 100% equity-financed firm, investors receive $63.2 million net after corporate and personal taxes. There is still a tax advantage to debt financing, but it is reduced in both absolute and relative terms.
Importantly, in the Table 6.3 example, we assume the capital gains were immediate. If an investor defers the capital gains, which they can do merely by not selling the stock (if you recall, earlier we explained that capital gains are only taxed when they are realized), then the effective capital gains tax rate is less than 20%. That is, the capital gains rate is 20% in the future, the present value of which is less today.
Additionally, in reality, tax rates change frequently. For example, the capital gains and dividends tax rates only increased to a maximum of 20% in 2013. This means the size of the advantage for debt financing versus equity financing also changes.
If the stockholders are not individuals but corporations or fiduciaries, the tax rates on interest payments, dividends, and capital gains are usually lower. These different rates do not change the logic of our example above. To avoid adding further complexity to this section, we will not address all the possible tax rates within the United States or between countries.
COSTS OF FINANCIAL DISTRESS
If taxes were the only consideration and all interest was deductible (as it was prior to 2018 in the U.S. and still is in most countries), then the tax shields from debt suggest that most companies should be 100% debt financed. However, the empirical evidence suggests otherwise. If a firm's debt burden is too high, the firm may have trouble paying it off. What happens if the firm does not pay its debt holders? The debt holders can force the firm into bankruptcy. We define a firm experiencing difficulties paying its debt as one in financial distress.
By contrast, if a firm does not pay its equity holders (or if the firm reduces its dividend payments), the shareholders may be hostile at the annual meeting and elect new directors.21 However, the shareholders, unlike the debt holders, can't force a firm into bankruptcy. Furthermore, as we saw in the last chapter detailing the experience of Massey Ferguson, firms in financial distress are also open to competitive attack and loss of management focus, as well as increased administrative costs.
In an M&M world, bankruptcy costs are assumed to be zero and therefore can be ignored. More importantly, M&M argue that a firm is in bankruptcy only when the firm's cash flows are below the amount required to pay the creditors. The big assumption here—and you should highlight it—is that in an M&M world, cash flows do not change because of financial distress. The primary reason a firm enters financial distress is falling sales and/or rising costs. This is what causes lower cash flows. Since financial distress in an M&M world has no cost, it does not affect cash flows. Thus, in an M&M world, financial distress does not affect firm value.
However, as we described in the Massey Ferguson case, in practice this is not true. There are costs of financial distress that can reduce the firm's cash flows. Thus, to use M&M sensibly, it is important to understand that the M&M theory is not a statement about the real world but rather a useful starting point to think about financial distress.
The question now becomes: How does being in financial distress reduce a firm's cash flows? To consider this question, let's divide the costs of financial distress into direct costs and indirect costs. The direct costs are the costs of the process itself: the legal, accounting, and administrative costs. The indirect costs are the impact on the firm's operations (its customers, suppliers, managers, agency costs, debt overhang, ability to raise new funds, inability to invest in positive NPV projects, and so on).
First, what are and how large are direct bankruptcy costs? Empirically, it has been estimated that the direct costs (legal expenses, court costs, advisory fees, etc.) average 2–5% of total firm value for large (Fortune 500) companies and maybe 20–25% for medium-sized (mid-cap) firms.22 So for a large firm like Massey, the lawyers' bills, the accountants' fees, the investment bankers' fees, and the costs of the Dorchester Hotel were not that large relative to the size of the debt being restructured. Furthermore, to properly compute a firm's direct bankruptcy costs, these costs should be weighted by the likelihood the firm will go into bankruptcy. This means that if firm bankruptcy costs are 2–5% and the probability any firm will go into bankruptcy is, for example, 1%, then the expected costs are between 0.02% and 0.05%. Thus, direct bankruptcy costs for large firms tend to be very low and don't impact firm value much.
The indirect costs of bankruptcy are another story. It is the indirect costs of financial distress that can substantially reduce firm value. Once a firm approaches financial distress, it is likely to lose customers and potentially suppliers. Customers are likely to disappear as they worry about future service and warranties as well as resale values. This may not be much of an issue for a hotel customer, who stays the night and then leaves. It matters a lot, however, if you are buying a combine from Massey Ferguson. If Massey Ferguson is in financial distress, farmers are more likely to buy a John Deere combine, as opposed to one from Massey Ferguson. A farmer owns a combine for many years and must be able to get parts to repair and maintain it. (Interestingly, when Chrysler was in financial difficulty in the early 1980s, they offered a free, five-year, 100,000-mile warranty to entice customers. Unfortunately, this may not have persuaded many buyers who worried about Chrysler being in existence long enough to honor the warranty.) Thus, one cost of financial distress is the loss of customers.
Similarly, a firm in financial distress may lose suppliers. If a supplier sells to a firm that now enters financial distress, the supplier may change the terms of sale from credit to cash on delivery. However, a firm in financial distress may have insufficient cash to pay on delivery. Furthermore, the new requirement that a firm must finance its former accounts payable is an additional financial burden. This is especially true if lenders are unlikely to extend new loans that may increase the firm's probability of bankruptcy. Finally, the firm's cost of capital will also likely rise as investors require higher returns to compensate for the increased risk.
Financial distress also affects a firm's management and employees. Management time and effort is spent dealing with the financial distress rather than focusing on the firm's operations and strategy. In addition, key employees may leave the firm for its competitors. This will weaken the firm further. Also, it has been suggested that employee theft is higher for firms in financial distress, because employees have less loyalty.
Agency costs may also affect management behavior during financial distress. Being in financial distress may motivate managers to act in value-destroying ways. For example, managers may delay liquidation because they want to keep getting their paychecks, despite the fact that the delay will lower the value that will be available to shareholders. Managers may also engage in excessive risk taking. Suppose a firm is bankrupt, owes $100, and if the managers liquidate the firm on Friday they will have $80 in cash to pay the debt holders on Monday. The debt holders won't be happy that they are paid less than they are owed, but they should receive 80 cents on the dollar. What will the equity holders get? Nothing. So what might managers do over the weekend? Take a trip to Las Vegas, check into the nicest hotel, go down to the roulette wheel, and put all that money on 00. If they win, they get paid 35 to 1 and everyone is happy. The debt holders are paid in full, and the equity holders receive a windfall. If they lose, the equity holders are no worse off (and the managers had a nice weekend in Las Vegas). This is why managers have an incentive to gamble (i.e., undertake high-risk ventures) when a firm is in financial distress.
It is not necessary for the firm to be facing financial distress for managers to take excessive risk or make negative NPV investments. For example, assume a firm has $100 million in cash and has an opportunity to acquire an Internet start-up for $50 million. The start-up is estimated to have a future value of $0 with a probability of 2/3 or $120 million with a probability of 1/3. The expected value of the start-up is therefore $40 million (2/3 * $0 + 1/3 * $120). It cost the firm $50 million to invest in a project with an expected future value of $40 million.
Ordinarily, managers would not make this investment. But suppose you are the manager of a firm worth $100 million with $90 million of debt outstanding. Without the new investment, the firm continues to be worth $100 million, with debt of $90 million and equity of $10 million. If the firm undertakes the project and is lucky, the value of the firm goes up by $70 million ($120 million from the new project being successful less the investment of $50 million). There is a one-in-three chance of this happening. In that case, the firm's value is $170 million ($100 million plus $70 million). The debt is still worth $90 million, and the equity is now worth $80 million. On the other hand, if the firm is unlucky and the investment fails, the firm's value will be $50 million ($100 million initial value plus $0 from the investment less the $50 million paid for the investment). The value of the firm falls from $100 million to $50 million. This means the debt holders won't get repaid their full $90 million and that the equity is wiped out: the firm is bankrupt. This is shown in Table 6.4.
TABLE 6.4 Agency Cost Example
| Probability | Firm Value ($ millions) | Debt | Equity | |
| No investment | 100% | 100 | 90 | 10 |
| New investment | ||||
| Good state | 33% | 100 + 120 − 50 = 170 | 90 | 80 |
| Bad state | 67% | 100 + 0 − 50 = 50 | 50 | 0 |
| Expected | 0.33 * 170 + 0.67 * 50 = 90 | 63.3 | 26.7 |
However, from an equity holder's perspective, what is the value of the firm with and without the investment? With the investment, the equity is worth $26.7 million (1/3 * $80 million + 2/3 * $0). Without the investment, the equity is worth $10 million. Doing the investment increases the value of the equity by $16.7 million. So the equity holders may actually decide to take on a negative NPV investment. The investment is a bad gamble, it has a negative NPV, but the shareholders are essentially gambling with someone else's money. They are gambling with the debt holders' money. This is similar to the reason why a firm in distress may adopt excessively risky strategies.
A third indirect cost of financial distress occurs when a firm rejects a profitable project. Why would the firm do this? Because of what is called the debt overhang. Essentially, if equity holders have to invest new money to undertake a new profitable project, but the current debt holders get most or all of the gain, the equity holders won't invest.
Let's explain with an example. Imagine a firm with two potential future states: half the time, the firm will be worth $100; half the time, the firm will be worth $10. So the expected value of the firm is $55 (50% * $100 + 50% * $10). Next assume the firm can undertake a new project for an investment of $15 with a guaranteed return of $22 in a year. If the discount rate is 10%, the project has an NPV of $5. The $22 in a year discounted back at 10% is $20 today ($22/1.1).
Should the firm do the project? Absolutely. It is a guaranteed NPV of $5 (you generate a value of $20 today at a cost of $15 today). Will the firm do it? Maybe, maybe not. It depends on how the project is financed, the firm's current financing, and whether there is a debt overhang. Let us explain further.
Assume the firm has $40 of debt. This means that in the good future state, where the firm's assets will be worth $100 (which occurs with a 50% probability), the creditors will be fully repaid their $40, and the shareholders will get the remaining $60. In the bad future state, where the assets will be worth $10 (which also occurs with a 50% probability), the creditors will only get $10 (losing $30) and the equity holders will get $0.
In our example above, what is the total value of the debt and equity? The value of the debt is $25 (50% * $40 + 50% * $10). The value of the equity is $30 (50% * $60 + 50% * 0). Thus, as noted above, the firm is worth $55, which is the combined value of the debt ($25) and the equity ($30), as shown in Table 6.5.
TABLE 6.5 Debt Overhang Example
| Without the New Investment | ||||
| State | Probability | Assets | Debt Holders | Equity Holders |
| Good | 50% | 100 | 40.0 | 60.0 |
| Bad | 50% | 10 | 10.0 | 0.0 |
| Expected | 55 | 25.0 | 30.0 | |
| With the New Investment | ||||
| State | Probability | Assets | Debt Holders | Equity Holders |
| Good | 50% | 100 + 20 =120 | 40.0 | 80.0 |
| Bad | 50% | 10 + 20 = 30 | 30.0 | 0.0 |
| Expected | 55 + 20 = 75 | 35.0 | 40.0 | |
Now, assume the new project can only be undertaken with new equity. This means that shareholders have to put in the extra $15. How does this affect the value of the firm, the debt, and the equity? As seen in Table 6.5, in the good state of the world, the firm will now be worth $120 (the prior $100 plus the $20 from the new project), the debt holders will get paid back their $40, and the equity holders will get $80. In the bad state of the world, the firm will be worth $30 (the prior $10 plus the $20 from the new project), and the debt holders will get the entire $30 while the shareholders still get $0 even though they invested an additional $15.
What is the present value of the equity if the firm does the new project and it is funded by the shareholders? $40 (50% * $80 + 50% * $0). What was their old equity value? $30. Will the equity holders pay $15 to raise their expected equity value from $30 to $40? No, even though it is a guaranteed positive NPV. Shareholders will not fund the project because they incur the full investment cost and only receive a return in the good state of the world. The existing debt holders invest nothing and still receive part of the return even in the bad state of the world. This is called a debt overhang (due to financial distress, the expected value of the debt, $25, is less than the face value of the debt, which is $40 in our original state). The failure to invest in a positive-NPV project is an indirect cost of financial distress.
This is why it is very hard to issue equity in a firm that is financially distressed. For example: If Massey Ferguson issued equity to undertake a new investment project, who would have received any increase in firm value? It would not be the equity holders (who put the new funds in) but rather the debt holders who were underwater. The existence of risky debt acts as a disincentive to new investments. Shareholders of a firm with high leverage may be reluctant to fund new projects where most of the benefits go to the firm's existing creditors. This effect becomes stronger as financial distress increases.
Thus, we have seen that if the equity holders can gamble with the debt holders' money, they will happily take risks that the debt holders do not want them to take. By contrast, if the equity holders have to put in extra money but don't get all of the upside, there are some profitable projects they won't undertake.
So, what can be done about this? The obvious answer seems to be to issue debt instead of equity to fund the new project. That is, have new debt holders put in the $15. However, if the new debt has a lower seniority than the old debt, then this is the same as issuing equity. (Lower seniority may get paid only after those with higher seniority.) In our example, everyone (old debt, new debt, and equity) gets paid in the good state of the world. In the bad state, the senior debt gets the increase in value coming from the new project while the new debt holders and the equity holders get nothing. If the new debt has the same seniority as the old debt, then it is a mixed case: the increase in value due to the project is split between the new and old debt holders in the bad state. If the firm could issue new debt with a higher seniority than existing debt, the new debt holders who put in $15 would get back $15 plus interest in all states of the world. The problem with this approach is that it is usually prohibited by the covenants on the existing debt. Debt usually has covenants that will not allow new debt to be issued senior to it. Thus, the solution of issuing debt instead of equity is usually not possible because you typically cannot issue new debt senior to existing debt and because, consequently, new lenders will not want to loan money to a financially distressed firm.
Another solution is for the firm to restructure its debt obligations. Remember, the new project delivers $5 of extra value without risk. The debt holders in the current firm (without the new project) have an expected value of $25 ($40 half the time and $10 half the time). Suppose the firm offers a restructuring where it guarantees the old debt holders $1 of the $5 NPV from the new project. The old debt holders should accept this as it makes them better off. And what happens to the shareholders? They get $4 of the $5 NPV from the new project. Currently they expect to get $30 (50% * $60). With a restructuring, the shareholders have an expected value of $34 (50% * $64 + 50% * $4). The restructuring has split the $5 gain, giving $1 to the old debt holders and $4 to the equity holders.
The firm could also change the split in the restructuring and give the old debt holders $2, $3, or $4. However, if the old debt holders receive $5, it is not clear why the shareholders would agree to the scheme. That is, there is some range in which both parties are better off and the restructuring can be done. We will cover restructurings and workouts in Chapter 13. A key element is to find gains that result from the restructuring and share them so that all parties are better off and will agree to the deal. That is, compared to no restructuring and no new investments, everyone will be better off. The problem is that the cost of negotiating the restructuring may prevent it from happening (in the example above we assume the cost of restructuring is zero).
The way to minimize the costs of financial distress is for a firm to reduce its costs of distress in advance and avoid agency and debt overhang issues. This can be accomplished by anticipating the firm's need to raise funds in the future and avoiding having too much debt (how much is too much will be discussed in the coming chapters). If a firm can't avoid excess leverage, it should at least actively manage the leverage to facilitate future restructurings. For example, the 250 banks Massey Ferguson had without a lead bank to manage the group makes it hard to renegotiate and share the benefit from a good project. With a single bank or one lead bank, the costs of restructuring will be lower (often significantly).
THE TEXTBOOK VIEW OF CAPITAL STRUCTURE
Understanding capital structure theory starts with the M&M (1958) irrelevance proposition—capital structure does not matter in a pure M&M world. We next relax the first two of M&M's underlying assumptions by adding taxes and the costs of financial distress. When adding taxes, we discuss the trade-off between corporate (which give firms an incentive to increase debt) and personal taxes (where investors prefer income from equity). Next, we consider the costs of financial distress that can affect a firm's operations and cash flows (and give firms an incentive to lower, or at least limit, debt). Finally, we examine the trade-off between the benefits from debt and the costs of financial distress. This trade-off, in the “textbook” view, results in a static optimum for a firm where the debt level is stable over time.
The above paragraph is shown graphically in Figure 6.3. M&M's (1958) assertion that the value of the firm is not affected by leverage is shown by the solid line at Vu. The dotted line in Figure 6.3 is M&M (1963) with taxes. It shows that firm valuation increases with debt once we include taxes because with more debt, the firm has a larger tax shield (thereby increasing firm value). It is assumed here that the tax shield is available over the entire range graphed. If the tax shield is limited the dotted line flattens where interest deductibility is limited. The solid line, labeled Max Vf, adds in the value of financial distress and shows that increasing the level of debt also increases the risk of financial distress, which causes firm value to start to go down.
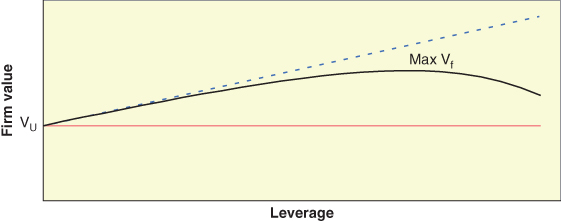
FIGURE 6.3 “Textbook” View of Optimal Capital Structure
The expected costs of financial distress (the likelihood of distress times the costs) are assumed to be small at first. This means the net advantage to a firm from its first tier of debt is close to the full tax shield. As the firm incurs more debt, the cost of financial distress rises and reduces the net value of the firm. The value of the firm with the tax shield and the cost of financial distress is shown in Figure 6.3 by the solid black line. The cost of financial distress is the distance between the solid black line and the dotted line above. At some point, the firm's debt reaches a level where the tax shield from more debt equals the increase in the expected costs of financial distress. This is the firm's optimal capital structure. This is shown as Max Vf in Figure 6.3.
THE COST OF CAPITAL
The cost of capital is how much it costs a firm to obtain the funds to finance the assets it uses to operate its business. In this chapter, we compute the cost as a blended rate: the weighted average of the cost of debt and equity, which is called the Weighted Average Cost of Capital (WACC). The standard way to compute this rate is by taking the percentage of debt times the after-tax cost of debt plus the percentage of equity times the cost of equity.24
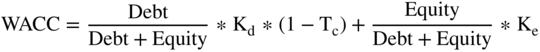
where:
| Kd | = | the cost of debt |
| Tc | = | the corporate tax rate |
| Ke | = | the cost of equity |
Reminder
Minimizing the cost of debt is not the CFO's objective. Minimizing the cost of capital is. Doing so maximizes the value of the firm. Students often state that a firm should minimize the cost of its debt. This is a fallacy. You can always minimize the cost of debt by maintaining very little debt and an AAA rating.25 In addition, debt is almost always cheaper than equity (by definition, even without the tax shield, it is less risky to investors so it has a lower cost). Thus, a firm can almost always borrow at a lower cost than the cost of issuing new equity. But a CFO's job is not about minimizing the cost of debt or about minimizing the cost of new incremental funding. One of a CFO's three major tasks, which we stated in Chapter 1, is to make good financing decisions. This means the CFO's job is to minimize the weighted average cost of capital by getting the trade-off between debt and equity to its optimal point. Minimizing the overall cost of capital is not done by simply minimizing the cost of debt.
SUMMARY
Let's review what we have covered so far. We started with the empirical evidence on corporate capital structures. We noted that leverage measured by market value of equity and leverage measured by book value of equity had fluctuated but remained within a small band. In addition, capital structure varied widely by industry. Much more importantly, we compared how firms funded themselves. Overwhelmingly, in the United States and internationally, firms use internally generated funds first, then they use debt financing, with equity the third choice.
After these empirical facts, we examined capital structure theory, the true focus of this chapter. We began with M&M's seminal work in 1958, which showed that in an M&M world, capital structure does not matter. We next listed the five important assumptions that are necessary for an M&M world.
Our discussion subsequently addressed the implications of relaxing the first two of M&M's assumptions. We allowed for the existence of taxes (both corporate and personal) and the costs of financial distress.26
Relaxing these two assumptions provided us with the “textbook” view of corporate finance (circa 1980), where there is a trade-off between the tax shield and the increased costs of financial distress due to the additional debt.
While the theory is nice, how is capital structure actually set in practice? We now present a checklist with three questions:
- Internal: How much debt can the firm service with internally generated funds? This is calculated by projecting future cash flows using pro formas. It involves computing likely best-case and worst-case scenarios. It also involves answering questions such as: Can the firm pay its debt obligations, interest, and principal in all the expected states of the world? Will the firm ever violate its debt covenants? Are there scenarios where the firm enters financial distress? By answering these questions, we know the level of debt that the firm can afford using its internally generated funds.
- External: What level of debt do external evaluators believe the firm can support? The external evaluations come from rating agencies, analysts, banks, and investors. What is the firm's credit rating, will issuing more debt lower it, will the banks lend the firm money and on what terms?
- Cross-sectional: How does the firm's capital structure compare to its competitors? Is the firm's debt ratio outside the range, either much lower or much higher than the rest of its industry? More explicitly (if you read Chapter 5), if John Deere has a 30% debt level, does Massey Ferguson really want to be at a 47% level? The question can be rephrased as: Is the firm at the right debt level, or are its competitors at the right level? In an industry downturn: Which firms will survive and which won't, and does the firm's debt ratio affect the likelihood of survival?
The three questions above explain the capital structure differences across industries (e.g., electric and gas utilities versus computer hardware and software firms). It is not as good, however, at explaining differences within an industry because there are other factors that are important as well. We will add some of these other factors, such as the impact of asymmetric information and transaction costs, in Chapter 12.
Coming Attractions
The next two chapters are on the Marriott Corporation, one of the most important parts of the book because it illustrates all the key elements of financing a firm. This is where we really start doing corporate finance and where we are going to bring in asymmetric information and other variables. As noted, the current chapter has taken corporate finance to circa 1980. In the next two chapters, we examine how corporate finance has evolved to the present.
We saw the tension in PIPES (Chapter 2) between product market goals and the necessity to fund those goals. In PIPES, the issue was funding sales growth. In Chapter 5, we saw that fast-growing firms that are reluctant to issue equity, such as Massey Ferguson, end up with a debt ratio higher than their target (or optimal) debt ratio. Slow-growing firms that don't buy back their stock wind up with too little debt and pay higher taxes than they should. While it is okay for a firm to stray somewhat from its optimal capital structure, because there is a dynamic element to capital structure, the firm must keep in mind where it ultimately wants to be. Importantly, firms that stray too far from their optimal capital structure in one direction increase their risk of financial distress. As we will see in the chapters ahead, straying too far in the other direction results in too high a cost of capital and too low a stock price; this also has negative consequences, such as a hostile takeover. Ultimately, firms have to be consistent in trading off between the tax savings from debt and the costs from increasing their risk of financial distress.