2  Rainbows in the History of Scientific Enquiry

We use the classical theory on Mondays, Wednesdays and Fridays and the quantum theory on Tuesdays, Thursdays and Saturdays. Sir William Bragg1

The exact origin of what might be termed a scientific approach to the natural world remains a matter of some debate, amid competing claims that the scientific method originated in ancient Egypt or in seventeenth-century Europe or at various points in between. In any case, the history of the study of rainbows as scientific phenomena closely parallels the history of science itself. Dating from the fourth century BCE, Aristotle’s rainbow theory owed something to earlier authors, especially Anaxagoras (d. 428 BCE), Anaximenes of Miletus (fl. 550 BCE) and Hesiod (fl. 700 BCE).² But in its level of detail and its power over subsequent generations, it was quite unparalleled, despite fatal flaws stemming from the fact that ‘avoidance of experiment’ lay ‘at the heart of Aristotle’s methodology on the rainbow’.³ The history of the bow as an object of scientific enquiry is therefore largely the story of the acceptance, loss, rediscovery, re-acceptance and gradual abandonment of Aristotelian ideas over a period of two millennia. In comparison to this slow yet fascinating trudge from deference to self-confidence, the arrival of the ‘modern’ rainbow in the seventeenth century can seem like a sudden explosion, since which improvements to our understanding have again been relatively incremental and slow. While it is not feasible in the space of this chapter to provide a complete narrative of all the pre-modern rainbow theories and experiments about which anything is known, it is certainly possible to trace some of the most important turning points, and dead ends, in the study of this extraordinary phenomenon.

Rainbow, bottled rainbow, dragons, demon and warrior from the Thesaurus thesaurorum et secretum secretissimum in quo omnia Mundi arcana latent, a European alchemical text of c. 1725.

Aristotle: a half-baked solution becomes a new problem

Aristotle, who lived in the fourth century bce, correctly understood several aspects of the rainbow: that it could not appear without the presence of water droplets in the atmosphere; that there were ‘geometrical uniformities’ in the relative positions of the bow, the observer and the Sun; and that the bow’s shape might also be accounted for geometrically.4 His belief that the bow consisted of only three colours – red, green and violet – was not necessarily wrong in itself, as such judgements are to some extent culturally based. However, other aspects of his explanation had manifest problems – for instance, his conviction that each of these three colours was a mixture (in different proportions) of white and black, with red containing the most white of the three, and violet the least. At any rate, these were the real colours; Aristotle saw yellow in the rainbow, too, but considered this to be a mere trick of perception.⁵ That there should be exactly three colours was given a variety of non-scientific or pseudoscientific justifications, including the division of events into three parts (beginnings, middles and ends), the division of space into three dimensions and even the use of the number three ‘in the worship of the gods’.⁶ Aristotle further held that the red band of the rainbow was the fattest in primary rainbows and thinnest in secondary ones. While aware of the existence of refraction – and even that this process might be ‘effective’ in the production of colour – he never suggested that rainbows were caused by anything other than reflection.⁷ Violating his own dictum that the Sun was larger than the Earth, Aristotle also used reflection as a broad explanation for why daylight can be seen everywhere and not merely in ‘that spot on which the sun’s rays directly fall’.⁸ He recognized that reflection operated according to natural laws of some sort, but expressed little or no interest in what these laws might be; and if Euclid’s law of reflection was known during Aristotle’s lifetime, Aristotle either rejected it out of hand, or was wholly unaware of it.⁹

Woodcut of Aristotle pointing to the heavens, in a 1496 French edition of his Physics.

An imagined conversation between Aristotle, Ptolemy and Copernicus, engraved in 1632 by Stefano della Bella (1610–1664).

Because he also supposed that every reflection represented a drastic weakening of the original image – as in the primitive metal mirrors with which he was familiar – Aristotle held that no tertiary rainbow could exist; following their exertions in creating the secondary bow, the reflections required to create a third would be too weak.10 (It did not bother most of Aristotle’s followers that if the secondary bow were in fact merely a reflection of the primary, it would be U-shaped and not a second, larger arch.)

The apparent strength of the red band in the secondary bow, Aristotle said, was because this band, being lowest relative to the ground, is nearest to the observer.11 However, this explanation was subverted by the fact that the red band in the primary bow was, by Aristotle’s reckoning, the farthest from the observer yet also the brightest. So in the case of the primary bow, he explained this away using a separate argument that the redness/brightness of the outermost/highest band was due to it having the greatest overall area, much as the outside lane on a race course is the longest, and that it therefore had the most opportunity for reflection.¹² But obviously, these two explanations cannot be reconciled. Nor can Aristotle have spent much time observing rainbows in the mountains, since he maintained that ‘the rainbow never forms a full circle, nor any segment greater than a semicircle’.¹³

Most importantly, in terms of his blockage of correct understanding of the rainbow by generations of later observers, Aristotle maintained that it was always reflected from clouds. This was an echo of the work of Anaximenes, who, two centuries earlier, had suggested that rainbows consisted of ‘sunlight . . . returned to an observer from an impenetrable cloud’.¹⁴ For Aristotle, however, the water droplets that gave rise to the rainbow did so because, though flat like household mirrors rather than spherical or spheroid, they were far too small to reflect the Sun as it actually appears, and in place of the Sun’s image could reflect colours only. And crucially, Aristotle’s clouds (and Sun, and everything else located in what we moderns would call both the sky and outer space) are attached to the inside of an imaginary sphere with the observer at its centre, and are thus necessarily concave.

The biggest of many problems with a rainbow based entirely on reflection is that it ought to grow taller as the Sun rises and shrink as it sets, rather than rise as the Sun sets and vice versa, which rainbows always do in reality. Another key implication of Aristotle’s ideas was that the rainbow was exactly the same distance from the observer as the observer was from the Sun, regardless of whether the observer moved; and one wonders if this troubled even his ancient contemporaries, despite them being accustomed to thinking of the sky as the flat Earth’s domed roof.15

The ancients after Aristotle

Though Posidonius took issue with minor aspects of Aristotle’s rainbow in the second century BCE, the first major challenge came from Seneca the Younger (d. 65 CE), who hacked at the roots of the Aristotelian shrub by attacking its source material: the rainbow theory of Anaximenes.¹⁶ If rainbows were indeed caused by some water particles in a cloud transmitting sunlight and others not transmitting it, Seneca asked, why was the bow not merely of two colours, light and dark? While at first tentatively accepting the Aristotelian view that the shape of the rainbow was produced ‘by a cloud formed like a concave, round mirror’, Seneca expressed nagging doubts about the fact that rainbows resembled the Sun in neither colour nor size.¹⁷ He also moved ‘acutely to deny from the outset that a rainbow can be formed by the reflection of the sun in cloud’ on the grounds that clouds do not contain any raindrops, only matter from which raindrops are later produced.¹⁸ Moreover,

it is obvious that in the case of a rainbow no actual color is formed, but only the appearance of illusory color, the sort which . . . the neck of a pigeon takes on or gives up whenever it changes position. This is also the case in a mirror, which assumes no actual color, but only a kind of copy of the color of something else.¹⁹

Alexander of Aphrodisias (fl. 200 CE) was the pre-eminent ancient Greek commentator on Aristotle’s works. He raised a question that cut right through the master’s problematic dual explanation for the primary bow being brightest in the top band and the secondary bow brightest at the bottom: why is the whole area between the primary and secondary bows not also red? Indeed, why does it appear darker than either the area inside the primary bow, or the area outside the secondary bow? This darker inter-bow area is still known today as Alexander’s band. But such a challenge was exceptional. Olympiodorus the Younger provided a staunch, programmatic defence of the Aristotelian theory, and authors in the West mostly followed his example until after the fall of Rome, when knowledge of the Greek language (and with it, direct knowledge of what Aristotle had said) rapidly faded away.20

Frontispiece to the 1549 Venetian edition of the Commentaria of Alexander of Aphrodisias.

By the seventh century, despite the appeal of arguments that a three-colour rainbow accorded well with the Holy Trinity, a number of Christian thinkers had decided that the rainbow contained four colours corresponding to the four elements. However, they disagreed over which colours represented each of them. Saint Isidore (d. 636), for instance, saw a red, purple, black and white bow representing fire, water, earth and air, whereas the Venerable Bede (d. 735) saw the same elements as producing the rainbow colours red, blue, green and brown. But for the time being, European investigation of the bow’s other aspects had effectively ceased.21

Clear image of Alexander’s Band, the dark inter-bow area named for Alexander of Aphrodisias, who deployed it as part of an important early challenge to Aristotle’s deeply flawed rainbow theory.

Rainbow scholarship in the Islamic world

King Ptolemy II of Egypt (r. 283–46 BCE) had purchased a great quantity of Aristotle’s books, and this – along with the ongoing use of Greek in the region – may have helped prop up the Aristotelian rainbow theory in the Eastern Mediterranean.22 But it was the emergence of Islam in the seventh century CE that gave new impetus to the study of Aristotle’s rainbow writings, among many other ancient Greek scientific texts. In the 820s, the Syrian scholar Ayyub al-Ruhawi – better known as Job of Edessa – provided the first serious departure from Aristotle since Alexander of Aphrodisias. Al-Ruhawi did not dispute that the sky was domed, or specifically that it ‘appears to us like a vault’, but he jettisoned Aristotle’s demonstrably false assumption that rainbows are only ever seen against a background of clouds.²³ He still maintained that they were caused by reflection only, but reflection from ‘thin’ and ‘thick’ forms of humidity in the air – even air that appears ‘clear’ to the naked eye. Like Aristotle, Al-Ruhawi saw the rainbow as being of three colours, but in his case, yellow replaced violet; and to explain why three different colours were produced, he again relied on fairly vague references to humidity.²⁴

This was merely a small down payment, however, on the advancements provided by later scholars in the Islamic world. The Persian Ibn-Sīnā (d. 1037), known in the West as Avicenna, rejected the cloud-mirror concept on the grounds of his own observations, and further argued that water drops in the atmosphere were ‘a necessary, rather than merely a sufficient, condition for the rainbow’.²⁵ And while he accepted that the bow was of the same three colours assigned to it by Aristotle, Ibn-Sīnā was deeply troubled by the reversal of colours in the primary and secondary bows, which he felt that neither Aristotle’s theories nor his own could do anything to explain.

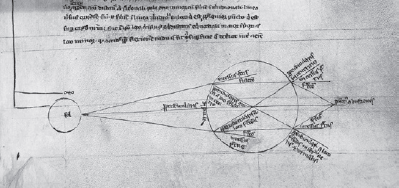
It fell to Ibn-Sīnā’s Basra-born contemporary Ibn al-Haytham (‘Alhazen’, d. 1039) to bring the notion of refraction to the problem. Through carefully designed experiments involving water-filled glass globes, al-Haytham established the first mathematical rules for the refractive bending of light. Though these laws were not perfectly accurate, and he did not apply them to his fundamentally Aristotelian explanation of the rainbow, they laid the groundwork for further experimentation by similar methods. In particular, Qutb al-Din al-Shirazi (1236–1311) ‘at a stroke laid bare the essence of the rainbow’s optics’ – namely, that it is caused by two refractions and one reflection of light within a raindrop.26 In Europe, unfortunately, Qutb al-Din’s unprecedented insight barely became known; and even if it had been, it would have had to compete head-to-head against Aristotle’s original theory, newly rediscovered.

The Western rediscovery of Aristotle

With the Spanish conquest of the city of Toledo in the late eleventh century, a great library containing the works of Aristotle, Euclid and Alexander of Aphrodisias, as well as Islamic authors including Ibn-Sīnā, suddenly became available to the Christian West. The supply of newly translated scientific texts was matched by demand for curricula from the wave of European universities that were founded from the mid-twelfth century onwards. As in so many other areas of science, the medieval universities’ nearly universal support for Aristotle would have a great deal to answer for in the sphere of rainbow theory. However, a University of Paris graduate working in Oxford, Robert Grosseteste (Bishop of Lincoln from 1235; d. 1253), was the first Westerner to work out a rainbow theory involving refraction. Proceeding from the problem that a rainbow produced by reflection would rise and fall with the Sun, rather than inversely to it, he proposed that refraction must instead be the key to the process of rainbow production. And, in perhaps the strongest departure from Aristotle up to that time, he assigned the inception of his series of three refractions to a mostly round cloud behind the observer. However, in a convoluted description that would have troubled even the writers of Doctor Who, Grosseteste’s refracting cloud had to be concave in some places and convex in others, and also able to emit an invisible ‘pyramid or cone’ of dense moisture.27 Modern experts disagree vigorously as to whether this cone was meant to point steeply upwards from the ground into a round cloud, or downwards to the centre of the Earth from a cloud shaped like an inverted bowl.²⁸ In any case, somewhat like Aristotle’s rainbow, Grosseteste’s was ‘projected . . . as though on a screen’ onto a (second) cloud.²⁹ But in contrast to Aristotle’s, this receiving cloud was also externally convex, not concave: in other words, the ancients’ dome-of-heaven concept did not enter into the bishop’s explanation at all. It is frankly astonishing that people had believed for so long that all rainbows were projected onto (or perhaps from) the literal edge of the world. For, as Philip Fisher rather poetically puts it,

Conventional portrait of Ibn-Sīnā (Avicenna) on a silver vase in Iran.

Woodcut scene illustrating various properties or ‘feats’ of light, from a 1572 edition of the Opticae thesaurus of Ibn al-Haytham (Alhazen).

The rainbow was always . . . the one part of heaven that occurred here on earth, just over there, touching a neighbor’s barn and that familiar tree, in front of the hill, closer than the nearest town.30

Thirteenth-century optical experiment utilizing a water-filled glass sphere, variously attributed to Roger Bacon and to Bacon’s teacher, Robert Grosseteste.

And yet, as we shall see, this idea did persist – in some circles, for centuries after Grosseteste’s death.

Despite his precocious appreciation that refraction had a role in rainbow production, Grosseteste was ‘concerned primarily with the shape of the bow’, and left only a ‘hint’ that he might have associated refraction with the rainbow’s colours.³¹ Moreover, in abandoning the Aristotelian dome-of-heaven idea, or at any rate the notion that rainbows appear on the interior surface of that dome, Grosseteste also jettisoned the only extant explanation for the fact that rainbows move as the observer moves – namely, that they are exactly as far away as the Sun. Though tortuous, ‘crude’ and ultimately quite wrong, Grosseteste’s rainbow theory must nevertheless be counted as an important step in the right direction, for it was arguably the first to challenge Aristotle fundamentally, and certainly the first refraction-based explanation of the bow to be presented to a wide European audience.³²

Grosseteste’s pyramid-of-moisture idea was adopted – some would say stolen – as part of the ‘correct’ explanation of the rainbow in a voluminous history of rainbow theories compiled by Albertus Magnus (d. 1280). It was also accepted by John Peckham, Archbishop of Canterbury (d. 1292). But the credit for Grosseteste’s real insight, that refraction played a major role, was, until fairly recently, assigned to the Polish-German scholar Witelo of Viterbo (fl. 1270), an expert on the works of al-Haytham.33 Witelo’s genuinely original contributions were twofold. First, he suggested – much like his exact contemporary Qutb al-Din, but to a European audience – that refraction and reflection were both involved in the rainbow’s production. This particular part of Witelo’s work was far less satisfactory than Qutb’s, however, in that Witelo postulated an interplay between multiple raindrops, in which the refractions were internal to the drops, but the reflections external. Second, Witelo insisted that refraction be studied via ‘experiments with instruments’ rather than the suppositions and analogies that previous scholars had tended to rely upon.³⁴

Witelo’s main rival and nearest European contemporary, Roger Bacon (d. 1292), had been a student of Grosseteste’s at Oxford and has sometimes been erroneously given credit for the authorship of Grosseteste’s De iride.³⁵ Bacon is often derided for his rejection of the role of refraction and defence of a reflection-only rainbow. Other aspects of his work on the subject have also been critiqued as ‘thoroughly “medieval” in the popular sense of the word’: for instance, he expanded the number of rainbow colours to five – red, blue, green, black and white – but on the grounds that the human eye contained ‘five bodies . . . three humors and two coatings’.³⁶ Nevertheless, Bacon made four significant contributions to the growing debate. First, ‘he rejected refraction for good reasons, by advancing sound criticisms against some of the more absurd aspects of Grosseteste’s refraction theory’.³⁷ For instance, the appearance of rainbows in small, localized sprays of water ruled out Grosseteste’s triple refraction starting from an extraordinary cloud-cone, which could hardly exist indoors – if, indeed, it could exist at all. Second, Bacon used direct observation to establish that the maximum elevation of the bow was 42 degrees: a figure that was very close to correct and would not be bettered for nearly four centuries.³⁸ Third, he pointed out that

if two people stand observing the rainbow in the north and one moves westward, the rainbow will move parallel to him; if the other observer moves eastward, the rainbow will move parallel to him; and if he stands still, the rainbow will remain stationary. It is evident, therefore, that there are as many rainbows as observers . . . and each observer must see his own rainbow.39

As well as being quite true, this is of course fundamentally at odds with the idea that the bow is projected as if on a screen, which had been promoted by Grosseteste and a high proportion of his predecessors.⁴⁰ Finally, Bacon ‘called attention to the function fulfilled by individual drops, arguing that the rainbow appears in a different set of drops for each observer’.⁴¹ But a key question, as D. C. Lindberg reminds us, remained unanswered:

Why does the rainbow appear as an arc and not a full circle (or semicircle) of color? . . . This is one phenomenon that neither a simple reflection theory nor a simple refraction theory can satisfactorily explain.⁴²

The 1535 engraved title page of De natura by Witelo of Viterbo, one of the first scholars to suggest that refraction and reflection were both involved in the rainbow’s production, and that the former should be studied via formal experiments.

The ‘modern’ theory from Theodoric to Descartes

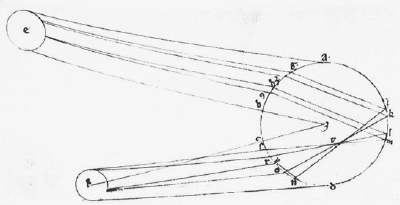
In or before 1304, inspired chiefly by the works of al-Haytham, a German Dominican cleric and former University of Paris student named Theodoric of Freiberg (d. c. 1310) conducted a series of experiments involving the use of water-filled spheres of glass to simulate raindrops. While his methods in and of themselves were ‘particularly pregnant for the future’, his results allowed him to argue correctly that the rainbow colours red, yellow, green and blue always occur in this ‘inviolable order’.43 Moreover, he established valid reasons for the relative positions of the primary and secondary rainbows; for why Alexander’s band was darker than the areas outside the two bows; for why the colours of the secondary bow occur in reverse order; and most significantly, for how the two bows were produced via a particular number and sequence of refractions and reflections. ‘Gone is the need for a problematic reflecting (or refracting) cloud – each raindrop is a self-contained prism and mirror.’⁴⁴ His initial decision to focus his enquiry on the raindrop may have been partly inspired by the work of Roger Bacon, but in any case, Theodoric was a prolific scholar who ‘probably was familiar with all major thirteenth-century writers on the rainbow’, with the exception of Qutb al-Din.⁴⁵

Ray-tracing from Theodoric of Freiberg’s De iride (c. 1305).

As correct as he was about the rainbow in many respects, however, Theodoric was wildly wrong in others. In contrast to the nearly correct measurements provided by Bacon, Theodoric measured the primary bow’s height as just 22 degrees, and that of the secondary bow as 33 degrees. Unlike Bishop Grosseteste, Theodoric implicitly accepted the Aristotelian dome-of-heaven idea – and even went beyond it, in the sense that his own model of rainfall implied the drops falling not straight to the ground, but along the same curvature as the world’s ‘roof’, or what he referred to as the ‘altitude circle’. He held that the rainbow contained only the four colours red, yellow, green and blue, and also seemed to think that rays of sunlight are not parallel to each other, but spread out from the Sun in an array, perhaps implying that the Earth is larger than the Sun. None of this, however, should detract from the fact that Theodoric’s work on the production of rainbows was substantially correct in its ‘qualitative insights’ and faulty only in its ‘quantitative details’.46

This diagram from De iride clearly shows how the traditional ‘dome of heaven’ concept added a needless layer of complexity to Theodoric’s rainbow theory.

It is widely reported that Theodoric’s breakthroughs were swiftly and tragically forgotten for five centuries, until their discovery and publication by Giambatista Venturi shocked the world in 1814.47 This particular myth accords nicely with the ‘naïve’ but ‘widely held’ idea that ‘the first theory of the rainbow was given by Descartes in 1637’.⁴⁸ In fact, the years between 1500 and 1700 saw more books on the rainbow published than in all time before or since, though in fairness, many of these were fundamentally non-scientific works devoted to prognostication, alchemy and the like, even where men of science were credited with their authorship.⁴⁹ Certainly, the sixteenth and seventeenth centuries saw determined elaborations of the Aristotelian reflection-only rainbow by, among others, Francesco Maurolico (1494–1575). Attacking Peckham and Witelo for their ‘obscurity’, Maurolico proposed a theory which, though right in a few respects, fundamentally required sunlight to have ‘terminal points’ on an imaginary plane standing perpendicular to the surface of the Earth.50 In effect, he had replaced the ancients’ inverted bowl of heaven with an inverted box. Yet the idea that Theodoric’s rainbow theory had been lost is not quite correct, insofar as it was evidently known to Themo Judaei (fl. 1360), Regiomontanus (1436–1476) and Jodocus Trutfetter (fl. 1514), and it may even have been taught at the University of Erfurt in Trutfetter’s time and beyond.⁵¹ Marco Antonio de Dominis (1560–1624), renegade Catholic Archbishop of Spalatro – and later, Protestant Dean of Windsor – mysteriously ‘gave a rather better explanation of the primary rainbow than any published before 1637, when Descartes gave the correct elementary theory of both bows’.⁵² But de Dominis’ contribution of 1611 was mysterious only to the extent that we believe Theodoric’s rainbow theory had been definitively lost by that date, for we now recognize de Dominis’ work as being an only ‘somewhat distorted’ version of Theodoric’s.⁵³ Its greatest flaw was that it ‘overlooked the fact that the rays must be refracted on emerging from the raindrops, as well as upon entering’.⁵⁴

Johannes Kepler, who associated each of the six known planets with a particular musical scale (as shown), also compared the colours of the rainbow to ‘the infinity of tones in the musical octave’.

Johannes Kepler (1571–1630) came at the rainbow from a decidedly oblique direction: a quest to apply the harmonies of music and mathematics to the mystery of colours. Perhaps the most remarkable aspect of his views on the rainbow, however, was how much they changed over time. Writing around 1599, Kepler compared the colours of the rainbow to ‘the infinity of tones in the musical octave’, with yellow operating as ‘a sort of mean’. The darkening of the rainbow from yellow via red into black was caused by ‘crass material in the cloud’, while refraction was responsible for the bow’s brightening from yellow via green, blue, purple and violet.55 It is clear that Kepler initially followed pre-Aristotelian views that a cloud located in front of the observer – but acting as a whole, and not via its individual particles of moisture – was responsible for the phenomenon. Also, Kepler’s ‘refraction’ at this early period may have been merely a reproduction of the ancients’ confusing but commonplace use of ‘reflection’ and ‘refraction’ as synonyms. By 1604, however, Kepler had changed his tune completely, and was supporting an extreme version of Grosseteste’s view that the rainbow was caused by light refracted through a cloud placed between the Sun and the observer’s back.⁵⁶ It was only after this that Kepler first resorted to model-raindrop experiments, allowing him to conclude that colour ‘seems to depend upon the magnitude of the angle of incidence’, and struck up a correspondence with the Oxford mathematician Thomas Harriot (1560–1621), who had established – but not publicized – the law of refraction between 1597 and 1606.⁵⁷ Even following this interchange of ideas with Harriot, however, Kepler’s work on refraction and reflection within the raindrop was hampered by an assumption – shared with many of his predecessors, ancient and modern – that the primary rainbow’s radius was 45 degrees, not 42.⁵⁸ Never realizing that this was the problem, he ascribed the errors in his calculations of refracted rays to variations in water temperature. Though Kepler was right about refraction decreasing as water temperature increases, this effect is far too small to account for the discrepancies in his research.

As previously mentioned, René Descartes (1596–1650) is perhaps the person most widely credited with cracking the secrets of the rainbow, even if no one would nowadays dare to suggest he was the first person to try. In spite of or because of this primacy, however, ‘few scientists have been subjected to charges of plagiarism more frequently’.⁵⁹ Though ‘it is quite probable that he had never even seen’ the work of de Dominis, Descartes was accused of plagiarizing from him by Gottfried Leibniz (1646–1716) and Isaac Newton (1642–1727), among many others; and the opinion that Descartes ‘was unjust in not acknowledging’ his great intellectual debts to de Dominis was ‘widely held’ as recently as the mid-twentieth century.60 But Carl Boyer, the pre-eminent historian of rainbow theory and experimentation, concluded in 1952 that

Descartes believed, mistakenly, that he was the first one to study the rainbow through experiments with a large spherical globe of water which served as a magnified raindrop.⁶¹

Descartes also may have independently arrived at the correct law of refraction, though this had been taught at the University of Leiden by Willebrord Snellius (1580–1626), who died about two years before Descartes’ rainbow work commenced. The key difference here between Snellius and Descartes was that the latter knew ‘that he had discovered a completely general and powerful description of the path of light rays within transparent media’. Neither man, however, thought to link the precise angle of a light ray’s deviation to its colour.⁶²

Though largely ‘indifferent’ to hands-on experimentation, Descartes did not ‘entirely reject’ it either, and in the case of the rainbow he performed ‘endless’ observations.⁶³ Following the voyages of Columbus and Magellan, the dome of heaven was no longer seriously believed in, except by ‘illiterate persons’.⁶⁴ But within the field of rainbow research, Descartes’ experiments finally put paid to it once and for all: by showing that only the angle of observation, and not the linear distance between the raindrops and the observer, determines what rainbow colours he can see.⁶⁵ To all of the correct aspects of Theodoric’s theory, Descartes added the crucial insight that there is a particular point near the top of a spherical water drop, at and above which all rays entering the drop (via the correct sequence of refraction, reflection and refraction) become concentrated at roughly the same angle as one another when they exit the drop’s lower hemisphere – that is, head back in the general direction of the Sun and the observer, but now nearly rather than exactly parallel, in a tight bundle 40 to 42 degrees below the level at which the sunlight first entered the drop. Bluntly put, ‘this concentration of sunlight at exit angles near 41 degrees produces rainbows.’66 Descartes also came to realize that the other side of the coin of this concentration process is that the sky is starved of light within the 9-degree inter-rainbow area known as Alexander’s band.

Ancient and medieval authors had been aware of prisms, and even conducted experiments with them, but tended to reject the relationship of the spectrum to the rainbow as apparent rather than actual. This was due to a widespread belief that rainbows were mere optical illusions, whereas prismatic spectra could be projected onto walls, approached and touched, and were therefore real – though perhaps not as real as the colours of dyed cloth. Descartes rejected such distinctions. Because prisms do not operate either via curved surfaces or reflection, he was also able correctly to surmise that the rainbow’s colours were produced by some other aspect of the rainbow-formation process. From this point, however, his colour theory began to fall apart quite rapidly. Briefly put, Descartes came to believe that colours were caused by microscopic globes of air, struck initially by the force emanating from a light source and then rolling onwards in a great mass and striking each other like billiard balls; the forward travel of the balls transmitted light per se, while their differing rates of spin produced colours. Moreover, in seeming contradiction to this (itself quite wrong and strange) theory, Descartes’ work also wrongly implied that light travels faster in water or glass than it does in air – in reality it slows down by nearly 25 per cent in water and around 33 per cent in glass – and this notion ‘hung on stubbornly for more than two centuries’.⁶⁷ Unsurprisingly, his work on the rainbow could not be used to explain its colour-order.

‘Formation of the Rainbow’, illustration from the Physica sacra, by Johann Jakob Scheuchzer (1672–1733).

Newton and beyond

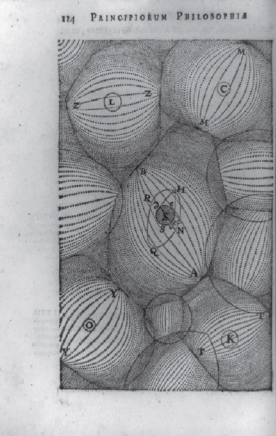
Right though much of it was, Descartes’ work on rainbows was not immediately accepted as such even by a large minority of his fellow European scientists, for whom ‘the Aristotelian rainbow remained a fixture of the intellectual landscape.’68 Both Pierre Gassendi (1592–1655) and Francesco Grimaldi (1618–1663) were rare exceptions proving the rule; but by and large, Descartes was not generally accepted as the principal authority on the subject until the 1680s, some thirty years after his death.⁶⁹ Descartes’ colour theory, which was obviously unsatisfactory even when newly written, was quickly supplanted by the theory of Edme Mariotte (1620–1684), who held – also quite incorrectly – that white light operated under wholly different laws of refraction than those that governed coloured light.

No-one abhorred a vacuum quite as much as René Descartes, for whom even outer space was made up of solids in collision. From the 1644 Amsterdam edition of Principia philosophiae.

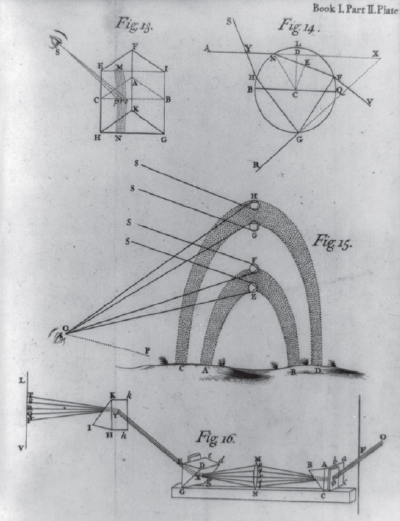
The problem of colours was also being approached from a more practical perspective – namely, the desire to eliminate colour distortions from new devices including the first practical microscopes (invented c. 1590) and refracting telescopes (1608). It was from this direction that Newton first embarked on his ‘singular mental voyage’.70 Aware of Descartes’ theory of the rainbow by 1666, when he was aged just 23, Newton had already had the insight that the process of refraction might be colour-dependent; but he later conducted a dramatic series of experiments that demonstrated this conclusively.⁷¹ A prism was placed over a hole in the wall of a building, and natural sunlight shining through the hole was projected onto the interior wall opposite. Newton found that the image of the Sun thus projected was always an oblong, four or five times longer than it was wide – regardless of the position of the prism, the position of the Sun or the size of the hole. Because nothing he did in this scenario could make the Sun appear round, Newton realized that his initial insight had been correct: angles of refraction vary by colour. He later repeated the experiment with the planet Venus replacing the Sun, and achieved much the same results.72

Rainbow and prism diagrams from Isaac Newton’s Opticks (1704).

Initially, Newton believed that there were five main rainbow colours – red, yellow, green, blue and purple – separated by four or more ‘intermediate ones’.⁷³ Eventually, through painstaking experimentation, he would arrive at the seven ‘canonical’ colours still generally accepted today, though these were considered ‘heretical’ by many in his own time.74 In part, this hostile response was because Newton had suggested – correctly – that all of the rainbow colours were present in white light, and not the result of mixing light with darkness in differing proportions, as had been generally believed from at least the time of Aristotle onwards.

To Roger Bacon’s key realization that no two people see the same rainbow, Newton added the idea that it is impossible for ‘any one perceiver [to] see the identical rainbow from moment to moment’, further focusing our attention on ‘the crucial completing role of the viewer in achieving the rainbow image’.⁷⁵ Newton also gave the most accurate measurements so far of both the primary and secondary bows – that is, that the former stretched from 40.283 to 42.033 degrees, and the latter from 50.950 to 54.117 degrees. Moreover, he recognized that it would be possible to arrive at a general law of the dispersion of light, which, if joined to the already discovered law of refraction, would allow one to ‘completely specify refraction of colors between any two media’.⁷⁶ Unfortunately, this insight was not matched by any success (or indeed sustained interest) in actually establishing such a law. Yet, the main flaw in Newton’s understanding of colours – which would nevertheless stand all but unchallenged through the eighteenth century – was that he conceived of light as a particle rather than a wave. And like Descartes, Newton assumed that light moved more quickly through denser substances.⁷⁷ It is hard to say if Newton’s rejection of light as a ‘pulse’ and his insistence that it was ‘corpuscular’ was more an effect or a cause of his deep personal loathing for Robert Hooke (1635–1703), who had proposed a rudimentary wave theory of light in 1665.⁷⁸ But in a curious parallel to the thirteenth-century debate on the all-reflection versus all-refraction rainbow, neither an all-particle nor an all-wave theory of light would prove entirely satisfactory. By the twentieth century, both would give way to ‘a new ontology’ in which, as A. Lande explains,

objective physical reality in the traditional sense is discounted as old-fashioned, at least in the microphysical domain where we can only form pictures of a subjective kind, even opposite ones as those of discrete particles and of continuous waves.79

Though much better known for his contributions to microscopy, seen here in this page from his Micrographia, Robert Hooke proposed a rudimentary wave theory of light in 1665.

With regard to the rainbow in particular, the modification of Newton’s ideas was slow indeed, amid what can fairly be described as his eighteenth-century deification. It would fall to Thomas Young to begin the reconciliation of ‘everyday perceptual experience’ to ‘Newton’s essentially correct physical model of light’, a process that would be further refined by James Clerk Maxwell’s (1831–1879) identification of light as waves of electromagnetic radiation in 1865.⁸⁰ Because it was largely rejected by scientists, though accepted by artists, the colour theory published by J. W. von Goethe in 1810 will be addressed in Chapter Five, below.

The rainbow surmounting a vista of mankind’s actual and expected scientific and technical achievements. By Etienne Voysard (1746–1812) after Claude-Louis Desrais (1746–1816).

Of course, nothing in the present chapter is intended to suggest that myriad other understandings of what rainbows were, how and why they formed, and what they meant had not been arrived at in other historical and cultural contexts. The next chapter will survey these alternatives.