 PROBLEM 8-1
PROBLEM 8-1Logic gives rise to an important branch of mathematics known as set theory. Mathematicians define a set as a collection or group of objects called elements or members. An element of a set can be anything real or imagined, concrete or abstract.
CHAPTER OBJECTIVES
In this chapter, you will
• Define and symbolize sets.
• See how sets relate to each other.
• Draw diagrams to illustrate set behavior.
• Learn basic set operations.
• Compare set operations with logical operations.
If you have a set of a dozen eggs, you have something more than mere eggs. You have the right to claim that those eggs all belong to a specific group. If you think about the group of all people in the state of South Dakota, you’re thinking about something more than people. You’re thinking about a specific set of people.
If we want to call some entity x an element of a defined set A, then we write
x ∈ A
The “lazy pitchfork” symbol means “is an element of.” We can also say that x “belongs” to set A, or that x “is in” set A. If some other entity y is not an element of set A, then we write
y ∉ A
An element constitutes a “smallest possible piece” that can exist in any set. We can’t break an element down into anything smaller and have it remain a legitimate member of the original set. This concept becomes important whenever we have a set that contains another set as one of its elements.
When we list the elements of a set, we enclose the list in “curly brackets,” technically known as braces. The order of the list doesn’t matter. Repetition in the list doesn’t make any difference either. The following sets are all identical:
{1, 2, 3}
{3, 2, 1}
{1, 3, 3, 2, 1}
{1, 2, 3, 1, 2, 3, 1, 2, 3, …}
The ellipsis (string of three dots) means that the list goes on forever in the pattern shown. Now look at this example of a set with five elements:
S = {2, 4, 6, 8, 10}
Whether the elements of S are numbers or numerals depends on the context. Usually, when we see a set with numerals listed like this, the author means to define the set containing the numerical values that those numerals represent. Here’s another example of a set with five elements:
P = {Mercury, Venus, Earth, Mars, Jupiter}
We can reasonably assume that the elements of this set are the first five planets in our solar system, not the words representing those planets!
A set can exist even if it contains no elements. When we have a set lacking elements altogether, we call it the empty set or the null set. We can symbolize the null set by writing two braces facing each other with a space between:
{}
We can also denote the null set as a circle with a forward slash through it:
Ø
You might ask, “How can a set have no elements? That would be like a club with no members.” That’s exactly right! If all the members of the Pingoville Ping-Pong club quit today and no new members join, the club still exists as long as it has a charter and by-laws. The set of members of the Pingoville Ping-Pong Club might be empty, but it’s a legitimate set as long as someone says that the club exists.
Mathematicians categorize sets as either finite or infinite. We can name all of the elements of a finite set if we have enough time. This includes the null set. We can utter the words “This set has no elements,” and we’ve named all the elements of the null set. We cannot name all the elements of an infinite set, no matter how much time we have. Nevertheless, we can sometimes write an “implied list” of the elements of an infinite set that describes that set in unambiguous, clear terms. When we encounter a set like this, we call it denumerably infinite. Consider the following infinite set:
W = {0, 1, 2, 3, 4, 5, …}
We recognize W as the set of nonnegative integers, also called whole numbers. We know whether or not something constitutes an element of set W, even if we don’t see it in the above “short list,” and even if we couldn’t reach it if we started to scribble down the “long list” right now and kept at it for years. We can tell straightaway which of the following numbers belong to W and which do not:
12
1/2
23
100/3
78,883,505
356.75
90,120,801,000,000,000
−65,457,333
The first, third, fifth, and seventh numbers belong to W, but the second, fourth, sixth, and eighth numbers don’t.
TIP Sometimes, we’ll encounter an infinite set that we cannot define by means of any list, even an “implied list.” The set of real numbers falls into this category. So does the set of irrational numbers. Theorists call sets of this sort nondenumerably infinite or simply nondenumerable.
A set can act as an element of another set. Remember again, anything can serve as a member of a set! When you allow sets to compose members of other sets, you get end up with sets that get confusing! Following are some examples, in increasing order of strangeness:
{1, 2, {3, 4, 5}}
{1, {2, {3, {4, {5}}}
{1, {2, {3, 4, 5}}}
{1, {2, {3, {4, 5}}}}
TIP An “inner” or “member” set can sometimes contain more elements than the set to which it belongs. Consider the following example:
{1, 2, {3, 4, 5, 6, 7, 8}}
In this case, the “main” set has three elements, one of which is a set with six elements.
Here, the “main” set has three elements, one of which is a set with six elements.
 PROBLEM 8-1
PROBLEM 8-1
Name a set that’s an element of itself.
 SOLUTION
SOLUTION
The set of all abstract ideas is abstract idea, so it’s an element of itself.
 PROBLEM 8-2
PROBLEM 8-2
Build up an infinite set of sets, starting with the null set.
 SOLUTION
SOLUTION
Consider the set containing the null set, that is, {Ø}. This set is a mathematical object, but it’s not the null set. It’s the sole element of {{Ø}}. Now imagine the following “top-down” list of sets, in which any given set acts as the sole element of the next one:
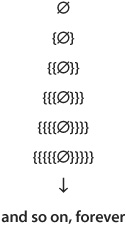
Relationships among sets of similar objects lend themselves to a special type of illustration called the Venn diagram, in which sets appear as groups of points or geometric figures.
Figure 8-1 illustrates a simple Venn diagram. The large, heavy rectangle represents the set of all things that can exist, whether real or imaginary (including all possible sets). We call this infinite set the universal set or the universe. In Fig. 8-1, we see three finite sets and two infinite sets within the universe. Note how the objects overlap, lie within one another, or are entirely separated from one another.
FIGURE 8-1. A Venn diagram showing the set of all sets (the universe), along with a few specific sets within it.
All the women in Chicago are people in Illinois, but there are plenty of people in Illinois who aren’t people in Chicago. The numbers 2, 4, and 6 are positive whole numbers, but there are lots of positive whole numbers different from 2, 4, or 6. The sets of positive and negative whole numbers are entirely separate, even though both sets are infinite. None of the positive or negative whole numbers is a person in Illinois, and no person in Illinois is a number (except according to the government, maybe).
When all the elements of a set also belong to a second set, we call the first set a subset of the second set. If we encounter two sets A and B, such that every element of A also belongs to B, then A is a subset of B. We symbolize that fact as
A ⊆ B
Figure 8-1 shows that the set of all the women in Chicago forms a subset of the set of all the people in Illinois. We indicate that fact (in this example, anyhow) by drawing a hatched square inside a shaded oval. Figure 8-1 also shows that the set {2, 4, 6} constitutes a subset of the set of positive whole numbers. We express that fact by placing the numerals 2, 4, and 6 inside the rectangle representing the positive whole numbers. All five of the figures inside the large, heavy rectangle portray subsets of the universe. Any set we can imagine, no matter how large, small, or strange, whether finite or infinite, forms a subset of the universe. A set is always a subset of itself, too.
Often, a subset represents part, but not all, of the “main set.” In a situation like that, we call the smaller set a proper subset of the larger set. In the scenario of Fig. 8-1, the set of all women in Chicago constitutes a proper subset of the set of all people in Illinois. The set {2, 4, 6} is a proper subset of the set of positive whole numbers. All five of the sets inside the large, outermost rectangle are proper subsets of the universe. When a certain set C is a proper subset of another set D, we write this fact as
C ⊂ D
Name a set that’s a subset of every possible set.
 SOLUTION
SOLUTION
The null set is a subset of any set we care to imagine. If we have a set A with known elements, we can add nothing to its roster of members, and we’ll always get the same set A. The null set is a subset of itself, although not a proper subset of itself. Here’s an example. If you let the written word “nothing” actually stand for nothing, then
Ø = { } = {nothing}
and
{nothing} ⊆ {nothing, 1, 2, 3}
so therefore
Ø ⊆ {1, 2, 3}
but
{nothing} ⊄ {nothing}
Here, the symbol ⊄ means “is not a proper subset of.”
TIP Keep in mind that a subset does not constitute the same thing as a set element. The null set contains nothing, but the null set is not itself nothing.
Once in awhile, you’ll encounter two sets that have different denotations or expressions, but you discover that they’re identical when you scrutinize them. Consider the following:
E = {1, 2, 3, 4, 5, …}
and
F = {7/7, 14/7, 21/7, 28/7, 35/7, …}
At first glance, these two sets look completely different. But if you think of their elements as numbers (not as symbols representing numbers), you can see that both lists represent the same set. You know this because
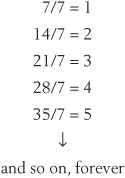
Every element in set E has exactly one “mate” in set F, and every element in set F has exactly one “mate” in set E. We can pair off the elements of E and F in a one-to-one correspondence.
When two sets contain identical elements, and we can pair off the elements of one set in a one-to-one correspondence with the elements in the other, we call the two sets congruent sets. Some mathematicians call them equal sets or coincident sets. In the above situation, we can write
E = F
Once in awhile, an author will use a three-barred equals sign to indicate congruence between sets, as follows:
E = F
When two sets have no elements in common, we call them disjoint sets. Here’s an example of two disjoint sets of numbers:
G = {1, 2, 3, 4}
and
H = {5, 6, 7, 8}
FIGURE 8-2 Two disjoint sets, Jand K.They have no elements in common.
Both of these sets happen to be finite, but infinite sets can also be disjoint. Consider the set of all the even whole numbers and the set of all the odd whole numbers:
Weven = {0, 2, 4, 6, 8, …}
and
Wodd = {1, 3, 5, 7, 9, …}
No matter how far out along the list for Weven we go, we’ll never find any element that’s also in Wodd. No matter how far out along the list for Wodd we go, we’ll never find any element that’s also in Weven. We won’t try to prove this fact now, but your “mathematical sixth sense” should assure you of its truth.
The Venn diagram of Fig. 8-2 illustrates two sets, J and K, with no elements in common. Imagine J as the set of all the points on or inside the circle, and K as the set of all the points on or inside the oval. Sets J and K are disjoint. When we have two disjoint sets, neither of them forms a subset of the other.
When two sets have at least one element in common, we call them overlapping sets. Formal texts might call them nondisjoint sets. Congruent sets overlap in the strongest possible sense, because they share all of their elements. More often, you’ll see cases in which two overlapping sets share some, but not all, of their elements. Following are two sets of numbers that overlap with one element in common:
L = {2, 3, 4, 5, 6}
and
M = {6, 7, 8, 9, 10}
Here’s a pair of sets that overlap with several elements in common:
P = {21, 23, 25, 27, 29, 31, 33}
and
Q = {25, 27, 29, 31, 33, 35, 37}
Technically, the following two sets overlap as well:
R = {11, 12, 13, 14, 15, 16, 17, 18, 19}
and
S = {12, 13, 14}
In the last case above, S constitutes a subset of R. In fact, S is a proper subset of R. Now, let’s look at a pair of infinite sets that overlap with four elements in common:
W3− = {…, −5, −4, −3, −2, −1, 0, 1, 2, 3}
and
W0+ = {0, 1, 2, 3, 4, 5, …}
The notation W3− (read “W sub three-minus”) means the set of integers starting at 3 and decreasing, one by one, without end. The notation W0+ (read “W sub zero-plus”) means the set of integers starting with 0 and increasing, one by one, without end.
Figure 8-3 shows two sets, T and U, with some elements in common, so they overlap. You can imagine T as the set of all the points on or inside the circle, and U as the set of all the points on or inside the oval. When you have two overlapping sets, one of them can compose a subset of the other, but that doesn’t have to be the case. It’s clearly not true for T and U in Fig. 8-3.
FIGURE 8-3 Two overlapping sets, T and U. They have some elements in common.
 PROBLEM 8-4
PROBLEM 8-4
Is the universal set a subset of itself? Is it a proper subset of itself?
 SOLUTION
SOLUTION
The universal set (call it U) is a subset of itself. That’s a trivial notion, because any set forms a subset of itself. But U is not a proper subset of itself. Remember, we define U as the set of all entities, real or imaginary, past, present, future—everything! If U were a proper subset of itself, then there would exist some entity that did not belong to U. That’s impossible because it contradicts the very definition of the universal set!
TIP The foregoing convoluted argument offers a “massive” example of reductio ad absurdum, which you first encountered in Chap. 2.
 PROBLEM 8-5
PROBLEM 8-5
Provide an example of two sets, both with infinitely many elements, but such that one set forms a proper subset of the other.
 SOLUTION
SOLUTION
Plenty of set pairs will satisfy this requirement! The set of all even whole numbers (nonnegative integers), Weven, is a proper subset of the set of all whole numbers, W. Both of these sets have infinitely many elements. Amazingly enough, you can pair the elements of both sets off one-to-one, even though one of them is a proper subset of the other! You can get an idea of how this pairing-off works if you divide every element of Weven by 2, one at a time, and then write down the first few elements of the resulting set. When you do that, you get
{0/2, 2/2, 4/2, 6/2, 8/2, 10/2, …}
That’s exactly the same as W, because when you perform the divisions, you get
{0, 1, 2, 3, 4, 5, …}
 PROBLEM 8-6
PROBLEM 8-6
List all the subsets of the set {1, 2, 3}. Here’s a hint: When you want to denote all the subsets of a small set, start by listing the null set (which is a subset of any set). Then list all of the set’s individual elements and enclose them in set braces one by one. Finally list every possible set that contains at least one of those elements.
 SOLUTION
SOLUTION
First, write down the symbol for the null set. Then isolate the individual elements of {1, 2, 3} and enclose the numerals in braces. Finally assemble and list all the sets you can, using one or more of the elements 1,2, and 3. You’ll get the following list:
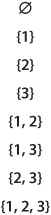
List all the subsets of {1, {2, 3}}. Be careful! You must strictly follow the instructions in the hint that goes along with Problem 8-6.
 SOLUTION
SOLUTION
The set {1, {2,3}} has only two elements: the number 1 and the set {2,3}. You can’t break {2,3} down and have it remain an element of the original set {1, {2, 3}}. The list of all possible subsets of {1, {2, 3}} is surprisingly short:

 PROBLEM 8-8
PROBLEM 8-8
List all the subsets of {1, {2, {3}}}. Be extra careful! The hint given with Problem 8-6 is critical here.
 SOLUTION
SOLUTION
The set {1, {2, {3}}} has two elements: the number 1 and the set {2, {3}}. You can’t break {2, {3}} down and have it remain an element of the original set {1, {2, {3}}}. Therefore, all the possible subsets of {1, {2, {3}}} are as follows:

TIP When you write down arcane sets such as the foregoing, you must use the same total number of opening braces and closing braces in every set expression. Count up the braces after you’ve written each item. If there are more or fewer opening braces than closing braces, you’ve made a mistake somewhere.
The intersection of two sets comprises all the elements, but only the elements, that belong to both sets. When you have two sets, say V and W, their intersection is a set that you denote by writing V ∩ W. The upside-down U-like symbol translates to the word “intersect,” so you say “V intersect W.”
The intersection of two congruent (identical) sets is the set of all elements in either set. For any two sets X and Y,
If X = Y
then
X ∩ Y = X
and
X ∩ Y = Y
TIP Because X and Y are identical, you’re actually dealing with only one set in the above situation, not two sets! You can just as well write
X ∩ X = X
The intersection of the null set with any other set always gives you the null set. For any set V,
V ∩ Ø = Ø
Remember, any element in the intersection of two sets must belong to both of those sets. Nothing can belong to a set that contains no elements! Therefore, nothing can belong to the intersection of the null set with any other set.
When two sets are disjoint, they have no elements in common, so nothing can belong to them both. The intersection of two disjoint sets always equals the null set. The set size makes no difference. For example, recall the sets of even and odd whole numbers, Weven and Wodd. They both contain infinitely many elements, but even so,
Weven ∩ Wodd = Ø
When two sets overlap, their intersection contains at least one element. There’s no limit to how many elements the intersection of two sets can have. You have to keep in mind only one requirement: Every element in the intersection set must belong to both of the original sets.
Let’s look at the examples of overlapping sets you saw a little while ago, and figure out the intersection sets. First, examine the following two sets:
L = {2, 3, 4, 5, 6}
and
M = {6, 7, 8, 9, 10}
Here, the intersection set contains one element:
L ∩ M = {6}
This expression refers to the set containing the number 6, not just the number 6 itself. Now look at the following two sets:
P = {21, 23, 25, 27, 29, 31, 33}
and
Q = {25, 27, 29, 31, 33, 35, 37}
In this case, the intersection set contains five elements:
P ∩ Q = {25, 27, 29, 31, 33}
Now check out the following two sets:
R = {11, 12, 13, 14, 15, 16, 17, 18, 19}
and
S = {12, 13, 14}
In this situation, S ⊂ R, so the intersection equals set S. You can write that fact as follows:
R ∩ S = S = {12, 13, 14}
How about the set W3− of all positive, negative, or zero whole numbers less than or equal to 3, and the set W0+ of all the nonnegative whole numbers? You can write down these two sets as follows:
W3− = {…, −5, −4, −3, −2, −1, 0, 1, 2, 3}
and
W0+ = {0, 1, 2, 3, 4, 5, …}
The intersection set has four elements:
W3− ∩ W0+ = {0, 1, 2, 3}
The Venn diagram of Fig. 8-4 shows two overlapping sets. Think of the set V as the rectangle and all the points inside. Imagine the set W as the oval and all the points inside. The two regions are hatched diagonally, but in different directions. The intersection set V ∩ W shows up as an irregular cross-hatched region.
FIGURE 8-4 • Two overlapping sets V and W. The double-hatched region illustrates their intersection.
Find two sets of whole numbers that overlap, with neither set forming a subset of the other, and whose intersection set contains infinitely many elements.
 SOLUTION
SOLUTION
You can come up with many examples of set pairs like this. Look at the set of all positive whole numbers divisible by 4 without a remainder. (When a quotient has no remainder, that quotient always equals a whole number.) Call this set W4d. Similarly, let W6d be the set of all positive whole numbers divisible by 6 without a remainder. You can list the first few elements of each set as follows:
W4d = {0, 4, 8, 12, 16, 20, 24, 28, 32, 36, …}
and
W6d = {0, 6, 12, 18, 24, 30, 36, 42, 48, …}
Both of the sets W4d and W6d contain infinitely many elements. The two sets overlap because they share certain elements. But neither set forms a subset of the other; they both have some elements all their own. The intersection is the set of all elements divisible by both 4 and 6; call it W4d6d. If you write out both of the above lists up to all values less than or equal to 100 and then identify the elements common to both sets, you’ll obtain
W4d ∩ W6d = W4d6d
= {0, 12, 24, 36, 48, 60, 72, 84, 96, …}
This set happens to contain all positive whole numbers divisible by 12 without a remainder. If you call it W12d′ then you can write
W4d ∩ W6d = W12d
The union of two sets contains all of the elements that belong to one set or the other, where you take “or” in the inclusive sense. When you have two sets, say X and Y, their union also forms a set, written X ∪ Y. You can read the U-like symbol as “union” and say “X union Y.”
When you have two congruent sets, their union equals either set taken alone. For any sets X and Y,
If X = Y
then
X ∪ Y = X
and
X ∪ Y = Y
You’re actually dealing with only one set here, so you could just as well write
X ∪ X = X
For the null set you have
Ø ∪ Ø = Ø
TIP When you have two congruent sets, their union equals their intersection! This fact might seem trivial right now, but you’ll sometimes encounter situations where the congruence of two sets isn’t obvious. In cases like that, you can compare the union with the intersection to perform a “congruence test.” If the union of two sets corresponds precisely to their intersection, then the sets are congruent.
The union of the null set with any nonempty set gives you that nonempty set. For any nonempty set X, you can write
X ∪ Ø = X
Remember, any element in the union of two sets only has to belong to one of them.
When two nonempty sets are disjoint, they have no elements in common, but their union always contains some elements. Consider again the sets of even and odd whole numbers, Weven and Wodd. Their union equals the set of all the whole numbers:
Weven ∪ Wodd = {0, 1, 2, 3, 4, 5, …}
Again, let’s look at the same examples of overlapping sets we checked out when we worked with intersection. First, consider the following two sets:
L = {2, 3, 4, 5, 6}
and
M = {6, 7, 8, 9, 10}
The union set is
L ∪ M = {2, 3, 4, 5, 6, 7, 8, 9, 10}
The number 6 appears in both sets, but we count it only once in the union. (Any specific element can “belong to a set only once.”) Now look at these two sets:
P = {21, 23, 25, 27, 29, 31, 33}
and
Q = {25, 27, 29, 31, 33, 35, 37}
The union set in this case is
P ∪ Q = {21, 23, 25, …, 33, 35, 37}
That’s all the odd whole numbers between, and including, 21 and 37. We count each individual duplicate element 25 through 33 only once. Now examine the following two sets:
R = {11, 12, 13, 14, 15, 16, 17, 18, 19}
and
S = {12, 13, 14}
In this situation, S ⊂ R, so the union set equals R. We can write that down as
R ∪ S = R
= {11, 12, 13, 14, 15, 16, 17, 18, 19}
We count each individual element 12, 13, and 14 only once. Now consider the sets
W3− = {…, −5, −4, −3, −2, −1, 0, 1, 2, 3}
and
W0+ = {0, 1, 2, 3, 4, 5, …}
Here, the union set consists of all the positive and negative whole numbers, along with 0. Let’s write that set as W0± (read “W sub zero plus-or-minus”). Then:
W3− ∪ W0± = W0±
= {…, −5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5, …}
We count each individual element 0, 1, 2, and 3 only once. As you know from basic number theory, W0± is the set of integers.
Figure 8-5 shows two overlapping sets. Think of X as the rectangle and everything inside it. Imagine Y as the oval and everything inside it. We represent the union of the two sets, X ∪ Y, as the entire shaded region.
FIGURE 8-5 Two overlapping sets X and Y. The entire shaded region illustrates their union.
FIGURE 8-6 Illustration for Problems and Solutions 8-10 through 8-12.
 PROBLEM 8-10
PROBLEM 8-10
Figure 8-6 is a Venn diagram that shows five sets A, B, C, D, and E, in a rather complicated relationship. What does the small, dark-shaded triangle marked P represent?
 SOLUTION
SOLUTION
All of the elements in set P belong to the intersection of sets A and C. You know this because the dark-shaded triangle constitutes exactly that region where the rectangle representing A and the triangle representing C overlap. Symbolically,
P = A ∩ C
What set does the dark-shaded, irregular, four-sided figure Q represent in Fig. 8-6?
 SOLUTION
SOLUTION
The points in region Q are fully shared by the points in B and D. Therefore, region Q represents the intersection of sets B and D, which you can write as
Q = B ∩ D
 PROBLEM 8-12
PROBLEM 8-12
If you consider all the possible intersections of two sets in Fig. 8-6, which of those intersection sets are empty?
 SOLUTION
SOLUTION
Whenever two regions share no area at all, the sets they represent are disjoint, so their intersection set is empty. In Fig. 8-6, the only pairs of regions that don’t overlap are A and D, B and C, and C and D. Therefore, the null-set Intersection pairs in this scenario are as follows:
A ∩ D = Ø
B ∩ C = Ø
C ∩ D = Ø
 PROBLEM 8-13
PROBLEM 8-13
What is the intersection of the following two sets? What is their union?
A = {1, 1/2, 1/3, 1/4, 1/5, 1/6, …}
and
G = {1, 1/2, 1/4, 1/8, 1/16, 1/32, …}
In set A, the denominator of the fraction increases by 1 as you go down the list. In set G, the denominator doubles as you go down the list. All the numerators in both sets are equal to 1.
Notice that set G contains all the elements, but only those elements, that belong to both sets. Therefore, the intersection of sets A and G equals set G. You symbolize this fact by writing
A ∩ G = G
If you start with set A and then add in all the elements of G, you get the same set A (with certain elements listed twice, but they can count only once). Therefore, set A contains precisely those elements that belong to one set or the other. The union of the two sets equals set A. You symbolize this fact as
A ∪ G = A
 PROBLEM 8-14
PROBLEM 8-14
Can you find two sets of whole numbers, with one of the sets infinite, but such that their union contains only a finite number of elements?
 SOLUTION
SOLUTION
No, you can’t. Any element in the union of two sets must belong to one or both sets. If a set has infinitely many elements, then the union of that set with any other set—even the null set—must have infinitely many elements.
You may refer to the text in this chapter while taking this quiz. A good score is at least 8 correct. Answers are in the back of the book.
1. Which of the following statements holds true under all circumstances?
A. If A is a proper subset of B, then A is a subset of B.
B. If A is a subset of B, then A is a proper subset of B.
C. If A and B are identical sets, then A is a proper subset of B.
D. Sets A and B are coincident if and only A is a subset of B.
2. Suppose that you have two nonempty sets P and Q. Which of the following statements can’t hold true under any circumstances?
A. P ∩ Q is infinite.
B. P ∪ Q is infinite.
C. P ∩ Q is empty.
D. P ∪ Q is empty.
3. Figure 8-7 illustrates two nonempty sets E and P. The entire shaded region represents the set of all elements that belong to
A. set E and set P.
B. set E if and only if set P.
C. set E or set P.
D. set E with set P.
FIGURE 8-7 Illustration for Quiz Question 3.
4. How many elements does the set {1, 2, 3, 4, 3, 2, 1} have?
A. Three.
B. Four.
C. Seven.
D. We can’t say because the list is redundant.
5. What is the union of {1, 2, 3, 4, 3, 2, 1} with the set of all strictly negative integers?
A. Ø
B. {…, −4, −3, −2, −1}
C. {…, −4, −3, −2, −1, 1, 2, 3, 4}
D. {1, 2, 3, 4, …}
6. Consider two sets G and H, such that G ∩ H ≠ Ø. In this situation,
A. G and H overlap.
B. G and H are disjoint.
C. G and H share a single element.
D. G and H are congruent.
7. Suppose that you encounter two nonempty sets P and Q. The set P ∩ Q contains exactly those elements belonging to
A. both P and Q.
B. P or Q, or both.
C. either P or Q, but not both.
D. the universal set.
8. What is the intersection of {1, 2, 3, 4, 3, 2,1} with the set of all strictly negative integers?
A. Ø
B. {…, −4, −3, −2, −1}
C. {…, −4, −3, −2, −1, 1, 2, 3, 4}
D. {1, 2, 3, 4}
9. Which of the following sets is a subset of the null set?
A. The set containing the null set.
B. No such set exists.
C. The null set.
D. The set of all sets.
10. Two sets are congruent if and only if
A. they have the same number of elements, and those elements can be paired off in a one-to-one correspondence.
B. neither set is a subset of the other.
C. they both contain infinitely many elements that can be paired off in a one-to-one correspondence.
D. their elements are identical and can be paired off in a one-to-one correspondence.