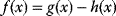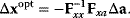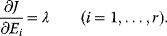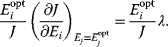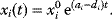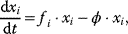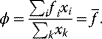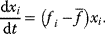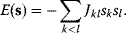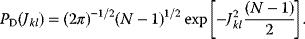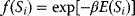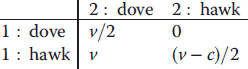11
Optimality and Evolution
- 11.1 Optimality in Systems Biology Models
- 11.2 Optimal Enzyme Concentrations
- 11.3 Evolution and Self-Organization
- 11.4 Evolutionary Game Theory
- Exercises
- References
- Further Reading
Evolution is an open process without any goals. However, there is a general trend toward increasing complexity, and phenotypes arising from mutation and selection often look as if they were optimized for specific biological functions. The evolution toward optimal solutions can be studied experimentally: in a competition among bacteria, faster growing mutants are likely to outcompete the wild-type population until bacterial genomes, after many such changes, become enriched with features needed for fast growth. Dekel and Alon [1] grew Escherichia coli bacteria under different combinations of lactose levels and under artificially induced expression levels of the Lac operon (which includes the gene lacZ). From the measured growth rates, they predicted that there exists, for each lactose level, an optimal LacZ expression level that maximizes growth and, therefore, the fitness advantage in a direct competition. The prediction was tested by having bacteria evolve in serial dilution experiments at given lactose levels. After a few hundred generations, the wild-type population was in fact replaced by mutants with the predicted optimal LacZ expression levels.
To picture the mechanism of evolution, we can imagine individuals as points in a phenotype space (see Figure 11.1), and a population forming a cloud (or distribution) of points. Individuals' chances to replicate (or their expected number of descendants) depend on the phenotype and can be described by a fitness function. Due to mutations and recombination of genes, offspring may show new phenotypes and may spread in this fitness landscape. Due to a selection for high fitness, a population of individuals will change from generation to generation, tending to move toward a fitness maximum. The fitness landscape can have local optima, each surrounded by a basin of attraction. If rare mutations are needed to jump into another basin of attraction, the population may be confined to a current local optimum even if better optima exist elsewhere. The fitness function can also be drawn directly as a landscape in genotype space. Since the same phenotype, on which selection primarily acts, can emerge from various genotypes, movements in genotype space will often be fitness-neutral. Moreover, analogous traits can evolve, under similar selective pressures, in organisms that are genetically very distant.
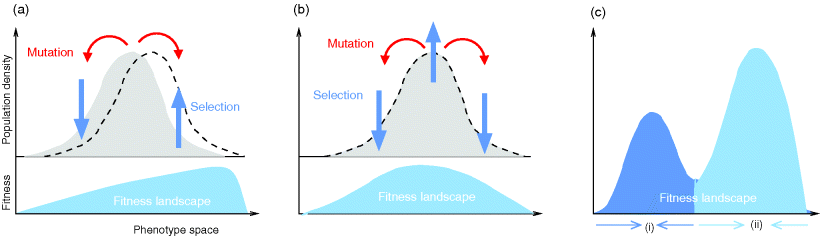
Figure 11.1 Evolution in a fitness landscape. (a) Evolution by mutation and selection. A population, shown as a frequency density in phenotype space (gray), changes by mutation and selection. A higher fitness value (shown at the bottom) represents a selection advantage and leads to an increase in frequency. As the different phenotypes change in their frequencies, the distribution gradually moves along the fitness gradient (dashed line). (b) Stationary population around a local fitness optimum. Mutation and selection are balanced and the population is stable. (c) Fitness landscape with two optima and their basins of attraction (marked by (i) and (ii)).
Evolution as a Search Strategy
Evolution by mutation and selection is an efficient search strategy for optima in complex fitness landscapes and can lead to relatively predictable outcomes. This may sound surprising because mutations are random events. Any innovation emerges from individuals in which certain mutations first occurred and which had to survive and pass it on. However, the number of possible favorable mutations is usually large, and so is the number of individuals in which these mutations can occur: thus, even if a certain change is very unlikely to occur in a single individual, it may be very likely to occur in a species. This is how evolution, the “tinkerer,” can act as an engineer [2].
Biomechanical problems solved by evolution are numerous and complex, and the solutions are often so good that engineers try to learn from them. Evolution has even inspired the development of very successful algorithms for numerical optimization [3]. Genetic algorithms (see Section 6.1) can tackle general, not necessarily biological optimization problems: metaphorically, candidate solutions to a problem are described as “genotypes” (usually encoded by numbers). A population of such potential solutions is then optimized in a series of mutation and selection steps. Since genetic algorithms simulate populations of individuals and not single individuals (as in, for example, simulated annealing; see Section 6.1), they allow for recombination of advantageous “partial solutions” from different individuals. This can considerably speed up the convergence toward optimal solutions.
What makes mutation and selection such a powerful search strategy? One reason is that the search for alternatives happens in a massively parallel way. A bacterial population produces huge numbers of mutants in every generation, and there is a constant selection for advantageous mutations that can be integrated into the complex physiology and genetics of existing cells. In constant environments, well-adapted genotypes are continuously tested and advantageous traits are actively conserved. At the same time, the population remains genetically flexible: when conditions are changing, it can move along a fitness gradient toward the next local optimum (see Figure 11.1a).
During evolution, there were long periods of relatively stable conditions, in which species could adapt to specific ecological niches. These periods, however, were interrupted by sudden environmental changes in which specialists went extinct and new species arose from the remaining generalists. Thus, to succeed in evolution, species should be not only well adapted, but also evolvable, that is, able to further adapt genetically [4]. As we saw in Sections 8.3 and 10.2, evolvability can be improved by the existence of robust physiological modules. Simulations suggest that varying external conditions can speed up evolution toward modular, well-adapted phenotypes [5]. Evolvability is further facilitated by exaptation – the reuse of existing traits to perform new functions. An example of exaptation are crystallin proteins, which were originally enzymes, but adopted a second unrelated function, namely, to increase the refraction index of the eye lens. Also in metabolism, potentially useful traits can emerge as by-products: for instance, the metabolic networks that enable cells to grow on one carbon source will, typically, also allow them to live on many other carbon sources. Even if a carbon source has never been present during evolution, the evolutionary step to using it as a nutrient can be relatively small [6].
Finally, we should remember that genotypes and phenotypes are not linked by abstract rules, but through very concrete physiological processes – the processes we attempt to understand in systems biology. Accordingly, what appears to be a selection for phenotypic traits may actually be a selection for regulation mechanisms that shape and control these traits and adapt them to an individual's needs and environment. An example is given by the way in which bones grow to their functional shapes, adapt to typical mechanical stresses, and re-enforce their structures after a fracture. This adaptation is based on feedback mechanisms. Higher stresses will cause bone growth and a strengthening of internal structures, while stresses below average cause a remodeling, that is, a removal of material [7]. The result of this regulation, described by the mechanostat model [8], are well-adapted bone shapes and microstructures. The physiological processes underlying this adaptation have been studied in detail [9] and the resulting microstructures of bones can be simulated [10]. Similar principles hold for other structures that emerge from self-organized processes, for example, cell organelles [11]: an evolutionary selection for good shapes may, effectively, consist in a selection for regulation mechanisms that produce the right shapes under the right circumstances.
Control of Evolution Processes
Evolution can proceed quite predictably. We saw an example in the artificial evolution of Lac operon expression levels, where the expression level after evolution could be predicted from previous experiments. Another known example is the evolution from C3 to C4 carbon fixation systems in plants, which occurred independently more than 60 times in evolution. The evolution toward C4 metabolism involves a number of changes in metabolism. In theory, these changes could take place in various orders. However, simulations of the evolutionary process, based on fitness evaluation in metabolic models, showed that the evolutionary trajectory (i.e., the best sequence of adaptation steps) is almost uniquely determined [12]. Even if individual gene mutations cannot be foreseen, the order of phenotypic changes seems to be quite predictable.
Can evolutionary dynamics, for example, the evolution of microbes in experiments, be steered by controlling the environment or by applying genetic modifications that constrain further evolution? Avoiding unintended evolution is important in biotechnology: if genetic changes, meant to increase the production of chemicals, burden cells excessively, the cells' growth rate will be severely reduced and the engineered cells may be outcompeted by faster growing mutants. This can be avoided, for instance, by applying genetic changes that stoichiometrically couple biomass production to production of the desired product.
Another case in which controlling evolution would matter is the prevention of bacterial resistances. Resistant bacteria carry mutations that make them less sensitive to antibiotic drugs. The resistant mutants have better chances to survive, so their resistance genes will be selected for. Chait et al. [13] have developed a method to prevent this. A combined administration of antibiotics can either increase or reduce antibiotics' effects on cell proliferation (synergism or antagonism). In extreme cases of antagonism, drug combinations can even have a weaker effect than either of the drugs alone. This phenomenon, known as suppressive drug combination, has a paradoxical consequence: mutants that have become resistant to one drug will suffer more strongly from the other one (because the first drug cannot exert its suppressive effect) and will be selected against. Thus, a suppressive combination of antibiotics traps bacteria in a local fitness optimum where resistances cannot spread. In experiments, this was shown to prevent the emergence of resistances [13,14].
There is, however, another lesson to be learned from this: if both drugs are applied, their effect decreases. For somebody who does not care about resistances spreading, taking only one of the drugs would be more effective. The fight against bacterial resistance – from which we all benefit – can thus be undermined by everyone's desire to get the most effective drug treatment now. This means that we're also trapped in a dilemma called “tragedy of the commons,” which we encounter again in Section 11.4.
11.1 Optimality in Systems Biology Models
Optimality principles play a central role in many fields of research and development, including engineering, economics, and physics. Whenever we build a machine, steer a technical process, or produce goods, we want to do this effectively (i.e., realize some objective, which we define) and efficiently (i.e., do so with the least possible effort). Often, we need to deal with trade-offs, for instance, if machines that are built to be more durable and energy-efficient become more costly. Moreover, what is optimal for one person may be detrimental for society. In such cases, the solution to a problem depends crucially on what the optimality problem is considered exactly.
In physics, optimality principles are central, but they are used in a more abstract sense and without referring to human intentions. Many physical laws can be formulated in a way as if nature maximized or minimized certain functions. In classical mechanics, laws as basic as Newton's laws of motion can be derived from variational principles [15]: in Lagrangian mechanics, instead of integrating the system equations in time, we consider the system's entire trajectory and compare it with other conceivable (but unphysical) trajectories. Each trajectory is scored by a so-called action functional, and the real, physical trajectory is a trajectory for which this functional shows an extremal value. Variational principles exist for many physical laws, and they sometimes connect different theories of the same phenomenon. For instance, Fermat's principle states that light rays from point A to point B follow paths of extremal duration: small deviations from the path would always increase (or, in some cases, always decrease) the time to reach point B. Fermat's principle entails not only straight light rays, but also the law of diffraction. An explanation comes from wave optics: light waves following extremal paths and the paths surrounding them show constructive interference, allowing for light to be detected at the end point; in quantum electrodynamics, the same principle holds for the wave function of photons [16]. Another variational principle, defining thermodynamically feasible flux distributions [17], is described in Section 15.6.
The idea of optimality is also common in biology and bioengineering. On the one hand, we can assume that phenotypic traits of organisms, for example, the body shapes of animals, are optimized during evolution. On the other hand, engineered microorganisms are supposed to maximize, for instance, the yield of some chemical product. In both cases, optimality assumptions can be translated into a mathematical model. Optimality-based (or “teleological”) models follow a common scheme: we consider different possible variants  of a biological system, score them by a fitness function
of a biological system, score them by a fitness function 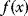 , and select variants of maximal fitness. In studies of cellular networks, model variants considered can differ in their structure, kinetic parameters, or regulation and may be constrained by physical limitations. The fitness function can represent either the expected evolutionary success or our goals in metabolic engineering. In models, the fitness is expressed as a function of the system's behavior and, possibly, of costs caused by the system.
, and select variants of maximal fitness. In studies of cellular networks, model variants considered can differ in their structure, kinetic parameters, or regulation and may be constrained by physical limitations. The fitness function can represent either the expected evolutionary success or our goals in metabolic engineering. In models, the fitness is expressed as a function of the system's behavior and, possibly, of costs caused by the system.
Teleological models not only describe how a system works, but also explore why it works in this way and why it shows its specific dynamics. Thus, these models incorporate mechanisms, but their main focus is on how a system may have been optimized, according to what principles, and under what constraints. Optimality studies can also tell us about potential limits of a system. We may ask: if a known fitness function had to be maximized in evolution or biotechnology, what fitness value could be maximally achieved, and how? Turning this around, if a system is close to its theoretical optimum, we may suspect that natural selection, with fitness criteria similar to the ones assumed, has acted upon the system. Finally, optimality studies force us to think about the typical environment to which systems are adapted. A general assumption is that species are optimized for routine situations, but also rare severe events can exert considerable selective pressures. Generally, variable environments entail different types of selective pressure (e.g., toward robustness or versatility) than constant environments (adaptation to minimal effort and specialization).
Teleological Modeling Approaches
How does the concept of optimality fit into the mechanistic framework of molecular biology? As noted in Section 8.1.5, observations can be explained not only by cause and effect (Aristotle's causa efficiens), but also by objectives (Aristotle's causa finalis). In our languages, we do this quite naturally, for instance, when saying “E. coli bacteria produce flagella in order to swim.” The sentence not only describes a physical process, but also relates it to a task. This does not mean that we ascribe intentions to cells or to evolution – it simply expresses the fact that flagella can increase cells' chances to proliferate, and this is a reason why E. coli bacteria – which have outcompeted many mutants in the past – can express flagella.
Teleological statements are statements about biological function. But then, what exactly is meant by “function,” and why do we need such a concept? Can't we simply describe what is happening inside cells? In fact, cell biology combines two very different levels of description: on the one hand, the physical dynamics within cells and, on the other hand, the evolutionary mechanisms that lead to these cells and can be seen at work in evolution experiments. The two perspectives inform each other: the cellular dynamics we observe today is the one that has succeeded in evolution, and changes in this dynamics will affect the species' further evolution. The entanglement of long-term selection and short-term cell physiology is subsumed in the concept of biological function.
Thus, “cells express flagella in order to swim” can be read as a short form of “cells that cease to produce flagella may be less vital due to shortage of nutrients” or, one step further, “without producing flagella in the right moment, cells would have been outcompeted by other cells (maybe, by cells producing flagella).” Optimality-based models translate such hypotheses into mathematical formulas. Here, “in order to” is represented by scoring a system by an objective function, and optimizing it. Dynamic models relate cause and mechanistic effect; optimality models, in contrast, relate mechanisms and fitness effects.
Epistemologically, the concept of “function” has a similar justification as the concept of randomness. Random noise can be used as a proxy for processes that we omit from our models, either because they are too difficult to describe or because their details are unknown. Since we cannot neglect them completely, we account for them in a simple way – by random noise. Similarly, a functional objective can be a proxy for evolutionary selection, which by itself has no place in biochemical models. Since we cannot neglect evolution completely, we may account for it in a simple way – by a hypothetical optimization with some presumable objective. The biological justification lies in the assumption that evolution would already have selected out system variants that are clearly suboptimal. How much nonoptimality can be tolerated depends on many factors, including the strictness of selection (reflected by the steepness of the fitness function in models), population size, and the evolutionary time span considered.
Optimality and Model Fitting
Another point in systems biology modeling where optimization matters is parameter estimation. As mathematical problems, estimation and optimization of biochemical parameters are very similar: to find the most likely model, parameters are optimized for goodness of fit, and to find the most performant one, they are optimized for some fitness function. Biochemical constraints play a central role in both cases. Algorithms for numerical optimization are described in Section 6.1. They range from an optimization of structural model variants to linear flux optimization (as in flux balance analysis (FBA)) or a nonlinear optimization of enzyme levels or rate constants.
11.1.1 Mathematical Concepts for Optimality and Compromise
In an optimality perspective, all biological traits result from compromise. In the case of the Lac operon, an increased expression level increases the cell's energy supply (if lactose is present), but also demands resources (e.g., energy and ribosomes) and causes a major physiological burden due to side effects of the Lac permease activity [18]. To capture such trade-offs, optimality models typically combine four components: a system to be optimized, a fitness function (which may comprise costs and benefits), ways in which the system can be varied, and constraints under which these variations take place. We will now see how such trade-offs can be treated mathematically (Figure 11.2 gives an overview).
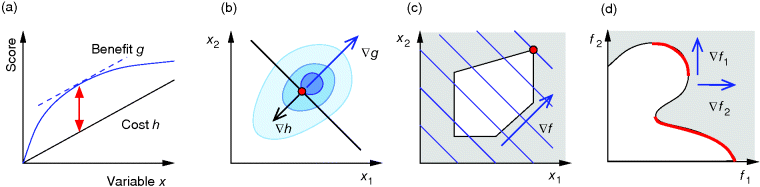
Figure 11.2 Optimization under constraints. (a) Cost–benefit optimization. A fitness function, defined as the difference 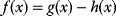 between benefit and cost, becomes maximal where both curves have the same slope (dashed). (b) Local optimum under an equality constraint (black line). A fitness function
between benefit and cost, becomes maximal where both curves have the same slope (dashed). (b) Local optimum under an equality constraint (black line). A fitness function 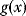 in two dimensions is shown by contour lines. The constraint is defined by an equality
in two dimensions is shown by contour lines. The constraint is defined by an equality 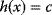 . In the constrained optimum point (red circle), contour lines and constraint line are parallel, so the gradients must satisfy an equation
. In the constrained optimum point (red circle), contour lines and constraint line are parallel, so the gradients must satisfy an equation 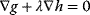 with a Lagrange multiplier
with a Lagrange multiplier 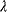 . (c) Linear programming: a feasible region (white) is defined by linear inequality constraints for the arguments
. (c) Linear programming: a feasible region (white) is defined by linear inequality constraints for the arguments 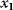 and
and 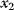 . The linear fitness function is shown by contour lines and gradient (arrow). (d) Pareto (multi-objective) optimization with two objectives
. The linear fitness function is shown by contour lines and gradient (arrow). (d) Pareto (multi-objective) optimization with two objectives 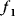 and
and 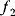 (shown on the axes). Feasible combinations
(shown on the axes). Feasible combinations 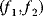 lie within the white region. States in which none of the objectives can be increased without decreasing the other objective are Pareto-optimal (red). Pareto optimization yields a continuous set of solutions, the so-called Pareto front.
lie within the white region. States in which none of the objectives can be increased without decreasing the other objective are Pareto-optimal (red). Pareto optimization yields a continuous set of solutions, the so-called Pareto front.
Cost–Benefit Models
In cost–benefit calculations for metabolic systems [1,19–21], a difference
between a benefit 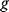 and a cost
and a cost 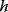 is assumed as a fitness function (see Figure 11.2a). The variable
is assumed as a fitness function (see Figure 11.2a). The variable  is a vector describing quantitative traits to be varied, for example, enzyme abundances in a kinetic model. In the model for Lac expression [1], bacterial growth is treated as a function of two variables: external lactose concentration (an external parameter) and expression of LacZ (regarded as a control parameter, optimized by evolution). The function was first fitted to measured growth rates and then used to predict the optimal LacZ expression levels for different lactose concentrations. A local optimum of the variable
is a vector describing quantitative traits to be varied, for example, enzyme abundances in a kinetic model. In the model for Lac expression [1], bacterial growth is treated as a function of two variables: external lactose concentration (an external parameter) and expression of LacZ (regarded as a control parameter, optimized by evolution). The function was first fitted to measured growth rates and then used to predict the optimal LacZ expression levels for different lactose concentrations. A local optimum of the variable  – in this case, the enzyme level – implies a vanishing fitness slope
– in this case, the enzyme level – implies a vanishing fitness slope 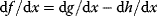 . The marginal benefit
. The marginal benefit 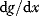 and the marginal cost
and the marginal cost 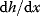 must therefore be equal. In an optimal state, the benefit obtained from expressing an additional enzyme molecule and the cost for producing this molecule must exactly be balanced. Figure 11.2a illustrates this: since the benefit saturates at high
must therefore be equal. In an optimal state, the benefit obtained from expressing an additional enzyme molecule and the cost for producing this molecule must exactly be balanced. Figure 11.2a illustrates this: since the benefit saturates at high  values while the cost keeps increasing, the fitness function shows a local maximum. If the cost function were much steeper, the marginal cost would exceed the marginal benefit already at the level
values while the cost keeps increasing, the fitness function shows a local maximum. If the cost function were much steeper, the marginal cost would exceed the marginal benefit already at the level 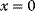 . Since enzyme levels cannot be negative, this point would be a boundary optimum, and in this case the enzyme should not be expressed.
. Since enzyme levels cannot be negative, this point would be a boundary optimum, and in this case the enzyme should not be expressed.
Inequality Constraints
Which constraints need to be considered in optimization? This depends very much on our models and questions. Typically, there are nonnegativity constraints (e.g., for enzyme levels) and physical restrictions (e.g., upper bounds on substance concentrations, bounds on rate constants due to diffusion limitation, or Haldane relationships between rate constants to be optimized). However, inequality constraints can also represent biological costs. In fact, various important constraints on cell function, including limits on cell sizes and growth rates, the dense packing of proteins in cells, and cell death at higher temperatures, can be derived from basic information such as protein sizes, stabilities, and rates of folding and diffusion, as well as the known protein length distribution [22].
Mathematically, costs and constraints are, to an extent, interchangeable, which provides some freedom in how to formulate a model. As an example, consider a cost–benefit problem as in Eq. (11.1), but with several variables 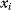 . In a unique global optimum
. In a unique global optimum 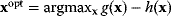 , the cost function has a certain value
, the cost function has a certain value 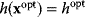 . We can now reformulate the model: we drop the cost terms and require that
. We can now reformulate the model: we drop the cost terms and require that 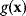 be maximized under the constraint
be maximized under the constraint 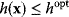 . Our state
. Our state 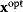 will be a global optimum of the new problem. Likewise, if we start from a local optimum
will be a global optimum of the new problem. Likewise, if we start from a local optimum 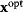 with cost
with cost 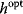 and introduce the equality constraint
and introduce the equality constraint 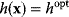 , the optimum
, the optimum 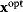 will also be a local optimum to the new problem. In this way, a quantitative cost term for enzyme levels, for instance, can formally be replaced by a bound on enzyme levels. The advantage a cost constraint over an additive cost term is that benefits and costs can be measured on different scales and in different units. There is no need to quantify their “relative importance.”
will also be a local optimum to the new problem. In this way, a quantitative cost term for enzyme levels, for instance, can formally be replaced by a bound on enzyme levels. The advantage a cost constraint over an additive cost term is that benefits and costs can be measured on different scales and in different units. There is no need to quantify their “relative importance.”
In some case, however, it can be practical to do exactly the opposite: to replace a constraint by a cost term. If our system state hits some upper bound 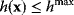 , we can express this by an equality constraint
, we can express this by an equality constraint 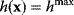 . This constraint can be treated by the method of Lagrange multipliers: instead of maximizing
. This constraint can be treated by the method of Lagrange multipliers: instead of maximizing 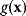 under the constraint
under the constraint 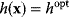 , we search for a number
, we search for a number 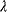 , called the Lagrange multiplier, such that
, called the Lagrange multiplier, such that 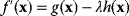 becomes maximal with respect to
becomes maximal with respect to  (where the constraint
(where the constraint 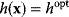 must still hold). The necessary optimality condition reads
must still hold). The necessary optimality condition reads 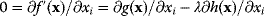 . Effectively, the original constraint is replaced by a virtual cost term that is subtracted from the objective function. The relative importance of costs and benefits is determined by the value of the Lagrange multiplier in the original optimal state.
. Effectively, the original constraint is replaced by a virtual cost term that is subtracted from the objective function. The relative importance of costs and benefits is determined by the value of the Lagrange multiplier in the original optimal state.
Pareto Optimality
If an organism is subject to multiple objectives, its potential phenotypes can be depicted as points in a space spanned by these objective functions (see Figure 11.3a). If there are trade-offs between the objectives, only a limited region of this space will be accessible. Boundary points of this region in which none of the objectives can be improved without compromising the others form the Pareto front. We will see an example – a Pareto front of metabolic fluxes in bacterial metabolism – further below. Pareto optimality problems allow for many solutions, and unlike local minima in single-objective problems, these solutions are not directly comparable: one solution is not better or worse than another one – it is just different. Moreover, each objective can be scored on a different scale – there is no need to make them directly comparable.
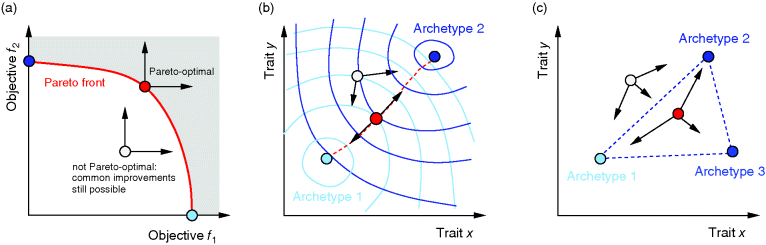
Figure 11.3 Pareto optimality for a system with multiple objectives. (a) Variants of a system, shown as points in the space of objective functions. (b) The same system variants, shown in phenotype space (axes correspond to phenotypical traits) [23]. The two objective functions are shown by contour lines; their optimum points are called archetypes. In a Pareto-optimal point (red), the gradients of both objective functions are parallel, but with opposite directions: none of the objectives can be simultaneously improved without compromising the other one. In a nonoptimum point (gray), both objectives could still be improved. (c) In a problem with three objectives, the archetypes form a triangle in phenotype space. The criterion for a Pareto optimum (red) is that the gradients, weighted by positive prefactors, must sum to zero. This resembles the balance between objective and constraint in Lagrange optimization (Figure 11.2b). With simple objective functions (circular contour lines, not shown), this condition is satisfied exactly within the triangle, so the Pareto optima are also convex combinations of the archetypes.
Pareto optimality can be depicted very intuitively with the concept of archetypes, introduced by Shoval et al. to refer to phenotypes that optimize, individually, one of the different objectives [23,24]. The role of archetypes becomes clear when phenotypes are displayed in another space, the space of phenotype variables (Figure 11.3b). In a problem with three objectives and two phenotypical traits, the three archetypes would define a triangle in a plane. If the objectives, as functions in this space, have circular contour lines, as we assume as an approximation, the possible Pareto optima will fill this triangle. Each of them will thus be a convex combination of the archetype vectors. The same concept applies also to higher dimensions (i.e., more objectives and traits).
Shoval et al. applied this approach to different kinds of data, for instance, Darwin's data on the body shapes of ground finches. When plotting body size against a quantitative measure of beak shape, they obtained a triangle of data points. The three archetypes, with their extreme combinations of the traits, could be explained as optimal adaptations to particular diets. All other species, located within the triangle, represent less specialized adaptations, possibly adaptations to mixed diets. In the theoretical model, triangles are expected to appear for simple objective functions with circular contour lines. With more general objective functions, the triangles will be distorted [24]. In general, whether a cloud of data points forms a triangle (or, more generally, an  -dimensional convex polytope in
-dimensional convex polytope in  -dimensional space) needs to be tested statistically.
-dimensional space) needs to be tested statistically.
Compromises in the Choice of Catalytic Constants
As an example of optimality considerations, including compromises and possibly nonoptimality, let us consider the choice of 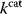 values in metabolic systems. Empirically,
values in metabolic systems. Empirically, 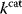 values tend to be higher in central metabolism, where fluxes are large and enzyme levels are high [25]. This suggests that
values tend to be higher in central metabolism, where fluxes are large and enzyme levels are high [25]. This suggests that 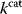 values in other regions stay below their biochemically possible maximum, contradicting the optimality assumption whereby each
values in other regions stay below their biochemically possible maximum, contradicting the optimality assumption whereby each 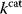 value should be as high as possible. Thus, what prevents some
value should be as high as possible. Thus, what prevents some 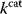 values from increasing? In some cases, enzymes with higher
values from increasing? In some cases, enzymes with higher 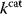 values become larger and therefore more costly. In other cases, high
values become larger and therefore more costly. In other cases, high 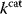 values could compromise substrate specificity (which may be more relevant in secondary than in central metabolism), allosteric regulation (as in the case of phosphofructokinase, a highly regulated enzyme with a rather low catalytic constant), or a favorable temperature dependence of kinetic properties. Finally, enzymes can also exert additional functions (e.g., metabolize alternative substrates or act as a signaling, structural, or cell cycle protein), which may compromise their
values could compromise substrate specificity (which may be more relevant in secondary than in central metabolism), allosteric regulation (as in the case of phosphofructokinase, a highly regulated enzyme with a rather low catalytic constant), or a favorable temperature dependence of kinetic properties. Finally, enzymes can also exert additional functions (e.g., metabolize alternative substrates or act as a signaling, structural, or cell cycle protein), which may compromise their 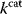 values.
values.
However, we may also assume an evolutionary balance between a selection for high 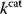 values and a tendency toward lower
values and a tendency toward lower 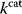 values caused by random mutations. Formally, this nonoptimal balance can be treated in an optimality framework by framing the effect of mutations as an effective evolutionary cost. This cost appears as a fitness term, but it actually reflects the fact that random mutations of an enzyme are much more likely to decrease than to increase its
values caused by random mutations. Formally, this nonoptimal balance can be treated in an optimality framework by framing the effect of mutations as an effective evolutionary cost. This cost appears as a fitness term, but it actually reflects the fact that random mutations of an enzyme are much more likely to decrease than to increase its 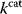 value. The prior probability
value. The prior probability 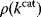 , that is, the number of gene sequences that realize a certain
, that is, the number of gene sequences that realize a certain 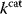 value, defines the evolutionary cost
value, defines the evolutionary cost 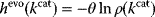 . The constant parameter
. The constant parameter 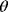 describes the strictness of selection [25]. The most likely
describes the strictness of selection [25]. The most likely 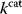 value after an evolution is thus not expected to maximize an organism's actual fitness
value after an evolution is thus not expected to maximize an organism's actual fitness 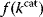 , but the apparent fitness
, but the apparent fitness 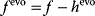 .
.
The concept of apparent fitness is analogous to the concept of free energy in thermodynamics. To describe systems at given temperature 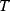 , the principle of minimal energy
, the principle of minimal energy 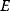 (a stability condition from classical mechanics) is replaced by a principle of minimal free energy
(a stability condition from classical mechanics) is replaced by a principle of minimal free energy 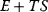 , where the entropy
, where the entropy 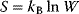 refers to the number
refers to the number 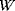 of microstates showing the energy
of microstates showing the energy 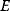 . The term
. The term 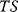 appears formally as an energy, but it actually reflects the fact that macrostates of higher energy contain much more microstates (Section 15.6).
appears formally as an energy, but it actually reflects the fact that macrostates of higher energy contain much more microstates (Section 15.6).
Of course, the notion of evolutionary costs is not restricted to 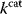 values, but applies very generally. A similar type of effective cost is the evolutionary effort, quantified by counting the number of mutations or events necessary to attain a given state [26].
values, but applies very generally. A similar type of effective cost is the evolutionary effort, quantified by counting the number of mutations or events necessary to attain a given state [26].
Table 11.1 Some optimality approaches used in metabolic modeling.
| Name | Formalism | Objective | Control variables | Main constraints | Reference |
| FBA | Stoichiometric | Flux benefit | Fluxes | Stationary fluxes | [27] |
| FBA with minimal fluxes | Stoichiometric | Flux cost | Fluxes | Stationary, flux benefit | [28] |
| Resource balance analysis | Stoichiometric | Growth rate | Fluxes | Stationary, whole cell | [29] |
| Enzyme rate constants | Reaction kinetics | Different objectives | Rate constants | Haldane relations | [30] |
| Enzyme allocation | Kinetic | Pathway flux | Enzymes (static) | Total enzyme | [31] |
| Temporal enzyme allocation | Kinetic | Substrate conversion | Enzymes (dynamic) | Total enzyme | [32] |
| Transcriptional regulation | Kinetic | Substrate conversion | Rate constants | Feedback structure | [33] |
| Enzyme adaptation | Kinetic | General fitness | Enzymes (changes) | Model structure | [20] |
| Growth rate optimization | Kinetic, growing cell | Growth rate | Protein allocation | Total protein | [34] |
11.1.2 Metabolism Is Shaped by Optimality
A field within systems biology in which optimality considerations are central is metabolic modeling. Aside from standard methods such as FBA, which take optimality as one of their basic assumptions, there are dedicated optimality-based studies on pathway architecture, choices between pathways, metabolic flux distributions, the enzyme levels supporting them, and the regulatory systems controlling these enzyme levels (Table 11.1). In the forthcoming sections, we shall see a number of examples of these approaches.
When describing metabolic systems as optimized, we first need to specify an objective function. The objective does not reflect an absolute truth, but is related to the evolution scenario we consider. In natural environments, organisms will experience times of plenty, where fast growth is possible and maybe crucial for evolutionary success, and times of limitation, where efficient, sustainable usage of resources is most important. Both situations can be mimicked by artificial evolution experiments and studied with models. If bacteria are experimentally selected for fast growth – and nothing else – their growth rate will be a meaningful fitness function: mutants that grow faster will be those that survive, and those are also the ones we are going to model as optimized. However, setting up an experiment that selects for growth and nothing else is difficult: in a bioreactor with continuous dilution, cells could evolve to stick to the walls of the bioreactor, which would allow them not to be washed out. Even if these cells replicate slowly, their strategy provides a selection advantage in this setting. In serial dilution experiments, this drawback is avoided by transferring the microbial population between different flasks every day. However, if the cultures are grown as batch cultures, the cells will experience different conditions during the course of each day and may switch between growth and stationary phases. Again, many more traits, not just for a fast growth under constant conditions, will be selected for in the experiment.
Thus, it is the experimental setup that determines what is selected for and what objective should be used in our models. There is also a version of serial dilution that can select for nutrient efficiency instead of fast inefficient growth [35]. Unlike normal serial dilution experiments, this experiment requires – and allows for – models in which nutrient efficiency is the objective function. Not surprisingly, selection processes in natural environments are even more complicated: a species' long-term survival depends on many factors, including the populating of new habitats, defenses against pathogens, and complex social behavior. How evolution depends on interactions between organisms and environment can be studied through evolutionary game theory, which we discuss in Section 11.4.
Given a fitness function for an entire cell, how can we derive from it objectives for individual pathways? Metabolic pathways contribute to a cell's fitness by performing some local function (e.g., production of fatty acids), which contributes to more general cell functions (e.g., maintenance of cell membranes) and thereby to cell viability in general. Compromises between opposing subobjectives may be inevitable, for example, between high production fluxes, large product yields, and low enzyme investment. The relative importance of the different objectives may depend on the cell's current environment [36]. Once we have identified an objective, we can ask how pathway structure, flux distribution, or enzyme profile should be chosen, and also how regulation systems can ensure optimal behavior under various physiological conditions.
What Functional Reasons Can Explain Metabolic Network Structures?
If the laws of chemistry (e.g., conservation of atom numbers) were the only restriction, an enormous number of metabolic network structures could exist (see Section 8.1). The actual network structures, however, are determined by the set of enzymes encoded in cells' genomes or, more specifically, by the set of enzymes expressed by cells. The sizes and capabilities of metabolic networks vary widely, but their structures follow some general principles. Important precursors (such as nucleotides and amino acids in growing cells) form the central nodes that are connected by pathways. Many reactions involve cofactors, which connect these pathways very tightly. A relatively small set of cofactors has probably been used since the early times of metabolic network evolution [37].
By which chemical reactions will two substances be connected? In fact, the number of possibilities is vast: already for the route from chorismate to tyrosine, realized by three reactions in E. coli, a computational screen yielded more than 350 000 potential pathway variants [38]. Out of numerous possible pathways, only very few are actually used by organisms, and we may wonder what determines this selection. Some of the choices may be due to specific functional advantages [39]: for instance, glucose molecules are phosphorylated at the very beginning of glycolysis; this prevents them from diffusing through membranes, thus keeping them inside the cell. But there are also more general reasons informing pathway structure. We shall discuss three important principles: the preferences for yield-efficient, short, and thermodynamically efficient pathways [38,40].
Yield Efficiency
Alternative pathways may produce different amounts of product from the same substrate amount. At given substrate uptake rates, high-yield pathways produce more product per time and should therefore be preferable in evolution. However, there may be a trade-off between a high product yield and a high product production per amount of enzyme needed to catalyze the pathway flux. The reason is that yield-efficient pathways tend to operate closer to equilibrium, where enzymes are used inefficiently. At equal enzyme investment, yield-inefficient pathways may thus provide larger fluxes, enabling faster cell growth. This is why some metabolic pathways exist in alternative versions with different yields, even in the same organism. We will come back to this point, using glycolysis as an example.
Preference for Short Pathways
The preference for short pathways is exemplified by the non-oxidative part of the pentose phosphate pathway, a pathway with the intricate task of converting six pentose molecules into five hexose molecules. If we additionally require that intermediates have at least three carbon atoms and that enzymes can transfer two or three carbon atoms, the pentose phosphate pathway solves this task in a minimal number of enzymatic steps [41] (Figure 11.4). A trend toward minimal size is also visible more generally in central metabolism: Noor et al. showed that glycolysis, pentose phosphate pathway, and TCA cycle are composed of reaction modules that connect a number of central precursor metabolites and that, in each case, consist of minimal possible numbers of enzymatic steps [42].
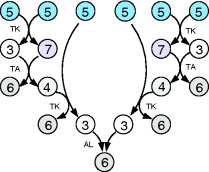
Figure 11.4 A metabolic pathway of minimal size. The non-oxidative phase pentose phosphate pathway converts six pentose molecules into five hexose molecules in a minimal number of reactions. Metabolites shown (numbers of carbon atoms in parentheses): D-ribose 5-phosphate and D-xylulose 5-phosphate (5); D-glyceraldehyde 3-phospate (3); D-sedoheptulose 7-phosphate (7); D-fructose 6-phosphate and D-fructose 1,6-bisphosphate (6); D-erythrose 4-phosphate (4). Enzymes: transketolase (TK); transaldolase (TA); aldolase (AL).
Pathways Must Be Thermodynamically Feasible
A third general factor that affects pathway structure is thermodynamic efficiency. The metabolic flux directions, in each single reaction, are determined by the negative Gibbs energies of reactions (also called reaction affinity or thermodynamic driving force; see Section 15.6). To allow for a forward flux, the driving force must be positive. This holds not only for an entire pathway, but also for each single reaction within a pathway. However, the driving force has also a quantitative meaning: it determines the percentage of enzyme capacity that is wasted by the backward flux within that reaction. If the force approaches zero (i.e., a chemical equilibrium), the enzyme demand for realizing a given flux rises fast. Therefore, a sufficiently large positive driving force must exist in every reaction (see Section 15.6).
Glycolysis examplifies the role of thermodynamics in determining pathway structure. The typical chemical potential difference between glucose and lactate would allow for producing four molecules of ATP per glucose molecule; however, this would leave practically no energy to be dissipated and thus to drive a flux in the forward direction. Assuming that the flux is proportional to the thermodynamic force 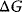 along the pathway – which, far from equilibrium, is only a rough approximation – a maximal rate of ATP production will be reached by glycolytic pathways that produce only half of the maximal number of ATP molecules [43]. In glycolytic pathways found in nature, this is indeed the typical case. The two ATP molecules, however, are not produced directly. First, two ATP molecules are consumed in upper glycolysis, and then four ATP molecules are produced in lower glycolysis. A comparison with other potential pathway structures shows that this procedure allows for a maximal glycolytic flux at given enzyme investment [40,44]. A systematic way to assess the thermodynamic efficiency of a pathway is the max–min driving force (MDF) method [45]. Based on equilibrium constants and bounds on metabolite concentrations, it distributes the reaction driving forces in such a way (by choosing the metabolite concentrations) that small forces are avoided. Specifically, concentrations are arranged in such a way that the lowest reaction driving force in the pathway is as high as possible. The minimal driving force can be used as a quality criterion to compare pathway structures. If the minimal driving force is low, a pathway is unfavorable in terms of enzyme demand. Like shorter pathways, also pathways with favorable thermodynamics allow cells to reduce their enzyme investments. Also the ATP investment in upper glycolysis can be explained with this concept: without the early phosphorylation by ATP, a sufficient driving force in the pathway would require very high concentrations of the first intermediates. With the phosphorylation, the chemical potentials of the first intermediates can be high, but their concentrations will be much lower!
along the pathway – which, far from equilibrium, is only a rough approximation – a maximal rate of ATP production will be reached by glycolytic pathways that produce only half of the maximal number of ATP molecules [43]. In glycolytic pathways found in nature, this is indeed the typical case. The two ATP molecules, however, are not produced directly. First, two ATP molecules are consumed in upper glycolysis, and then four ATP molecules are produced in lower glycolysis. A comparison with other potential pathway structures shows that this procedure allows for a maximal glycolytic flux at given enzyme investment [40,44]. A systematic way to assess the thermodynamic efficiency of a pathway is the max–min driving force (MDF) method [45]. Based on equilibrium constants and bounds on metabolite concentrations, it distributes the reaction driving forces in such a way (by choosing the metabolite concentrations) that small forces are avoided. Specifically, concentrations are arranged in such a way that the lowest reaction driving force in the pathway is as high as possible. The minimal driving force can be used as a quality criterion to compare pathway structures. If the minimal driving force is low, a pathway is unfavorable in terms of enzyme demand. Like shorter pathways, also pathways with favorable thermodynamics allow cells to reduce their enzyme investments. Also the ATP investment in upper glycolysis can be explained with this concept: without the early phosphorylation by ATP, a sufficient driving force in the pathway would require very high concentrations of the first intermediates. With the phosphorylation, the chemical potentials of the first intermediates can be high, but their concentrations will be much lower!
Enzyme Investments
The preferences for short pathways and the avoidance of small driving forces may be explained by a single requirement: the need to realize flux distributions at a minimal enzyme cost. If enzyme investments are a main factor driving the choice of pathways, how can we quantify them? Typically, the notion of protein investment captures marginal biological costs, that is, a fitness reduction caused by an additional expression of proteins. For growing bacteria, the costs can be defined as the measured reduction in growth rate caused by artificially induced proteins. To ensure that the measurement concerns only costs, and not benefits caused by the proteins, one studies proteins without a normal physiological function (e.g., fluorescent marker proteins) or enzymes without available substrate [1,46].
For use in models, various proxies for enzyme cost have been proposed, including the total amount of enzyme in cells or specific pathways [19] or the total energy utilization [47]. To define simple cost functions, we can assume that protein cost increases linearly with the protein production rate, that is, with the amount of amino acids invested per time in translation [48]. With these definitions, protein cost will increase with protein abundance, protein chain length, and the effective protein turnover rate (which may include dilution in growing cells) [49].
11.1.3 Optimality Approaches in Metabolic Modeling
Based on known requirements for efficient metabolism (high product yields, short pathways, sufficient thermodynamic forces, and low enzyme investment), one may attempt to predict metabolic flux distributions as well as the enzyme levels driving them.
Flux Optimization
Flux prediction has many possible applications: for instance, as a sanity check in network reconstruction or for scoring possible pathway variants in metabolic engineering [50,51]. Understanding how flux distributions are chosen in nature can also shed light on the allocation of protein resources, for instance, on the enzyme investments in different metabolic pathways (see Figure 8.15). Flux distributions in metabolic networks can be predicted by FBA (see Chapter 3). In a typical FBA, flux distributions are predicted by maximizing a linear flux benefit 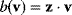 under the stationarity constraint
under the stationarity constraint 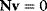 and bounds on individual fluxes. FBA can predict optimal yields and the viability of cells after enzyme deletions. The flux distribution itself, however, is usually underdetermined, and flux predictions are often unreliable. One reason is that FBA, by placing a bound on the substrate supply, effectively maximizes the product yield per substrate invested. When cells need to grow fast, however, it is more plausible to assume that cells maximize the product yield per enzyme investment.
and bounds on individual fluxes. FBA can predict optimal yields and the viability of cells after enzyme deletions. The flux distribution itself, however, is usually underdetermined, and flux predictions are often unreliable. One reason is that FBA, by placing a bound on the substrate supply, effectively maximizes the product yield per substrate invested. When cells need to grow fast, however, it is more plausible to assume that cells maximize the product yield per enzyme investment.
To account for this fact, some variants of FBA suppress unnecessary pathway fluxes in their solutions. The principle of minimal fluxes [28] states that a flux distribution  must achieve a given benefit
must achieve a given benefit 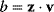 at a minimal sum of absolute fluxes
at a minimal sum of absolute fluxes 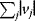 . In this sum, the fluxes can also be individually weighted (see Chapter 3). This flux cost may be seen as a proxy for the (unknown) enzyme costs required to realize the fluxes. In contrast to standard FBA, FBA with flux minimization resolves many of the underdetermined fluxes and yields more realistic flux predictions [36,52]. FBA with molecular crowding [53], an alternative method, pursues a similar, yet contrary approach: it translates absolute fluxes into approximate enzyme demands and puts upper bounds on the latter while maximizing the linear flux benefit. Resource balance analysis (RBA), finally, not only covers metabolism, but also brings macromolecule production into the picture [29]. It assumes a growing cell in which macromolecules, including enzymes, are diluted. Therefore, metabolic reactions depend on a continuous production of enzymes and, indirectly, on ribosome production. Macromolecule synthesis, in turn, depends on precursors and energy to be supplied by metabolism. RBA checks, for different possible growth rates, whether a consistent cell state can be sustained, and determines the maximal possible growth rate and the corresponding metabolic fluxes and macromolecule concentrations.
. In this sum, the fluxes can also be individually weighted (see Chapter 3). This flux cost may be seen as a proxy for the (unknown) enzyme costs required to realize the fluxes. In contrast to standard FBA, FBA with flux minimization resolves many of the underdetermined fluxes and yields more realistic flux predictions [36,52]. FBA with molecular crowding [53], an alternative method, pursues a similar, yet contrary approach: it translates absolute fluxes into approximate enzyme demands and puts upper bounds on the latter while maximizing the linear flux benefit. Resource balance analysis (RBA), finally, not only covers metabolism, but also brings macromolecule production into the picture [29]. It assumes a growing cell in which macromolecules, including enzymes, are diluted. Therefore, metabolic reactions depend on a continuous production of enzymes and, indirectly, on ribosome production. Macromolecule synthesis, in turn, depends on precursors and energy to be supplied by metabolism. RBA checks, for different possible growth rates, whether a consistent cell state can be sustained, and determines the maximal possible growth rate and the corresponding metabolic fluxes and macromolecule concentrations.
All these methods assume, in one way or another, a trade-off between flux benefits and flux costs, which sometimes appear in the form of constraints. However, this trade-off can be studied more directly by adopting a multi-objective approach. Instead of being optimized in only one way, flux distributions may be chosen to optimize different objectives under different growth conditions [36] or compromises between different objectives. For flux distributions in the central metabolism of E. coli, measured by isotope labeling of carbon atoms, this has been demonstrated [52]. Each flux distribution can be characterized by three objectives: ATP yield and biomass yield (both to be maximized), and the sum of absolute fluxes (to be minimized). By assessing all possible flux distributions in an FBA model, the Pareto surface for these objectives can be computed. As shown in Figure 11.5, the measured flux distributions are close to the Pareto surface; each of them represents a different compromise under a different experimental condition. The fact that the flux distributions are not exactly on the Pareto surface can mean two things: either that these are not optimized or that other optimality criteria, aside from those considered in the analysis, play a role. One such possibility could be anticipation behavior: by deviating from the momentary optimum, flux distributions could facilitate future flux changes and thus the adaptation to new environmental conditions.
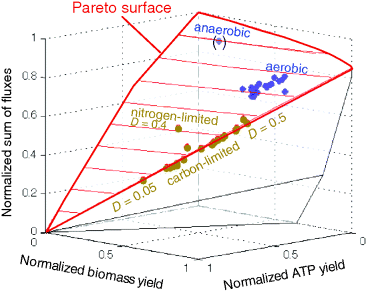
Figure 11.5 Metabolic flux distributions in E. coli central metabolism are close to being Pareto-optimal. Axes correspond to three metabolic objectives: biomass yield, ATP yield, and the sum of absolute fluxes. Dots represent measured flux distributions under different growth conditions. The polyhedron comprises all possible combinations of objective values, determined from a stoichiometric model. The Pareto surface is marked in red. The measured flux distributions are close to, but not exactly on the Pareto surface. (From Ref. [52].)
Optimization of Enzyme Levels
If flux distributions are thought to be optimized, optimality should also hold for enzyme levels and the regulation systems behind them. In models, the question of optimal enzyme levels can be addressed in two ways. Either we assume that some predefined flux distribution must be realized or we directly optimize cell fitness as a function of enzyme levels. In both cases, fluxes and enzyme investments are linked by enzyme kinetics.
In the first approach, we use flux analysis to determine a flux distribution and then search for enzyme profiles (and corresponding metabolite profiles) that can realize this flux distribution with a given choice of rate laws [54,55]. Since the fluxes do not uniquely determine the enzyme profile, an additional optimality criterion is needed to pick a solution, for instance, minimization of total enzyme cost. Since reactions with low driving forces would automatically imply larger enzyme levels, they will automatically be avoided: either by shutting down the enzyme or by an arrangement of enzyme profiles that ensures sufficient reaction affinities in all reactions.
Effectively, this approach translates a given flux distribution into an optimal enzyme profile and thereby into an overall enzyme cost. In theory, cost functions of this sort could also be used to define nonlinear flux costs for FBA, but these would be hard to compute in practice. It can be generally proven, though, that such flux cost functions, at equal flux benefits, are minimized by elementary flux modes [56,57].
In the second approach, the metabolic objective is directly written as a function 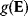 of the enzyme levels
of the enzyme levels 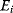 , mediated through enzyme-dependent steady-state concentrations and fluxes. The enzyme levels are optimized for a high fitness value, either at a given total enzyme investment or with a cost term for enzymes (following Eq. (11.1), where
, mediated through enzyme-dependent steady-state concentrations and fluxes. The enzyme levels are optimized for a high fitness value, either at a given total enzyme investment or with a cost term for enzymes (following Eq. (11.1), where  is a metabolic objective scoring the stationary fluxes and concentrations and
is a metabolic objective scoring the stationary fluxes and concentrations and  scores the enzyme investments). Given the fitness function, we can compute optimal protein profiles and study how they should be adapted after perturbations. Modeling approaches of this sort will be discussed further below.
scores the enzyme investments). Given the fitness function, we can compute optimal protein profiles and study how they should be adapted after perturbations. Modeling approaches of this sort will be discussed further below.
Measurements of Enzyme Fitness Functions
The fitness as a function of enzyme levels can also be explored by experiments. If the fitness function is given by the cell growth rate, the fitness landscape can be experimentally screened by varying the expression of a protein and recording the resulting growth rates [1]. The protein levels in E. coli, for instance, can be varied by manipulating the ribosome binding sites. By modifying the ribosome binding sites of several genes combinatorially, one can produce a library of bacterial clones with different expression profiles of these genes. In this way, suitable expression profiles for a recombinant carotenoid synthesis pathway in E. coli have been determined [58]. A similar approach was applied to constitutive gene promoters in Saccharomyces cerevisiae. A large number of variants of the engineered violacein biosynthetic pathway, differing in their combinations of promoter strengths, were obtained by combinatorial assembly. Based on measured production rates, a statistical model could be trained to predict the preferential production of different pathway products depending on the promoter strengths [59].
Another way to measure the benefits from single genes is the genetic tug-of-war (gTOW) method [60], which allows for systematic measurements of maximal tolerable gene copy numbers, that is, copy numbers at which the selective pressure against an even higher expression begins to be strong. The method, established for the yeast S. cerevisiae, uses a plasmid vector whose copy number in cells ranges typically from 10 to 40. In a yeast strain with a deletion of the gene leu2 (coding for a leucine biosynthesis enzyme needed for growth on leucine-free media) and with plasmids containing a low-expression variant of the same gene, larger copy numbers of the plasmid lead to a growth advantage. Due to a selection for higher copy numbers, the typical numbers rise to more than 100. Now a second gene, the target gene under study, is inserted into the plasmid, and thus expressed depending on the plasmid's copy number. The gene's expression can have beneficial or (especially at very high copy numbers) deleterious fitness effects, which are overlaid with the (mostly beneficial) effect of leu expression. Eventually, the cells arrive at an optimal copy number, the number at which a small further change in copy number has no net effect because marginal advantage (due to increased leu expression) and marginal disadvantage (from increased target gene expression) cancel out. By measuring this optimal copy number, one can compare the fitness effects (or, a bit simplified, the maximal tolerable gene copy numbers) of different target genes.
11.1.4 Metabolic Strategies
Fermentation and Respiration as Examples of High-Rate and High-Yield Strategies
Cell choices between high-flux and high-yield strategies are exemplified by the choice between two metabolic strategies in central metabolism, fermentation and respiration. Glycolysis realizes fermentation, producing incompletely oxidized substances such as lactate or ethanol. In terms of yield, this is rather inefficient: only two ATP molecules are produced per glucose molecule. Exactly because of this, however, large amounts of Gibbs energy are dissipated, which suppresses backward fluxes and thereby increases the metabolic flux. Respiration, performed by the TCA cycle and oxidative phosphorylation, uses oxygen to oxidize carbohydrates completely into CO2. It has a much higher yield than glycolysis, producing up to 36 molecules of ATP per glucose molecule. However, this leaves little Gibbs energy for driving the reactions, so more enzyme may need to be invested to obtain the same ATP production flux. The details depend on the concentrations of extracellular compounds (e.g., oxygen and carbon dioxide), which affect the overall Gibbs free energy of the pathway.
Cells tend to use high-yield strategies under nutrient limitation and in multicellular organisms (although microbes such as E. coli can also be engineered to use high-yield strategies [61]). Low-yield strategies, such as additional fermentation on top of respiration in yeast (Crabtree effect) [62] and the Warburg effect in cancer cells [63], are preferred when nutrients are abundant and in situations of strong competition. Low-yield strategies may be profitable when enzyme levels are costly or constrained, or when the capacity for respiration is limited. For instance, when the maximal capacity of oxidative phosphorylation has been reached (because of limited space on mitochondrial membranes), additional fermentation could increase the ATP production flux [64]. Moreover, a higher thermodynamic driving force may lead to a higher ATP production per time at the same total enzyme investment, which in turn would allow for faster growth [53,65].
Paradoxically, low-yield strategies can outperform high-yield strategies even if their performance is worse. Grown separately on equal substrates, a high-yield strategy leads to higher cell densities (in continuous cultures) and longer survival (in batch cultures). However, when grown on a shared food source, microbes using a low-yield strategy initiate a competition in which they use their waste of nutrients as a weapon to outperform yield-efficient microbes. Therefore, inefficient metabolism can provide a selection advantage for individual cells that is paid by a permanent loss of the cell population. But this is not the end of the story: excreted fermentation products, such as lactate or ethanol, can serve as nutrients for other cells or for later times. Thus, depending on the frame of description, fermentation can also appear as a cooperative strategy. In Section 11.4, we will see how the social behavior of microbes is framed by evolutionary game theory.
Trade-off between Product Yield and Enzyme Cost
Aside from the most typically studied variant of glycolysis, called Embden–Meyerhof–Parnas (EMP) pathway, there are other variants of glycolysis with different ATP yields. EMP glycolysis produces two ATP molecules from one molecule of glucose and is common in eukaryotes. An alternative variant, the Entner–Doudoroff (ED) pathway, produces one ATP molecule only (see Figure 11.6). If the two variants are compared at equal ATP production rates, the ED pathway consumes twice as much glucose. Nevertheless, many bacteria use the ED pathway, either as an alternative or in addition to the EMP pathway.
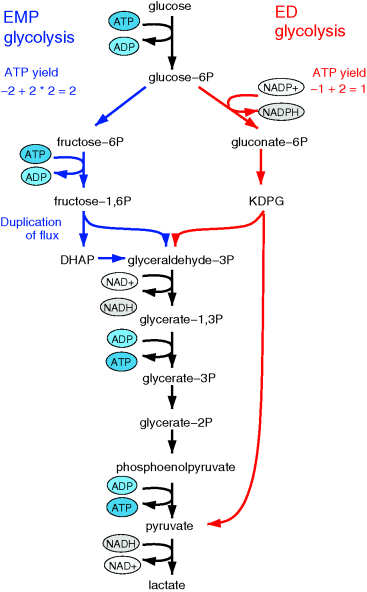
Figure 11.6 Comparison between two variants of glycolysis. The EMP pathway shows a higher ATP yield (two ATP molecules per molecule of glucose) than the ED pathway (one ATP molecule per glucose molecule). However, its enzyme demand per ATP flux is more than twice as high [45].
We already saw that pathways with lower yields may be justified by their larger energy dissipation, which can lower the enzyme demand. By modeling the energetics of both pathways, Flamholz et al. [55] showed that the enzyme demand of the EMP pathway, at equal ATP production rates, is about twice as high. Thus, the choice between the two pathways will depend on what is more critical in a given environment – an efficient usage of glucose or a low enzyme demand. If ATP production matters less (e.g., because other ATP sources, such as respiration or photosynthesis, exist), or if glucose can be assumed to be abundant (as in the case of Zymomonas mobilis, which is adapted to very large glucose concentrations), the ED pathway will be preferable. This prediction has been confirmed by a broad comparison of microbes with different lifestyles [55].
Molenaar et al. modeled the choice between high-yield and low-yield strategies as a problem of optimal resource allocation [34]. In their models, cells can choose between two pathways for biomass precursor production: one with high cost and high yield and another one with low cost and low yield. Given a fixed substrate concentration and aiming at maximal growth, cells can allocate a fixed total amount of protein resources between the two pathways. After numerical optimization, the simulated cells employ the high-yield pathway when substrate is scarce, and the low-yield pathway when the substrate level increases. The two cases correspond, respectively, to slow-growth and fast-growth conditions.
11.1.5 Optimal Metabolic Adaptation
Metabolic enzymes show characteristic expression patterns across the metabolic network, but also characteristic temporal patterns during adaptation. Mechanistically, expression patterns follow, for instance, from the regulation functions encoded in the genes' promoter sequences (see Section 9.3). If a pathway is controlled by a single transcription factor, the enzymes in that pathway will tend to show a coherent expression. However, we may still ask why the regulation system works in this way: why is it that transcription factor regulons and metabolic pathway structures match, even if the metabolic network and its transcriptional regulation evolve independently? In terms of function, coherent expression patterns may simply be the best way to regulate metabolism. This hypothesis can be studied by models in which enzyme profiles control the metabolic state and are chosen to optimize the metabolic performance.
Optimal Adaptation of Enzyme Activities
Using such models, we can address a number of questions. If a metabolic state is perturbed, how should cells adapt their enzyme levels? And, in particular, if an enzyme level itself is perturbed, how should the other enzymes respond? To predict such adaptations, we may consider a kinetic pathway model and determine its enzyme levels from an optimality principle as in Eq. (11.1). We start in an initially optimal state. When an external perturbation is applied, this will change the fitness landscape in enzyme space and shift the optimum point. Similarly, when a knockdown forces one enzyme level to a lower value, this will lead to a new, constrained optimum for the other enzymes. In both cases, the cell should adapt its enzyme activities to reach the new optimum. Given a model, the necessary enzyme adaptations can be computationally optimized.
A mathematical approach for such scenarios was developed in Ref. [20]: under the assumption of small perturbations, the optimal adaptations can be directly computed from the metabolic response coefficients and the local curvatures of the fitness landscape (i.e., the Hessian matrix). Consider a kinetic model with steady-state metabolite concentrations and fluxes (in a state vector 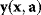 ) depending on control variables (e.g., enzyme activities, in a vector
) depending on control variables (e.g., enzyme activities, in a vector  ) and environment variables (in a vector
) and environment variables (in a vector  ). The possible control profiles
). The possible control profiles  are scored by a fitness function
are scored by a fitness function
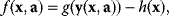
which describes the trade-off between a metabolic objective 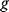 and a cost function
and a cost function 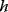 . The optimality principle requires that, given the environment
. The optimality principle requires that, given the environment  , the control profile
, the control profile  must be chosen to maximize
must be chosen to maximize 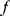 . As a condition for a local optimum, the gradient
. As a condition for a local optimum, the gradient 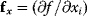 must vanish and the Hessian matrix
must vanish and the Hessian matrix 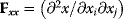 must be negative definite. Now we assume a change
must be negative definite. Now we assume a change 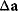 of the environment parameters, causing a shift in the optimal enzyme profile. The adaptation
of the environment parameters, causing a shift in the optimal enzyme profile. The adaptation 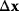 that brings the cell from the old to the new optimal state can be determined as follows. To provide an optimal adaptation, the change
that brings the cell from the old to the new optimal state can be determined as follows. To provide an optimal adaptation, the change 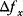 of the fitness gradient during the adaptation must vanish. We approximate the fitness landscape to second order around the initial optimum and obtain the optimality condition
of the fitness gradient during the adaptation must vanish. We approximate the fitness landscape to second order around the initial optimum and obtain the optimality condition
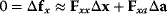
and thus
The Hessian matrices 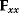 and
and 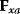 can be obtained from gradients and curvatures of
can be obtained from gradients and curvatures of 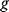 and
and 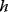 and from the first- and second-order response coefficients of the state variables in
and from the first- and second-order response coefficients of the state variables in 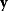 with respect to
with respect to  or
or  . In the second adaptation scenario, we assume that one control variable
. In the second adaptation scenario, we assume that one control variable 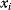 is constrained to some higher or lower value (in the case of enzyme levels, by overexpression or knockdown). How should the other control variables be adapted? If a change
is constrained to some higher or lower value (in the case of enzyme levels, by overexpression or knockdown). How should the other control variables be adapted? If a change 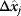 is enforced on the
is enforced on the 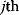 enzyme, the optimal adaptation profile of all enzymes can be written as
enzyme, the optimal adaptation profile of all enzymes can be written as
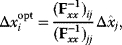
where  automatically assumes its perturbed value
automatically assumes its perturbed value 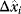 . Even if the Hessian matrix
. Even if the Hessian matrix 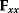 is unknown, its symmetry implies a general symmetry between perturbation and response. We can see this as follows: in the initial optimum state, the matrix
is unknown, its symmetry implies a general symmetry between perturbation and response. We can see this as follows: in the initial optimum state, the matrix 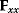 must be negative definite, so the elements
must be negative definite, so the elements 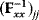 will all be negative. Since
will all be negative. Since 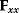 itself is symmetric, the coefficients
itself is symmetric, the coefficients 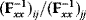 must form a matrix with a symmetric sign pattern. This means that whenever a knockdown of enzyme A necessitates an adaptive upregulation of enzyme B, a knockdown of B should also necessitate an adaptive upregulation of A. An analogous relationship holds for cases of adaptive downregulation. Symmetric behavior, as predicted, has been found in expression data.
must form a matrix with a symmetric sign pattern. This means that whenever a knockdown of enzyme A necessitates an adaptive upregulation of enzyme B, a knockdown of B should also necessitate an adaptive upregulation of A. An analogous relationship holds for cases of adaptive downregulation. Symmetric behavior, as predicted, has been found in expression data.
Optimal Control Profiles Reflect the Objective and the System Controlled
What can we learn about proteins' function by observing their expression profiles? For instance, is there a reason why correlations in expression should reflect metabolic pathway structures? Or, turning this question around, when a metabolic pathway is induced, should all enzyme levels be upregulated, or only some of them? In protein complexes, subunits often come in fixed proportions, and should therefore be expressed as such. The ribosomal subunits, for instance, are combined in a fixed stoichiometry; if the expression ratios did not match this stoichiometry, some subunits would remain unused and protein resources would be wasted. This argument can be framed mathematically as an optimality principle (e.g., minimal protein production at a fixed number of functional ribosomes). The stoichiometric expression is confirmed by proteomics and ribosome profiling [66] and visible, for instance, in Figure 8.15. A proportional expression can also make sense for forming a metabolic pathway – even if the enzymes do not form a complex. In theory, the same predefined pathway flux could be achieved by various different enzyme profiles. Accordingly, a small increase in flux could be achieved either by a proportional induction of all enzymes or by a selective induction of one enzyme, for instance, the one with the highest control. Thus, the question is not how the flux change can be achieved, but how it can be achieved most economically.
Here, the answer depends on details. In a simple case – if the external metabolite concentrations are fixed and if enzyme cost depends linearly on the enzyme levels – we can employ a scaling argument. We imagine a proportional scaling of fluxes and enzyme levels at constant metabolite levels. If we start with optimal expression ratios along the pathway, the fact that these ratios are optimal should be unaffected by scaling (see Section 10.2.6). In other words, if the flux needs to be increased, the best way of doing so is a proportional induction of all enzymes. In other cases, for instance, after a change of substrate, product, or cofactor levels, a nonproportional induction may be more favorable. According to Eq. (11.4), the optimal enzyme adaptations depend on how enzyme levels affect the steady-state variables, how these variables affect fitness, and how enzyme levels affect the fitness directly via their costs. The Hessian matrices, which encode this information, are partially based on the metabolic control coefficients. Accordingly, as a rough approximation, enzymes with a similar control over fitness-relevant variables can be expected to show similar differential expression. Loosely speaking, we can see optimal control problems as an inverted form of MCA. Instead of going from cause to effect (i.e., from enzyme changes to the resulting metabolic state changes), we go backward and ask, teleologically, how enzyme levels should be adjusted in order to achieve a given metabolic change. Thus, what the differential activity patterns can be expected to portray – if any – is not the shape of the metabolic network, but the enzymes' control coefficients, which, to an extent, reflect the network structure [20].
11.2 Optimal Enzyme Concentrations
11.2.1 Optimization of Catalytic Properties of Single Enzymes
An important function of enzymes is to increase the rate of a reaction. Therefore, evolutionary pressure should lead toward a maximization of the reaction rate  [67–70]. High reaction rates may only be achieved if the kinetic properties of the enzymes are suitably adapted. We identify the optimal kinetic parameters that maximize the rate for the reversible conversion of substrate S into product P [71].
[67–70]. High reaction rates may only be achieved if the kinetic properties of the enzymes are suitably adapted. We identify the optimal kinetic parameters that maximize the rate for the reversible conversion of substrate S into product P [71].
Two constraints must be considered. First, the action of an enzyme cannot alter the thermodynamic equilibrium constant for the conversion of S to P (Section 4.1, Eqs. (4.5) and (4.10)). Changes of kinetic properties must obey the thermodynamic constraint. Second, the values of the kinetic parameters are limited by physical constraints even for the best enzymes, such as diffusion limits or maximal velocity of intramolecular rearrangements. In the following, the maximal possible values are denoted by  and all rate constants are normalized by their respective
and all rate constants are normalized by their respective  , such that the normalized kinetic constants have a maximal value of 1. Likewise, concentrations and rates are normalized to yield dimensionless quantities. For a simple reaction
, such that the normalized kinetic constants have a maximal value of 1. Likewise, concentrations and rates are normalized to yield dimensionless quantities. For a simple reaction
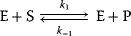
that can be described with mass action kinetics with the thermodynamic equilibrium constant 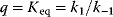 , the rate equation reads
, the rate equation reads
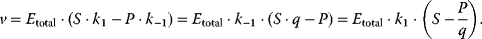
It is easy to see that v becomes maximal for fixed values of Etotal, S, P, and q, if 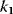 or
or 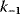 becomes maximal. This is mathematically equivalent to a minimal transition time
becomes maximal. This is mathematically equivalent to a minimal transition time 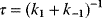 . Note that usually only one of the two rate constants may attain its maximal value. The value of the other, submaximal constant is given by the relation to the equilibrium constant.
. Note that usually only one of the two rate constants may attain its maximal value. The value of the other, submaximal constant is given by the relation to the equilibrium constant.
For a reversible reaction obeying Michaelis–Menten kinetics
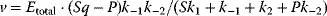
with 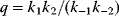 , the optimal result depends on the value of P. For
, the optimal result depends on the value of P. For 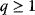 and
and 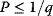 , the rate becomes maximal if
, the rate becomes maximal if 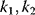 , and
, and 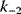 assume maximal values and
assume maximal values and 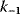 is submaximal (region R1 in Figure 11.7). For
is submaximal (region R1 in Figure 11.7). For 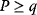 , we obtain submaximal values of only
, we obtain submaximal values of only 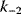 (region R2). For
(region R2). For 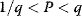 , the optimal solution is characterized by submaximal values of
, the optimal solution is characterized by submaximal values of 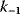 and
and 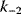 with
with 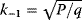 and
and 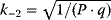 (region R3).
(region R3).
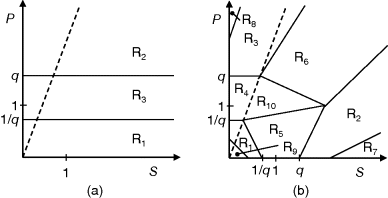
Figure 11.7 Subdivision of the plane of substrate and product concentrations (S, P) into regions of different solutions for the optimal microscopic rate constants (schematic representation). The dashed lines indicate the function  . (a) Solution regions for the two-step mechanism. (b) Solution regions for the three-step mechanism.
. (a) Solution regions for the two-step mechanism. (b) Solution regions for the three-step mechanism.
Comparison of the optimal state with a reference state can assess the effect of the optimization. One simple choice for a reference state is 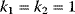 and
and 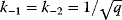 , that is, equal distribution of the free energy difference (see Section 4.1) represented by the equilibrium constant in the first and the second step. The respective reference rate reads
, that is, equal distribution of the free energy difference (see Section 4.1) represented by the equilibrium constant in the first and the second step. The respective reference rate reads
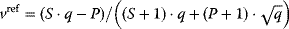
and the optimal rates in regions R1, R2, and R3 are
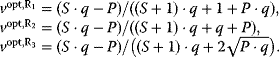
For example, in the case  and
and  , the maximal rate for optimal kinetic constants is
, the maximal rate for optimal kinetic constants is 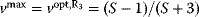 and the reference rate is calculated as
and the reference rate is calculated as 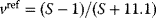 , which is lower than the maximal rate.
, which is lower than the maximal rate.
For the reversible three-step mechanism involving the binding of the substrate to the enzyme, the isomerization of the ES complex to an EP complex, and the release of product from the enzyme,
the reaction rate is given as
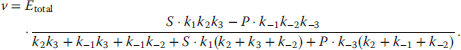
It turns out that the optimal solution for this mechanism depends on the values of both S and P. There are 10 different solutions, shown in Table 11.2 and Figure 11.7.
Table 11.2 Optimal solutions for the rate constants of the three-step enzymatic reaction as functions of the concentrations of substrate and product for 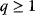 .
.
| Solution | k1 | k−1 | k2 | k−2 | k3 | k−3 |
| R1 | 1 | 1/q | 1 | 1 | 1 | 1 |
| R2 | 1 | 1 | 1 | 1/q | 1 | 1 |
| R3 | 1 | 1 | 1 | 1 | 1 | 1/q |
| R4 | 1 | 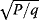 |
1 | 1 | 1 | 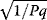 |
| R5 | 1 | 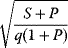 |
1 | 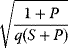 |
1 | 1 |
| R6 | 1 | 1 | 1 | 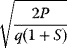 |
1 |  |
| R7 | 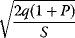 |
1 | 1 | 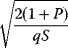 |
1 | 1 |
| R8 | 1 | 1 | 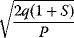 |
1 | 1 | 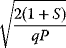 |
| R9 | 1 | 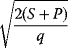 |
1 | 1 | 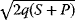 |
1 |
| R10 | 1 | a | 1 | 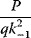 |
1 | 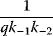 |
ak−1 is solution of the equation 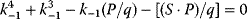 . . |
||||||
Among the 10 solutions, there are three solutions with a submaximal value of one backward rate constant, three solutions with submaximal values of two backward rate constants, three solutions with submaximal values of one backward and one forward rate constant, and one solution with submaximal values of all three backward rate constants. The constraint imposed by the thermodynamic equilibrium constant leads to the following effects. At very low substrate and product concentrations, a maximal rate is achieved by enhancing the binding of S and P to the enzyme (so-called high (S, P)-affinity solution). If S or P is present in very high concentrations, they should be weakly bound (low S- or P-affinity solutions). For intermediate values of S and P, only backward constants assume submaximal values. For concentrations of S and P equal to unity, the optimal solution reads
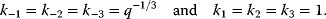
This case represents an equal distribution of the drop in free energy in all three elementary steps.
In summary, we find that when normalized substrate concentrations are close to 1, then the maximal rates are favored by maximal forward rate constants and equal distribution of the thermodynamic constraints to the backward rate constants. If S or P deviates from the mean value, optimal rate constants compensate for the thermodynamic burden.
11.2.2 Optimal Distribution of Enzyme Concentrations in a Metabolic Pathway
By means of regulated gene expression and protein degradation, cells can adjust the amount of enzyme allocated to the reactions of a metabolic pathway according to the current metabolic supply or demand. In many cases, the individual amounts of enzymes are regulated such that the metabolic fluxes necessary to maintain cell functions are achieved while the total enzyme amount is low. A reason for keeping enzyme concentrations this low is that proteins are osmotically active substances. One strategy to achieve osmotic balance is, therefore, to keep the total amount of enzyme constrained. Furthermore, enzyme synthesis is expensive for the cell, with respect to both energy and material. Therefore, it is sensible to assume that various pathways or even individual reactions compete for the available resources.
We can study theoretically how a maximal steady-state flux through a pathway is achieved with a given fixed total amount of enzyme [72]. The optimization problem is to distribute the total protein concentration 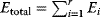 optimally among the r reactions. We will exemplify this for the simple unbranched pathway presented in Chapter 4, Eq. (4.100). To assess the effect of optimization we will again compare the optimal state to a reference state where the given total concentration of enzymes is distributed uniformly such that
optimally among the r reactions. We will exemplify this for the simple unbranched pathway presented in Chapter 4, Eq. (4.100). To assess the effect of optimization we will again compare the optimal state to a reference state where the given total concentration of enzymes is distributed uniformly such that 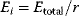 .
.
The optimal enzyme concentrations 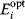 in states of maximal steady-state flux can be determined by the variational equation
in states of maximal steady-state flux can be determined by the variational equation
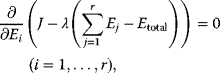
where 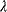 denotes the Lagrange multiplier. From this equation, it follows that
denotes the Lagrange multiplier. From this equation, it follows that
(Equation 11.15) indicates that all nonnormalized flux response coefficients with respect to enzyme concentrations (Chapter 4) have the same value. By multiplication with 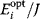 , we find
, we find
The left-hand term of Eq. (11.16) represents the normalized flux control coefficient (Eq. (4.65)) 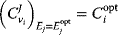 of reaction i over steady-state flux J in optimal states. Since the sum of the flux control coefficients over all reactions equals unity (summation theorem, Eq. (4.70)), it follows that
of reaction i over steady-state flux J in optimal states. Since the sum of the flux control coefficients over all reactions equals unity (summation theorem, Eq. (4.70)), it follows that
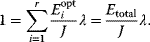
Therefore,
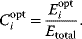
This means that the allocation of flux control coefficient in optimal states (here, states of maximal steady-state fluxes), 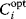 , is equal to the allocation of the relative enzyme concentrations along the pathway: the flux only becomes maximal if enzymes with higher or lower control are present in higher or lower concentration, respectively.
, is equal to the allocation of the relative enzyme concentrations along the pathway: the flux only becomes maximal if enzymes with higher or lower control are present in higher or lower concentration, respectively.
The problem of maximizing the steady-state flux at a given total amount of enzyme is related to the problem of minimizing the total enzyme concentration that allows for a given steady-state flux. For an unbranched reaction pathway (Eq. (4.100)) obeying the flux equation 4.101, minimization of 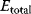 results in the same optimal allocation of relative enzyme concentrations and flux control coefficients as maximization of J.
results in the same optimal allocation of relative enzyme concentrations and flux control coefficients as maximization of J.
The principle of minimizing the total enzyme concentration at fixed steady-state fluxes is more general since it may be applied also to branched reaction networks. Application of the principle of maximal steady-state flux to branched networks requires an objective function that balances the different fluxes by specific weights or could lead to conflicting interests between different fluxes in different branches.
Special conditions hold for the flux control coefficients in states of minimal total enzyme concentration at fixed steady-state fluxes. Since the reaction rates 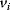 are proportional to the enzyme concentrations, that is,
are proportional to the enzyme concentrations, that is, 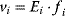 , keeping fixed the steady-state fluxes
, keeping fixed the steady-state fluxes 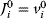 leads to the following relation between enzyme concentrations and substrate concentrations:
leads to the following relation between enzyme concentrations and substrate concentrations:
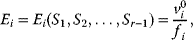
where the function 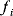 expresses the kinetic part of the reaction rate that is independent of the enzyme concentration. The principle of minimal total enzyme concentration implies
expresses the kinetic part of the reaction rate that is independent of the enzyme concentration. The principle of minimal total enzyme concentration implies
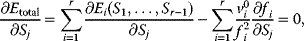
which determines the metabolite concentrations in the optimal state. Since 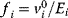 , it follows that
, it follows that
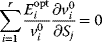
and in matrix representation
where  is the vector containing the optimal enzyme concentrations. An expression for the flux control coefficients in matrix representation has been given in Eq. (4.98). Its transposed matrix reads
is the vector containing the optimal enzyme concentrations. An expression for the flux control coefficients in matrix representation has been given in Eq. (4.98). Its transposed matrix reads
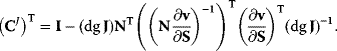
Postmultiplication with the vector  and considering Eq. (11.24) leads to
and considering Eq. (11.24) leads to
This expression represents a functional relation between enzyme concentrations and flux control coefficients for enzymatic networks in states of minimal total enzyme concentration.
11.2.3 Temporal Transcription Programs
In this section, temporal adaptation of enzyme concentration is studied, instead of steady-state solutions as in the previous section. Consider an unbranched metabolic pathway that can be switched on or off by the cell depending on actual requirements. The product Sr of the pathway is desirable, but not essential for the reproduction of the cell. The faster the initial substrate S0 can be converted into Sr, the more efficiently the cell may reproduce and outcompete other individuals. If S0 is available, then the cell produces the enzymes of the pathway to make use of the substrate. If the substrate is not available, then the cell does not synthesize the respective enzymes for economic reasons. Bacterial amino acid synthesis is frequently organized in this way. This scenario has been studied theoretically [73] by starting with a resting pathway; that is, although the genes for the enzymes are present, they are not expressed due to lack of the substrate. Suddenly S0 appears in the environment (by feeding or change of place). How can the cell make as soon as possible use of S0 and convert it into Sr?
The system of ordinary differential equations (ODEs) describing the dynamics of the pathway reads
For the sake of simplicity, we first assume that the cell can make the enzymes instantaneously when necessary (neglecting the time necessary for transcription and translation), but the total amount of enzyme is limited due to limited capacity of the cell to produce and store proteins. The time necessary to produce Sr from S0 is measured by the transition time
The optimization problem to be solved is to find a temporal profile of enzyme concentrations that minimizes the transition time ( ) at fixed value of
) at fixed value of 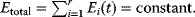
To solve the above optimization problem for pathways with n enzymes, we divide the time axis into m intervals in each of which the enzyme concentrations are constant. The quantities to be optimized are the switching times  defining the time intervals and the enzyme concentrations during these intervals. In the reference case with only one interval (
defining the time intervals and the enzyme concentrations during these intervals. In the reference case with only one interval ( switches), the optimal enzyme concentrations are all equal:
switches), the optimal enzyme concentrations are all equal: 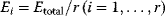 . The transition time for this case reads
. The transition time for this case reads 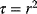 in units of
in units of 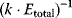 . Permitting one switch (
. Permitting one switch ( ) between intervals of constant enzyme concentrations allows for a considerably lower transition time. An increase in the number of possible switches (
) between intervals of constant enzyme concentrations allows for a considerably lower transition time. An increase in the number of possible switches ( ) leads to a decrease in the transition time until the number of switches reaches
) leads to a decrease in the transition time until the number of switches reaches 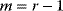 . The corresponding optimal enzyme profiles have the following characteristics: within any time interval, except for the last one, only a single enzyme is fully active whereas all others are shut off. At the beginning of the process, the whole amount of available protein is allocated exclusively to the first enzyme of the chain. Each of the following switches turns off the active enzyme and allocates the total amount of protein to the enzyme that catalyzes the following reaction. The last switch allocates finite fractions of the protein amount to all enzymes with increasing amounts from the first one to the last one (Figure 11.9).
. The corresponding optimal enzyme profiles have the following characteristics: within any time interval, except for the last one, only a single enzyme is fully active whereas all others are shut off. At the beginning of the process, the whole amount of available protein is allocated exclusively to the first enzyme of the chain. Each of the following switches turns off the active enzyme and allocates the total amount of protein to the enzyme that catalyzes the following reaction. The last switch allocates finite fractions of the protein amount to all enzymes with increasing amounts from the first one to the last one (Figure 11.9).
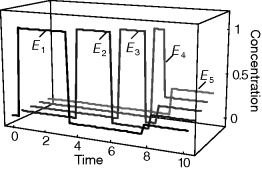
Figure 11.9 Optimal temporal enzyme profiles yielding the minimal transition time for a pathway of five reactions. The switching times are 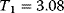 ,
, 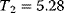 ,
, 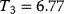 , and
, and 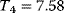 .
.
If one compares the case of no switch (the reference case) with the case of 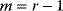 switches, the drop in transition time (gain in turnover speed) amplifies with increasing length r of the reaction chain.
switches, the drop in transition time (gain in turnover speed) amplifies with increasing length r of the reaction chain.
If we impose a weaker condition for the conversion of substrate 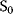 into product
into product 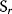 by demanding only conversion of 90% instead of 100%, then the optimal solution looks as follows: enzymes
by demanding only conversion of 90% instead of 100%, then the optimal solution looks as follows: enzymes 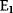 to
to 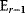 are switched on and off successively in the same way as in the case of 100% conversion except for the last interval, where enzyme
are switched on and off successively in the same way as in the case of 100% conversion except for the last interval, where enzyme 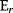 is fully activated, but none of the other enzymes (Bartl, 2008). The transition time is considerably reduced compared with the strict case. In conclusion, abandonment of perfection (here demanding 90% metabolite conversion instead of 100%) may lead to incomplete, but faster metabolite conversion.
is fully activated, but none of the other enzymes (Bartl, 2008). The transition time is considerably reduced compared with the strict case. In conclusion, abandonment of perfection (here demanding 90% metabolite conversion instead of 100%) may lead to incomplete, but faster metabolite conversion.
When cells have to survive in a complicated environment, it can be assumed that they should optimize several properties simultaneously, for example, to minimize the time needed for proper response to an external stimulus or to minimize the amount of enzyme necessary for the respective metabolic conversion or to minimize the amount of accumulated intermediates. This multi-objective case has been studied extensively [74]. It leads to multiple optimal solutions, that is, solutions that cannot be improved in one property without impairing another property. This is called a Pareto front. Figure 11.10 shows an example for a linear pathway with three reactions in a row converting substrate S1 into product S4. The objectives are to minimize the accumulation of S2 and S3  and to minimize the time needed to reach a certain amount of S4.
and to minimize the time needed to reach a certain amount of S4.
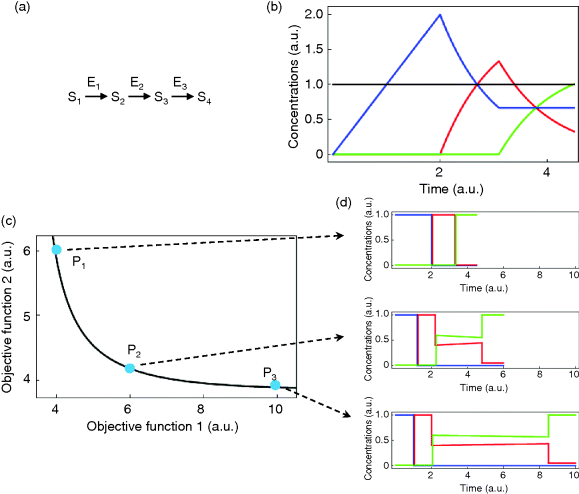
Figure 11.10 Multiple objective functions. (a) Linear pathway of three consecutive reactions. The objective functions are the minimization of intermediates (S2 and S3) over time and the minimization of the time needed for substrate S4 to reach a certain amount. (b) Metabolite dynamics in the optimal case P1. (c) Pareto front obtained in the minimization process. At each point, one property can only be improved at the cost of the other property. For different points, the optimal enzyme profiles are represented in (d).
The simple example of a metabolic pathway shows that temporal adjustment of enzyme activities, for instance, by regulation of gene expression, may lead to a considerable improvement of metabolic efficiency. As detailed in Example 11.3, bacterial amino acid production pathways are possibly regulated in the described manner.
11.3 Evolution and Self-Organization
11.3.1 Introduction
Since Darwin's famous book “On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life” (1859) [77], it is a widely accepted view that biological species have gradually developed from a few common ancestors in an iterative process of mutations and natural selection during millions of years. Throughout this evolution, new species appeared and existing species adapted themselves to changing environmental conditions; others became extinct.
Mutations are changes in the genetic material (genotype) of organisms. They usually cause changes of properties of the organisms (phenotype). They occur by chance. Natural selection proves fitness with respect to survival and reproduction in the actual environment with no further goal or plan. The fittest in gaining and using the necessary resources will win and survive, while the others become extinct. The term natural selection has to be distinguished from artificial selection. Artificial selection chooses specific features to be retained or eliminated depending on a goal or intention (e.g., the objective of a farmer to improve the growth of corn such that it permits maximal harvest).
The view that biological systems developed during evolution can be applied not only to species, but also to other units of biological consideration, such as cells, metabolic pathways, and gene expression networks. It has been questioned though whether the principle of development by mutation and selection can be used to understand evolution in a theoretical way, to learn how and why biological systems assumed their current state, and to predict structures of biological networks using simple analogies.
A basic assumption of theoretical considerations is that evolution is based on the trial-and-error process of variation and natural selection of systems at all levels of complexity. The development of biological systems further involves the feature of self-organization, that is, assuming stable structures that (i) employ a global cooperation between the elements, (ii) are inherent in the system, and (iii) are contained independently of external pressure.
Biological evolution is a quite complex process. Like for other subjects of systems biology, this complexity conflicts with the attempt of developing general models for evolution. Biological diversity increases the number of components to be considered in models. Therefore, it seems unrealistic to develop a detailed and fundamental description of phenomena, as it is sometimes possible in theoretical physics. In general, evolutionary models can rarely be experimentally tested, since we will not survive the necessary time span. Nevertheless, the step has been undertaken to clarify with mathematical modeling features of biological phenomena such as competition and cooperativity, self-organization, or emergence of new species. Such models provide a better understanding of biological evolution; they also give generalized descriptions of biological experiments. The following types of evolutionary models have been developed.
Models of the origin of self-replicating systems have been constructed in connection with the origin of life problem. Manfred Eigen and Peter Schuster [78–82] introduced the concept of quasispecies and hypercycles. These models describe mathematically some hypothetical evolutionary stages of prebiological self-reproducing macromolecular systems. The quasispecies model is a description of the process of the Darwinian evolution of self-replicating entities within the framework of physical chemistry. It is useful mainly in providing a qualitative understanding of the evolutionary processes of self-replicating macromolecules such as RNA or DNA or simple asexual organisms such as bacteria or viruses. Quantitative predictions based on this model are difficult because the parameters that serve as its input are hard to obtain from actual biological systems.
The model relies on four assumptions:
- The self-replicating entities can be represented as sequences composed of letters from an alphabet, for example, sequences of DNA consisting of the four bases A, C, G, and T.
- New sequences enter the system solely as either correct or erroneous copies of other sequences that are already present.
- The substrates, or raw materials, necessary for ongoing replication are always present in sufficient quantity in the considered volume. Excess sequences are washed away in an outgoing flux.
- Sequences may decay into their building blocks.
In the quasispecies model, mutations occur by errors made during copying of already existing sequences. Further, selection arises because different types of sequences tend to replicate at different rates, which leads to the suppression of sequences that replicate more slowly in favor of sequences that replicate faster. In the following chapters, we will show how to put these assumptions into equations. Note that these models still disregard some aspects of evolution, which nowadays are also considered important, such as recombination, that is, the exchange of parts of sequences between DNA molecules during meiosis, or the transfer of sequences among species such as from a virus to its host.
General models of evolution describe some informational and cybernetic aspects of evolution such as the neutral evolution theory by Motoo Kimura [83–86] and Stuart Kauffman's automata [87–90]. Models of artificial life are aimed at understanding the formal laws of life and evolution. These models analyze the evolution of artificial “organisms,” living in computer program worlds.
Computer algorithms have been developed, which use evolutionary methods of optimization to solve practical problems. The genetic algorithm by J.H. Holland [91–93] and the evolutionary programming initiated by Lawrence Fogel et al. [94], evolution strategies by Ingo Rechenberg [95], and genetic programming propagated by J. Koza [96] are well-known examples of these researches. Evolutionary optimization has been applied to models of biological systems. The idea is to predict features of a biological system from the requirement that it functions optimally in order to be the fittest that survives.
These models are usually very abstract and much simpler than biological processes. But the abstractness is necessary to find a general representation of the investigated features despite their real complexity and diversity. Furthermore, the concepts must be simple enough to be perceived and to be applicable.
11.3.2 Selection Equations for Biological Macromolecules
The dynamics of selection processes in early evolution may be described with equations of the type used in population dynamics. Instead of species, we consider here as model the macromolecules that are able to self-replicate. For example, DNA molecules are replicated by complementary base pairing (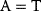 and
and  ):
):
A population is defined as a set  of n DNA sequences. Each sequence is a string of N symbols,
of n DNA sequences. Each sequence is a string of N symbols, 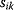 , with
, with 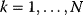 and
and  . The symbols are taken from an alphabet containing λ letters. For the DNA as example, we have a four-letter alphabet (
. The symbols are taken from an alphabet containing λ letters. For the DNA as example, we have a four-letter alphabet ( ,
, 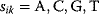 ). Thus, the space of possible sequences covers λN different sequences. The sequence length N and the population size
). Thus, the space of possible sequences covers λN different sequences. The sequence length N and the population size  are assumed to be large:
are assumed to be large: 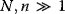 . The concentration of molecules with identical sequences
. The concentration of molecules with identical sequences 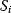 is
is 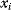 . We assume that the DNA molecules have some selective value
. We assume that the DNA molecules have some selective value 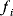 that depends on the sequence of nucleotides. During propagation of the replication process, the molecules with higher selective value will have an advantage compared with those with a lower value. The evolution character depends strongly on the population size n. If n is very large (
that depends on the sequence of nucleotides. During propagation of the replication process, the molecules with higher selective value will have an advantage compared with those with a lower value. The evolution character depends strongly on the population size n. If n is very large ( ), the number of all sequences in a population is large and evolution can be considered as a deterministic process. In this case, the population dynamics can be described in terms of the ordinary differential equations. In the opposite case (
), the number of all sequences in a population is large and evolution can be considered as a deterministic process. In this case, the population dynamics can be described in terms of the ordinary differential equations. In the opposite case ( ), the evolution process should be handled as stochastic (not done here).
), the evolution process should be handled as stochastic (not done here).
A basic assumption of this concept is that there is a master sequence, 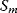 , having the maximal selective value
, having the maximal selective value 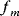 . The selective value
. The selective value 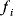 of any other sequence
of any other sequence 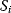 depends on the Hamming distance h (the number of different symbols at corresponding places in sequences) between
depends on the Hamming distance h (the number of different symbols at corresponding places in sequences) between 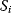 and the master sequence
and the master sequence 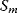 :
: 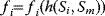 – the smaller the distance h, the greater the selective value
– the smaller the distance h, the greater the selective value 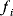 .
.
In the following, we present a number of scenarios for replication of sequences with or without additional constraints and characterize the resulting population dynamics.
11.3.2.1 Self-Replication without Interactions
Assume that DNA molecules perform identical replication and are also subject of decay. The time course of their concentration 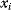 is determined by the following differential equation:
is determined by the following differential equation:
where 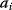 and
and 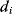 are the rate constants for replication and decay, respectively. For constant values of
are the rate constants for replication and decay, respectively. For constant values of 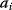 and
and 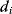 and an initial concentration
and an initial concentration  for
for  , the solution of Eq. (11.32) is given by
, the solution of Eq. (11.32) is given by
Depending on the difference 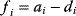 , Eq. (11.33) describes a monotonous increase (
, Eq. (11.33) describes a monotonous increase (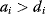 ), decrease (
), decrease (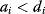 ), or a constant concentration (
), or a constant concentration (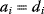 ). Therefore, the difference
). Therefore, the difference 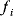 can be considered as the selective value (also called excess productivity).
can be considered as the selective value (also called excess productivity).
11.3.2.2 Selection at Constant Total Concentration of Self-Replicating Molecules
In Eq. (11.33), the dynamics of species 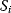 is independent of the behavior of the other species. However, selection will only happen if there is interaction between the species, leading to selective pressure. This is given if, for example, the number of building blocks (mononucleotides) is limited or if the concentration may not exceed a certain maximum. In the latter case, the total concentration of species can be kept constant by introducing a term describing elimination of supernumerary individuals or dilution by flow out of the considered volume. This is called selection at constant organization [97]. Assuming that the dilution rate is proportional to the actual concentration of the species, it follows that
is independent of the behavior of the other species. However, selection will only happen if there is interaction between the species, leading to selective pressure. This is given if, for example, the number of building blocks (mononucleotides) is limited or if the concentration may not exceed a certain maximum. In the latter case, the total concentration of species can be kept constant by introducing a term describing elimination of supernumerary individuals or dilution by flow out of the considered volume. This is called selection at constant organization [97]. Assuming that the dilution rate is proportional to the actual concentration of the species, it follows that
where again 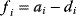 . Under the condition of constant total concentration
. Under the condition of constant total concentration  , it follows that
, it follows that
Since 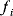 denotes the excess productivity of species
denotes the excess productivity of species 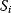 ,
, 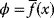 is the mean excess productivity. Introducing Eq. (11.35) into (11.34) yields the selection equations
is the mean excess productivity. Introducing Eq. (11.35) into (11.34) yields the selection equations
This is a system of coupled nonlinear ODEs. Nevertheless, it is easy to see that the concentrations increase over time for all species with 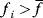 and that the concentrations decrease for all species with
and that the concentrations decrease for all species with 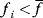 . The mean excess productivity
. The mean excess productivity  is, therefore, a selection threshold. (Equation 11.36) shows that the concentrations of species with high selective value increase with time. Hence, also the mean excess productivity increases according to Eq. (11.35). Successively, the selective values of more and more species become lower than
is, therefore, a selection threshold. (Equation 11.36) shows that the concentrations of species with high selective value increase with time. Hence, also the mean excess productivity increases according to Eq. (11.35). Successively, the selective values of more and more species become lower than  , their concentrations start to decrease, and eventually they die out. Finally, only the species with the highest initial selective value will survive, that is, the so-called master species.
, their concentrations start to decrease, and eventually they die out. Finally, only the species with the highest initial selective value will survive, that is, the so-called master species.
The explicit solution of the equation system (11.36) reads
The species with the highest excess productivity is the master sequence 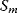 . In the current scenario, it will survive and the other species will become extinct.
. In the current scenario, it will survive and the other species will become extinct.
11.3.3 The Quasispecies Model: Self-Replication with Mutations
Up to now, we considered only the case of identical self-replication. However, mutations are an important feature of evolution. In the case of erroneous replication of sequence 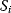 , a molecule of sequence
, a molecule of sequence 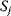 is produced that also belongs to the space of possible sequences. The right-hand side of Eq. (11.34) can be extended in the following way:
is produced that also belongs to the space of possible sequences. The right-hand side of Eq. (11.34) can be extended in the following way:
The expression 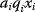 denotes the rate of identical self-replication, where
denotes the rate of identical self-replication, where 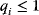 is the ratio of correctly replicated sequences. The quantity
is the ratio of correctly replicated sequences. The quantity 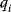 characterizes the quality of replication. The term
characterizes the quality of replication. The term 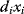 denotes again the decay rate of sequence
denotes again the decay rate of sequence 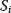 , and
, and 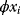 is the dilution term ensuring constant total concentration. The expression
is the dilution term ensuring constant total concentration. The expression 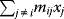 characterizes the synthesis rate of sequence
characterizes the synthesis rate of sequence 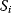 from other sequences
from other sequences 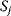 by mutation.
by mutation.
Since every replication results in the production of a sequence from the possible sequence space, the rate of erroneous replication of all sequences must be equal to the synthesis rate of sequences by mutation. Therefore,
Taking again into account the constant total concentration and Eq. (11.39) yields
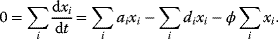
This way, Eq. (11.35) again holds for 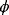 . The selection equation for self-replication with mutation reads
. The selection equation for self-replication with mutation reads
(Equation 11.41) differs from Eq. (11.36) by an additional coupling term that is due to the mutations. A high precision of replication requires small coupling constants 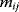 . For small
. For small 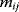 , one may expect similar behavior as in the case without mutation: the sequences with the high selective value will accumulate, whereas sequences with low selective value die out. But the existing sequences always produce erroneous sequences that are closely related to them and differ only in a small number of mutations. A species and its close relatives that appeared by mutation are referred to as quasispecies. Therefore, there is not selection of a single master species, but of a set of species. The species with the highest selective value and its close relatives form the master quasispecies distribution.
, one may expect similar behavior as in the case without mutation: the sequences with the high selective value will accumulate, whereas sequences with low selective value die out. But the existing sequences always produce erroneous sequences that are closely related to them and differ only in a small number of mutations. A species and its close relatives that appeared by mutation are referred to as quasispecies. Therefore, there is not selection of a single master species, but of a set of species. The species with the highest selective value and its close relatives form the master quasispecies distribution.
In conclusion, the quasispecies model does not predict the ultimate extinction of all but the fastest replicating sequence. Although the sequences that replicate more slowly cannot sustain their abundance level by themselves, they are constantly replenished as sequences that replicate faster mutate into them. At equilibrium, removal of slowly replicating sequences due to decay or outflow is balanced by replenishing, so that even relatively slowly replicating sequences can remain present in finite abundance.
Due to the ongoing production of mutant sequences, selection does not act on single sequences, but on so-called mutational clouds of closely related sequences, the quasispecies. In other words, the evolutionary success of a particular sequence depends not only on its own replication rate, but also on the replication rates of the mutant sequences it produces, and on the replication rates of the sequences of which it is a mutant. As a consequence, the sequence that replicates fastest may even disappear completely in selection–mutation equilibrium, in favor of more slowly replicating sequences that are part of a quasispecies with a higher average growth rate [98]. Mutational clouds as predicted by the quasispecies model have been observed in RNA viruses and in in vitro RNA replication [92,99].
11.3.3.1 The Genetic Algorithm
The evolution process in the quasispecies concept can also be viewed as a stochastic algorithm. This has been widely used as a strategy for a computer search algorithm. The evolution process produces consequent generations. We start with an initial population  at time
at time  . A new generation
. A new generation 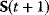 is obtained from the old one
is obtained from the old one 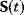 by random selection and mutation of sequences
by random selection and mutation of sequences 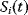 , where t corresponds to the generation number. Assume that all
, where t corresponds to the generation number. Assume that all 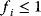 , which can be ensured by normalization. The model evolution process can be described formally in the following computer program-like manner.
, which can be ensured by normalization. The model evolution process can be described formally in the following computer program-like manner.
- Initialization.Form an initial population
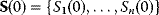 by choosing for every sequence
by choosing for every sequence 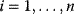 and for every position
and for every position 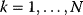 in the sequence randomly a symbol from the given alphabet (e.g., A, T, C, G, or “0” and “1”).
in the sequence randomly a symbol from the given alphabet (e.g., A, T, C, G, or “0” and “1”). - Sequence selection for the new generation.Select sequences by choosing randomly numbers
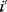 with the probability
with the probability 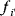 and adding a copy of the old sequence
and adding a copy of the old sequence 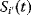 to the new population as
to the new population as 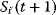 .
. - Control of population size.Repeat (ii) until the new population has reached size n of the initial population.
- Mutation.Change with a certain probability for every sequence
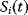 with
with 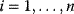 and for every position
and for every position 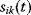 with
with 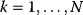 the current symbol to another symbol of the alphabet.
the current symbol to another symbol of the alphabet. - Recombination.As a possible extension to the previous steps, dice a number
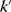 with
with 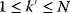 and two numbers
and two numbers 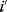 and
and 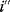 with
with 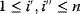 and then exchange positions
and then exchange positions 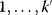 between sequences
between sequences 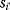 and
and 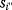 .
. - Iteration.Repeat steps (ii) to (iv) or (v) for successive time points.
The application of this algorithm allows for a visualization of the emergence of quasispecies and the master quasispecies distribution from an initial set of sequences during time.
11.3.3.2 Assessment of Sequence Length for Stable Passing On of Sequence Information
The number of possible mutants of a certain sequence depends on its length N. Since the alphabet for DNA molecules has four letters, each sequence has 3N neighboring sequences (mutants) with Hamming distance  . For mutants with arbitrary distance h, there are
. For mutants with arbitrary distance h, there are 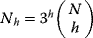 possibilities. Therefore, the number of sequences belonging to a quasispecies can be very high.
possibilities. Therefore, the number of sequences belonging to a quasispecies can be very high.
The quality measure q entering Eq. (11.38) for a sequence of length N can be expressed by the probability 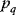 of correct replication of the individual nucleotides. Assuming that this probability is independent of position and type of the nucleotide, the quality measure reads
of correct replication of the individual nucleotides. Assuming that this probability is independent of position and type of the nucleotide, the quality measure reads
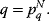
Mathematical investigation confirms that stable passing on of information is only possible if the value of the quality measure is above a certain threshold  . The parameter s is the relative growth rate of the master sequence, which is referred to as superiority. The generation of new species, and therefore development during evolution, is only possible with mutations. But too large mutation rates lead to destruction of already accumulated information. The closer q is to 1, the longer sequences may replicate in a stable manner. For the maximal length of a sequence, Eigen and coworkers [100] determined the relation
. The parameter s is the relative growth rate of the master sequence, which is referred to as superiority. The generation of new species, and therefore development during evolution, is only possible with mutations. But too large mutation rates lead to destruction of already accumulated information. The closer q is to 1, the longer sequences may replicate in a stable manner. For the maximal length of a sequence, Eigen and coworkers [100] determined the relation
During evolution, self-reproducing systems became more and more complex and the respective sequences became longer. Hence, the accuracy of replication also had to increase. Since the number of nucleotides in mammalian cells is about 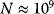 , Eq. (11.43) implies that the error rate per nucleotide is on the order of
, Eq. (11.43) implies that the error rate per nucleotide is on the order of 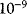 or lower. This is in good agreement with the accuracy of the replication in mammalian cells. Such a level of accuracy cannot be reached by simple self-replication based on chemical base pairing; it necessitates help from polymerases that catalyze the replication. For uncatalyzed replication of nucleic acids, the error rate is at least
or lower. This is in good agreement with the accuracy of the replication in mammalian cells. Such a level of accuracy cannot be reached by simple self-replication based on chemical base pairing; it necessitates help from polymerases that catalyze the replication. For uncatalyzed replication of nucleic acids, the error rate is at least 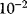 , which implies a maximal sequence length of
, which implies a maximal sequence length of 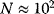 .
.
11.3.3.3 Coexistence of Self-Replicating Sequences: Complementary Replication of RNA
As we saw, only mutation and selection cannot explain the complexity of currently existing sequences and replication mechanisms. Their stable existence necessitates cooperation between different types of molecules besides their competition.
Consider the replication of RNA molecules, a mechanism used by RNA phages. The RNA replicates by complementary base pairing. There are two complementary strands, 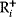 and
and  . The synthesis of one strand always requires the presence of the complementary strand, that is,
. The synthesis of one strand always requires the presence of the complementary strand, that is, 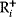 derives from
derives from 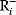 and vice versa. Thus, both strands have to cooperate for replication.
and vice versa. Thus, both strands have to cooperate for replication.
For a single pair of complementary strands, we have the following cartoon:

with the kinetic constants 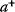 and
and 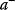 for replication and the kinetic constants
for replication and the kinetic constants 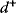 and
and 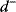 for degradation. Denoting the concentrations of
for degradation. Denoting the concentrations of 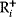 and
and  with
with 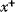 and
and  , respectively, the corresponding ODE system reads
, respectively, the corresponding ODE system reads
and in matrix notation
The eigenvalues of the Jacobian matrix (see Chapter 15) in Eq. (11.46) are
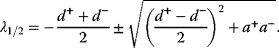
They are always real, since the kinetic constants have nonnegative values. While  (the “−” solution) is always negative,
(the “−” solution) is always negative,  (the “+” solution) may assume positive or negative values depending on the parameters:
(the “+” solution) may assume positive or negative values depending on the parameters:
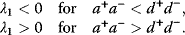
The solution of Eq. (11.46) reads
with concentration vector 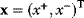 and eigenvectors
and eigenvectors 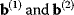 of the Jacobian.
of the Jacobian.
According to Eq. (11.49), a negative eigenvalue 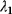 indicates the extinction of both strands
indicates the extinction of both strands 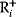 and
and 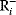 . For a positive eigenvalue
. For a positive eigenvalue 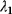 , the right-hand side of Eq. (11.49) comprises an exponentially increasing and an exponentially decreasing term, the first of which dominates for progressing time. Thus, the concentration of both strands rises exponentially. Furthermore, the growth of each strand depends not only on its own kinetic constants but also on the kinetic constants of the other strand.
, the right-hand side of Eq. (11.49) comprises an exponentially increasing and an exponentially decreasing term, the first of which dominates for progressing time. Thus, the concentration of both strands rises exponentially. Furthermore, the growth of each strand depends not only on its own kinetic constants but also on the kinetic constants of the other strand.
11.3.4 The Hypercycle
The hypercycle model describes a self-reproducing macromolecular system, in which RNAs and enzymes cooperate in the following manner. There are n RNA species; the ith RNA codes for the ith enzyme (i = 1, 2,…, n). The enzymes cyclically increase the replication rates of the RNAs, that is, the first enzyme increases replication rate of the second RNA, the second enzyme increases replication rate of the third RNA,…, and eventually the nth enzyme increases replication rate of the first RNA. In addition, the described system possesses primitive translation abilities, in that the information stored in RNA sequences is translated into enzymes, analogously to the usual translation processes in contemporary cells. M. Eigen and P. Schuster consider hypercycles as predecessors of protocells (primitive unicellular biological organisms). The action of the enzymes accelerates the replication of the RNA species and enhances the accuracy. Although the hypercycle concept may explain the advantages of the cooperation of RNA and enzymes, it cannot explain how it aroused during evolution. A special problem in this regard is the emergence of a genetic code.
The simplest cooperation between enzymes and nucleotide sequences is given when (i) the enzyme Ei is the translation product of the nucleic acid Ii and (ii) the enzyme Ei catalyzes primarily the identical replication of Ii as depicted below.
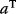 and
and 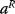 are the kinetic constants of translation and replication, respectively.
are the kinetic constants of translation and replication, respectively.
In general, a hypercycle involves several enzymes and RNA molecules. In addition, the mentioned macromolecules cooperate to provide primitive translation abilities; thus, the information encoded in RNA sequences is translated into enzymes, analogously to the usual translation processes in biological objects. The cyclic organization of the hypercycle shown in Figure 11.14 ensures its structural stability.
Figure 11.14 Schematic representation of the hypercycle consisting of RNA molecules Ii and enzymes Ei (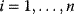 ). The ith RNA codes for the ith enzyme Ei. The enzymes cyclically increase RNA's replication rates, namely, E1 increases the replication rate of I2, E2 increases the replication rate of I3,…, and, eventually, En increases the replication rate of I1.
). The ith RNA codes for the ith enzyme Ei. The enzymes cyclically increase RNA's replication rates, namely, E1 increases the replication rate of I2, E2 increases the replication rate of I3,…, and, eventually, En increases the replication rate of I1.
In the following, we will consider the dynamics for the competition of two hypercycles of the type depicted in Eq. (11.50). Under the condition of constant total concentration and negligible decay of compounds, the ODE system for RNAs with concentrations 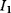 and
and 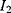 and enzymes
and enzymes 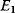 and
and 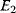 reads
reads
For the ODE system (11.51), it is assumed that all reactions follow simple mass action kinetics. Since the total concentrations of RNAs and enzymes are constant (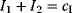 and
and 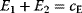 ), it follows for the dilution terms that
), it follows for the dilution terms that
There are three steady-state solutions of (Eqs. 11.51) and (11.52) with nonnegative concentration values. The following two steady states are stable:
and the third steady state is not stable (a saddle, see Chapter 15). In both stable steady states, one of the hypercycle survives and the other one dies out.
For competing hypercycles, the dynamics depends both on the individual kinetic parameters of the hypercycles and on the initial conditions. Both steady states are attractive for a certain region of the concentration space. If the initial state belongs to the basin of attraction of a steady state, the system will always move toward this state. The hypercycle with less favorable parameters and lower growth rate may survive if it is present with high initial concentration. Nevertheless, the steady state that ensures the survival of the hypercycle with higher growth rates has a larger basin of attraction, and this hypercycle may also win with a lower initial concentration.
The dependence on initial conditions in the selection of hypercycles is a new property compared with the identical or complementary self-replication without catalysts. If a new hypercycle would emerge due to mutation, the initial concentrations of its compounds are very low. It can only win against the other hypercycles if its growth rate is much larger. Even then it may happen that it becomes extinct – depending on the actual basins of attraction for the different steady states. This dependence causes that during evolution even nonoptimal systems may succeed if they are present in sufficiently high initial concentration. This is called once forever selection favoring the survival of systems that had by chance good conditions, independent of their actual quality. This behavior is quite different from the classical Darwinian selection process.
Even the nonoptimal hypercycles combine advantageously the properties of polynucleotides (self-reproduction) with the properties of enzymes (enhancement of speed and accuracy of polynucleotide replication). The cyclic organization of the hypercycle ensures its structural stability. This stability is even enhanced if hypercycles are organized in compartments [101]. This way, external perturbations by parasites can be limited and functionally advantageous mutations can be selected for.
In conclusion, one may state that the considered models, of course, can't explain the real-life origin process, because these models are based on various plausible assumptions rather than on a strong experimental evidence. Nevertheless, quasispecies and hypercycles provide a well-defined mathematical background for understanding the evolution of first molecular genetic systems. These models can be considered a step toward development of more realistic models.
11.3.5 Other Mathematical Models of Evolution: Spin Glass Model
The quasispecies concept as model of evolution (Section 11.3.3) implies a strong assumption: the Hamming distance between the particular and unique master sequences determines the selective value. Only one maximum of the selective value exists. Using the physical spin glass concept, we can construct a similar model, where the fitness function can have many local maxima.
D. Sherrington and S. Kirkpatrick [102,103] proposed a simple spin glass model to interpret the physical properties of the systems, consisting of randomly interacting spins. This well-known model can be described briefly as follows:
- There is a system s of spins
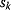 with
with 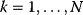 , where N is large (
, where N is large ( ). Each spin has a value of either 1 or
). Each spin has a value of either 1 or  .
. - Spins can exchange their values by random interactions, which lead to spin reversals.
- The energy
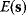 of the spin system is
of the spin system is
The values
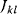 are elements of the exchange interaction matrix with normally distributed random values and a probability density PD of
are elements of the exchange interaction matrix with normally distributed random values and a probability density PD ofAccording to (Eqs. 11.54) and (11.55), the mean spin glass energy is zero,
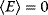 , and for one-spin reversal the mean square root of energy variation is equal to 2.
, and for one-spin reversal the mean square root of energy variation is equal to 2.
The interesting feature of the spin glass concept is the large number of local energy minima M, where a local energy minimum is defined as a state 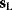 at which any one-spin reversal would increase the energy E. Furthermore, there is a global energy minimum
at which any one-spin reversal would increase the energy E. Furthermore, there is a global energy minimum 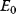 with
with 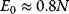 .
.
A spin glass model of evolution represents a model sequence as a vector 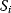 of spins and a population as a set
of spins and a population as a set 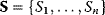 of n sequences. Each sequence has a selective value that depends on its energy:
of n sequences. Each sequence has a selective value that depends on its energy:
for a choice of 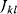 .
. 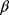 is a parameter for the selection intensity.
is a parameter for the selection intensity.
Spins 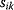 and
and 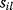 interact according to the interaction matrix
interact according to the interaction matrix 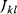 . The selective value of a sequence becomes maximal and its energy minimal when the combinations of spins in the sequences provide maximally cooperative interactions for a given matrix
. The selective value of a sequence becomes maximal and its energy minimal when the combinations of spins in the sequences provide maximally cooperative interactions for a given matrix 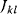 .
.
To this end, we consider again an evolutionary process with subsequent generations (compare with Section 11.3.3.1). The initial population is generated by chance. New generations are obtained by selection and mutation. Selection occurs with respect to the selective value defined in Eq. (11.56). Mutation is a sign reversal of a spin 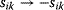 with certain probability P.
with certain probability P.
The evolutionary process can be followed by considering for successive generations Ti the number of sequences possessing certain energy 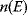 as illustrated in Figure 11.16.
as illustrated in Figure 11.16.
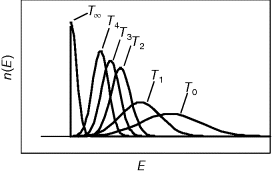
Figure 11.16 Schematic representation of sequence distributions  for subsequent generations
for subsequent generations  . For
. For  , the system is trapped into a local energy minimum
, the system is trapped into a local energy minimum 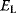 . The global energy minimum is
. The global energy minimum is 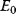 .
.
In the spin glass-type of evolution, the system converges to one of the local energy minima 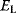 , which can be different for different runs of simulation.
, which can be different for different runs of simulation.
One may compare the evolutionary method with the sequential method of energy minimization, that is, consequent changes of symbols (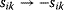 ) of one sequence and fixation of only successful reversals. The sequential search is computationally simpler than the evolutionary search. Nevertheless, the evolutionary search results on average in a deeper local energy minimum
) of one sequence and fixation of only successful reversals. The sequential search is computationally simpler than the evolutionary search. Nevertheless, the evolutionary search results on average in a deeper local energy minimum 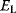 , because different valleys in energy landscape are examined in the evolution process simultaneously that are never reached in the sequential method. Thus, in the spin glass case, the evolutionary search has a certain advantage with respect to the sequential search: it results on average in the greater selective value.
, because different valleys in energy landscape are examined in the evolution process simultaneously that are never reached in the sequential method. Thus, in the spin glass case, the evolutionary search has a certain advantage with respect to the sequential search: it results on average in the greater selective value.
11.3.6 The Neutral Theory of Molecular Evolution
The neutral theory of molecular evolution introduced by Motoo Kimura [83] states that mutations are mostly neutral or only slightly disadvantageous. The historical background for this statement was the deciphering of the genetic code and the structure of DNA by Watson and Crick in 1953 [104–106] and the understanding of the principle of protein synthesis. In addition, the evolutionary rate of amino acid substitutions and the protein polymorphism were estimated. The assumption of neutrality of mutations agrees with the mutational molecular substitution rate observed experimentally and with the fact that the rate of the substitutions for the less biologically important part of macromolecules is greater than that for the active centers of macromolecules.
The mathematical models of the neutral theory are essentially stochastic; that is, a relatively small population size plays an important role in the fixation of the neutral mutations.
The features of the neutral selection can easily be explained using the game of neutral evolution.
Consider populations (of sequences or organisms or, in the following example, of balls) with a finite population size n. The rules describing the evolutionary process are the following:
- The population contains black and white balls with a total population size n.
- The next generation is created in two steps. First, all balls are duplicated preserving their color. A black ball has a black offspring, and a white ball a white one. Second, half of the population is removed irrespective of the “age” of a ball (i.e., whether it is an offspring or a parent ball) and with equal probability for black and white balls.
The state of the population is given by the number l of black balls. Consequently, there are  white balls. The evolution is characterized by the probability
white balls. The evolution is characterized by the probability 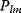 for the transition from a state with l black balls to a state with m black balls in the next generation.
for the transition from a state with l black balls to a state with m black balls in the next generation. 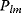 can be calculated by applying combinatorial considerations:
can be calculated by applying combinatorial considerations:
with 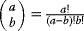 .
.
Possible evolutionary processes for a population of size 10 with initially 5 black and 5 white balls are illustrated in Figure 11.17.
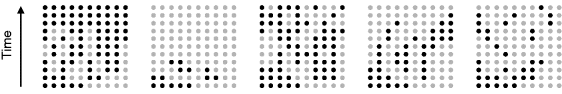
Figure 11.17 Representative runs for the game of neutral evolution. Starting with five black balls and five white balls at generation  (bottom line), the system converges within several generations to a state with either only black balls (left panel) or only white balls (second and fourth panels from left). For the third and fifth panels, the final state is not yet decided at generation
(bottom line), the system converges within several generations to a state with either only black balls (left panel) or only white balls (second and fourth panels from left). For the third and fifth panels, the final state is not yet decided at generation  .
.
The matrix 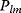 determines a random Markovian process, which can be considered as an example of a simple stochastic genetic process. For the behavior of this process, the following hold:
determines a random Markovian process, which can be considered as an example of a simple stochastic genetic process. For the behavior of this process, the following hold:
- The process always converges to one of the two states
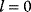 (only white balls) or
(only white balls) or 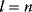 (only black balls).
(only black balls). - For large population size n, the characteristic number of generations needed to converge to either of these states is equal to
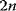 .
.
Thus, although this evolution is purely neutral (black and white balls have equal chances to survive), only one species is selected.
It can be questioned how progressive evolution is possible if molecular substitutions are neutral. To answer this question, M. Kimura used the concept of gene duplication developed by S. Ohno [107]. According to M. Kimura, gene duplications create unnecessary, surplus DNA sequences, which in turn drift further because of random mutations, providing the raw material for the creation of new, biologically useful genes.
The evolutionary concepts of the neutral theory came from interpretations of biological experiments; this theory was strongly empirically inspired. The other type of theory, a more abstract one, was proposed by Stuart A. Kauffman: NK automata or Boolean networks (see Section 7.1).
11.4 Evolutionary Game Theory
Evolutionary theory suggests that mutation and selection can increase the average fitness of a population in a given environment. However, evolution need not lead to an optimization: first, gene mutations can spread and be fixed in a population without providing a fitness advantage – a phenomenon called neutral evolution. Second, nonoptimal traits may arise as by-products of other traits that are under selective pressure. But the optimality assumption also ignores a third, very common phenomenon: by their very presence, organisms influence their environment and can change their own fitness landscape; trying to maximize fitness within such flexible fitness landscapes may lead, paradoxically, to an overall fitness decrease: if you change your own fitness landscape while running, you may run uphill, but in fact move down.
Let us illustrate this point with an example. Natural selection favors trees that grow higher and thereby receive more light than their neighbors. This makes the selection pressure on height even stronger, and trees need to allocate more and more of their resources to growth, forcing other trees to do the same. Eventually, they reach a limit where growing taller would consume more resources than it provides – but the tree population does not receive more light than in the beginning. This deadlock (in terms of cost efficiency) is hard to avoid because a population of small trees – which would entail the least effort for all individuals – can always be invaded by higher growing mutants or outcompeted by other species of taller trees and is therefore inherently unstable. Similar competition scenarios exist for other characteristics of plants, such as average foliage heights, shading and self-shading, temporal growth strategies, flowering times, or the fraction of biomass allocated to leafs, stems, branches, and roots [108]. Thinking in terms of optimality only, we cannot grasp such phenomena: instead, we need to describe how an optimization of individuals affects their environment and thus the conditions under which their own optimization takes place. Evolutionary game theory provides concepts for this.
11.4.1 Social Interactions
Notions of “social behavior” also play a role in systems biology [109], for instance, when describing the production of beneficial or toxic substances or the consumption of nutrients, which can be described as public goods. Growing on a common substrate, cells could push their metabolism toward either maximal production rates (product per time) or maximal efficiency (product yield per substrate molecule), which often oppose each other. Optimality studies would start from such objectives and study how they can be maximized, or which of them seem to play a role [110,111]. However, why certain objectives matter for selection depends on how individuals interact and how they shape their environment.
Some central aspects of evolution can be understood from population dynamics. Figure 11.18 shows a simple scheme of neutral evolution as described in Section 11.3.6: individuals produce offspring, but only some of the children reach an age at which they also have offspring themselves. In a simple stochastic model, each individual has a certain number of children:  children from the population are randomly chosen to form the next generation, and the entire process is iterated. In a scenario of neutral evolution, each individual has the same number of children and the sizes of subpopulations (blue and brown in Figure 11.18) will drift randomly. A new mutant has a fixation probability (probability to spread in the entire population) of
children from the population are randomly chosen to form the next generation, and the entire process is iterated. In a scenario of neutral evolution, each individual has the same number of children and the sizes of subpopulations (blue and brown in Figure 11.18) will drift randomly. A new mutant has a fixation probability (probability to spread in the entire population) of  , where
, where  is the population size. If subpopulations have different reproduction rates, those with more offspring are more likely to outcompete others.
is the population size. If subpopulations have different reproduction rates, those with more offspring are more likely to outcompete others.
Figure 11.18 Simple model of reproduction and selection. A population consists of two subtypes (blue and brown), which differ in their numbers of offspring. Generation 1 consists of two blue and two brown individuals. They grow up and have offspring, which form the next generation. In a stochastic model, the number of children depends on the type of individual, and new adults are picked randomly from the previous generation of children such that the total population size is preserved. For large populations, this scheme can be approximated by the deterministic replicator (equation 11.62).
As a further complication, we may assume that reproduction rates are not fixed, but depend on the subpopulation sizes. For instance, if survival and reproduction of individuals are affected by random encounters between individuals, each genotype's fitness will depend on the probability to meet individuals of certain genotypes, that is, on the relative subpopulation sizes.
With such a dependence, a mutant that exploits other individuals may lose its advantage when it becomes abundant. Examples are “selfish” virus mutants that cannot produce certain proteins and that instead use proteins produced by wild-type viruses in the same cell [112]. By reducing their genome size, the mutants reach a higher fitness. However, they also become dependent on the presence of wild-type viruses; as the mutant spreads in the population, its fitness decreases. In other cases, mutants may require a “critical mass” of individuals to become beneficial; such mutants may easily disappear before they can start spreading. This effect of a “critical mass” is why some evolutionary steps (e.g., the usage of L-amino acids as building blocks of proteins) could hardly be reverted, even in case such reversion was beneficial (“once forever selection”). Finally, different species can influence each other's evolution: pathogens, for instance, force the immune system to evolve, which in turn exerts a selection pressure on the pathogen strains.
11.4.2 Game Theory
Game theory [113] studies rational decisions in strategic games. In a two-player game, each player can choose between several strategies, and the payoff depends on the player's and the coplayer's choice. Both players try to maximize their own return. The payoffs are defined by a payoff matrix  : in a game with two strategies
: in a game with two strategies  and
and  , the payoffs for the first player read
, the payoffs for the first player read

Rows correspond to the first player's choice, and columns correspond to the choice of his/her coplayer. If a game is symmetric (as we assume for simplicity), the payoffs for the second player are given by the transposed matrix.
Hawk–Dove Game and Prisoner's Dilemma
Figure 11.19 shows two well-studied games, called hawk–dove game [114] (or “snow drift game”) and prisoner's dilemma. In both games, a cooperative strategy is confronted by an aggressive strategy. If both players act aggressively, both will lose. The payoff matrix of the hawk–dove game has the form
with positive parameters  and
and  . The matrix
. The matrix  contains the payoffs for player 1 (left player in Figure 11.19) and the game is symmetric, so the payoff matrix for player 2 is the transposed matrix
contains the payoffs for player 1 (left player in Figure 11.19) and the game is symmetric, so the payoff matrix for player 2 is the transposed matrix  .
.
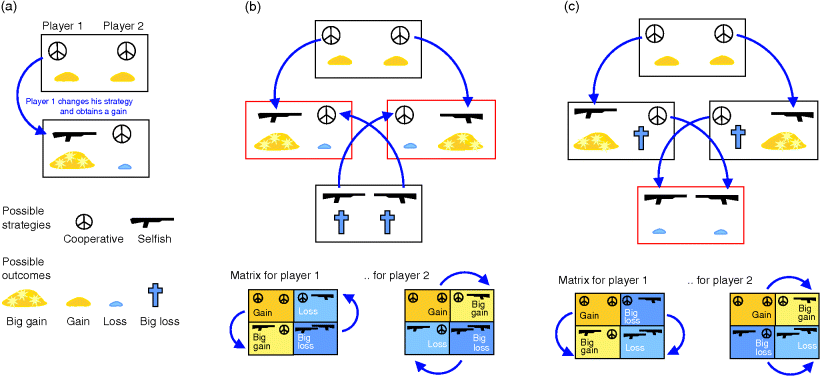
Figure 11.19 Hawk–dove game and prisoner's dilemma. (a) Scheme of a two-player game with two strategies (cooperative and selfish). Knowing the opponent's choice, a player may increase his/her payoff by a change of strategy (arrow). (b) Hawk–dove game. The four boxes illustrate all of the choices available to the two players (peaceful or aggressive behavior) and the possible payoffs. If none of the players can further increase his/her payoff, a stable situation – a so-called Nash equilibrium – is reached (red boxes). Tables at the bottom show the qualitative payoffs for both players as described by the payoff matrices. (c) Prisoner's dilemma, shown in the same way.
The elements of matrix (11.59) can be seen as expected payoffs in the following scenario: players compete for a common resource (for instance, food) and can choose between two strategies, termed “hawk” and “dove.” A hawk initiates aggressive behavior and maintains it until he/she either wins the conflict or loses and gets seriously injured. A dove retreats immediately if the other player is aggressive. Figure 11.19 illustrates the four types of encounters and the resulting payoffs: if two doves meet, the resource is shared equally and each player obtains 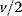 as a payoff. If a hawk meets a dove, the hawk obtains the full resource
as a payoff. If a hawk meets a dove, the hawk obtains the full resource  and the dove gets nothing. If a hawk meets another hawk, he/she wins (payoff
and the dove gets nothing. If a hawk meets another hawk, he/she wins (payoff  ) or becomes injured (cost
) or becomes injured (cost  ) with equal probabilities, so the expected payoff is
) with equal probabilities, so the expected payoff is 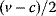 . In the hawk–dove game, the cost of injury
. In the hawk–dove game, the cost of injury  is assumed to exceed the value of the resource
is assumed to exceed the value of the resource  . The prisoner's dilemma has a similar structure: its two strategies “cooperate” and “defect” correspond to “dove” and “hawk,” and the same type of payoff matrix is used. However, we assume that
. The prisoner's dilemma has a similar structure: its two strategies “cooperate” and “defect” correspond to “dove” and “hawk,” and the same type of payoff matrix is used. However, we assume that 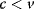 , which means that the best response to a defector is to defect as well.
, which means that the best response to a defector is to defect as well.
Nash Equilibrium
In both games, the optimal response to a coplayer's strategy can be seen from the payoff matrix. In the hawk–dove game, one should choose “hawk” if the coplayer plays “dove,” but “dove” if the coplayer plays “hawk.” Hence, players should always respond with the opposite strategy. In the prisoner's dilemma, this is different: here it is always best to defect, no matter which strategy the coplayer chooses. Paradoxically, the fact that both players choose their optimal strategies does not mean that the outcome is good for them. To predict the outcome, we need to search for states in which none of the players can improve his/her payoff by a change of strategy. Such a state is called a Nash equilibrium. The Nash equilibria for the above games are (1: hawk/2: dove) or (1: dove/2: hawk) for the hawk–dove game and (1: defect/2: defect) for the prisoner's dilemma. Once a Nash equilibrium has been reached, none of the players has an incentive to deviate from his/her strategy, even if another state (e.g., 1: cooperate/2: cooperate) would provide higher payoffs for both players. In the prisoner's dilemma, this leads to the paradoxical situation that both players end up in the unfavorable selfish state because all other states (including the favorable “cooperative” state) would be locally nonoptimal for one of the players. Even if both players had an agreement to choose “cooperate,” the agreement itself would be threatened because of the initial advantage of defecting.
Repeated Games
So far, we assumed that a game is played only once. Additional complexity emerges in sequential games, in which games are played repeatedly and players can respond to the coplayer's behavior in previous rounds. A successful sequential strategy for the repeated prisoner's dilemma is “tit for tat,” a form of reciprocal altruism: the player plays “cooperate” in the first round, and then responds in kind to each of the coplayer's previous actions. Confronted with itself, this strategy is able to maintain the beneficial cooperate/cooperate state, but in contrast to the pure “cooperate” strategy, it also contains a threat against strategies that would attempt to exploit it.
11.4.3 Evolutionary Game Theory
Game theory was originally developed to study rational decisions based on an intention to maximize one's own profit. However, later it became clear that the same formalism also applies to the evolution of biological traits, without any reference to conscious decisions. Evolutionary game theory [115] describes this evolution in population models, assuming that evolutionary fitness depends on the success in hypothetical games. Strategies are not chosen by rational consideration, but genetically determined, and their prevalence in a population changes dynamically, depending on how they perform in the game. The language of game theory can be helpful to describe such processes, but it is not absolutely necessary: the same results can also be obtained from population dynamics models without an explicit usage of game theoretical terminology.
In a common scenario, individuals encounter each other randomly. Depending on their genotypes, they play different strategies and the obtained average payoffs determine how fast each genotype will replicate. Given a two-player game, we can define a frequency-dependent fitness for each strategy. Assume two subpopulations playing strategies  and
and 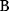 with respective frequencies
with respective frequencies 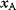 and
and 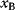 , satisfying
, satisfying 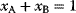 ; with the payoff matrix
; with the payoff matrix  , an individual of type A will obtain an expected payoff
, an individual of type A will obtain an expected payoff
In a direct competition, successful genotypes will replicate faster and spread in the population. However, this will change the frequency of strategies, which then, following Eq. (11.60), affects the fitness functions. For example, a strategy may first spread, but then impair its own success at higher frequencies.
11.4.4 Replicator Equation for Population Dynamics
Population dynamics can be described by different mathematical frameworks, including deterministic and stochastic approaches and models with spatial structure (e.g., partial differential equations or cellular automata; see Section 7.3.1). In the following, we employ the deterministic replicator equation, a rate equation for the relative subpopulation sizes in a well-mixed population.
The Replicator Equation
In the replicator equation, the reproduction rate of a subpopulation is given by a baseline rate plus an average payoff from pairwise random encounters between individuals. The probabilities to meet members of different subpopulations are given by their frequencies 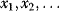 , which sum up to 1. When individuals of type
, which sum up to 1. When individuals of type  meet individuals of type
meet individuals of type  , they obtain a payoff
, they obtain a payoff 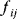 . Such encounters happen with probability
. Such encounters happen with probability 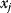 , so the average payoff of strategy
, so the average payoff of strategy 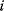 is
is
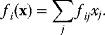
In a simple deterministic model, the frequencies 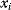 evolve in time according to a selection equation
evolve in time according to a selection equation
called the replicator equation. The term 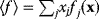 denotes the current average fitness of the population. Subtracting it in Eq. (11.62) ensures that the frequencies remain normalized (i.e.,
denotes the current average fitness of the population. Subtracting it in Eq. (11.62) ensures that the frequencies remain normalized (i.e., 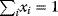 ) and that the baseline fitness value cancels out.
) and that the baseline fitness value cancels out.
A competition between subpopulations  and
and 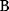 can lead to different types of dynamics, including sustained oscillations (see Section 11.4.6) and convergence to a fixed point. A subpopulation frequency
can lead to different types of dynamics, including sustained oscillations (see Section 11.4.6) and convergence to a fixed point. A subpopulation frequency 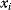 remains constant if
remains constant if
that is, if the strategy has died out (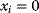 ) or if its fitness
) or if its fitness 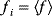 matches the average fitness of the entire population. Thus, in a fixed point of Eq. (11.62), all surviving subpopulations have the same fitness – given the subpopulation frequencies in this state.
matches the average fitness of the entire population. Thus, in a fixed point of Eq. (11.62), all surviving subpopulations have the same fitness – given the subpopulation frequencies in this state.
Outcomes of Frequency-Dependent Selection
The number and types of fixed points of Eq. (11.62) depend on the payoff matrix. There are different cases: (i) A dominant strategy is a best reply to itself and to the other strategy (e.g., “defect” in the prisoner's dilemma); it always wins, that is, its frequency will approach 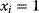 . (ii) Coexistence: if two strategies are best replies to each other, they can coexist in stable proportions (like, for instance, in the hawk–dove game). (iii) Bistability: if each strategy is a best reply to itself, many individuals of the other strategy would be needed to undermine it. In this bistable case, one of the strategies eventually wins (
. (ii) Coexistence: if two strategies are best replies to each other, they can coexist in stable proportions (like, for instance, in the hawk–dove game). (iii) Bistability: if each strategy is a best reply to itself, many individuals of the other strategy would be needed to undermine it. In this bistable case, one of the strategies eventually wins (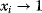 ), and who the winner is depends on their initial frequencies. Strategy
), and who the winner is depends on their initial frequencies. Strategy 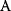 is called risk-dominant if it has the larger basin of attraction (
is called risk-dominant if it has the larger basin of attraction (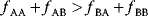 ). Such a strategy will win if both strategies start at equal subpopulation frequencies. (iv) Neutrality: both strategies have the same expected payoff independently of the subpopulation frequencies: in terms of fitness, they are effectively identical. According to the deterministic (equation 11.62), the subpopulation sizes will be constant in time; in stochastic population models, they would drift randomly.
). Such a strategy will win if both strategies start at equal subpopulation frequencies. (iv) Neutrality: both strategies have the same expected payoff independently of the subpopulation frequencies: in terms of fitness, they are effectively identical. According to the deterministic (equation 11.62), the subpopulation sizes will be constant in time; in stochastic population models, they would drift randomly.
Figure 11.20 shows simulations for a payoff matrix (11.59) with values 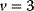 ,
, 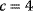 ((a), hawk–dove game) and
((a), hawk–dove game) and 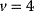 ,
, 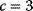 ((b), prisoner's dilemma). For each type of game, curves with different initial frequencies between 0.1 and 0.9 are shown. The hawk–dove game leads to a coexistence at a frequency
((b), prisoner's dilemma). For each type of game, curves with different initial frequencies between 0.1 and 0.9 are shown. The hawk–dove game leads to a coexistence at a frequency 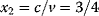 of hawks; in the prisoner's dilemma, the cooperative strategy always dies out. In a third game (Figure 11.20c), with an identity payoff matrix
of hawks; in the prisoner's dilemma, the cooperative strategy always dies out. In a third game (Figure 11.20c), with an identity payoff matrix 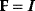 , each strategy is a best response to itself. The dynamics is bistable, so different initial conditions can lead to success of either
, each strategy is a best response to itself. The dynamics is bistable, so different initial conditions can lead to success of either 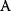 or
or 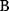 .
.
Figure 11.20 Population dynamics simulated by the replicator (equation 11.62). Two populations playing different strategies are represented by their time-dependent frequencies (normalized population sizes  ). The curves show simulation results starting from different initial frequencies. (a) The hawk–dove game leads to coexistence of individual strategies. (b) In the prisoner's dilemma, the strategy “defect” dominates “cooperate,” which eventually dies out. (c) Two evolutionarily stable strategies forming a bistable pair: who the winner is depends on the initial frequencies.
). The curves show simulation results starting from different initial frequencies. (a) The hawk–dove game leads to coexistence of individual strategies. (b) In the prisoner's dilemma, the strategy “defect” dominates “cooperate,” which eventually dies out. (c) Two evolutionarily stable strategies forming a bistable pair: who the winner is depends on the initial frequencies.
11.4.5 Evolutionarily Stable Strategies
A basic type of question in evolutionary game theory is whether some population can be invaded by mutants playing a different strategy. If the resident strategy dominates all possible mutant strategies, it will outcompete any mutants and is called unbeatable. However, strategies need not be dominant to persist in evolution. The weaker concept of evolutionarily stable strategies (ESS) takes into account that a mutant initially appears in small numbers. Strategy 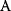 is evolutionary stable if competing strategies
is evolutionary stable if competing strategies 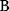 , starting at a small frequency, cannot invade a population of type
, starting at a small frequency, cannot invade a population of type 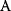 . There are two ways by which
. There are two ways by which 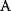 can be evolutionary stable: either
can be evolutionary stable: either  dominates
dominates  or
or 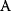 and
and 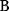 form a bistable pair and the mutant subpopulation does not reach the critical size for taking over the population. An evolutionarily stable strategy, confronted with itself, is always a Nash equilibrium. However, the opposite does not hold: a strategy may form a Nash equilibrium with itself, but may still be invaded by new mutants, so the resident strategy is not evolutionarily stable.
form a bistable pair and the mutant subpopulation does not reach the critical size for taking over the population. An evolutionarily stable strategy, confronted with itself, is always a Nash equilibrium. However, the opposite does not hold: a strategy may form a Nash equilibrium with itself, but may still be invaded by new mutants, so the resident strategy is not evolutionarily stable.
What is the mathematical criterion for evolutionarily stable strategies? Assume that 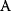 is the strategy of the resident population and
is the strategy of the resident population and 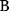 is a possible mutant strategy. With relative frequencies
is a possible mutant strategy. With relative frequencies 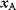 and
and 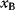 , the average payoffs for individuals of type
, the average payoffs for individuals of type  and
and  read
read
By definition, 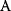 is evolutionarily stable if it cannot be invaded by a few individuals of type
is evolutionarily stable if it cannot be invaded by a few individuals of type 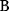 : thus,
: thus, 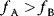 must hold for small frequencies
must hold for small frequencies 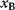 . If
. If 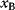 is very small, an individual (of type A or B) will almost never encounter an individual of type B. Therefore, we can disregard the second terms in (11.64) and obtain the simple condition
is very small, an individual (of type A or B) will almost never encounter an individual of type B. Therefore, we can disregard the second terms in (11.64) and obtain the simple condition 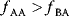 . However, in the case of equality (
. However, in the case of equality (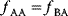 ), the rare encounters with
), the rare encounters with 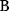 individuals will play a role, and we must additionally require that
individuals will play a role, and we must additionally require that 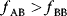 . Thus, an evolutionarily stable strategy
. Thus, an evolutionarily stable strategy  must perform better than
must perform better than  when encountering individuals of type
when encountering individuals of type  ; if it performs only equally well, it must at least perform better in encounters with individuals of type
; if it performs only equally well, it must at least perform better in encounters with individuals of type  .
.
11.4.6 Dynamical Behavior in the Rock–Scissors–Paper Game
Frequency-dependent selection can lead not only to stationary states in population dynamics, but also to sustained dynamic behavior [116] as in the following example. The rock–scissors–paper game consists of the three strategies rock ( ), paper (
), paper ( ), scissors (
), scissors ( ), which beat each other in a circle (Figure 11.21a):
), which beat each other in a circle (Figure 11.21a): 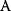 dominates
dominates 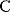 ,
, 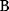 dominates
dominates  , and
, and 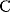 dominates
dominates 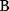 . This game can be used to describe an arms race between three strains of E. coli bacteria [117]. A strain
. This game can be used to describe an arms race between three strains of E. coli bacteria [117]. A strain  (“killer”) produces the toxin colicin against other bacteria, together with an immunity protein to protect itself. Strain
(“killer”) produces the toxin colicin against other bacteria, together with an immunity protein to protect itself. Strain  (“immune”) produces the immunity protein, but not the toxin, and strain
(“immune”) produces the immunity protein, but not the toxin, and strain 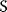 (“sensitive”) produces neither of them. In pairwise competitions,
(“sensitive”) produces neither of them. In pairwise competitions, 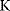 kills
kills 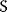 with its toxin,
with its toxin, 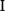 outcompetes
outcompetes 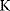 because it does not produce toxin and saves resources for growth, and
because it does not produce toxin and saves resources for growth, and 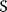 outcompetes
outcompetes 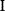 because it saves the effort of producing the immunity protein.
because it saves the effort of producing the immunity protein.

Figure 11.21 Population dynamics in the rock–scissors–paper game. (a) Each strategy (A: rock; B: paper; C: scissors) beats the previous one in a circle (arrowheads point to the winning strategy). (b) Simulated dynamics based on the replicator equation. The population frequencies vary periodically. Depending on the specific payoff matrix chosen, the subpopulations replace each other periodically (top) or converge to a stable mixture (bottom).
In a direct competition, each strategy can invade the previous one, so the subpopulation sizes will oscillate. Figure 11.21 shows dynamic behavior resulting from two different payoff matrices
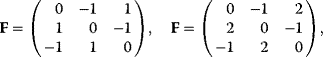
which lead, respectively, to sustained and damped oscillations. Ongoing arms races have been suggested [118] as an explanation for the huge diversity found in microbial communities. At first sight, such diversity would contradict the competitive exclusion principle, which states that the number of species surviving in a fixed environment must equal the number of limited resources (“paradox of the plankton”) [119].
11.4.7 Evolution of Cooperative Behavior
Many types of behavior in people, animals, and even in microbes can be seen as forms of cooperation. Formally, cooperation can be defined as follows: a cooperator 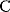 pays a cost
pays a cost  for another individual to receive a benefit
for another individual to receive a benefit 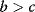 . A defector
. A defector  does not deal out benefits, but will receive benefits from cooperators. The payoff matrix
does not deal out benefits, but will receive benefits from cooperators. The payoff matrix
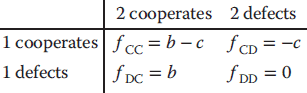
shows that defectors will dominate cooperators because 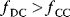 and
and 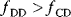 . In this basic scenario, cooperation will not be evolutionarily stable because
. In this basic scenario, cooperation will not be evolutionarily stable because 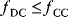 can never be satisfied. The prediction would be that evolution selects for noncooperative, “selfish” traits. However, various examples of cooperation have evolved, and evolutionary theory has found ways to explain this. In fact, cooperation can emerge in a number of specific evolution scenarios [120], which we shall now discuss.
can never be satisfied. The prediction would be that evolution selects for noncooperative, “selfish” traits. However, various examples of cooperation have evolved, and evolutionary theory has found ways to explain this. In fact, cooperation can emerge in a number of specific evolution scenarios [120], which we shall now discuss.
Kin Selection
Altruism toward one's own genetic relatives can evolve by a mechanism called kin selection. To see how this works, let us consider a gene in a single individual: for the gene's long-term reproduction, it does not matter whether it is reproduced via its “host” individual or via other individuals that carry the same gene. This second possibility provides a selection advantage to genes that promote altruistic behavior. If two individuals X and Y are relatives, there is a chance  that an arbitrarily chosen gene of X is shared by Y because of common inheritance. This so-called coefficient of relatedness has a value of
that an arbitrarily chosen gene of X is shared by Y because of common inheritance. This so-called coefficient of relatedness has a value of 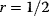 for siblings and
for siblings and 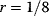 for cousins. Altruistic behavior toward relatives can help the relatives reproduce, and thereby reproduce some shared genes: therefore, the payoff (seen from the perspective of a single gene) is increased by the amount of the coplayer's payoff (given by the transposed payoff matrix), multiplied by
for cousins. Altruistic behavior toward relatives can help the relatives reproduce, and thereby reproduce some shared genes: therefore, the payoff (seen from the perspective of a single gene) is increased by the amount of the coplayer's payoff (given by the transposed payoff matrix), multiplied by  . According to the modified payoff matrix
. According to the modified payoff matrix
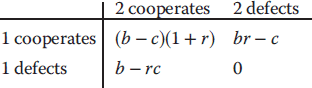
kin selection will take place (i.e., altruism toward kins will be evolutionarily stable) if 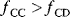 , that is,
, that is, 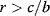 . J.B.S. Haldane has expressed this criterion, called Hamilton's rule, as “I'd lay down my life for two brothers or eight cousins.” The higher the typical coefficient of relatedness in encounters (large
. J.B.S. Haldane has expressed this criterion, called Hamilton's rule, as “I'd lay down my life for two brothers or eight cousins.” The higher the typical coefficient of relatedness in encounters (large  ), the more easily the rule can be satisfied. Hamilton's rule has been studied in detail with bacteria, where cooperators produce a beneficial substance (an activator for the expression of an antibiotic resistance gene), while defectors only benefit from it [121].
), the more easily the rule can be satisfied. Hamilton's rule has been studied in detail with bacteria, where cooperators produce a beneficial substance (an activator for the expression of an antibiotic resistance gene), while defectors only benefit from it [121].
Cooperation with relatives – and therefore kin selection – requires kin recognition. The plant Cakile edentula, for instance, grows stronger roots when it shares a pot with other plants, thus competing with them for water and nutrients. However, when groups of siblings share one pot, they grow weaker roots [122]. This suggests two things: that competition among siblings is weaker, and that siblings can recognize each other, possibly by sensing chemicals via their roots.
Reciprocity and Group Selection
Cooperation can also evolve if individuals recompense each other for earlier cooperative behavior: different scenarios presuppose that individuals can remember earlier encounters (direct reciprocity), know the reputation of other individuals (indirect reciprocity), or interact locally with neighbors in a network (network reciprocity). In spatially structured models, cooperators can grow in local clusters, which makes them less prone to exploitation by defectors. Moreover, cooperative behavior can evolve by a mechanism called group selection, which involves two levels of competition: individuals compete within groups, and groups compete with each other. In this scenario, selfish behavior within the group may be selected against because it can lead to extinction of the entire group and, thus, of the selfish individual itself.
In a group selection model by Nowak [120], individuals obtain a fitness value  from encounters within their group and replicate with a rate
from encounters within their group and replicate with a rate 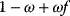 , where
, where 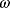 is a parameter describing the intensity of selection. Groups can only grow to a maximum size of
is a parameter describing the intensity of selection. Groups can only grow to a maximum size of  – when a larger size is reached, one of the two things will happen: either a randomly selected individual from the group dies (with probability
– when a larger size is reached, one of the two things will happen: either a randomly selected individual from the group dies (with probability 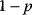 ) or the group is split into two and another randomly selected group dies (with probability
) or the group is split into two and another randomly selected group dies (with probability 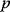 ). Due to the second possibility, groups must replicate fast to evade extinction.
). Due to the second possibility, groups must replicate fast to evade extinction.
In this model, defectors have a direct growth advantage within their own group, but this advantage is counterbalanced by the risk of killing their group as a result of their selfish behavior. If  denotes the size at which groups are split and
denotes the size at which groups are split and  is the total number of groups, then in cases of weak selection
is the total number of groups, then in cases of weak selection  and small splitting probability
and small splitting probability  , we obtain the effective payoff matrix [120]
, we obtain the effective payoff matrix [120]
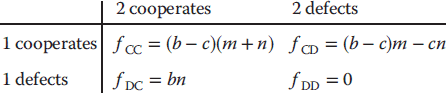
Again, cooperation becomes evolutionarily stable if 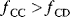 , in this case if
, in this case if 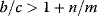 . This criterion is more likely to be satisfied when groups are small (small
. This criterion is more likely to be satisfied when groups are small (small  ) and numerous (large
) and numerous (large 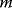 ).
).
11.4.8 Compromises between Metabolic Yield and Efficiency
In Section 11.1, we saw that choices between high-yield and low-yield metabolic strategies can be predicted from optimality considerations, assuming that protein resources are allocated in a way that maximizes cell growth. Which of the strategies is optimal depends on several factors, in particular nutrient supply and the extra protein cost of the high-yield strategy [123]. However, a fundamental problem remained open: with a low-yield strategy, cell populations grow to smaller sizes and are less sustainable because they deplete the nutrients in their environment. But still, in a direct competition with efficient cells, this strategy brings a growth advantage. If this is true, how can sustainable, high-yield strategies, in which growth is deliberately restricted, evolve at all? The existence of multicellular organisms, which strictly control cell growth, shows that this must be possible.
High-Yield and Low-Yield Fluxes Seen as Strategies
Pfeiffer et al. [124] applied a game theoretical perspective to the study of high-flux or high-yield strategies in metabolism. Instead of using a notion of “optimal” strategies, they asked whether each of the strategies can be evolutionarily stable. Since high-yield strategies spare resources for other cells, they can be seen as “cooperative,” while low-yield strategies can be seen as “selfish.” The competition between selfish and cooperative individuals for shared nutrients leads to a dilemma called “tragedy of the commons”. If respirators and fermenters grow separately on a constant sugar supply, the respirators will grow to a higher cell density than the fermenters, so their fitness as a population will be higher. However, in a direct competition for sugar, respirators are outperformed by fermenters, so their population may be invaded by fermenting mutants. Only fermentation is evolutionarily stable in this scenario.
Nevertheless, respiration has evolved. Unicellular organisms, which compete for external resources, tend to use fermentation, while cells in higher animals tend to use respiration, with cancer cells being a prominent exception (Warburg effect) [125]. In a multicellular organism, ingested nutrients are shared among cells, so there is no competition for food: instead, the well-being of the entire organism requires cooperative behavior. Since cells in an organism are genetically identical, this can be seen as an example of Hamilton's rule.
Pfeiffer et al. suggested that the evolution of multicellularity, which has appeared at least 10 times independently in the tree of life, may have been triggered by a competition between fermenting and respiring cells [124]. When oxygen accumulated in the atmosphere as a waste product of photosynthesis, respiration arose as a new, efficient energy source. However, as a downside of their high yield, respiring cells would have grown more slowly than the existing fermenters and would have been outcompeted. This dilemma could have been solved by group selection: the formation of cell aggregates may have enabled respirators to evade competition and, thus, to benefit from their new energy source.
Spatial Structure Can Promote Cooperative Behavior
The evolution of yield-efficient strategies can be favored by spatially structured environments. This has been shown for bacteria undergoing an evolution in the laboratory. In a normal serial dilution experiment, cells are suspended in a growth medium and share the same resources; this leads to a selection for fast-growing cells. To create an incentive for yield-efficient behavior, Bachmann et al. grew Lactococcus lactis bacteria in an emulsion of small water droplets in oil, each containing only a few cells [126] (see Figure 11.22). In each dilution step, the emulsion was broken, cells were diluted in fresh medium, and a new emulsion was prepared. The shared resources within droplets lead to an evolution toward yield-efficient behavior, namely, mixed acid fermentation (producing three molecules of ATP per glucose molecule) instead of lactate excretion (producing only two molecules of ATP, but at a faster flux), as well as a measurable higher biomass yield, but also smaller cell sizes.
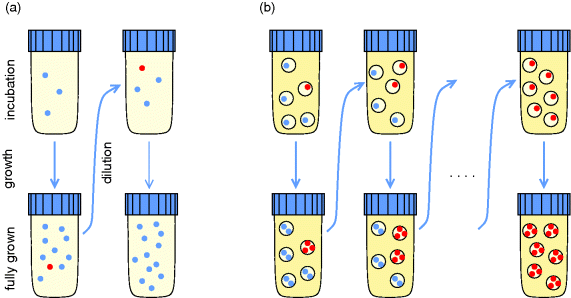
Figure 11.22 A serial dilution experiment in which yield-efficient behavior can evolve. Slowly growing bacteria mutants with a high ATP yield (red) compete with the low-yield, fast-growing wild-type bacteria (blue). (a) In a cell suspension, mutants would be outcompeted due to their slower growth. (b) In a water-in-oil emulsion (bacteria living within small droplets), the mutants can replicate to larger numbers within droplets, allowing them to take over the population. (Redrawn from Ref. [126].)
Exercises
Section 11.1
- 1) ATP production in glycolysis. A glycolytic pathway converts glucose into lactate and effectively turns two ADP molecules into two ATP molecules. (a) Is this process thermodynamically feasible? Assume a decrease of Gibbs free energy by 205 kJ mol−1 for the conversion of glucose into two lactate molecules and an increase of 49 kJ mol−1 for each ADP molecule converted to ATP. (b) Imagine alternative variants of glycolysis that also convert glucose into lactate, but produce different numbers of ATP molecules. What are the minimal and maximal numbers possible? (c) Assume, for simplicity, that the glycolytic flux is proportional to the total decrease of Gibbs free energy. Which number of ATP molecules produced would lead to (i) a maximal rate of ATP production or (ii) maximal yield efficiency, that is, maximal ATP production per amount of glucose consumed?
Section 11.2
- 2) Calculate the steady-state flux for an unbranched metabolic pathway with four reactions. Use formula (4.15). Use the parameter and concentration values
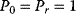 ,
, 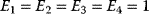 ,
, 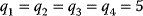 , and
, and 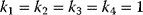 .
. - 3) Determine the maximal steady-state flux for the case where the enzyme concentrations may vary in the range from 0 to 2. Compare with the steady-state flux for the case where all enzyme concentrations are equal to 2.
- 4) Repeat Exercise 11.3 by applying the conditions (i) that the sum of enzyme concentrations is 8 and (ii) all individual enzyme concentrations are positive.
- 5) Calculate optimal enzyme concentrations according to formula (11.19) and the resulting steady-state flux.
- 6) Consider the temporal regulation of enzymatic pathways. Calculate the transition time for the case where (i) the enzyme concentrations are constant and (ii) the pathway contains only one reaction,
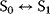 , and the temporal change of the reaction is given by the decay of
, and the temporal change of the reaction is given by the decay of 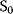 .
.
Note: First integrate the appropriate set of equations for the dynamics of 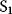 (Eq. (11.27) and then introduce the result into Eq. (11.28).
(Eq. (11.27) and then introduce the result into Eq. (11.28).
Repeat for a pathway consisting of two consecutive enzymes.
Section 11.3
- 7) Consider the case of selection under constant total concentration. Could you predict which species will survive if you would describe the system with a stochastic approach?
- 8) Can you find general conditions under which hypercycles become extinct?
- 9) Compute steady states for a system of three competing hypercycles (choose reasonable parameter values).
Section 11.4
- 10) Fixed point of the replicator equation. Consider the deterministic replicator equation with a fitness function defined by the hawk–dove game (1: dove; 2: hawk). Show that the stationary ratio x1/x2 of subpopulation frequencies is given by (c − v)/v.
- 11) Maximal efficiency or maximal rate? Consider the following model of competition for a common resource [127]: several microbial strains (denoted by i) compete for a resource S (with concentration s), which arrives at a constant rate v. The consumption rates
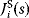 per cell and the efficiencies
per cell and the efficiencies 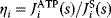 differ between the strains. Cells replicate at a rate proportional to their ATP production and die at a constant rate, with the same constants for all strains. Show that (a) for a single strain (no competition with other strains), the steady-state population size is proportional to the efficiency ηi of ATP production and that (b) If several strains compete for the resource, a strain's success depends on the rate
differ between the strains. Cells replicate at a rate proportional to their ATP production and die at a constant rate, with the same constants for all strains. Show that (a) for a single strain (no competition with other strains), the steady-state population size is proportional to the efficiency ηi of ATP production and that (b) If several strains compete for the resource, a strain's success depends on the rate 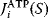 of ATP production.
of ATP production.
References
- 1. Dekel, E. and Alon, U. (2005) Optimality and evolutionary tuning of the expression level of a protein. Nature, 436, 588–692.
- 2. Alon, U. (2003) Biological networks: the tinkerer as an engineer. Science, 301, 1866–1867.
- 3. Holland, J.H. (1975) Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence, University of Michigan Press, Ann Arbor, MI.
- 4. Kirschner, M. and Gerhart, J. (1998) Evolvability. Proc. Natl. Acad. Sci. USA, 95 (15), 8420–8427.
- 5. Kashtan, N., Noor, E., and Alon, U. (2007) Varying environments can speed up evolution. Proc. Natl. Acad. Sci. USA, 104 (34), 13711–13716.
- 6. Barve, A. and Wagner, A. (2013) A latent capacity for evolutionary innovation through exaptation in metabolic systems. Nature, 500, 203–206.
- 7. Wolff, J. (1892) Das Gesetz der Transformation der Knochen, Verlag von August, Berlin.
- 8. Frost, H.M. (2001) From Wolff's law to the Utah paradigm: insights about bone physiology and its clinical applications. Anat. Rec., 262, 398–419.
- 9. Robling, A.G., Castillo, A.B., and Turner, C.H. (2006) Biomechanical and molecular regulation of bone remodeling. Annu. Rev. Biomed. Eng., 8, 455–498.
- 10. Huiskes, R. et al. (2000) Effects of mechanical forces on maintenance and adaptation of form in trabecular bone. Nature, 405, 704–706.
- 11. Heinrich, R. and Rapoport, T.A. (2005) Generation of nonidentical compartments in vesicular transport systems. J. Cell Biol., 168, 271–280.
- 12. Heckmann, D., Schulze, S., Denton, A., Gowik, U., Westhoff, P., Weber, A.P.M., and Lercher, M.J. (2013) Predicting C4 photosynthesis evolution: modular, individually adaptive steps on a Mount Fuji fitness landscape. Cell, 153 (7), 1579–1588.
- 13. Chait, R., Craney, A., and Kishony, R. (2007) Antibiotic interactions that select against resistance. Nature, 446, 668–671.
- 14. Gomes, A.L.C., Galagan, J.E., and Segrè, D. (2013) Resource competition may lead to effective treatment of antibiotic resistant infections. PLoS One, 8 (12), e80775.
- 15. Trigg, G.L. (2005) Mathematical Tools for Physicists, Wiley-VCH Verlag GmbH, Weinheim.
- 16. Feynman, R. (1985) QED: The Strange Theory of Light and Matter, Princeton University Press, Princeton, NJ.
- 17. Fleming, R.M.T., Maes, C.M., Saunders, M.A., Ye, Y., and Palsson, B.Ø. (2012) A variational principle for computing nonequilibrium fluxes and potentials in genome-scale biochemical networks. J. Theor. Biol., 292, 71–77.
- 18. Eames, M. and Kortemme, T. (2012) Cost–benefit tradeoffs in engineered lac operons. Science, 336, 911–915.
- 19. Reich, J.G. (1983) Zur Ökonomie im Proteinhaushalt der lebenden Zelle. Biomed. Biochim. Acta, 42 (7/8), 839–848.
- 20. Liebermeister, W., Klipp, E., Schuster, S., and Heinrich, R. (2004) A theory of optimal differential gene expression. Biosystems, 76, 261–278.
- 21. Kalisky, T., Dekel, E., and Alon, U. (2007) Cost–benefit theory and optimal design of gene regulation functions. Phys. Biol., 4, 229–245.
- 22. Dill, K.A., Ghosh, K., and Schmit, J.D. (2011) Physical limits of cells and proteomes. Proc. Natl. Acad. Sci. USA, 108 (44), 17876–17882.
- 23. Shoval, O., Sheftel, H., Shinar, G., Hart, Y., Ramote, O., Mayo, A., Dekel, E., Kavanagh, K., and Alon, U. (2012) Evolutionary trade-offs, Pareto optimality, and the geometry of phenotype space. Science, 336, 1157–1160.
- 24. Sheftel, H., Shoval, O., Mayo, A., and Alon, U. (2013) The geometry of the Pareto front in biological phenotype space. Ecol. Evol., 3 (6), 1471–1483.
- 25. Bar-Even, A., Noor, E., Savir, Y., Liebermeister, W., Davidi, D., Tawfik, D.S., and Milo, R. (2011) The moderately efficient enzyme: evolutionary and physicochemical trends shaping enzyme parameters. Biochemistry, 21, 4402–4410.
- 26. Heinrich, R. and Holzhütter, H.-G. (1985) Efficiency and design of simple metabolic systems. Biomed. Biochim. Acta, 44 (6), 959–969.
- 27. Edwards, J.S. and Palsson, B.Ø. (2000) Metabolic flux balance analysis and the in silico analysis of Escherichia coli K-12 gene deletions. BMC Bioinform., 1, 1.
- 28. Holzhütter, H.-G. (2004) The principle of flux minimization and its application to estimate stationary fluxes in metabolic networks. Eur. J. Biochem., 271 (14), 2905–2922.
- 29. Goelzer, A. and Fromion, V. (2011) Bacterial growth rate reflects a bottleneck in resource allocation. Biochim. Biophys. Acta, 1810 (10), 978–988.
- 30. Heinrich, R. and Hoffmann, E. (1991) Kinetic parameters of enzymatic reactions in states of maximal activity: an evolutionary approach. J. Theor. Biol., 151, 249–283.
- 31. Klipp, E. and Heinrich, R. (1999) Competition for enzymes in metabolic pathways: implications for optimal distributions of enzyme concentrations and for the distribution of flux control. Biosystems, 54, 1–14.
- 32. Klipp, E., Heinrich, R., and Holzhütter, H.-G. (2002) Prediction of temporal gene expression. Metabolic optimization by re-distribution of enzyme activities. Eur. J. Biochem., 269, 1–8.
- 33. Zaslaver, A., Mayo, A.E., Rosenberg, R., Bashkin, P., Sberro, H., Tsalyuk, M., Surette, M.G., and Alon, U. (2004) Just-in-time transcription program in metabolic pathways. Nat. Genet., 36, 486–491.
- 34. Molenaar, D., van Berlo, R., de Ridder, D., and Teusink, B. (2009) Shifts in growth strategies reflect tradeoffs in cellular economics. Mol. Syst. Biol., 5, 323.
- 35. Bachmann, H., Fischlechner, M., Rabbers, I., Barfa, N., Branco dos Santos, F., Molenaar, D., and Teusink, B. (2013) Availability of public goods shapes the evolution of competing metabolic strategies. Proc. Natl. Acad. Sci. USA, 110 (35), 14302–14307.
- 36. Schuetz, R., Kuepfer, L., and Sauer, U. (2007) Systematic evaluation of objective functions for predicting intracellular fluxes in Escherichia coli. Mol. Syst. Biol., 3, 119.
- 37. Wagner, A. and Fell, D.A. (2001) The small world inside large metabolic networks. Proc. Biol. Sci., 268 (1478), 1803–1810.
- 38. Hatzimanikatis, V., Li, C., Ionita, J.A., Henry, C.S., Jankowski, M.D., and Broadbelt, L.J. (2005) Exploring the diversity of complex metabolic networks. Bioinformatics, 21 (8), 1603–1609.
- 39. Bar-Even, A., Flamholz, A., Noor, E., and Milo, R. (2012) Rethinking glycolysis: a perspective on the biochemical logic of glucose fermentation. Nat. Chem. Biol., 8, 509–517.
- 40. Stephani, A., Nuño, J.C., and Heinrich, R. (1999) Optimal stoichiometric designs of ATP-producing systems as determined by an evolutionary algorithm. J. Theor. Biol., 199, 45–61.
- 41. Melendez-Hevia, E. and Isodoro, A. (1985) The game of the pentose phosphate cycle. J. Theor. Biol., 117, 251–263.
- 42. Noor, E., Eden, E., Milo, R., and Alon, U. (2010) Central carbon metabolism as a minimal biochemical walk between precursors for biomass and energy. Mol. Cell, 39, 809–820.
- 43. Waddell, T.G., Repovic, P., Meléndez-Hevia, E., Heinrich, R., and Montero, F. (1999) Optimization of glycolysis: new discussions. Biochem. Educ., 27 (1), 12–13.
- 44. Meléndez-Hevia, E., Waddell, T.G., Heinrich, R., and Montero, F. (1997) Theoretical approaches to the evolutionary optimization of glycolysis – chemical analysis. Eur. J. Biochem., 244, 527–543.
- 45. Noor, E., Bar-Even, A., Flamholz, A., Reznik, E., Liebermeister, W., and Milo, R. (2014) Pathway thermodynamics uncovers kinetic obstacles in central metabolism. PLoS Comput. Biol., 10, e100348.
- 46. Shachrai, I., Zaslaver, A., Alon, U., and Dekel, E. (2010) Cost of unneeded proteins in E. coli is reduced after several generations in exponential growth. Mol. Cell, 38, 1–10.
- 47. Stucki, J.W. (1980) The optimal efficiency and the economic degrees of coupling of oxidative phosphorylation. Eur. J. Biochem., 109, 269–283.
- 48. Stoebel, D.M., Dean, A.M., and Dykhuizen, D.E. (2008) The cost of expression of Escherichia coli lac operon proteins is in the process, not in the products. Genetics, 178 (3), 1653–1660.
- 49. Hoppe, A., Richter, C., and Holzhütter, H.-G. (2011) Enzyme maintenance effort as criterion for the characterization of alternative pathways and length distribution of isofunctional enzymes. Biosystems, 105 (2), 122–129.
- 50. Bar-Even, A., Noor, E., Lewis, N.E., and Milo, R. (2010) Design and analysis of synthetic carbon fixation pathways. Proc. Natl. Acad. Sci. USA, 107 (19), 8889–8894.
- 51. Byrne, D., Dumitriu, A., and Segrè, D. (2012) Comparative multi-goal tradeoffs in systems engineering of microbial metabolism. BMC Syst. Biol., 6, 127.
- 52. Schuetz, R., Zamboni, N., Zampieri, M., Heinemann, M., and Sauer, U. (2012) Multidimensional optimality of microbial metabolism. Science, 336 (6081), 601–604.
- 53. Beg, Q.K., Vazquez, A., Ernst, J., de Menezes, M.A., Bar-Joseph, Z., Barabási, A.-L., and Oltvai, Z.N. (2007) Intracellular crowding defines the mode and sequence of substrate uptake by Escherichia coli and constrains its metabolic activity. Proc. Natl. Acad. Sci. USA, 104 (31), 12663–12668.
- 54. Tepper, N., Noor, E., Amador-Noguez, D., Haraldsdóttir, H.S., Milo, R., Rabinowitz, J., Liebermeister, W., and Shlomi, T. (2013) Steady-state metabolite concentrations reflect a balance between maximizing enzyme efficiency and minimizing total metabolite load. PLoS One, 8 (9), e75370.
- 55. Flamholz, A., Noor, E., Bar-Even, A., Liebermeister, W., and Milo, R. (2013) Glycolytic strategy as a tradeoff between energy yield and protein cost. Proc. Natl. Acad. Sci. USA, 110 (24), 10039–10044.
- 56. Wortel, M.T., Peters, H., Hulshof, J., Teusink, B., and Bruggeman, F.J. (2014) Metabolic states with maximal specific rate carry flux through an elementary flux mode. FEBS J., 281 (6), 1547–1555.
- 57. Müller, S., Regensburger, G., and Steuer, R. (2014) Enzyme allocation problems in kinetic metabolic networks: optimal solutions are elementary flux modes. J. Theor. Biol., 347, 182–190.
- 58. Zelcbuch, L., Antonovsky, N., Bar-Even, A., Levin-Karp, A., Barenholz, U., Dayagi, M., Liebermeister, W., Flamholz, A., Noor, E., Amram, S., Brandis, A., Bareia, T., Yofe, I., Jubran, H., and Milo, R. (2013.) Spanning high-dimensional expression space using ribosome-binding site combinatorics. Nucleic Acids Res., 41 (9), e98.
- 59. Lee, M.E., Aswani, A., Han, A.S., Tomlin, C.J., and Dueber, J.E. (2013) Expression-level optimization of a multi-enzyme pathway in the absence of a high-throughput assay. Nucleic Acids Res., 41 (22), 10668–10678.
- 60. Moriya, H., Shimizu-Yoshida, Y., and Kitano, H. (2006) In vivo robustness analysis of cell division cycle genes in Saccharomyces cerevisiae. PLoS Genet., 2 (7), e111.
- 61. Trinh, C.T., Carlson, R., Wlaschin, A., and Srienc, F. (2006) Design, construction and performance of the most efficient biomass producing E. coli bacterium. Metab. Eng., 8 (6), 628–638.
- 62. Crabtree, H.G. (1928) The carbohydrate metabolism of certain pathological overgrowths. Biochem. J., 22 (5), 1289–1298.
- 63. Warburg, O., Posener, K., and Negelein, E. (1924) Ueber den Stoffwechsel der Tumoren. Biochem. Z., 152, 319–344.
- 64. Zhuang, K., Vemuri, G.N., and Mahadevan, R. (2011) Economics of membrane occupancy and respiro-fermentation. Mol. Syst. Biol., 7, 500.
- 65. Schuster, S., Pfeiffer, T., and Fell, D. (2008) Is maximization of molar yield in metabolic networks favoured by evolution? J. Theor. Biol., 252, 497–504.
- 66. Li, G.-W., Burkhardt, D., Gross, C., and Weissman, J.S. (2014) Quantifying absolute protein synthesis rates reveals principles underlying allocation of cellular resources. Cell, 157, 624–635.
- 67. Pettersson, G. (1989) Effect of evolution on the kinetic properties of enzymes. Eur. J. Biochem., 184 (3), 561–566.
- 68. Pettersson, G. (1992) Evolutionary optimization of the catalytic efficiency of enzymes. Eur. J. Biochem., 206 (1), 289–295.
- 69. Heinrich, R. and Hoffmann, E. (1991) Kinetic parameters of enzymatic reactions in states of maximal activity: an evolutionary approach. J. Theor. Biol., 151 (2), 249–283.
- 70. Wilhelm, T., Hoffmann-Klipp, E., and Heinrich, R. (1994) An evolutionary approach to enzyme kinetics: optimization of ordered mechanisms. Bull. Math. Biol., 56, 65–106.
- 71. Klipp, E. and Heinrich, R. (1994) Evolutionary optimization of enzyme kinetic parameters: effect of constraints. J. Theor. Biol., 171 (3), 309–323.
- 72. Klipp, E. and Heinrich, R. (1999) Competition for enzymes in metabolic pathways: implications for optimal distributions of enzyme concentrations and for the distribution of flux control. Biosystems, 54 (1–2), 1–14.
- 73. Klipp, E., Heinrich, R., and Holzhutter, H.G. (2002) Prediction of temporal gene expression. Metabolic optimization by re-distribution of enzyme activities. Eur. J. Biochem., 269 (22), 5406–5413.
- 74. de Hijas-Liste, G.M., Klipp, E., Balsa-Canto, E., and Banga, J.R. (2014) Global dynamic optimization approach to predict activation in metabolic pathways. BMC Syst. Biol., 8, 1.
- 75. Zaslaver, A., Mayo, A.E., Rosenberg, R., Bashkin, P., Sberro, H., Tsalyuk, M. et al. (2004) Just-in-time transcription program in metabolic pathways. Nat. Genet., 36 (5), 486–491.
- 76. Ibarra, R.U., Edwards, J.S., and Palsson, B.O. (2002) Escherichia coli K-12 undergoes adaptive evolution to achieve in silico predicted optimal growth. Nature, 420 (6912), 186–189.
- 77. Darwin, C. (1859) On the Origin of Species by Means of Natural Selection, or the Preservation of Favoured Races in the Struggle for Life, John Murray, London.
- 78. Eigen, M. (1971) Molekulare Selbstorganisation und Evolution (Self-organization of matter and the evolution of biological macromolecules). Naturwissenschaften, 58 (10), 465–523.
- 79. Eigen, M. and Schuster, P. (1979) The Hypercycle: A Principle of Natural Self-Organization, Springer, Berlin.
- 80. Eigen, M. and Schuster, P. (1977) The hypercycle. A principle of natural self-organization. Part A. Emergence of the hypercycle. Naturwissenschaften, 64 (11), 541–565.
- 81. Eigen, M. and Schuster, P. (1982) Stages of emerging life: five principles of early organization. J. Mol. Evol., 19 (1), 47–61.
- 82. Eigen, M. and Schuster, P. (1978) The hypercycle. A principle of natural self organization. Part B. The abstract hypercycle. Naturwissenschaften, 65 (1), 7–41.
- 83. Kimura, M. (1983) The Neutral Theory of Molecular Evolution, Cambridge University Press, Cambridge.
- 84. Kimura, M. (1979) The neutral theory of molecular evolution. Sci. Am., 241 (5), 98–100, 102, 108 passim.
- 85. Kimura, M. and Ota, T. (1971) On the rate of molecular evolution. J. Mol. Evol., 1 (1), 1–17.
- 86. Kimura, M. and Ota, T. (1974) On some principles governing molecular evolution. Proc. Natl. Acad. Sci. USA, 71 (7), 2848–2852.
- 87. Kauffman, S.A. and Weinberger, E.D. (1989) The NK model of rugged fitness landscapes and its application to maturation of the immune response. J. Theor. Biol., 141 (2), 211–245.
- 88. Kauffman, S.A. (1991) Antichaos and adaptation. Sci. Am., 265 (2), 78–84.
- 89. Kauffman, S.A. and Macready, W.G. (1995) Search strategies for applied molecular evolution. J. Theor. Biol., 173 (4), 427–440.
- 90. Kauffman, S.A. (1993) The Origins of Order: Self-Organization and Selection in Evolution, Oxford University Press, New York.
- 91. Holland, J.H. (1975) Adaptation in Natural and Artificial Systems, MIT Press, Boston, MA.
- 92. Domingo, E. and Holland, J.H. (1997) RNA virus mutations and fitness for survival. Annu. Rev. Microbiol., 51, 151–178.
- 93. Holland, J.H. (1992) Adaptation in Natural and Artificial Systems, MIT Press, Cambridge, MA.
- 94. Fogel, L.J., Owens, A.J., and Walsh, M.J. (1966) Artificial Intelligence Through Simulated Evolution, John Wiley & Sons, Inc., New York.
- 95. Rechenberg, I. (1994) Evolutionsstrategie '94, Friedrich Frommann Verlag.
- 96. Koza, J.R., Mydlowec, W., Lanza, G., Yu, J., and Keane, M.A. (2001) Reverse engineering of metabolic pathways from observed data using genetic programming. Pac. Symp. Biocomput., 434–445.
- 97. Schuster, P., Sigmund, K., and Wolff, R. (1978) Dynamical systems under constant organization. I. Topological analysis of a family of non-linear differential equations: a model for catalytic hypercycles. Bull. Math. Biol., 40 (6), 743–769.
- 98. Swetina, J. and Schuster, P. (1982) Self-replication with errors. A model for polynucleotide replication. Biophys. Chem., 16 (4), 329–345.
- 99. Burch, C.L. and Chao, L. (2000) Evolvability of an RNA virus is determined by its mutational neighbourhood. Nature, 406 (6796), 625–628.
- 100. Eigen, M. (1971) Molecular self-organization and the early stages of evolution. Q. Rev. Biophys., 4 (2), 149–212.
- 101. Eigen, M., Gardiner, W.C., Jr., and Schuster, P. (1980) Hypercycles and compartments. Compartments assist – but do not replace – hypercyclic organization of early genetic information. J. Theor. Biol., 85 (3), 407–411.
- 102. Sherrington, D. and Kirkpatrick, S. (1975) Solvable model of a spin glass. Phys. Rev. Lett., 35 (26), 1792–1796.
- 103. Sherrington, D. and Kirkpatrick, S. (1978) Infinite-ranged models of spin-glasses. Phys. Rev. B, 17, 4384.
- 104. Watson, J.D. and Crick, F.H. (1953) Genetical implications of the structure of deoxyribonucleic acid. Nature, 171 (4361), 964–967.
- 105. Watson, J.D. and Crick, F.H. (1953) The structure of DNA. Cold Spring Harb. Symp. Quant. Biol., 18, 123–131.
- 106. Watson, J.D. and Crick, F.H. (1953) Molecular structure of nucleic acids: a structure for deoxyribose nucleic acid. Nature, 171 (4356), 737–738.
- 107. Ohno, S. (1970) Evolution by Gene Duplication, Springer, Berlin.
- 108. Falster, D.S. and Westoby, M. (2003) Plant height and evolutionary games. Trends Ecol. Evol., 18, 337–343.
- 109. Pfeiffer, T. and Schuster, S. (2005) Game-theoretical approaches to studying the evolution of biochemical systems. Trends Biochem. Sci., 30 (1), 20–25.
- 110. Schuetz, R., Kuepfer, L., and Sauer, U. (2007) Systematic evaluation of objective functions for predicting intracellular fluxes in Escherichia coli. Mol. Syst. Biol., 3, 119.
- 111. Schuetz, R., Zamboni, N., Zampieri, M., Heinemann, M., and Sauer, U. (2012) Multidimensional optimality of microbial metabolism. Science, 336 (6081), 601–604.
- 112. Turner, P.E. (2005) Cheating viruses and game theory. Am. Sci., 93, 428–435.
- 113. von Neumann, J. and Morgenstern, O. (1944) Theory of Games and Economic Behavior, Princeton University Press, Princeton, NJ.
- 114. Smith, J.M. and Price, G.R. (1973) The logic of animal conflict. Nature, 246, 15–18.
- 115. Smith, J.M. (1982) Evolution and the Theory of Games, Cambridge University Press, Cambridge.
- 116. Nowak, A. and Sigmund, K. (2004) Evolutionary dynamics of biological games. Science, 303, 793–799.
- 117. Kerr, B., Riley, M.A., Feldman, M.W., and Bohannan, B.J.M. (2002) Local dispersal promotes biodiversity in a real-life game of rock–paper–scissors. Nature, 418, 171–174.
- 118. Czárń, T.L., Hoekstra, R.F., and Pagie, L. (2002) Chemical warfare between microbes promotes biodiversity. Proc. Natl. Acad. Sci. USA, 99, 786–790.
- 119. Hutchinson, G.E. (1961) The paradox of the plankton. Am. Nat., 95, 137–145.
- 120. Nowak, M.A. (2006) Five rules for the evolution of cooperation. Science, 314 (5805), 1560–1563.
- 121. Chuang, J.S., Rivoire, O., and Leibler, S. (2010) Cooperation and Hamilton's rule in a simple synthetic microbial system. Mol. Syst. Biol., 6, 398.
- 122. Dudley, S.A. and File, A.L. (2007) Kin recognition in an annual plant. Biol. Lett., 4, 435–438.
- 123. Schuster, S., de Figueiredo, L.F., Schroeter, A., and Kaleta, C. (2011) Combining metabolic pathway analysis with evolutionary game theory. Explaining the occurrence of low-yield pathways by an analytic optimization approach. Biosystems, 105, 147–153.
- 124. Pfeiffer, T., Schuster, S., and Bonhoeffer, S. (2001) Cooperation and competition in the evolution of ATP-producing pathways. Science, 292, 504–507.
- 125. Warburg, O., Posener, K., and Negelein, E. (1924) Ueber den Stoffwechsel der Tumoren. Biochem. Z., 152, 319–344.
- 126. Bachmann, H., Fischlechner, M., Rabbers, I., Barfa, N., Branco dos Santos, F., Molenaar, D., and Teusink, B. (2013) Availability of public goods shapes the evolution of competing metabolic strategies. Proc. Natl. Acad. Sci. USA, 110 (35), 14302–14307.
- 127. Pfeiffer, T., Schuster, S., and Bonhoeffer, S. (2001) Cooperation and competition in the evolution of ATP-producing pathways. Science, 292, 504–507.
Further Reading
- Optimality in metabolic systems: Heinrich, R. and Schuster, S. (1998) The modelling of metabolic systems. Structure, control, and optimality. Biosystems, 47, 61–77.
- Temporal optimization: Klipp, E., Heinrich, R., and Holzhütter, H.-G. (2002) Prediction of temporal gene expression. Metabolic optimization by re-distribution of enzyme activities. Eur. J. Biochem., 269 (22), 5406–5413.
- Experimental cost–benefit analysis of Lac operon: Dekel, E. and Alon, U. (2005) Optimality and evolutionary tuning of the expression level of a protein. Nature, 436, 588–692.
- Evolvability: Kirschner, M. and Gerhart, J. (1998) Evolvability. Proc. Natl. Acad. Sci. USA, 95 (15), 8420–8427.
- Flux minimization: Holzhütter, H.-G. (2004) The principle of flux minimization and its application to estimate stationary fluxes in metabolic networks. Eur. J. Biochem., 271 (14), 2905–2922.
- Multi-objective flux optimization: Schuetz, R., Zamboni, N., Zampieri, M., Heinemann, M., and Sauer, U. (2012) Multidimensional optimality of microbial metabolism. Science, 336 (6081), 601–604.
- Enzyme allocation for maximal growth: Molenaar, D., van Berlo, R., de Ridder, D., and Teusink, B. (2009) Shifts in growth strategies reflect tradeoffs in cellular economics. Mol. Syst. Biol., 5, 323.
- Metabolic flux and yield in FBA: Schuster, S., Pfeiffer, T., and Fell, D. (2008) Is maximization of molar yield in metabolic networks favoured by evolution? J. Theor. Biol., 252, 497–504.
- Trade-off between enzyme cost and yield: Flamholz, A., Noor, E., Bar-Even, A., Liebermeister, W., and Milo, R. (2013) Glycolytic strategy as a tradeoff between energy yield and protein cost. Proc. Natl. Acad. Sci. USA, 110 (24), 10039–10044.
- Evolutionary game theory: Smith, J.M. (1982) Evolution and the Theory of Games, Cambridge University Press, Cambridge.
- Evolution and self-organization: Kauffman, S.A. (1993) Origins of Order: Self-Organization and Selection in Evolution, Oxford University Press, New York.
- Evolution of cooperation: Nowak, M.A. (2006) Five rules for the evolution of cooperation. Science, 314 (5805), 1560–1563.
- Metabolic flux and yield studied by game theory: Pfeiffer, T., Schuster, S., and Bonhoeffer, S. (2001) Cooperation and competition in the evolution of ATP-producing pathways. Science, 292, 504–507.
- Evolution of yield-efficient behavior: Bachmann, H., Fischlechner, M., Rabbers, I., Barfa, N., Branco dos Santos, F., Molenaar, D., and Teusink, B. (2013) Availability of public goods shapes the evolution of competing metabolic strategies. Proc. Natl. Acad. Sci. USA, 110 (35), 14302–14307.