and π, to take two examples. The set of real numbers is the name for the collection of all numbers on the number line, which are those that can be represented by decimal expansions of any kind, as shown in Figure 7.The counting numbers, 1, 2, 3, ··· are just the tip of the number iceberg. This tip is of course the first part we discover, and for a time we might believe there is no more to the iceberg than the tip, especially if we remain reluctant to look below the waterline. In the course of this chapter, we first introduce the negative integers and coupling this extension with fractions, both positive and negative, gives the collection we call the set of rational numbers. This number collection is often pictured to lie along the number line, with the positive numbers lying to the right of zero, with their negatives forming the mirror image to the left. However, the number line turns out to be the home of other numbers that cannot be expressed as fractions, such as and π, to take two examples. The set of real numbers is the name for the collection of all numbers on the number line, which are those that can be represented by decimal expansions of any kind, as shown in Figure 7.
However, one of the great achievements of the 19th century was the full realization that the true domain of number is not one-, but rather is two-dimensional. The plane of the complex numbers is the natural arena of discourse for much of mathematics. This has been brought home to mathematicians and scientists through problem solving – to be able to carry out the investigations required to solve real-world problems, many of which seem to be only about ordinary counting numbers, it becomes necessary to expand your number horizon. The explanation as to how this extra dimension emerges will come towards the end of this chapter and be explored further in Chapter 8.
7. Central portion of the number line near 0
The integers is the name applied to the set of all whole numbers, positive negative, and zero. This set, often symbolized by the letter Z, is therefore infinite in both directions:
{··· − 4, −3, −2, −1, 0, 1, 2, 3, 4, ···}.
The integers are often pictured as lying at equally spaced points along a horizontal number line, in the order indicated. The additional rules that we need to know in order to do arithmetic with the integers can be summarized as follows:
(a) to add or subtract a negative integer, − m, we move m spaces to the left in the case of addition, and m spaces to the right for subtraction;
(b) to multiply an integer by − m, we multiply the integer by m, and then change sign.
In other words, the direction of addition and subtraction of negative numbers is the opposite to that of positive numbers, while multiplying a number by −1 swaps its sign for the alternative. For example, 8 + (−11) = −3, 3 × (−8) = −24, and (−1) × (−1) = 1.
You should not be troubled by this last sum. First, it is reasonable that multiplying a negative number by a positive one yields a negative answer: when a debt (a negative amount) is subject to interest (a positive multiplier greater than 1) the outcome is greater debt, that is to say a larger negative number. We are all well aware of this. That multiplication of a negative number by another negative number should have the opposite outcome, that is a positive result, would then appear consistent. The fact that the product of two negative numbers is positive can readily be given formal proof. The proof is based on the assumptions that we want our expanded number system of the integers to subsume the original one of the natural numbers, and that the augmented system should continue to obey all the normal rules of algebra. Indeed, the result on the product of two negatives follows from the fact that any number multiplied by zero equals zero. (This too is not an assumption but rather is also a consequence of the laws of algebra.) For we now have:
−1 × (−1 + 1) = −1 × 0 = 0;
if we then multiply out the brackets, we see that in order that the left-hand side equal zero, (−1) × (−1) must take the opposite sign to (−1) × 1 = −1; in other words (−1) × (−1) = 1.
In a similar way that subtraction leads to the negative numbers, the operation of division also leads us out of the set of natural counting numbers into the larger realm of fractions. However, the nature of the new arithmetic we encounter is of a different character. When adding or subtracting, fractions with different denominators (bottom lines) are incompatible. The fractions in question need to be expressed with a common denominator before the sum can be completed. Multiplication is a comparatively simple process in that we only need to multiply the numerators (top lines) and denominators together in order to get the answer. Division is the inverse operation to multiplication so that division by n corresponds to multiplication by the reciprocal,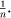 
. In general, this carries over to fractions in that to divide by the fraction 
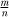we multiply by its reciprocal, 
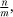for that reverses the effect of multiplication by 
.
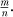The Ancient Egyptians were only happy with unit fractions, which are those that are simple reciprocals of whole numbers,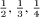 
etc. (although they retained a special symbol for 
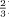). A fraction such as 
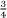was not thought of as a meaningful entity in its own right, and they would record this quantity as the sum of two reciprocals: 
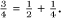(The notation for fractions used here is of course the modern European type, which has its origins in Greek mathematics.) It is not, however, obvious that it is necessarily possible to write any fraction as the sum of a number of different unit fractions, which is what they insisted on. It can, however, always be done and explaining this will allow you to brush up your skills on dealing with fractions.
If you wish to find an Egyptian decomposition of a fraction such as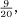 
, you need only subtract the largest unit fraction you can from the given number, and repeat this process until the remainder is itself a unit fraction. This will always work, and the number of fractions involved never exceeds the numerator of your original fraction. This is because, at each stage, the numerator of the fraction that still remains is always less than the previous one: not obvious but true. In this example the first stage will give:
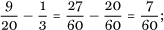
next we find that the largest unit fraction less than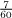 
is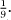 
.(To test this, compare the result of the cross-multiplication: 
< 
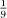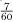because 1 × 60 = 60 < 63 = 7 × 9.) Subtracting again, we see that
and so we recover the Egyptian decomposition: 9 20
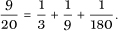
This greedy approach of always subtracting the largest unit fraction available does work but may not yield the shortest decomposition there is, as we can see even in this case as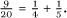 
This two-fraction decomposition of 
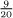can be found, however, through use of the technique of the Akhmim papyrus, a Greek parchment discovered at the city of Akhmim on the Nile and dated to AD 500–800. In modern notation, the trick can be expressed as the readily verified algebraic identity:
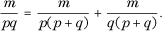
Applying this with m = 9, p = 4, q = 5 immediately gives us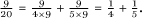 
It may well have been years since you last added even simple fractions together because nearly all practical arithmetic is now carried out in decimal format. The use of decimal fractions is found in ancient China and medieval Arabic nations but only came into widespread use in Europe in the latter part of the 16th century when serious efforts were made to improve practical methods of computation. There is a price to be paid, however, for this commitment to decimal forms. In normal base ten arithmetic we exploit the fact that any number can be written as a sum of multiples of powers of ten. When expressing a fraction as a decimal, we are attempting to write the number as a sum of powers of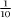 
= 0.1. Unfortunately, even for very simple fractions such as 
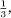, this cannot be done, and the decimal expansion goes on without end: 
= 0.333 …. In practice, we appreciate that by truncating the decimal expansion after a certain number of places (depending on the accuracy we demand), we can get by with the resulting terminating decimal that approximates the exact fraction. Any inaccuracy is trivial in comparison with the convenience of carrying out all our number work in the standard base ten frame of reference. Decimal expansions can be thought of as the closest we can get to having a single common denominator for all fractions.
It is natural to ask, though, which fractions will have terminating expansions (and which will not)? The answer is, not very many. More often than not, the decimal expansion of a fraction goes into a recurring pattern: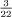 
= 0.1363636··· with the 36 part repeating forever. Every fraction generates a recurring decimal in one way or another, although in the case of a terminating decimal such as 
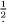= 0.5, the recurring part is simply an unending string of zeros: 
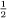= 0.5000 ···, and so is not explicitly mentioned. In any event, the length of the recurring block in a recurring decimal expansion is no longer than one less than the value of the denominator. This can be seen by considering what happens when we carry out the corresponding long division sum: if the denominator is n, then the remainder after each step in the division takes on one of the values 0, 1, ···, n − 1. If at some stage the remainder is 0, the division terminates and so does the decimal expansion: for example, 
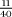is exactly equal to 0.275. Otherwise the division continues forever, but once a remainder is repeated, which is inevitable, we shall be forced into the same cycle of divisions once more, thus giving a recurring pattern whose block can be no longer than n − 1. The expansion will terminate exactly when the denominator is a product of the prime factors 2 and 5 of our base 10 but not if there is any other factor involved. For example, fractions with denominators 16, 40, and 50 are terminating, but fractions like 
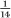and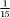 
will not terminate because the respective prime factors of 7 and 3 in their denominators force the expansion into a recurring cycle.
This does show, however, that whether or not a fraction’s expansion terminates is not determined just by the number itself but rather depends on the relationship of the number to the base in which you are operating. If, for instance, we worked in ternary (base three) then 0.1 would represent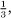 
, as the 1 after the decimal point would stand for 
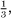and not 
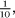, the way it does in decimal expansions.
The reverse process of turning a recurring decimal back into a fraction is also quite simple, showing that there is a one-to-one correspondence between fractions and recurring decimals, and we can use whichever representation best suits our current purpose. A simple example is as follows: let a = 0.212121 ···. Since the length of the recurring block is 2, we can simplify this, as you will see, by multiplying by 102 = 100 to obtain 100a = 21.212121 ···. This has been set up so that, upon subtraction, the recurring parts of the two numbers a and 100a, being identical, will cancel, allowing us to infer that 99a = 21, whence a =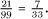 
This kind of trick is often used to simplify an expression that involves an infinite repeating process. For example, consider the following little monster:
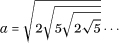
By squaring, and then squaring again, the left-hand side becomes a4, while the expression on the right gives:
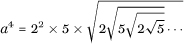
Since what follows the 5 is another copy of the expression for a, we infer that a4 = 20a so that a3 = 20 or, if you prefer, a is the cube root of 20. We will call on this technique again in Chapter 7 when we introduce so-called continued fractions.
Does the class of fractions provide us with all the numbers we could ever need? As mentioned earlier, the collection of all fractions, together with their negatives, form the set of numbers known as the rationals, that is all numbers that result from whole numbers and the ratios between them. They are adequate for arithmetic in that any sum involving the four basic arithmetic operations of addition, subtraction, multiplication, and division will never take you outside the world of rational numbers. If we are happy with that, this set of numbers is all we require. However, we explain in the next section how numbers such as a above are not rational.
The word irrational applied to a number a means simply that the number is not rational, that is to say cannot be written as a fraction. Irrational numbers were first discovered a very long time ago, in ancient Greece. Pythagoras understood the irrational nature of . The Greeks did not think in terms of decimal expansions but were happy to recognize a length constructed in the geometry of straightedge and compass as representing a real quantity. In particular, Pythagoras’ Theorem tells us that the longer side of a right-angled triangle whose shorter sides are each of length 1 unit is exactly equal to the square root of 2.
Pythagoras was able to prove that the square root of 2 was not equal to any fraction, thereby showing that irrational numbers truly exist. In particular, you cannot exactly measure the diagonal of a square with the same units with which you measure the side, for if you could the diagonal would be an exact fractional multiple of the side, in which case would be equal to this fraction. The two lengths are however fundamentally incompatible, or incommensurable as they are described in the classical texts. The story is the same for π, which is approximately equal to the fraction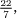 
, but is different from it, and from any fraction that you care to nominate. (However, the easily remembered ‘double 1, double 3, double 5’ ratio: 355/113 = 3.1415929 ··· accurately approximates the value of π to better than one part in one million.)
Although it is very difficult to prove that π is irrational, the question for the square root of 2 can be settled easily by a simple contradiction argument. First, we note that for any number c, the highest power of 2 that is a factor of c2, is twice the highest power of 2 that is a factor of c, and so in particular the highest power of 2 that divides any square must itself be an even number. For example, 24 = 23 × 3 while 576 = 242 = 26 × 32, and in this case the highest power of 2 dividing the number does indeed double from 3 to 6 when we take the square. This is always the case, and indeed applies not only to powers of 2 but to any prime factor of the original number.
Suppose now that were equal to the fraction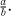 
. Squaring both sides of this equation allows us to deduce that 2 = 
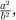which gives 2b2 = a2. By the previous observation, the highest power of 2 that divides the right-hand side of this equation is even, while the highest power that divides the left-hand side is odd (because of the presence of the extra 2). This shows the equation to be nonsense, and so it must not be possible to write as a fraction in the first place. Like Pythagoras, we come face to face with the irrationals.
Arguments along these lines allow us to show that quite generally, when we take the square root (or indeed the cube or a higher root) of a number, the answer, if not a whole number, is always irrational, thus explaining why the decimal displays on your calculator never show a recurring pattern when asked to calculate such a root.
Pythagoras discovered that in order to do his mathematics, he required a wider field of numbers than mere fractions. The Greeks regarded a number to be ‘real’ if its length could be constructed from a standard unit interval using only a straightedge (not a marked ruler, just an edge) and compass. It turns out that although the square root operation does introduce irrationals, the full collection itself does not go very far beyond the rational. The set of euclidean numbers, as we shall refer to them, are all those that can be arrived at from the number 1 through carrying out any or all of the four operations of arithmetic and the taking of square roots, any number of times. For example, the number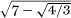 
is therefore a number of this kind. Even cube roots are beyond the grasp of the euclidean tools. This was the basis of perhaps the first great unsolved problem in mathematics. The first of the three Delian Problems as they were known was the call to construct the cube root of 2, using only straightedge and compass. Legend has it that this was the task set by the god when the citizens of Delos consulted the Oracle of Delphi to learn what they should do in order to banish the plague from Athens–the problem was put in the form of exactly doubling the volume of an altar that was a perfect cube.
This problem remained untouchable in classical times. That the cube root of 2 lies outside the range of the euclidean tools was only settled in 1837 by Pierre Wantzel (1814–38), as it requires a precise algebraic description of what is possible using the classical tools in order to see that the cube root of 2 is a number of a fundamentally different type. It does indeed come down to showing that you can never manufacture a cube root out of square roots and rationals. When put that way, the impossibility sounds more plausible. However, that in no way constitutes a proof.
Within the class of irrationals lies the mysterious family of transcendental numbers. These numbers do not arise through the ordinary calculations of arithmetic and the extraction of roots. For the precise definition, we first introduce the complementary collection of algebraic numbers, which are those that solve some polynomial equation with integer coefficients: for example x5 − 3x + 1 = 0 is such an equation. The transcendentals are then defined to be the class of non-algebraic numbers.
It is not at all clear that there are any such numbers. However, they do exist and they form a very secretive society, with those in it not readily divulging their membership of the club. For example, the number π is an instance of a transcendental but this is not a fact that it openly reveals. It will be explained in the next chapter when we explore the nature of infinite sets why it is that ‘most’ numbers are transcendental, in a sense that will be made precise.
For the time being, I will settle for introducing perhaps the most famous transcendental of all, the number e = 2.71828 …. This number arises constantly in higher mathematics and calculus: it is the base of the so-called natural logarithm, the function that tells you the area under the graph of the reciprocal function. It is also the limiting value of the sequence of numbers you get when you raise the ratio of two consecutive integers,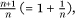 
to the power n. (Ask your calculator for the value of (129/128)128 –you can ‘fast exponentiate’ this, just calculate 129/128 and then square 7 times, as 27 = 128.)
This sequence arises when we consider the problem of the limiting value of a compound interest rate as you reduce the interval of repayment shorter and shorter from annually, to monthly, to daily, and so on. To best illustrate the point, suppose that interest is paid at an annual rate of 100%, compounding in n instalments per year, which means that your initial investment is multiplied by the factor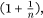 
, n times in all, throughout the course of the year. Your principal will then be multiplied by the factor 
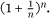. The more often you are paid interest, the more you will earn as you begin to collect interest on your interest earlier and earlier as n becomes higher and higher. However, as n increases, the effective APR (Annual Percentage Rate) does not increase beyond all bounds but rather approaches a ceiling, an upper limit as mathematicians call it. This limiting multiplier that would apply to your principal in the continuous interest case is the limiting value, as n increases, of the number
Another way in which the mysterious e arises is through the sum of the reciprocals of the factorials, and this gives a way of calculating e to a high degree of accuracy as this series converges rapidly because its terms approach zero very quickly indeed:
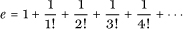
This representation allows you to show by a relatively simple contradiction argument, outlined here, that e is an irrational number. We suppose that the preceding series for e equals a fraction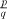 
and then we multiply both sides by q!. The left-hand side is then an integer but the right-hand side consists of terms that are integers followed by an infinite sequence of non-integral terms. By comparing to a simple geometric series, we deduce that this ‘tail’ sums to less than 1, and so the right-hand side cannot be a whole number, and therein lies the required contradiction. Showing that e is not just irrational, but transcendental, requires quite a bit more work.
The relationship of e with the factorials also manifests itself in a remarkable formula of the Scottish mathematician James Stirling (1692–1770), after whom Stirling numbers (see Chapter 5) are named. He showed that as n increases, the value of n! is approximated better and better by the expression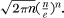 
Since e crops up in a variety of distinct and fairly simple ways, it persistently appears throughout mathematics, often where you would not expect to meet it. For example, take two well-shuffled packs of playing cards, turn over the top card of each deck, and compare. Continue doing this until you have exhausted the packs. What are the chances that, at some stage, there is a perfect match? That is to say, on one turn or another the cards showing are exactly the same, be they the seven of clubs, queen of hearts, or whatever. It works out that the proportion of times this experiment yields at least one such match is as near as makes no difference to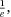 
which is about 36.8%. This comes about through application of what is known as the inclusion–exclusion principle, which arrives at the solution through a sum of terms each of which represent alternating corrections and reverse corrections. In this example, the principle furnishes the series of reciprocals of the factorials but this time with alternating signs, which converges to 
.
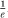The first five chapters of this Very Short Introduction dealt mainly with positive integers. We emphasized factorization properties of integers, which led us to consider numbers that have no proper factorizations, which are the primes, a set that occupies a pivotal position in modern cryptography. We also looked at particular types of numbers, such as the Mersenne primes, which are intimately connected with perfect numbers and took time to introduce some special classes of integers that are important in counting certain naturally occurring collections. Throughout all this, the backdrop was the system of integers, which are the counting numbers, positive, negative, and zero.
In this chapter we have gone beyond integers, first to the rationals (the fractions, positive and otherwise), then to the irrationals, and within the class of irrationals we have identified the transcendental numbers. The underlying system in which all this is taking place is the system of the real numbers, which can be thought of as the collection of all possible decimal expansions. Any positive real number can be represented in the form r = n.a1 a2 ··· where n is a non-negative integer and the decimal point is followed by an infinite trail of digits. If this trail eventually falls into a recurring pattern, then r is in fact rational and we have shown how to convert this representation into an ordinary fraction. If not, then r is irrational, so the real numbers come in those two distinct flavours, the rational and the irrational.
In our mathematical imaginations, we often picture the real numbers as corresponding to all the points along the number line as we look out from zero, to the right for the positive reals, and to the left for the negative reals. This leaves us with a symmetrical picture with the negative real numbers being a mirror image of the positive reals, and this symmetry is preserved when dealing with addition and subtraction – but not with multiplication. Once we pass to multiplication, the positive and negative numbers no longer have equal status as the number 1 is endowed with a property that no other number possesses, for it is the multiplicative identity, meaning that 1 × r = r × 1 = r for any real number r. Multiplication by 1 fixes the position of any number, but in contrast multiplication by −1 swaps a number for its mirror image on the far side of 0. Once multiplication enters the scene, the fundamental differences in the nature of positive and negative numbers are revealed. In particular, negative numbers lack square roots within the real number system because the square of any real number is always greater than or equal to zero.
This is the cue for imaginary numbers to make their entrance. This topic is one that we shall take up again in the final chapter; for the time being, we will just make some introductory comments.
These numbers arise through the search for solutions to simple polynomial equations. In particular, since the square of any real number is never negative, we can find no solution to the equation x2 = −1. Undaunted, mathematicians invented one, denoted by i, which is endowed with that property, so that i2 = −1. At first sight, this seems artificial and arbitrary but it is not too much different from the kind of behaviour we have indulged in before. After all, while recognizing that the counting numbers 1, 2, 3, ··· are pre-eminent, in order to deal smoothly with general number matters we are led to the wider number system of the rationals, which is the collection of all fractions, positive, negative, and zero. We then find, however, that we have no solution to the equation x2 = 2, as we have shown that the square of a rational number cannot exactly equal 2. To deal with this, we have to ‘invent’ . At this point we could take the alternative attitude and say that we have proved that the square root of 2 simply does not exist and that is the end of the matter. However, few would feel happy to haul up the drawbridge in this way. The ancient Greeks certainly were not content to let things stand at that, for they could construct a length representing with compass and straightedge and so the number was, to their way of thinking, definitely real and any mathematical system that denied this was inadequate.
We might agree with Pythagoras for quite a different reason. We may react by saying that we can approximate to any degree of accuracy via its decimal expansion: = 1.414213 ···, and so is the number that is represented exactly by the totality of this expansion. A modern person might find more force in this argument and so insist for this reason that the number system needs to be expanded beyond the rationals.
However, at first glance we might say that things are different when it comes to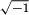 
as there seems no immediate need to worry about its non-appearance among the collection of numbers that we habitually call ‘real’. It transpires though that as our mathematics progresses a little further, the need for imaginary numbers becomes very pressing, and any initial reluctance to deal with them is dispelled as our understanding of things mathematical grows.
This first struck home in the 16th century when Italian mathematicians learnt how to solve cubic and fourth-degree polynomial equations in a fashion that extended that used to solve quadratic equations. The Cardano method, as it came to be known, would often involve square roots of negatives even though the solutions to the equations eventually turned out to be positive integers. By stages from this point, the use of complex numbers, which are those of the form a + bi, where a and b are ordinary real numbers, was shown to facilitate a variety of mathematical calculations. For example, in the 18th century Euler revealed and exploited the stunning little equation eiπ = −1, which cannot fail to surprise anyone on their first encounter.
Around the beginning of the 19th century, the geometric interpretation of complex numbers as points in the coordinate plane (the standard system of xy -coordinates), was investigated by Wessell and Argand, from which point the use of the ‘imaginary’ became accepted as normal mathematics. Identifying the complex number x + iy with the point with coordinates (x, y) allows examination of the behaviour of complex numbers in terms of the behaviour of points in the plane, and this proves to be very illuminating. The theory of so-called complex variables, whose subject matter is represented by functions of complex numbers, rather than just real numbers, flourished spectacularly in the hands of Augustin Cauchy (1789–1857). It is now a cornerstone of mathematics, underpins much of electrical signal theory, and the entire field of X-ray diffraction is built on complex numbers. These numbers have proved to have real meaning, and moreover the system is complete in that every polynomial equation has its full complement of solutions within the system of complex numbers. We shall return to these matters in the final chapter. Before doing that, however, we shall in the next chapter look more closely at the infinite nature of the real number line.
