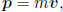
The previous chapter analyzed how particles “move” in space and time without considering the interactions that led to their motion. In this chapter, relativistic formulations of various physical concepts such as momentum and energy will be introduced. The elegant 4-vector formulation, which captures the quintessence of relativistic dynamics, in simple matrices with just four entries, will also be explored. The prefix “relativistic” that appears in front of many concepts in this chapter is misleading in certain aspects as the principle of relativity also exists in the classical regime — with the caveat that Galilean relativity is assumed instead. However, this prefix shall still be used to distinguish quantities in this chapter from their classical counterparts.
In classical mechanics, the momentum of a particle in a particular inertial frame S is defined as
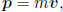
where m is the mass of the particle and v is the velocity of the particle in frame S. There is no ambiguity about which frame m is measured with respect to as the mass of a particle is assumed to be an intrinsic property that is invariant across inertial frames. The importance of this formulation lies in the law of conservation of momentum. It is empirically observed that the total momentum of a system that is not under the influence of net external forces is conserved. In an isolated system of particles, even if the particles interacted with one another in a certain manner, the total momentum of the particles remains constant.
The combination of the classical definition of momentum, mass invariance and the principle of relativity (that all laws hold similar forms in all inertial frames) implies the conservation of mass in closed systems. Take note of the distinction between mass invariance and the conservation of mass. Mass invariance means that if a particle is observed to have a certain mass m in an inertial frame S, its observed mass in another inertial frame S’ is also m. On the other hand, the conservation of mass means that the total mass in a closed system remains the same, regardless of the inner workings of the system.
Consider a closed system of n particles in which the ith particle has an initial mass mi and an initial velocity ui as observed in an inertial frame S. The particles may undergo arbitrary interactions with one another. Nonconservative forces such as friction may exist such that the total mechanical energy of the system is not conserved. Furthermore, there may also be changes in the mass of each individual particle and the total number of particles as atoms may be scraped off during collisions, particles may stick together or decay. After the particles are allowed to interact for a certain amount of time, there are n′ particles and the ith particle has a mass 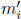 and a velocity vi in the same frame S. By the conservation of momentum in this frame,
and a velocity vi in the same frame S. By the conservation of momentum in this frame,

Now if we were to switch to another inertial frame S’ that moves at a velocity V relative to frame S, the law of the conservation of momentum should also be valid in frame S’ by the principle of relativity as all inertial frames are “equivalent.” Based on Galilean relativity, if a particle is observed to have a velocity u in frame S, it will be observed to possess a velocity u – V in frame S’. Furthermore, since the mass of a particle is assumed to be invariant across inertial frames (that is, the particle with mass mi in S still has mass mi in S’), the conservation of momentum in frame S’ becomes
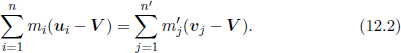
Subtracting Eq. (12.1) from Eq. (12.2) and simplifying,

Equation (12.3) states the conservation of mass in a closed system. If a closed system has a certain amount of total mass at a certain instance, it will also contain the same amount of mass at the next instance. This is what allows us to conclude that the perfectly inelastic collision of a particle of mass m and another particle of mass M produces a combined particle of mass m + M.
Relativistic Momentum
It turns out that the classical definition of momentum is not quite conserved in an isolated system. Instead, the relativistic momentum is conserved and is defined for a particle with respect to an inertial frame S as

where

u is the velocity of the particle in frame S and m refers to the mass of the particle observed in a frame in which it is at rest — a quantity denoted as the rest mass of the particle. Henceforth, the term “mass” will refer to the rest mass, unless explicitly stated otherwise. Again, the rest mass of a particle is presumed to be an intrinsic property of the particle and is invariant across inertial frames.
The total relativistic momentum of particles in a system that is free from a net external force, is conserved. This assertion, similar to the classical conservation of momentum, cannot be proven and should be regarded as an axiom. However, it has been empirically verified by rigorous test and hence shall be believed to be true.
An immediate consequence of this new postulate is that the total (rest) mass of a closed system may not be conserved! The premise of the previous section (Eq. (12.1) and the Galilean velocity transformation) is inaccurate. To illustrate the mutability of the total rest mass, consider the set-up in Fig. 12.1.

Figure 12.1:Two particles in frame S
Two identical particles, of rest mass m, initially travel at speed u in opposite directions in an inertial frame S. They collide with one another and stick together to form a resultant particle of rest mass M, which is not necessarily 2m. Due to the symmetry of this set-up, there is zero total momentum and the resultant particle remains stationary in this frame S by the conservation of momentum (analogous to the right-hand side of Eq. (12.1) being zero). Similar to how we proceeded from Eq. (12.1) to (12.2), consider the inertial frame S’ that travels at the initial velocity of the particle on the right. In this frame, the situation is depicted by Fig. 12.2.

Figure 12.2:Two particles in frame S’
The velocity u′ of the left mass in frame S’ can be computed via the relativistic velocity addition formula as  Again, the invariance of the rest mass allows us to conclude that the rest masses of these particles are the same in frame S’. By the principle of relativity, the total momenta of the system before and after the collision are identical.
Again, the invariance of the rest mass allows us to conclude that the rest masses of these particles are the same in frame S’. By the principle of relativity, the total momenta of the system before and after the collision are identical.

Solving for M,
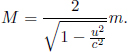
It can be seen that the rest mass of the resultant particle is larger than the rest mass of its constituents! It is natural to question where this additional mass comes from. Answering this shall be the goal of the next section.
At this point, we underscore the fact that we will adopt the same conventional definitions as the previous chapter. The velocity of a particle or wave in frame S will be denoted by u by default. Usually, we will be concerned with switching to another inertial frame S’. Hence, we will reserve v to be the velocity that S’ travels with respect to S in the positive x-direction in general. A similar statement holds for 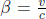 which is only associated with the transformations. Sometimes, we will switch to the frame of the particle and will thus substitute a quantity related to u into v.
which is only associated with the transformations. Sometimes, we will switch to the frame of the particle and will thus substitute a quantity related to u into v.
In a general inertial frame S, we will append the prefix “coordinate” to the measurements to explicitly indicate that they are measured with respect to a general frame. For example, the coordinate time refers to time measured in S. Often, we will be concerned with quantities observed in the frame of a particle. We then append the prefix “proper” to such measurements.
It is postulated that the total relativistic energy in an isolated system is conserved. The total energy of a particle, which includes both its kinetic energy and internal energy, in a particular inertial frame S is proposed to be

where

m and u are again the rest mass and the speed of the particle in frame S, respectively. Once again, this is another axiom which cannot be derived from first principles.1 However, it has also been extensively tested by experimentalists as it establishes a fundamental basis in many branches of physics such as nuclear physics. Next, let us analyze the constituents of this energy in greater detail.
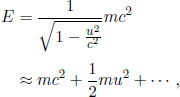
where we have expanded the Taylor series of γu. We begin to see a familiar  term followed by other higher order terms in
term followed by other higher order terms in  that are not shown. However, there is an enormous mc2 term in the expression as well, depending only on the rest mass of the particle. This is known as the rest energy of the particle, E0.
that are not shown. However, there is an enormous mc2 term in the expression as well, depending only on the rest mass of the particle. This is known as the rest energy of the particle, E0.

The rest energy of a particle is equivalent to its internal energy and is an intrinsic property of the particle. The rest energy is eponymously the energy of the particle when it is at rest and remains constant regardless of the particle’s motion. Furthermore, since the rest mass is invariant across inertial frames, the rest energy of a particle is also invariant. In general, the internal energy of a particle or system consists of the (microscopic) kinetic and rest energy of its constituents as well as the potential energy associated with its constituents due to interactions between its constituents or fields produced by its constituents (this excludes fields generated by sources external to the system). A consequence of this postulate is that heating a system increases its rest mass, as its internal energy is increased.
Next, the kinetic energy of a particle is then the remaining portion of energy associated with the motion of the particle.

As seen from the previous Taylor series expansion, this expression indeed reduces to the familiar formula for kinetic energy in the classical limit.
Lastly, note that the potential energy of a particle by virtue of its position in an external field is not included in the particle’s total energy. This is because this potential energy is “associated” with the particle and not possessed by it. The concept of potential energy is merely a “book-keeping” device that simplifies our calculations. When the kinetic energy of a particle increases as it is acted upon by a force due to an external field, the gain in kinetic energy should not be ascribed to its loss in potential energy. Rather, it should be understood that the field itself loses an equivalent amount of energy. Potential energy is an imaginary construct that helps us to keep track of the total energy of a system without taking into account where this energy “belongs” to. The “location” of energy matters in the context of relativity as it manifests itself in the local distortion of space and time. Hence, the potential energy due to an external field cannot be ascribed to a particle as a “real” form of energy and is forgone in special relativity.
Armed with the knowledge of relativistic energy and the conservation of relativistic energy (we will drop the “relativistic” prefix henceforth), let us revisit the previous question and verify if the total energy of the system is indeed conserved in Fig. 12.1. The total energy in the system of two particles before the collision in frame S is

As we have previously computed that the rest mass of the resultant particle is M = 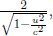 the energy of the system after the collision is
the energy of the system after the collision is
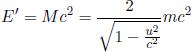
as the resultant particle is at rest. It can be seen that they are indeed equal. But wait! How can the total energy in this perfectly inelastic collision be conserved? Furthermore, we have yet to answer the question regarding the origin of the additional mass. Well, the resolution to these problems is that the kinetic energy of the particles is converted into their internal energy due to the heat released during the collision. Hence, the total energy, which includes the internal energy of the particles, of the system is still conserved. Furthermore, this additional internal energy also “shows up” as the additional mass of the resultant particle. In this particular sense, relativistic dynamics may actually be simpler than its classical counterpart, as the total energy of an isolated system is always conserved. In real life, you would expect the total energy of the resultant particle to be less than the sum of the original two. However, this deviation is due to heat transfer with the surroundings which means that the system of particles is no longer isolated and that the conservation of energy is inapplicable (but not violated). Lastly, be cautious that though the total energy of an isolated system is definitely conserved, the total kinetic energy may not necessarily be conserved — evident from the situation above.
The conservation of energy and momentum can be directly applied to solve many problems in a manner similar to the classical situation.
Problem: In Fig. 12.3, a particle of rest mass M initially travels at a velocity u in the x-direction in inertial frame S. It then decays into two identical particles of rest mass m that travel at a certain velocity v that makes a certain angle θ with the x-axis. Determine v and θ.

Figure 12.3:Decay
The conservation of momentum in the x-direction implies

where vx is the component of the resultant particles’ velocities in the x-direction. By the conservation of energy,

Dividing the two equations above and simplifying,

Substituting this into the first equation,

Useful Identities
In light of how the velocity u is horrendously coupled in the γ factors in the definitions of momentum and energy, there are a few neat identities that are commonly exploited in problem-solving. Firstly, consider the expression

This is a convenient identity that can be used to relate the energy of a particle to its momentum. Furthermore, it can be used to isolate and eliminate the dynamical properties of a particle (energy or momentum) which is not of concern. This will be illustrated in the next example. What’s more, notice that the right-hand side of the equation is frame-independent! That is, regardless of the inertial frame in which the energy E and momentum p of the particle are measured, substituting them into the equation above will always produce m2c4 where m is the rest or invariant mass of the particle! Perhaps, the deeper reason behind this invariance can be understood once the method of four-vectors is introduced.
The next useful identity is obtained by dividing p by E.

The equation above is especially helpful in determining the speed of a particle in a certain inertial frame given its momentum and energy in that frame. Note that in general, we do not wish to work in terms of u as it is usually entangled with annoying surds that are cumbersome to isolate. Hence, the momenta and energies will be the main avenues through which a dynamical problem can be solved.
Next, Eqs. (12.8) and (12.9) are particularly enlightening in the case of massless particles such as photons, which are inherently relativistic. Equations (12.5) and (12.6) are less so as γu tends to infinity while m tends to zero in the case of such massless particles which travel at the speed of light (we will soon see that all massless particles must travel at c) — leaving the values of those expressions indeterminate. Substituting m = 0 into Eq. (12.8),

Applying Eq. (12.9) with this relationship would show that u = c in the case of massless particles. Similarly, it is not difficult to show that the speed of a massive particle must be less than c in any given inertial frame. Moving on, from quantum mechanics, the energy of a photon in an inertial frame S is

where f and λ are its frequency and wavelength in frame S, related by c = fλ. Correspondingly, the momentum of a photon in frame S is

which is just the de Broglie relationship.
Problem: In inertial frame S, a photon of wavelength λ, that is initially traveling the x-direction, collides with a stationary electron with rest mass m. If the photon scatters at an angle θ from the x-axis, determine the resultant wavelength of the photon. This effect is known as Compton scattering.

Figure 12.4:Compton scattering
Referring to Fig. 12.4, let u be the resultant speed of the electron and let ux and uy be its components in the horizontal and vertical directions, positive rightwards and downwards. By the conservation of momentum and energy,
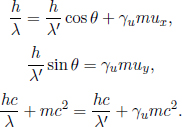
These equations appear tricky to solve because of ux and uy which are coupled in γu. However, notice that the resultant momentum and energy of the electron are not germane. Hence, we can eliminate them by using Eq. (12.8) astutely. Rewriting the equations in terms of the components of the momentum and the energy of the electron (via 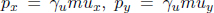 and
and 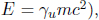

Applying E2 – p2c2 = m2c4 by taking the square of the last equation and subtracting it by the first and second equations squared and multiplied by c2,

Simplifying,

Multiplying both sides of the equation by 

Rest Energy and Mass of a System
The rest or invariant mass of a system msys is related to the total energy of the particles, combined with the potential energy due to internal interactions between the constituent particles (this component was excluded from the definition of the energy of a particle), denoted as Etot,CM, in the inertial frame in which the total momentum of the system is zero — this frame is known as the center-of-momentum frame. By definition,

Evidently, there are two factors that can affect the invariant mass of a system. Firstly, the total energy of each particle in the center-of-momentum frame may increase in a non-isolated system. In the case of an ideal gas whose particles lack potential energy, heating the gas causes the rest mass of the system to increase as the kinetic energy of the particles increases.
Another factor that affects the internal energy and thus the rest mass of the system would be the microscopic potential energy of its constituents due to their interactions (this was excluded from the total energy of each particle). This is the reason behind the large discrepancy between the mass of a proton and the sum of the individual rest masses of the component quarks.
As the rest mass of a system is dependent on both microscopic kinetic and potential energy, it is generally not equal to the sum of the rest masses of its constituents. In the case of non-interacting particles (collisions and decays are not counted here), the potential energy of the constituents is zero and the left-hand side of Eq. (12.13) is simply the sum of the energies of the constituent particles in the center-of-momentum (CoM) frame, ECM.

Furthermore, we claim that ECM can be expressed in terms of the dynamical properties observed in a general inertial frame in the following manner.
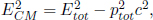
where Etot and ptot are the total energy and momentum of the system of particles in an arbitrary inertial frame S. This leap is not obvious now as we have yet to discuss how energy and momentum transform between inertial frames. However, the reader should just accept this for now. We will deduce this result and examine why the “invariant mass of a system” is indeed invariant later. Then,
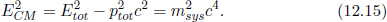
Let us consider the example in Fig. 12.5 to convince ourselves that the rest mass of a system indeed deviates from the sum of the rest masses of its constituents. In inertial frame S, a particle of mass 2m travels at a speed u in the positive x-direction while another particle of mass m travels at a speed u in the negative x-direction.

Figure 12.5:Two particles
Then the rest mass of the system comprising the two particles is given by Eq. (12.15).

which differs from the sum of the individual rest masses, 3m. In general, since the total energy and momentum is conserved in an isolated system, the rest mass of an isolated system remains unchanged too by Eq. (12.15). This is the conservation rule that replaces the classical conservation of mass. However, this is merely tautology as we have only created a new definition for 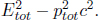 The important part lies in the fact that this quantity is in fact invariant across all inertial frames (and hence we term it the “invariant mass of a system”), as we shall prove. In practice, the rest mass of a system is not particularly useful as it is easily superseded by the formulation of four-vectors (as we shall see).
The important part lies in the fact that this quantity is in fact invariant across all inertial frames (and hence we term it the “invariant mass of a system”), as we shall prove. In practice, the rest mass of a system is not particularly useful as it is easily superseded by the formulation of four-vectors (as we shall see).
In the relativistic case, a net force on a system still leads to a rate of change of relativistic momentum. The forces are still of the same form as their classical counterparts (e.g. the elecromagnetic force is given by the Lorentz force law). However, the rate of change of relativistic momentum of a massive particle is no longer ma where a is its acceleration. The net external force f on a particle, as observed in an inertial frame S, engenders a rate of change of relativistic momentum.

where u and t are the coordinate velocity of the particle and coordinate time as observed in frame S. The lower-case letter shall be used to avoid confusion with the four-force four-vector which will later be defined with the uppercase letter. Note that there are two time-dependent terms in the expression above, γu and u. The time derivative of γu shall be evaluated first.


where a dot is used to denote a derivative with respect to coordinate time. The coordinate acceleration a of a particle is the derivative of its coordinate velocity u with respect to coordinate time t.

Hence, the expression above can be rewritten as

If the x-axis of the Cartesian coordinate system in frame S is defined to be along the direction of the particle’s instantaneous coordinate velocity u,

Now, the chain rule can be applied to Eq. (12.16) to obtain a simpler expression for f. Assuming that the rest mass of the particle remains constant,

it can be seen that the force on a particle f in an inertial frame S is not proportional to the coordinate acceleration of the particle a in the same inertial frame S. It is in fact easier to accelerate a particle in the transverse direction rather than the longitudinal direction! As a result, the force vector f is no longer necessarily parallel to the coordinate acceleration a.

Figure 12.6:Force and acceleration vectors
In Fig. 12.6, a force of magnitude f is exerted on a particle traveling at speed u in the x-direction, at an angle θ anti-clockwise relative to the positive x-axis in the lab frame S. Then, the angle θ′ that the coordinate acceleration makes with the x-axis in S is given by
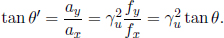
Furthermore, not only does the force not point along the direction of coordinate acceleration in most cases, the force vector varies across inertial frames as the coordinate velocity u in Eq. (12.16) changes in a way that affects its coordinate time derivative — contrary to the case in Galilean relativity. The transformation rules for force and coordinate acceleration will be derived in a later section.
Moving on, the confluence of the conservation of momentum and the definition of force implies a relativistic analog of Newton’s third law. If a particle A exerts a force on another particle B, A also experiences an equal and opposite force such that the total momentum of the two particles is conserved.
Another fact that one needs to get used to would be that the velocities of a particle in different directions are no longer independent. If a particle is initially traveling in the positive x-direction and a constant force is exerted on it in the y-direction, the x component of the velocity of the particle must decrease — without which, γu will increase as uy increases, leading to a violation of the conservation of momentum in the x-direction. However, the momentum of the particle in the x-direction in this case will still remain the same. The key takeaway from this is that one should focus on dynamical properties such as momentum and energy which often describe a system in a fashion that is more elegant than kinematic quantities such as coordinate velocities and accelerations directly.
Impulse-Momentum Theorem
Considering the definition of force, the impulse-momentum theorem can be expressed as

Power
Taking the derivative of 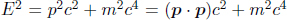 with respect to coordinate time and assuming that the rest mass m remains constant,
with respect to coordinate time and assuming that the rest mass m remains constant,

Since the force  and
and  where u is the coordinate velocity of the particle,
where u is the coordinate velocity of the particle,

It can be observed that the dot product of force and the particle’s coordinate velocity in frame S is equal to the power delivered by the net force in S, analogous to the classical scenario.
Work-Energy Theorem
If the dt in the denominator of Eq. (12.19) is shifted to the other side and the entire equation is integrated, the work-energy theorem is obtained.

where dr is an infinitesimal displacement of the particle in frame S. Again, this equation is built on the assumption that the rest mass of the particle remains constant. Lastly, if the instantaneous velocity of the particle is defined to be in the x-direction, Eq. (12.19) becomes

Hence,

At a certain instant in frame S, the force exerted on the particle in the direction of its instantaneous velocity is the change in the energy of particle due to an infinitesimal displacement, which must be along the direction of its instantaneous velocity.
Problem: In inertial frame S, a constant force f is exerted on an initially stationary particle of rest mass m. Find the time required for the particle to travel a distance s.
Well, this looks like an innocuous and typical kinematics question about a particle undergoing a one-dimensional acceleration. However, solving this problem by analyzing the equations of motion is incredibly tedious due to the γu terms. Instead, the dynamical equations should be used in an elegant manner. By the work-energy theorem, the final energy E of the particle is related to its initial energy (the rest energy) by

By the impulse-momentum theorem, the final momentum of the particle when it has traveled a distance s is

where t is the time interval between the start of the particle’s motion and the juncture at which it has traveled a distance s. Lastly, as 
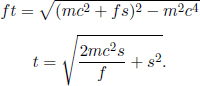
By now, you may have realized that the additional c’s popping up everywhere are extremely frustrating. Hence, we shall adopt the units c = 1 for the rest of the chapter to maintain our sanity and to simplify the equations. The c’s can always be added back to the expressions via dimensional analysis. So far, we have endured with the c’s to present a more “formal” formulation of the various dynamical properties of a particle so that one can clearly distinguish the relationship between these and the speed of light.
In the sections above, the definitions of various dynamical properties of a particle in a certain inertial frame S have been covered. However, since the chapter is on relativity after all, it is interesting to determine how these properties transform between inertial frames. The formulation of four-vectors encapsulates these transformations in a terse manner while also keeping the quintessential conservation laws. As such, the next few sections will elaborate on four-vectors and how these properties vary across inertial frames.
A four-vector is a matrix consisting of four entries that transforms between inertial frames according to the Lorentz transformations, in a manner similar to (ct, x, y, z). Four-vectors will be denoted by capital letters and units of c = 1 will be adopted henceforth. Consider a four-vector A, of the form:

A0 is known as the time-like component and is similar to t in the four-vector (t, x, y, z) while A1, A2 and A3 are known as the space-like components that correspond to x, y and z respectively. In an inertial frame S, the entries of A are shown above. The corresponding values as observed in an inertial frame S’ that travels at a velocity v in the positive x-direction relative to S are obtained by the Lorentz transformations.

where β = v in units of c. The above expressions can be represented more compactly via a matrix equation.

The matrix above will be referred to as the Lorentz transformation matrix  . The inverse transformation matrix
. The inverse transformation matrix  –1 can be obtained by adding a negative sign in front of the β’s while retaining the magnitude of v, which is equivalent to substituting v for –v.
–1 can be obtained by adding a negative sign in front of the β’s while retaining the magnitude of v, which is equivalent to substituting v for –v.
Property 1: Multiplying a four-vector by a constant or Lorentz scalar produces another four-vector. A Lorentz scalar is a quantity that has the same value in all inertial frames (e.g. the invariant interval (Δs)2).
Proof: Consider X = cA where A is a four-vector and c is a constant or Lorentz scalar. Then, X′ in another inertial frame obeys

where we have used the fact that c′ = c. This shows that X is a four-vector as it transforms according to the Lorentz transformations. Now, it is tempting to exploit the seemingly distributive nature of the Lorentz transformations and claim that any linear combination of four-vectors produces another four-vector. However, we have to understand that four-vectors are generally associated with physical properties of particles. A linear combination of four-vectors may be the sum of four-vectors (multiplied by constants or scalars) evaluated at the same time in a frame S but applying a Lorentz transformation to it and using the distributive rule would result in a linear combination of four-vectors evaluated at different times! This is the result of the loss of simultaneity between events that are spatially separated (this occurs as the four-vectors usually correspond to properties of different particles). Therefore, the linear combination of four-vectors is, foremost, meaningless. Its value at a certain instance in another inertial frame (i.e. all of its component four-vectors are determined simultaneously) most definitely cannot be computed via a Lorentz transformation of its value at a certain instance in a precedent inertial frame.
Definition: The inner product of two four-vectors A and B is defined as

Note that the inner product is commutative and distributive. In other words,
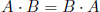
and
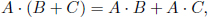
where A, B and C are four-vectors.
Property 2: The inner product of any two four-vectors is Lorentz invariant (i.e. a scalar).
Proof: Consider a Lorentz transformation in the x-direction.

A similar statement can be made for Lorentz transformations in the other spatial directions.
Corollary: The inner product of a four-vector with itself, |A|2, is Lorentz-invariant and is defined as its squared norm. This immediately follows from above.

An apt illustration of this invariance would be the invariant interval (Δs)2 introduced in the previous chapter which is basically the norm of 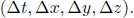
Property 3: If the inner product of A and B produces the same scalar in all inertial frames while A is a four-vector, then B must also be a four-vector.
The premise is basically stating that

for all pairs of frames. Now, we know from the proof in Property 2 that
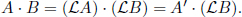
Therefore,

Now, we can prove that B′ = 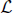 B by astutely substituting appropriate values for A′ (since it can be tweaked). Substituting A′ = (1, 0, 0, 0) would show that the first entries of B′ and
B by astutely substituting appropriate values for A′ (since it can be tweaked). Substituting A′ = (1, 0, 0, 0) would show that the first entries of B′ and 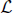 B are equal. Repeating this for similar “unit vectors” would prove that
B are equal. Repeating this for similar “unit vectors” would prove that

Therefore, B must be a four-vector.
Leveraging Properties 1 and 3, we can develop a repository of four-vectors that will be immensely expeditious in the problems that we will encounter.
The four-coordinate vector is defined as
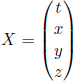
where t, x, y and z are the temporal and spatial coordinates of an event in an arbitrary inertial frame S. Its squared norm guarantees the invariance of s2 = t2 – x2 – y2 – z2.
If the coordinates describe the world line of a particle, then the invariant interval must be time-like (i.e. (Δs)2 > 0). Now, recall that the infinitesimal proper time interval between two events separated by an infinitesimal segment along the world line of a particle is defined as the infinitesimal time between them as measured in the frame of the particle. Since the particle remains still in its own rest frame, ds2 = dτ2. Expressing this in terms of the coordinates observed in a general inertial frame S,
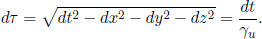
Note that the infinitesimal proper time interval dτ is measured in the frame of the particle while the infinitesimal coordinate time interval dt is measured in the current inertial frame S. The last equality is obtained from extracting dt from the brackets in the second last expression (γu is associated with the velocity of the particle in frame S, u). The proper time elapsed between two events is then obtained from integrating the above expression.
The concept of proper time is particularly useful in two areas. Firstly, it presents another way to describe the motion of a particle by considering the proper coordinates, which are coordinates as measured in its own rest frame. Then, the corresponding coordinates in a general inertial frame can be obtained via the Lorentz transformations. Secondly and more importantly, the proper time interval is a Lorentz scalar — evident from the fact that it is directly related to the invariant interval. Invariant quantities are sacrosanct in the context of special relativity. Utilising the invariance of proper time, many other four-vectors can be formulated via the following procedure.
Property 4: If A(t) is a four-vector ascribed to a particle where t is the coordinate time in the current inertial frame,  where τ is the proper time elapsed in the particle’s rest frame — is a four-vector.
where τ is the proper time elapsed in the particle’s rest frame — is a four-vector.
Proof: From the first principles of calculus,

where the coordinate time t(τ) is a function of proper time τ such that 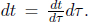 We can deem the above as dividing A(t + dt) – A(t) by dτ. Since dτ has been shown to be Lorentz invariant, we just have to show that A(t + dt) – A(t) is a valid four-vector to prove that X is a four-vector (as we can subsequently apply Property 1).
We can deem the above as dividing A(t + dt) – A(t) by dτ. Since dτ has been shown to be Lorentz invariant, we just have to show that A(t + dt) – A(t) is a valid four-vector to prove that X is a four-vector (as we can subsequently apply Property 1).
Now, even though A(t + dt) – A(t) is a linear combination of four-vectors, the issue highlighted in the comments of Property 1 does not crop up here because A(t + dt) and A(t) describe the same particle, and the time interval dt between them is infinitesimal such that the loss of simultaneity (due to the particle being at possibly different locations at t and t + dt) in a new inertial frame S’ is infinitesimal2 and can be absorbed into the infinitesimal time interval dt′ in S’. With this clarification, it is easy to prove that A(t + dt) – A(t) is a four-vector. A′(t + dt′) – A(t′) in another inertial frame S’ obeys
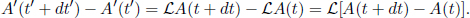
Thus,  is a valid four-vector.
is a valid four-vector.
By Property 4, taking the derivative of the four-coordinate of a particle in an arbitrary inertial frame S with respect to its proper time produces a new four-vector, known as the four-velocity U of the particle. Since 

where u is the velocity of the particle in frame S. Notice that the spatial component of the four-velocity does not describe the velocity of the particle in frame S directly. It is the derivative of spatial coordinates observed in frame S with respect to the proper time interval which is observed in the frame of the particle. Hence, the four-vector itself lacks physical meaning. However, it is indirectly related to the coordinate velocity u. The sole purpose of such a definition is its utility as a four-vector — namely, its transformations and inner product invariance. This will be a recurring theme for many of the other four-vectors in the following sections.
An example of the utility of the four-velocity would pertain to the derivation of the velocity-addition formulae. Let u and u′ be the three-velocities in inertial frames S and S’ respectively. Then, the four-velocity in S’ can be obtained from that in S via a Lorentz transformation.
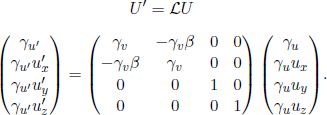
Comparing first entries, we obtain the relationship between the gamma factors in both frames.
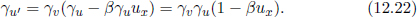
Comparing the second entries, the longitudinal velocity addition formula can be obtained.

where we have used the previous result. Comparing the third entries, the transverse velocity addition formula can be obtained.

A similar statement can be made for uz′.
Next, the squared norm of the four-velocity can be easily computed by considering the rest frame of the particle as the squared norm is Lorentz invariant. In the rest frame of the particle,
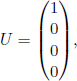
as the velocity of the particle in its own frame is zero. Hence, the squared norm of the four-velocity is

Another important property is the inner product of the four-velocities of two different particles, U1 and U2. This can be evaluated in the rest frame of one of the particles. Then, let urel denote the velocity of the other particle in this rest frame. The inner product of the two four-velocities in this frame is then

It can be observed that this inner product is minimized when the relative velocity urel is zero (i.e. the two particles travel at the same velocity in any arbitrary inertial frame). When considering the rest frame of a particle, it was implicitly assumed that the particle traveled at a subluminal speed. If not, there would not have been a rest frame for that particle. However, this is perfectly fine as the four-velocity is ill-defined for massless particles which travel at the speed of light.
Next, the consideration of the rest frame of the particle in computing the inner product of its four-velocity with another four-vector enables the isolation of the first entry of the other four-vector, as the first entry of the four-velocity is one while the others are all zero in the rest frame of the particle. The utility of this will be illustrated in a later section.
Once again, the four-velocity can be differentiated with respect to the proper time τ to produce yet another four-vector which is termed as the four-acceleration. The four-acceleration in an arbitrary inertial frame S is

It has been shown that

where a is the coordinate acceleration, 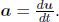 Hence, the four-acceleration can be expressed as
Hence, the four-acceleration can be expressed as

If the x-axis of frame S is chosen such that it is aligned with the instantaneous coordinate velocity of the particle u, the four-acceleration becomes

where we have used the fact that

Once again, individual entries of the four-acceleration do not have obvious physical meanings. However, the four-acceleration provides a convenient pathway to derive how different components of acceleration transform between inertial frames.
Sometimes, a need to relate the coordinate acceleration in an inertial frame S to the proper acceleration in the rest frame of the particle may arise. Let the four-accelerations in frame S and the rest frame of the particle be A and A’ respectively. Assuming that the particle travels at a speed u in the positive x-direction in frame S,
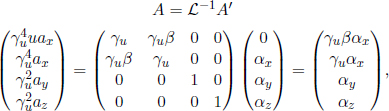
where we have substituted v = u to switch between S and the rest frame of the particle. Comparing the corresponding terms, the proper accelerations, which are denoted by the symbol α, are given by

Multiplying the four-velocity of a particle by its rest mass produces the four-momentum of the particle in an arbitrary inertial frame S.
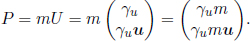
Observe that the first entry is simply the energy of the particle in frame S while the three-vector below corresponds to the momentum of the particle in frame S. Hence,
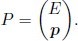
Note that even though the four-velocity is ill-defined for massless particles, the four-momentum remains well-defined. Since the total energy and momentum in an isolated system is conserved, the sum of all relevant four-momenta should be equal at two different instances in the same frame — encapsulating the two conservation laws into a single four-vector equation. This combined with the squared norm of a four-momentum can greatly simplify calculations. The squared norm of a four-momentum can be computed in the rest frame of the particle (if it is massive). In this frame,

Hence, the squared norm of the four-momentum of a massive particle is
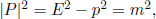
which is basically Eq. (12.8). Actually, the above equation is also valid for massless particles (m = 0) for which E = p such that E2 – p2 = 0 – it is therefore entirely general. Next, we make a rather bold claim that the sum of four-momenta in a system undergoing purely local interactions is another four-vector. This seemingly contradicts what we have said in the comments of Property 1 of four-vectors but we are saved by the conservation of momentum and energy here. Let the total four-momentum of a system be

When evaluating Ptot at a certain time t = t0 in a certain frame S, we mean to sum up all Pi’s evaluated at time t = t0. However, note that the actual value of Ptot should be irrespective of time t, as it is conserved. Now, consider another inertial frame S’ with the conventional definition. When calculating  at a certain time
at a certain time  , we similarly add all P′i’s evaluated at time
, we similarly add all P′i’s evaluated at time  but these cannot possibly correspond to events that are simultaneous in frame S, due to the spatial separations of particles. Then, the constituent P′i’s cannot simply be obtained from the Lorentz transformations,
but these cannot possibly correspond to events that are simultaneous in frame S, due to the spatial separations of particles. Then, the constituent P′i’s cannot simply be obtained from the Lorentz transformations,  in general. However, by asserting that Ptot is a four-vector, we are claiming that
in general. However, by asserting that Ptot is a four-vector, we are claiming that

as a whole. Again, 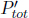 should be independent of time, as energy and momentum are also conserved in S’ by the principle of relativity.
should be independent of time, as energy and momentum are also conserved in S’ by the principle of relativity.

Figure 12.7:World lines of particles and lines of simultaneity
If a system of particles only undergoes short-range interactions, the energies and momenta of individual particles (and possibly new particles formed) can only change when they come into the immediate vicinity of one another (i.e. when their world lines intersect in Fig. 12.7). Then, when evaluating Ptot, we can deliberately choose to evaluate Pi at non-simultaneous times in S but simultaneous times in S’ while capitalizing on the fact that the individual energies and momenta of particles can only vary at space-time junctions and will remain constant at other times. The existence of a valid set of times that should be chosen is best visualized by the Minkowski diagram depicting the world lines of various particles in frame S in Fig. 12.7. A line of simultaneity in frame S’ superimposed on the diagram is a line that subtends an angle smaller than 45° from the horizontal. Since the slope of a world line must be larger than or equal to 45°, it is impossible for a line of simultaneity to cut across the world lines of interacting particles and divide the intersected events into two groups — those before their interaction and those after their interaction. The times of the intersected events must always lie on one temporal side, with respect to the time of interaction of the particles. Therefore, it is always possible to choose a set of events that both correctly represent Ptot collectively and are simultaneous in S’. For the diagram in Fig. 12.7, three possible lines of simultaneity are drawn and the intersections along a single line form a possible set of events at which the individual Pi’s can be evaluated. Then, applying a Lorentz transformation to each of these distinct four-momenta would yield four-momenta evaluated concurrently in S’, after which they can be summed to determine  . Therefore,
. Therefore,  is simply obtained from the Lorentz transformation of Ptot.
is simply obtained from the Lorentz transformation of Ptot.

This proves that Ptot is a valid four-vector for collisions (and decays). Another perspective to this is that we can gradually rotate a horizontal line — anchored about a certain point — into the final line of simultaneity (akin to considering the lines of simultaneity of a continuous set of frames). The sum of the individual energies and momenta of the particles along an intermediate line of simultaneity during this rotation cannot change. This is because the individual energy and momentum of a particle recorded during this rotation will only change during an interaction. However, even during such interactions which occur at space-time intersections between particles, the total energy and momentum of the system of particles do not change by the conservation laws.
Armed with this machinery, the square of the total energy of the particles in the center-of-momentum frame of a system  can be proven to be
can be proven to be  where Etot and ptot are the total energy and momentum of the system of particles in an arbitrary inertial frame S; this was used to derive Eq. (12.15). Let the sum of all four-momenta of the particles in the system in frame S and the center-of-momentum frame be Ptot and
where Etot and ptot are the total energy and momentum of the system of particles in an arbitrary inertial frame S; this was used to derive Eq. (12.15). Let the sum of all four-momenta of the particles in the system in frame S and the center-of-momentum frame be Ptot and  respectively. Then,
respectively. Then,

The squared norm of the two matrices above should be equal as they are the same four-vector observed in different inertial frames. Thus,

The last equality stems from the fact that the total mass of a system msys of non-interacting particles is, by definition, given by 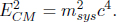 This relationship also proves the invariant nature of the invariant mass of a system, msys.
This relationship also proves the invariant nature of the invariant mass of a system, msys.
Problem: A particle of rest mass m1 and initial momentum p1 collides with another stationary particle of rest mass m2. It is known that the final velocities of these particles are perpendicular to each other and non-zero. If the rest masses of the particles remain constant, determine the magnitudes of the resultant momenta of the two particles.

Figure 12.8:Collision with perpendicular final velocities
Define the coordinate axes to be parallel to the final velocities and define angle θ as shown in Fig. 12.8. Then, let the four-momenta of particles m1 and m2, before and after collision, be

By the conservation of energy and momentum,
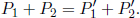
Now, we may be tempted to equate each of the rows of the four-vectors and solve for the required expressions. However, this will be extremely tedious due to the energies E1, 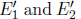 being surds in terms of their corresponding momenta. A better method would entail taking the squared norm of both sides of the equations.
being surds in terms of their corresponding momenta. A better method would entail taking the squared norm of both sides of the equations.
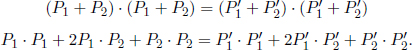
Since the rest masses of the particles remain unchanged after the collision,
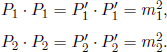
The equation above then becomes

Up till now, we have not assumed anything about the exact expression of any of the four-momenta in the equation above. Hence, this equation is valid for all collisions between two particles that are rest-mass preserving — such collisions are known as elastic collisions in the context of special relativity. The reason behind this terminology will be explicated immediately after this problem. Substituting the expressions for the four-momenta into the equation above,
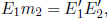
where we have deliberately tweaked the coordinate axes to elucidate the orthogonality of the three-momenta of 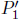 and
and 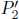 . Using the fact that E2 = p2 + m2 for a particle,
. Using the fact that E2 = p2 + m2 for a particle,

Squaring and simplifying,
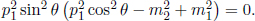
Since the final momentum of the second particle must be non-zero, sin θ ≠ 0.

Notice that the condition for the resultant configuration of velocities after the collision to be possible is 
Inner Product of Two Four-Momenta
The inner product of the four-momenta of two different particles of rest masses m1 > 0 and m2 > 0 can be evaluated in the rest frame of one particle as

where urel is the speed of one particle in the rest frame of the other particle. The second equality is obtained from applying Eq. (12.23). Hence in the case of a rest-mass preserving collision described in the previous example, the speed of one particle in the rest frame of the other particle must be the same before and after the collision (note that these are two different rest frames as the particle’s velocity may have changed). Since this “relative speed” remains unchanged, such a collision is known as an elastic collision.
When m1 > 0 and m2 ≥ 0, we can evaluate the inner product in the rest frame of the first particle. In this frame, P1 = (m1, 0) and P2 = (Erel, prel), where Erel and prel are the energy and momentum of the second particle.

Moving on, Eq. (12.24) implies that two massive particles should have zero relative velocity to minimize the inner product of their four-momenta. On another note, it can be easily shown, by using the fact that E = pc for a massless particle, that the inner product of the four-momenta of a mass-less particle and a massive particle or of two massless particles, is similarly minimized when both particles move in the same direction in an inertial frame.
Threshold Energy
Often, reactions are initiated by bombarding a stationary particle with another particle, producing new particles of various rest masses. The problem of finding the threshold energy entails determining the minimum amount of energy that the incoming particle must possess to spark off the reaction. Note that the required condition in such situations is not that the kinetic energy of the incoming particle must be equal to the sum of the additional rest masses of the final configuration as the product particles must still possess a certain amount of kinetic energy by the conservation of momentum. Let us derive a general formula for the threshold energy of a reaction that produces only massive products. Let the four-momenta of the incident and stationary particles be Pa and Pb respectively, and let there be k final particles with the ith particle having a four-momentum Pi and mass mi > 0. The incident particle is possibly massless (but if it is, it must be absorbed as all products are massive) while the receiving particle is massive. By the conservation of momentum and energy,
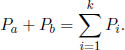
Taking the inner product of both sides of the equation,
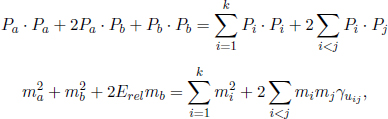
where Erel is the energy of the incident particle in the rest frame of the receiving particle — it is simply the energy Ea of the incident particle in the current inertial frame, since the receiving particle is stationary in this frame! Meanwhile, uij is the relative speed between the ith and jth particle in one of their rest frames. Using Erel = Ea and rearranging,

Note that all quantities are predetermined except γuij. To minimize Ea, γuij must attain its minimum value of unity, which occurs when uij = 0, for all i and j. This implies that all resultant particles travel together in a “blob” after the process, akin to a perfectly inelastic collision in classical mechanics. Then, the threshold energy is

Transformations of Energy and Momentum
The combination of the three-momentum and energy of a particle as a four-vector elucidates their transformations across inertial frames. If the components of the momentum of a particle in the x, y and z-directions are px, py and pz respectively and if its energy is E in an inertial frame S, the corresponding quantities, denoted by appending a prime, in an inertial frame S’ that travels at a velocity v in the x-direction are obtained from the Lorentz transformations.

Four-Frequency
As illustrated previously, the energy and momentum of a photon in an inertial frame are E = hf and  respectively. Hence the four-momentum of a photon in an inertial frame S is
respectively. Hence the four-momentum of a photon in an inertial frame S is
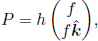
where f is the frequency of the photon as observed in frame S. 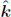 is a unit vector along the velocity of the photon in frame S. For the sake of convenience, we define a new four-frequency four-vector as
is a unit vector along the velocity of the photon in frame S. For the sake of convenience, we define a new four-frequency four-vector as

since multiplying a four-vector by a constant generates another four-vector. Notably, the squared norms of the four-momentum of a photon and the four-frequency are zero.
Surprisingly, the particulate nature of light allows us to deduce many relativistic effects pertaining to the wave nature3 of light via the four-frequency vector. Consider a photon, of frequency f, that is traveling at an angle θ relative to the x-axis in an inertial frame S. We define the y-axis such that the motion of the particle is solely confined to the xy-plane.
We would like to determine the frequency f′ of this photon and the angle θ′ it makes with the x’-axis in an inertial frame S’ that is traveling at a velocity u in the positive x-direction with respect to frame S. Let the four-frequencies of the photon in S and S’ be
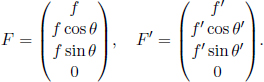
F′ can be obtained from F via a Lorentz transformation.

Comparing the first entries,

This is the formula for the relativistic Doppler effect! Consider Fig. 12.9, in which a photon emanates from a source and reaches the eye of an observer. The left diagram shows frame S, which is the rest frame of the source. In this frame, the observer is traveling at a speed u in the positive x-direction and f is the frequency of the photon. On the other hand, the right diagram depicts the rest frame of the observer, S’. The source now travels at the same speed in the opposite direction while the frequency of the photon is now f′.

Figure 12.9:Source emitting photons in different frames
The longitudinal case can be easily derived by setting θ = 0.

Similar to Problem 12 in the previous chapter, there are two cases to consider in the transverse situation — namely, the frequencies of the received photons, observed by the observer, emitted as the source crosses the line of sight of the observer and that of photons reaching the eyes of the observer when the source crosses the vertical line of sight of the observer. In the second case,  as the photon reaching the observer’s eyes would have taken a vertical path in frame S (i.e. the photons were already emitted before the observer and the source formed a vertical line). Then,
as the photon reaching the observer’s eyes would have taken a vertical path in frame S (i.e. the photons were already emitted before the observer and the source formed a vertical line). Then,

In the first case, the photons are emitted when the observer crosses the vertical line in frame S (see Fig. 12.10) and thus reach the observer after the observer crosses the vertical line.
In this case, cos θ will be u. Substituting this back into the equation,
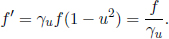
The four-frequency can also be used to derive the aberration formula (Problem 6 in Chapter 11). Comparing the second entries,
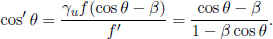

Figure 12.10:Emission of photon when observer crosses line of sight
Problem: A photon of frequency f is normally incident on an infinitely massive and perfectly reflective mirror that is retracting at a velocity u in inertial frame S. Determine the frequency f′ of the photon after the reflection in frame S.
The initial four-frequency of the photon in frame S is

Let S’ be the frame that travels at a velocity u relative to S (i.e. the mirror is initially at rest in this frame). The initial four-frequency in S’ is obtained from the Lorentz transformations.
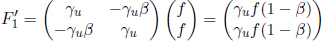
where β = u. After the reflection, the four-frequency in frame S’ is

as the photon just reverses its momentum after its collision with the stationary massive mirror (for energy to be conserved, since the infinitely massive mirror gains negligible kinetic energy). Lastly, an inverse Lorentz transformation can be applied to return to the original frame S.
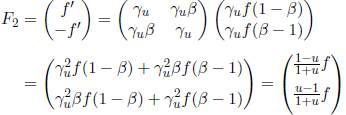
The four-force is obtained by differentiating the four-momentum with respect to proper time.
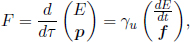
as the definition of the three-force is  To simplify the first entry, consider the inner product of the four-force with the four-velocity in the rest frame of the particle (which exists because the four-force is usually only defined for massive particles).
To simplify the first entry, consider the inner product of the four-force with the four-velocity in the rest frame of the particle (which exists because the four-force is usually only defined for massive particles).
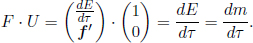
It can be seen that F · U is just the rate at which the internal energy of the particle changes in its rest frame, which is also equal to the rate of change of its rest mass in its rest frame. This expression is Lorentz invariant as it is an inner product of two four-vectors. Evaluating this in a general inertial frame S, in which the velocity of the particle is u,
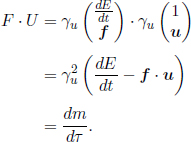
Usually, the problems that we will encounter do not involve a change in the rest mass of the particle. In such cases,  and
and

as expected from the previous discussion on the three-force. The four-force can then be rewritten as

Furthermore, observe that when the rest mass of the particle remains constant,

where A is the four-acceleration. This is the relativistic counterpart of the F = ma equation in classical mechanics, except that the respective terms are now four-vectors instead of three-vectors.
Force Transformations
Equipped with the four-force, the transformation of forces between a lab frame S and a particle’s rest frame S’ can be derived. It is assumed that the particle travels at a velocity u in the positive x-direction in frame S and that the rest mass of the particle remains unchanged. The four-force in S’ is

The first entry is zero as the velocity of the particle is zero in its own rest frame. The four-force in S is related to that in S’ by a Lorentz transformation.
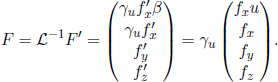
Comparing the terms,

These are the transformation rules for forces in an arbitrary frame S and the rest frame of the particle.
In general, a traveling plane wave can be described by the equation
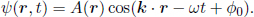
Setting the source of the wave as the origin, ψ is the displacement at a point whose position vector is r, at time t in frame S. k is the wave-vector and ω is the angular frequency. A is the amplitude of the wave which varies as some function of r while ϕ0 is the constant phase offset of the source. The phase of the wave, which is enclosed in the brackets, is

The important observation here is that the phase of a wave at a particular point in time and space in an inertial frame S should be the same as that at the corresponding time and space, after a Lorentz transformation, in another inertial frame S’, as the phase corresponds to a physical event. It measures the state of the displacement at a certain point in space, relative to all other points, at a given time. If an event is a peak in frame S, the corresponding event will still be a peak in frame S’. Hence, the phase must be a Lorentz scalar. Then, as the second vector is a four-vector and the right-hand side is a Lorentz scalar,

is a four-vector in units of c by Property 3 — referred to as the four-wave vector. Note that the relationship

still holds in any inertial frame S where u is the phase velocity of the wave. The fact that the angular frequency and the wave numbers of a plane wave form a four-vector is extremely convenient in determining the transformation of properties related to waves.
For example, the longitudinal Doppler effect for a wave with a frequency f and speed u in an inertial frame S can be computed relatively easily. Let f′ be the frequency of the wave as observed in the frame S’ that is traveling at a velocity v longitudinally relative to frame S. Then, the four-wave vectors in S and S’ are

respectively. From the Lorentz transformations,
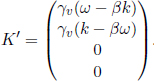
Hence,

Since u = fλ,

One of Einstein’s motivations behind special relativity was how similar effects in electromagnetism were attributed to the different entities — electric and magnetic fields. Consider a charged particle and a stationary magnet in frame S. The moving charge experiences a magnetic force due to the magnetic field but no electric force due to the absence of an external electric field. Now consider the instantaneous rest frame of the particle S’, in which the magnet is now moving. Though there is still a magnetic field, there is no magnetic force on the particle as it remains stationary. However, there is now a non-conservative electric field induced by the time-varying magnetic field which causes the charge to experience an electric force. Einstein firmly believed that these seemingly disparate effects were linked by a more general theory.
It turns out that electric and magnetic fields are essentially the same entity, as observed in different frames. The electric and magnetic fields at corresponding points in space and time in inertial frames S and S’ (which travels at v relative to S) are related by
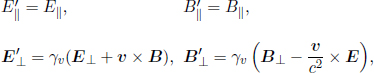
where || and 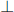 denote directions parallel and perpendicular to the velocity v, respectively. Note that the equations on the second row are vectors. It can be seen that the perpendicular components of the electric and magnetic field in frame S’ need not lie along the same direction as their counterparts in frame S. If frame S’ travels at a speed v in the positive x-direction relative to frame S, the transformations can be expressed in Cartesian coordinates as
denote directions parallel and perpendicular to the velocity v, respectively. Note that the equations on the second row are vectors. It can be seen that the perpendicular components of the electric and magnetic field in frame S’ need not lie along the same direction as their counterparts in frame S. If frame S’ travels at a speed v in the positive x-direction relative to frame S, the transformations can be expressed in Cartesian coordinates as
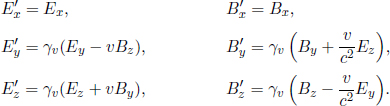
Proof: The transformations above can be deduced from the four-force vector corresponding to the Lorentz force on a charged particle in an electromagnetic region. Note that the transformations should actually be independent of the physical existence of such a particle as the external fields4 themselves are physical entities which persist without regard of anything besides their sources. The charged particle is merely a construct — a stepping stone — in identifying these transformations.
The Lorentz force law exerts that the force on a charge q in frame S is
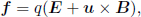
where u is the velocity of the particle in S. The idea here is to relate the forces (and power) in two inertial frames to deduce the electromagnetic field transformations.
Firstly, consider a charged particle, with unit charge5 for the sake of convenience, and velocity u = (u, 0, 0) in frame S. The Lorentz force on the particle is
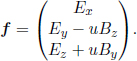
The four-force vector in frame S is then
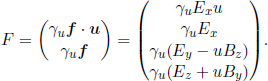
Now, we proceed to an inertial frame S’ which travels at velocity u in the x-direction relative to S such that the charge is stationary in this frame. The force on the charge in S’ is then

where E′ is the electric field in frame S’. The four-force vector in S’ is thus

Furthermore, we know that F′ and F are related by the Lorentz transformations.

with β = u. Comparing the two expressions for F′,

where we have substituted v for u as we have the prerogative to choose u (i.e. because u is arbitrary). The transformations for the magnetic field can in fact be obtained from the above via some astute manipulations. Firstly, the above implies that the inverse transformations are
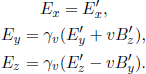
From the second equation,

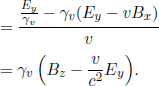
Similarly, from the third equation,

Now, we need to consider a separate charged particle to determine  as the force on a charged particle that is traveling solely along the x-direction will be independent of the x-component of the magnetic field. Consider a unit charge which travels at u = (0, 0, u) in S. The four-force in S is
as the force on a charged particle that is traveling solely along the x-direction will be independent of the x-component of the magnetic field. Consider a unit charge which travels at u = (0, 0, u) in S. The four-force in S is
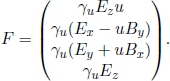
In frame S’ which travels at velocity v relative to S, in the x-direction, the velocity of the particle is  by the velocity addition formula. The y-component of the four-force F′ in S’ is thus
by the velocity addition formula. The y-component of the four-force F′ in S’ is thus

Another expression for  can be obtained from applying a Lorentz transformation to the four-force F.
can be obtained from applying a Lorentz transformation to the four-force F.

Since  by Eq. (12.22) with ux = 0,
by Eq. (12.22) with ux = 0,

Since 

We have hence completed the derivation of the field transformations.
Finally, note that the laws of electromagnetism (Maxwell’s equations) are still valid in the relativistic case. Meanwhile, the Lorentz force law now engenders a rate of change of relativistic momentum. Moreover, a crucial property when switching between inertial frames is that the quantity of electric charge is invariant, though charge densities may differ due to length contraction.
Let us verify the transformation rules using the following example. Consider a standard parallel plate capacitor that consists of two large plates with width w and length l, separated by a distance d (d  w and d
w and d  i). Each plate carries a charge Q. In inertial frame S, the plates are stationary at the coordinates depicted in Fig. 12.11.
i). Each plate carries a charge Q. In inertial frame S, the plates are stationary at the coordinates depicted in Fig. 12.11.

Figure 12.11:Capacitor plates in frame S
In this frame, there is an electric field (by Gauss’ law) between the plates with components:

where  is the surface charge density of the positive plate. The magnetic field in frame S is zero everywhere due to the absence of moving charge. Now, consider a frame S’ that travels at a velocity v in the x-direction relative to frame S. The configuration of the plates as observed in S’ is depicted in Fig. 12.12.
is the surface charge density of the positive plate. The magnetic field in frame S is zero everywhere due to the absence of moving charge. Now, consider a frame S’ that travels at a velocity v in the x-direction relative to frame S. The configuration of the plates as observed in S’ is depicted in Fig. 12.12.
Firstly, the new surface charge density σ′ is larger than that in S by a factor of γv due to length contraction.
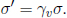
The electric field between the capacitor plates in this frame at any instant is then

Figure 12.12:Capacitor plates in frame S’

in correspondence with the electric field transformations stated at the start of this section. However, we are not done here. The charged plates are now traveling at a speed v in the negative x’-direction. Hence, they constitute a current similar to an infinite current sheet (the y’z’-plane is akin to the cross section). Drawing an Amperian loop, with edges parallel to the y’ and z’ axes, that cuts only one plate and extends to infinity, we obtain

The magnetic field in the region between the plates is taken to be uniform, as the plates are large. The total enclosed current in this case is the charge crossing the loop per unit time and is given by
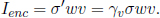
Hence,

Let us verify that this is consistent with the purported electric and magnetic field transformations.

Next, by using the fact that 
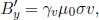
which is the answer that we had obtained from applying Ampere’s law in frame S’. One can also check that the transformations imply that there is no component of the magnetic field in the x’ and z’-directions.
In this section, the electric and magnetic fields due to a point charge traveling at a constant velocity v in frame S will be determined by considering the corresponding quantities in the rest frame S’ of the charge; this is a very important result. We define the vectors shown in Fig. 12.13 (the diagrams are drawn in 2-D and the velocity v is depicted to be along the x-axis for convenience).
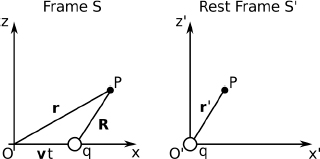
Figure 12.13:Frame S and rest frame S’
The charge lies at the origin O in frame S at t = 0. Hence, the position vector of the charge q at time t in frame S is given by vt. r and r′ are the position vectors of point P, the location at which the electromagnetic field is of interest, with respect to the origins of S and S’ respectively. R is the vector pointing from the instantaneous position of the charge to point P in frame S. The components of the electric field in frame S’ are given by Coulomb’s law as

where  The magnetic field due to the charge is zero everywhere in frame S’. Hence, the transformations of the electric fields give
The magnetic field due to the charge is zero everywhere in frame S’. Hence, the transformations of the electric fields give
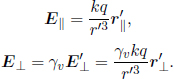
Therefore,

Ideally, we wish to express this in terms of the quantities in frame S. From the Lorentz transformations,

as  and
and  as illustrated in Fig. 12.13. Then,
as illustrated in Fig. 12.13. Then,

The electric field in frame S can then be expressed as

If we define θ to be the angle subtended by the vectors vt and R when they are placed tail to tail,
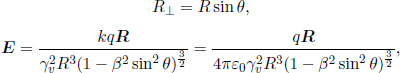
with 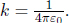 In the non-relativistic limit β → 0, this expression reduces to the familiar Coulomb’s law.
In the non-relativistic limit β → 0, this expression reduces to the familiar Coulomb’s law.

Now, the magnetic field can similarly be obtained from the transformations.

as 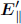 is defined to be in the direction of v, causing
is defined to be in the direction of v, causing 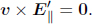 Then,
Then,

Therefore, the magnetic field at point P in frame S is simply
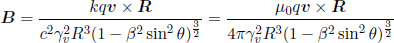
as  and
and  In the non-relativistic limit, β → 0,
In the non-relativistic limit, β → 0,
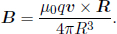
This expression is similar to substituting qv for 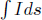 in the Biot-Savart law. However, they arise from different premises. The Biot-Savart law is only valid for steady currents and a single moving charge most definitely does not constitute a steady current (as the net charge at various positions varies with time) and is an empirical law. The above derivation is a consequence of Coulomb’s law, charge invariance and special relativity. It just happens that in the non-relativistic limit, the above expression reduces to something similar to the Biot-Savart law. The derivation of this result from purely classical tools (specifically, the Ampere–Maxwell law) was the subject of Problem 25 (Chapter 8).
in the Biot-Savart law. However, they arise from different premises. The Biot-Savart law is only valid for steady currents and a single moving charge most definitely does not constitute a steady current (as the net charge at various positions varies with time) and is an empirical law. The above derivation is a consequence of Coulomb’s law, charge invariance and special relativity. It just happens that in the non-relativistic limit, the above expression reduces to something similar to the Biot-Savart law. The derivation of this result from purely classical tools (specifically, the Ampere–Maxwell law) was the subject of Problem 25 (Chapter 8).
Problems
Problems without Four-Vectors
1.“Infinite” Energy Generator*
Tom proposes the following mechanism to generate “infinite” energy. Orient two perfectly reflective mirrors (of arbitrary masses) such that they are mutually parallel and stationary initially. Now, place a photon between the two mirrors such that it impinges the mirrors normally. As the photon bounces back and forth between the two mirrors, it imparts momentum and thus kinetic energy to the two mirrors. Furthermore, the photon can always catch up with the mirrors, even if the mirrors begin to pick up speed so this process will continue indefinitely — producing “infinite” kinetic energy. What is wrong with Tom’s reasoning? Now, consider a new set-up where the two mirrors are identical and initially stationary. Two photons, with initial velocities in opposite directions and initial frequency f each, impinge normally on the two mirrors repeatedly. What is the final kinetic energy of each mirror after a long time?
2.Exploding Particle*
A particle of rest mass m is traveling in the positive x-direction at velocity u in the lab frame. It then disintegrates into two identical particles of rest mass  each. Determine the velocities of the product particles in the lab frame if they are aligned with the x-axis.
each. Determine the velocities of the product particles in the lab frame if they are aligned with the x-axis.
3.Available Energy*
A particle of rest mass m1 is bombarded at another stationary particle of rest mass m2 at initial velocity u. If this collision triggers the production of a third particle (while retaining the rest masses of the other two), determine the maximum rest mass of the third particle.
A particle of unknown mass M decays into two particles of known masses ma = 0.5GeV/c2 and mb = 1.0GeV/c2, whose momenta are measured to be pa = 2.0GeV/c directed along the y-axis and pb = 1.5GeV/c directed along the x-axis. Find the unknown mass M and its speed (in units of c).
5.Positron-Electron Collision*

Determine the minimum initial energy of the electron or positron for this reaction to occur in the center-of-momentum (CoM) frame in terms of the rest masses mψ and me. Hence, find the threshold energy of the positron if the positron is bombarded at the stationary electron in the lab frame, without the aid of Eq. (12.26).
6.Relativistic Photon Rocket*
A rocket is initially stationary with a rest mass Mi in the lab frame S. The rocket then begins to convert mass into photons and ejects them from the back. When the rest mass of the rocket is Mf, prove that its speed u in frame S fulfils
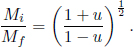
7.Relativistic Mass Rocket**
In the lab frame S, a relativistic rocket of initial rest mass Mi is initially stationary. The rocket then begins to eject mass continuously in minuscule amounts at one instant, towards the back, at a velocity u relative to its instantaneous rest frame. When the rest mass of the rocket is Mf, prove that the velocity v of the rocket in frame S satisfies
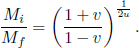
Hint: Consider the conservation of energy and momentum in the instantaneous rest frame and their relationship to the rest mass of the object.
8.Bucket**
A bucket of initial rest mass M0 has an initial velocity u0 in frame S. It begins to collect sand aligned in a line with a linear mass density λ in S. Assuming that the line of sand extends forever,
(a)Find the rate of rest mass increase of the bucket when the bucket has speed u. Why is this greater than λu? Find the rest mass of the bucket, M(t), as a function of time.
(b)Find the energy and velocity of the bucket as functions of time, E(t) and u(t).
(c)Find the energy and velocity of the bucket as functions of the displacement of the bucket relative to the bucket’s initial position, E(x) and u(x).
(Adapted from “Introduction to Mechanics”)
9.Leaking Bucket**
Referring to the previous scenario, the bucket-and-contained-sand system now loses a fraction f of its remaining rest mass per unit distance traveled. Find E(x), p(x) and t(x). (Adapted from “Introduction to Mechanics”)
Problems with Four-Vectors
A common trick in solving equations involving four-momenta involves isolating a single four-momentum that is not of interest and then taking the squared norm of both sides to eliminate the irrelevant four-momentum (as its squared norm produces the mass of the particle). This will be a common denominator in many problems.
10.Four-Vectors*
(a)Let A be a four-vector, and suppose that one component of A is found to be zero in all inertial frames. Show that all four components of A are zero in all frames. This is known as the zero-component theorem.
(b)The four-momentum of a particle in the lab frame S is P while the four-velocity of an observer is U with respect to S. Show that the particle’s energy in the rest frame of the observer is P · U.
(c)Prove that the inner product of the four-velocity U and the four-acceleration A of a massive particle is zero.
(d)Show that the instantaneous charge density ρ and the instantaneous current density j at a particular location forms a four-vector J = (ρc, j) in an arbitrary inertial frame S. J is known as the four-current. Hint: consider the four-velocity.
11.Chasing Particles*
A particle ma with speed va is pursuing another particle mb with vb (vb < va) along the x-axis of an inertial frame S. When particle a catches up with particle b, they collide and coalesce to form a single particle of mass m. Show that

12.Disintegration*
A particle of rest mass m1 is initially stationary in the lab frame S. It then disintegrates into a photon and another particle of rest mass m2 < m1. Find the energies of the photon and the final particle.
13.Reflected Photon*
In an inertial frame S, a photon of frequency f is normally incident on a perfect plane mirror, of mass m, retracting at a velocity u from the photon. Find the frequency f′ of the reflected photon in frame S.
14.Proton Collision*
A proton of energy E collides elastically with a second proton of rest energy E0 that is initially stationary. Subsequently, the two protons are directed at angles  relative to the initial velocity of the incident proton. Find cos ϕ.
relative to the initial velocity of the incident proton. Find cos ϕ.
15.Electron-Photon Collision*
A massive particle with energy E0 and speed β0c undergoes a head-on elastic collision with a photon with energy Eγ0. Show that the final energy Eγ of the photon is

Show that Eγ < E0 but if  That is, a high-energy particle loses most of its energy to the photon (in the ideal β0 → 1 limit, the particle retains energy Eγ0 by the conservation of energy).
That is, a high-energy particle loses most of its energy to the photon (in the ideal β0 → 1 limit, the particle retains energy Eγ0 by the conservation of energy).
16.Emission by Excited Atom*
An excited atom A* at rest drops to its ground state A by emitting a photon. In atomic physics, it is usually assumed that the energy Eγ of the emitted photon is equal to the difference in energies of the two atomic states, ΔE = (M* – M)c2, where M and M* are the rest masses of the ground and excited states of the atom. This cannot be exactly true, since the recoiling atom X must carry away part of ΔE. Show that in fact

Given that ΔE is of order eV while the lightest atom has M of order GeV/c2. Discuss the validity of the approximation Eγ = ΔE.
17.Neutrino Beam*
High-energy neutrino beams are produced by allowing an excited pion π+ to decay into an excited muon μ+ and neutrino v according to the equation

The masses of a pion and muon are 140MeV/c2 and 106MeV/c2. The mass of a neutrino is negligible.
(a)Find the energy of the neutrino in the rest frame of the pion.
(b)In the lab frame, the pion has an energy of 200GeV. If the momentum of the neutrino is aligned with the initial momentum of the pion, determine the energy of the neutrino.
(c)Referring to (b), let θ be the angle between the momentum of the neutrino and the initial momentum of the pion. Find the value of θ for which the neutrino’s energy is half of its maximum possible energy.
18.Mad Scientist*
A mad scientist asserts to have observed the decay of a particle of mass M into two identical particles of mass m > 0, with M < 2m. He dismisses objections about the violation of the conservation of energy by this process with the claim that if M were traveling fast enough, its energy could easily exceed 2mc2 and could hence decay into the two particles of mass m. Prove that he is wrong and qualitatively describe the flaw in his rebuttal.
19.Photon Decay*
Show that a photon cannot spontaneously decay into a particle with a non-zero rest mass, accompanied by an arbitrary number of other particles of arbitrary masses, which may be zero.
20.Compton Scattering**
In frame S, a photon of frequency f is incident on an electron with momentum p1 and energy E1. Determine the minimum frequency of the scattered photon and the directions of the velocities of the incident photon and the scattered photon in such a situation. The rest mass of the electron is constant.
21.Pion Photoproduction**
Consider the reaction
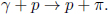
The rest energies of a proton and pion are 938 MeV and 135 MeV respectively.
(a)If the proton is initially at rest in the laboratory, find the laboratory threshold photon energy for this reaction to occur.
(b)If the photon’s energy is 10–3eV, find the minimum proton energy that can spark off this reaction.
22.Energy Transfer**
In the lab frame S, particle 1 of rest mass m1 is traveling at velocity u in the positive x-direction and subsequently collides with an initially stationary particle 2 of rest mass m2. If the final velocities of the particles are still aligned with the x-direction and their rest masses remain constant, find the final energy of particle 2. Determine the fraction of the total energy in the lab frame that is possessed by particle 2 in the limit where u tends to c. Hint: Consider the center-of-momentum frame. You will discover the ratio in fact tends to unity. Here’s another subtler way of proving this. Let  and P2 be the final four-momentum of particle 1 and the initial four-momentum of particle 2 in the center-of-momentum frame. Firstly, show that the inner product of
and P2 be the final four-momentum of particle 1 and the initial four-momentum of particle 2 in the center-of-momentum frame. Firstly, show that the inner product of  – P2 with itself is larger than zero in the center-of-momentum frame (be wary that
– P2 with itself is larger than zero in the center-of-momentum frame (be wary that  – P2 is not a four-vector and its inner product is not invariant). Armed with this inequality, show that the final energy of particle 1 must not exceed
– P2 is not a four-vector and its inner product is not invariant). Armed with this inequality, show that the final energy of particle 1 must not exceed  This value is independent of u and hence shows that particle 2 absorbs most of the energy if u is large.
This value is independent of u and hence shows that particle 2 absorbs most of the energy if u is large.
23.Maximum Frequency**
In inertial frame S, a particle of rest mass m is incident at a speed u on a nucleus of rest mass M. During the collision, a photon is emitted. The rest masses of the particle and the nucleus remain unchanged. Show that the maximum energy of the photon in frame S is

Show that this occurs when the direction of the photon is parallel to the initial velocity of the particle u and when the nucleus and the particle “stick together” after the collision in frame S. Hint: from the four-vector equation 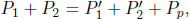 where
where  are the four-momenta of the particle and the nucleus before and after the collision and Pp is the four-momentum of the photon, obtain
are the four-momenta of the particle and the nucleus before and after the collision and Pp is the four-momentum of the photon, obtain  and consider the squared norm of both sides.
and consider the squared norm of both sides.
Force, Impulse-Momentum and Work-Energy
24.Two Particles Connected by String*
Two particles of rest masses m and M are connected by a flexible rope of constant tension T. If the two particles are initially at rest and are separated by an initial distance L in frame S, what is the distance x between the point at which the particles meet and the initial position of the particle of rest mass m? (“Introduction to Mechanics” by David Morin)
25.Projectile Motion**
A particle initially possesses an x-component of momentum p0 and energy E0 in the lab frame. It is then acted upon by a constant –F force in the y-direction. Determine the trajectory of the particle in the lab frame. Show that the resultant expression reduces to the familiar parabolic path in the non-relativistic limit.
26.Pulling a Leaking Bucket**
In frame S, there is an initially stationary bucket with zero initial rest mass that is pulled along by a string of constant tension T. The bucket begins to gather sand of linear mass density λ. Find the velocity u of the bucket. (“Introduction to Mechanics”)
Waves and Electromagnetism
27.Light in Moving Glass**
In the lab frame S, a source emits light of frequency f towards a glass block of refractive index n that is retracting at velocity v. By considering the four-wave vector and the rest frame of the block S’, determine the frequency and wavelength of light inside the block in the lab frame S.
28.Crossed Fields**
In the lab frame S, there are uniform electric and magnetic fields E = (0, E, 0) and B = (0, 0, B) where E < 0 and B > 0. A charged particle of rest mass m and charge q initially possesses velocity v0 in the x-direction when it is at the origin. Determine the maximum x-coordinate that the particle attains in its subsequent motion. Hint: Consider another inertial frame.
29.Magnetic Field***
In this problem, we shall see how the magnetic field is the manifestation of the electric field in another frame. In frame S, an infinitely long wire carries a current I in the positive x-direction. The current comprises electrons of linear charge density –λ traveling at a velocity u in the negative x-direction in frame S (I = λu). In frame S, there are also stationary positive ions of linear charge density λ in the wire such that the wire is neutral. A point charge q travels at a velocity v in the positive x-direction, at a distance r from the wire. Without any knowledge of the existence of a magnetic field and by considering the electric field in the rest frame of the charge S’, show that the charge experiences a force of the form
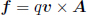
in frame S where A is a certain vector. Now let A be defined as the magnetic field B. Verify that the expression for the magnetic field is consistent with that obtained from Ampere’s law in frame S. Do not use the transformations for the electromagnetic fields in this problem.
Solutions
1.“Infinite” Energy Generator*
Tom’s reasoning is fallacious because the frequency (and thus energy) of the photon will decrease after reflection from a retracting mirror. Therefore, the photon imparts less momentum with each reflection until it ultimately disappears (or becomes insignificant) when it loses all of its initial energy. The total kinetic energy imparted to the two mirrors will be equal to the initial energy of the photon by the conservation of energy.
Because the second set-up is symmetrical, the final kinetic energies of the mirrors are identical and are each equal to the initial energy of one photon hf, by the conservation of energy.
2.Exploding Particle*
This problem is beckoning for us to consider it in the rest frame of the initial particle, S’. In this frame, the initial energy of the system is m while the initial momentum is zero. By symmetry, the final energy of each particle in this rest frame is  Then, the magnitude of their momenta is
Then, the magnitude of their momenta is
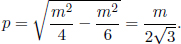
They are directed in opposite directions, parallel to the x’-axis. The magnitude of the velocities of the product particles in frame S’ is
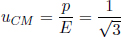
and the velocities point in opposite directions. The velocities of these particles in the lab frame S can then be obtained from the velocity addition formula.

An equivalent method is to transform the individual four-momenta of the particles and subsequently use the relationship 
3.Available Energy*
In the center-of-momentum frame S’, energy and momentum must also be conserved. By definition, the total momentum in S’ should be zero. Therefore, the most energy can be channeled into the creation of the new particle if all particles possess zero final momentum in S’ (so that no energy is wasted on kinetic energy). The maximum rest mass of the new particle m′ is thus the total energy in the center of momentum frame ECM, minus m1 and m2.

Applying Eq. (12.15),
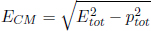
where Etot and ptot are the total energy and momentum in any arbitrary inertial frame, as the above expression is a scalar. Substituting the corresponding expressions in the lab frame,

Then,

4.Unknown Mass Decay*
Let the momentum of M be p. Since pa · pb = 0,

Meanwhile, the energies of particles a and b are

The energy of M is thus

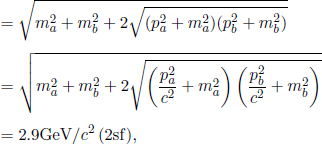
where the c’s have been added back in the second-last expression. The velocity of M is

5.Positron-Electron Collision*
In the CoM frame, let the initial energies of the electron and positron be E. The minimum final total energy occurs when all products are stationary and is of value 2me + mψ. By the conservation of energy,

Next, suppose that the total energy in the CoM frame is Etot = 2E and that the electron and positron travel towards each other at speed u. By the energy-momentum transformations, the total energy in the rest frame of the electron is

Therefore, the initial energy of the positron in this frame is

Observe that γu decreases as E decreases (since the electron and positron possess less kinetic energy). Therefore, the minimum E+ (i.e. the threshold energy) occurs when E = Emin.
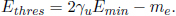
From the definition of the relativistic energy, we have

Thus,
6.Relativistic Photon Rocket*
The initial energy of the entire system is Mi. If we let the total energy of the radiated photons in frame S be E,

Since the momentum of the photons differs from their energy only by a factor of c, the conservation of momentum gives

Hence,

7.Relativistic Mass Rocket**
Figure 12.14 depicts an ejection event in the instantaneous rest frame of the rocket, S’. This rest frame travels at a velocity v relative to S.
Immediately after the ejection, let the velocity of the rocket be dv′ in S’ and let the rest mass of the rocket be m + dm. The fuel travels at a velocity –u in the new instantaneous rest frame of the rocket which travels at dv′ relative to the first instantaneous rest frame. Using the velocity addition formula, the fuel travels at speed  in the original instantaneous rest frame S’.
in the original instantaneous rest frame S’.
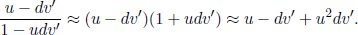
Then, let γf and dmf denote the gamma factor associated with the velocity of the fuel in S’ and the rest mass of the fuel. By the conservation of energy in frame S’, the total final energy of the system consisting of the ejected fuel and the rocket must be equal to m which is the initial energy.

Figure 12.14:Ejection event in instantaneous rest frame

Ignoring second order terms,

Furthermore, by the conservation of momentum,

Discarding the preponderance of second order terms,

Now, we cannot directly integrate this expression in the current instantaneous rest frame as this expression for dv′ will no longer be valid as the rocket begins to acquire a non-negligible velocity in this frame. Hence, there is a need to transform back to frame S. Let the speed of the rocket in frame S after the ejection event be v + dv. By the velocity addition formula,
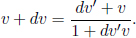
Performing a binomial expansion 

Substituting this into the previous relevant equation,

8.Bucket**
(a) Consider a collision event between the bucket, with an instantaneous mass M and instantaneous velocity u, and an infinitesimal segment of sand of rest mass dm. The total energy before and after the collision are γuM and γuM + dm respectively. The total momenta before and after collision are still γuMu. Hence, the new rest mass M + dM after the collision is

Ignoring the second order infinitesimal terms,
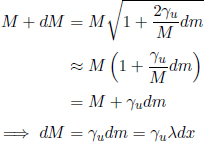
where dx is the length of an infinitesimal segment of sand swept by the bucket in time dt in the lab frame. Since 

This is greater than λu due to the increase in internal energy of the combined bucket-and-sand system during the inelastic collision, as part of the kinetic energy of the bucket is converted into heat. Next, we can use the fact that the total momentum of the bucket always remains at p = γu0 M0u0 to rewrite the differential equation above as

where p = γu0 M0u0.
(b) The increase in the total energy of the bucket is due to the rest energy of the additional sand collected. Hence,

Next, since 
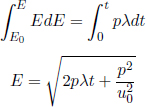
where the initial energy E0 has been expressed as  Lastly,
Lastly,

where p = γu0M0u0.
(c) The energy of the bucket as a function of x can be computed via

Then,

where p = γu0M0u0.
9.Leaking Bucket**
This time, the change in the total energy per unit distance traveled is both due to the absorption of the sand, which has a certain amount of rest energy, and the amount of rest mass lost by the bucket-and-sand system. Since the bucket losses rest mass (which is assumed to be homogeneous) at a fraction per unit distance of f, its fractional rate of energy loss is also f. Hence,

Note that E – 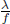 (at all times) must have the same sign as E0 –
(at all times) must have the same sign as E0 – 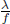 . This is evident from the
. This is evident from the  equation. E will always tend towards
equation. E will always tend towards 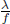 , after which it stops changing. Therefore, the term in the absolute value brackets is definitely positive.
, after which it stops changing. Therefore, the term in the absolute value brackets is definitely positive.

where E0 is the initial energy of the bucket, E0 = γu0 M0. On the other hand, the change in momentum of the bucket per unit distance is similarly,
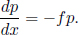
p is now the instantaneous momentum of the bucket-and-sand system. Solving this differential equation,

where p0 = γu0M0u0. Then, using 
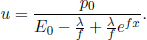
Using the fact that  and separating variables,
and separating variables,
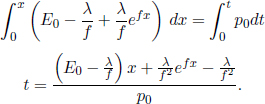
10.Four-Vectors*
(a) Suppose that the ith component of A is found to be zero in all inertial frames. Given Ai in frame S, we can compute  in frame S’ in the following manner, under a Lorentz transformation in an appropriate direction.
in frame S’ in the following manner, under a Lorentz transformation in an appropriate direction.
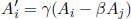
where Aj is the time-like component if Ai is a space-like component and vice-versa, Aj is a space-like component if Ai is the time-like component. Evidently, for  = 0, given Ai = 0, we must have Aj = 0. Since the definition of the inertial frame S is arbitrary, the jth component of A must be zero in all inertial frames. As such, if Ai is the time-like component, we can perform Lorentz transformations along all three spatial directions to deduce that all spatial components of A are zero in all inertial frames.
= 0, given Ai = 0, we must have Aj = 0. Since the definition of the inertial frame S is arbitrary, the jth component of A must be zero in all inertial frames. As such, if Ai is the time-like component, we can perform Lorentz transformations along all three spatial directions to deduce that all spatial components of A are zero in all inertial frames.
Otherwise, if Ai is a space-like component, we can first apply the same argument to conclude that the time-like component A0 is zero in all inertial frames. Then, by using the final result of the previous paragraph, we conclude that all components of A are zero in all inertial frames.
(b) Let the four-momentum of the particle and the four-velocity of the observer be P′ and U′ in the rest frame of the observer, S’, respectively.

where E′ and p′ are the energy and momentum of the particle in S’. Evidently,

By the invariance of the inner product of two four-vectors across Lorentz transformations,

which is our desired result.
(c) In the rest frame S’ of the particle (which exists because it is massive and cannot travel at the speed of light in any inertial frame),

where α is the proper acceleration of the particle. Observe that

Since the inner product of two four-vectors is Lorentz invariant,

where U and A are the particle’s four-velocity and four-acceleration with respect to an arbitrary inertial frame S.
(d) Suppose for now that the charges at the location P of interest all possess the same velocity u in inertial frame S. Since the longitudinal length of the moving charges are shrunk by a factor of  as compared to that in their rest frame S’, due to length contraction and because the total amount of charge in a given volume must be Lorentz invariant,
as compared to that in their rest frame S’, due to length contraction and because the total amount of charge in a given volume must be Lorentz invariant,

where ρ0 is the proper charge density at the corresponding location P’ in S’. Next, the current density j in S is simply

Now, observe that the four-current in this case is merely the four-velocity U of the charges multiplied by the constant ρ0!

By Property 1 of four-vectors, J is hence a four-vector in this case. In the more general case where there are a total of k classes of charge velocities at P, with the ith class having a charge density ρi traveling at velocity ui in S, we can consider the four-current 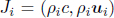 associated with each individual class. Since Ji is a four-vector for all 1 ≤ i ≤ k by the above proof,
associated with each individual class. Since Ji is a four-vector for all 1 ≤ i ≤ k by the above proof,

is a valid four-vector because
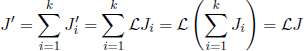
in an arbitrary inertial frame S’, where 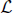 is the Lorentz transformation matrix. Note that the addition of four-vectors to produce another four-vector is valid in this case only because the addition is performed at the same location and at the same time in every inertial frame — the loss of simultaneity across inertial frames has been precluded.
is the Lorentz transformation matrix. Note that the addition of four-vectors to produce another four-vector is valid in this case only because the addition is performed at the same location and at the same time in every inertial frame — the loss of simultaneity across inertial frames has been precluded.
11.Chasing Particles*
Let the initial four-momenta of the particles be Pa and Pb. Denote the four-momentum of the final particle as P. The four-vector equation associated with this process is
Taking the inner product of both sides,
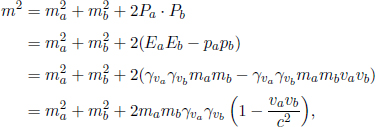
where we have added back the c’s in the last equation.
12.Disintegration*
The conservation of energy and momentum implies:

Taking the squared norm of both sides,
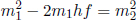

13.Reflected Photon*
Let the final four-momentum of the mirror be (E, p) where the only spatial direction of concern has been defined to be along the x-axis. Then, the conservation of energy and momentum entails

This can be rewritten in terms of four-vectors.

Shifting P3 to the left-hand side and finding the squared norm of both sides,
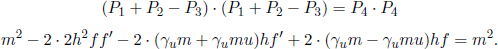
Simplifying,

14.Proton Collision*
Let the initial four-momenta of the incident and stationary protons be Pl and P2 respectively. Denote their final four-momenta as  and
and 
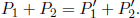
Taking the inner product of both sides,

since  (they are in fact, the squared mass of a proton
(they are in fact, the squared mass of a proton  can be easily computed as EE0 since the three-momentum in P2 is the null vector.
can be easily computed as EE0 since the three-momentum in P2 is the null vector.  requires more work, but observe that the two protons must possess identical final momentum and thus final energy to fulfil the conservation of momentum in directions perpendicular to the incident photon’s initial velocity. The final energy and squared momentum of each proton is thus
requires more work, but observe that the two protons must possess identical final momentum and thus final energy to fulfil the conservation of momentum in directions perpendicular to the incident photon’s initial velocity. The final energy and squared momentum of each proton is thus 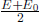 and
and  Since
Since 

since E ≠ E0.
15.Electron-Photon Collision*
Let the initial and final four-momenta of the massive particle be P and P′ and those of the photon be Pγ and  The germane four-vector equation is
The germane four-vector equation is
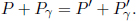
Since the particle is irrelevant after the collision, we isolate P′.

Taking the inner product of both sides,
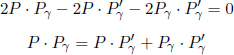
where we have canceled the squared rest mass of the particle on both sides. Since this problem is solely one-dimensional, we have 
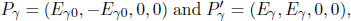 where we note that the velocity of the photon must be reversed after the collision because it cannot penetrate the particle.
where we note that the velocity of the photon must be reversed after the collision because it cannot penetrate the particle.
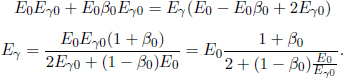
Since  which implies that Eγ < E0. When
which implies that Eγ < E0. When 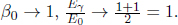
16.Emission by Excited Atom*
Let the four-momenta of the excited and ground states of the atom be P* and P. Denote the four-momentum of the emitted photon as Pγ. The relevant four-vector equation is
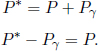
Taking the inner product of both sides,

Since P* = (M*, 0) while Pγ = (Eγ, Eγ ),
),

where we have added back the c’s in the last step. Evidently, the fractional error in assuming Eγ = ΔE is maximum when M* → M. Even then, the fractional error is 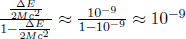 for ΔE of order eV and the minimum M (and thus maximum error) of order GeV/c2. Therefore, Eγ = ΔE is typically a good approximation.
for ΔE of order eV and the minimum M (and thus maximum error) of order GeV/c2. Therefore, Eγ = ΔE is typically a good approximation.
17.Neutrino Beam*
(a) Let the four-momenta of the pion, muon and neutrino be Pπ, Pμ and Pv respectively. In the rest frame of the pion,

where p is the unknown momentum of the neutron. The four-vector equation is

Since the muon is not of concern, it is customary to isolate Pμ even though it is not really necessary here.

Taking the inner product of each side with itself,

where we have added the c back. The energy of the neutrino is

(b) There are multiple ways of solving this. The direct method is to repeat the process of (a) with

Since  the inner products of both sides yield
the inner products of both sides yield

where we have added back the c’s. Alternatively, we can apply the energy-momentum transformations to the momentum p computed in (a) to obtain

(c) Denoting the momentum of the neutrino as pv and repeating the same process in (b) with 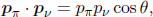 one would obtain
one would obtain

Evidently, the maximum neutrino energy occurs when θ = 0.

For 


18.Mad Scientist*
A simple proof for M > 0 (such that its rest frame exists) is to observe the situation in the rest frame of M. Presuming that such a reaction is possible, the initial total energy is only Mc2 while the final total energy is at least 2mc2 > Mc2, contradicting the conservation of energy.
For a more general rebuttal which works even when M = 0, let the four-momentum of M be P1 and the four-momenta of the products be P2 and P3. The four-vector equation is

Taking the inner product of each side with itself,

where γrel is the gamma factor associated with the velocity of one particle of mass m, as observed in the other. As γrel ≥ 1, the right-hand side obeys the inequality
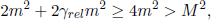
which establishes a contradiction. Therefore, the scientist is wrong. Qualitatively, his refutation of the violation of energy conservation is flawed because when M has a certain velocity and thus momentum in the lab frame, the products must possess some kinetic energy in addition to their rest energies, by the conservation of momentum. The total energy of the proposed products is always larger than the energy of M.
19.Photon Decay*
Let Pp be the four-momentum of the photon and let the photon disintegrate into k particles with the ith particle having a four-momentum Pi. Then,

Taking the squared norm of both sides,
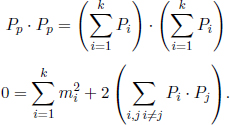
One can show that 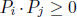 for all possible combinations of particles. If at least one particle is massive (suppose that it is the ith particle without the loss of generality),
for all possible combinations of particles. If at least one particle is massive (suppose that it is the ith particle without the loss of generality),  (as both rest mass and energy must be non-negative) where Ejrev is the energy of the jth particle as observed in the rest frame of the ith particle. If both particles are massless, pi · pj, =
(as both rest mass and energy must be non-negative) where Ejrev is the energy of the jth particle as observed in the rest frame of the ith particle. If both particles are massless, pi · pj, =  as E = p for a massless particle. Since the left-hand side of the previous equation is zero while the right-hand side is a sum of non-negative numbers, all terms on the right-hand side must be zero — implying that a particle with a non-zero rest mass cannot be produced.
as E = p for a massless particle. Since the left-hand side of the previous equation is zero while the right-hand side is a sum of non-negative numbers, all terms on the right-hand side must be zero — implying that a particle with a non-zero rest mass cannot be produced.
20.Compton Scattering**
By the conservation of energy and momentum,

Shifting the first term on the right-hand side to the left-hand side and taking the squared norm of both sides,
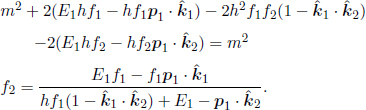
Evidently, the minimum f2 occurs when  and
and 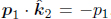 That is,
That is,  1 is parallel to p1 while
1 is parallel to p1 while  2 is anti-parallel to p1. Then,
2 is anti-parallel to p1. Then,

21.Pion Photoproduction**
(a) Applying Eq. (12.26), the threshold photon energy is

(b) Let the initial four-momenta of the proton be Pp = (E, p) and the photon be  where
where 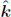 is the unit vector along the photon’s velocity. The four-vector equation associated with the reaction is
is the unit vector along the photon’s velocity. The four-vector equation associated with the reaction is

Taking the inner product of both sides with itself,

Noting that  and
and  where γpπ is the gamma factor associated with the final velocity of the proton as observed in the rest frame of the pion,
where γpπ is the gamma factor associated with the final velocity of the proton as observed in the rest frame of the pion,

Since γpπ ≥ 1, the minimum E occurs when γpπ = 1 and p · 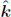 = –p. Then,
= –p. Then,
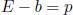
where 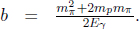 Squaring both sides and using the identity
Squaring both sides and using the identity 

22.Energy Transfer**
In the lab frame, the total energy and momentum are given by γum1 + m2 and γum1u. As the energy and momentum obey the Lorentz transformations, the momentum in another inertial frame S’ is

Therefore, in order for p′ = 0, the center-of-momentum frame S’ must travel  relative to S. v must also be the initial speed of particle 2 in S’. In the center-of-momentum frame, the momenta of the two particles must simply reverse after the collision for both energy and momentum to be conserved (if one momentum increases or decreases in magnitude, the other must follow suit by the conservation of momentum, and hence lead to a violation of the conservation of energy). Therefore, the final velocity of particle 2 in S’ is v in the positive x’-direction. The final velocity of particle 2 in the lab frame S is then
relative to S. v must also be the initial speed of particle 2 in S’. In the center-of-momentum frame, the momenta of the two particles must simply reverse after the collision for both energy and momentum to be conserved (if one momentum increases or decreases in magnitude, the other must follow suit by the conservation of momentum, and hence lead to a violation of the conservation of energy). Therefore, the final velocity of particle 2 in S’ is v in the positive x’-direction. The final velocity of particle 2 in the lab frame S is then  by the velocity addition formula. The resultant energy of particle 2 in S is then
by the velocity addition formula. The resultant energy of particle 2 in S is then
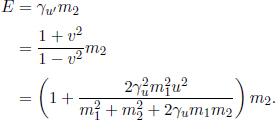
The ratio of E to the total energy in S is

As u → l and  in the denominator
in the denominator 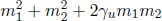 and m2 in the denominator γum1 + m2 become negligible comparatively. The ratio then tends to
and m2 in the denominator γum1 + m2 become negligible comparatively. The ratio then tends to

Moving on to the more indirect approach, the three-momentum components of  and P2 are identical in the center-of-momentum frame. Therefore, the inner product of
and P2 are identical in the center-of-momentum frame. Therefore, the inner product of  – P2 with itself in the center-of-momentum frame must be non-zero as it is simply the square of the difference of the two energies in the center-of-momentum frame. Then,
– P2 with itself in the center-of-momentum frame must be non-zero as it is simply the square of the difference of the two energies in the center-of-momentum frame. Then,

Substituting the squared norm of a four-momentum and Eq. (12.24),
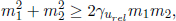
where γurel is the γ factor associated with the final velocity of particle 1 in the frame that is at rest with the initial velocity of the particle 2, urel. However, notice that the initial velocity of particle 2 is v in the negative x’-direction in the center-of-momentum frame. Therefore, the final velocity of particle 1 in the frame that is at rest with the initial velocity of the particle 2 effectively performs a –v velocity addition to the final velocity of particle 1 in the center-of-momentum frame — transforming it back to the final value in the lab frame ulab. Since the final energy of particle 1 is Elab = γulabm1 in the lab frame,

which sets a fixed upper bound on the energy retained by particle 1.
23.Maximum Frequency**
By the conservation of energy and momentum,

where  is a unit vector in the direction of the photon’s velocity. Taking the squared norm of both sides,
is a unit vector in the direction of the photon’s velocity. Taking the squared norm of both sides,
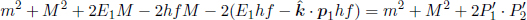
where  and
and  are the final four-momenta of the particle and the nucleus respectively. Solving for hf,
are the final four-momenta of the particle and the nucleus respectively. Solving for hf,

Evidently, hf is maximized when 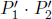 is minimized and when
is minimized and when 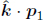 is maximized. The former expression is
is maximized. The former expression is
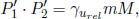
where urel is the velocity of one particle in the rest frame of the other. This quantity is minimized when there is no relative velocity between the nucleus and the particle (i.e. γurel = 1). Next, 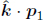 is maximized when these two vectors are parallel. In other words, the ejected photon travels in the same direction as the initial velocity of the particle. Then the maximum energy of the photon in frame S is
is maximized when these two vectors are parallel. In other words, the ejected photon travels in the same direction as the initial velocity of the particle. Then the maximum energy of the photon in frame S is
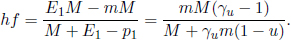
24.Two Particles Connected by String*
Let E1 and E2 be the final energies of the particles of rest masses m and M respectively. Then, by the work-energy theorem,
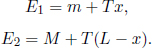
Let the magnitudes of the final momenta of the particles, which must be equal by the conservation of momentum or by Newton’s third law, be p. Then,

25.Projectile Motion**
Let x, y and t denote the spatial and temporal coordinates of the particle in the lab frame S. Define the origin at the initial position of the particle. The x and y components of the particle’s momentum are

Furthermore, the work-energy theorem states that the energy of the particle at (x, y) is

Then, y(t) can first be solved for

Solving for y,
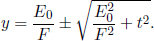
The y-coordinate must be negative for t > 0. Thus, we choose the negative expression.

Armed with y(t), x(t) can be determined.
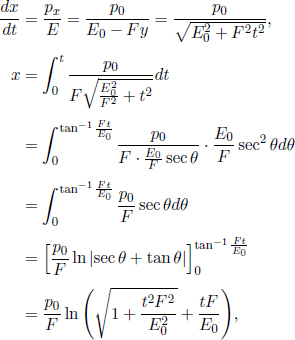
where we have adopted the trigonometric substitution  along the way. After some algebraic manipulation, we can show that
along the way. After some algebraic manipulation, we can show that

For readers familiar with hyperbolic functions, we can instead adopt the substitutions  such that
such that

where we have used the identity cosh2 θ = 1 + sinh2 θ.
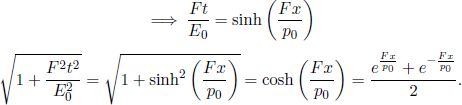
Then,

Note that in SI units, the exponents are actually  . Therefore in the non-relativistic limit where
. Therefore in the non-relativistic limit where 
 1, we can perform a Maclaurin expansion for the exponential functions.
1, we can perform a Maclaurin expansion for the exponential functions.
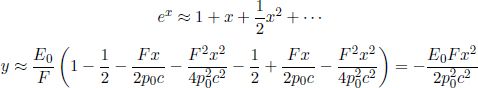
which is a parabola. What’s more, in the non-relativistic limit, E0 is dominated by the rest energy (E0 ≈ mc2) where m is the rest mass of the particle, while p0 ≈ mv0 where v0 is the initial velocity of the particle. Then,

When F is of the form of gravity, F = mg classically.

which is the trajectory of a particle with initial x-velocity v0 under free fall. The latter set-up is described by the equations

Hence,

26.Pulling a Leaking Bucket**
The only external force on the bucket is the tension in the string. Hence,

as the initial momentum of the bucket is zero. Next, the rate of increase of the energy of the bucket is equal to the sum of the rate of the rest mass of sand gathered by the bucket and the power delivered by the tension.
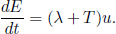
Next, using the relationship 
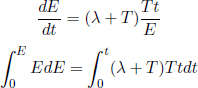

which is independent of time except for the discontinuity in velocity at t = 0.
27.Light in Moving Glass**
In the rest frame of the block S’, the block is stationary while the light source emits light of Doppler-shifted frequency  The speed of light inside the block is
The speed of light inside the block is  in units of c. Hence, the wavelength of light inside the block in S’ is
in units of c. Hence, the wavelength of light inside the block in S’ is  Thus, the four-wave vector inside the glass block in S’ is
Thus, the four-wave vector inside the glass block in S’ is

The four-wave vector K inside the glass block in S can be obtained from applying the inverse Lorentz transformation to K′.
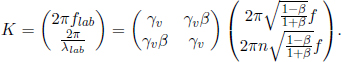
Equating the corresponding entries,

where we have added back the c’s.
28.Crossed Fields**
One can show that in an inertial frame S’ that travels at 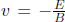 in the negative x-direction relative to S (we define v this way such that v > 0), the electric field is null while the magnetic field is
in the negative x-direction relative to S (we define v this way such that v > 0), the electric field is null while the magnetic field is  In this frame S’, the particle’s kinetic energy cannot change as the magnetic force does no work. Furthermore, the magnetic force is perpetually perpendicular to the particle’s velocity — implying that the particle undergoes circular motion (this holds in the classical case as well). The initial speed of the particle in S’ is given by the velocity addition formula as
In this frame S’, the particle’s kinetic energy cannot change as the magnetic force does no work. Furthermore, the magnetic force is perpetually perpendicular to the particle’s velocity — implying that the particle undergoes circular motion (this holds in the classical case as well). The initial speed of the particle in S’ is given by the velocity addition formula as  (directed initially along the x’-axis), and remains constant afterwards. The magnetic force quB′ provides the centripetal force. Since this force is perpendicular to the instantaneous velocity of the particle,
(directed initially along the x’-axis), and remains constant afterwards. The magnetic force quB′ provides the centripetal force. Since this force is perpendicular to the instantaneous velocity of the particle,

by Eq. (12.17) where  is the centripetal acceleration and R is the radius of rotation. The radius of rotation can then be computed as
is the centripetal acceleration and R is the radius of rotation. The radius of rotation can then be computed as
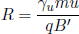
while the angular velocity is

Now, if we define the initial position of the particle in S’ to be at the origin O’, the center of rotation must lie at x′ = 0 and y′ = –R. Therefore, the x-coordinate of the particle as a function of time t′ in S’ is
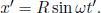
The x-coordinate of the particle in S is then obtained from the Lorentz transformations.

The maximum value of x occurs when  This yields
This yields
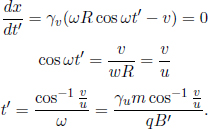
Note that  exists as
exists as  when v0 < 1 and v < 1 (just shift the terms around). When the above condition is satisfied,
when v0 < 1 and v < 1 (just shift the terms around). When the above condition is satisfied,
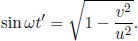
We choose the positive value such that the second derivative 
 is negative at this stationary point — ensuring that it is a maximum point. Observe from
is negative at this stationary point — ensuring that it is a maximum point. Observe from  that the global maxima evidently occurs for the smallest t′ that satisfies
that the global maxima evidently occurs for the smallest t′ that satisfies  Hence, our choice of
Hence, our choice of  above is justified. Then, the maximum x value is
above is justified. Then, the maximum x value is
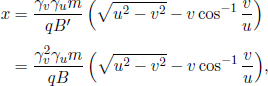
where 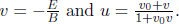
29.Magnetic Field***
The crux of this problem is to observe that the wire is no longer neutral in frame S’ due to the different extents of length contraction of positive ions and electrons (as they were moving at different speeds in S). Let us determine the charge density of the electrons in frame S’,  first. Let L be the proper distance between adjacent electrons. Then, the distance between adjacent electrons in frame S is given by the length contraction formula:
first. Let L be the proper distance between adjacent electrons. Then, the distance between adjacent electrons in frame S is given by the length contraction formula:
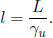
The distance between adjacent electrons as observed in frame S’ is
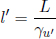
where u′ is the velocity of the electrons in frame S’. Referring to Eq. (12.22),

where  and we have included the c’s for clarity. Then, the charge density of the electrons in frame S’ is given by
and we have included the c’s for clarity. Then, the charge density of the electrons in frame S’ is given by

A similar argument can be made to conclude that the charge density of the positive ions in frame S’ is

Hence, the total linear charge density of the wire in frame S’ is
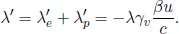
A much more efficient alternative is to consider the four-current J = (ρc, j) introduced in part (d) of Problem 10, where ρ is the charge density and j is the current density. The four-current everywhere along the infinite wire in S is J = (0, λu, 0, 0), for one-dimensional charge distributions. Meanwhile, the four-current in S’ is  where
where  and
and 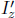 are the current components in S’. λ′ can then be computed from the Lorentz transformations.
are the current components in S’. λ′ can then be computed from the Lorentz transformations.
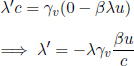
everywhere along the wire in S’. Applying Gauss’ law to the wire (by drawing a cylindrical Gaussian surface whose axis coincides with the wire), the electric field in frame S’ is

where r′ is the vector pointing perpendicularly outwards from the closest point on the axis of the wire to the charge in frame S’. Hence, the force on the charge in frame S’ (note that there is no velocity-dependent force, such as the magnetic force, as the charge is stationary) is
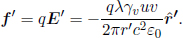
Notice that the net force on the charge in frame S’ is purely radial and is perpendicular to the velocity of frame S relative to frame S’. Hence, from the force transformations, the net force on the charge in frame S is
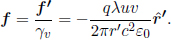
Furthermore, notice that since r′ is also perpendicular to the velocity v, r′ = r where r is the radial vector from the wire to the charge in frame S. Hence,
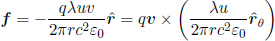
where  is the azimuthal unit vector, whose positive direction is given by the right-hand-grip rule (applied to the positive current). Hence, it can be seen that the force takes a form similar to the magnetic force. We can show that the last term indeed gives the correct expression for the magnetic field. λu is simply the current I and
is the azimuthal unit vector, whose positive direction is given by the right-hand-grip rule (applied to the positive current). Hence, it can be seen that the force takes a form similar to the magnetic force. We can show that the last term indeed gives the correct expression for the magnetic field. λu is simply the current I and  Hence,
Hence,

which is consistent with Ampere’s law.
1The expression for the kinetic energy of the particle (in the section after this) can be deduced from integrating the rate of change of relativistic momentum (relativistic force) with respect to displacement, which is the relativistic analog of work. However, the “rest energy” is indeed a bold assertion.
2This is also partly due to the finite speed of the particle which causes the separation between its positions at t + dt and t to be infinitesimal.
3The proofs of these effects begin from different premises but are coherent. Hence, the four-frequency is a useful way to recall wave-like effects of light by considering its particulate nature.
4We are only considering the external fields and are ignoring the fields generated by the hypothetical charged particle.
5Note that charge is presumed to be invariant across inertial frames. Therefore, the particle possesses unit charge in all inertial frames.