

Deep learning is a type of machine learning that has advanced rapidly in the past few years, due to improvements in processing power and deep learning techniques. Usually, deep learning refers to deep, or many-layered, neural networks, which excel at performing very complex, often historically human-centric tasks, like image recognition and language translation.
For example, detecting whether a file contains an exact copy of some malicious code you’ve seen before is simple for a computer program and doesn’t require advanced machine learning. But detecting whether a file contains malicious code that is somewhat similar to malicious code you’ve seen before is a far more complex task. Traditional signature-based detection schemes are rigid and perform poorly on never-before-seen or obfuscated malware, whereas deep learning models can see through superficial changes and identify core features that make a sample malicious. The same goes for network activity, behavioral analysis, and other related fields. This ability to pick out useful characteristics within a mass of noise makes deep learning an extremely powerful tool for cybersecurity applications.
Deep learning is just a type of machine learning (we covered machine learning in general in Chapters 6 and 7). But it often leads to models that achieve better accuracy than approaches we discussed in these preceding chapters, which is why the entire field of machine learning has emphasized deep learning in the last five years or so. If you’re interested in working at the cutting edge of security data science, it’s essential to learn how to use deep learning. A note of caution, however: deep learning is harder to understand than the machine learning approaches we discussed early in this book, and it requires some commitment, and high-school level calculus, to fully understand. You’ll find that the time you invest in understanding it will pay dividends in your security data science work in terms of your ability to build more accurate machine learning systems. So we urge you to read this chapter carefully and work at understanding it until you get it! Let’s get started.
Deep learning models learn to view their training data as a nested hierarchy of concepts, which allows them to represent incredibly complex patterns. In other words, these models not only take into consideration the original features you give them, but automatically combine these features to form new, optimized meta-features, which they then combine to form even more features, and so on.
“Deep” also refers to the architecture used to accomplish this, which usually consists of multiple layers of processing units, each using the previous layer’s outputs as its inputs. Each of these processing units is called a neuron, and the model architecture as a whole is called a neural network, or a deep neural network when there are many layers.
To see how this architecture can be helpful, let’s think about a program that attempts to classify images either as a bicycle or a unicycle. For a human, this is an easy task, but programming a computer to look at a grid of pixels and tell which object it represents is quite difficult. Certain pixels that indicate that a unicycle exists in one image will mean something else entirely in the next if the unicycle has moved slightly, been placed at a different angle, or has a different color.
Deep learning models get past this by breaking the problem down into more manageable pieces. For example, a deep neural network’s first layer of neurons might first break down the image into parts and just identify low-level visual features, like edges and borders of shapes in the image. These created features are fed into the next layer of the network to find patterns among the features. These patterns are then fed into subsequent layers, until the network is identifying general shapes and, eventually, complete objects. In our unicycle example, the first layer might find lines, the second might see lines forming circles, and the third might identify that certain circles are actually wheels. In this way, instead of looking at a mass of pixels, the model can see that each image has a certain number of “wheel” meta-features. It can then, for example, learn that two wheels likely indicate a bicycle, whereas one wheel means a unicycle.
In this chapter, we focus on how neural networks actually work, both mathematically and structurally. First, I use a very basic neural network as an example to explain exactly what a neuron is and how it connects to other neurons to create a neural network. Second, I describe the mathematical processes used to train these networks. Finally, I describe some popular types of neural networks, how they’re special, and what they’re good at. This will set you up nicely for Chapter 11, where you’ll actually create deep learning models in Python.
Machine learning models are simply big mathematical functions. For example, we take input data (such as an HTML file represented as a series of numbers), apply a machine learning function (such as a neural network), and we get an output that tells us how malicious the HTML file looks. Every machine learning model is just a function containing adjustable parameters that get optimized during the training process.
But how does a deep learning function actually work and what does it look like? Neural networks are, as the name implies, just networks of many neurons. So, before we can understand how neural networks work, we first need to know what a neuron is.
Neurons themselves are just a type of small, simple function. Figure 10-1 shows what a single neuron looks like.
Figure 10-1: Visualization of a single neuron
You can see that input data comes in from the left, and a single output number comes out on the right (though some types of neurons generate multiple outputs). The value of the output is a function of the neuron’s input data and some parameters (which are optimized during training). Two steps occur inside every neuron to transform the input data into the output.
First, a weighted sum of the neuron’s inputs is calculated. In Figuree 10-1, each input number, xi, travelling into the neuron gets multiplied by an associated weight value, wi. The resulting values are added together (yielding a weighted sum) to which a bias term is added. The bias and weights are the parameters of the neuron that are modified during training to optimize the model.
Second, an activation function is applied to the weighted sum plus bias value. The purpose of an activation function is to apply a nonlinear transformation to the weighted sum, which is a linear transformation of the neuron’s input data. There are many common types of activation functions, and they tend to be quite simple. The only requirement of an activation function is that it’s differentiable, which enables us to use backpropagation to optimize parameters (we discuss this process shortly in “Training Neural Networks” on page 189).
Table 10-1 shows a variety of other common activation functions and explains which ones tend to be good for which purposes.
Table 10-1: Common Activation Functions
Name |
Plot |
Equation |
Description |
Identity |
|
f(x) = x |
Basically: no activation function! |
ReLU |
|
|
Just max(0, x). ReLUs enable fast learning and are more resilient to the vanishing gradient problem (explained later in this chapter) compared to other functions, like the sigmoid. |
Leaky ReLU |
|
|
Like normal ReLU, but instead of 0, a small constant fraction of x is returned. Generally you choose α to be very small, like 0.01. Also, α stays fixed during training. |
PReLU |
|
|
This is just like leaky ReLU, but in PReLU, α is a parameter whose value is optimized during the training process, along with the standard weight and bias parameters. |
ELU |
|
|
Like PReLU in that α is a parameter, but instead of going down infinitely with a slope of α when x < 0, the curve is bounded by α, because ex will always be between 0 and 1 when x < 0. |
Step |
|
|
Just a step function: the function returns 0 unless x ≤ 0, in which case the function returns 1. |
Gaussian |
|
f(x) = e-x2 |
A bell-shaped curve whose maximum value tops out at 1 when x = 0. |
Sigmoid |
|
|
Because of the vanishing gradient problem (explained later in this chapter), sigmoid activation functions are often only used in the final layer of a neural network. Because the output is continuous and bounded between 0 and 1, sigmoid neurons are a good proxy for output probabilities. |
Softmax |
(multi-output) |
|
Outputs multiple values that sum to 1. Softmax activation functions are often used in the final layer of a network to represent classification probabilities, because Softmax forces all outputs from a neuron to sum to 1. |
Rectified linear unit (ReLU) is by far the most common activation function used today, and it’s simply max(0, s). For example, let’s say your weighted sum plus bias value is called s. If s is above zero, then your neuron’s output is s, and if s is equal to or below zero, then your neuron’s output is 0. You can express the entire function of a ReLU neuron as simply max(0, weighted-sum-of-inputs + bias), or more concretely, as the following for n inputs:
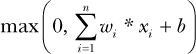
Nonlinear activation functions are actually a key reason why networks of such neurons are able to approximate any continuous function, which is a big reason why they’re so powerful. In the following sections, you learn how neurons are connected together to form a network, and later you’ll gain an understanding of why nonlinear activation functions are so important.
To create a neural network, you arrange neurons in a directed graph (a network) with a number of layers, connecting to form a much larger function. Figure 10-2 shows an example of a small neural network.
Figure 10-2: Example of a very small, four-neuron neural network, where data is passed from neuron to neuron via the connections.
In Figure 10-2, we have our original inputs: x1, x2, and x3 on the left side. Copies of these xi values are sent along the connections to each neuron in the hidden layer (a layer of neurons whose output is not the final output of the model), resulting in three output values, one from each neuron. Finally, each output of these three neurons is sent to a final neuron, which outputs the neural network’s final result.
Every connection in a neural network is associated with a weight parameter, w, and every neuron also contains a bias parameter, b (added to the weighted sum), so the total number of optimizable parameters in a basic neural network is the number of edges connecting an input to a neuron, plus the number of neurons. For example, in the network shown in Figure 10-2, there are 4 total neurons, plus 9 + 3 edges, yielding a total of 16 optimizable parameters. Because this is just an example, we’re using a very small neural network—real neural networks often have thousands of neurons and millions of connections.
A striking aspect of neural networks is that they are universal approximators: given enough neurons, and the right weight and bias values, a neural network can emulate basically any type of behavior. The neural network shown in Figure 10-2 is feed-forward, which means the data is always flowing forward (from left to right in the image).
The universal approximation theorem describes the concept of universality more formally. It states that a feed-forward network with a single hidden layer of neurons with nonlinear activation functions can approximate (with an arbitrarily small error) any continuous function on a compact subset of Rn.1 That’s a bit of a mouthful, but it just means that with enough neurons, a neural network can very closely approximate any continuous, bounded function with a finite number of inputs and outputs.
In other words, the theorem states that regardless of the function we want to approximate, there’s theoretically some neural network with the right parameters that can do the job. For example, if you draw a squiggly, continuous function, f(x), like in Figure 10-3, there exists some neural network such that for every possible input of x, f(x) ≈ network(x), no matter how complicated the function f(x). This is one reason neural networks can be so powerful.
Figure 10-3: Example of how a small neural net could approximate a funky function. As the number of neurons grows, the difference between y and ŷ will approach 0.
In the next sections, we build a simple neural network by hand to help you understand how and why we can model such different types of behavior, given the right parameters. Although we do this on a very small scale using just a single input and output, the same principle holds true when you’re dealing with multiple inputs and outputs, and incredibly complex behaviors.
To see this universality in action, let’s try building our own neural network. We start with two ReLU neurons, using a single input x, as shown in Figure 10-4. Then, we see how different weight and bias values (parameters) can be used to model different functions and outcomes.
Figure 10-4: Visualization of two neurons being fed input data x
Here, both neurons have a weight of 1, and both use a ReLU activation function. The only difference between the two is that neuron1 applies a bias value of –1, while neuron2 applies a bias value of –2. Let’s see what happens when we feed neuron1 a few different values of x. Table 10-2 summarizes the results.
Table 10-2: Neuron1
Input |
Weighted sum |
Weighted sum + bias |
Output |
x |
x* wx→1 |
x* wx→1 + bias1 |
max(0, x* wx→1 + bias1) |
0 |
0 * 1 = 0 |
0 + –1 = –1 |
max(0, –1) = 0 |
1 |
1 * 1 = 1 |
1 + –1 = 0 |
max(0, 0) = 0 |
2 |
2 * 1 = 2 |
2 + –1 = 1 |
max(0, 1) = 1 |
3 |
3 * 1 = 3 |
3 + –1 = 2 |
max(0, 2) = 2 |
4 |
4 * 1 = 4 |
4 + –1 = 3 |
max(0, 3) = 3 |
5 |
5 * 1 = 5 |
5 + –1 = 4 |
max(0, 4) = 4 |
The first column shows some sample inputs for x, and the second shows the resulting weighted sum. The third column adds the bias parameter, and the fourth column applies the ReLU activation function to yield the neuron’s output for a given input of x. Figure 10-5 shows the graph of the neuron1 function.
Figure 10-5: Visualization of neuron1 as a function. The x-axis represents the neuron’s single input value, and the y-axis represents the neuron’s output.
Because neuron1 has a bias of –1, the output of neuron1 stays at 0 until the weighted sum goes above 1, and then it goes up with a certain slope, as you can see in Figure 10-5. That slope of 1 is associated with the wx→1 weight value of 1. Think about what would happen with a weight of 2: because the weighted sum value would double, the angle in Figure 10-5 would occur at x = 0.5 instead of x = 1, and the line would go up with a slope of 2 instead of 1.
Now let’s look at neuron2, which has a bias value of –2 (see Table 10-3).
Table 10-3: Neuron2
Input |
Weighted sum |
Weighted sum + bias |
Output |
x |
x* wx→2 |
x* wx→2 + bias2 |
max(0, x* wx→2) + bias2) |
0 |
0 * 1 = 0 |
0 + –2 = –2 |
max(0, –2) = 0 |
1 |
1 * 1 = 1 |
1 + –2 = –1 |
max(0, –1) = 0 |
2 |
2 * 1 = 2 |
2 + –2 = 0 |
max(0, 0) = 0 |
3 |
3 * 1 = 3 |
3 + –2 = 1 |
max(0, 1) = 1 |
4 |
4 * 1 = 4 |
4 + –2 = 2 |
max(0, 2) = 2 |
5 |
5 * 1 = 5 |
5 + –2 = 3 |
max(0, 3) = 3 |
Because neuron2’s bias is –2, the angle in Figure 10-6 occurs at x = 2 instead of x = 1.
Figure 10-6: Visualization of neuron2 as a function
So now we’ve built two very simple functions (neurons), both doing nothing over a set period, then going up infinitely with a slope of 1. Because we’re using ReLU neurons, the slope of each neuron’s function is affected by its weights, while its bias and weight terms both affect where the slope begins. When you use other activation functions, similar rules apply. By adjusting parameters, we could change the angle and slope of each neuron’s function however we wanted.
In order to achieve universality, however, we need to combine neurons together, which will allow us to approximate more complex functions. Let’s connect our two neurons up to a third neuron, as shown in Figure 10-7. This will create a small three-neuron network with a single hidden layer, composed of neuron1 and neuron2.
In Figure 10-7, input data x is sent to both neuron1 and neuron2. Then, neuron1 and neuron2’s outputs are sent as inputs to neuron3, which yields the network’s final output.
Figure 10-7: Visualization of a small three-neuron network
If you inspect the weights in Figure 10-7, you’ll notice that the weight w1→3 is 2, doubling neuron1’s contribution to neuron3. Meanwhile, w2→3 is –1, inverting neuron2’s contribution. In essence, neuron3 is simply applying its activation function to neuron1 * 2 – neuron2. Table 10-4 summarizes the inputs and corresponding outputs for the resulting network.
Table 10-4: A Three-Neuron Network
Original network input |
Inputs to neuron3 |
Weighted sum |
Weighted sum + bias |
Final network output |
|
x |
neuron1 |
neuron2 |
(neuron1 * w1→3) + (neuron2 * w2→3) |
(neuron1 * w1→3) + (neuron2 * w2→3) + bias3 |
max(0, (neuron1 * w1→3) + (neuron2 * w2→3) + bias3) |
0 |
0 |
0 |
(0 * 2) + (0 * –1) = 0 |
0 + 0 + 0 = 0 |
max(0, 0) = 0 |
1 |
0 |
0 |
(0 * 2) + (0 * –1) = 0 |
0 + 0 + 0 = 0 |
max(0, 0) = 0 |
2 |
1 |
0 |
(1 * 2) + (0 * –1) = 2 |
2 + 0 + 0 = 2 |
max(0, 2) = 2 |
3 |
2 |
1 |
(2 * 2) + (1 * –1) = 3 |
4 + –1 + 0 = 3 |
max(0, 3) = 3 |
4 |
3 |
2 |
(3 * 2) + (2 * –1) = 4 |
6 + –2 + 0 = 4 |
max(0, 4) = 4 |
5 |
4 |
3 |
(4 * 2) + (3 * –1) = 5 |
8 + –3 + 0 = 5 |
max(0, 5) = 5 |
The first column shows original network input, x, followed by the resulting outputs of neuron1 and neuron2. The rest of the columns show how neuron3 processes the outputs: the weighted sum is calculated, bias is added, and finally in the last column the ReLU activation function is applied to achieve the neuron and network outputs for each original input value for x. Figure 10-8 shows the network’s function graph.
Figure 10-8: Visualization of our network’s inputs and associated outputs
We can see that through the combination of these simple functions, we can create a graph that goes up for any period or slope desired over different points, as we did in Figure 10-8. In other words, we’re much closer to being able to represent any finite function for our input x!
We’ve seen how to make our network’s function’s graph go up (with any slope) by adding neurons, but how would we make the graph go down? Let’s add another neuron (neuron4) to the mix, as shown in Figure 10-9.
Figure 10-9: Visualization of a small four-neuron network with a single hidden layer
In Figure 10-9, input data x is sent to neuron1, neuron2, and neuron4. Their outputs are then fed as inputs to neuron3, which yields the network’s final output. Neuron4 is the same as neuron1 and neuron2, but with its bias set to –4. Table 10-5 summarizes the output of neuron4.
Table 10-5: Neuron4
Input |
Weighted sum |
Weighted sum + bias |
Output |
x |
x * wx→4 |
(x * wx→4) + bias4 |
max(0, (x * wx→4) + bias4) |
0 |
0 * 1 = 0 |
0 + –4 = –4 |
max(0, –4) = 0 |
1 |
1 * 1 = 1 |
1 + –4 = –3 |
max(0, –3) = 0 |
2 |
2 * 1 = 2 |
2 + –4 = –2 |
max(0, –2) = 0 |
3 |
3 * 1 = 3 |
3 + –4 = –1 |
max(0, –1) = 0 |
4 |
4 * 1 = 4 |
4 + –4 = 0 |
max(0, 0) = 0 |
5 |
5 * 1 = 5 |
5 + –4 = 1 |
max(0, 1) = 1 |
To make our network graph descend, we subtract neuron4’s function from that of neuron1 and neuron2 in neuron3’s weighted sum by setting the weight connecting neuron4 to neuron3 to –2. Table 10-6 shows the new output of the entire network.
Table 10-6: A Four-Neuron Network
Original network input |
Inputs to neuron3 |
Weighted sum |
Weighted sum + bias |
Final network output |
||
x |
neuron1 |
neuron2 |
neuron4 |
(neuron1 * w1→3) + (neuron2 * w2→3) + (neuron4 * w4→3) |
(neuron1 * w1→3) + (neuron2 * w2→3) + (neuron4 * w4→3) + bias3 |
max(0, (neuron1 * w1→3) + (neuron2 * w2→3) + (neuron4 * w4→3) + bias3) |
0 |
0 |
0 |
0 |
(0 * 2) + (0 * –1) + (0 * –2) = 0 |
0 + 0 + 0 + 0 = 0 |
max(0, 0) = 0 |
1 |
0 |
0 |
0 |
(0 * 2) + (0 * –1) + (0 * –2) = 0 |
0 + 0 + 0 + 0 = 0 |
max (0, 0) = 1 |
2 |
1 |
0 |
0 |
(1 * 2) + (0 * –1) + (0 * –2) = 2 |
2 + 0 + 0 + 0 = 2 |
max (0, 2) = 2 |
3 |
2 |
1 |
0 |
(2 * 2) + (1 * –1) + (0 * –2) = 3 |
4 + –1 + 0 + 0 = 3 |
max (0, 3) = 3 |
4 |
3 |
2 |
0 |
(3 * 2) + (2 * –1) + (0 * –2) = 4 |
6 + –2 + 0 + 0 = 4 |
max (0, 4) = 4 |
5 |
4 |
3 |
1 |
(4 * 2) + (3 * –1) + (1 * –2) = 5 |
8 + –3 + –2 + 0 = 3 |
max (0, 3) = 3 |
Figure 10-10 shows what this looks like.
Figure 10-10: Visualization of our four-neuron network
Hopefully, now you can see how the neural network architecture allows us to move up and down at any rate over any points on the graph, just by combining a number of simple neurons (universality!). We could continue adding more neurons to create far more sophisticated functions.
You’ve learned that a neural network with a single hidden layer can approximate any finite function with enough neurons. That’s a pretty powerful idea. But what happens when we have multiple hidden layers of neurons? In short, automatic feature generation happens, which is perhaps an even more powerful aspect of neural networks.
Historically, a big part of the process of building machine learning models was feature extraction. For an HTML file, a lot of time would be spent deciding what numeric aspects of an HTML file (number of section headers, number of unique words, and so on) might aid the model.
Neural networks with multiple layers and automatic feature generation allow us to offload a lot of that work. In general, if you give fairly raw features (such as characters or words in an HTML file) to a neural network, each layer of neurons can learn to represent those raw features in ways that work well as inputs to later layers. In other words, a neural network will learn to count the number of times the letter a shows up in an HTML document, if that’s particularly relevant to detecting malware, with no real input from a human saying that it is or isn’t.
In our image-processing bicycle example, nobody specifically told the network that edges or wheel meta-features were useful. The model learned that those features were useful as inputs to the next neuron layer during the training process. What’s especially useful is that these lower-level learned features can be used in different ways by later layers, which means that deep neural networks can estimate many incredibly complex patterns using far fewer neurons and parameters than a single-layered network could.
Not only do neural networks perform a lot of the feature extraction work that previously took a lot of time and effort, they do it in an optimized and space-efficient way, guided by the training process.
So far, we’ve explored how, given a large number of neurons and the right weights and bias terms, a neural network can approximate complex functions. In all our examples so far, we set those weight and bias parameters manually. However, because real neural networks normally contain thousands of neurons and millions of parameters, we need an efficient way to optimize these values.
Normally, when training a model, we start with a training dataset and a network with a bunch of non-optimized (randomly initialized) parameters. Training requires optimizing parameters to minimize an objective function. In supervised learning, where we’re trying to train our model to be able to predict a label, like 0 for “benign” and 1 for “malware,” that objective function is going to be related to the network’s prediction error during training. For some given input x (for example, a specific HTML file), this is the difference between the label y we know is correct (for example, 1.0 for “is malware”) and the output ŷ we get from the current network (for example, 0.7). You can think of the error as the difference between the predicted label ŷ and the known, true label y, where network (x) = ŷ, and the network is trying to approximate some unknown function f, such that f(x) = y. In other words, network = 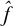 .
.
The basic idea behind training networks is to feed a network an observation, x, from your training dataset, receive some output, ŷ , and then figure out how changing your parameters will shift ŷ closer to your goal, y. Imagine you’re in a spaceship with various knobs. You don’t know what each knob does, but you know the direction you want to go in (y). To solve the problem, you step on the gas and note the direction you went (ŷ ). Then, you turn a knob just a tiny bit and step on the gas again. The difference between your first and second directions tells you how much that knob affects your direction. In this way, you can eventually figure out how to fly the spaceship quite well.
Training a neural network is similar. First, you feed a network an observation, x, from your training dataset, and you receive some output, ŷ . This step is called forward propagation because you feed your input x forward through the network to get your final output ŷ . Next, you determine how each parameter affects your output ŷ . For example, if your network’s output is 0.7, but you know the correct output should be closer to 1, you can try increasing a parameter, w, just a little bit, seeing whether ŷ gets closer to or further away from y, and by how much.2 This is called the partial derivative of ŷ with respect to w, or ∂ŷ/∂w.
Parameters all throughout the network are then nudged just a tiny bit in a direction that causes ŷ to shift a little closer to y (and therefore network closer to f ). If ∂ŷ/∂w is positive, then you know you should increase w by a small amount (specifically, proportional to ∂(y – ŷ)/∂w), so that your new ŷ will move slightly away from 0.7 and toward 1 (y). In other words, you teach your network to approximate the unknown function f by correcting its mistakes on training data with known labels.
The process of iteratively calculating these partial derivatives, updating parameters, and then repeating is called gradient descent. However, with a network of thousands of neurons, millions of parameters, and often millions of training observations, all of that calculus requires a lot of computation. To get around this, we use a neat algorithm called backpropagation that makes these calculations computationally feasible. At its core, backpropagation allows us to efficiently calculate partial derivatives along computational graphs like a neural network!
In this section, we construct a simple neural network to showcase how backpropagation works. Let’s assume that we have a training example whose value is x = 2 and an associated true label of y = 10. Usually, x would be an array of many values, but let’s stick to a single value to keep things simple. Plugging in these values, we can see in Figure 10-11 that our network outputs a ŷ value of 5 with an input x value of 2.
Figure 10-11: Visualization of our three-neuron network, with an input of x = 2
To nudge our parameters so that our network’s output ŷ , given x = 2, moves closer to our known y value of 10, we need to calculate how w1→3 affects our final output ŷ . Let’s see what happens when we increase w1→3 by just a bit (say, 0.01). The weighted sum in neuron3 becomes 1.01 * 2 + (1 * 3), making the final output ŷ change from 5 to 5.02, resulting in an increase of 0.02. In other words, the partial derivative of ŷ with respect to w1→3 is 2, because changing w1→3 yields twice that change in ŷ .
Because y is 10 and our current output ŷ (given our current parameter values and x = 2) is 5, we now know that we should increase w1→3 by a small amount to move y closer to 10.
That’s fairly simple. But we need to be able to know which direction to push all parameters in our network, not just ones in a neuron in the final layer. For example, what about wx→1? Calculating ∂ŷ/∂wx→1 is more complicated because it only indirectly affects ŷ . First, we ask neuron3’s function how ŷ is affected by neuron1’s output. If we change the output of neuron1 from 2 to 2.01, the final output of the neuron3 changes from 5 to 5.01, so ∂ŷ/∂neuron1 = 1. To know how much wx→1 affects ŷ , we just have to multiply ∂ŷ/∂neuron1 by how much wx→1 affects the output of neuron1. If we change wx→1 from 1 to 1.01, the output of neuron1 changes from 2 to 2.02, so ∂neuron1/∂wx→1 is 2. Therefore:
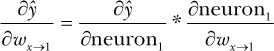
Or:
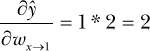
You may have noticed that we just used the chain rule.3
In other words, to figure out how a parameter like wx→1 deep inside a network affects our final output ŷ , we multiply the partial derivatives at each point along the path between our parameter wx→1 and ŷ . This means that if wx→1 is fed into a neuron whose outputs are fed into ten other neurons, calculating wx→1’s effect on ŷ would involve summing over all the paths that led from wx→1 to ŷ , instead of just one. Figure 10-12 visualizes the paths affected by the sample weight parameter wx→2.
Figure 10-12: Visualization of the paths affected by wx→2 (shown in dark gray): the weight associated with the connection between input data x and the middle neuron in the first (leftmost) layer
Note that the hidden layers in this network are not fully connected layers, which helps explain why the second hidden layer’s bottom neuron isn’t highlighted.
But what happens when our network gets even larger? The number of paths we need to add to calculate the partial derivative of a low-level parameter increases exponentially. Consider a neuron whose output is fed into a layer of 1,000 neurons, whose outputs are fed into 1,000 more neurons, whose outputs are then fed into a final output neuron.
That results in one million paths! Luckily, going over every single path and then summing them to get the ∂ŷ/(∂parameter) is not necessary. This is where backpropagation comes in handy. Instead of walking along every single path that leads to our final output(s), ŷ , partial derivatives are calculated layer by layer, starting from the top down, or backward.
Using the chain rule logic from the last section, we can calculate any partial derivative ∂ŷ/∂w, where w is a parameter connecting an output from layeri–1 to a neuroni in layeri, by summing over the following for all neuroni+1, where each neuroni+1 is a neuron in layeri+1 to which neuroni (w’s neuron) is connected:

By doing this layer by layer from the top down, we limit path explosion by consolidating derivatives at each layer. In other words, derivatives calculated in a top-level layeri+1 (like ∂ŷ/∂neuroni+1) are recorded to help calculate derivatives in layeri. Then to calculate derivatives in layeri–1, we use the saved derivatives from layeri (like ∂ŷ/∂neuroni). Then, layeri–2 uses derivatives from layeri–1, and so on and so forth. This trick greatly reduces the amount of calculations we have to repeat and helps us to train neural networks quickly.
One issue that very deep neural networks face is the vanishing gradient problem. Consider a weight parameter in the first layer of a neural network that has ten layers. The signal it gets from backpropagation is the summation of all paths’ signals from this weight’s neuron to the final output.
The problem is that each path’s signal is likely to be incredibly tiny, because we calculate that signal by multiplying partial derivatives at each point along the ten-neuron-deep path, all of which tend to be numbers smaller than 1. This means that a low-level neuron’s parameters are updated based on the summation of a massive number of very tiny numbers, many of which end up canceling one another out. As a result, it can be difficult for a network to coordinate sending a strong signal down to parameters in lower layers. This problem gets exponentially worse as you add more layers. As you learn in the following section, certain network designs try to get around this pervasive problem.
For simplicity’s sake, every example I’ve shown you so far uses a type of network called a feed-forward neural network. In reality, there are many other useful network structures you can use for different classes of problems. Let’s discuss some of the most common classes of neural networks and how they could be applied in a cybersecurity context.
The simplest (and first) kind of neural network, a feed-forward neural network, is kind of like a Barbie doll with no accessories: other types of neural networks are usually just variations on this “default” structure. The feed-forward architecture should sound familiar: it consists of stacks of layers of neurons. Each layer of neurons is connected to some or all neurons in the next layer, but connections never go backward or form cycles, hence the name “feed forward.”
In feed-forward neural networks, every connection that exists is connecting a neuron (or original input) in layer i to a neuron in layer j > i. Each neuron in layer i doesn’t necessarily have to connect to every neuron in layer i + 1, but all connections must be feeding forward, connecting previous layers to later layers.
Feed-forward networks are generally the kind of network you throw at a problem first, unless you already know of another architecture that works particularly well on the problem at hand (such as convolutional neural networks for image recognition).
A convolutional neural network (CNN) contains convolutional layers, where the input that feeds into each neuron is defined by a window that slides over the input space. Imagine a small square window sliding over a larger picture where only the pixels visible through the window will be connected to a specific neuron in the next layer. Then, the window slides, and the new set of pixels are connected to a new neuron. Figure 10-13 illustrates this.
The structure of these networks encourages localized feature learning. For example, it’s more useful for a network’s lower layers to focus on the relationship between nearby pixels in an image (which form edges, shapes, and so on) than to focus on the relationship between pixels randomly scattered across an image (which are unlikely to mean much). The sliding windows explicitly force this focus, which improves and speeds up learning in areas where local feature extraction is especially important.
Figure 10-13: Visualization of a 2 × 2 convolutional window sliding over a 3 × 3 input space with a stride (step size) of 1, to yield a 2 × 2 output
Because of their ability to focus on localized sections of the input data, convolutional neural networks are extremely effective at image recognition and classification. They’ve also been shown to be effective for certain types of natural language processing, which has implications for cybersecurity.
After each convolutional window’s values are fed to specific neurons in a convolutional layer, a sliding window is again slid over these neurons’ outputs, but instead of them being fed to standard neurons (for example, ReLUs) with weights associated with each input, they’re fed to neurons that have no weights (that is, fixed at 1) and a max (or similar) activation function. In other words, a small window is slid over the convolutional layer’s outputs, and the maximum value of each window is taken and passed to the next layer. This is called a pooling layer. The purpose of pooling layers is to “zoom out” on the data (usually, an image), thereby reducing the size of the features for faster computation, while retaining the most important information.
Convolutional neural networks can have one or multiple sets of convolutional and pooling layers. A standard architecture might include a convolutional layer, a pooling layer, followed by another set of convolutional and pooling layers, and finally a few fully connected layers, like in feed-forward networks. The goal of this architecture is that these final fully connected layers receive fairly high-level features as inputs (think wheels on a unicycle), and as a result are able to accurately classify complex data (such as images).
An autoencoder is a type of neural network that tries to compress and then decompress an input with minimal difference between the original training input and the decompressed output. The goal of an autoencoder is to learn an efficient representation for a set of data. In other words, autoencoders act like optimized lossy compression programs, where they compress input data into a smaller representation, then decompress it back to its original input size.
Instead of the neural network optimizing parameters by minimizing the difference between known labels (y) and predicted labels (ŷ ) for a given input x, the network tries to minimize the difference between the original input x and the reconstructed output  .
.
Structurally, autoencoders are usually very similar to standard feed-forward neural networks, except that middle layers contain fewer neurons than early and later stage layers, as shown in Figure 10-14.
Figure 10-14: Visualization of an autoencoder network
As you can see, the middle layer is much smaller than the leftmost (input) and rightmost (output) layers, which each have the same size. The last layer should always contain the same number of outputs as the original inputs, so each training input xi can be compared to its compressed and reconstructed cousin  .
.
After an autoencoder network has been trained, it can be used for different purposes. Autoencoder networks can simply be used as efficient compress/decompress programs. For example, autoencoders trained to compress image files can create images that look far clearer than the same image compressed via JPEG to the same size.
A generative adversarial network (GAN) is a system of two neural networks competing with each other to improve themselves at their respective tasks. Typically, the generative network tries to create fake samples (for example, some sort of image) from random noise. Then a second discriminator network attempts to tell the difference between real samples and the fake, generated samples (for example, distinguishing between real images of a bedroom and generated images).
Both neural networks in a GAN are optimized with backpropagation. The generator network optimizes its parameters based on how well it fooled the discriminator network in a given round, while the discriminator network optimizes its parameters based on how accurately it could discriminate between generated and real samples. In other words, their loss functions are direct opposites of one another.
GANs can be been used to generate real-looking data or enhance low-quality or corrupted data.
Recurrent networks (RRNs) are a relatively broad class of neural networks in which connections between neurons form directed cycles whose activation functions are dependent on time-steps. This allows the network to develop a memory, which helps it learn patterns in sequences of data. In RNNs, the inputs, the outputs, or both the inputs and outputs are some sort of time series.
RNNs are great for tasks where data order matters, like connected handwriting recognition, speech recognition, language translation, and time series analysis. In the context of cybersecurity, they’re relevant to problems like network traffic analysis, behavioral detection, and static file analysis. Because program code is similar to natural language in that order matters, it can be treated as a time series.
One issue with RNNs is that due to the vanishing gradient problem, each time-step introduced in an RNN is similar to an entire extra layer in a feed-forward neural network. During backpropagation, the vanishing gradient problem causes signals in lower-level layers (or in this case, earlier time-steps) to become incredibly faint.
A long short-term memory (LSTM) network is a special type of RNN designed to address this problem. LSTMs contain memory cells and special neurons that try to decide what information to remember and what information to forget. Tossing out most information greatly limits the vanishing gradient problem because it reduces path explosion.
A ResNet (short for residual network) is a type of neural network that creates skip connections between neurons in early/shallow layers of the network to deeper layers by skipping one or more intermediate layers. Here the word residual refers to the fact that these networks learn to pass numerical information directly between layers, without that numerical information having to pass through the kinds of activation functions we illustrated in Table 10-1.
This structure helps greatly reduce the vanishing gradient problem, which enables ResNets to be incredibly deep—sometimes more than 100 layers.
Very deep neural networks excel at modeling extremely complex, odd relationships in input data. Because ResNets are able to have so many layers, they are especially suited to complex problems. Like feed-forward neural networks, ResNets are important more because of their general effectiveness at solving complex problems rather than their expertise in very specific problem areas.
In this chapter, you learned about the structure of neurons and how they are connected together to form neural networks. You also explored how these networks are trained via backpropagation, and you discovered some benefits and issues that neural networks have, such as universality, automatic feature generation, and the vanishing gradient problem. Finally, you learned the structures and benefits of a few common types of neural networks.
In the next chapter, you’ll actually build neural networks to detect malware, using Python’s Keras package.