Big Ideas

IN CONTEXT

BRANCH

Physics

BEFORE

1925 Werner Heisenberg, Max Born, and Pascual Jordan develop matrix mechanics to describe the wave-like behaviour of particles.

1926 Erwin Schrödinger develops a wavefunction describing the change in an electron over time.

AFTER

1932 The existence of the positron, the antiparticle to the electron, is confirmed by Carl Anderson.

1940s Richard Feynman, Sin-Itiro Tomonaga, and Julian Schwinger develop quantum electrodynamics – a mathematical way to describe the interaction between light and matter, which fully unites quantum theory with special relativity.

English physicist Paul Dirac contributed a huge amount to the theoretical framework of quantum physics in the 1920s, but is probably best known today for predicting the existence of antiparticles through mathematics.

Dirac was a postgraduate student at Cambridge University when he read Werner Heisenberg’s groundbreaking paper on matrix mechanics, which described how particles jump from one quantum state to another. Dirac was one of the few people capable of grasping the paper’s difficult mathematics, and noticed parallels between Heisenberg’s equations and parts of the classical (pre-quantum) theory of particle motion known as Hamiltonian mechanics. This allowed Dirac to develop a method by which classical systems could be understood on a quantum level.

One early result of this work was a derivation of the idea of quantum spin. Dirac formulated a set of rules now known as “Fermi-Dirac statistics” (since they were also independently found by Enrico Fermi). Dirac named particles such as electrons that have a half-integer spin value “fermions”, after Fermi. The rules describe how large numbers of fermions interact with one another. In 1926, Dirac’s PhD supervisor Ralph Fowler used his statistics to calculate the behaviour of a collapsing stellar core and explain the origin of superdense white dwarf stars.

Quantum field theory

While much of schoolbook physics focuses on the properties and dynamics of individual particles and bodies under the influence of forces, a deeper understanding can be gained by developing field theories. These describe the way that forces make their influence felt across space. The importance of fields as independent entities was first recognized in the mid-19th century by James Clerk Maxwell while he was developing his theory of electromagnetic radiation. Einstein’s general relativity is another example of a field theory.

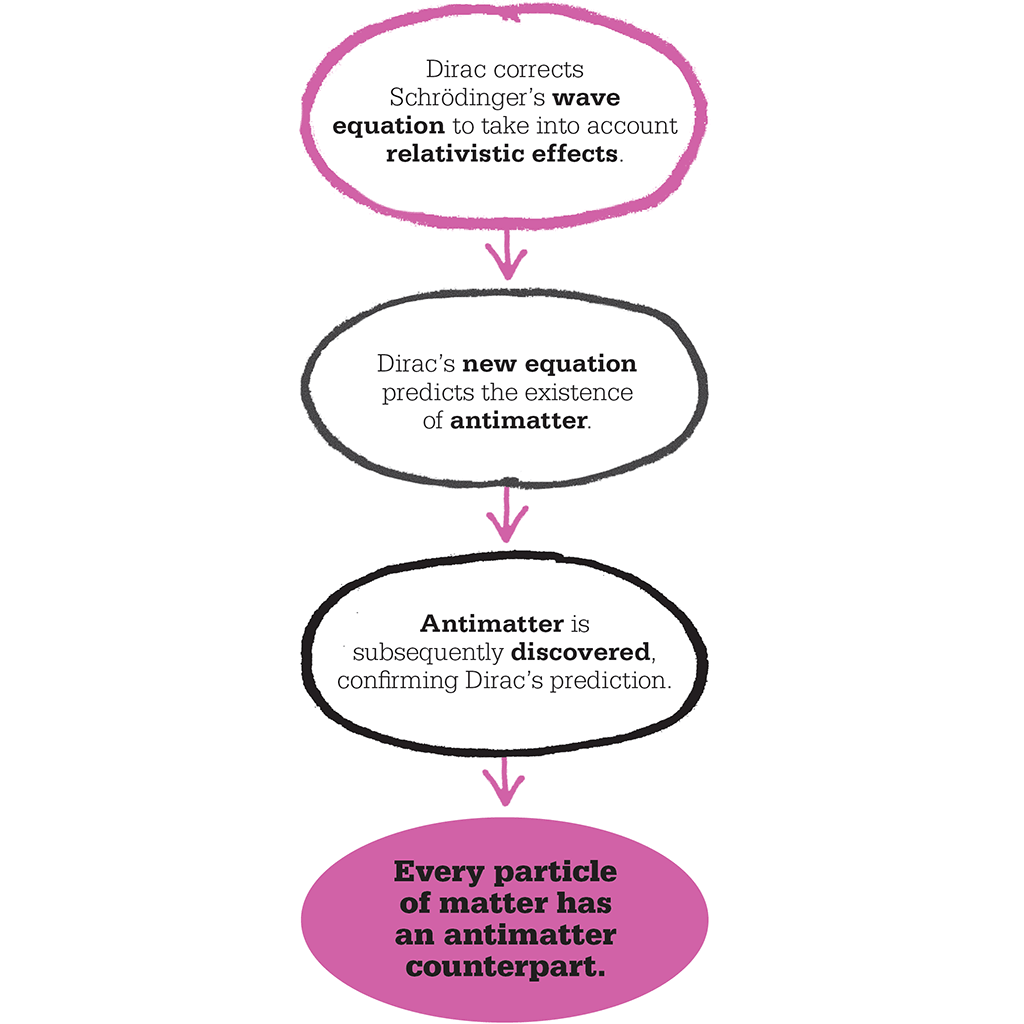
Dirac’s new interpretation of the quantum world was a quantum field theory. In 1928, it allowed him to produce a relativistic version of Schrödinger’s wave equation for the electron (that is, one that could take into account the effects of particles moving close to the speed of light, and therefore model the quantum world more accurately than Schrödinger’s non-relativistic equation). The so-called “Dirac equation” also predicted the existence of particles with identical properties to particles of matter but with opposite electric charge. They were dubbed “antimatter” (a term that had been bandied around in wilder speculations since the late 19th century).

The antielectron particle, or positron, was experimentally confirmed by US physicist Carl Anderson in 1932, detected first in cosmic rays (high-energy particles showered into Earth’s atmosphere from deep space), and then in certain types of radioactive decay. Since then, antimatter has become a subject for intense physical research, and also beloved of science-fiction writers (particularly for its habit of “annihilating” with a burst of energy on contact with normal matter). Perhaps more importantly, however, Dirac’s quantum field theory laid the foundations for the theory of quantum electrodynamics brought to fruition by a later generation of physicists.

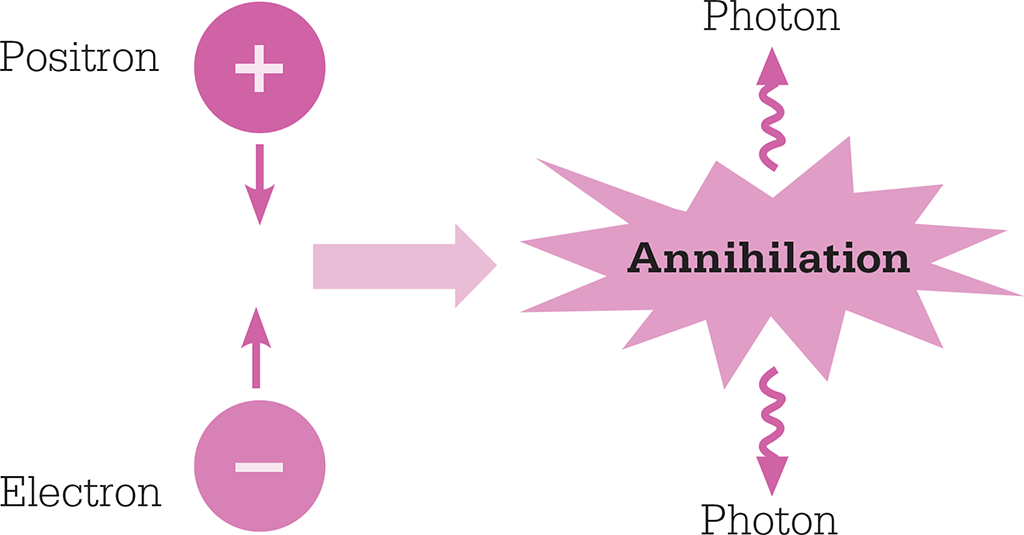
When a particle and its antiparticle come together, they annihilate. Their mass turns into photons of electromagnetic energy in accord with the equation E = mc².

PAUL DIRAC

Paul Dirac was a mathematical genius who made several key contributions to quantum physics, sharing the Nobel Prize in Physics with Erwin Schrödinger in 1933. Born in Bristol, England, to a Swiss father and an English mother, he took degrees in electrical engineering and mathematics at the city’s university, before continuing his studies at Cambridge, where he pursued his fascination with general relativity and quantum theory. After his groundbreaking advances of the mid-1920s, he continued his work at Göttingen and Copenhagen before returning to Cambridge to take up the Lucasian Chair in Mathematics. Much of his later career was focused on quantum electrodynamics. He also pursued the idea of unifying quantum theory with general relativity, but this endeavour met with limited success.

Key works

1930 Principles of Quantum Mechanics

1966 Lectures on Quantum Field Theory