
IN CONTEXT
Physics
1900 A crisis in the understanding of light inspires Max Planck to find a theoretical solution that involves treating light as quantized packets of energy.
1905 Albert Einstein demonstrates the reality of Planck’s quantized light through his explanation of the photoelectric effect.
1913 Niels Bohr’s model of the atom uses the idea that electrons shifting between energy levels within an atom emit or absorb individual quanta of light (photons).
1930s Schrödinger’s work, along with that of Paul Dirac and Werner Heisenberg, forms the foundation of modern particle physics.
Erwin Schrödinger was a key figure in the advancement of quantum physics – the science that explains the tiniest levels of subatomic matter. His star contribution was a famous equation that showed how particles moved in waves. It formed the basis of today’s quantum mechanics and revolutionized the way we perceive the world. But this revolution did not happen suddenly. The process of discovery was a long one, with many pioneers along the way.
Quantum theory was originally limited to the understanding of light. In 1900, as part of an attempt to solve a troubling problem in theoretical physics known as the “ultraviolet catastrophe”, the German physicist Max Planck proposed treating light as though it came in discrete packets, or quanta, of energy. Albert Einstein then took the next step and argued that light quanta were indeed a real physical phenomenon.
Danish physicist Niels Bohr knew that Einstein’s idea was saying something fundamental about the nature of light and atoms, and in 1913 used it to solve an old problem – the precise wavelengths of light emitted when certain elements were heated. By modelling the structure of the atom with electrons orbiting in discrete “shells” whose distance from the nucleus determined their energy, Bohr could explain the emission spectra (distribution of light wavelengths) of atoms in terms of photons of energy given off as electrons jumped between orbits. However, Bohr’s model lacked a theoretical explanation, and could only predict the emissions from hydrogen, the simplest atom.
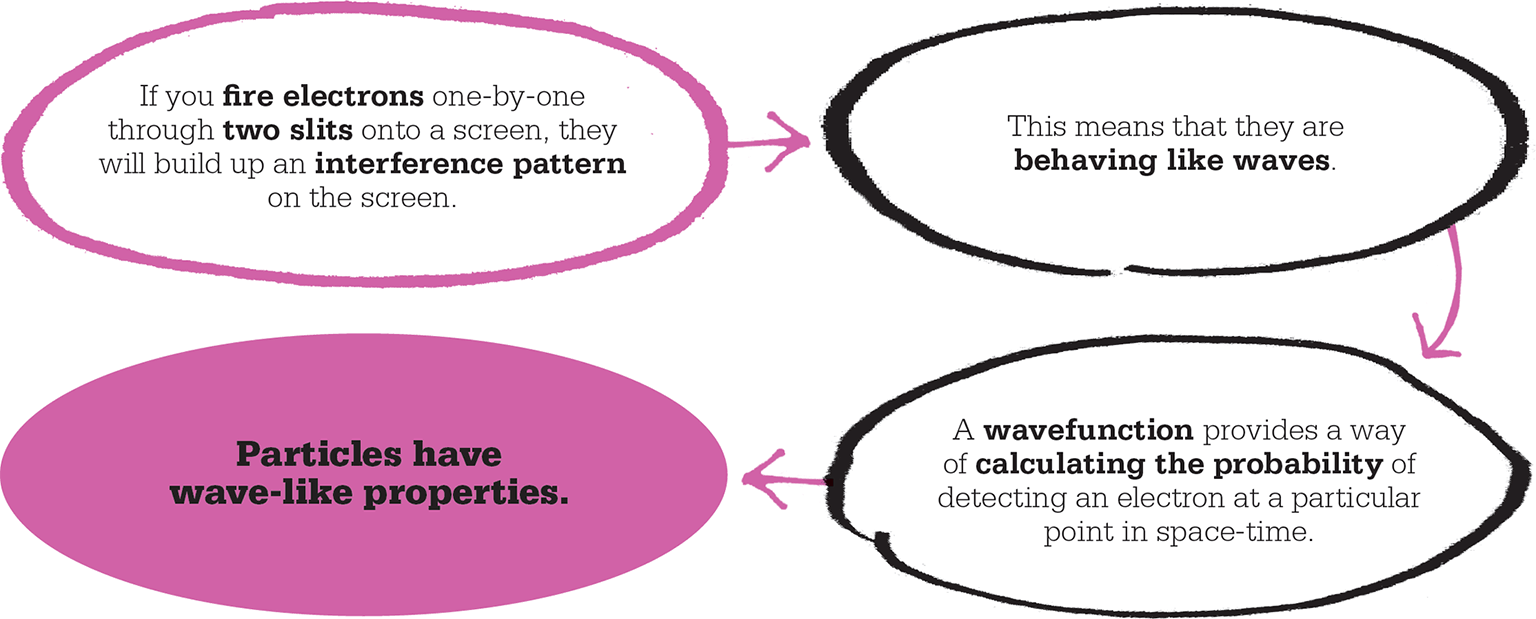
Wave-like atoms?
Einstein’s idea had breathed new life into the old theory of light as streams of particles, even though light had also been proved, through Thomas Young’s double-slit experiment, to behave as a wave. The puzzle of how light could possibly be both particle and wave received a new twist in 1924 from a French PhD student, Louis de Broglie, whose suggestion led the quantum revolution into a dramatic new phase. Not only did de Broglie demonstrate with a simple equation how, in the subatomic world, particles could equally be waves, he also showed how any object, of whatever mass, could behave as a wave to some extent. In other words, if light waves had particle-like properties, then particles of matter – such as electrons – must have wave-like properties.
Planck had calculated the energy of a light photon with the simple equation E = hv, where E is the energy of the electromagnetic quanta, v is the wavelength of the radiation involved, and h is a constant, today known as the Planck constant. De Broglie showed that a light photon also has momentum, something normally only associated with particles with mass and given by multiplying the particle’s mass with its speed. De Broglie showed that a light photon had a momentum of h divided by its wavelength. However, since he was dealing with particles whose energy and mass might be affected by motion at speeds close to that of light, de Broglie incorporated the Lorentz factor into his equation. This produced a more sophisticated version that took into account the effects of relativity.
De Broglie’s idea was radical and daring, but it soon had influential supporters, including Einstein. The hypothesis was also relatively easy to test. By 1927, scientists in two separate laboratories had conducted experiments to show that electrons diffracted and interfered with each other in exactly the same way as photons of light. De Broglie’s hypothesis was proved.

1927 saw a gathering of greats at the Solvay Conference of physics in Brussels. Among others are: 1. Schrödinger, 2. Pauli, 3. Heisenberg, 4. Dirac, 5. de Broglie, 6. Born, 7. Bohr, 8. Planck, 9. Curie, 10. Lorentz, 11. Einstein.
"Two seemingly incompatible conceptions can each represent an aspect of the truth."
Louis de Broglie
Growing significance
In the meantime, a number of theoretical physicists were sufficiently intrigued by de Broglie’s hypothesis to investigate it further. In particular, they wanted to know how the properties of such matter waves could give rise to the pattern of specific energy levels among the electron orbitals of the hydrogen atom proposed by Bohr’s model of the atom. De Broglie himself had suggested that the pattern arose because the circumference of each orbital must accommodate a whole number of wavelengths of the matter wave. Since the electron’s energy level depends on its distance from the atom’s positively charged nucleus, this meant that only certain distances, and certain energy levels, would be stable. However, de Broglie’s solution relied on treating the matter wave as a one-dimensional wave trapped in orbit around the nucleus – a full description would need to describe the wave in three dimensions.
The wave equation
In 1925, three German physicists, Werner Heisenberg, Max Born, and Pascual Jordan, tried to explain the quantum jumps that occurred in Bohr’s model of the atom with a method called matrix mechanics, in which the properties of an atom were treated as a mathematical system that could change over time. However, the method could not explain what was actually happening inside the atom, and its obscure mathematical language did not make it very popular.
A year later, an Austrian physicist working in Zurich, Erwin Schrödinger, hit upon a better approach. He took de Broglie’s wave-particle duality a step further and began to consider whether there was a mathematical equation of wave motion that would describe how a subatomic particle might move. To formulate his wave equation, he began with the laws governing energy and momentum in ordinary mechanics, then amended them to include the Planck constant and de Broglie’s law connecting the momentum of a particle to its wavelength.
When he applied the resulting equation to the hydrogen atom, it predicted exactly the specific energy levels for the atom that had been observed in experiments. The equation was a success. But one awkward issue remained, because no one, not even Schrödinger, knew exactly what the wave equation really described. Schrödinger tried to interpret it as the density of electric charge, but this was not entirely successful. It was Max Born who eventually suggested what it really was – it was a probability amplitude. In other words, it expressed the likelihood of a measurement finding the electron in that particular place. Unlike matrix mechanics, the Schrödinger wave equation or “wavefunction” was embraced by physicists, although it threw open a whole range of wider questions about its proper interpretation.
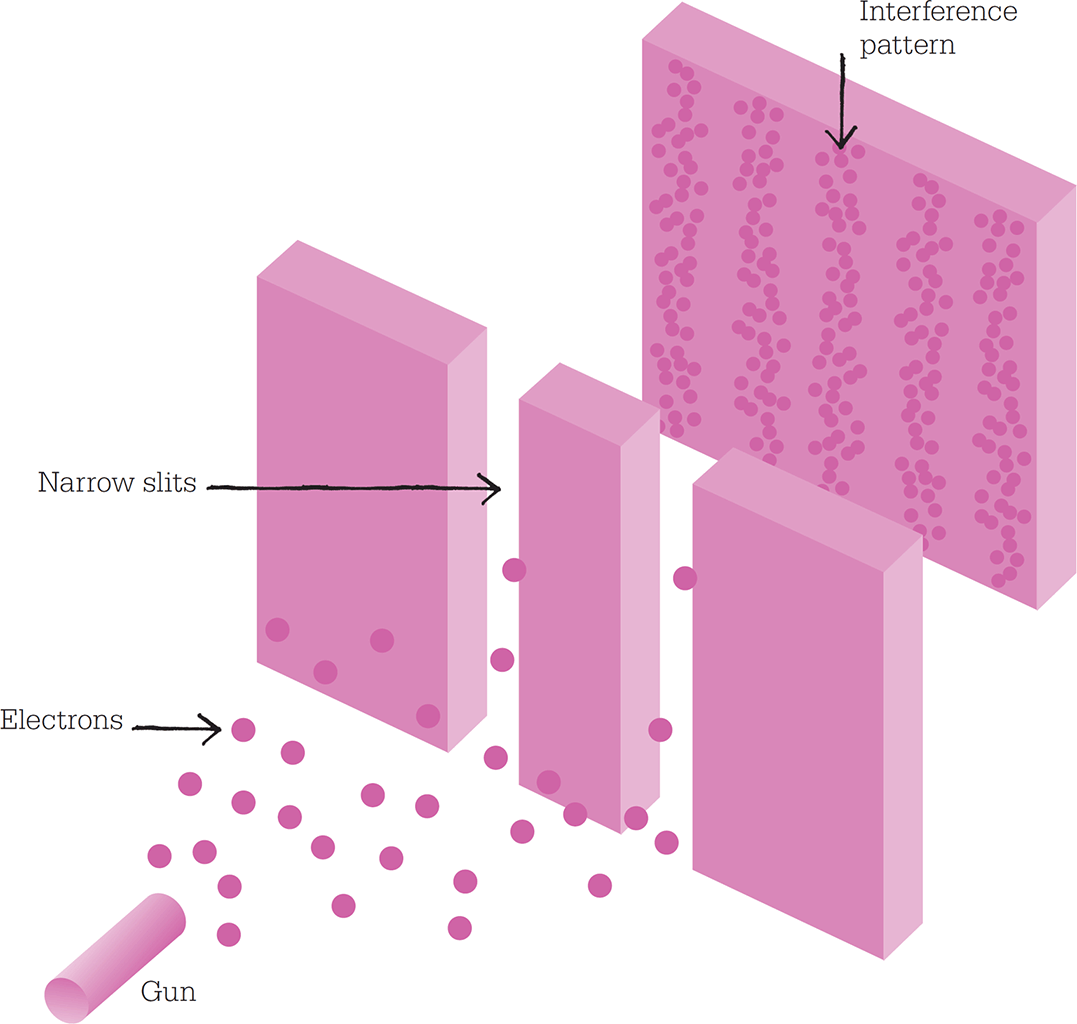
A classic illustration of wave-particle duality involves firing electrons from a “gun” through a barrier with two slits in it. If electrons are allowed to build up over time, an interference pattern forms, just as it would for light waves.
Pauli’s exclusion principle
Another important piece of the puzzle fell into place in 1925 courtesy of another Austrian, Wolfgang Pauli. In order to describe why the electrons within an atom did not all automatically fall directly into the lowest possible energy state, Pauli developed the exclusion principle. Reasoning that a particle’s overall quantum state could be defined by a certain number of properties, each with a fixed number of possible discrete values, his principle stated that it was impossible for two particles within the same system to have the same quantum state simultaneously.
In order to explain the pattern of electron shells that was apparent from the periodic table, Pauli calculated that electrons must be described by four distinct quantum numbers. Three of these – the principal, azimuthal, and magnetic quantum numbers – define the electron’s precise place within the available orbital shells and subshells, with the values of the latter pair limited by the value of the principal number. The fourth number, with two possible values, was needed to explain why two electrons can exist in each subshell with slightly different energy levels. Together, the numbers neatly explained the existence of atomic orbitals that accept 2, 6, 10, and 14 electrons respectively.
Today, the fourth quantum number is known as spin; it is a particle’s intrinsic angular momentum (which is created by its rotation as it orbits), and has positive or negative values that are either whole- or half-integer numbers. A few years later, Pauli would demonstrate that values of spin split all particles into two major groups – fermions such as electrons (with half-integer spins), which obey a set of rules known as Fermi–Dirac statistics, and bosons such as photons (with zero or whole-number spin), which obey different rules known as Bose–Einstein statistics. Only fermions obey the exclusion principle, and this has important implications for the understanding of everything from collapsing stars to the elementary particles that make up the Universe.
Schrödinger’s success
Combined with Pauli’s exclusion principle, Schrödinger’s wave equation allowed a new and deeper understanding of the orbitals, shells, and subshells within an atom. Rather than imagining them as classical orbits – well-defined paths on which the electrons circle the nucleus – the wave equation shows that they are actually clouds of probability – doughnut-shaped and lobe-shaped regions in which a particular electron with certain quantum numbers is likely to be found.
Another major success for Schrödinger’s approach was that it offered an explanation for radioactive alpha decay – in which a fully formed alpha particle (consisting of two protons and two neutrons) escapes from an atomic nucleus. According to classical physics, in order to remain intact, the nucleus had to be surrounded by a potential well steep enough to prevent particles escaping from it. (A potential well is a region in space where the potential energy is lower than its surroundings, meaning that it traps particles.) If the well was not sufficiently steep, the nucleus would disintegrate completely. How, then, could the intermittent emissions seen in alpha decay happen while allowing the remaining nucleus to survive intact? The wave equations overcame the problem because they allowed the energy of the alpha particle within the nucleus to vary. Most of the time, its energy would be low enough to keep it trapped, but occasionally it would rise high enough to overcome the wall and escape (an effect now known as quantum tunnelling). The probability predictions of the wave equation matched the unpredictable nature of the radioactive decay.

Schrödinger’s equation, in its most general form, shows the development of a quantum system over time. It requires the use of complex numbers.
Uncertainty principle
The great debate that shaped the development of quantum physics during the middle years of the 20th century (and remains essentially unresolved today) surrounded what the wavefunction actually meant for reality. In an echo of the Planck/Einstein debate two decades previously, de Broglie saw his and Schrödinger’s equations as mere mathematical tools for describing movement: for de Broglie, the electron was still essentially a particle – just one that had a wave property governing its motion and location. For Schrödinger, however, the wave equation was far more fundamental – it described the way in which the properties of the electron were physically “smeared out” across space. Opposition to Schrödinger’s approach inspired Werner Heisenberg to develop another of the century’s great ideas – the uncertainty principle. This was a realization that the wavefunction meant that a particle can never be “localized” to a point in space and at the same time have a defined wavelength. The more accurately a particle’s position was pinned down, for example, the harder its momentum was to measure. Thus, particles defined by a quantum wavefunction existed in a general state of uncertainty.
"God knows I am no friend of probability theory, I have hated it from the first moment when our dear friend Max Born gave it birth."
Erwin Schrödinger

Dane Niels Bohr (left) collaborated with Werner Heisenberg, to formulate the Copenhagen interpretation of Schrödinger’s wavefunction.
The road to Copenhagen
Measuring the properties of a quantum system always revealed the particle to be in one location, rather than in its wave-like smear. On the scale of classical physics and everyday life, most situations involved definite measurements and definite outcomes, rather than myriad overlapping possibilities. The challenge of reconciling quantum uncertainty with reality is called the measurement problem, and various approaches to it have been put forward, known as interpretations.
The most famous of these is the Copenhagen interpretation, devised by Niels Bohr and Werner Heisenberg in 1927. This states simply that it is the very interaction between the quantum system and a large-scale, external observer or apparatus (subject to the classical laws of physics) that causes the wavefunction to “collapse” and a definite outcome to arise. This interpretation is perhaps the most widely (though not universally) accepted, and appears to be borne out by experiments such as electron diffraction and the double-slit experiment for light waves. It is possible to devise an experiment that reveals the wave-like aspects of light or electrons, but impossible to record the properties of individual particles in the same apparatus.
However, while the Copenhagen interpretation seems reasonable when dealing with small-scale systems such as particles, its implication that nothing is determined until it is measured troubled many physicists. Einstein famously commented that “God does not throw dice”, while Schrödinger devised a thought-experiment to illustrate what he viewed as a ridiculous situation.
Schrödinger’s cat
Taken to its logical conclusion, the Copenhagen interpretation resulted in a seemingly absurd paradox. Schrödinger imagined a cat sealed in a box that contains a vial of poison linked to a radioactive source. If the source decays and emits a particle of radiation, a mechanism will release a hammer that breaks the vial of poison. According to the Copenhagen interpretation, the radioactive source remains in its wavefunction form (as a so-called “superposition” of two possible outcomes) until it is observed. But if that is the case, the same has to be said of the cat.
New interpretations
Dissatisfaction with apparent paradoxes such as Schrödinger’s cat has spurred scientists to develop various alternative interpretations of quantum mechanics. One of the best known is the “Many Worlds Interpretation” put forward in 1956 by American physicist Hugh Everett III. This resolved the paradox by suggesting that during any quantum event, the Universe splits into mutually unobservable alternate histories for each of the possible outcomes. In other words, Schrödinger’s cat would both live and die.
The “Consistent Histories” approach addresses the problem in a rather less radical way, using complex mathematics to generalize the Copenhagen interpretation. This avoids the issues around the collapse of the wavefunction, but instead allows probabilities to be assigned to various scenarios, or “histories”, on both a quantum and classical scale. The approach accepts that only one of these histories eventually conforms to reality, but does not allow prediction of which outcome that will be – instead it simply describes how quantum physics can give rise to the Universe we see without wavefunction collapse.
The ensemble, or statistical, approach is a minimalist mathematical interpretation that was favoured by Einstein. The de Broglie–Bohm theory, which developed from de Broglie’s initial reaction to the wave equation, is an attempt at a strictly causal, rather than probabilistic, explanation, and postulates the existence of a hidden “implicate” order to the Universe. The transactional approach involves waves travelling both forwards and backwards in time.
Perhaps the most intriguing possibility of all, however, is one that verges on the theological. Working in the 1930s, Hungarian-born mathematician John von Neumann concluded that the measurement problem implied that the entire Universe is subject to an all-encompassing wave equation known as the universal wavefunction, and that it is constantly collapsing as we measure its various aspects. Von Neumann’s colleague and countryman Eugene Wigner took the theory and expanded it to suggest that it was not simply interaction with large-scale systems (as in the Copenhagen interpretation) that caused the wavefunction to collapse – it was the presence of intelligent consciousness itself.

Schrödinger’s thought experiment produces a situation in which, according to a strict reading of the Copenhagen interpretation, a cat is both alive and dead at the same time.
ERWIN SCHRÖDINGER

Born in Vienna, Austria, in 1887, Erwin Schrödinger studied physics at the University of Vienna, gaining an assistant’s post there before serving in World War I. After the war, he moved first to Germany, and then to the University of Zurich, Switzerland, where he did his most important work, immersing himself in the emerging field of quantum physics. In 1927, he returned to Germany, and succeeded Max Planck at the Humboldt University of Berlin.
Schrödinger was a vocal opponent of the Nazis, and left Germany for a post at Oxford University in 1934. It was there that he learned he had been awarded the 1933 Nobel Prize in Physics, with Paul Dirac, for the quantum wave equation. By 1936, he was back in Austria, but had to flee again following Germany’s annexation of the country. He settled in Ireland for the rest of his career before retiring to Austria in the 1950s.
Key works
1920 Colour Measurement
1926 Quantization as an Eigenvalue Problem
See also: Thomas Young • Albert Einstein • Werner Heisenberg • Paul Dirac • Richard Feynman • Hugh Everett III