In the multiple-choice section, this topic appears in about 7 out of 75 questions.
In the free-response section, this topic appears almost every year.
When you do calculations on the AP Chemistry Exam, you’ll be expected to present your answers with the proper number of significant figures, so let’s review the rules.
| 245 | 3 significant figures |
| 7.907 | 4 significant figures |
| 907.08 | 5 significant figures |
| 0.005 | 1 significant figure |
| 0.0709 | 3 significant figures |
| 12.000 | 5 significant figures |
| 0.080 | 2 significant figures |
| 1.0 | 2 significant figures |
| 1,200 | 2 significant figures |
| 1,200. | 4 significant figures |
| 10 | 1 significant figure |
| 10. | 2 significant figures |
moles of carbon.0.352 × 0.90876 = 0.320
864 × 12 = 1.0 × 104
7 ÷ 0.567 = 10
26 + 45.88 + 0.09534 = 72
780 + 35 + 4 = 819
The whole point is that the result of a calculation cannot be more accurate than the least accurate number in the calculation.
Let’s review some basic facts about logarithms.
If 10x = y, then log y = x
If ex= y, then ln y = x
e = 2.7183
ln y = 2.303 log y
log (ab) = log a + log b
The mole (Avogadro’s number) is the most important number in chemistry, serving as a bridge that connects all the different quantities that you’ll come across in chemical calculations. The coefficients in chemical reactions tell you about the reactants and products in terms of moles, so most of the stoichiometry questions you’ll see on the test will be exercises in converting between moles and grams, liters, molarities, and other units.
The definition of Avogadro’s number gives you the information you need to convert between moles and individual molecules and atoms.
Moles and grams can be related by using the atomic weights given in the periodic table. Atomic weights on the periodic table are given in terms of atomic mass units (amu), but an amu is the same as a gram per mole, so if 1 carbon atom weighs 12 amu, then 1 mole of carbon atoms weighs 12 grams.
You can use the relationship between amu and g/mol to convert between grams and moles by using the following equation:
We’ll talk more about the ideal gas equation in Chapter 6, but for now, you should know that you can use it to calculate the number of moles of a gas if you know some of the gas’s physical properties. All you need to remember at this point is that in the equation PV = nRT, n stands for moles of gas.
The equation above gives the general rule for finding the number of moles of a gas. Many gas problems will take place at STP, or standard temperature and pressure, where P = 1 atmosphere and T = 273 K. At STP, the situation is much simpler and you can convert directly between the volume of a gas and the number of moles. That’s because at STP, one mole of gas always occupies 22.4 liters.
We’ll talk more about molarity and molality in Chapter 9, but for now you should realize that you can use the equations that define these common measures of concentration to find the number of moles of solute in a solution. Just rearrange the equations to isolate moles of solute.
Moles = (molarity)(liters of solution)
Moles = (molality)(kilograms of solvent)
To solve many problems on the exam, you will need to use percent composition, or mass percents. Percent composition is the percent by mass of each element that makes up a compound. It is calculated by dividing the mass of each element or component in a compound by the total molar mass for the substance.
You will also need to know how to determine the empirical and molecular formula of a compound given masses or mass percents of the components of that compound. Remember that the empirical formula represents the simplest ratio of one element to another in a compound (e.g. C6H12O6), while the molecular formula represents the actual formula for the substance (e.g. C12H24O12).
Normally, balancing a chemical equation is a trial-and-error process. You start with the most complicated-looking compound in the equation and work from there. There is, however, an old Princeton Review SAT trick that you may want to try if you see a balancing equation question on the multiple-choice section. The trick is called backsolving.
It works like this: To make a balancing equation question work in a multiple-choice format, one of the answer choices is the correct coefficient for one of the species in the reaction. So instead of starting blind in the trial-and-error process, you can insert the answer choices one by one to see which one works. You probably won’t have to try all five, and if you start in the middle and the number doesn’t work, it might be obviously too small or large, eliminating other choices before you have to try them. Let’s try it.
1. If the equation above were balanced with lowest whole number coefficients, the coefficient for NH3 would be
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
Start at (C) because it’s the middle number. If there are 3 NH3’s, then there can’t be a whole number coefficient for N2, so (C) is wrong, and so are the other odd number answers, (A) and (E).
Try (D).
If there are 4 NH3’s, then there must be 2 N2’s and 6 H2O’s.
If there are 6 H2O’s, then there must be 3 O2’s, and the equation is balanced with lowest whole number coefficients.
Backsolving is more efficient than the methods that you’re accustomed to. If you use the answer choices that you’re given, you streamline the trial-and-error process and allow yourself to use POE as you work on the problem.
Many of the stoichiometry problems on the test will be formatted in the following way: You will be given a balanced chemical equation and told that you have some number of grams (or liters of gas, or molar concentration, and so on) of reactant. Then you will be asked what number of grams (or liters of gas, or molar concentration, and so on) of products are generated.
In these cases, follow this simple series of steps.
Let’s try one.
2 HBr(aq) + Zn(s) → ZnBr2(aq) + H2(g)
2. A piece of solid zinc weighing 98 grams was added to a solution containing 324 grams of HBr. What is the volume of H2 produced at standard temperature and pressure if the reaction above runs to completion?
(A) 11 liters
(B) 22 liters
(C) 34 liters
(D) 45 liters
(E) 67 liters
So (C) is correct.
Let’s try another one using the same reaction.
2 HBr(aq) + Zn(s) → ZnBr2(aq) + H2(g)
3. A piece of solid zinc weighing 13.1 grams was placed in a container. A 0.10-molar solution of HBr was slowly added to the container until the zinc was completely dissolved. What was the volume of HBr solution required to completely dissolve the solid zinc?
(A) 1.0 L
(B) 2.0 L
(C) 3.0 L
(D) 4.0 L
(E) 5.0 L
In this case, we’re using the balanced reaction to find out how much of one reactant is required to consume the other reactant. It’s a slight variation on the process described in (2) and (3).
We can see from the balanced equation that it takes 2 moles of HBr to react completely with 1 mole of Zn, so it will take 0.400 moles of HBr to react completely with 0.200 moles of Zn.
So (D) is correct.
When you perform calculations, always include units. Including units in your calculations will help you (and the person scoring your test) keep track of what you are doing. Including units will also get you partial credit points on the free-response section.
Questions 1–3
(A) Moles
(B) Liters
(C) Grams
(D) Atmospheres
(E) Volts
1. One mole of solid zinc has a mass of 65.39 of these.
2. These units can be calculated by dividing a quantity by 6.02 × 1023.
3. Four grams of helium gas occupy 22.4 of these at standard temperature and pressure.
4. What is the mass ratio of fluorine to boron in a boron trifluoride molecule?
(A) 1.8 to 1
(B) 3.0 to 1
(C) 3.5 to 1
(D) 5.3 to 1
(E) 6.0 to 1
5. A hydrocarbon sample with a mass of 6 grams underwent combustion, producing 11 grams of carbon dioxide. If all of the carbon initially present in the compound was converted to carbon dioxide, what was the percent of carbon, by mass, in the hydrocarbon sample?
(A) 25%
(B) 33%
(C) 50%
(D) 66%
(E) 75%
6. What is the mass of oxygen in 148 grams of calcium hydroxide (Ca(OH)2)?
(A) 16 grams
(B) 24 grams
(C) 32 grams
(D) 48 grams
(E) 64 grams
7. An ion containing only oxygen and chlorine is 31% oxygen by mass. What is its empirical formula?
(A) ClO–
(B) ClO2–
(C) ClO3–
(D) ClO4–
(E) Cl2O–
8. A sample of propane, C3H8, was completely burned in air at STP. The reaction occurred as shown below.
C3H8 + O2 → 3 CO2 + 4 H2O
If 67.2 liters of CO2 were produced and all of the carbon in the CO2 came from the propane, what was the mass of the propane sample?
(A) 11 grams
(B) 22 grams
(C) 33 grams
(D) 44 grams
(E) 55 grams
9. What is the percent composition by mass of the elements in the compound NaNO3?
(A) Na 20%, N 20%, O 60%
(B) Na 23%, N 14%, O 48%
(C) Na 23%, N 14%, O 63%
(D) Na 27%, N 16%, O 57%
(E) Na 36%, N 28%, O 36%
10. CaCO3(s) → CaO(s) + CO2(g)
A sample of pure CaCO3 was heated and decomposed according to the reaction given above. If 28 grams of CaO were produced by the reaction, what was the initial mass of CaCO3?
(A) 14 grams
(B) 25 grams
(C) 42 grams
(D) 50 grams
(E) 84 grams
11. The composition of a typical glass used in bottles is 12.0% Na2O, 12.0% CaO, and 76.0% SiO2. Which of the following lists the three compounds in order of greatest to least number of moles present in a typical sample of bottle glass?
(A) SiO2, CaO, Na2O
(B) SiO2, Na2O, CaO
(C) Na2O, SiO2, CaO
(D) Na2O, CaO, SiO2
(E) CaO, Na2O, SiO2
12. The concentration of sodium chloride in sea water is about 0.5 molar. How many grams of NaCl are present in 1 kg of sea water?
(A) 30 grams
(B) 60 grams
(C) 100 grams
(D) 300 grams
(E) 600 grams
13. A sample of a hydrate of CuSO4 with a mass of 250 grams was heated until all the water was removed. The sample was then weighed and found to have a mass of 160 grams. What is the formula for the hydrate?
(A) CuSO4 • 10 H2O
(B) CuSO4 • 7 H2O
(C) CuSO4 • 5 H2O
(D) CuSO4 • 2 H2O
(E) CuSO4 • H2O
14. A compound containing only sulfur and oxygen is 50% sulfur by weight. What is the empirical formula for the compound?
(A) SO
(B) SO2
(C) SO3
(D) S2O
(E) S3O
15. 2 Na(s) + 2 H2O(l) → 2 NaOH(aq) + H2(g)
Elemental sodium reacts with water to form hydrogen gas as shown above. If a sample of sodium reacts completely to form 20 liters of hydrogen gas, measured at standard temperature and pressure, what was the mass of the sodium?
(A) 5 grams
(B) 10 grams
(C) 20 grams
(D) 30 grams
(E) 40 grams
16. ZnSO3(s) → ZnO(s) + SO2(g)
What is the STP volume of SO2 gas produced by the above reaction when 145 grams of ZnSO3 are consumed?
(A) 23 liters
(B) 36 liters
(C) 45 liters
(D) 56 liters
(E) 90 liters
17.…CN– +…OH– →…CNO– +…H2O +…e–
When the half reaction above is balanced, what is the coefficient for OH– if all the coefficients are reduced to the lowest whole number?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
18.…MnO4– +…I– +…H2O →…MnO2 +…IO3– +…OH–
The oxidation-reduction reaction above is to be balanced with lowest whole number coefficients. What is the coefficient for OH–?
(A) 1
(B) 2
(C) 3
(D) 4
(E) 5
19. CaCO3(s) + 2 H+(aq) → Ca2+(aq) + H2O(l) + CO2(g)
If the reaction above took place at standard temperature and pressure and 150 grams of CaCO3(s) were consumed, what was the volume of CO2 (g) produced at STP?
(A) 11 L
(B) 22 L
(C) 34 L
(D) 45 L
(E) 56 L
20. A gaseous mixture at 25°C contained 1 mole of CH4 and 2 moles of O2 and the pressure was measured at 2 atm. The gases then underwent the reaction shown below.
CH4(g) + 2 O2(g) → CO2(g) + 2 H2O(g)
What was the pressure in the container after the reaction had gone to completion and the temperature was allowed to return to 25°C?
(A) 1 atm
(B) 2 atm
(C) 3 atm
(D) 4 atm
(E) 5 atm
21. A sample of a hydrate of BaCl2 with a mass of 61 grams was heated until all the water was removed. The sample was then weighed and found to have a mass of 52 grams. What is the formula for the hydrate?
(A) BaCl2 • 5 H2O
(B) BaCl2 • 4 H2O
(C) BaCl2 • 3 H2O
(D) BaCl2 • 2 H2O
(E) BaCl2 • H2O
22. A hydrocarbon was found to be 20% hydrogen by weight. If 1 mole of the hydrocarbon has a mass of 30 grams, what is its molecular formula?
(A) CH
(B) CH2
(C) CH3
(D) C2H4
(E) C2H6
23.…CuFeS2 +…O2 → Cu2S +…FeO +…SO2
When the half-reaction above is balanced, what is the coefficient for O2 if all the coefficients are reduced to the lowest whole number?
(A) 2
(B) 3
(C) 4
(D) 6
(E) 8
24. A hydrocarbon contains 75% carbon by mass. What is the empirical formula for the compound?
(A) CH2
(B) CH3
(C) CH4
(D) C2H5
(E) C3H8
25. When chlorine gas is combined with fluorine gas, a compound is formed that is 38% chlorine and 62% fluorine. What is the empirical formula of the compound?
(A) ClF
(B) ClF2
(C) ClF3
(D) ClF5
(E) ClF7
1. A 10.0 gram sample containing calcium carbonate and an inert material was placed in excess hydrochloric acid. A reaction occurred producing calcium chloride, water, and carbon dioxide.
(a) Write the balanced equation for the reaction.
(b) When the reaction was complete, 900 milliliters of carbon dioxide gas were collected at 740 mmHg and 30°C. How many moles of calcium carbonate were consumed in the reaction?
(c) If all of the calcium carbonate initially present in the sample was consumed in the reaction, what percent by mass of the sample was due to calcium carbonate?
(d) If the inert material was silicon dioxide, what was the molar ratio of calcium carbonate to silicon dioxide in the original sample?
2. A gaseous hydrocarbon sample is completely burned in air, producing 1.80 liters of carbon dioxide at standard temperature and pressure and 2.16 grams of water.
(a) What is the empirical formula for the hydrocarbon?
(b) What was the mass of the hydrocarbon consumed?
(c) The hydrocarbon was initially contained in a closed 1.00 liter vessel at a temperature of 32°C and a pressure of 760 millimeters of mercury. What is the molecular formula of the hydrocarbon?
(d) Write the balanced equation for the combustion of the hydrocarbon.
3. The table below shows three common forms of copper ore.
(a) What is the percent by weight of copper in Cu2S?
(b) What is the empirical formula of ore #2?
(c) If a sample of ore #3 contains 11.0 grams of iron, how many grams of sulfur does it contain?
(d) Cu can be extracted from Cu2S by the following process:
3 Cu2S + 3 O2 → 3 SO2 + 6 Cu
If 3.84 grams of O2 are consumed in the process, how many grams of Cu are produced?
4. 2 Mg(s) + 2 CuSO4(aq) + H2O(l) → 2 MgSO4(aq) + Cu2O(s) + H2(g)
(a) If 1.46 grams of Mg(s) are added to 500 milliliters of a 0.200-molar solution of CuSO4, what is the maximum molar yield of H2(g)?
(b) When all of the limiting reagent has been consumed in (a), how many moles of the other reactant (not water) remain?
(c) What is the mass of the Cu2O produced in (a)?
(d) What is the value of [Mg2+] in the solution at the end of the experiment? (Assume that the volume of the solution remains unchanged.)
1. C The units for atomic weight are grams/mole.
2. A A mole is equal to 6.02 × 1023.
3. B Four grams of helium is a mole. A mole of gas occupies 22.4 liters at STP.
4. D The empirical formula of boron trifluoride is BF3.
Grams = (moles)(MW)
Grams of boron = (1 mol)(10.8 g/mol) = 10.8 g
Grams of fluorine = (3 mol)(19.0 g/mol) = 57.0 g
So the mass ratio is about 57 to 11, which is about 5.3 to 1.
5.
C Moles = 
If 
mole of CO2 was produced, then mole of C was consumed.
Grams = (moles)(MW)
Grams of carbon = ( mol)(12 g/mol) = 3 g
So the percent by mass of carbon was 
6.
E Moles =
Moles of calcium hydroxide = 
= 2 moles
Every mole of Ca(OH)2 contains 2 moles of oxygen.
So there are (2)(2) = 4 moles of oxygen
Grams = (moles)(MW)
So grams of oxygen = (4 mol)(16 g/mol) = 64 grams
7. A Assume that we have 100 grams of the compound. That means that we have 31 grams of oxygen and 69 grams of chlorine.
Moles =
Moles of oxygen =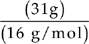 
= slightly less than 2 mol
Moles of chlorine =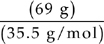 
= slightly less than 2 mol
So the ratio of chlorine to oxygen is 1 to 1, and the empirical formula is ClO–.
8.
D Moles = 
Moles of CO2 = 
= 3 mol
According to the balanced equation, if 3 moles of CO2 were produced, 1 mole of C3H8 was consumed.
Grams = (moles)(MW)
So grams of C3H8 = (1 mol)(44 g/mol) = 44 grams
9.
D The molecular weight of NaNO3 is: (23) + (14) + (3)(16) = 85 g/mol
We can get the answer using pretty rough estimates.
The percent by mass of Na = 
= between 25% () and 33% (
)
The percent by mass of N = 
= between 10% (
) and 20% (
)
The percent by mass of O = 
= between 50% (
) and 60% (
)
You can use POE to get choice (D).
10.
D Moles =
Moles of CaO = 
= 0.50 mol
From the balanced equation, if 0.50 mol of CaO was produced, then 0.50 mol of CaCO3 was consumed.
Grams = (moles)(MW)
Grams of CaCO3 = (0.50 mol)(100 g/mol) = 50 g
11.
A The molecular weights of the three compounds are as follows:
Na2O – 62 g/mol
CaO – 56 g/mol
SiO2 – 60 g/mol
Because the molecular weights are close together, we can safely say that SiO2, which makes up a much greater percentage by mass of bottle glass than the other two, will have far and away the most moles in a sample. So the answer must be (A) or
(B).
Remember, (grams) = (moles)(MW). Because a sample of bottle glass will have the same number of grams of Na2O and CaO, the one with the smaller molecular weight must have the greater number of moles. So there must be more moles of CaO than Na2O.
12.
A First, you have to remember that 1 liter of water has a mass of 1 kg.
Moles = (molarity)(liters)
Moles of NaCl = (0.5 M)(1 L) = 0.5 moles
Grams = (moles)(MW)
Grams of NaCl = (0.5 mol)(59 g/mol) = 30 g
13. C The molecular weight of CuSO4 is 160 g/mol, so we have only 1 mole of the hydrate. The lost mass was due to water, so 1 mole of the hydrate must have contained 90 grams of H2O.
Moles =
Moles of water = 
= 5 moles
So if 1 mole of hydrate contains 5 moles of H2O, then the formula for the hydrate must be CuSO4 • 5 H2O.
14. B You might be able to do this one in your head just from knowing that sulfur’s molecular weight is twice as large as oxygen’s. If not, let’s say you have 100 grams of the compound. So you have 50 grams of sulfur and 50 grams of oxygen.
Moles =
Moles of sulfur = 
= a little more than 1.5
Moles of oxygen = 
= a little more than 3
The molar ratio of O to S is 2 to 1, so the empirical formula must be SO2.
15.
E Moles = 
Moles of H2 = 
= about 0.9 moles
From the balanced equation, for every mole of H2 produced, 2 moles of Na are consumed, so 1.8 moles of Na are consumed.
Grams = (moles)(MW)
Grams of Na = (1.8 mol)(23 g/mol) = about 40 grams
You don’t really have to do the math, because you can get the answer by using rough estimates.
16.
A Moles =
Moles of ZnSO3 = 
= 1 mole
From the balanced equation, when 1 mole of ZnSO3 is consumed, 1 mole of SO2 will be produced. So about 1 mole of SO2 is produced.
Liters = (moles)(22.4 L/mol)
Liters of SO2 = (about 1 mol)(22.4 L) = 23 liters
17.
B Use trial and error or backsolve.
Start with (C). If there are 3 OH–, there can’t be a whole number coefficient for H2O, so (C) is wrong. You should also be able to see that the answer can’t be an odd number, so (A) and (E) are also wrong.
Try (D). If there are 4 OH–, then there are 2 H2O.
That leaves 2 more Os on the
product side, so there must be 2 CNO–.
If there are 2 CNO– then there are 2 CN–.
These are all whole numbers, but they are not the lowest whole numbers, so (D) is wrong.
If we divide all the coefficients by 2, we get the lowest whole number coefficients. That leaves us with 2 OH–, which is choice (B).
By the way, N5– (in CN–) is oxidized to N3– (in CNO–), so there are 2 e–.
18.
B Use trial and error or backsolve.
Start at (C).
If there are 3 OH–, there can’t be a whole number coefficient for H2O, so (C) is wrong. Also, the answer can’t be an odd number, so (A) and (E) are wrong.
Notice that you don’t have to test both of the remaining answers. If the one you pick works, you’re done. If the one you pick doesn’t work,
then the one that’s left must be correct. With a choice of only two answers, pick the one that looks easier to work with.
Try (B) because it’s smaller. If there are 2 OH–, then there is 1 H2O. If you put in 1 for I– and IO–3 and 2 for MnO–4 and MnO2, the equation is balanced. So (B) is correct.
19.
C Moles =
Moles of CaCO3 =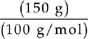 
= 1.5 moles
From the balanced equation, for every mole of CaCO3 consumed, one mole of CO2 is produced. So 1.5 moles of CO2 are produced.
At STP, volume of gas = (moles)(22.4 L)
So volume of CO2 = (1.5)(22.4) = 34 L
20. B All of the reactants are consumed in the reaction and the temperature doesn’t change, so the pressure will only change if the number of moles of gas changes over the course of the reaction. The number of moles of gas (3 moles) doesn’t change in the balanced equation, so the pressure will remain the same (2 atm) at the end of the reaction as at the beginning.
21. D The molecular weight of BaCl2 is 208 g/mol, so we can figure out how many moles of the hydrate we have.
Moles =
Moles of hydrate = 
mole
The lost mass was due to water, so 1 mole of the hydrate must have contained 9 grams of H2O.
Moles =
Moles of water =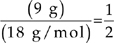 
moles
So if mole of hydrate contains mole of H2O, there must be 2 moles of H2O for every mole of hydrate, and the formula for the hydrate must be BaCl2 • 2 H2O.
22. E Let’s say we have 100 grams of the compound.
Moles =
So moles of carbon = 
= 6.7 moles
and moles of hydrogen = 
= 20 moles
According to our rough calculation, there are about three times as many moles of hydrogen in the compound as there are moles of carbon, so the empirical formula is CH3.
The molar mass for the empirical formula is 15 g/mol, so we need to double the moles of each element to get a compound with a molar mass of 30 g/mol. That makes the molecular formula of the compound C2H6.
23. C Backsolving doesn’t work so well in this case because there are two different compounds that contain oxygen on the right side of the equation, which makes the process kind of confusing. Instead, let’s just try plugging in values for the most complicated compound in the equation, CuFeS2.
What if there’s 1 CuFeS2? That’s impossible because there are 2 Cu’s on the right.
What if there are 2 CuFeS2’s? Then the right side has 1 Cu2S to balance the Cu and 2 FeO to balance the Fe. The right side must also have 3 SO2 to balance the S.
Now there are 8 O’s on the right, so there must be 4 O2’s on the left, and the equation is balanced.
2 CuFeS2 + 4 O2 → 1 Cu2S + 2 FeO + 3 SO2
24. C Let’s say we have 100 grams of the compound.
Moles =
So moles of carbon = 
= 6 moles
and moles of hydrogen = 
= 25 moles
According to our rough calculation, there are about four times as many moles of hydrogen in the compound as there are moles of carbon, so the empirical formula is CH4.
25. C Let’s say we have 100 grams of the compound.
Moles =
Moles of chlorine = 
= about 1 mole
Moles of fluorine = 
= about 3 moles
According to our rough calculation, there are about three times as many moles of fluorine in the compound as there are moles of chlorine, so the empirical formula is ClF3.
1. (a) CaCO3 + 2 HCl → CaCl2 + H2O + CO2
(b) Use the ideal gas equation to find the number of moles of CO2 produced. Remember to convert to the proper units.
From the balanced equation, for every mole of CO2 produced, 1 mole of CaCO3 was consumed.
So 0.035 moles of CaCO3 were consumed.
(c) We know the number of moles of CaCO3, so we can find the mass.
Grams = (moles)(MW)
Grams of CaCO3 = (0.035 mol)(100 g/mol) = 3.50 grams
Percent by mass =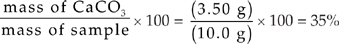 
(d) Mass of SiO2 = 10.0 g – 3.5 g = 6.5 g
Moles =
Moles of SiO2 = 
= 0.11 mol
Molar ratio = 
= 0.32
2. (a) All of the hydrogen in the water and all of the carbon in the carbon dioxide must have come from the hydrocarbon.
Moles of H2O =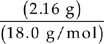 
= 0.120 moles
Every mole of water contains 2 moles of hydrogen, so there are 0.240 moles of hydrogen.
Moles of CO2 = 
= 0.080 moles
Every mole of CO2 contains 1 mole of carbon, so there are 0.080 moles of carbon.
There are three times as many moles of hydrogen as there are moles of carbon, so the empirical formula of the hydrocarbon is CH3.
(b) In (a), we found the number of moles of hydrogen and carbon consumed, so we can find the mass of the hydrocarbon.
Grams = (moles)(MW)
Grams of H = (0.240 mol)(1.01 g/mol) = 0.242 g
Grams of C = (0.080 mol)(12.01 g/mol) = 0.961 g
Grams of hydrocarbon = (0.242) + (0.961) = 1.203 g
(c) First let’s find the number of moles of hydrocarbon from the ideal gas law. Don’t forget to convert to the appropriate units (760 mmHg = 1 atm, 32°C = 305 K).
Now we can use the mass we found in (b) to find the molecular weight of the hydrocarbon.
CH3 would have a molecular weight of 15, so we can just double the empirical formula to get the molecular formula, which is C2H6.
(d) 2 C2H6 + 7 O2 → 4 CO2 + 6 H2O
3. (a) First find the molecular weight of Cu2S.
MW of Cu2S = (2)(63.6) + (1)(32.1) = 159.3% by mass of Cu =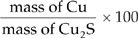 
= 
× 100 = 79.8%
(b) Assume that we have 100 grams of ore #2. So we have 34.6 g of Cu, 30.5 g of Fe, and 34.9 g of S. To get the empirical formula, we need to find the number of moles of each element.
Moles =
Moles of Cu = 
= 0.544 moles of Cu
>Moles of Fe = 
= 0.546 moles of Fe
Moles of S =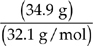 
= 1.09 moles of S
So the molar ratio of Cu:Fe:S is 1:1:2 and the empirical formula for ore #2 is CuFeS2.
(c) You can use the ratio of the percents by weight.
Mass of S =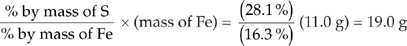 
(d) First find the moles of O2 consumed.
Moles =
Moles of O2 = 
= 0.120 moles
From the balanced equation, for every 3 moles of O2 consumed, 6 moles of Cu are produced, so the number of moles of Cu produced will be twice the number of moles of O2 consumed. So 0.240 moles of Cu are produced.
Grams = (moles)(MW)
Grams of Cu = (0.240 mol)(63.6 g/mol) = 15.3 grams
4. (a) We need to find the limiting reagent. There’s plenty of water, so it must be one of the other two reactants.
Moles =
Moles of Mg =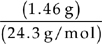 
= 0.060 moles
Moles = (molarity)(volume)
Moles of CuSO4 = (0.200 M)(0.500 L) = 0.100 moles
From the balanced equation, Mg and CuSO4 are consumed in a 1:1 ratio, so we’ll run out of Mg first. Mg is the limiting reagent, and we’ll use it to find the yield of H2.
From the balanced equation, 1 mole of H2 is produced for every 2 moles of Mg consumed, so the number of moles of H2 produced will be half the number of moles of Mg consumed.
Moles of H2 = (0.060 mol) = 0.030 moles
(b) Mg is the limiting reagent, so some CuSO4 will remain. From the balanced equation, Mg and CuSO4 are consumed in a 1:1 ratio, so when 0.060 moles of Mg are consumed, 0.060 moles of CuSO4 are also consumed.
Moles of CuSO4 remaining = (0.100 mol) – (0.060 mol) = 0.040 moles
(c) From the balanced equation, 1 mole of Cu2O is produced for every 2 moles of Mg consumed, so the number of moles of Cu2O produced will be half the number of moles of Mg consumed.
Moles of Cu2O = (0.060 mol) = 0.030 moles
>Grams = (moles)(MW)
Grams of Cu2O = (0.030 mol)(143 g/mol) = 4.29 grams
(d) All of the Mg consumed ends up as Mg2+ ions in the solution.
Molarity = 
[Mg2+] = 