How to Gamble If You Must

ONE-LOTTERY STRATEGIES

1. INTRODUCTION.

This chapter is basically an application of part of the familiar theory of sums of independent and identically distributed random variables.

A casino Γ has a superfair lottery θ available at 1 if and only if Γ is superfair; equivalently, if and only if, for the usual u, U is the indicator of (0, ∞). The proof of this in Section 4.4 is indirect; so there is some interest in finding a stationary family of optimal strategies based on θ. One natural possibility, the θ -proportional family, is always to use [fθ + f] for f < 1 and δ(f) for f ≥ 1, that is, to use θ in proportion to your wealth until the goal is achieved. Somewhat surprisingly, this is not always optimal, even for quite ordinary lotteries θ. What is needed for it to be optimal is roughly that ∫ log (1 + z) dθ(z) ≥ 0; when this integral is undefined, the θ proportional family may or may not be optimal. Though the integral can be negative for θ itself, it is bound to be positive for the contraction [sθ] for sufficiently small positive s; so the [sθ]-proportional family is optimal for small s. This result, the main one of this chapter, will be used as two technical points in the next chapter.

Those who do not wish to enter into the formal proof and the refinements of the preceding paragraph can skip or skim this chapter.

To replace multiplication by addition and to take advantage of the established theory of sums of independent and identically distributed random variables, study of proportional families will be founded upon that of translational families, defined as follows: If ϕ is a lottery on [− ∞, ∞), the ϕ-translational family of strategies is the family of strategies generated by the gambles if f < 0 and δ(f) if f ≥ 0. It is to be understood that . The utility u of interest now and until Section 5 is the indicator of [0, ∞), and the main question, which we cannot—and need not—answer completely, is “For which ϕ is for all f > − ∞ ?”

For a useful reformulation, consider the gambling house Γ_ϕ for which Γ_ϕ (f) consists only of [ϕ + f]. This house is leavable only in the trivial case that ϕ = δ(0). It has only one strategy available at each f; this stationary family σ* is the family generated by ϕ* (f) = [ϕ + f] at all f in [− ∞, ∞).

THEOREM 1. is an optimal strategy at f of , the leavable closure of Γϕ; is the U of and of Γ_ϕ.

Proof: The two assertions are plainly equivalent to each other. The first is an instance of Theorem 3.9.5, the proof of which we did not give. But the second is easily proved directly, thus: Plainly, majorizes u. According to Theorem 3.2.1, ; the basic Theorem 2.12.1 now applies.

2. LIMITED PLAYING TIME

Let U_m (m = 0, 1, · · ·, ω) be defined for as in Section 2.15. It will ultimately be shown that U of and Γ_ϕ is U_ω. All these functions are plainly 1 for f ≥ 0.

LEMMA 1. is nondecreasing in the stop rule t.

Proof: Apply Theorem 3.4.7.

LEMMA 2.

LEMMA 3. For 0 < m < ω,

The next two lemmas are instances of Theorem 8.2.4 and of (8.3.1), (8.3.2), and (8.3.3), except for the minor detail that − ∞ was not included as a fortune there.

LEMMA 4. U_m(f), U_ω(f), and U(f) are nondecreasing in m and in f for 0 ≤ m < ω and − ∞ ≤ f < ∞.

LEMMA 5. U_m+n(f + g) ≥ U_m(f)U_n(g), U_ω(f + g) ≥ U_ω(f)U_ω(g), and U(f + g) ≥ U(f)U(g) for 0 ≤ m < ω and − ∞ < f, g < ∞.

LEMMA 6. , and U(nf) ≥ Uⁿ(f).

THEOREM 1. U_ω(f) = 1 either for all f in (− ∞, 0) or for none; similarly for U(f).

THEOREM 2. U₀(f) is the indicator of [0, ∞), U₁(f) = ϕ[− f, ∞] for f < 0, and more generally,

3. CONVENTIONAL LOTTERIES

If the lottery ϕ that generates σ* is conventional, that is, countably additive on the Borel sets of [− ∞, ∞), then the distribution of (f₁, · · · , f_m) under σ* on the Borel sets of the m-fold Cartesian product of [− ∞, ∞) is the same as that of (f + s₁, · · · , f + s_m), where

and the y_j are random variables independently distributed according to ϕ .

The inclusion of − ∞as a possible value of y_j (to provide a logarithm for 0) is a little unusual but not unheard of. The reader will easily see that it does not interfere.

When ϕ is conventional, U_m(f) is the probability that at least one of the partial sums 0, s₁, · · ·, s_m is as large as − f, according to Lemma 2.3. And, in conventional terms, U_ω(f) is the probability that 0 or some s_n is as large as − f. Thus, much of the literature on sums like the s_n can be brought to bear. In the last decade there have been studies of U(f) and U_m(f) for conventional ϕ that go far beyond what is needed in this book. A central work in this literature is (Spitzer 1956). Theorem 4.1 of that paper includes the following lemma. You may find the alternative demonstration presented below interesting or convenient.

LEMMA 1. lim sup s_n is a constant almost surely. This constant can be only ∞, 0, or − ∞. It is 0 if and only if y_j = 0 almost surely; it is ∞ (− ∞) if and only if sup s_n > 0 (inf s_n < 0) almost surely.

Proof: Apply a variant of the zero-one law (Hewitt and Savage 1955, Theorem 11.3) to see that lim sup s_n is some constant c almost surely. Suppose 0 < c < ∞. Some s_n is almost sure to exceed c/2; let n₁ be the first n for which this happens. Then some is almost sure to exceed c/2, since the have the same distribution as the s_n (Doob 1953, p. 145). Proceeding in this way, construct s_n₁, s_n₁+n₂, · · · converging to ∞. Therefore lim sup s_n = ∞, contradicting the assumption 0 < c < ∞. Likewise, − ∞ < c < 0 is impossible. As is not difficult to show, if c = 0, then y_j = 0 almost surely.

LEMMA 2. For a conventional ϕ, U_ω(f) = 1 for − ∞ < f < 0 if and only if lim sup s_n = ∞ almost surely, or, equivalently, if and only if sup s_n > 0 almost surely. Otherwise, U_ω(f) < 1 for − ∞ < f < 0, and s_n = 0 for all n almost surely or s_n converges to − ∞ almost surely.

Proof: Apply Lemma 1 and the above remark that U_ω(f) is the conventional probability that 0 or some s_n is at least − f.

Theorems 1, 2, and 3 will be proved in this section for conventional lotteries only. But the proofs will be extended to all lotteries in the next section.

THEOREM 1. If U_ω(f) < 1 for − ∞ < f < 0, then U_n(f) converges uniformly to U_ω(f).

Proof: For f ≥ 0, U_n(f) = U_ω(f) = 1. For f < 0, U_ω(f) − U_n(f) − U_n(f) is the probability that, for some m > n, but for no m ≤ n, s_m ≥ − f. This is at most the probability that, for some m > n, s_m > 0, which approaches zero in n.

THEOREM 2. U = U_ω.

Proof: The conclusion is obvious if U_ω(f) = 1 for − ∞ < f < ∞. In the other case, it follows immediately from the preceding theorem and part (b) of Theorem 2.15.5.

Necessary and sufficient conditions on ϕ, the distribution of y_j, for lim sup s_n to be infinite, that are convenient for this chapter, are not known to us. (See, however, (Spitzer 1956, Theorem 4.1).) If Ey_j is well defined, perhaps infinite, then Kolmogorov’s law of large numbers (Loève 1955, page 423; Doob 1953, page 141) supplemented by an interesting theorem of Chung and Fuchs (1951, Theorem 5) readily supplies a convenient condition.

LEMMA 3. If Ey_j > 0, s_n converges to ∞ almost surely; if Ey_j < 0, s_n converges to − ∞ almost surely; if Ey_j = 0, and y_j is not almost identically 0, then lim sup s_n = ∞ and lim inf s_n = − ∞ almost surely. If and are both infinite, then lim sup s_n can be almost surely ∞ and can be almost surely − ∞.

Proof: The discussion above suggests the proof for all except the last sentence. If y_j has a standard Cauchy distribution, then lim sup s_n = ∞. But if, for example, prob (y_j = − ∞) > 0, then lim sup s_n = − ∞.

There are also examples with prob (y_j = − ∞) = 0, and both infinite, and lim sup s_n = − ∞ (Derman and Robbins 1955).

THEOREM 3. For each lottery ϕ on [− ∞, ∞):

(a) If for all positive , then U(f) = 0 for − ∞ < f < 0.

(b) If for some positive , and ∫ f dϕ(f) ≥ 0, then U(f) = 1 for − ∞ < f < 0.

(d) If ∫ f dϕ(f) is not defined, then either 0 < U(f) < 1 for − ∞ < f < 0 or U(f) = 1 for − ∞ < f < 0. Both cases are possible, and the first obtains if ϕ{− ∞} > 0.

Theorem 3 is the main goal of this section. It has been so expressed as to make the hypothesis that ϕ is conventional superfluous, as will be shown in the next section.

4. GENERAL LOTTERIES

This section extends to arbitrary lotteries on [− ∞, ∞) the main conclusions about conventional lotteries in the preceding section.

One possible peculiarity of a nonconventional ϕ on [ − ∞, ∞) is that it can be partially remote, that is, ϕ(c, ∞) can be uniformly positive for finite c. The facts catalogued in the next theorem are easy to prove from first principles.

THEOREM 1. If ϕ is partially remote:

(a) ∫ f dϕ(f) is infinite or undefined.

(b) If ϕ{− ∞} = 0, U(f) = 1 for − ∞ < f < 0.

In harmony with Section 4.5, two lotteries ϕ and ϕ′ are companions if ϕυ = ϕ′υ for every υ bounded and continuous on F, which here is the whole of [− ∞, ∞). This concept admits of wide topological generalization, and much of this section can be correspondingly generalized. It will soon be clear that, at least for the purposes of this chapter, a pair of companions really are very much alike. On this account, Lemma 2 below reduces the general situation nearly to that for conventional gambles.

LEMMA 1. The not partially remote lotteries, ϕ and ϕ′, are companions if and only if and for all f in (− ∞ , ∞) and all positive e.

Proof: Let υ be any continuous function bounded between 0 and 1, with υ(g) = 1 for g ≥ f and υ(g) = 0 for . If ϕ and ϕ′ are companions, . This proves the “only if” clause.

If and for all f in (− ∞, ∞) and all positive , it is easy to see that ϕυ = ϕ′υ for every bounded, continuous, monotonic υ. Therefore, ϕυ = ϕ′υ if υ is continuous and of bounded variation on [− ∞, ∞) or is the uniform limit of such functions. If υ is any function bounded and continuous on [− ∞, ∞), let υ_c(f) = υ(f) for f ≤ c and υ_c(f) = υ(c) for f ≥ c. Then ϕυ_c = ϕ′υ_c, and since ϕ and ϕ′ are not partially remote, lim ϕυ_c = ϕυ and lim ϕ′υ_c = ϕ′υ.

LEMMA 2. Every not partially remote ϕ has one and only one conventional companion ϕ*, and ϕ* is characterized by the condition that

Proof: Plainly (1) does define a conventional ϕ*. In view of (1), ;

so Lemma 1 applies to show that ϕ and ϕ* are companions. Lemma 1 shows also that distinct conventional lotteries cannot be companions.

LEMMA 3. If ϕ and ϕ′ are companions, then ∫fdϕ(f) = ∫fdϕ′(f) if either integral is defined.

A pair of bounded, nondecreasing functions V and V′ on [− ∞, ∞) are companions if and for all f in [− ∞, ∞) and all positive .

LEMMA 4. V and V′ are companions if and only if they have the same points of continuity and agree with each other there and at − ∞.

LEMMA 5. If V_n approaches V and approaches V′, and if V_n and are companions for each n, then V and V′ are companions. If, further, V_n approaches V uniformly, then approaches V′ uniformly.

Proof: To see that V and V′ are companions, calculate thus for fixed f, , and δ and for sufficiently large n: .

If V_n approaches V uniformly, then, in view of Lemma 4, approaches V′ uniformly on the set of those fortunes that are points of continuity of V′ and of every . Let G be the denumerable set of fortunes not covered by this conclusion. For any δ there are only a finite number of elements of G where the magnitude of the discontinuity of V′ is as great as δ.

LEMMA 6. If V and V′ are companions and ϕ and ϕ′ are companions, then the functions of f defined by ∫ V(f + g)dϕ(g) and ∫ V′(f + g) dϕ′(g) are companions.

Proof:

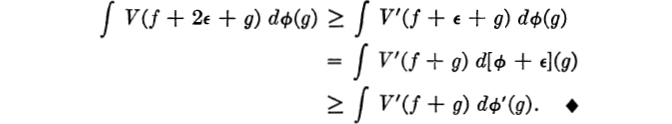
Let U_n, U_ω, and U be defined for ϕ as in Section 2, and let and be the corresponding functions for the conventional companion of ϕ.

LEMMA 7. U_n and , and U_ω and , are companions. Both U_ω and are identically 1 in (−∞, 0), or both are less than 1 there. If U_ω is less than 1 in (− ∞, 0), then U_n converges uniformly to U_ω. In either case, U_ω = U, and U and are companions.

Proof: Lemma 6 and Theorem 2.2 show that U_n and are companions. Lemma 5 then shows that U_ω and are companions, which implies that both are 1 in (− ∞, 0) or neither is. The assertion about uniform convergence follows from Theorem 3.1 and the last sentence of Lemma 5. The final assertion is now an application of part (b) of Theorem 2.15.5.

Lemma 7 contains Theorems 3.1 and 3.2 without the hypothesis that ϕ is conventional. Since the central Theorem 3.3 without the hypothesis that ϕ is conventional is a corollary of Lemmas 3 and 7, the objectives of this section have been attained.

5. PROPORTIONAL STRATEGIES

Let u(θ)(f) be the utility of the θ-proportional strategy initiating at f in [0, ∞), and let ϕ be the lottery on [− ∞,∞) such that ϕ log (A + 1) = θA for every A ⊂ [−1, ∞). Then u(θ)(f) is the utility of the ϕ-translational strategy initiating at log f. Through the final paragraph of Section 4, this observation leads to the following conclusions.

THEOREM 1. If f = 0, u(θ)(f) = 0. If f ≥ 1, u(θ)(f) = 1. One of the following cases applies for all f in (0, 1) and each can occur:

(a) for all positive, , and u(θ)(f) = 0.

(b) for some positive, , ∫ log (1 + x) dθ(x) < 0, and 0 < u(θ)(f) < 1.

(d) ∫ log (1 + x) dθ(x) is undefined, and u(θ)(f) = 1.

(d′) ∫ log (1 + x)dθ (x) is undefined, and 0 < u(θ)(f) < 1.

On [−1, ∞), m(θ) = ∫dθ(x) is, of course, defined for all θ. If m(θ) ≤ 0, θ is at most fair, and cases (a) and (b) of Theorem 1 are the actual possibilities. If m(θ) > 0, case (a) is excluded, but all the others are possible, as examples will soon show.

Thus, even if θ is superfair, the θ-proportional strategies may have probability less than 1 of attaining the goal 1 from every fortune f in (0, 1). Nonetheless, for sufficiently small positive s; so the [sθ]-proportional strategies do attain the goal with probability 1 from every positive fortune if θ is superfair. Letting

it will in fact be shown that B(s) > 0, so that case (c) obtains for [sθ], for all sufficiently small positive s if θ is superfair.

THEOREM 2. For every θ on [−1, ∞) with ∫x dθ(x) > 0, B(s) is defined for s in [0, 1). It is 0 for s = 0. Either B(s) = ∞ for all s in (0, 1) or B(s) < ∞ and is concave for s in [0, 1), and B′(0) > 0. B(s) is positive for sufficiently small s. The following cases, and only these, can occur:

1. B(s) < ∞ in [0, 1].

1.1. B(s) > 0 in (0, 1).

1.2. For a unique s₀ in (0, 1), B(s) > 0 in (0, s₀), B(s₀) = 0, and B(s) < 0 in (s₀, 1].

2. B(s) = ∞ for all s in (0, 1).

2.1. B(1) = ∞.

2.2. B(1) is undefined.

2.2.1. u(θ) ≡ 1.

2.2.2. 0 < u(θ)(f) < 1 for f in (0, 1).

Both subcases of case 1 are compatible both with ∫ x dθ(x) < ∞ and with ∫x dθ(x) = ∞, but case 2 is compatible only with ∫ x dθ(x) = ∞.

Proof: Since log (1 + sx) ≥ log (1 − s), B(s) is defined and is at least log (1 − s) in [0, 1), and B(0) is obviously 0.

Since, for s and s’ in (0, 1), log (1 + sx) − log (1 + s′x) is bounded for x in [− 1, ∝), B(s) is either infinite for all s in (0, 1) or for none. If the first of these possibilities obtains, , and cases 2.1 and 2.2 are the only ones possible. Since

these cases cannot occur unless ∫ x dθ(x) = ∞.

If B(s) is finite in [0, 1), then, according to the usual techniques, B(s) has two derivatives in s for s in [0, 1) that are computable by differentiation under the expectation sign. It is seen thus that B is concave in s for s in [0, 1) and, since θ is superfair, . Also, B(0) = 0. Since, for s in (0, 1), log (1 + x) − log (1 + sx) is bounded for x > 0, ; so B(1) is well defined though possibly − ∞. Also,

because log (1 + sx) approaches log (1 + x) uniformly in x ≥ 0. By a slightly different but equally easy argument,

So B(s) approaches B(1) as s approaches 1. Putting these facts together, B(s) is positive for sufficiently small positive s, and if it is not positive for all s in (0, 1) (case 1.1), it has a unique zero s₀ as required by case 1.2.

It has thus been shown that one of the five mutually exclusive cases 1.1, 1.2, 2.1, 2.2.1, or 2.2.2 must obtain. Examples will now show that these cases are all possible and will illustrate some other phenomena.

Example 1. θ is uniform on [− 1, g + 1] for some positive g.

B(1) = ∫ log (1 + x) dθ(x) = log (g + 2) − 1. This can be positive, 0, or negative, illustrating both parts of case 1 with ∫θ dθ (x) < ∞.

Exaple 2. θ is a convex combination of the uniform distribu-bution on [−1, 0] and a distribution on (0, ∞) with density λ (1 + x)^-1-λ for some λ in (0, 1). Thus θ has density b on [−1, 0) and density on (0, ∞) for some b in (0, 1).

Manipulating b for any fixed λ illustrates both parts of case 1 again, this time with ∫ x dθ (x) = ∞.

Example 3. Paralleling the proof of Lemma 3.3, let θ be the distribution of e^y − 1 for a random variable y with E max (0, y) = ∞; so B(1) = Ey is ∞ or is undefined. For any such θ, case 1 does not obtain. If B(1) = ∞, it is case 2.1 that does. If B(1) is undefined, then, according to part (d) of Theorem 3.4, either of the two remaining subcases can occur.

THEOREM 3. If Γ is a casino with a superfair lottery θ available at 1, then Γ is superfair, U(f) = 1 for f > 0, and the [sθ]-proportional family of strategies is optimal for all sufficiently small positive s.

Proof: According to Theorem 2, B(s) = ∫ log (1 + x) d[sθ](x) > 0 for sufficiently small s > 0; so, according to part (c) of Theorem 1, u([sθ])(f) = 1 for f in (0,1).

Even if every expected gain and every expected fortune f_n is infinite, the fortunes f_n can converge to 0 if you repeatedly stake too large a fraction of your fortune, as Example 2 illustrates.

An example of some interest is a superfair simple lottery, that is, a lottery under which the gambler either gains g with probability w or loses l with probability , where . Here

and B(1), of course, is . In a primitive casino, l = 1, and B(1) = − ∞. Therefore, in a superfair primitive casino, it is imprudent to stake a large share of your fortune repeatedly. Even if 0 < l < 1, w and g can be so manipulated as to ensure ∫ x dθ(x) > 0 and B(1)< 0.

It is not to be expected that the root s₀ of the equation B(s) = 0 can be calculated explicitly in terms of w, g, and l. However, a stake s less than s₀ can easily be found for a simple superfair θ. An elementary differentiation gives Solving B’(s) = 0 gives . For s, the minimum of s′ and 1, the [sθ]-proportional strategies attain the goal with probability 1 from every f₀ > 0.

How does the expected number of gambles E(N|f, s, θ) required to attain the goal from a given f in (0, 1) depend on s for s in (0, s₀], presuming the expected number is finite? Breiman (1961) has found results along these lines. We ourselves know little about the dependence of this function on s, but it seems implausible that it should not have discontinuities if, for example, θ is two-valued and superfair. The function is not always monotonic, for according to a well-known theorem of Wald and Blackwell (Blackwell 1946; Doob 1953, p. 351), the expectation is large near s = 0 and, if there is an s₀, near s₀.