This chapter determines when a casino Γ is fair, that is, such that U(f) = f in (0, 1). It is necessary that Γ contain no superfair lottery (Section 4.4 and Theorem 10.5.3); in the presence of this condition, Γ is fair if and only if it is at least fair, that is, if and only if U(f) ≥ f for all f—or, equivalently, for some f—in (0, 1).
Suppose Θ(1) contains no superfair lottery but does contain a fair nontrivial θ. If θ has bounded support, then it is easy to show that Γ is fair. But what if θ does not have bounded support? That a lottery can generate a fair casino though it has no bounded support was seen in Section 4.4. Donald Ornstein showed us, in the spring of 1958, that a fair lottery can generate an arbitrarily subfair casino. Therefore, some fair lotteries generate fair casinos, and others generate subfair casinos.
Which do which? For θ to generate a fair casino it is necessary and sufficient that
and
A main purpose of this chapter is to prove this (Theorem 6.1). Another is to find necessary and sufficient conditions for any casino, not only one generated by a single lottery, to be fair (Theorem 3.1 and Theorem 3.2).
This section demonstrates Donald Ornstein’s conclusion that some fair lotteries generate arbitrarily subfair casinos, but by a method different from the one used by him. This conclusion will not be formally relied on later, so this section could be read only casually.
Let γ0 be a fixed gamble and Γ0 the smallest casino for which γ0 ∈ Γ0(1). Thus, 
. If Q is any nonnegative function that is fairly regular, increasing on [0, 1], and equal to 1 on [1, ∞), it will prove possible to choose γ0 fair and yet such that γQ ≤ Q(f) for all f and all γ in Γ0(f). According to Theorem 2.12.1, this implies that Q majorizes U; so Γ0 is subfair if Q also satisfies Q(f) < f for some f in (0, 1).
Specifically, let Q restricted to [0, 1] have the following properties: (a) Q(f) ≥ 0 and Q(1) = 1; (b) 
for some α; 
≤ 2αβ for some β > 0. Such functions exist in abundance. In fact, Q(f’) can be arbitrarily small for any f ‘in (0, 1). Consider, for example, 
for f in [0, 1] with 
As one preliminary to deriving an upper bound for γQ, note that, for f and f + g in [0,1],
Also, since 
is a bounded function of f; that is, for all f in [0, 1],
for some sufficiently large p.
To prepare for computation in this and later sections, define, for each nonnegative integer a, the ath partial moment ma(z; 6) (or simply ma(z)) of any θ at z in [−1, ∞) thus:
for all positive s.
If γ = [θ + f] is a fair or subfair gamble available in a casino at f for some f ∈ (0, 1), then, using (1), (3), and (2), γQ can be estimated thus:
where, in view of (2) and of the nonpositivity of 
,
say.
If now γ0 ∈ Γ0 (f)and γ ≠ δ(f), then θ = [fsθ0] for some s in (0, 1], where θ0 = [γ0 − 1]. Using (4) and abbreviating 
by z,
where
In summary, if θ0 is such that T(z; θ0) ≤ 0 for all nonnegative z, then the U of Γ0 is majorized by Q. It remains to construct a fair θ0 on [−1, ∞) that satisfies this inequality for all z ≥ 0. This will be done by choosing a suitable member of the family of probability densities,
with 0 < b < 1 and δ > 0. As is easily checked, ρ is a probability density of mean
Let b henceforth be so chosen that (10) vanishes, which will ensure m(θ0) = 0. It will be enough to remember that 
for small δ. If θ0 is the distribution corresponding to ρ(w|δ, b), this table shows the computation of T(z; θ0).
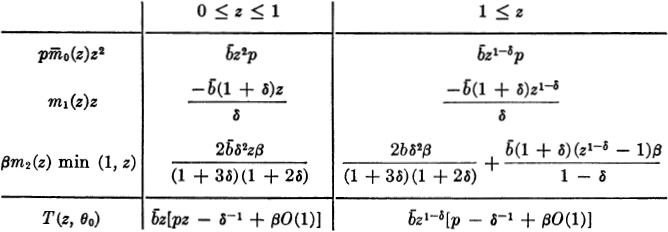
Clearly, for sufficiently small δ, T(z; θ0) is nonpositive for all z ≥ 0. There is great latitude in the choice of a θ0 that makes (8) nonpositive; we have made a simple choice showing that γ0 can have a density and attach positive probability to all neighborhoods of − 1.
The section is summarized by a theorem.
THEOREM 1. For every positive є and for f in (0, 1), there is a rich man’s casino Γ for which 
and such that Γ(1) contains a fair, conventional gamble other than δ(1).
A casino that contains superfair gambles has been shown to be superfair. With this case out of the way, the fundamental question concerning fair casinos is answered in terms of the set of lotteries Θ(1) = [Γ(1) − 1] by Theorem 2 and, in a preliminary way, by Theorem 1. (As usual, w ∧ z is the minimum of the two numbers w and z.)
THEOREM 1. For a casino Γ that contains no superfair lotteries, these three conditions are equivalent:
(a) Γ is fair.
(b) There is a positive z such that, for every positive 
, there is a θ in Θ(1) with
(c) For every positive z and , (1) has a solution in Θ(1).
The content of Theorem 1 would plainly be unchanged by the removal of “z” before the first integral of (1). But this “z” serves to make dimensionless.
Proof that (b) and (c) are equivalent: Clearly, (c) implies (b). The reverse implication will develop from the next few paragraphs, which are of some interest in themselves.
If , z, and θ satisfy (1), then so do , sz, and [sθ] Thus, if (1) can be solved in Θ(1) for a specified positive , and z, it can also be solved for that and all smaller z.
If , z, and θ satisfy (1), and z′ ≥ z > 0, let 
, and note that 
, z′, and θ also satisfy (1).
It is now evident that, if some positive z satisfies condition (b) of the theorem, all positive z do; so (b) does imply (c). Still more, if some positive z fails to satisfy condition (b) for some positive , then all larger values of z fail for that , and all smaller z, say sz, fail for 
.
The next two lemmas are used in the proof that (a) implies (b).
LEMMA 1. Suppose that, for some in (0, 1), every lottery θ available in a house Γ on the nonnegative reals is permitted by the quadratic function Q, 
, that is, ∫ Q(x) dθ(x) ≤ 0. Then Q is excessive for Γ. Consequently, for any u, if Q ≥ u, then Q ≥ U. If it is supposed only that every θ available at every f in [0, 1] is permitted by Q, then Q ∧ 1 is excessive and Q ≥ U for the usual u.
Proof: For θ permitted by Q, and γ = [f + θ], compute thus:
Therefore, if every available θ is permitted by Q, Q is excessive; if every θ available at every f in [0, 1] is permitted by Q, then Q ∧ 1 is excessive. In either event, Theorem 2.12.1 applies. 
(Lemma 1 is weaker, but also considerably simpler, than Theorem 9.4.1.)
For each measure θ and real number z, the curtailment θ ∧ z of θ at z is the measure that agrees with θ on subsets of (− ∞, z) and that assigns to {z} the value θ[z, ∞]. The curtailment Γ ∧ z of a house Γ based on a set of real numbers is defined by
LEMMA 2. If Γ1 is the curtailment at 1 of a house Γ on a set of real numbers and if u is the indicator of [1, ∞), then U1 = U.
Proof that condition (a) of Theorem 1 implies (b): If Γ is fair, then, according to Lemma 2, so is Γ ∧ 1. Lemma 1 then provides for each 
a θ* available in Γ ∧ 1 at some f in [0, 1], for which
where θ is available in Γ at f and hence at 1.
Proof that condition (c) of Theorem 1 implies (a): The program is to show that the utility function f ∧ 1 is nearly attained by a stationary family of strategies that resembles the proportional family studied in Chapter 10. For every lottery θ carried on [−1, ∞) and for every z and α, where z > α > 0, the standard stationary family of strategies σ(f; θ, z, α) is defined for each f by the gamble
The abbreviations σ(f) and γ(f) will be used for σ(f; θ, z, α) and γ (f; θ, z, α). The idea behind the definition of standard strategy is this: If the gambler moves at all under σ(f), he chooses the fraction fs of the lottery θ that will make γ(f)[1 + α, ∞) = [fsθ + f][1 + α, ∞) = θ[z, ∞); he stands pat with δ(f) if the goal of 1 is already attained, or if the requisite s, namely, 
, would exceed 1, since, for s < 1, [fsθ + f] is not generally in Γ(f). If [θ + 1] ∈ Γ(1), then γ(f) ∈ Γ(f) and σ(f) is available in Γ at f. It is helpful to think of α as small and z as large.
Denote the σ(f)-probabilities that fn < (1 + α)/(1 + z) and fn ≥ 1 by An and Bn, respectively. Of course, An and Bn are nonde-creasing in n. It will now be shown that, unless θ is trivial, An + Bn approaches 1 for large n. Let β = θ[z, ∞). Since each essential gamble used by σ(f) has probability β of leading to a fortune of at least 1 + α, An + Bn ≥ 1 − (1 − β)n. This proves the required point if β > 0. Otherwise, for every n, 0 ≤ fn < 1 + α. almost certainly, and σ(f; θ, z, α) is very like a proportional strategy in which (1 + α) plays the role of 0, fortunes are measured down from 1 + α, and the goal is (1 + α)/(1 + z). The only difference is that γ(f) = δ(f) between 1 and 1 + α. Formally, consider the proportional strategy p based on the lottery [ − θ/z], beginning with the fortune 
. It is easy to see that An + Bn is the probability under p that some fortune among 
falls outside of (α, (1 + α)z/(1 + z)]. This approaches 1 in n if θ is nontrivial, as can be seen by applying Lemma 10.3.1 modified in the spirit of Section 10.4 so as to apply to general lotteries.
Let Q be any strictly convex, increasing, quadratic function of f such that Q(f) < f in [0, 1] and Q(f) > 0. As will be shown in the next paragraph, there is a θ in Θ(1), and a z and an α such that
Consider the implications of this anticipated conclusion. First, Lemma 2.12.1 can be applied to 1 − (Q ∧ 1), and to the gambling house Γθ, where Γθ(f) = {γ(f)} (or {γ(f), δ(f)] if one prefers not to depart from the usual assumption that δ(f) is always available). Hence,
for every stop rule t. Next, if t > n, Q(ft) < 0 with σ(f)-probability at least An; so the left side of (7) is at most 1 − An. But An + Bn approaches 1, so lim Bn ≥ Q(f) for f in [0, 1], whence also u(a) (f) ≥ Q(f)in (0, 1). (This argument is foreshadowed in Theorem 2.12.4.) Finally, since Q(f)can be arbitrarily close to f in [0, 1], the promised inequalities (5) and (6) will indeed complete the proof.
Choose a such that Q(1 + α) = 1 and z such that
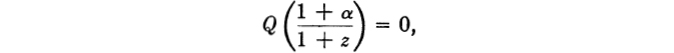
as is compatible with the assumptions about Q and the requirement that z > α > 0. This choice ensures (5). For the interesting range of f, namely, [(1 + a)/(I + z), 1), and for any θ,
The coefficient of ∫ w d[θ ∧ z](w) is bounded from above, and the coefficient of ∫ w2 d[θ ∧ z](w) is positive and bounded from below for ∫ in the interesting range. In view of hypothesis (c), θ can therefore be so chosen that { } > 0 for all f of interest.
Theorem 1 remains true if the curtailed moments to which it refers are replaced by partial moments.
THEOREM 2. For a casino Γ that contains no superfair lotteries these three conditions are equivalent:
(a) Γ is fair.
(b′) There is a positive z such that, for every positive , there is a θ in Θ(1) with
(c′) For every positive z and , (9) has a solution in Θ(1).
(As in Theorem 1, the “z” before the first integral is to make dimensionless.)
Proof that (b′) and (c’) are equivalent: The argument that (b) and (c) are equivalent applies verbatim.
Proof that (b′) implies (b): The left side of (1) is at most the left side of (9), and the right side of (9) is at most the right side of (1).
The following lemma, of possible analytical interest, will be used to show that (b) implies (b′):
LEMMA 3. Suppose that and z′ are positive, and θ is any not partially remote, probability measure on [−1, ∞]. If
for all z in (z′, ∞), then for all z in (z′, ∞)
and
Proof: There is no loss in generality in assuming that θ is conventional. To see this, note that the left side of (10) can never increase rapidly, and the right side is nondecreasing. If (10) is ever violated in (z′, ∞), it must then be violated throughout some nontrivial subinterval. Therefore, (10) obtains throughout (z′, ∞)if and only if it obtains at the points of continuity of the functions on the right-hand and left-hand sides of (10), which are functions of bounded variation. At these points of continuity the values of the two functions are unchanged if θ′, the conventional companion of θ, is substituted for θ; so (10) is satisfied throughout (z′, ∞) for θ if and only if it is satisfied for θ′. A similar argument applies to (11) and (12). Specialization to conventional lotteries is now justified.
The proof involves several integrations by parts, which can be justified by, for example, (Widder 1941, Theorem 4b, p. 7), (Saks 1932, Theorem 14.1, p. 102), or (Hewitt 1960, Theorem A). Some instances of the general formula
where ϕ and ψ are bounded and Borel measurable and F is of bounded variation and continuous from the right, are also involved.
Calculate thus for z > 0, in the notation of Section 2.
If (10) obtains in (z′, ∞), then, according to (15),
for w in (z′, ∝). Therefore,
for z in (z′, ∞). Therefore,
for z in (z′, ∞). Now, using (14), (18), and (15) in that order,
so (11) obtains for z in (z′, ∞).
To see that (10) and (11) imply (12), add 
times (10) to 
times (11).
Proof that (b) implies (b′): If (9) fails for some and z′, it fails for that and all z > z′, and (12) applies to show that (1) fails for 
and for all z > z′.
The proof of Theorem 2 is now complete.
Lemma 3 is not true in reverse:
Example 1. Suppose that θ is fair and conventional, with density Ax−(t+2) for z in (1, ∞), where t is an arbitrary number larger than 1 and A is some positive number. Then,
where 
. Therefore, (11) is satisfied. That (10) is not satisfied is easily seen thus:
which converges to 0 as z approaches infinity; but m2(z) approaches a finite positive limit.
The following sufficient condition for a casino to be at least fair is an immediate consequence of Theorem 2 and Lemma 3.
THEOREM 3. A casino Γ is at least fair if, for some positive z and for every positive , there is a θ in Θ(1) for which
If (23) is satisfied by z, , and θ, it is also satisfied by sz, , and [sθ]; therefore if some z satisfies the condition of Theorem 3, so does any smaller z, though some z may be too large to satisfy it.
Example 2. Let Γ be generated by a single fair θ carried on [− 1, r], with r the least such number. The theorem applies with z any number less than r, but it does not apply with any z as large as r, since the right side of (23) vanishes for such z.
It is easy to prove Theorem 3 directly, along the lines of the proof that condition (c) of Theorem 1 implies condition (a), with the simplification that linear functions can play the role here that quadratic ones do there. This was almost done in Section 4.4.
We mention Theorem 3 because (23) is simpler than (9). As will be apparent later, however, the sufficient condition of Theorem 3 is vastly more restrictive than conditions (b′) and (c′) of Theorem 2.
To apply and illustrate the general conclusions of the preceding section, specialize Θ(1) in this section to consist of a set of simple lotteries. A simple lottery θ is characterized by the triple (s, t, w); θ loses the stake s with probability 
and wins a prize t with probability w. The immediate object is to determine which sets of triples correspond to fair casinos. Denote the first and second moments of θ simply by m1 and m2, and introduce a subfairness coefficient ϕ, ϕ = −m1/m2. Written out,
To set aside superfair lotteries as uninteresting here, assume throughout this section that m1 ≤ 0 for all θ in Θ(1).
THEOREM 1. If Θ(1) consists of simple lotteries none of which are superfair, these four conditions are equivalent:
(a) The casino is fair.
(b) For every positive z and there is a θ in Θ(1) such that t < z and 
.
(c) For every positive there is a θ ∈ Θ(1) such that 
and 
.
(d) For every positive there is a θ in Θ(1) such that 
and 
.
Proof: According to Theorem 3.2, if the casino is fair, there is, for every positive z and , a θ in Θ(1) such that 
. This inequality cannot obtain if 
, for it would mean 
, or 
. Thus, for 
there must be a θ with t ≤ z and 
. And the inequality t ≤ z can be made strict by contracting θ slightly. Since the condition t < z and 
can be satisfied for all positive z and small positive , it can be satisfied for all positive z and ; so (a) implies (b).
(b) implies that, for a certain θ, 
. So, according to Theorem 3.2, (b)also implies (a).
If (b) obtains, substitute for z and 
for in (b) to conclude (c). Conversely, if (c) obtains, choose the in (c) smaller than both the z and 
of (b). Thus (b) and (c) are equivalent.
It is evident that (c) implies (d). Finally, it will be shown that, under (d), there are θ’s with t and ϕ arbitrarily small, as required by (c). For if (t, ϕ) corresponds to a θ in Θ(1), then so do all points (t′, ϕ′) on the semihyperbola 0 < t′ ≤ t, t′ϕ′ = tϕ. Specifically, if there is a θ with 
and 
for some 
in (0, 1), there is also a θ′ with 
and 
. First, if 
, let t′ = t and ϕ′ = ϕ. Otherwise, 
is in Θ(1) along with θ. But 
, and 
.
COROLLARY 1. If t is bounded, the casino is fair if and only if there are θ‘s with ϕ arbitrarily small.
If, for every bounded lottery θ, t is interpreted as the essential upper bound of θ, the four conditions of Theorem 1 are meaningful for any casino all of whose lotteries are bounded. The proofs given in Theorem 1 that conditions (b), (c), and (d) are equivalent and imply condition (a) apply to any casino whose lotteries have bounded carriers, with almost no change. However, condition (a) does not imply condition (b) for all such casinos.
Example 1. For 0 < δ < 1/3, let θδ attach probability 
to − 1, 
to 1, and δ2 to δ−1. Let Γ be the casino for which Θ(f) = {[aθδ]: 0 ≤ a ≤ f, 0 < δ < 1/3}. As is easily verified, Γ is fair but does not satisfy condition (b) of Theorem 1.
For some questions it is convenient to introduce the shape parameters 
of a lottery, where
These are “shape parameters” in that the 
and 
of a lottery θ are equal, respectively, to the 
and 
of [aθ] for any positive number a. If Θ* is a set of simple lotteries, all with s ≤ 1, then there is a smallest casino for which Θ(1) ⊃ Θ*. For this casino,
If this smallest casino is at least fair, and only then, every casino for which Θ(1) ⊃ Θ* is at least fair. The following corollaries all refer to the smallest casino associated with Θ*, called the casino of Θ*, and it is to be understood that Θ* includes no superfair gambles.
COROLLARY 2. The casino of Θ* is fair if and only if, for every positive , 
and 
for some θ in Θ*,.
COROLLARY 3. If t is bounded on Θ*, the casino of Θ*, is fair if and only if, for every positive 
for some θ in Θ*.
COROLLARY 4. If s is bounded away from 0 on Θ*, the casino of Θ* is fair if and only if, for every positive 
and 
for some θ in Θ*.
COROLLARY 5. If t is bounded and s is bounded away from 0 on Θ*, the casino of Θ* is fair if, and only if, for every positive , 
for some θ in Θ*.
Example 2. Let Θ* consist of simple lotteries θδ for which s = − 1, 
. For θδ, 
; so the casino of Θ* is fair according to Corollary 5. On the other hand, as is easy to verify, the condition of Theorem 3.3 is not satisfied for this uniformly bounded casino. This suggests how far the sufficient condition for fairness stated by that theorem is from being necessary.
Recall from Section 4.7 that a casino is a one-game casino generated by θ if θ ∈ Θ (1) and every element of Θ(1) is of the form [sθ] for some nonnegative s. The definition was so phrased that the set of s for which [sθ] ∈ Θ(1) can be a half-open or a closed interval with 0 as its lower endpoint.
THEOREM 1. If Γ is a one-game casino generated by a θ for which θ(z, ∞) approaches 0 as z approaches ∞, these three conditions are equivalent:
(a) The casino Γ is fair.
(b) θ is nontrivial, and
(c) θ is nontrivial, satisfies (1), and is a fair lottery; that is, θ has mean 0.
Proof: Suppose first that Γ is fair. Then, according to Section 4.4, θ is at most fair and is nontrivial. Consequently, m2(z) is uniformly positive for positive z, the limit inferior in (1) is at least 0, and the numbers s for which [sθ] ∈ Θ(1) are bounded from above. According to Theorem 3.2, for every positive z and there must be an s with [sθ] in Θ(1) and 
. In view of (2.4), 
. Since s is bounded, this shows that (1) obtains, and (a) implies (b).
Calculating in the opposite direction, (b) implies (a).
Clearly, (c) implies (b). What remains to be shown is only this: If (b) obtains, θ is at least fair. But if θ were not at least fair, m1(z; θ) would be uniformly negative in z and (3.15) would contradict (1).
THEOREM 2. Each of the following conditions on a nontrivial lottery θ of mean 0 implies all of its successors and none of its predecessors:
(b) θ has finite variance.
(c) θ is such that
is 0.
(d) θ is such that (2) is finite.
(e) The one-game casino generated by θ is fair.
Proof: Obviously, (a) implies, but is not implied by, (b). If (b) obtains,
and the final integral in (3) approaches 0 as z approaches infinity. Therefore (b) implies (c). If −m1(z) = A(z log z)−1 for z in (2, ∞), then (c) obtains but (b) does not.
Obviously, (c) implies (d). If −m1(z) = Az−1, then (d) obtains but (c) does not.
If (d) obtains but (b) does not, then (e) is obvious in view of Theorem 1. If (d) and (b) obtain, then so does (c), but (b) with (c) implies (e) in view of Theorem 1. So (d) implies (e).
If −m1(z) = Az−1 log z for z > 1, then (d) fails but, according to Theorem 1, (e) obtains.
According to condition (b) of Theorem 2, a fair θ that has a finite moment of order 2 generates a fair casino. The order 2 is critical; that is, for every r, 1 ≤ r < 2, there is a fair θ that has a finite moment of order r but generates a subfair casino.
Example 1. If θ has a density proportional to w−1−r for w in (2, ∞), then θ has moments of all orders up to but not including r and, by Theorem 1, is subfair if r is less than 2. If r = 2, θ has an infinite second moment and does not even satisfy (2), but it generates a fair casino. If r > 2, the second moment is plainly finite and the casino is fair.
Theorem 1 is of course a specialization of Theorem 3.2. In the same spirit, the next theorem, partially proved in Section 4.4, specializes the rather feeble Theorem 3.3.
THEOREM 3. If Γ is a one-game casino generated by a not super-fair θ, then Γ satisfies the condition of Theorem 3.3 (and is therefore fair) if and only if, for every positive , there is a positive z for which
Applied to a fair lottery, (4) has a neat interpretation. Namely, the expectation of the prize, given that it is more than z, is less than 
. But the condition (4), like that of Theorem 3.3 from which it is derived, is excessively strong. In fact, Example 3.1 shows that some very simple distributions having finite variance (or any other moment of fixed order) do not satisfy the condition of Theorem 3.
An example will now be adduced to show that “lim inf” cannot be replaced by “lim” in Theorem 1. The same example will show incidentally that the condition of Theorem 3 can apply to a 0 for which even condition (d) of Theorem 2 fails.
Example 2. Let θ attach probability 1 to the set consisting of −1 and the integers n!, n = 1, 2, · · · . Further, let −m1(n!) = A2n/(n + 2)!, where A is of course determined by normalization. According to (3.15),
Therefore, −n!m1(n!)/m2(n!) ∼ (n + 1)−1; so (1) is satisfied, and θ generates a fair casino. But, for n > 1,
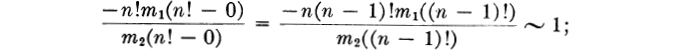
so (1) would not be true with “lim” in place of “lim inf”.
According to (3.14),
Therefore,
and condition (4) of Theorem 3 is satisfied, though condition (2) of Theorem 2 is not, and θ has infinite variance.
As Example 2 shows, “lim inf” in (1) cannot be replaced by “lim.” It cannot be replaced by “inf” either, though in a sense it nearly can. If the denominator in (1) is bounded away from 0 for all positive z, that is, if 
for some 
, then the fraction in (1) approaches 0 for small z. But if the infimum of the fraction outside of some neighborhood of 0 is 0, then its lower limit as z approaches ∞ is also 0. More fully, if θ is fair and nontrivial, either −zm1(z)/m2(z) is bounded away from 0 on every interval bounded away from both 0 and ∞ or it is identically 0 for sufficiently large z. This follows from calculation, for z > 0 and t ≥ 1, thus:
For fair θ, (1) can be rewritten
The numerator in (8) is equal to that in (1), and the denominator of (8) differs from that of (1) only at points of discontinuity of θ. Thus, in view of (7), (1) and (8) really are equivalent. Obviously, (8) implies that
and this is known to be a necessary and sufficient condition for the distribution θ, which is bounded from below, to belong to the domain of partial attraction of the normal law; see, for example, (Gnedenko and Kolmogorov 1954, p. 190).
Equation (8) is definitely stronger than (9), even for fair θ, according to this example.
Example 3. Let θ be a fair lottery confined to −1 and numbers of the form zn = 2n2/n2, n = 1, 2, · · ·, with θ{zn} = A2−n2, as is possible. The fraction in (9) is, at zn + 0, asymptotic to 2−2n−1; so θ is in the domain of partial attraction of the normal law. But the fractions in (1) and (8) approach ∞; so θ does not generate fair casinos.
If θ is fair and 
is sufficiently small for large z, then θ will generate a fair casino. For in this case, θ will have finite variance. One might conjecture that, conversely, if θ (z, ∞), for a fair θ, is sufficiently large, then θ cannot generate a fair casino. Surprisingly, this conjecture is far from true. In fact, for any lottery θ of finite mean carried on [−1, ∞), there is a conventional lottery ϕ of mean 0 carried on [−1, ∞) that generates a fair casino and is such that ϕ (z, ∞) ≥ θ (z, ∞) for all z in some interval [z0, ∞). Still more, ϕ can be made to satisfy the relatively severe condition of Theorem 3, as the next theorem states.
LEMMA 1. If θ has a finite mean, there is a conventional ϕ with finite mean such that ϕ(x, ∞) ≥ θ[x, ∞) for all x.
Proof: For some positive y, let 
F is the distribution function of a conventional ϕ, and 
.
LEMMA 2. If θ is conventional and has finite mean m, there is, for each positive , a conventional ϕ such that the mean of ϕ is at most 
, ϕ(x, ∞) ≥ θ(x, ∞) for all x, and for each positive δ there is a positive 2 for which
Proof: If θ(x, ∞) = 0 for some finite x, then θ itself can serve for ϕ, as is easy to see. Assume, therefore, that θ(x, ∞) is positive for all finite x. Let 
, · · · be a sequence of numbers in (0, 1) such that
for all i. For instance, let 
. Choose a1 > 0 so that
There is a unique b1 for which 
, and b1 > a1. Choose ai+1 > bi such that
and let bi be the number for which
Since the ai approach ∞, and
the bi approach ∞.
For each x, let i(x) be the least i for which x < bi. Let T(x) = θ(− ∞, x] and G(x) = T(ai(x)). Clearly, G(x) is nondecreasing and continuous on the right, and satisfies
Let F(x) = min (T(x), G(x)). Clearly, F is a distribution function, and, for some conventional ϕ, 
for all x, as required.
LEMMA 3. If θ is conventional and has a finite mean, there is a conventional ϕ with 0 mean such that ϕ(x, ∞), = θ(x, ∞) for all sufficiently large x. If θ[−1, ∞) = 1, ϕ can be so chosen that ϕ[−1, ∞) = 1.
THEOREM 4. If θ has a finite mean, there is a conventional ϕ with mean 0 such that ϕ(x, ∞) ≥ θ[x, ∞) for all sufficiently large x, and such that (10) has a solution in z for each positive δ. If θ[− 1, ∞) = 1, ϕ can be chosen so that ϕ[− 1, ∞) = 1.
Suppose that every γ ∈ Γ(1) is countably additive on the Borel subsets of [0, ∞). It is then natural to inquire about the existence of optimal Borel-measurable strategies, where σ = σ0, · · ·, σn, · · · is, as usual, Borel measurable if each σn is countably additive on the Borel sets A, and σn(f1, · · ·, fn) A is Borel measurable in f1, · · ·, fn for each A.
As is not difficult to see, unless there is some γ ∈ Γ(1) other than δ(1) that is fair, has bounded support, and attains its upper bound with positive probability, there is no optimal Borel-measurable σ. On the other hand, the presence of such a gamble in a fair casino ensures the existence of an optimal Borel-measurable strategy. The simplest one is the bold strategy based on that γ. As usual, to play boldly means to stake just enough to reach the goal when rich enough to do so and otherwise to stake all.
If a conventional fair gamble γ attains its essential upper bound with positive probability but does not attain its essential lower bound with positive probability, then a gambler who uses the bold strategy based on γ, or indeed any optimal strategy based on γ, is in the uncomfortable position of having positive probability of gambling forever. Equivalently, there is no optimal Borel-measurable wide-sense policy based on such a γ, where (σ, t) is a wide-sense policy if t stops with inner σ-probability 1. A necessary and sufficient condition for the existence of a Borel-measurable, optimal wide-sense policy based on a given fair, conventional γ is that both the essential least upper bound and the essential greatest lower bound of γ be attained with positive probability and that they differ from each other. Clearly, the bold strategy σ, with the associated natural incomplete stop rule t—stop when the fortune is 0 or 1—is such an optimal widesense policy. Thus, if a fair Γ has available such a fair γ, then measurable, optimal wide-sense policies do exist. The existence of such a fair γ is, however, not necessary for the existence of measurable, optimal wide-sense policies. It suffices that there be in Γ(1) a fair, conventional gamble γ, other than δ(1), that attains its least upper bound with positive probability, and a fair, conventional gamble γ′, other than δ(1), with bounded support, that attains its lower bound with positive probability. Indeed, this condition is both necessary and sufficient.
Return now to the question of the existence of optimal strategies when no gamble attains its least upper bound with positive probability. As was observed above, under these conditions no Borel-measurable, optimal strategies exist. Yet there are optimal strategies for at least some such fair casinos.
Example 1. Let Γ(f) = [f Θ(1) + f] for all f in [0, ∞), where 0(1) contains all lotteries that are fair and countably additive on the Borel sets of [−1, ∞) except those that attain their upper bounds with positive probability. An optimal family of strategies, and of policies with two moves, can be constructed for this casino. Let (0, 1) be partitioned into a denumerable number of sets Bn, each of inner Lebesgue measure 0. Let σ0 = σ0(f), for f in (0, 1), be any element of Γ(f) that is carried by (0, 1) and that attaches probability 0 to each of the Bn; let σ0(f) = δ(f) elsewhere. (Though completely additive on Borel sets, σ0 is not, and is not here expected to be, completely additive on all the sets for which it is defined.) Let σ1(f), for f in Bn, be any element of Γ(f) that is carried by {0} ∪ (1 + (2n)−1, 1 + n−1]; let σ1(f) = δ(f) elsewhere. Let σn(f) = δ(f) for all n ≥ 2 and all f. The strategy just defined stagnates with probability 1 but almost never at f = 1. With evident notation,
So the strategy σ is worth f and is therefore optimal.
