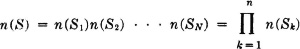
The fundamental task in the classical theory of probability is to count the number of ways that an event can occur. The discipline of counting (which can become quite sophisticated) is commonly known as combinatorial analysis. We shall discuss only the most elementary principles and results in this theory.
A fundamental principle of counting
A basic strategy of counting is the following. Break a selection process S into a finite sequence of selections S1, S2, …, SN such that the number of ways of making selection Sk does not depend upon the results of the previous selections in the sequence. Then the number of ways of realizing S is the product of the numbers of ways of realizing the various selections in the sequence.
A simple set representation of this situation can be made in terms of the cartesian product of sets. Suppose we let S be a set of points—one point for each way of carrying out the selection process. Similarly, we let Sk be a set of points—one point for each way of carrying out the kth step. The selection of a point in S is equivalent to a sequence of selections of points in the spaces Sk, k = 1, 2, …, N. Thus we may think of S as the cartesian product space S1 × S2 × · · · × SN. Determination of a sequence of components is tantamount to selection of a point in S. If we let n(S) represent the number of points in space S and n(Sk) be the number of points in space Sk, we have the fundamental relation for product spaces
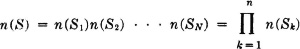
Permutations and combinations
In selecting (or displaying) a finite set of distinct objects chosen from a given set, we may take two points of view:
1. We may be interested only in the membership of the set selected, without regard to the order in which the objects are selected or displayed. Each distinguishable set in this case is called a combination. Two sets having the same number of objects represent different combinations iffi (if and only if) there is at least one element in one of the sets which is different from every element in the other set.
2. We may be interested in the order in which the elements are arranged, as well as the combination which is ordered. Each ordered arrangement of a given combination is called a permutation. Two permutations of the same combination differ iffi they differ in the element found in at least one place in the ordering scheme. Two sets represent the same combination iffi for any one permutation of the first set there is a permutation of the second set which does not differ from the given permutation of the first set.
Some basic formulas
1. The number Prn of permutations of r objects (i.e., the number of ordered r-tuples) selected from a set of n objects is given by
2. The number Crn of combinations of r objects selected from a set of n objects is given by
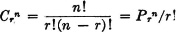
3. Let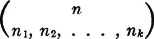 
be the number of ways that n objects may be placed in k cells, with n1 objects in the first, n2 objects in the second, etc. (n1 + n2 + · · · + nk = n). The order of placing the objects in any cell is immaterial. Then we have
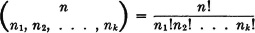
Derivation of the basic formulas
The formulas above may be derived by using the basic counting strategy.
(1) (a) Select from the n objects one object for the first position (there are n possibilities).
(b) Select from the n − 1 remaining objects one object for the second position (there are n − 1 possibilities, regardless of the result of the previous step).
(c) Continue the process until finally one selects from the n – r + 1 remaining objects one object for the rth place (there are n − r + 1 possibilities for this step, regardless of the results of the previous steps).
Then, by the fundamental counting rule,
(2) Obtain a permutation in two steps:
(a) Select a combination of r objects (Crn possibilities).
(b) Select a permutation of the r objects (there are Prr = r! possibilities for each combination chosen).
By the fundamental counting rule
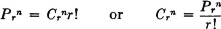
(3) Obtain a permutation of the entire n objects in the following steps:
(a) Select a combination of the desired type; there are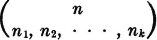 
possibilities.
(b) Select a permutation of the n1 objects in the first cell (there are n1! possibilities).
(c) In a similar manner, for each of the k cells, obtain a permutation of the objects in that cell (there are ni! possibilities in the ith cell).
By the fundamental counting rule, the number of permutations of the entire set of n objects must be given by
so that the desired result follows immediately.
By an inductive proof it may be shown that
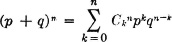
so that the number Ckn appears as a coefficient in the binomial expansion, and is hence called a binomial coefficient. Since this coefficient appears naturally in a wide variety of applications, we note some properties.
If we put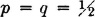 
, we obtain
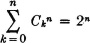
In terms of combinations, this says that the number of combinations of n or fewer elements (including zero) from a set of n elements is 2n. This is the well-known fact that a space with n elements has 2n subsets (including the whole space and the empty set).
It is sometimes convenient to extend the range of r in the expression Crn by putting
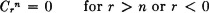
By examining the basic formulas, the following relations may be derived easily:
A wide variety of other formulas may be developed.
Treatments of combinatorial analysis are found in many books on probability. For a simple but good introductory treatment, one may consult Goldberg [1960]: for a much more extensive treatment, see Feller [1957, chaps. 2 through 4].