The discussion in Chap. 1 has shown that the classical theory of probability, based upon a finite set of equally likely possible outcomes of a trial, has severe limitations which make it inadequate for many applications. This is not to dismiss the classical case as trivial, for an extensive mathematical theory and a wide range of applications are based upon this model. It has been possible, by the use of various strategies, to extend the classical case in such a way that the restriction to equally likely outcomes is greatly relaxed. So widespread is the use of the classical model and so ingrained is it in the thinking of those who use it that many people have difficulty in understanding that there can be any other model. In fact, there is a tendency to suppose that one is dealing with physical reality itself, rather than with a model which represents certain aspects of that reality. In spite of this appeal of the classical model, with both its conceptual simplicity and its theoretical power, there are many situations in which it does not provide a suitable theoretical framework for dealing with problems arising in practice. What is needed is a generalization of the notion of probability in a manner that preserves the essential properties of the classical model, but which allows the freedom to encompass a much broader class of phenomena.
In the attempt to develop a more satisfactory theory, we shall seek in a deliberate way to describe a mathematical model whose essential features may be correlated with the appropriate features of real-world problems. The history of probability theory (as is true of most theories) is marked both by brilliant intuition and discovery and by confusion and controversy. Until certain patterns had emerged to form the basis of a clear-cut theoretical model, investigators could not formulate problems with precision, and reason about them with mathematical assurance. Long experience was required before the essential patterns were discovered and abstracted. We stand in the fortunate position of having the fruits of this experience distilled in the formulation of a remarkably successful mathematical model.
A mathematical model shares common features with any other type of model. Consider, for example, the type of model, or “mock-up,” used extensively in the design of automobiles or aircraft. These models display various essential features: shape, proportion, aerodynamic characteristics, interrelation of certain component parts, etc. Other features, such as weight, details of steering mechanism, and specific materials, may not be incorporated into the particular model used. Such a model is not equivalent to the entity it represents. Its usefulness depends on how well it displays the features it is designed to portray; that is, its value depends upon how successfully the appropriate features of the model may be related to the “real-life” situation, system, or entity modeled. To develop a model, one must be aware of its limitations as well as its useful properties.
What we seek, in developing a mathematical model of probability, is a mathematical system whose concepts and relationships correspond to the appropriate concepts and relationships in the “real world.” Once we set up the model (i.e., the mathematical system), we shall study its mathematical behavior in the hope that the patterns revealed in the mathematical system will help in identifying and understanding the corresponding features in real life.
We must be clear about the fact that the mathematical model cannot be used to prove anything about the real world, although a study of the model may help us to discover important facts about the real world. A model is not true or false; rather, a model fits (i.e., corresponds properly to) or does not fit the real-life situation. A model is useful, or it is not. A model is useful if the three following conditions are met:
1. Problems and situations in the real world can be translated into problems and situations in the mathematical model.
2. The model can be studied as a mathematical system to obtain solutions to the model problems which are formulated by the translation of real-world problems.
3. The solutions of a model problem can be correlated with or interpreted in terms of the corresponding real-world problem.
The mathematical model must be a consistent mathematical system. As such, it has a “life of its own.” It may be studied by the mathematician without reference to the translation of real-world problems or the interpretation of its features in terms of real-world counterparts. To be useful from the standpoint of applications, however, not only must it be mathematically sound, but also its results must be physically meaningful when proper interpretation is made. Put negatively, a model is considered unsatisfactory if either (1) the solutions of model problems lead to unrealistic solutions of real-world problems or (2) the model is incomplete or inconsistent mathematically.
Although long experience was needed to produce a satisfactory theory, we need not retrace and relive the mistakes and fumblings which delayed the discovery of an appropriate model. Once the model has been discovered, studied, and refined, it becomes possible for ordinary minds to grasp, in reasonably short time, a pattern which took decades of effort and the insight of genius to develop in the first place.
The most successful model known at present is characterized by considerable mathematical abstractness. A complete study of all the important mathematical questions raised in the process of establishing this system would require a mathematical sophistication and a budget of time and energy not properly to be expected of those whose primary interest is in application (i.e., in solutions to real-world problems). Two facts motivate the study begun in this chapter:
1. Although the details of the mathematics may be sophisticated and difficult, the central ideas are simple and the essential results are often plausible, even when difficult to prove.
2. A mastery of the ideas and a reasonable skill in translating real-world problems into model problems make it possible to grasp and solve problems which otherwise are difficult, if not impossible, to solve. Mastery of this model extends considerably one’s ability to deal with real-world problems.
In addition to developing the fundamental mathematical model, we shall develop certain auxiliary representations which facilitate the grasp of the mathematical model and aid in discovering strategies of solution for problems posed in its terms. We may refer to the combination of these auxiliary representations as the auxiliary model.
Although the primary goal of this study is the ability to solve real-world problems, success in achieving this goal requires a reasonable mastery of the mathematical model and of the strategies and techniques of solution of problems posed in terms of this model. Thus considerable attention must be given to the model itself. As we have already noted, the model may be studied as a thing in itself, with a “life of its own.” This means that we shall be engaged in developing a mathematical theory. The study of this mathematics can be an interesting and challenging game in itself, with important dividends in training in analytical thought. At times we must be content to play the game, until a stage is reached at which we may attempt a new correlation of the model with the real world. But as we reach these points in the development of the theory, repeated success in the act of interpretation will serve to increase our confidence in the model and to make it easier to comprehend its character and see its implications for the real world.
The model to be developed is essentially the axiomatic system described by the mathematician A. N. Kolmogorov (1903– ), who brought together in a classical monograph [1933] many streams of development. This monograph is now available in English translation under the title Foundations of the Theory of Probability [1956]. The Kolmogorov model presents mathematical probability as a special case of abstract measure theory. Our exposition utilizes some concrete but essentially sound representations to aid in grasping the abstract concepts and relations of this model. We present the concepts and their relations with considerable precision, although we do not always attempt to give the most general formulation. At many places we borrow mathematical theorems without proof. We sometimes note critical questions without making a detailed examination; we merely indicate how they have been resolved. Emphasis is on concepts, content of theorems, interpretations, and strategies of problem solution suggested by a grasp of the essential content of the theory. Applications emphasize the translation of physical assumptions into statements involving the precise concepts of the mathematical model.
It is assumed in this chapter that the reader is reasonably familiar with the elements of set theory and the elementary operations with sets. Adequate treatments of this material are readily available in the literature. A sketch of some of these ideas is given in Appendix B, for ready reference. Some specialized results, which have been developed largely in connection with the application of set theory and boolean algebra to switching circuits, are summarized in Sec. 2–6. A number of references for supplementary reading are listed at the end of this chapter.
Sets, Events, and Switching [1964]. A number of references for supplementary reading are listed at the end of this chapter.
The discussion in the previous introductory paragraphs has indicated that, to establish a mathematical model, we must first identify the significant concepts, patterns, relations, and entities in the “real world” which we wish to represent. Once these features are identified, we must seek appropriate mathematical counterparts. These mathematical counterparts involve concepts and relations which must be defined or postulated and given appropriate names and symbolic representations.
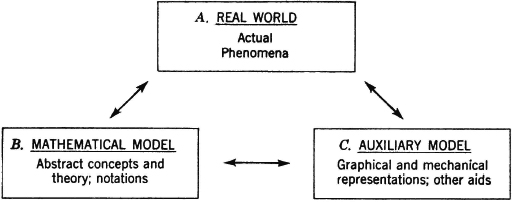
Fig. 2-1-1 Diagrammatic representation of the relationships between the “real world” and the models.
In order to be clear about the situation that exists when we utilize mathematical models, let us make a diagrammatic representation as in Fig. 2-1-1. In this diagram, we analyze the object of our investigation into three component parts:
A. The real world of actual phenomena, known to us through the various means of experiencing these phenomena.
B. The imaginary world of the mathematical model, with its abstract concepts and theory. An important feature of this model is the use of symbolic notational schemes which enable us to state relationships and facts with great precision and economy.
C. An auxiliary model, consisting of various graphical, mechanical, and other aids to visualization, remembering, and even discovering important features about the mathematical model. It seems likely that even the purest of mathematicians, dealing with the most abstract mathematical systems, employ, consciously or unconsciously, concrete mental images as the carriers of their thought patterns. We shall develop explicitly some concrete representations to aid in thinking about the abstract mathematical model; these in turn will help us to think clearly and systematically about the patterns abstracted from (i.e., lifted out of) our experience of the real world of phenomena.
Much of our attention and effort will be devoted to establishing the mathematical model B and to a study of its characteristics. In doing this, we shall be concerned to relate the various aspects of the mathematical model to corresponding aspects of the auxiliary model C, as an aid to learning and remembering the important characteristics of the mathematical model. Our real goal as engineers and scientists, however, is to use our knowledge of the mathematical model as an aid in dealing with problems in the real world. This means that we must be able to move from one part of our system to another with freedom and insight. For clarity and emphasis, we may find it helpful to indicate the important transitions in the following manner:
A → B: Translation of real-world concepts, relations, and problems into terms of the concepts of the mathematical model.
B → A: Interpretation of the mathematical concepts and results in terms of real-world phenomena. This may be referred to as the primary interpretation.
B → C: Interpretation of the mathematical concepts and results in terms of various concrete representations (mass picture, mapping concepts, etc.). This may be referred to as a secondary interpretation.
C → B: The movement from the auxiliary model to the mathematical model exploits the concrete imagery of the former to aid in discovering new results, remembering and extending previously discovered results, and evolving strategies for the solution of model problems.
A ↔ C: The correlation of features in A and C often aids both the translation of real-world problems into model problems and the interpretation of the mathematical results. In other words, the best path from A to B or from B to A may be through C.
The first element to be modeled is the relative frequency of the occurrence of an event. It is an empirical fact that in many investigations the relative frequencies of occurrence of various events exhibit a remarkable statistical regularity when a large number of trials are made. This feature of many games of chance served (as we noted in Chap. 1) to motivate much of the early development of probability theory. In fact, many of the questions posed by gamblers to the mathematicians of their time were evoked by the fact that observed frequencies deviated slightly from that which they expected.
This phenomenon of constant relative frequencies is in no way limited to games of chance. Modern statistical communication theory, for example, makes considerable use of the remarkable statistical regularities which characterize languages. The relative frequencies of occurrence of symbols of the alphabet (including all symbols such as space, numbers, punctuation, etc.), of symbol pairs, triples, etc., and of words, word combinations, etc., have been studied extensively and are known to be quite stable. Of course, exceptions are known. For example, Pierce [1961] quotes a paragraph from a novel which is written without the use of a single letter E in its entire 267 pages. In ordinary English, the letter E is used more frequently than any other letter of the alphabet. Such marked deviations from the usual patterns require special effort or indicate unusual situations. In the normal course of affairs one may expect rather close adherence to the common patterns of statistical regularity.
The whole life insurance industry is based upon so-called mortality tables, which predict the relative frequency of deaths at various ages (or give information equivalent to specifying these frequencies). In a similar manner, reliability engineering makes extensive use of the life expectancy of articles manufactured by a given process. These life expectancies are based on the equivalent of mortality tables for the products manufactured. Closely related is the theory of errors, in which the relative frequencies of errors of various magnitudes may be assumed to follow quite closely certain well-known patterns.
The empirical fact of a stable (i.e., constant) relative frequency serves as the basis in experience for choosing a mathematical model of probability. This empirical fact cannot in any way imply logically the existence of a probability number. We set up a model by postulating the existence of an ideal number, which we call the probability of an event. If this is a sound model and we have chosen the number properly, we may expect the relative frequency of occurrence of the event in a large number of trials to lie quite close to this number. But we cannot “prove” the existence in the real world of such an ideal limiting frequency. We simply set up a model. We then examine the “behavior” of the model, interpret the probabilities as relative frequencies, check or test these probabilities against observed frequencies (where possible), and try to determine experimentally whether the model fits the real-world situation to be modeled. We can build up confidence in our model; we cannot prove or disprove our model. If it works for enough different problems, we move with considerable confidence to new problems. Continued success tends to increase our confidence, so that we come to place a large degree of reliance upon the adequacy of the model to predict behavior in the real world.
If the feature of the real world to be represented by probability is the relative frequency of occurrence of a given event in a large number of trials, then the probability must be a number associated with this event. These numbers must obey the same laws as relative frequencies. We can readily list several elementary properties which must therefore be possessed by the probability model.
1. If an event is sure to occur, its relative frequency, and hence its probability, must be unity. Similarly, if an event cannot possibly occur, its probability must be 0.
2. Probabilities are real numbers, lying between 0 and 1.
3. If two events are mutually exclusive (i.e., cannot both happen on any one trial), the probability of the compound event that either one or the other of the original events will occur is the sum of the individual probabilities.
4. The probability that an event will not occur is 1 minus the probability of the occurrence of the event.
5. If the occurrence of one event implies the occurrence of a second event, the relative frequency of occurrence of the second event must be at least as great as that of the first event. Thus the probability of the second event must be at least as great as that of the first event.
Many more such properties could be enumerated. One of the concerns of the model maker is to discover the most basic list, in the sense that the properties included in this list imply as logical consequences all the other desirable or necessary properties. When we come to the formal presentation of our mathematical model in Sec. 2-3, we shall see that the basic list desired is contained in the list of properties above.
In order to realize an economy of expression, we shall need to introduce an appropriate notational scheme to be used in formulating probability statements. Before attempting to do this, however, we should take note of the fact that we have used the term event in the previous discussion without attempting to characterize or represent this concept. Since probability theory deals in a fundamental way with events and various combinations of events, it is desirable that we give attention to a precise formulation of the concept of event in a manner that will be mathematically useful and precise and that will be meaningful in terms of real-world phenomena. We turn our attention to that problem in the next section.
In order to produce a mathematical model of an event, it is necessary to have a clear idea of the situations to which probability theory may be applied. Historically, the ideas developed principally in connection with games of chance. In such games the concept of some sort of trial or test or experiment is fundamental. One draws a card from a deck, throws a pair of dice, or selects a colored ball from a jar. The trial may be composite. A single composite trial may consist of drawing, successively, five cards from a deck to form a hand, or of flipping a coin ten times and noting the sequence of heads and tails that turn up. But in any case, there must be a well-defined trial and a set of possible outcomes. In the coin-flipping trial, for example, it is physically conceivable that the coin may land neither “heads” nor “tails.” It may stand on edge. It is necessary to decide whether the latter eventuality is to be considered a satisfactory performance of the experiment of flipping the coin.
It is perhaps helpful to realize that each of the situations described above is equivalent to drawing balls from a jar or urn. Each throw of a pair of dice, for instance, results in an identifiable outcome. Each such outcome can be represented by a single ball, appropriately marked. Throwing the dice is then equivalent to choosing at random a ball from the urn. Similarly, the composite trial of drawing five cards from a deck may be equivalent to drawing a single ball. Suppose we were to lay out each of the possible hands of five cards, with the cards arranged in the order of their drawing; a picture could be taken of each possible hand; the set of all pictures (or a set of balls, each with one of the pictures of a hand printed thereon) could be put in a large urn. Drawing a single picture (or ball) from the urn would then be equivalent to the composite trial of drawing five cards from the deck to form a hand.
The concept of the outcome of a trial, which is so natural to a game of chance, is readily extended to situations of more practical and scientific importance. One may be sampling opinions or recording the ages at death of members of a population. One may be making a physical measurement in which the precise outcome is uncertain. Or one may be receiving a message on a communication system. In each case, the result observed may be considered to be the result of a trial which yields one of a set of possible outcomes. This set of possible outcomes is clearly defined, in principle, at least. Even here we may use the mental image of drawing balls from a jar, provided we are willing to suppose, our jar may contain an infinite number of balls. Making a trial, no matter what physical procedure is required, is then equivalent to choosing a ball from the jar.
We have a simple mathematical counterpart of a jar full of balls. This is the fundamental mathematical notion of an abstract set of elements. We consider a basic set S of elements 
. Each element represents one of the possible outcomes of the trial. The basic set, or basic space (also commonly called the sample space), S represents the collection of all allowed outcomes. The single element is referred to as an elementary outcome. Regardless of the nature of the physical trial referred to, the performance of a trial is represented mathematically as the choice of an element . In many considerations it is, in fact, convenient to refer to the element as the choice variable.
Events
Probability theory refers to the occurrence of events. Let us now see how this idea may be expressed in terms of sets and elements. Suppose, for example, a trial consists of drawing a hand of five cards from an ordinary deck of playing cards. We may think in terms of our equivalent urn experiment in which each ball has the picture of one of the possible hands, with one ball for each such hand. Selecting a ball is equivalent to drawing the hand pictured thereon. What is meant by the statement “A hand with one or more aces is drawn”? This can mean but one thing. The ball drawn is one of those having a picture of a hand with one or more aces. But the set of balls satisfying this condition constitutes a well-defined subset of the set of all the balls in the jar.
Our mathematical counterpart of the jar full of balls is the abstract basic space S. There is an element corresponding to each ball in the urn. We suppose that it is possible, in principle at least, to identify each element in terms of the properties of the ball (and hence the hand) it represents. The occurrence of the event is the selection of one of the elements in the subset of those elements which have the properties determining the event. In our example, this is the property of having one or more aces. Viewed in this way, it seems natural to identify the event with the subset of elements (balls or hands) having the desired properties. The occurrence of the event is the act of choosing one of the elements in this subset. In probability investigations, we suppose the choice is “random,” in the sense that it is uncertain which of the balls or elements will be chosen before the actual trial is made. It should be apparent that the occurrence of events is not dependent upon this concept of randomness. A deliberate choice—say, one in which the balls are examined in the process of selection—would still lead to the occurrence or nonoccurrence of an event.
In general, an event may be defined by a proposition. The event occurs whenever the proposition is true about the outcome of a trial. On the other hand, a proposition about elements defines a set in the following manner. Suppose the symbol πA(·) represents a proposition about elements in the basic set S. In the example above, the symbol πA() is understood to mean “the hand represented by has one or more aces.” This statement may or may not be true, depending upon which element is being considered. Let us consider the set A of those elements for which the proposition πA() is true. We use the symbolic representation A = {:πA()} to mean “A is the set of those for which the proposition πA() is true.” Thus, in our example, A is the set of those hands which have one or more aces. We identify this set with the event A. The event A occurs iffi (if and only if) the chosen is a member of the set A.
Let us illustrate further. Consider the result of flipping a coin three times. Each resulting sequence may be represented by writing a sequence of H’s and T’s, corresponding to throws of heads or tails, respectively. Thus the symbol THT indicates a sequence in which a tail appears on the first and third throws and a head appears on the second throw. There are eight elementary outcomes, each of which is represented by an element. We may list them as follows:
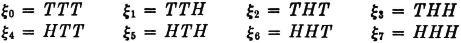
Consider the event that a tail turns up on the second throw. This is the event T2 = {0, 1, 4, 5}. This event occurs if any one of the elements in this list is chosen, which means that any one of the sequences represented by 0, 1, 4, or 5 is thrown. Similarly, the set H1 = {4, 5, 6, 7} corresponds to the event that a head is obtained on the first throw. Many other events could be defined and the elements belonging to them listed in a similar manner.
We have made considerable progress in developing a mathematical model for probability theory. The essential features may be outlined as follows:
Some aspects of the formulation of the model have not been made precise as yet. Some of the flexibility and possibilities of the representation of events as sets have not yet been demonstrated. But considerable groundwork has been laid.
Special events and combinations of events
In probability theory we are concerned not only with single events and their probabilities, but also with various combinations of events and relations between them. These combinations and relations are precisely those developed in elementary set theory. Thus, having introduced the concept of an event as a set, we have at our disposal an important mathematical resource in the theory of sets. In the following treatment, it is assumed that the reader is reasonably familiar with elementary topics in set theory. A brief exposition of the facts needed is given in Appendix B, for ready reference.
Before considering combinations of events, it may be well to note the following fact. When a trial or choice is made, one and only one element is chosen—i.e., only one elementary outcome is observed—but a large number of events may have occurred. Suppose, in throwing a pair of dice, the pair of numbers 2, 4 turn up. Only one of the possible outcomes of the trial has been selected. But the following events (among many others) have occurred:
1. A “six” is thrown.
2. A number less than seven is thrown.
3. An even number is thrown.
4. Both of the numbers appearing are even numbers.
5. The larger number in the pair thrown is twice the smaller.
These are distinct events, and not just different names for the same event, as may be verified by enumerating the elements in each of the events described. Each of these events has occurred; yet only one outcome has been observed.
It is important to distinguish between the elementary outcome and the elementary event {} whose only member is the elementary outcome . Whenever the result of a trial is the elementary outcome , the elementary event {} occurs; so also, in general, do many other events. We have here an example of the necessity in set theory of distinguishing logically between an element and the single-element set {}. The reader should be warned of an unfortunate anomaly in terminology found in much of the literature. In his fundamental work, Kolmogorov [1933, 1956] used the term elementary event for the elementary outcome ; he used no specific term for the event {}. Although he does not confuse logically the elementary outcome with the event {}, his terminology is inconsistent at this point. We shall attempt to be consistent in our usage. A little care will prevent confusion in reading the literature which follows Kolmogorov’s usage.
Let us consider now several special events, combinations of events, and relations between events. We shall illustrate these by reference to the coin-flipping experiment described earlier in this section. We let Hk be the event of a head on the kth throw in the sequence (k is 1, 2, or 3 in this experiment) and Tk be the event of a tail on the kth throw. For convenience, we list the corresponding sets as follows:
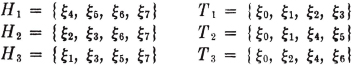
Suppose we are interested in the compound event of “a head on the first throw or a tail on the second throw.” To what set of elementary outcomes does this correspond? The event “a head on the first throw” is the set of elementary outcomes H1; the event “a tail on the second throw” is the set of elementary outcomes T2. The compound event occurs iffi an element from either of these sets is chosen. Thus the desired event is the set of elementary outcomes H1 ∪ T2, that is, the set of all those elementary outcomes which are in at least one of the events H1, T2. The argument carried out for this illustration could be repeated without essential change for any two events A and B. Thus, for any pair of events A, B, the event “A or B” is the event A ∪ B. We commonly refer to this as the or event; also, we may use the language of sets and refer to this as the union of the events A, B.
In a similar way, the event of “a head on the first throw and a tail on the second throw” can be represented by the intersection H1T2 = H1 ∩ T2. From the point of view of set theory, this is the set of those elements which are in both H1 and T2. This is precisely what is required by the joint occurrence of H1 and T2; the element chosen must belong to both of the events (sets) H1 and T2, which is the same as saying that it belongs to H1T2. We may refer to this as the joint event, or as the intersection of the events, H1 and T2. Again, the argument does not depend upon the specific illustration, and we may speak of the joint event AB for any two events A and B.
If we consider the intersection H1T1 of the events H1 and T1, we find that it contains no element; i.e., there is no sequence which has both a head on the first throw and a tail on the first throw. As a set, the intersection H1T1 is the empty set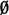 
; as an event, the intersection is impossible, since no possible outcome can meet the conditions which determine the event. It is immediately evident that the impossible event always corresponds to the empty set. In abstract set theory, the symbol is commonly used to represent the empty set; we shall also use it to indicate the impossible event. When two events A,B have the relation that their joint occurrence is impossible, they are commonly called mutually exclusive events. Thus two mutually exclusive events are characterized by having an empty intersection; in the language of sets, we may refer to these as disjoint events.
It may be noted that the set T1 has as members all the elements that are not in H1. T1 is thus the set known as the complement of H1, designated H1c. The event T1 occurs whenever H1 fails to occur—if a head does not appear on the first throw, a tail must appear there. We speak of the event H1c as the complementary event for H1. Inspection of the list above shows that, for each k = 1, 2, or 3, we must have Hkc = Tk and Tkc = Hk, as common sense requires. If we take the event Hk ∪ Tk for any k, we have the set of all possible outcomes. This means that the event Hk ∪ Tk is sure to happen. Every sequence must have either a head or a tail (but not both) in the kth place. The event S, corresponding to the basic set of all possible outcomes, is thus naturally referred to as the sure event.
We have noted that two events A and B may stand in the relation of being mutually exclusive, in the sense that if one occurs the other cannot occur on the same trial. At the other extreme, we may have the situation in which the occurrence of the event A implies the occurrence of the event B. This, in terms of set theory, means that set A is contained in set B, a relationship indicated by the notation A ⊂ B. We shall utilize the same notation for events; if the occurrence of event A requires the occurrence of event B (this means that every element in A is also in B), we shall indicate the fact by writing A ⊂ B. In keeping with the custom in set theory, we shall suppose the impossible event implies any event A. It certainly is true that every element which is in event is also in event A. The convention involved in this seemingly pointless statement, denoted in symbols by ⊂ A for any A ⊂ S, is often useful in the symbolic manipulation of events.
Because of the essential identity of the notions of sets and events, as we have formulated our model, we shall find it convenient to use the language of sets and that of events interchangeably, or even in a manner which mixes the terminology. We have, in fact, already done so in the discussions of the preceding paragraphs. The resulting usage is so natural and obvious that no confusion is likely to result.
A systematic tabulation of the terminology and concepts discussed above may be useful for emphasis and for reference. We emphasize the fact that the language of events comes largely from our ordinary experience by listing various terms in this language in the “real-world” column. In the same column, however, we include symbols which are taken from the set theoretic formulation of our concept of events. In spite of some anomalies here, the tabulation may be useful in making the tie between the real world, where events actually happen, and the mathematical model, in which they are represented in an extremely useful way.
We have extended our mathematical model by the use of the theory of sets. An important addition to our auxiliary model is provided by the Venn diagrams (Appendix B), used as an aid in visualizing set combinations and relations. These now afford a means of visualizing combinations of events and relations among them. The Venn diagram, in fact, provides a somewhat simplified version of the urn or jar model. Points in the appropriate regions on the Venn diagram correspond to the balls in the urn. Various subsets may be designated by designating appropriate regions. Determining the outcome of a trial corresponds to picking a point on the Venn diagram. The occurrence of an event A corresponds to the choice of one of that set of points determined by the region delineating the event A. We shall illustrate the use of Venn diagrams in the following discussion.
Classes of events
In the foregoing discussion, events are defined as sets which are subsets of the basic space S; relationships between pairs of events are specified in terms of the appropriate concepts of set theory. These relations and concepts may be extended to much larger (finite or infinite) classes of events in a straightforward manner, utilizing the appropriate features of abstract set theory. Thus we may speak of finite classes of events, sequences of events, mutually exclusive (or disjoint) classes of events, monotone classes of events, etc. The and and or (intersection and union) combinations may be extended to general classes of events. Where necessary or desirable, we make the modifications of terminology required to adapt to the language of events.
Notation for classes
It frequently occurs that the most difficult part of a mathematical development is to find a way of stating precisely and concisely various conditions or relationships pertinent to the problem. To this end, skill in the use of mathematical notation may play a key role. In dealing with classes of events (sets), we shall often find it expedient to exploit the notational devices described below.
A class of events is a set of events. We shall ordinarily use capital letters A, B, C, etc., to designate events and shall use capital script letters 
, 
, 
, etc., to indicate classes of events. To designate the membership of a class, we use an adaptation of the notation employed for subsets of the basic space S. For example,
is the class having the four member events listed inside the braces.
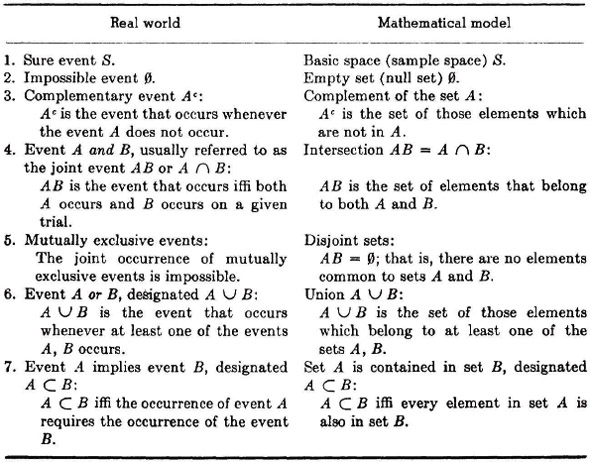
One of the common means of designating the member events in a class of events is to use the same letter for all events in the class and to distinguish between the various events in the class by appropriate subscripts (or perhaps in some cases, superscripts). When this scheme is used, the membership of the class may be designated by an appropriate specification of which indices are to be allowed. This means that we designate the membership of the class when we specify the index set, i.e., the set of all those indices such that the corresponding event is a member of the class. For example, suppose is the class consisting of four member events A1, A2, A3, and A4. Then we may write
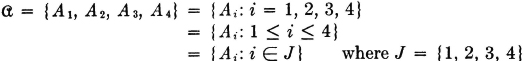
We may thus (1) list the member events, (2) list the indices in the index set, (3) give a condition determining the indices in the index set, or (4) simply indicate symbolically the index set, which is then described elsewhere. It is obvious that the last two schemes may be used to advantage when the class has a very large (possibly infinite) number of members. Also, the symbolic designation of the index set J is useful in expressions in which the index set may be any of a large class of index sets. For example, we may simply require that J be any finite index set. We say class is countable iffi the number of member sets is either finite or countably infinite, in which case the index set J is a finite or countably infinite set.
Suppose we wish to consider the union of the events in the class just described. This is the event that occurs iffi at least one of the member events occurs. We speak of this event as the union of the class and designate it in symbols in one of the following ways:
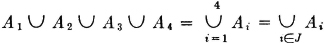
The latter notation is particularly useful when we may want to consider a general statement true for a large class of different index sets.
If the class of events under consideration is a mutually exclusive class, we may designate the union of the class by replacing the symbol ∪ by the symbol 
. Use of the latter symbol not only indicates the union of the class, but implies the stipulation “the events are mutually exclusive.” Thus, when we write
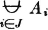
we are thereby adding the requirement that the Ai be mutually exclusive. It is not incorrect in such a case, however, to use the ordinary union symbol ∪ if we are not concerned to display the fact that the events are mutually exclusive.
In a similar way, we may deal with the intersection of the events of the class . This is the event that occurs iffi all the member events occur. We speak of this event as the intersection of the class (or sometimes as the joint event of the class) and designate it in symbols in one of the following ways:
Extensions of this notational scheme to various finite and infinite cases are immediate and should be obvious.
Use of the index-set notation is also useful in the case of dealing with sums of numbers. Suppose a1, a2, a3, and a4 are numbers. We may designate the sum of these numbers in any of the following ways:
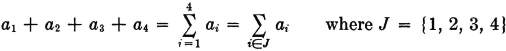
Here we have used the conventional sigma Σ to indicate summation. Extensions to sums of larger classes of numbers parallels the extension of the convention for unions of events to larger classes. We shall find this notational scheme extremely useful in later developments.
Partitions
As our theory develops, we shall find that expressing an event as the union of a class of mutually exclusive events plays a particularly important role. In anticipation of this fact, we introduce and illustrate some concepts and terminology which will be quite useful. As a first step, we make the following
Definition 2-2a
A class of events is said to form a complete system of events if at least one of them is sure to occur.
It is immediately apparent that the class = {A1, A2, …, An} consisting of the indicated n events is a complete system iffi
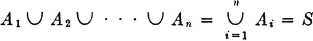
If any element is chosen, it must be in at least one of the Ai (it could be in more than one). A class thus forms a complete system iffi the union of the class is the sure event.
One of the simplest complete systems is formed by taking any event A and its complement Ac. One of these two events is sure to occur. Suppose, for example, that during a storm a photographer sets up his camera and opens the shutter for 10 seconds. Let the event A be the event that one or more lightning strokes are recorded. Then the event Ac is the event that no lightning stroke is recorded. One of the two events A or Ac must occur, for A ∪ Ac = S, the sure event.
As a more complicated complete system, suppose we take a sample of 10 electrical resistors from a large stock. We suppose this choice of 10 resistors corresponds to one trial. The resistors are tested individually to see that their resistance values lie within specified limits of the nominal value marked upon them. Let Ak, for any integer k between 0 and 10, be the event that, for the sample taken, k or more of the resistors meet specification. Then the 11 events A0, A1, …, A10 form a complete system of events. In any sample taken, some number (possibly zero) of resistors must meet specification. Suppose in a given sample this number is three. Then the element representing this particular sample is an element of each of the events A3, A2, A1, and A0 and hence is an element of the union of all the events. We may note that we have a class of events satisfying A0 ⊃ A1 … ⊃ A10; that is, we have a monotone-decreasing class. As a matter of fact, the event A0 is the sure event, for every sample must have zero or more resistors which meet specification.
A more interesting class of events in the resistor-sampling problem is the class = {Bk: 0 ≤ k ≤ 10}, where for each k the event Bk is the event that the sample has exactly k resistors which meet specification. In this case, the different events in the class are mutually exclusive, since no sample can have exactly k and also exactly j ≠ k resistors which meet tolerance. Thus is a mutually exclusive class. Now it is apparent that the class forms a complete system of events, for every element corresponding to a sample must belong to one (and only one) of the Bk. The particular k in each case is determined by counting the number of resistors in the sample which meet specification.
Complete systems of events in which the members are mutually exclusive are so important that we find it convenient to give them a name as follows:
Definition 2-2b
A class of events is said to form a partition iffi one and only one of the member events must occur on each trial.
It is apparent that the class of events = {Bk: 0 ≤ k ≤ 10} defined in the resistor-sampling problem above is a partition; so also is the complete system of events {A, Ac} illustrated in the photography example. It is also apparent that a partition is characterized by the two properties
Fig. 2-2-1 Venn-diagram representation of a partition.
1. The class is mutually exclusive.
2. The union of the class is the sure event S.
The name partition is suggested by the fact that a partition divides the Venn diagram representing the basic space S into nonoverlapping sets. While the members of the partition may be quite complicated sets (representing events), the essential features of a partition are exhibited in a schematic representation such as that in Fig. 2-2-1. One deficiency of such a representation is that it is not clear to which set the points on the boundary are assigned. If it is kept in mind that disjoint sets are being represented, this need cause no difficulty in interpretation.
We may extend the notion of a partition in the following useful way:
Definition 2-2c
A mutually exclusive class of events whose union is the event A is called a partition of the event A (or sometimes a decomposition of A).
It is obvious that a partition of the sure event S is a partition in the sense of Def. 2-2b. A Venn diagram of a partition of an event A is illustrated in Fig. 2-2-2.
As an illustration of the partition of an event, we consider some partitions of the union of two events. A certain type of rocket is known to fail for one of two reasons: (1) failure of the rocket engine because the fuel does not burn evenly or (2) failure of the guidance system. Let the elementary outcome correspond to the firing of a rocket. We let A be the event the rocket fails because of engine malfunction and B be the event the rocket fails because of guidance failure. The event F of a failure of the rocket is thus given by F = A ∪ B. Now we cannot assert that events A and B are mutually exclusive. We may assert, however, that
Fig. 2-2-2 Venn-diagram representation of a partition of an event A.
We thus have three partitions of A ∪ B, namely, {A, AcB}, {B, ABc}, and {AcB, AB, ABc}. The first and third of these are illustrated in Fig. 2-2-3.
As a second example, which is quite important in probability theory, consider a mutually exclusive class of events
where in this case J = {1, 2, 3, 4}. Suppose
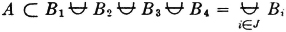
Then the class {AB1, AB2, AB3, AB4} = {ABi: i ∈ J} is a mutually exclusive class whose union is the event A. Thus {ABi: i ∈ J} is a partition of the event A. If the class is a partition (of the sure event S), then every A is contained in the union of the class. This manner of producing a partition of an event A by taking the intersections of A with the members of a partition is illustrated in the Venn diagram of Fig. 2-2-4. Note that some of the members of the partition may be impossible events (empty sets). These may be ignored when the fact is known. They do not affect the union if included, since they contribute no elementary outcomes. The use of the general-index-set notation in the argument above shows that the result is not limited to the special choice of the mutually exclusive sets.
Fig. 2-2-3 Partitions of the union of two events A and B.
Fig. 2-2-4 A partition of an event A produced by the intersection with a partition of the sure event S.
Because of its importance, we state the general case as
Theorem 2-2A
Let = {Bi: i ∈ J} be any mutually exclusive (disjoint) class of events. If the event A is such that 
, then the class {ABi: i ∈ J} is a partition of A, so that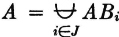 
.
We shall return to the important topic of partitions in Sec. 2-7.
Sigma fields of events
We have defined events as subsets of the basic space S and have developed a considerable mathematical system based on these ideas. Our discussion has proceeded as if every subset of S could be considered an event, and hence as if the class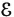 
of events could be considered the class of all subsets of S. In the case of a finite number of elementary outcomes, this is the usual procedure. In many investigations in which the basic space is infinite, there are technical mathematical reasons for defining a less extensive class of subsets as the class of events. Fortunately, in applications it is usually not important to examine the question of which of the subsets of S are to be considered as events. For the purposes of this book, we shall simply suppose that in each case a suitable class of subsets of S makes up the class of events. It is usually important to describe carefully the various individual events of interest, but once these are described, they are assumed, without further examination, to belong to an appropriate class.
Development of the mathematical foundations has shown that the class of events must be a sigma field of sets. A brief discussion of such classes is given in Appendix B. We simply note here that such classes are closed under the formation of unions, intersections, and complements. This means that if the class of events includes a countable class = {Ai: i ∈ J}, then the union of , the intersection of , and the complements of any of the Ai must be events also. This provides the mathematical flexibility required for building up composite events from various events defined in formulating a problem, as subsequent developments show.
Having noted some of the general properties which probability numbers must have and having examined the concept of an event in considerable detail, we are now ready to make a formal definition of probability.
In Sec. 2-1 we discussed informally several properties of probability which must hold if we are to consider the probability of an event as the relative frequency of occurrences of the event to be expected in a large number of trials. This informal discussion was restricted by the fact that the concept of an event had not been formulated in a precise way. The subsequent development in Sec. 2-2 was devoted to formulating carefully the concept of an event and relating the resulting mathematical model to the real-world phenomena which it represents. An event is represented as a set of elements from a basic space; each element of that space represents one of the possible outcomes of a trial or experiment under study; the occurrence of an event A corresponds to the choice of an element from that subset of the basic space which represents the event. As a result of this development, we have adopted the following mathematical apparatus:
1. A basic space S, consisting of elements (referred to as elementary outcomes)
2. Events which are subsets of S (more precisely, members of a suitable class of subsets of S)
In this model, the occurrence of the event A is the choice of an element in the set A (thus is sometimes referred to as the choice variable).
We now wish to introduce a third entity into this model: a mathematical representation of probability. It is desired to do this in a manner that extends the classical probability model and includes it as a special case. In particular, it is desired to preserve the properties which make possible the relative-frequency interpretation. We note first that probability is associated with events rather than with individual outcomes. In the classical case, the probability of an event A is the ratio of the number of elements in A (i.e., the number of ways that A can occur) to the total number of elements in the basic space S (i.e., the total number of possible outcomes). Thus, in our model, probability must be a function of sets; that is, it must associate a number with a set of elements rather than with an individual element.
An examination of the list of properties which probability must have, as developed in Sec. 2-1, shows that probability has the formal properties characterizing a class of functions of sets known in mathematics as measures. If we are able to use this well-known class of set functions as our probability model, we shall be able to appropriate a rich and extensive mathematical theory. It is precisely this notion of probability as a measure function which characterizes the highly successful Kolmogorov model for probability. An examination of the theory of measure shows that it is not necessary to postulate all the properties of probability discussed and listed in Sec. 2-1. Several of these properties can be taken as basic or axiomatic, and the others deduced from them. This trimming of the list of basic properties to a minimum or near minimum often results in an economy of effort in establishing the fact that a set function is a probability measure. It is also an aid in grasping the essential character of the function under study. At this point, we shall simply introduce the definition of probability in a formal manner; the justification for this choice rests upon the many mathematical consequences which follow and upon the success in relating these mathematical consequences in a meaningful way to phenomena of interest in the real world.
Probability systems
We are now ready to make the following
Definition 2-3a
A probability system (or probability space) consists of the triple:
1. A basic space S of elementary outcomes (elements)
2. A class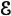 
of events (a sigma field of subsets of S)
3. A probability measure P(·) defined for each event A in the class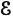 
and having the following properties:
(P1) P(S) = 1 (probability of the sure event is unity)
(P2) P(A) ≥ 0 (probability of an event is nonnegative)
(P3) If = {Ai: i ∈ J} is a countable partition of A (i.e., a mutually exclusive class whose union is A), then
The additivity property (P3) provides an essential characterization of a probability measure P(·). It may be stated in words by saying that the probability of the union of mutually exclusive events is the sum of the probabilities of the individual events. We have seen how this property is required for a finite number of events in order to preserve a fundamental property of relative frequencies. The extension in the mathematical model to an infinity of events is needed to allow the analytical flexibility required in many common problems. For technical mathematical reasons, this property is limited to a countable infinity of events. A countably infinite class is one whose members may be put into a one-to-one correspondence with the positive integers. It is in this sense that the infinity is “countable.” As an example of a simple situation in which an infinity of mutually exclusive events is required for analysis, consider
Example 2-3-1
Suppose a game is played in which two players alternately toss a coin. The player who first tosses a “head” is the winner. In principle, the game as defined may continue indefinitely, for it is not possible to specify in advance how many tosses will be required before one player wins. Let Ak be the event that the first player (i.e., the player who makes the first toss in the sequence) wins on the kth toss. We note that a win is impossible for this player on the even-numbered throws. Thus Ak = 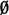for k even. We note that any two events Ak and Aj for different j and k must be mutually exclusive, since we cannot have a head appear for the first time in a given sequence on both the kth and the jth toss. Thus the class = {A1, A3, A5, …} = {Ai: i ∈ J0}, where J0 is the set of odd positive integers, is a mutually exclusive class. Also, the event A of the first man’s winning is the union of the class . This means that the first man wins iffi he wins on one of the odd-numbered throws in the sequence which corresponds to the compound trial defining the game. We thus have
If we can calculate the probabilities P(Ai), we can determine the probability of the event A by the relation
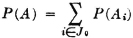
We shall see later that the P(Ai) may be determined quite easily under certain natural assumptions. 
We shall encounter a great many problems in which it is desirable to be able to deal with an infinity of events.
The example above illustrates a basic strategy in dealing with probability problems. It is desired to calculate the probability P(A) that the first man wins the game. The event A can be expressed as the union of the mutually exclusive events Ak. Under the usual conditions and assumptions (to be discussed later), it is easy to evaluate the probabilities P(Ak). Evaluation of P(A) is then made by use of the fundamental additivity rule. The key to the strategy consists in finding a partition of the event A such that the probabilities of the member events of the partition may be determined readily.
Before considering some of the properties of the probability measure P(·) which follow as consequences of the three axiomatic properties used in the definition, let us verify the fact that the new definition includes the classical probability as a special case. In order to do this, we must show that the three basic properties hold for the classical probability measure. In the classical case, the basic space has a finite number of elements and the class of events is the class of all subsets. Let the symbol n(A) indicate the number of elements in event A; that is, n(A) is the number of ways in which event A can occur. For disjoint (mutually exclusive) events, n(A B) = n(A) + n(B). The classical probability measure is defined by the expression P(A) = n(A)/n(S). From this it follows easily that
The property (P3) can easily be extended to any finite number of mutually exclusive events. In the case of a finite basic space, there can be only a finite number of nonempty, mutually exclusive events. The demonstration shows that the axioms are consistent, in the sense that there is at least one probability system satisfying the axioms. As we shall see, there are many others.
Other elementary properties
In order that the probability of an event be an indicator of the relative frequency of occurrence of that event in a large number of trials, it is immediately evident that several properties are required of the probability measure. Several of these are listed near the end of Sec. 2-1. In defining probability, we chose from this list three properties which are taken as basic or axiomatic. We now wish to see that the remaining properties in this list may be derived from the three basic properties. In addition, we shall obtain several other elementary properties which are fundamental to the development of the theory and to its application to real-world problems.
Property 4 in the list in Sec. 2-1 states that the probability that an event will not occur is 1 minus the probability of the occurrence of the event. This follows very easily from the fact that for any event A, the pair {A, Ac} forms a partition; that is, A Ac = S. From properties (P1) and (P3) we have immediately P(A) + P(Ac) = P(S) = 1, so that we may assert
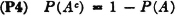
As a special case, we may let A = S, the sure event, so that Ac = 
. As a result we have
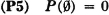
The probability of the impossible event is zero. This with property (P1) completes property 1 in Sec. 2-1.
We have now included in our model all the properties listed in Sec. 2-1 except property 5. This property states that if the occurrence of one event A implies the occurrence of a second event B on the same trial (i.e., if A ⊂ B), then P(B) ≥ P(A). We first note that the condition A ⊂ B implies A ∪ B = B, so that B = A AcB. Since every element in A is also in B, the elements in B must be those which are either in A or in that part of B not in A. By property (P3) we have P(B) = P(A) + P(AcB). Since the second term in the sum is non-negative, by property (P2), it follows immediately that P(A) ≤ P(B). For reference, we state this property formally as follows:
As an illustration of the implications of this fact, consider the following
Example 2-3-2 Serial Systems in Reliability Theory
In reliability theory one is concerned with the success or failure of a system or device. Usually the system is analyzed into several subsystems whose success or failure affects the success or failure of the larger system. The larger system is called a serial system if the failure of any one subsystem causes the complete system to fail. Such may be the case for a complex missile system with more than one stage. Failure of any stage results in failure of the entire system. If we let
then
A serial system composed of n subsystems is characterized by
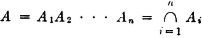
or equivalently by
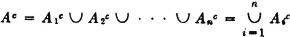
That is, the system succeeds iffi all the subsystems succeed, or the system fails iffi any one or more of the subsystems fail. This relationship requires A ⊂ Ai for each i = 1, 2, …, n. By property (P6) we must therefore have R ≤ Ri for each i. That is, the serial system reliability is no greater than the reliability of any subsystem.
We now wish to develop several other properties of the probability measure which are used repeatedly in both theory and applications. In Sec. 2-2 we discussed in terms of an example the following partitions of the event A ∪ B: {A, AcB}, {B, ABc}, and {AcB, ABc, AB}. The first and third of these are illustrated in Fig. 2-2-3. Use of property (P3) gives several alternative expressions for the probability of A ∪ B.
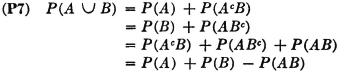
The first three expressions are obtained by direct application of property (P3) to the successive partitions. The fourth expression is obtained by an algebraic combination of the first three in the form P(A ∪ B) + P(A ∪ B) − P(A ∪ B). These expressions may be visualized with the aid of a Venn diagram, as in Fig. 2-3-1. Probabilities of nonoverlapping sets add to give the probability of the union. If one simply adds P(A) + P(B), he includes P(AB) twice; hence it is necessary to subtract P(AB) from the sum, as in the last expression in (P7). If the events A and B are mutually exclusive (i.e., if the sets are disjoint), AB = and, by property (P5), P(AB) = 0. Thus, for mutually exclusive events, property (P7) reduces to a special case of the additivity rule (P3).
The next example provides a simple illustration of a property which is frequently useful in analysis.
Example 2-3-3
A manufacturing process utilizes a basic raw material supplied by companies 1, 2, and 3. A batch of this material is drawn from stock and used in the manufacturing process. The material is selected at random but is packaged in such a way that the batch drawn is from only one of the suppliers. Let A be the event that the finished product meets specifications. Let Bk be the event that the raw material chosen is supplied by company numbered k (k = 1, 2, or 3). When event A occurs, one and only one of the events B1, B2, or B3 occurs. We thus have the situation formalized in Theorem 2-2A. The Bk form a mutually exclusive class. Occurrence of the event A implies the occurrence of one of the Bk. That is, A 
B1 B2 B3. From this it follows that A = AB1 AB2 AB3. By property (P3) we have P(A) = P(AB1) + P(AB2) + P(AB3). If the information about the selection process and the characteristics of the material supplied by the various companies is sufficient, it may be possible to evaluate each of the joint probabilities P(ABk). A discussion of the manner in which this is usually done must await the introduction of the idea of conditional probability, in Sec. 2-5.
Fig. 2-3-1 A partition of the union A ∪ B of two events.
The pattern illustrated in this example is quite general. We may utilize the formalism of Theorem 2-2A to give a general statement of this property as follows.
(P8) Let = {Bi: i ∈ J} be any countable class of mutually exclusive events. If the occurrence of the event A implies the occurrence of one of the Bi (i.e., if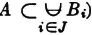 
), then 
.
It should be noted that if the class is a partition (of the whole space), then the occurrence of any event A implies the occurrence of one of the Bi, so that the theorem is applicable. The validity of the general theorem follows from Theorem 2-2A, which states that the class {ABi: i ∈ J} must be a partition of A, and from the additivity property (P3).
Example 2-3-4
Let us return to the coin-tossing game considered in Example 2-3-1. We let Ak be the event that the first man wins by tossing the first head in the sequence on the kth toss. We may let k be any positive integer; the fact that Ak = for k even will not affect our argument. Let us now consider the event Bk that the first man wins on the kth toss or sooner. We have a number of interesting relationships. For one thing, Bk ⊂ Bk+1 for any k since, if the man wins on the kth toss or sooner, he certainly wins on the (k + 1)st toss or sooner. Also,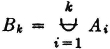 
since the man wins on the kth toss or sooner iffi he tosses a head for the first time on some toss between the first and the kth. We note also that 
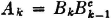; that is, the man tosses a head for the first time on the kth toss in the sequence iffi he tosses it on the kth toss or sooner but not on the (k − 1)st toss or sooner. We must also have the event A that the first man wins expressible as
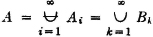
We note that the second union is not the union of a disjoint class. In fact, since the Bk form an increasing sequence, we may assert (see the discussion of limits of sequences in Appendix B) that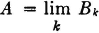 
. By the additivity property,
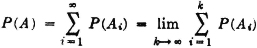
The last expression is the definition of the infinite sum given in the second expression. Again, by the additivity property,
From this we infer the interesting fact that
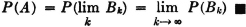
An examination of the argument in the example above shows that the last result does not depend upon the particular situation described. It depends upon the fact that the Bk form an increasing sequence and that the union of the Bk can be expressed as the disjoint union of the Ak in the manner shown. Further examination shows that if we had started with any increasing sequence {Bk: 1 ≤ k < 
} and had defined Ak by the relation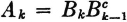 
, the Ak and Bk would have the properties and relationships utilized in the problem. Thus the final result holds generally for increasing sequences.
One can carry out a similar argument for a decreasing sequence. If {Ck: 1 ≤ k < ∞} is a sequence such that Ci ⊃ Ci + 1 for every i, we have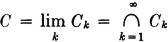 
. By well-known rules for complements,
and the events Ckc form an increasing sequence. We may use the result to assert
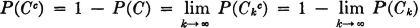
From this it follows that 
. We may summarize these results in the following statement.
(P9) If {An: 1 ≤ n < ∞} is a decreasing or an increasing sequence of events whose limit is the event A, then
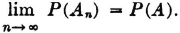
We add one more property which is frequently useful in making probability estimates. For the present we simply state it as a mathematical theorem whose usefulness remains to be demonstrated.
(P10) Let = {Ai: i ∈ J} be any finite or countably infinite class of events, and let A be the union of the class. Then
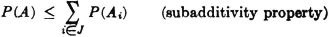
PROOF We consider the case of an infinite sequence of events; the finite case may be considered as a special case of the infinite case by setting all Ai = 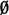for i > n.
We may use the following device to write A as a disjoint union. Let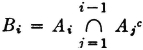 
; then, for any i ≠ j, the events Bi and Bj must be mutually exclusive. A careful reading of the following expressions shows that
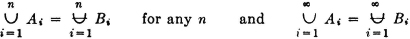
By property (P6), P(Bi) ≤ P(Ai) for each i, since Bi ⊂ Ai. By the additivity property (P3) and general rules on inequalities,
For the most part, the properties listed above have been discussed in terms of the frequency interpretation or have been illustrated in terms of real-world situations translated into the mathematical model. Their full significance for probability theory, however, will become evident only as the theory is developed further. Some of the properties have fairly obvious significance in terms of the relative-frequency interpretation; others find their principal importance as analytical tools for developing further special properties and for carrying out solutions of model problems in a systematic manner. The list of properties is certainly not exhaustive, but both the properties themselves and the arguments employed to verify them are useful in further development of the theory.
Determination of probabilities
The discerning reader will have noted that the mathematical model for probability introduced in this section does not tell how to determine the probabilities of events, except for those very special events the sure event S and the impossible event . This is characteristic of the theory. It tells how the probabilities of various events may be related when the events themselves stand in certain logical relationships. But the theory does not tell what the probability of a given event may be. In the classical case, to be sure, a specific rule is given for determining the probability of any event, once that event is characterized in terms of its membership, i.e., once it is known which elementary outcomes result in the occurrence of the event. But empirical evidence has shown that this rule is not always applicable in a good model. Generally, it is necessary to resort to empirical evidence to determine how probabilities are distributed among events of interest. Such evidence can never be conclusive. One must be content with assumptions or estimates based on experience. Even when the classical model is employed, we can merely assume and test against experience the fact that this is the best model available (or is at least a satisfactory approximation).
The nature of probability theory is such that if the probabilities can be determined for certain particular events (say, by assuming some rule of distribution of probabilities among these events, as in the classical case), then the probabilities for various other events of interest may be calculated. It often happens that it is difficult to observe directly the empirical evidence for the probability assumed for some particular event (or class of events). There may be reasons to guess what values these probabilities should have. From these assumed values it may then be possible to infer the consequent probabilities of other events which are more easily tested empirically. If the inferred probabilities agree sufficiently well with the empirically observed frequencies of occurrence, then one may use the originally assumed probabilities with a considerable measure of confidence. This is precisely the character of much of modern statistical theory. A distribution of probabilities over a given class of events is assumed; deductions are made concerning the probabilities of related events; these probabilities are tested against statistical evidence; if the “fit” is good enough, one proceeds to carry out the analysis on the basis of the assumed probabilities. Technique in these matters may become quite sophisticated and difficult.
We shall touch only briefly at a few points on the problem of determining empirically the correct probabilities to assume. For the most part, we shall assume that in any given problem it is possible to arrive at reasonable values for the required probabilities. We devote most of our attention—in so far as we attempt to solve problems—to the matter of determining other probabilities implied by these assumptions. We may rely on intuition, experience, or just exploratory guesses to obtain the basic probabilities. We shall be concerned, however, to formulate our problems so that it is plain what probabilities and what conditions among events are assumed. It is desirable to make these assumptions as simple and as natural as possible, and they should be stated in such a way that their validity is most easily tested against experience and judgment based on experience.
In this section we present an auxiliary model which serves as an aid in grasping the essential features of the basic mathematical model for probability. This auxiliary model provides concrete imagery to aid in thinking about the patterns and relations that exist in the abstract model. A probability measure has been characterized as a completely additive, nonnegative set function. Such measures seem to be somewhat strange and remote from the ordinary experience of life. As a matter of fact, the concept of measure arose in dealing with quite familiar physical and geometrical quantities. In our ordinary physical experience, we are quite familiar with several important quantities which may be represented by functions of this type.
At the most elementary level is the concept of the volume of a region in space. The set is the set of geometrical points usually taken to represent such regions. Volume is a number associated with such a set; it is nonnegative, and the volume of the combination (union) of any finite number of nonoverlapping regions is the sum of the volumes of the separate regions. For analytical purposes, it is usually assumed that this additivity extends to countably infinite combinations.
In a similar manner we may consider the mass located in a region of space. Again, the set is the set of geometrical points representing the region. A nonnegative number called the mass is associated with each such set of points. The mass in any two nonoverlapping (i.e., disjoint) regions is the sum of the masses in the two regions. This is the additivity property, which is usually assumed in physical theory to extend to masses in any countable infinity of nonoverlapping regions.
Mass may be viewed as continuously distributed. In such a situation, the mass associated with any region consisting of a single point is zero. But sets of points with positive volume may have nonzero masses. In addition to continuously distributed masses, there may be mass concentrations in the neighborhood of a point or along a line or over a surface; these may be idealized into point masses, line distributions of mass, or surface distributions of mass.
A similar concept is that of the electric charge in a region in space. The physical picture is similar to that of mass, except that the charge may be negative as well as positive.
The mathematical concepts corresponding to these physical concepts and, in fact, abstracted from them are:
1. Measure as a nonnegative, completely additive set function. In physical expressions, the basic space is the euclidean space, which is an idealization of physical, geometrical space. The more general mathematical model has been obtained by extending the domain of the measure function to abstract spaces, in which ordinary geometrical concepts of volume, continuity, and the like are not applicable. The essential patterns are, for the most part, those which are encountered in representations of ordinary physical situations.
2. Signed measure, which is the extension of the concept of measure obtained by removing the restriction to nonnegative values. It serves as the mathematical model of the classical concept of charge, when the space is euclidean. But mathematically, the space may be quite abstract, as in the case of ordinary measure functions.
A probability measure P(·) is a measure function on an abstract space. It is characterized by the fact that the value assigned to the whole space S is unity. If the space S is visualized as a set of points in ordinary physical space, as in the case of Venn diagrams, the probability of any event (set) may be visualized as a mass associated with the set of points. The total mass has unit value.
This physical picture is quite valid and serves as an important means of visualizing abstract relationships. To make the physical picture quite concrete, one may think of the Venn diagram as consisting of a thin sheet of material of variable density. When a set of points is determined by marking out a region, the mass associated with this region coincides with the usual physical picture. Thus, if probability is viewed as mass, we have a concrete physical picture of the abstract concept of a probability measure.
We shall frequently appeal to the mental image of probability as mass by referring to the probability mass associated with a given set of points corresponding to a specified event. We may exploit this conceptual image as an aid in visualizing or even discovering abstract relations. When the relations so visualized are precisely formulated, their validity may be established without dependence upon the geometrical picture. However, the construction of an analytical proof is often aided by proper mental visualization.
It should be apparent that a wide variety of mass distributions are possible on any given basic space. This is precisely in keeping with the fact that many probability measures may be defined on the same basic space. In order to illustrate the usefulness of the mass picture, we consider an important special class of probability systems.
Discrete probability spaces
In many investigations, only a finite number of outcomes of a trial have nonzero probabilities; these probabilities total to unity. In such a case, the probability mass is concentrated at a finite number of points on the basic space. For purposes of probability theory, any other points in the basic space may be ignored, so that the basic space is considered to be a finite space. In other investigations, the number of outcomes may be extended to a countable infinity of possibilities, with probabilities concentrated on a discrete set of points in the basic space. Such discrete probability spaces are quite important in applications.
We consider a basic space S which has a finite or countably infinite number of elements. Then S = {i: i ∈ J}, where J is a finite or countably infinite index set. As the class of events 
, we take the class of all subsets of S. We note that if S is finite with N elements,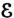 
has 2N sets as members. It is easy to see that this is a completely additive class.
In order to complete the probability space (or system), it is only necessary to assign a probability function. This is done by the simple expedient of associating with each point i in the space a probability mass pi. Strictly speaking, the probability mass is to be associated with the elementary event {i} rather than with the elementary outcome i, but this need cause no confusion. To each event (i.e., to each subset of the basic space) is associated the probability mass carried by the totality of the points in the set. The sum of the pi must be unity, and each number pi must be nonnegative (in fact, we often assume each pi to be strictly positive). It is sometimes helpful to consider the basic space as a collection of balls. Each ball has an appropriate mass. An event corresponds to an appropriate subcollection, or subset, of the balls. The probability of an event A is the total mass assigned to the balls in that subset. Since the mass of all the balls in the whole collection corresponding to the basic space is unity, the mass associated with the event A is equal to the fraction of the total mass assigned to the balls in the subset.
Example 2-4-1
The best-known example of such a space is the classical probability model, for which J = {1, 2, …, N} and pi = 1/N. The number of elements n(A) in an event A is the number of elements n(JA) in its index set JA. The probability assigned to any event A is, in these terms, P(A) = n(JA)/N = n(A)/N.
Example 2-4-2
Consider the results of throwing a pair of dice. Suppose (1) the dice are not distinguished and (2) that only the sum of the numbers of spots appearing is of interest. The possible numbers appearing are the integers 2 through 12. It is convenient to think of each of these as corresponding to one of the elements 2, 3, …, 12. The index set J consists of the integers 2 through 12. The elementary event {7}, for example, is the event that a seven is thrown. To each of these elementary events can be assigned the probabilities calculated from the classical model, under the usual assumptions. Thus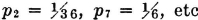 
etc. When these numbers are determined (or assumed), the probability measure P(·) is defined for all subsets of the basic space.
The foregoing example is of some interest because it shows that there may be no unique mathematical model for a given situation. The classical model could have been used for this situation. In fact, we derived the present model from the classical case. For some purposes, however, the model just described is the more convenient to use.
We may summarize once more the model we have developed in the following table.
Much of the success of the mathematical theory of probability is made possible by an extension of the basic model to include the idea of conditional probability. As we have developed the theory, a basic set S of possible outcomes is assumed. It frequently occurs, however, that one has information about a trial which assures the occurrence of a particular event E. If this condition exists, the set of possible outcomes is in effect modified and one would change his point of view in assessing the “chances” of the occurrence of an event A. If it is given that the event E must occur (or has occurred), the only possible elementary outcomes are those which are in the set E. Thus, if the event A occurs, the elementary outcome chosen must be in both A and E; that is, the event A E must occur. In such a situation, how should probabilities be assigned?
Again we may turn to the concept of relative frequency for the pattern to be incorporated into the mathematical model. If the outcome of a trial is to be conditioned by the requirement that the event E must occur, one would often be interested in the relative frequency of occurrences of the event A among the outcomes for which E also occurs. Suppose in a large number n of trials the event E occurs nE times; and suppose that among those trials resulting in the event E the event A also occurs nA E times. The number nA E is the number of occurrences of the joint event A E. The relative frequency of interest is nA E/nE. For sufficiently large n, we should expect this ratio to lie close to some ideal number, which we call the conditional probability of the event A, given the event E. Now we note that the relative frequency of occurrence of event E is fE = nE/n and that of event A E is fA E = nA E/n. Simple algebra shows that
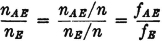
Since the relative frequency fA E is expected to lie close to the probability P(A E) and the relative frequency fE is expected to lie close to the probability P(E), the ratio nA E/nE should lie close to the ratio P(A E)/P(E).
Fig. 2-5-1 Diagram indicating the interpretation of conditional probability in terms of the mass picture.
On the basis of this argument, it would seem natural to introduce into the mathematical model the concept of conditional probability in the following manner:
Definition 2-5a
If E is an event with positive probability, the conditional probability of the event A, given E, written P(A|E), is defined by the relation
The analytical reason for requiring P(E) > 0 is evident from the definition. Generally, when we write a conditional probability, we shall assume tacitly that the conditioning event has positive probability. For any fixed E with positive probability, it is apparent that P(·|E) is a function defined for every event A.
We may examine this function in terms of the mass picture for probability. Suppose E is any fixed event with positive probability, as represented on the Venn diagram of Fig. 2-5-1. This event has assigned to it probability mass P(E). The event A E has assigned to it probability mass P(A E). The conditional probability of A, given E, is thus the fraction of the probability mass assigned to event E which is also assigned to event A. The probability P(A), on the other hand, is the fraction of the total probability mass (assigned to the sure event S) which is assigned to event A. In this regard, we note that
In fact, we require only that P(E) = 1 to ensure P(A|E) = P(A). To show that this is not a trivial observation, we must await further development of the theory.
On the basis of the mass picture, a number of properties of the conditional probability function P(·|E) are readily visualized. The conditional probability of an event is a nonnegative number which never exceeds unity. It must have the value 1 when A = S. Also, the conditional probability function must have the additivity property. This fact may be verified by the following analytical argument, although it should be apparent from the mass picture:
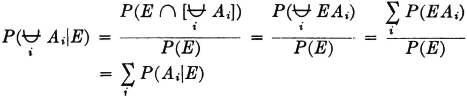
The properties just noted are precisely the fundamental properties (P1), (P2), and (P3) which characterize a probability measure; therefore we conclude that a conditional probability function is a probability measure. As such, the conditional probability measure must have all the properties common to other probability measures. In addition, it has special properties which follow from the fact that it is derived from the original probability measure P(·). In order to distinguish between the original probability measure P(·) and the conditional probability measure P(·|E), we shall refer to P(·) as a total probability measure and to its values as total probabilities.
Since a conditional probability is in fact a probability measure, it is sometimes difficult to know from a statement of a problem whether the total probability or a conditional probability is to be determined. In fact, in formulating a real-world problem it is not always clear which probability should be obtained to answer the question actually posed by the real-world situation. The following example presents such a dilemma.
Example 2-5-1
Three of five prisoners are to be shot. Their names are selected by drawing slips of paper from a hat. Prisoner 1 has figured the odds on his being selected. He then persuades the guard to point out one of the persons (other than himself) whose name has been chosen. Prisoner 3 is designated. Prisoner 1 then proceeds to recalculate his chances of being among those selected for execution. What probability does he calculate? Does the information that 3 is to be shot give him grounds for more hope that he will escape a similar fate?
SOLUTION The classical situation of equally likely choices is assumed for the selection process. We let A1 be the event prisoner 1 will be shot and A3 be the event prisoner 3 will be shot. It is apparent that the first probability calculated (before knowledge of the occurrence of event A3) is P(A1). Event A1 can occur in C24 ways, since this is the number of ways two objects can be chosen from among four (the fifth one having been fixed). The total number of selections of the three prisoners is C35. Hence, using the classical model, we have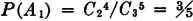 
. Once the fact of the occurrence of A3 is known, the question arises: What probability should serve as the basis of estimating the prisoner’s chances of being shot? Some would argue that nothing has been changed about the selection by the knowledge that A3 has occurred. Such an argument would suppose that P(A1) is the proper probability to use. A second possible argument is that since A3 has occurred, it is the event A1A3 that is of interest; thus the desired probability is P(A1A3). This may be calculated to be 
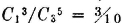. The third point of view—and the one most commonly taken in applications—argues that knowledge of the occurrence of A3 in effect sets up a new basic space. Thus the desired probability is P(A1|A3). This may be calculated as follows:
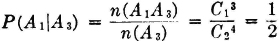
On the basis of this probability, prisoner 1 would be justified in having a little more hope for escape than before he learned of the fate of prisoner 3. This approach has been criticized on the ground that it is meaningless or improper to deal with the event A3. It is argued that some assumption must be made (or knowledge obtained) as to how the guard decides to tell prisoner 1 that prisoner 3 is to be shot. If, as is customary, it is assumed that the prisoner knows that the guard has selected at random from among the prisoners to be shot, after eliminating number 1 if present, then we have a different conditioning event B3. Under the usual assumptions about the meaning of “at random,” this gives
Under this condition, knowledge of the occurrence of B3 does not change the likelihood of A1, interpreted as probability conditioned by the information given. We are thus confronted with a second critical issue in formulating the problem. Exactly what information is given; hence, what conditioning event is determined? When clarity on this point is attained and a decision as to which probability is meaningful is reached, the purely mathematical problem posed admits of an unambiguous solution.
The defining relation for conditional probability may be rewritten as a product rule
P(A E) = P(E)P(A|E)
This rule may be extended to the case of the joint occurrence of three or more events in the following way:
We assume, of course, that P(A1) > 0 and P(A1A2) > 0, so that the conditional probabilities are defined. By a simple inductive argument, it is easy to extend the result to any finite number n of events. We thus have
As an illustration of the use of the product rule, consider the following example. There are several ways in which the solution might be carried out; the method chosen demonstrates the usefulness of the product rule (CP1).
Suppose a jar contains two white balls and three black balls. The balls are drawn from the jar and placed on the table in the order drawn. What is the probability that they are drawn in the order white, black, black, white, black?
SOLUTION
Let Wi be the event that the ith ball drawn is white
Bi be the event that the ith ball drawn is black (Bi = Wic)
By (CP1),
P(W1B2B3W4B5) = P(W1)P(B2|W1)P(B3|W1B2)P(W4|W1B2B3)P(B5|W1B2B3W4)
On the first choice, there are two white balls and three black balls, as shown in Fig. 2-5-2a. We therefore assume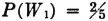 
. The situation for the second choice, given that the first choice resulted in drawing a white ball (i.e., given W1), is that there is one white ball and three black balls, as shown in Fig. 2-5-2b. It is natural to assume 
. Conditions for the third and fourth choices are shown in Fig. 2-5-2, leading to the assumptions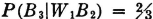 
and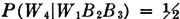 
. The final choice, under the conditions given, is the drawing of a black ball from one black ball. The conditional probability P(B5|W1B2B3W4) must be unity. Substitution of these values in the formula above gives the desired probability value of 
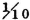. It may be noted that this result is consistent with one based on the classical probability model, where the result is determined by a careful counting of the ways the five balls could be chosen to satisfy the desired conditions.
Use of the product rule makes possible an extension of the basic strategy discussed in Sec. 2-3. There it is pointed out that a standard technique is to express an event as the disjoint union of events whose probabilities are known or which can be obtained from the assumed data. This strategy may be extended in many cases in the following way. The event of interest is expressed as the disjoint union of events, each of which is the intersection of one or more events. The probabilities are calculated by use of the product rule of conditional probability and then the additivity rule. We may illustrate this technique with the following:
Fig. 2-5-2 Basis for assumption of the values of conditional probabilities in Example 2-5-2. (a) First choice: 
; (b) second choice, given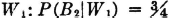 
; (c) third choice, given 
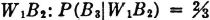: (d) fourth choice, given 
.
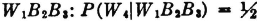A university is seeking to hire two men for positions on its faculty. One is an experienced teacher who is a leader of research in his field. The second is a young man just completing his graduate work in the field of the older man’s competence. His interest in accepting the position is conditioned by the decision of the older man, with whom he would like to work. It is estimated that there is a 50–50 chance that the older man will accept the offer. It is estimated that if the older man accepts the offer, there is a 90–10 chance that the younger man will do likewise; but if the experienced man declines the offer, the chances are reduced to about 40–60 that the younger man will accept the offer. What is the probability that the younger man will accept the offer? What is the probability that both men will accept the offer?
SOLUTION The problem is amenable to the application of probability theory only if the estimates of the “chances” are taken to be estimates of probabilities. Suppose we let A be the event that the experienced man will accept a position and B be the event that the younger man will accept the offer of a position. The estimates of chances are taken to be estimates of probabilities, as follows:
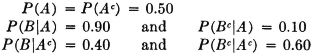
The problem is to find P(B) and P(AB).
We are concerned with the event B as conditioned by A or Ac. Now it is plain that B = BA BAc; that is, the occurrence of event B will be accompanied either by the occurrence of A or by the nonoccurrence of A. The possibilities are mutually exclusive. Hence
By the rule (CP1), we may write
Also
The specific pattern utilized in the preceding example is frequently encountered. It may be generalized by applying the product rule (CP1) to each term of the expansion in property (P8), in order to obtain the following important expansion:
(CP2) Let = {Bi: i ∈ J} be any countable class of mutually exclusive events, each with positive probability. If the occurrence of the event A implies the occurrence of one of the Bi (i.e., if 
), then
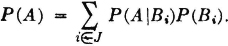
If the class is a partition, then the occurrence of any event A implies the occurrence of one of the Bi; in this case, the expansion is always applicable.
Example 2-5-4
Suppose in the problem of drawing the colored balls, posed in Example 2-5-2, it is desired to determine the probability P(B3) that the third ball drawn is a black one.
SOLUTION We may easily verify the fact that the class {W1W2; W1B2, B1W2, B1B2} is a partition. We may therefore use (CP2) to write
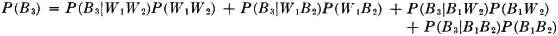
As before, we assume
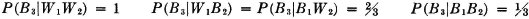
Also,
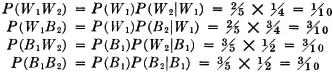
From this, it follows that 
. This result, also, is consistent with the usual result based on the classical model.
When the disjoint class in the statement of property (CP2) is a partition, the expansion is sometimes referred to as an average probability. On any trial, one of the events Bi must occur. For each such event, the conditional probability P(·|Bi) is a probability measure. The sum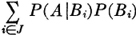 
can be considered a probability-weighted average of the various conditional probabilities of the event A. It is in this sense that the term average probability is used occasionally. Unfortunately, some writers do not make clear that the probabilities being “averaged” are in fact conditional probabilities.
The next example illustrates an interesting use of the expansion in property (CP2) and develops an important result.
Example 2-5-5 Random Coding
In information theory the concept of random coding has played an important role in developing certain theoretical expressions for bounds on the probability of error in decoding messages sent over noisy channels. In this theoretical approach, codes are chosen at random from a large set of possible codes. The message is encoded and decoded according to the code chosen. Let E be the event of an error in the random coding scheme, and let Ci be the event that the ith code is chosen. Note that {Ci: i ∈ J} is a partition, since one and only one code is chosen on each trial. By (CP2) we have
P(E|Ci) is the probability (conditional) of making an error if the ith code is used. P(E) is the average error of decoding over all the possible codes (in the sense discussed above). Now let Ja be the index set defined by
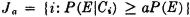
The event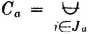 
is the event of choosing a code such that the conditional probability of an error, given that code, is greater than a times the average probability P(E). We wish to show that P(Ca) ≤ 1/a; that is, the probability of picking a code which gives a probability of error more than a times the average is no greater than 1/a.
SOLUTION We note first that 
. The following string of inequalities is justified by various basic properties and the condition defining Ja.
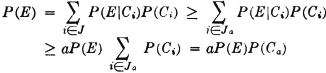
Dividing through by aP(E) gives the desired result.
When the disjoint class is a partition, property (CP2) may be viewed in another manner. If one begins with the conditional probability measures P(·|Bi) and the probabilities P(Bi), these may be combined according to (CP2) to give the total probability measure P(·). It frequently occurs that one makes calculations of the probabilities of various events and then realizes that he has assumed as a condition the occurrence of some specific event E. He has, in effect, restricted his set of allowed outcomes by the condition of the occurrence of E. Thus the probabilities are values of the conditional probability measure P(·|E). This causes no difficulty, since P(·|E) is a probability measure and obeys all the rules for such functions. In fact, as we discuss later in this section, further conditioning events may be introduced into the conditional probabilities, and these may be handled in the same manner as that by which ordinary conditional probabilities are derived from the total probability.
Suppose P(A|E) has been determined, with 0 < P(E) < 1. How may P(A) be determined? By property (CP2), we could use the partition {E, Ec} to get
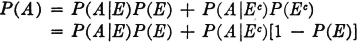
Thus, to determine P(A), we need P(E) and P(A|Ec), or the equivalent, say, P(Ec) and P(A Ec). It may be helpful to consider these results with the aid of Fig. 2-5-1 and the interpretation of conditional probabilities as fractions of the mass assigned to the conditioning event E. If it should turn out that P(E) = 1, a simpler situation exists. In this case we have already noted that P(·|E) = P(·).
It frequently occurs that conditional probabilities are given in one direction but the conditional probabilities in the other direction are desired. That is, we may have the conditional probability P(A|B) available from information about a system, whereas it is the conditional probability P(B|A) which is desired. This reversal is possible in the following general situation, in which we may utilize property (CP2) to give
(CP3) Bayes’ rule. Let = {Bi: i ∈ J} be any countable class of mutually exclusive events, each with positive probability. Let A be any event with positive probability such that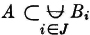 
. Then
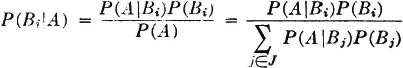
Note once more that the inclusion relation is automatically satisfied for any event A if the disjoint class is a partition. This rule is the celebrated Bayes’ rule, which has been the subject of much controversy in the historical development of probability theory. Because of misunderstanding (and misapplication) of this rule, it has often been suspect. It appears here as a logically derived implication of the probability model and is thus perfectly valid within the limitations of that model.
As a very simple example of the application of Bayes’ rule, we consider a problem which arises in many situations. We state the problem in a typical manner, which once more points to the need for distinguishing total probabilities and conditional probabilities.
Example 2-5-6
Two boxes on an electronics service bench contain transistors. Box A has two good and two defective transistors. Box B has three good and two defective units. One transistor is selected at random from box A and transferred to box B. One transistor is then selected at random from box B; it is tested and found to be good. What is the probability that the transistor transferred from box A to box B was good?
SOLUTION AND DISCUSSION As the question is posed, it is not clear what probability is asked for. If we let G1 be the event that the transistor moved from box A to box B was good and let G2 be the event that the transistor chosen on the second selection was good, three possible probabilities could be of interest here: P(G1), P(G1|G2), or P(G1|G2). From the point of view of the mathematical model, all three may be calculated. From the point of view of the real-world problem, one must decide which probability is the one desired. We shall suppose that the probability of interest is P(G1|(G2). Further, we shall suppose that in making a “random choice” of a transistor, the selection of any transistor in the box is “equally likely.” With the aid of the diagrams in Fig. 2-5-3, where defective transistors are shown as dark balls and good transistors are shown as white balls, we make the following assumptions:
Fig. 2-5-3 Distribution of good transistors (white balls) and defective transistors (dark balls) for Example 2-5-6. (a) Original situation; (b) situation after transfer of a good transistor; (c) situation after transfer of a defective transistor.
We note that the conditions of the problem lead naturally to the assumption of values for P(G2|G1) and P(G2|G1c). It is desired to reverse the first of these. This may be done in the following manner, which amounts to applying Bayes’ rule.
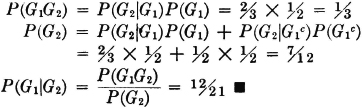
An example of some interest is provided by the following situation in communication theory.
Example 2-5-7
A noisy communication channel is transmitting a signal which consists of a binary coded message; i.e., the signal is a sequence of 0’s and 1’s. Noise acts upon one transmitted symbol at a time. A transmitted 0 or a 1 may or may not be perturbed into the opposite symbol in the process of transmission. Physical details of the process may be quite complicated, but in many cases it seems reasonable to suppose that probabilities of error (i.e., of a signal reversal) may be assigned. Let A be the event that a 1 is sent and let B be the event that a 1 is received at a certain time. Suppose that the following conditional probabilities may be assigned:
Suppose, moreover, that P(A) = p so that P(Ac) = 1 − p. These probabilities are essentially those determined at the sending end. Thus, to evaluate P(Bc|A), one would send 1’s and note how often they are perturbed in transmission. The process of reception must work from the receiving end. Thus, when a 1 is received, it is desired to know P(A|B) and P(Ac|B). Similarly, when a 0 is received, it is desired to know P(A|Bc) and P(Ac|Bc). Suppose we wish to know the value of P(A|Bc); that is, we wish to know what is the conditional probability that a 1 is sent, given that a 0 is received.
By Bayes’ rule (CP3),
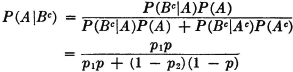
Similar calculations serve to evaluate the other conditional probabilities. Note that the denominator of the fraction is P(Bc), from which P(B) is easily determined, so that it is relatively simple to invert the other conditional probabilities.
A very similar problem is posed by the question of the reliability of a safety device or of a test for a dangerous condition.
Example 2-5-8
A safety device (or test for a dangerous condition) is designed to have a high conditional probability of operating (or indicating) when a failure (or dangerous condition) occurs and a high conditional probability of not operating (not indicating) when a failure (or dangerous condition) does not occur. Suppose F is the event that there is a failure and W is the event that the safety device works. Put P(W|F) = p and P(Wc|Fc) = q. It is desired to make p and q as near unity as possible. Suppose that P(F) = pF, which is normally assumed small. Note that these conditional probabilities are based on given knowledge of the event of a failure. What is really desired is the conditional probability of a failure, given that the safety device has or has not operated.
Again, by Bayes’ rule (CP3), we have
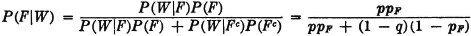
It is instructive to put in some numerical values. If we put pF = 0.001 and p = q = 0.98, we obtain
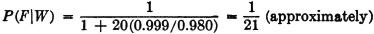
Although it is assumed that the safety device works 98 times in 100, the conditional probability of a failure given that the device operates is only 1 in 21. This seems to be a strange result. Note, however, that P(FWc) = (1 − p)pF = 2 × 10−5. The probability of simultaneous failure and nonoperation of the safety device is extremely small. On the other hand, P(FcW) = (1 − q)(1 − pF) = 0.02, so that the probability of operation of the safety device when there is no failure is approximately 
.
In the case of a test for a dangerous condition, it would be desirable to have P(F|W) as high as possible. It is instructive to consider the conditions required to make P(F|W) larger. The expression above may be rewritten
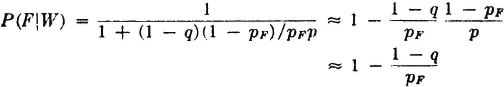
The first approximation assumes
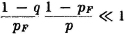
The second approximation is based on the assumption that 1 − pF and p are both quite close to unity, so that the ratio is also. To make P(F|W) approach unity, we must have 1 − q 
pF; that is, we must have P(W|Fc) P(F).
The effect on the probability of the occurrence of the event A produced by the knowledge that the event E must occur is incorporated into the mathematical model by means of the concept of the conditional probability of A, given E. The latter is derived from the total probability measure by taking the ratio of the probability mass P(A E) to the probability mass P(E). The receipt of additional information that event F has occurred also may be expected to modify further the conditional probability of the occurrence of event A. The new conditional probability, given the occurrence of both E and F, may be derived from the conditional probability given E, in the same manner that the latter is derived from the total probability. As a first step toward examining this fact, let us take note of a product rule closely related to property (CP1) and, in fact, derived therefrom.
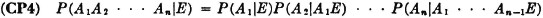
This may be derived by writing out the expansion (CP1) for the probability P(EA1A2 · · · An) and dividing both sides of the equation by P(E).
We may interpret this result with the aid of a hybrid notational scheme for conditional probabilities. The conditional probability P(·|E) is often written PE(·). This, as we have shown, is a true probability measure [derived, of course, from the total probability measure P(·)]. As a special case of (CP4), we may write P(AF|E) = P(F|E)P(A|EF). This may be rewritten
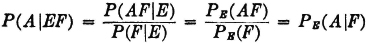
We thus have a sort of “conditional” conditional probability. The form used indicates that P(A|EF) is derived from the conditional probability measure P(·|E) = PE(·) by the same process that P(·|E) is derived from the total probability measure P(·). “Higher-order” conditional probabilities can be derived in similar fashion. For example,
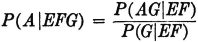
Using the hybrid notation, we may write
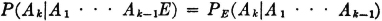
Also, we may rewrite (CP4) as follows:
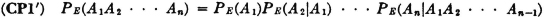
This form emphasizes the fact that in some sense (CP4) is an analog to (CP1). In fact, if E = S, this reduces to (CP1).
We may obtain analogs to (CP2) and (CP3). First, we obtain
(CP5) Let = {Bi: i ∈ J} be any finite or countably infinite class of mutually exclusive events, each with positive probability. If the occurrence of the event A E implies the occurrence of one of the Bi (i.e., if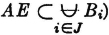 
), then
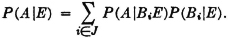
To see this we note from previous properties that
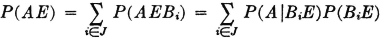
Dividing through by P(E) gives the desired result. Utilizing the hybrid notation once more, we may rewrite the expression to give
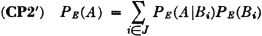
which is an analog to (CP2). A similar argument produces a Bayes’ rule (CP3′) for the conditional probability PE(·|Bi). We are thus able to operate with conditional probabilities with respect to further conditioning events in the same manner that we operate with total probabilities and conditional probabilities derived therefrom.
A variety of special results in particular circumstances may be derived with techniques similar to those utilized above. As a further illustration, we consider an analytical example that is of some interest in connection with the idea of independence, to be introduced in the next section.
Suppose {Bi: i ∈ J} is a finite or countably infinite disjoint class whose union is the event B. Suppose P(Bi) > 0 and P(A|Bi) = p for each i ∈ J. Show that P{A|B) = p.
SOLUTION The problem may be understood in terms of the mass picture. P(A|Bi) is the ratio of that part of the mass assigned to the common part of A and Bi to the mass assigned to Bi. If the ratio is the same for each part Bi of B, the ratio for that portion of the mass assigned to A and the union of the Bi to the mass assigned to the whole union must be the same. The result can be obtained analytically by the following argument.
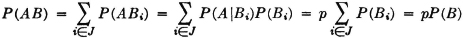
Dividing through by P(B) gives the desired result.
The concept of independence in probability theory, to which we turn attention in this section, has played an indispensable role in the development of the mathematical theory. The notion of independence in the physical world is one that is intuitively grasped but which is not precisely defined. Events are considered to be physically independent when they seem to have no causal relation. In order to develop a satisfactory mathematical counterpart of this vaguely formulated idea, we must identify a precise mathematical condition which seems to correspond to the condition of independence in the real world. Since there is no necessary logical connection between a concept introduced into the mathematical model and a (hopefully) corresponding one in the real world of physical phenomena, it is desirable to distinguish the real-world concept from the mathematical counterpart. It is customary to speak of stochastic independence when it is desired to emphasize that the probability concept is intended. Ordinarily, however, we simply speak of independence and know that, in dealing with a probability model, stochastic independence is intended.
Let us consider two events A and B, each with positive probability. We should probably be willing to consider these as independent events if the occurrence of one did not “condition” the probability of the occurrence of the other. Thus we should consider them independent if P(A|B) = P(A) or P(B|A) = P(B). It is easy to show that either of these equalities implies the other. Using the definition of conditional probability, we may express these equalities in the following manner:
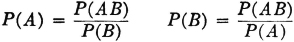
The two relationships may be combined into a single product relation
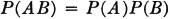
It would appear that independence may be characterized by this product rule.
Next, let us consider a simple physical situation in which the events under consideration would be judged to be independent in a physical sense.
Example 2-6-1
Suppose two ordinary dice are thrown. In observing the results, we distinguish between the dice. Let Ai be the event that the first die shows face number i (i = 1, 2, …, 6) and Bj the event that the second die shows face number j. On the classical assumption of equally likely outcomes, the events Ai and Bj and the joint event AiBj have the following probabilities:
Hence we have the product relation P(AiBj) = P(Ai)P(Bj).
Implicit in the assumption of equally likely outcomes is the notion that the outcome of the throw of the first die does not affect the outcome of the throw of the second die, and conversely. For any result of the throw of the first die, the various possibilities of the outcome of the throw of the second die are unaffected, i.e., are “equally likely.”
The condition that one outcome does not affect the other may be considered in terms of the relative frequency of occurrence of events in a large number n of trials of an experiment. Suppose nA is the number of these outcomes which result in the event A, with similar notation for the numbers of occurrences of other events. Under what condition would we be willing to say that events A and B do not affect one another physically? It seems natural to suppose that the occurrence of the event B does not affect the occurrence of the event A if the fraction of the occurrence of A among the occurrences of B is the same as the fraction of the occurrences of A among the nonoccurrences of B. That is, we suppose the occurrence of the event B does not affect the occurrence of the event A if
These results may be translated into relative frequencies as follows:
For large n it is supposed that the relative frequencies lie close to the corresponding probabilities. Hence, in the case of physical independence, we should expect the probabilities to satisfy the following conditions:
These are equivalent to the product rules
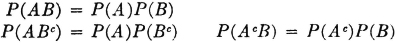
As we shall show in Theorem 2-6A, below, any one of these implies the other two.
On the basis of these arguments, it would seem promising to make the following
Definition 2-6a
Two events A and B are said to be (stochastically) independent iffi the following product rule holds:
P(AB) = P(A)P(B)
We emphasize that in this mathematical definition stochastic independence is characterized by a product rule. The definition is motivated by intuitive notions of physical independence, and we shall show that many of the mathematical consequences of this definition are readily interpreted in terms of ordinary notions of independence in the real world of phenomena. In fact, we may often anticipate mathematical conditions and relations related to stochastic independence by an appeal to intuitive notions based on physical experience. It must be kept firmly in mind, however, that to establish the independence of two events in the stochastic or probabilistic sense one must show that the product rule holds (or that some rule proved to be equivalent to it holds).
In the argument above, it may be noted that if A and B are physically independent events, so are A and Bc, Ac and B, and Ac and Bc. The following theorem shows that this pattern is preserved in the mathematical model.
Theorem 2-6A
If any one of the pairs {A, B}, {A, Bc}, {Ac, B}, or {Ac, Bc} is an independent pair, then all the pairs are independent pairs.
PROOF To establish independence we must establish the appropriate product rules. First we note that
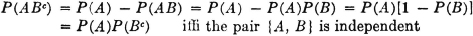
By interchanging the role of A and B in the previous argument, we obtain P{AcB} = P(Ac)P(B) iffi {A, B} is an independent pair. On replacing B by Bc, we may use the last result to assert P(AcBc) = P(Ac)P(Bc) iffi {A, Bc} is an independent pair. But this pair is independent iffi {A, B} is independent.
The argument leading up to the definition of independence presumes that the events under consideration have positive probabilities. This is because conditional probabilities or probability ratios are used. The formulation of the condition in terms of the product rule allows the removal of this restriction. In fact, it is almost trivially true that the impossible event and the sure event S are independent of any other events (including themselves). We may formalize this in the following.
Theorem 2-6B
Any event A is independent of the impossible event 0 and the sure event S.
PROOF
There is a constant tendency to confuse the idea of mutually exclusive events and the idea of independent events. The following theorem shows that these are quite different concepts.
Theorem 2-6C
If A and B are mutually exclusive events and each has positive probability, they cannot be independent; if they have positive probabilities and are independent, they cannot be mutually exclusive.
PROOF Under the hypothesis, P(A)P(B) > 0. The events can be mutually exclusive only if P(AB) = 0. Either the product rule does not hold or the events are not mutually exclusive.
This result, which frequently surprises the beginner, may be understood by realizing that if A and B are mutually exclusive, occurrence of the event A implies the occurrence of Bc and the occurrence of B implies the occurrence of Ac. Thus the occurrence of one of these events very definitely “conditions” the occurrence of the other.
We should note at this point that the independence condition must be introduced into any model problem as an assumption. As we have noted, independence is not precisely defined in the real world of phenomena. And by the very nature of a mathematical model, a condition in the real world does not imply logically a condition in a mathematical model; nor does a mathematical condition imply a real-world condition. The experiential basis for an independence assumption is usually the knowledge that the events to be represented in the mathematical model are physically independent in some appropriate sense. Where statistical examination of the result of a large number of trials is possible, one would check the appropriate product relations for the relative frequencies of occurrences. In introducing independence assumptions into the mathematical model for any problem, one should be guided by two basic considerations.
1. Assumptions should be made in a form most easily checked by physical experience. These are not always the simplest forms mathematically. One of the tasks of the theorist is to find equivalent forms of the assumptions which are more useful for work with the mathematical model.
2. Care should be taken to reduce the assumptions to a practical minimum and to ascertain the consistency of the assumptions made. Superfluous assumptions require unnecessary physical checks and introduce the risk of actual contradictions in assumed conditions. Again, it is the role of the theoretical investigator to determine what assumptions are really required in order that the model problem may be properly stated.
Before very much can be done with the idea of independence, it is necessary to extend the notion to classes of more than two events. Since the independence concept has been introduced in terms of a product rule, it seems natural to consider the possibility of extending it in these terms. As a first step we could consider the case in which the product rule applies to each pair of distinct members of the class. This condition is usually referred to as pairwise independence. While there are applications in which this condition is sufficient, experience has shown that a much more general extension is desirable. We shall simply state the more general condition and examine some of its mathematical consequences. The justification of the concept must lie in the nature of these consequences.
Definition 2-6b
A class of events = {Ai: i ∈ J), where J is a finite or an infinite index set, is said to be an independent class iffi the product rule holds for every finite subclass of .
We may state the defining condition analytically as follows: if J0 is any finite subset of the index set J, then
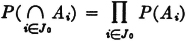
It should be emphasized that this product rule must hold for any, and hence every, finite subclass. As a simple example to illustrate the independence condition, we consider
The class {A, B, C} is independent iffi the following all hold:
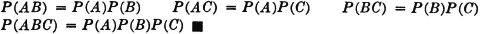
The following example shows that pairwise independence is not sufficient to guarantee independence of the whole class.
Example 2-6-3
Let {A1, A2, A3, A4} be a partition with each 
. Put
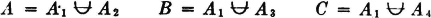
Then the class {A, B, C} has pairwise independence, but is not an independent class, as the following calculations show.
SOLUTION
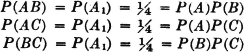
However,
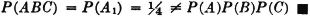
On the other hand, validity of the product rule for the entire class does not ensure its holding for subclasses. The following example illustrates this fact.
Example 2-6-4
Consider four events A, B, C, and D, satisfying the following conditions:
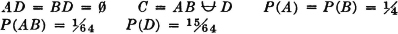
The product rule applies to the class {A, B, C}, but no two of these events are independent.
SOLUTION The relationships between the events and their probabilities are indicated in the Venn diagram of Fig. 2-6-1. It is apparent that
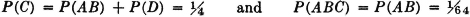
We have, therefore, P(ABC) = P(A)P(B)P(C). On the other hand, no two of the events are independent.
It should be noted that independence is a function of the probability measure and is not, except in special cases, a property of the events.
We have seen, in Sec. 2-5, that the product rule for conditional probabilities opens up possibilities for computing the probabilities of compound events. The product rule for independent events plays a similar role, augmented by the fact that the rule for independent events is inherently simpler than the product rule for conditional probabilities.
Fig. 2-6-1 Venn diagram for the events in Example 2-6-4. Probabilities are shown in parentheses.
As a simple example, we return to a consideration of the serial systems in reliability theory discussed briefly in Example 2-3-2.
Example 2-6-5 Serial Systems in Reliability Theory
As in the discussion in Example 2-3-2, we let A be the event of a success of the entire system and let Ai be the event of the success of the ith subsystem. A serial system is characterized by the condition
That is, the entire system operates successfully iffi all subsystems operate successfully. In many systems, the success or failure of any subsystem is not appreciably affected by the success or failure of any other subsystem. In such a case, it is natural to assume that the Ai are independent events. To be precise, we assume that the class = {Ai: 1 ≤ i ≤ n} is an independent class. This really is a model of the fact that the operation of any combination of the subsystems is not dependent upon the operation of any combination of other subsystems. Under the independence assumption, we have a simple formula for reliability of the whole system:
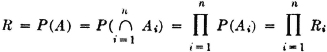
The reliability of the entire system is the product of the reliability factors for the various subsystems. Suppose, for example, there are 10 subsystems, each with reliability 0.99 = 1 − 0.01. The reliability of the entire system is (1 − 0.01)10. Since (1 − x)n ≈ 1 − nx, for small x, the reliability of the complete system is approximately 0.90.
Example 2-6-6 Parallel Systems in Reliability Theory
A second elementary type of system in reliability theory is the so-called parallel system. Such a system is characterized by the fact that the system operates if any one or more of the subsystems operate. Utilizing the notation of the previous example, we have
In the case of independent operation, we assume the class of events = {Ai: 1 ≤ i ≤ n) to be an independent class. In order to be able to use the product rule, we may use the rules on complements to obtain the following expression:
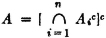
Now it seems reasonable to suppose (as we shall show in Theorem 2-6F, below) that the class ′ = {Aic: 1 ≤ i ≤ n} is also an independent class. In this case, we have
Translated into terms of the reliability factors, this becomes
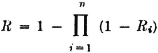
Again, we may use some numbers to get a feel for this relation. Suppose there are two subsystems, each with reliability 0.90. Then the system reliability is 1 − 0.102 = 1 − 10−2 = 0.99.
The figures in the preceding two examples illustrate the general fact that reliability of a serial system is generally smaller than that of any subsystem while the reliability of a parallel system is generally larger than that of any subsystem.
The definition for independent classes is stated for infinite as well as finite classes. It is important to note that even in the case of infinite classes, only finite subclasses need be considered. For reference, we state the essential fact in the following
Theorem 2-6D
A class of events is an independent class iffi every finite subclass consisting of two or more members is an independent class,
This is an obvious consequence of the definition.
We may reformulate the definition of an independent class in a useful manner, which we illustrate by the following analytical example.
Suppose {A, B, C, D, E} is an independent class of events. Then the following classes, among others, are independent classes: {ABC, E}, {AC, BE, D}, {B, C, DE}.
What we have done here is to select finite subclasses of the original class in such a way that no two of the subclasses have any member event in common. We have taken the intersections of the members of the various subclasses to form new events. These new events then are collected in a new class. It should be apparent—and the fact may easily be examined in detail—that the product rule holds for each newly formed class of events. On the other hand, if the product rule should hold for every such new class formulated in this manner, it must surely hold for the original class {A, B, C, D, E}. The pattern indicated here may be generalized into the following
Theorem 2-6E
Suppose = {Ai: i ∈ I} is any class of events. Let {j: j ∈ J} be a family of finite subclasses of such that no two have any member event Ai in common. Let Bj be the intersection of all the sets in j. Put = {Bj: j ∈ J}. Then is an independent class iffi every class so formed is an independent class.
Theorems 2-6A and 2-6B may be combined and interpreted in the following way. If {A, B} is an independent pair, we may replace either or both of the members by 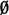, S, or the complement of the member and still have an independent pair. It would seem reasonable to suppose that this pattern could be extended to larger independent classes. For instance, we should suppose the following assertions to be true:
Example 2-6-8
If = {A, B, C, D} is an independent class, so also are the classes {A, Bc, Cc, Dc}, {A, Bc, C, }, {S, B, , Dc}, etc.
In order to verify this, it is just about as easy to develop the general theorem as to deal with the special case.
Theorem 2-6F
If = {Ai: i ∈ J} is an independent class, so also is the class ′ obtained by replacing the Ai in any subclass of by either , S, or Aic. The particular substitution for any given Ai may be made arbitrarily, without reference to the substitution for any other member of the subclass.
PROOF By Theorem 2-6D, it is sufficient to show the validity of the theorem for any arbitrarily chosen (and hence for every) finite subclass. We may argue as follows:
1. We may replace any single Aj in the finite class under consideration by its complement Ajc, by , or by S. By Theorems 2-6A and 2-6B, the product rule still holds if such a replacement is made.
2. Suppose j1, j2, …, jm is any sequence of indices where replacements are to be made. Suppose replacements have been made for all indices up to jr, and the independence of the modified class is preserved. Then an argument parallel to argument 1 shows that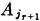 
may be replaced.
By mathematical induction, all members of the sequence may be replaced. Because of the arbitrariness of the sequence and of the finite subclass considered, the theorem is established.
This theorem allows considerable freedom in dealing with independent classes. It may be convenient to express independence in terms of a class of events; yet, for purposes of calculations, independence is needed in terms of the complements of at least some of the events in the class. We have already encountered such a situation in dealing with parallel reliability systems in Example 2-6-6. In this case we replaced each event in an independent class by its complement. We consider another such case in the next example, which also illustrates a basic strategy in probability calculations.
Example 2-6-9 Independent Trials
Suppose three independent tests are made on a physical system. Let A1 be the event of a satisfactory outcome on the first test, A2 on the second test, and A3 on the third test. We suppose these events are independent in the sense that the class {A1, A2, A3} is an independent class. Suppose P(Ai) = pi and P(Aic) = 1 − pi = qi. What is the probability of exactly two successful tests?
SOLUTION If C is the event of exactly two successes in the three tests, then it follows that
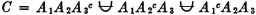
We have considered all the possible combinations of two successes and one failure. The terms in the union are disjoint, since we cannot have exactly one failure in the ith place and also exactly one failure in the jth place (i ≠ j). We have thus expressed the event C as the disjoint union of intersections of events whose probabilities are known. By Theorem 2-6F, the classes {A1, A2, A3c}, {A1, A2c, A3}, and {A1c, A2, A3} are independent classes for which the product rule holds. Utilizing the additivity property and the product rule, we have
It should be noted that we have used the same basic strategy employed in the section on conditional probability. We have expressed the event whose probability is desired as the disjoint union of intersections of events whose probabilities are known. The product rule for independent events is simpler in character and is therefore easier to use than the product rule for conditional probabilities. We shall employ this strategy frequently in dealing with independent events.
We next consider an example in which we study a slight variation of the game discussed in Example 2-3-1. The analysis further illustrates the basic strategy of expressing an event as the disjoint union of intersections of independent events whose probabilities are known. In this case, the number of events to be considered is countably infinite.
Example 2-6-10
Two men spin a roulette wheel alternately, each attempting to get one of several numbers which he has specified. The first man has probability p1 of spinning one of his numbers any time he spins. The second man has probability p2 of spinning one of his numbers. The results of the trials are assumed to be independent. The first man who succeeds in spinning one of his numbers wins the game. Determine the probability of each man’s winning. If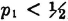 
, show what value p2 must have to make the probabilities of winning equal.
SOLUTION Each elementary outcome consists of a sequence of trials, which may not be limited in length. We may consider each sequence to be of infinite length. The elementary outcomes can be described, however, in terms of the results at any given trial in the sequence. We let Ai be the set of those outcomes in which the first man turns up one of his numbers on the ith spin. Since the men spin alternately, it is apparent that Ai = 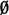(is impossible) for even values of i. Similarly, we let Bj be the event the second man spins one of his numbers on the jth trial. It follows that Bj = 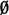for odd values of j. The independence condition is taken to mean that the Ai and Bj form an independent class. We assume P(A2k−1) = p1 and P(B2k) = p2 for k = 1, 2, …. For convenience, we put q1 = 1 − p1 and q2 = 1 − p2. Now we let A be the event the first man wins and B be the event the second man wins. We must find appropriate ways to express A and B, in order that the information provided may be utilized. A little thought shows that the first man wins if he spins his number on the first trial, or spins it on the third after failure of both on the first and second, etc. It is obvious that these are mutually exclusive possibilities. This can be expressed in symbols, as follows:
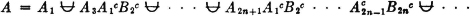
Event B can be expressed in a similar manner, as follows:
By virtue of Theorem 2-6F and the assumed independence condition, we may apply the product rule to each of the intersection terms. This gives for event A
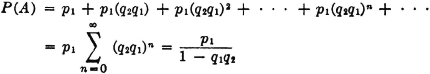
Here we have made use of the well-known expansion
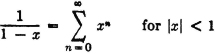
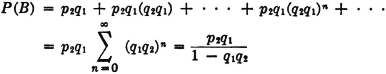
In order to make the probabilities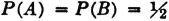 
, we must have p1 = q1p2 so that
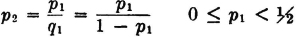
For 
, we should need p2 > 1, which is impossible. For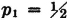 
, we should require p2 = 1, which makes it practically certain that the first man either wins on his first spin or he loses. It is interesting to note that P(A) + P(B) = 1, as may be shown by a little algebra. Since AB = , we must have S = A B AcBc. We cannot say that AcBc is empty, for there is at least one sequence for which neither man wins (i.e., there is at least one ∈ AcBc). It is true, however, that P(AcBc) = 0.
This example shows that while we can always assert that P() = 0, the fact that P(E) = 0 does not imply that E = . In such a case, however, E would be considered practically impossible, and it would ordinarily be ignored in considering events that could occur.
We consider next a pattern that frequently occurs in the theoretical examination of independence conditions. First we take a simple case.
Example 2-6-11
Suppose event A can occur in one of three mutually exclusive ways and event B can occur in one of two mutually exclusive ways. We have A = A1 A2 A3 and B = B1 B2. If the Ai and Bj are pairwise independent for each possible choice of i and j, then the events A and B are independent.
SOLUTION We first note that
Because of the additivity property
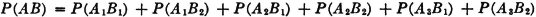
Because of the independence condition
Simple algebraic manipulations yield
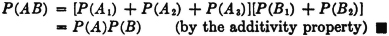
This result does not depend upon the small finite number of events Ai and Bj. The general pattern is expressed in the following
Suppose = {Ai: i ∈ I} and = {Bj: j ∈ J} are finite or countably infinite disjoint classes whose members have the property that any Ai is independent of any Bj, that is, that P(AiBj) = P(Ai)P(Bj) for any i ∈ I and j ∈ J. Then the events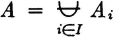 
and 
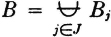are independent
PROOF
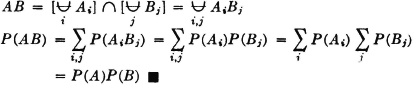
Further generalizations can be made by considering several disjoint classes, say, , , , 
, whose unions are A, B, C, D, respectively. If for any Ai ∈ , Bj ∈ , Ck ∈ , Dh ∈ we have {Ai Bj, Ck, Dh} is an independent class, then the class {A, B, C, D} is an independent class. Some notational skill but no new ideas are needed to establish such results.
The following example is of some interest in providing an illustration of typical methods in establishing independence. The conclusion is an immediate consequence of the result in Example 2-5-9, but we present the essentials of the analytical argument.
Example 2-6-12
Suppose {Bi: i ∈ J} is a partition and that P(A|Bi) = p for each i ∈ J. Then A is independent of each Bi and P(A) = p.
SOLUTION
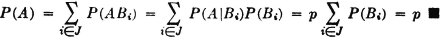
We shall return to the topic of independence in Sec. 2-8. First we shall consider, in the next section, some techniques for systematic handling of compound events which greatly facilitate the handling of both specific examples and general results.
