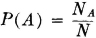
As is true of so much of mathematics, probability theory has a long history whose beginnings are largely unknown or obscure. In this chapter we examine very briefly the classical concept of probability which arose in early investigations and which still remains the basis of many applications. It seems reasonably certain that the principal impetus for the development of probability theory came from an interest in games of chance. Interest in gambling is ancient and widespread; games of chance involve an element of “randomness”; it is, in fact, puzzling that the idea of randomness and the attempt to describe it mathematically did not develop earlier. David [1962] discusses this cultural enigma in an interesting study of the early gropings toward a theory of probability and of the early work in the field.
The rudiments of a mathematical theory probably took shape in the sixteenth century. Some evidence of this is provided by a short note written in the early seventeenth century by the famous mathematician and astronomer Galileo Galilei. In a fragment known as Thoughts about Dice Games, Galileo dealt with certain problems posed to him by a gambler whose identity is not now known. One of the points of interest in this note (cf. David [1962, pp. 65ff.]) is that Galileo seems to assume that his reader would know how to calculate certain elementary probabilities.
The celebrated correspondence between Blaise Pascal and Pierre de Fermat in 1654, the treatise by Christianus Huygens, 1657, entitled De Ratiociniis in Aleae Ludo, and the work Ars Conjectandi by James Bernoulli (published posthumously in 1713, but probably written some time about 1690) are landmarks in the formulation and development of the classical theory. The fundamental definition of probability which was accepted in this period, vaguely assumed when not explicitly stated, remained the classical definition until the modern formulations developed in this century provided important extensions and generalizations.
We shall simply examine the classical concept, note some of its limitations, and try to identify the fundamental properties which underlie modern axiomatic formulations. It turns out that the key properties are extremely simple. All the results of the classical theory are obtained as easily in the more general system which we study in this book. Because of the success of the more general system, we shall not examine separately the extensive mathematical system developed upon the classical base. For such a development, one may consult the treatise by Uspensky [1937].
The interest in games of chance which stimulated early work in probability not only provided the motivation for that work but also influenced the character of the emerging theory. Almost instinctively, it seems, the best minds attempted to analyze the probability situations into sets of possible outcomes of a gaming operation. These possibilities were then assumed to be “equally likely.” The success of the analysis in predicting “chances” led eventually to the precise definition of probability, which remained the classical definition until early in the present century.
Definition 1-1a Classical Probability
A trial is made in which the outcome is one of N equally likely possible outcomes. If, among these N possible outcomes, there are NA possible outcomes which result in the occurrence of the event A, the probability of the event A is defined by
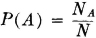
This definition seems to be motivated by two factors:
1. The intuitive idea of equally likely possible outcomes
2. The empirical fact of the statistical regularity of the relative frequencies of the occurrence of events to be studied
The statistical regularity of the relative frequencies of the occurrence of various events in gambling games has long been observed. In fact, some of the problems posed to noted mathematicians were the result of small variations of observed frequencies from those anticipated by the gamblers (David [1962, pp. 66, 89]). The character of the games was such that the notion of “equally likely” led to successful predictions. So natural did this concept seem that it has been defended vigorously upon philosophical grounds.
Once the definition is made—for whatever reasons—no further appeal to intuition or philosophy is needed. A situation is given; two questions must be answered :
1. How many possible outcomes are there (i.e., what is the value of N)?
2. How many of the possible outcomes result in the occurrence of event A (i.e., what is the value of NA)?
Once these questions are answered, the probability is determined by the ratio specified in the definition. The problem is to determine answers to these two questions. This, in turn, is a problem of counting the possibilities.
Consider a simple example. Two dice are thrown. Suppose the event A is the event that “a six is thrown.” This means that the pair of numbers which appear (in the form of spots) must add to six. What is the probability of throwing a six? First, we must identify the equally likely possible outcomes. Then we must perform the appropriate counting operations. If the dice are “fair,” it seems that it is equally likely that any one of the six sides of either of the dice will appear. It is thus natural to consider the appearance of each of the 36 possible pairs of sides of the two dice as equally likely. These various possibilities may be represented simply by pairs of numbers. The first number, being one of the integers 1 through 6, represents the corresponding side of one of the dice. The second number represents the corresponding side of the second die. Thus the number pair (3, 2) indicates the appearance of side 3 of the first die and of side 2 of the second die. The sides are usually numbered according to the number of spots thereon.
We have said there are 36 such pairs. For each possibility on the first die there are six possibilities on the second die. Thus, for the rolling of the dice, we take N to be 36. To determine NA, we may in this case simply enumerate those pairs for which the sum is 6. These are the pairs (1, 5), (2, 4), (3, 3), (4, 2), and (5, 1). There are five such outcomes, so that NA = 5. The desired probability is thus, by definition, 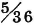 .
.
It should not be assumed from the simple example just discussed that probability theory is trivial. Counting, in complex situations, can be a very sophisticated matter, as references to the literature will show (cf. Uspensky [1937] or Feller [1957]). Much of the classical probability theory is devoted to the development of counting techniques. The principal tool is the theory of permutations and combinations. A brief summary of some of the more elementary results is given in Appendix A. An excellent introductory treatment is given in Goldberg [1960, chap. 3]; a more extensive treatment is given in Feller [1957, chaps. 2 through 4].
Upon this simple base a magnificent mathematical structure has been erected. Introduction of the laws of compound probability and of the concepts of conditional probability, random variables, and mathematical expectation have provided a mathematical system rich in content and powerful in its application. As an example of the range of such theory, one should examine a work such as the classical treatise by J. V. Uspensky [1937], entitled Introduction to Mathematical Probability. So successful was this development that Uspensky could venture the opinion that modern attempts to provide an axiomatic foundation would result in interesting mental exercises but would have little value for application [op. cit., p. 8].
The classical theory suffers some inherent limitations that inhibit its applications to many problems. Moreover, the success of modern mathematical models in extending the classical theory has provided a more flexible base for applications. Thus it seems desirable, both for applications and for purely mathematical investigations, to move beyond the classical model.
There are two rather obvious limitations of classical probability theory. For one thing, it is limited to situations in which there is only a finite set of possible outcomes. Very simple situations arise, even in classical gambling problems, in which a finite set of possibilities is not adequate. Suppose a game is played until one player is successful in performing a given act (i.e., until he “wins”). Any particular sequence of plays is likely to terminate in a finite number of trials. But there is no a priori assurance that this will happen. A man could conceivably flip a coin indefinitely without ever turning up a head. At any rate, no one can determine a number large enough to include all possible sequences ending in a successful toss. Other simple gaming operations can be conceived in which the game goes on endlessly. In order to account for these possibilities, there must be a model in which the possibilities are not limited to any finite number.
It is also desirable, both for theoretical and practical reasons, to extend the theory to situations in which there is a continuum of possibilities. In such situations, some physical variable may be observed: the height of an individual, the value of an electric current in a wire, the amount of water in a tank, etc. Each of the continuum of possible values of these variables is to be considered a possible outcome.
A second limitation inherent in the classical theory is the assumption of equally likely outcomes. It is noted above that the classical theory seems to be rooted in the two concepts of (1) equally likely outcomes and (2) statistical regularity of relative frequencies. It often occurs that these two concepts do not lead to the same definition. A simple example is the loaded die. For a die which is asymmetrical in terms of mass or shape, it is not intuitively expected that each side will turn up with equal frequency; as a matter of fact, both experience and intuition agree that the relative frequencies will not be the same for the different sides. But it is expected that the relative frequencies will show statistical regularity. Experience bears this out in many situations, of which the loaded die is a simple example.
These considerations suggest that the extension of the definition of probability should preserve the essential characteristics of relative frequencies. Two properties prove to be satisfactory for the extension:
1. If fA is the relative frequency of occurrence of an event A, then 0 ≤ fA ≤ 1.
2. If A and B are mutually exclusive events and C is the event which occurs iffi (if and only if) either A or B occurs, then fC = fA + fB.
In the next chapter we begin the development of a theory which defines probability as a function of events; the characteristic properties of the probability function are (1) that it takes values between zero and one and (2) that it has a fundamental additivity property for the probability of mutually exclusive events.
The idea of the relative frequency of the occurrence of events plays such an important role in motivating the concept of probability and in interpreting the meaning of the mathematical results that some competent mathematicians have developed mathematical models in which probability is defined as a limit of a relative frequency. This approach has the advantage of tying the fundamental concepts closely to the experiential basis for the introduction of the theoretical model. It has the disadvantage, however, of introducing certain complications into the formulation of the basic definitions and axioms.
It seems far more fruitful to postulate the existence of probabilities which have the simple fundamental properties discussed above. When these probabilities are interpreted as relative frequencies, the behavior of the mathematical model can be compared with the behavior of the physical (or other) system that it is intended to represent. The frequency interpretation is aided by the development of certain theorems known under the generic title of the law of large numbers. The high degree of correlation between suitable models based on this approach and the observed behavior of many practical systems have provided grounds for confidence in the suitability of such models. This approach is based philosophically on the view that one cannot “prove” anything about the physical world in terms of a mathematical model. One constructs a model, studies its “behavior,” uses the results to predict phenomena in the “real world,” and evaluates the usefulness of his model in terms of the degree to which the behavior of the mathematical model corresponds to the behavior of the real-world system. “The proof is in the pudding.” The growing literature on applications in a wide variety of fields indicates the extent to which such models have been successful (cf. the article by S. S. Shu in Bogdanoff and Kozin [1963] for a brief survey of the history of applications of probability theory in physics and engineering).
Because of these considerations, we do not attempt to examine the theory constructed upon the foundation of the classical definition of probability; instead, we turn immediately to the more general model. Not only does this general theory include the classical theory as a special case; it is often simpler to develop the more general concepts—in spite of certain abstractions—and then examine specific problems from the vantage point provided by this general approach. More elegant solutions and more satisfactory interpretations of problems and solutions are often obtainable with a smaller total effort.
DAVID [1962]: “Games, Gods, and Gambling.” This interesting work deals with “the origins and history of probability and statistical ideas from the earliest times to the Newtonian era.” A readable treatment, with many interesting personal and historical sidelights. The author has a keen interest in the history of ideas as well as in the development of the technical aspects of probability theory in its early stages.
FELLER [1957]: “An Introduction to Probability Theory and Its Applications,” vol. 1, 2d ed. An introduction and an extensive treatment of probability theory in the case of a finite or countably infinite number of possible outcomes. Chapters 2, 3, and 4 provide a rather extensive treatment of the problem of counting the ways an event can occur.
GOLDBERG [1960]: “Probability: An Introduction.” A lucid treatment of the modern point of view, which is mathematically easy because the author deals only with the case of a finite number of possible outcomes. Chapter 3 provides an excellent introduction to the theory of permutations and combinations needed for many probability problems, both in the classical and in the more general case.
USPENSKY [1937]: “Introduction to Mathematical Probability.” A classical treatment of classical probability. This work is still a major reference for many aspects of the mathematical theory and its applications, although its author takes a dim view of the modern axiomatic model which the present work attempts to expound. Available in a paperback edition, it probably should be on the bookshelf of any person having a serious interest in probability theory.