An equivalent condition for independence

We have seen that P_X(·), P_Y(·), and P_XY(·) are determined uniquely by specifying values for sets M_t, N_u, and M_t × N_u, respectively. From the product rule it follows immediately that if X(·), Y(·) form an independent pair, then for each real t, u we have P_XY(M_t × N_u) = P_X(M_t)P_Y(N_u). It is also known that if this condition ensures the product rule P_XY(M × N) = P_X(M)P_Y(N) holds for all M × N where M and N are Borel sets. Thus we have

Theorem 3-7B

Any two real-valued random variables X(·) and Y(·) are independent iffi, for all semi-infinite, half-open intervals M_t and N_u, defined above,

By definition, the latter condition is equivalent to the condition

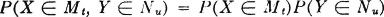
for all such half-open intervals.

To examine independence, then, it is not necessary to examine the product rule with respect to all Borel sets, but only with those special sets which are the semi-infinite, half-open intervals. In fact, we could replace the semi-infinite, half-open intervals with semi-infinite, open intervals or even with finite intervals of any kind.

Independence and joint distributions

Theorem 3-7B can be translated immediately into a condition on the distribution functions for independent random variables. Since

and

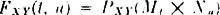
the independence condition becomes the following product rule for the distribution functions: F_XY(t, u) = F_X(t)F_Y(u) for each pair of real numbers t, u. If the joint and marginal density functions exist, the rules of differentiation for multiple integrals show that this is equivalent to the product rule f_XY(t, u) = f_X(t)f_Y(u) for the density functions. Thus we have the important

Theorem 3-7C

Two random variables X(·) and Y(·) are independent iffi their distribution functions satisfy the product rule F_XY(t, u) = F_X(t)F_Y(u).

    If the density functions exist, then independence of the random variables is equivalent to the product rule f_XY(t, u) = f_X(t)f_Y(u) for the density functions.

In the discrete case, as we have already established, the independence condition is p(i, j) = p(i, *)p(*, j). This could be considered to be a limiting situation, in which the probability masses are concentrated in smaller and smaller regions, which shrink to a point. The analytical expressions above, in terms of distribution or density functions, simply provide an analytical means for expressing the mass distribution property for independence.

Independent approximating simple functions

The problem of approximating random variables by simple random variables is discussed in Sec. 3-3. If X(·) and Y(·) are two independent random variables, and if X_i(·) and Y_j(·) are approximating simple random variables, formed in the manner discussed in connection with Theorem 3-3A, we must have independence of X_i(·) and Y_j(·). This follows easily from the results obtained in Example 3-7-2. The inverse image X_i⁻¹({t_r}) for any point t_r in the range of X_i(·) is the inverse image X⁻¹(M) for an appropriate interval; the inverse image Y_j⁻¹({u_s}) for any point u_s in the range of Y_j(·) is the inverse image Y⁻¹(N) for an appropriate interval. These must be independent events.

As a consequence of these facts, we may state the following theorem:

Theorem 3-7D

Suppose X(·) and Y(·) are independent random variables, each of which is nonnegative. Then there exist nondecreasing sequences of nonnegative simple random variables {X_n(·): 1 ≤ n < ∞} and {Y_m(·): 1 ≤ m < ∞} such that

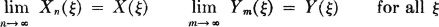
and

{X_n(·), Y_m(·)} is an independent pair for any choice of m, n

This theorem is used in Sec. 4-4 to develop an important property for integrals of independent random variables.

Independence of vector-valued random variables

Many results on the independence of real-valued random variables may be extended to the case of vector-valued random variables. The essential ideas of the proofs are usually quite similar to those used in the real-valued case, but are complicated by notational requirements for stating the relationships in higher dimensional space. We state two results for a pair of vector-valued random variables.

Let Z(·) and W(·) be vector-valued random variables with coordinate variables X_i(·), 1 ≤ i ≤ n, and Y_j(·), 1 ≤ j ≤ m, respectively. Let Z_*(·) and W_*(·) be random vectors whose coordinates comprise subclasses of the coordinate variables for Z(·) and W(·), respectively.

Theorem 3-7E

If Z(·), W(·) form an independent pair of random vectors, then Z_*(·), W_*(·) is an independent pair.

This follows from the fact that Z_*(·) is measurable 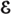(Z) and W_*(·) is measurable 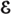(W). This result holds in the special case that Z_*(·) and W_*(·) may each consist of only one coordinate, and thus be real-valued.

Theorem 3-7F

If the coordinate random variables for Z(·) and W(·) together form an independent class of random variables, then Z(·), W(·) is an independent pair.

The proof of this theorem involves ideas similar to those used for establishing Theorem 3-7B in the real-valued case.

It should be apparent that these two theorems may be extended to the case of more than two random vectors.

3-8 Functions of random variables

It frequently occurs that it is desirable to consider not the random variable observed directly, but some variable derived therefrom. For example:

1. X(·) is the observed value of a physical quantity. When a value t is observed, the desired quantity is t², the square of the directly observed quantity.

2. Suppose X(·) and Y(·) are random variables which are the diameters and lengths of cylindrical shafts manufactured on an assembly line. When is such that X() = t and Y() = u, the number (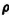π/4)t²u is the weight of the shaft.

3. Suppose X_k(·), k = 1, 2, …, 24, is the hourly recorded temperature in a room, throughout a single day. If values t₁, t₂, …, t₂₄ are observed, the number

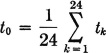
is the 24-hour mean temperature.

It is natural to introduce the

Definition 3-8a

If g(·) is a real-valued function of a single real variable t, the function Z(·) = g[X(·)] is defined to be the function on the basic space S which has the value v = g(t) when X() = t.

    Similarly, for two variables, if h(·, ·) is a real-valued function of two real variables t, u, the function Z(·) = h[X(·), Y(·)] is the function on the basic space which has the value v = h(t, u) when the pair X(·), Y(·) have the values t, u, respectively.

The extension to more than two variables is immediate. The function of interest in example (1) is Z(·) = X²(·); that in example (2) is Z(·) = (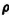π/4)X²(·)Y(·); and that in example (3) is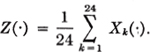

Before referring to a function of a random variable as a random variable, it is necessary to consider the measurability condition; i.e., it is necessary to show that Z⁻¹(M) is an event for each Borel set M. In order to see what is involved, we consider the mapping situation set up by a function of a random variable, as diagramed in Fig. 3-8-1. Figure 3-8-1a shows the direct mappings produced in the case of a single variable. The random variable X(·) maps into t on the real line R₁. The function g(·) maps t into v on the real line R₂. The resultant is a single mapping from into v, which is the mapping characterizing the function Z(·) = g[X(·)]. Figure 3-8-1b represents the inverse mappings. If M is any set in R₂, its inverse image N = g⁻¹(M) is the set of points in R₁ which are mapped into M by the function g(·). The set E = X⁻¹(N) is the set of those which are mapped into N by the random variable X(·). But these are precisely the which are mapped into M by the composite mapping. Thus Z⁻¹(M) = X⁻¹(N) = X⁻¹[g⁻¹(M)]. It is customary to indicate the last expression more simply by X⁻¹g⁻¹(M).

The function Z(·) = g[X(·)] is a random variable if g(·) has the property that g⁻¹(M) is a Borel set in R₁ for every Borel set M in R₂.

Fig. 3-8-1 (a) Direct mappings and (b) inverse mappings associated with a function of a single random variable.

Definition 3-8b

Let g(·) be a real-valued function, mapping points in the real line R₁ into points in the real line R₂. The function g(·) is called a Borel function iffi, for every Borel set M in R₂, the inverse image N = g⁻¹(M) is a Borel set in R₁. An exactly similar definition holds for a Borel function h(·, ·), mapping points in the plane R₁ × R₂ into points on the real line R₃.

The situation for functions of more than one variable is quite similar. The joint mapping from the basic space, in the case of two variables, is to points on the plane R₁ × R₂. The second mapping v = h(t, u) carries a point t, u in the plane into the point v on the real line, as illustrated in Fig. 3-8-2. If h(·, ·) is Borel, so that the inverse image Q of any Borel set M on R₃ is a Borel set on the plane, then the inverse image E of the Borel set Q is an event in the basic space S. Thus, the situation with respect to measurability is not essentially different in the case of two variables. For functions of more than two variables, the only difference is that the first mapping must be to higher-dimensional euclidean spaces.

These results may be summarized in the following

Theorem 3-8A

If W(·) is a random vector and g(·) is a Borel function of the appropriate number of variables, then Z(·) = g[W(·)] is a random variable measurable 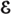(W).

It is known from more advanced measure theory that if Z(·) is an 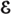(W)-measurable random variable, then there is a Borel function g(·) such that Z(·) = g[W(·)].

The class of Borel functions is sufficiently general to include most functions encountered in practice. For this reason, it is possible in most applications to assume that a function of one or more random variables is itself a random variable, without examining the measurability question. Suppose g(·) is continuous and there is a countable number of intervals on each of which g(·) is monotone; then g(·) is a Borel function, since the inverse image of any interval is a countable union of intervals and hence a Borel set.

The mappings for a function of a single random variable produce probability mass distributions on the lines R₁ and R₂, as indicated in Fig. 3-8-1b. The assignments are according to the scheme Distribution on R₁ by X(·):

Distribution on R₂ by Z(·) = g[X(·)]:

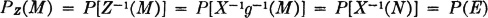
Fig. 3-8-2 Mappings and probability mass distributions for a function of two random variables.

Thus the probability mass distributions on the two real lines are related by the expression

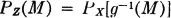
The situation for two random variables is shown on Fig. 3-8-2. The joint mapping from the basic space S is indicated by [X, Y](·). Sets M, Q, and E in R₃, R₁ × R₂, and S, respectively, stand in the relation

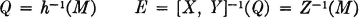
Each of these sets is assigned the same probability mass

It is apparent in later developments that it is sometimes convenient to work with the mass distribution on the plane R₁ × R₂ and sometimes with the distribution on the line R₃. Either course is at our disposal.

Simple random variables

For simple random variables, the formulas for functions of the random variables are of interest. Let X(·) and Y(·) be simple random variables which are expressed as follows:

If g(·) and h(·, ·) are any Borel functions, then g[X(·)] and h[X(·), Y(·)] are given by the formulas

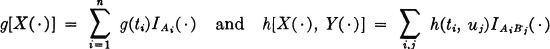
The expansion for g[X(·)] is in canonical form iffi no two of the t_i have the same image point under the mapping v = g(t). This requires that the expansion for X(·) be in canonical form and no two distinct t_i have the same image point. If they do, the canonical form may be achieved by combining the A_i for those t_i having the same image point. Similar statements hold for the expansion of h[X(·), Y(·)].

If the A_i do not form a partition, in general .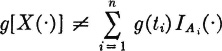

To illustrate this, we consider the following

Example 3-8-1

Suppose g(t) = t², and consider X(·) = 2I_A(·) − I_B(·) + 3I_C(·) with D = AB ≠ 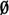, but ABC = 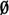. Compare X²(·) with Y(·) = 2²I_A(·) + (−1)²I_B(·) + 3²I_C(·).

SOLUTION For ∈ D, X() = 2 − 1 = 1. X²() = 1. Y() = 4 + 1 = 5 ≠ X² ().

Equality can hold only for very special functions g(·). For one thing, we should require that g(t_i + t_j) = g(t_i) + g(t_i) for any t_i and t_j in the range of X(·).

Independence of functions of random variables

We have defined independence of random variables X(·) and Y(·) in terms of independence of the sigma fields 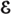(X) and 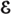(Y) determined by the random variables, with immediate extensions to arbitrary classes of random variables (real-valued or vector-valued). In view of the results on measurability of Borel functions of random variables, the following theorem, although trivial to prove, has far reaching consequences.

Theorem 3-8-B

If {X_i(·): i ∈ J} is an independent class of random variables and if, for each i ∈ J, W_i(·) is 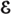(X_i) measurable, then {W_i(·): i ∈ J} is an independent class of random variables.

We give some examples which are important in themselves and which illustrate the usefulness of the previous development.

1. Suppose X(·) and Y(·) are independent random variables and A ∈ 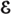(X) and B ∈ 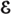(Y). Then I_A(·)X(·) and I_B(·)Y(·) are independent random variables.

2. As an application of (1), let A = {: X() ≤ a} and B = {: Y() ≤ b} Then A and A^c ∈ 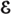(X) and B and B^c ∈ 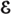(Y). We let X₁(·) = I_A(·)X(·) and X₂(·) = I_A^c(·)X(·), with similar definitions for Y₁(·) and Y₂(·). Then X(·) = X₁(·) + X₂(·) with X₁(·)X₂(·) = 0 and Y(·) = Y₁(·) + Y₂(·) with Y₁(·) Y₂(·) = 0. If X(·) and Y(·) are independent, so also are the pairs {X₁(·), Y₁(·)}, {X₁(·), Y₂(·)}, {X₂(·), Y₁(·)}, and {X₂(·), Y₂(·)}. This decomposition and the resulting independence is important in carrying out a classical argument known as the method of truncation.

3. If X(·) and Y(·) are independent and X_n(·) and Y_m(·) are two approximating simple functions of the kind described in Sec. 3-3, then X_n(·) must be measurable 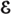(X) and Y_m(·) must be measurable 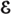(Y), so that X_n(·) and Y_m(·) are independent. This is a restatement of the proof of Theorem 3-7D.

Example 3-8-2

Suppose {X(·), Y(·), Z(·)} is an independent class of random variables. Then U(·) = X²(·) + 3Y(·) and V(·) = |Z(·)| are independent random variables. If W(·) = 2X(·)Z(·), then U(·) and W(·) are not, in general, independent random variables, since they involve a common function X(·).

3-9 Distributions for functions of random variables

We consider first the problem of determining the probability that Z(·) = g[X(·)] takes on values in a given set M when the probability distribution for X(·) is known. In particular, we consider the problem of determining F_z(·), and f_z(·) if it exists, when F_X(·) is known. We then extend the discussion to random variables which are functions of two or more random variables.

We shall develop a basic strategy with the aid of the mechanical picture of the probability mass distribution induced by the random variable X(·), or the joint distribution in the case of several random variables. When the problem is understood in terms of this mechanical picture, appropriate techniques for special problems may be discovered. Often the problem may not be amenable to straightforward analytical operations, but may be handled by approximate methods or by special methods which exploit some peculiarity of the distribution.

Functions of a single variable

Suppose X(·) is a real-valued random variable with distribution function F_X(·), and g(·) is a Borel function of a single real variable. We suppose that the domain of g(·) contains the range of X(·); that is, g(·) is defined for every value which X(·) can assume.

We begin by recalling the fundamental relationship

This may be seen by referring back to Fig. 3-8-1. We thus have the fundamental probability relationship

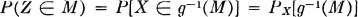
To determine the probability that Z(·) takes a value in M, we determine the probability mass assigned to the t set g⁻¹(M); this is the set of those t which are mapped into M by the mapping v = g(t).

For the determination of the distribution function F_Z(·), we consider the particular sets

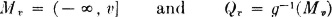
Now

so that

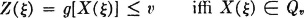
Hence we have as fundamental relationships

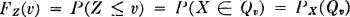
The value of the distribution function F_Z(·) for any particular v can be determined if Q_v can be determined and the probability mass P_X(Q_v) assigned to it can be evaluated. This determination may be made in any manner. We shall illustrate the basic strategy and the manner in which special methods arise by considering several simple examples.

Example 3-9-1

Suppose g(t) = t², so that Z(·) = X²(·). Determine F_Z(·) and f_Z(·).

SOLUTION We note that Z(·) cannot take on negative values, so that F_Z(v) = 0 for v < 0. For nonnegative values of r, F_Z(v) = P(Z ∈ (−∞, v]) = P(Z ∈ [0, v]).

Fig. 3-9-1 Mapping which gives the probability distribution for Z(·) = X²(·).

Now 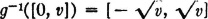. Hence , for v ≥ 0. A single formula can be used if the last expression is multiplied by u₊(v), to make it zero for negative v.

If the distribution for X(·) is absolutely continuous,

and

The essential facts of the argument are displayed geometrically in Fig. 3-9-1. The set M_v = (−∞, v] has the same inverse as does the set 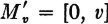, since the inverse image of (− ∞, 0) is 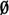; that is, g(·) does not take on negative values. The inverse of 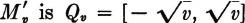for v ≥ 0 and Q_v = 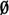for v < 0. The probability mass P_X(Q_v) assigned to this interval for nonnegative v is

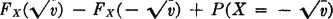
In the continuous case, the last term is zero, since there can be no concentration of probability mass on the real line.

Example 3-9-2

The current through a resistor with resistance R ohms is known to vary in such a manner that if the value of current is sampled at an arbitrary time, the probability distribution is gaussian. The power dissipated in the resistor is given by w = i²R, where i is the current in amperes, R is the resistance in ohms, and w is the power in watts. Suppose R is 1 ohm, I(·) is the random variable whose observed value is the current, and W(·) is the random variable whose value is the power dissipated in the resistor. We suppose

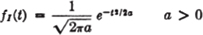
This is the density function for a gaussian random variable with the parameters = 0 and σ² = a (Example 3-4-3). Now W(·) = I²(·), since R = 1. According to the result in Example 3-9-1, we must have

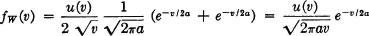
This density function is actually undefined at v = 0. The rate of growth is sufficiently slow, however, so that the mass in an interval, [0, v] goes to zero as v goes to zero. The unit step function u(v) ensures zero density for negative v, as is required physically by the fact that the power is never negative in the simple system under study.

In the case of a discrete random variable X(·), the resulting random variable Z(·) = g[X(·)] is also discrete. In this case it may be simpler to work directly with the probability mass distributions. The following simple example will illustrate the situation.

Example 3-9-3

A discrete positioning device may take the correct position or may be 1, 2, …, n units off the correct position in either direction. Let p₀ be the probability of taking the correct position. Let p_i be the probability of an error of i units to the right; also, let p_i be the probability of an error of i units to the left. In the design of positioning devices, position errors are often weighted according to the square of the magnitude. A negative error is as bad as a positive error; large errors are more serious than small errors. Let E(·) be the random variable whose value is the error on any reading. The range of E(·) is the set of integers running from −n through n. The probability P(E = i) = p_i, with p_−i = p_i. We wish to find the distribution for E²(·), the square of the position error. The result may be obtained with the aid of Fig. 3-9-2. E²(·) has range T = [v_i: 0 ≤ i ≤ n), with v_i = i². We have P(E² = 0) = p₀, and P(E² = i²) = 2p_i for 1 ≤ i ≤ n. The distribution function 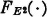may easily be written if desired. The density function does not exist.

The function considered in the next example is frequently encountered. It provides a change in origin and a change in scale for a random variable.

Fig. 3-9-2 Discrete probability distribution produced by the mapping g(t) = t² for the random variable in Example 3-9-3.

Fig. 3-9-3 Density functions for the random variables X(·) and Y(·) = 100X(·) – 1.00 in Example 3-9-5.

Example 3-9-4

Suppose g(t) = at + b, so that Z(·) = aX(·) + b.

DISCUSSION We need to consider two cases: (1) a > 0 and (2) a < 0 (the case a = 0 is trivial).

1. For a > 0,

2. For a < 0, so that a = −|a|,

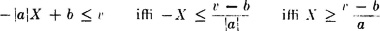
so that

In the absolutely continuous case, differentiation shows that for either sign of a, we have

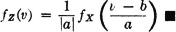
As a simple application, consider the following

Example 3-9-5

A random variable X(·) is found to have a triangular distribution, as shown in Fig. 3-9-3a. The triangle is symmetrical about the value t = 1.00. The base extends from t = 0.99 to 1.01. This means that the values of the random variable are clustered about the point t = 1.00. By subtracting off this value and expanding the scale by a factor of 100, we obtain the random variable Y(·) = 100[X(·) – 1.00]. The new random variable has a density function

The new density function f_Y(·) is thus obtained from f_X(·) by three operations: (1) scaling down the ordinates by a factor 0.01, (2) moving the graph to the left by 1.00 unit, and (3) expanding the scale by a factor of 100. The resulting graph is found in Fig. 3-9-3b.

The function in the following example is interesting from a theoretical point of view and is sometimes useful in practice.

Example 3-9-6

Suppose X(·) is uniformly distributed over the interval [0, 1]. Let F(·) be any probability distribution function which is continuous and strictly increasing except possibly where it has the value zero or one. In this case, the inverse function F⁻¹(·) is defined as a point function at least for the open interval (0, 1). Consider the random variable

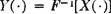
We wish to show that the distribution function F_Y(·) for the new random variable is just the function F(·) used to define Y(·).

SOLUTION Because of the nature of an inverse function

Thus P(Y ≤ a) = P[X ≤ F(a)]. Because of the uniform distribution of X(·) over [0, 1], P[X ≤ F(a)] = F(a). Hence we have F_Y(a) = P(Y ≤ a) = F(a), which is the desired result.

It is often desirable to be able to produce experimentally a sampling of numbers which vary according to some desired distribution. The following example shows how this may be done with the results of Example 3-9-6 and a table of random numbers.

Example 3-9-7

Suppose {X_i(·): 1 ≤ i ≤ n} is an independent class of random variables, each distributed uniformly over the integers 0, 1, …, 9. This class forms a model for the choice of n random digits (decimal). Consider the function

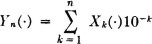
which is a random variable since it is a linear combination of random variables. For each choice of a set of values of the X_k(·) we determine a unique value of Y_n(·) on the set of numbers {0, 10⁻ⁿ, 2.10⁻ⁿ, …, 1-10⁻ⁿ}. The probability of any combination of values of the X_k(·) and hence of any value of Y_n(·) is 10⁻ⁿ, because of the independence of the X_k(·). This means that the graph of 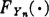takes a step of magnitude 10⁻ⁿ at points separated by 10⁻ⁿ, beginning at zero. Thus, 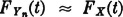, where X(·) is uniformly distributed [0, 1]. If Z_n(·) = F⁻¹[Y_n(·)], then for all real t.

Functions of two random variables

For functions of two random variables X(·) and Y(·), we suppose the joint distribution function F_XY(·, ·) of the joint probability measure P_XY(·) induced on the plane is known. If h(·, ·) is a Borel function of two real variables, we wish to determine the distribution function F_Z(·) for the random variable Z(·) = h[X(·), Y(·)]. The basic attack is the same as in the single-variable case. If

then

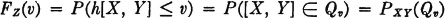
The problem amounts to determining the set Q_v of points (t, u) in the plane R₁ × R₂, for which h(t, u) ≤ v, and then determining the probability mass P_XY(Q_v) assigned to that set of points. Once the problem is thus understood, the particular techniques of solution may be determined for a given problem.

Fig. 3-9-4 Regions Q_v in which h(t, u) ≤ v for several functions h(·, ·). (a) h(t, u) = t + u; (b) h(t, u) = t − u; (c) h(t, u) = tu, v > 0; (d) h(t, u) = tu, v < 0.

We shall use a number of simple examples to illustrate some possibilities. As a first step, we consider the regions Q_v for various values of v and several common functions h(·, ·); these are shown on Fig. 3-9-4. Corresponding regions may be determined for other functions h(·, ·) encountered in practice by the use of analytical geometry.

As a first example, we consider a somewhat artificial problem designed to demonstrate the basic approach.

Example 3-9-8

Suppose h(t, u) = t + u, so that Z(·) = X(·) + Y(·). Determine F_Z(·) when the joint mass distribution is that shown in Fig. 3-9-5a.

SOLUTION By simple graphical operations, the distribution function F_Z(·) shown in Fig. 3-9-5b may be determined. At v = −2, the point mass of 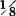is picked up. The continuously distributed mass in the region Q_v increases with the square of the increase in v until the two point masses of 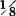each are picked up simultaneously to give a jump of 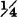at v = 0. Then F_Z(v) must vary as a constant minus the square of the distance from v to the value 2. At v = 2, the final point mass is picked up, to give a jump of 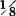. Since all the mass is included in Q₂, further increase in v does not increase F_Z(v).

Example 3-9-9

Suppose X(·) and Y(·) have an absolutely continuous joint distribution. Determine the density function f_Z(·) for the random variable Z(·) = X(·) + Y(·).

SOLUTION

Differentiating with respect to the variable v, which appears only in the upper limit for one of the integrals, we get

We have used the formula 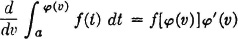. If we make the change of variable t = v − u, for any fixed v, the usual change-of-variable techniques show that we may also write

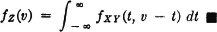
Again we use a simple illustration to demonstrate how the previous result may be employed analytically.

Fig. 3-9-5 A joint mass distribution and the probability distribution function for the sum of two random variables, (a) Joint mass distribution for X, Y; (b) mass distribution function F_Z(·).

Example 3-9-10

Suppose, for the problem posed generally in the preceding example, the joint density function is that shown in Fig. 3-9-6. We wish to evaluate

Fig. 3-9-6 Various probability density functions for Example 3-9-10.

We are aided graphically by noting that the points (t, v − t) lie on a slant line of the as a function of t for fixed v, is a step function. The length of the step is 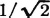times the length of that portion of the slant line in the region of positive density. The integral of this step function is twice the length of the positive part of the step function. This step function is twice the length of the positive part of the step function. This length obviously increases linearly with v for 0 ≤ v ≤ 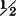; then it decreases linearly with v for 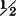≤ v ≤ 1; another cycle is completed for 1 ≤ v ≤ 2. The density function must be zero for v < 0 and v > 2. The resulting function is graphed in Fig. 3-9-6c. The same result could have been obtained by determining the distribution function, as in Example 3-9-8, and then differentiating.

The integration procedure in the preceding two examples can be given a simple graphical interpretation. If the joint density function f_XY(·, ·) is visualized graphically as producing a surface over the plane, in the manner discussed in Sec. 3-6 (Fig. 3-6-2), the value of the integral is 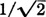times the area under that surface and over the line u = v − t. This is illustrated in Fig. 3-9-7 for the probability distribution, which is uniform over a rectangle. The region under the f_XY surface may be viewed as a solid block. For any given v, the block is sectioned by a vertical plane through the line u = v − t. The area of the section (shown shaded in Fig. 3-9-7) is 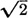times the value of f_Z(v). The simple distribution was chosen for ease in making the pictorial representation. The process is quite general and may be applied to any distribution for which a satisfactory representation can be made.

Fig. 3-9-7 Graphical interpretation of the integral ∫f_XY(t, v − t) dt.

Similar techniques may be applied to the difference of two random variables. The following may be verified easily:

Example 3-9-11

Suppose X(·) and Y(·) have an absolutely continuous joint distribution. The density function f_W(·) for the random variable W(·) = X(·) − Y(·) is given by

If the two random variables X(·) and Y(·) are independent, the product rule on the density functions may be utilized to give alternative forms, which may be easier to work with.

Example 3-9-12

Suppose X(·) and Y(·) are independent random variables, each of which has an absolutely continuous distribution. Let Z(·) = X(·) + Y(·) and W(·) = X(·) − Y(·). Because of the independence, we have

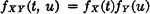
The results of Examples 3-9-9 and 3-9-11 may be written (with suitable change of the dummy variable of integration) as follows:

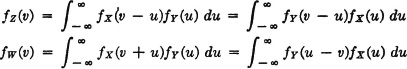
We may integrate these expressions with respect to v from −∞ to t to obtain

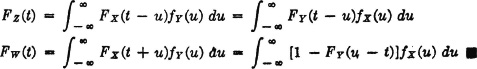
The integrals for f_Z(v) are known as the convolution of the two densities f_X(·) and f_Y(·). This operation is well known in the theory of Laplace and Fourier transforms. Techniques employing these transforms are often useful in obtaining the convolution. Since a knowledge of these transform methods lies outside the scope of this study, we shall not illustrate them. The following example from reliability theory provides an interesting application.

Example 3-9-13

A system is provided with standby redundancy in the following sense. There are two subsystems, only one of which operates at any time. At the beginning of operation, system 1 is turned on. If system 1 fails before a given time t, system 2 is turned on. Let X() be the length of time system 1 operates and Y() be the length of time system 2 operates. We suppose these are independent random variables. The system operates successfully if X() + Y() ≥ t, and fails otherwise. If F is the event of system failure, we have

Experience has shown that for a large class of systems the probability distribution for “time to failure” is exponential in character. Specifically, we assume

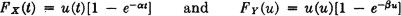
where the unit step functions ensure zero values for negative values of the arguments. This means that f_Y(u) = u(u)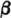e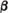^−u. The limits of integration may be adjusted to account for the fact that the integrand is zero for u < 0 or u > t (note that t is fixed for any integration). We thus have

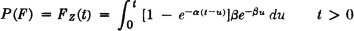
Combining the exponentials and evaluating the integrals, we obtain the result

The corresponding density function is given by

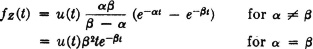
It is interesting to compare the reliability for the standby-redundancy case and the parallel case in which both subsystems operate simultaneously. For the former, we have R = 1 −P(F) = P(X + Y ≥ t). Now for the first subsystem we have R₁ = P(X ≥ t), and for the second subsystem we have R₂ = P(Y ≥ t). The reliability for parallel operation is R_p = P(X ≥ t or Y ≥ t).

The event {X ≥ t} ∪ {Y ≥ t} implies the event {X + Y ≥ t}. Thus R_p ≤ R, by property (P6). We cannot say, however, that the second event implies the first. We may have X() = 2t/3 and Y() = 2t/3, for example. Figure 3-9-8 shows plots of the density functions for the case α = 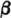. The density functions f_X(·) = f_Y(·) for the subsystems begin at value 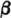for t = 0 and drop to 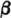/e = 0.37 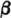at t = 1/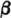. The density function for the sum increases to a maximum value of 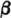/e = 0.37 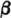at t = 1/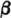. The distribution-function curves, which at any time t give the probability of failure on or before that time, are shown in Fig. 3-9-8b. At t = 1/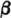, the probability of either subsystem having failed is 1 − 1/e = 0.63. The probability that the standby system has failed is 1 − 2/e = 0.26. The probability that the parallel system has failed is the product of the probabilities that either of the two subsystems has failed; this is (1 − 1/e)² = 1 − 2/e + 1/e² = 0.26 + 0.14 = 0.40.

Fig. 3-9-8 Density and distribution functions for the standby-redundancy system of Example 3-9-13.

Example 3-9-14

If X(·) and Y(·) are independent and both are uniformly distributed over the interval [a, b], the joint distribution is that shown in Fig. 3-9-9a. Use of the methods already discussed in this section shows that the sum Z(·) = X(·) + Y(·) is distributed according to the curves shown in Fig. 3-9-9a and b. The difference W(·) = X(·) − Y(·) has distribution function and density function whose graphs are identical in shape but which are symmetrical about v = 0, with the probability mass in the interval [a − b, b − a]. Note that a < b.

As an application of the result of Example 3-9-14, consider the following situation:

Fig. 3-9-9 Distribution and density for the sum of two uniformly distributed random variables. (a) Joint distribution; (b) distribution function for sum; (c) density function for sum.

Example 3-9-15

In the manufacture of an electric circuit, it is necessary to have a pair of resistors matched to within 0.05 ohm. The resistors are selected from a lot in which the values are uniformly distributed between R₀ − 0.05 ohms and R₀ + 0.05 ohms. Two resistors are chosen. What is the probability of a satisfactory match?

Fig. 3-9-10 Density function for the difference in resistor values in Example 3-9-15.

SOLUTION Let X() be the value of the first resistor chosen and Y() be the value of the second resistor chosen. Let W(·) = X(·) − Y(·). The event of a satisfactory match is {: −0.05 ≤ W() ≤ 0.05}. By Example 3-9-14, the density function for W(·) is that given in Fig. 3-9-10. The desired probability is equal to the shaded areas shown on that figure, which is equal to 1 minus the unshaded area in the triangle. Simple geometry shows this to be 1 − 0.05/0.20 = 0.75.

The following example of the breaking strength of a chain serves as an important model for certain types of systems in reliability theory. Such a system is a type of series system, which fails if any subsystem fails. We discuss the system in terms of a chain, but analogs may be visualized readily. For example, the links in the chain might be “identical” electronic-circuit units in a register of a digital computer. The system fails if any one of the units fails. Each unit is subjected to the same overvoltage, due to a variation in power-supply voltage. Being “identical” units, each unit has the same probability distribution for failure as a function of voltage.

Example 3-9-16 Chain Model

Consider a chain with n links manufactured “the same.” The same stress is applied to all links. What is the probability of failure? We let X_i(·) be the breaking strength of the ith link and let Y(·) be the applied stress. We suppose these are all random variables whose values are nonnegative (the chain does not have compressive strength, only tensile strength). We assume {X_i(·): 1 ≤ i ≤ n} is an independent class, all members of which have the same distribution. We let W(·) be the breaking strength of the n-link chain. Then

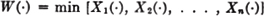
Now

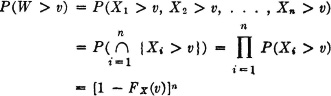
where F_X(·) is the common distribution function for the X_i(·). From this it follows that F_W(v) = P(W ≤ v) = 1 − [1 − F_X(v)]ⁿ. Note that F_W(v) = 0 for v < 0. The problem is to determine the probability that the breaking strength W(·) is greater than the value of the applied stress Y(·); that is, it is desired to determine P(W > Y). Now this is equivalent to determining P(Z > 0) = 1 − F_Z(0), where Z(·) = W(·) − Y(·). According to the result of Example 3-9-12 if we suppose the breaking strength W(·) and the applied stress Y(·) to be independent random variables, we have

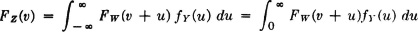
The limits in the last integral are based on the fact that f_Y(u) is zero for negative u. Since the integral of f_Y(·) over the positive real line must have the value 1, we may write

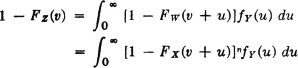
On putting v = 0, we have

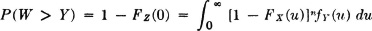
The problem is determined when the common distribution for the X_i(·) and the distribution for Y(·) are known. Let us suppose once more (Example 3-9-13) that the strength at failure is distributed exponentially; that is, we suppose F_X(u) = u(u)[1 − e^−αu]. Then 1 − F_X(u) = e^−αu for u > 0. We thus have

If Y(·) is distributed uniformly over the interval [0, f₀], it is easy to show that

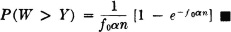
It may be noted that the integral expression for P(W > Y) is the Laplace transform of the density function f_Y(·), evaluated for the parameter s = αn. Tables of the Laplace transform may be utilized to determine the probability, once f_Y(·) is known.

We consider one more function of two random variables.

Example 3-9-17

Suppose X(·) and Y(·) are absolutely continuous. Determine the density function for the random variable Z(·) = X(·)Y(·). We have h(t, u) = tu, and the region Q_v is that shown in Fig. 3-9-4c and d. The most difficult part of the problem is to determine the limits of integration in the expression . It is necessary to divide the problem into two parts, one for v > 0 and one for v < 0. In the first case, examination of the region Q_v in Fig. 3-9-4c shows that the proper limits are given in the following expression:

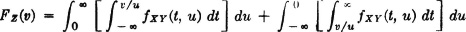
Differentiating with the aid of rules for differentiation with respect to limits of integration gives

Making use of the fact that in the second integral u < 0, we may combine this into a single-integral expression.

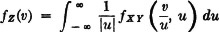
For the case v < 0, the regions are different, but an examination shows that the limits have the same formulas. Thus, the same formula is derived for f_Z(·) in either case.

Many other such formulas may be developed. Some of these are included in the problems at the end of this chapter. The strategy is simple. The difficulty comes in handling the details. Although there is no way to avoid some of these difficulties, a clear grasp of the task to be performed often makes it possible to discover how special features of the problem at hand may be exploited to simplify analysis and computations. Extensions to functions of higher numbers of random variables are equally simple, in principle, but generally difficult to carry out.

3-10 Almost-sure relationships

We have had occasion to note that P(E) = 0 does not imply that E is impossible. But for practical purposes, and in so far as probability calculations are concerned, such an event E is “almost impossible.” Similarly, P(A) = 1 does not imply that A is the sure event S. But A is “almost sure,” and for many purposes we need not distinguish between such an almost-sure event and the sure event. If two events have the same elements except possibly for a set whose total probability mass is zero, these could be considered essentially the same for many purposes in probability theory. And two random variables which have the same values for all elementary outcomes except for possibly a set of whose total probability mass is zero could be considered essentially the same. In this section, we wish to examine and formalize such relationships.

Events and classes of events equal with probability 1

We begin by considering two events.

Definition 3-10a

Two events A and B are said to be equal with probability 1, designated in symbols by

    A = B [P]

iffi

P(A) = P(B) = P(AB)

We also say A and B are almost surely equal.

This condition could have been stated in any of several equivalent ways, as the following theorem shows.

Theorem 3-10A

A = B [P] iffi any one of the following conditions holds:

1. P(AB^cA^cB) = P(AB^c) + P(A^cB) = 0

2. P(A ∪ B) = P(AB)

3. A^c = B^c [P]

PROOF Conditions 1 and 2 follow from the fact that

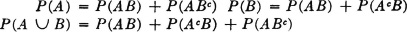
Condition 3 follows from condition 2 and the fact that

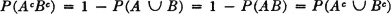
The condition of equality with probability 1 is illustrated in the Venn diagrams of Fig. 3-10-1. Figure 3-10-1a shows two sets A and B with the total probability mass in set A ∪ B actually located entirely in the common part AB. Figure 3-10-1b shows a case of probability mass concentrated at discrete points. Any two sets A and B which contain the same mass points must be equal with probability 1.

This concept may be extended to classes of events as follows:

Definition 3-10b

Two classes of events and are said to be equal with probability 1 or almost surely equal, designated = [P], iffi their members may be put into a one-to-one correspondence such that A_i = B_i [P] for each corresponding pair.

Fig. 3-10-1 Events equal with probability 1. (a) Probability mass in the shaded region is zero; (b) probability mass concentrated at discrete points.

We note immediately the following theorem, whose proof is given in Appendix D-1.

Theorem 3-10B

Let and 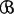be countable classes such that = 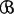[P], Then the following three conditions must hold:

1.

2.

3.

This theorem shows that calculations of the probabilities of events involving the usual combinations of member events of the class are not changed if any of the A_i are replaced by corresponding B_i. It is easy to show, also, that if is an independent class, so also is 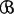, since the product rule for the latter is a ready consequence of the product rule for the class .

We have seen that partitions play an important role in probability theory. A finite or countably infinite partition has the properties

Now it may be that the class is not a partition, even though it has the two properties listed above. From the point of view of probability calculations, however, it has the essential character of a partition. In fact, we can make the following assertion, which is proved in Appendix D-1.

Theorem 3-10C

If a countable class of events has the properties 1 and 2 noted above, then there exists a partition 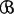such that = 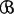[P].

Random variables

The concept of almost-sure equality extends readily to random variables as follows:

Definition 3-10c

Two random variables X(·) and Y(·) are said to be equal with probability 1, designated X(·) = Y(·) [P], iffi the elements for which they differ all belong to a set D having zero probability. We also say in this case that X(·) and Y(·) are almost surely equal.

This means that if we rule out the set of on which X(·) and Y(·) differ, we rule out a set which has zero probability mass. Over any other set the two random variables have the same values; hence any point in such a set must be mapped into the same t by both X(·) and Y(·). The mass picture would make it appear that two random variables that are almost surely equal must induce the same mass distribution on the real line.

The case of simple random variables is visualized easily. If two simple random variables are equal with probability 1, they have essentially the same range T and assign the same probability mass to each t_i ∈ T. If there are values of either variable which do not lie in the common range T, these points must be assigned 0 probability. Thus, for practical purposes, these do not represent values of the function to be encountered. These statements may be sharpened to give the following theorem, whose proof is found in Appendix D-2.

Theorem 3-10D

Consider two simple random variables X(·) and Y(·) with ranges T₁ and T₂, respectively. Let T = T₁ ∪ T₂, with t_i ∈ T. Put A_i = [: X() = t_i) and B_i = {: Y() = t_i}. Then X(·) = Y(·) [P] iffi A_i = B_i [P] for each i.

For the general case, we have the following theorem, which is also proved in Appendix D-2.

Theorem 3-10E

Two random variables X(·) and Y(·) are equal with probability 1 iffi X⁻¹(M) = Y⁻¹(M) [P] for each Borel set M on the real line.

This theorem shows that equality with probability 1 requires P_X(M) = P_Y(M) for any Borel set M, so that two almost surely equal random variables X(·) and Y(·) induce the same probability mass distribution on the real line. The converse does not follow, however. We have, in fact, illustrated in Example 3-2-3 that two quite different random variables may induce the same mass distribution.

In dealing with random variables, it is convenient to extend the ideas discussed above to various types of properties and relationships. We therefore make the following

Definition 3-10d

A property of a random variable or a relationship between two or more random variables is said to hold with probability 1 (indicated by the symbol [P] after the appropriate expression) iffi the elements for which the property or relationship fails to hold belong to a set D having 0 probability. In this case we may also say that the property or the relationship holds almost surely.

    A property or relationship is said to hold with probability 1 on (event) E (indicated by “[P] on E”) iffi the points of E for which the property or relationship fails to hold belong to a set having 0 probability. We also use the expression “almost surely on E.”

Thus we may say X(·) = 0 [P], X(·) ≤ Y(·) [P] on E, etc. Other examples of this usage appear in later discussions, particularly in Chaps. 4 and 6.

Problems

3-1. Suppose X(·) is a simple random variable given by

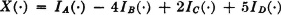
where {A, B, C, D} is a partition of the whole space S.

(a) What is the range of X(·)?

(b) Express in terms of members of the partition the set X⁻¹(M), where

(1) M = (0, 1)          i.e., the interval 0 < t < 1

(2) M = {− 1, 3, 5}

(3) M = (− ∞, 4]     i.e., the interval − ∞ < t ≤ 4

(4) M = (2, ∞)        i.e., the interval 2 < t < ∞

3-2. Consider the function X(·) = I_A(·) + 3I_B(·) − 4I_c(·). The class {A, B, C} is a partition of the whole space S.

(a) What is the range of X(·)?

(b) What is the inverse image X^{− 1}(M) when

(1) M = (−∞, 3]

(2) M = (1, 4]

ANSWER: B

(3) M = (2, 5)^c

3-3. Suppose X(·) is a random variable. For each real t let E_t = {: X() ≤ t}. Express the following sets in terms of sets of the form E_t for appropriate values of t.

(1) {: X() < a}

ANSWER: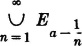

(2) {: X() ≥ a}

(3) {: X() ∈ [a, b)}

(4) {: X() ∈ (a, b)}

ANSWER:

3-4. Consider the random variable

where {A, C, D, E} is a disjoint class whose union is B^c. Suppose P(A) = 0.1, P(B) = 0.2, P(C) = 0.2, and P(D) = 0.2. Show the probability mass distribution produced on the real line by the mapping t = X().

ANSWER: Probability masses 0.1, 0.2, 0.2, 0.2, 0.3 at t = −4, 0, 1, 3, 5, respectively

3-5. Suppose X(·) is a simple random variable given by

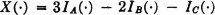
where {A, B, C} is a class which generates a partition, none of whose minterms are empty.

(a) Determine the range of X(·).

(b) Express the function in canonical form.

(c) Express the function in reduced canonical form.

3-6. A man stands in a certain position (which we may call the origin). He tosses a coin. If a head appears, he moves one unit to the left. If a tail appears, he moves one unit to the right.

(a) After 10 tosses of the coin, what are his possible positions and what are the probabilities?

(b) Show that the distance at the end of 10 trials is given by the random variable

where the distance to the left is considered negative. A_i is the event that a head appears on the ith trial. Make the usual assumption concerning coin-flipping experiments.

ANSWER: t = 2r − 10, where 0 ≤ r ≤ 10 is the number of tails; P(X = t) = C_r¹⁰2⁻¹⁰

3-7. The random variable X(·) has a distribution function F_X(·), which is a step function with jumps of 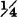at t = 0, 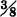at t = 1, 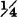at t = 2, and 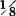at t = 3.

(a) Sketch the mass distribution produced by the variable X(·).

(b) Determine P(1 ≤ X ≤ 2), P(X > 1.5).

ANSWER: + , +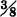

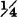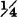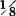
3-8. Suppose a random variable X(·) has distribution function

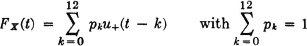
In terms of p₀, p₁, …, p₁₂, express the probabilities:

3-9. An experiment consists of a sequence of tosses of an honest coin (i.e., to each elementary event corresponds an infinite sequence of heads and tails). Let A_k be the event that a head appears for the first time at the kth toss in a sequence, and let H_k be the event of a head at the kth toss. Suppose the H_k form an independent class with P(H_k) = 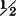for each k. For a given sequence corresponding to the elementary outcome , let X() be the number of the toss in the sequence for which the first head appears.

(a) Express X(·) in terms of indicator functions for the A_k.

(b) Determine the distribution function F_X(·).

3-10. A game is played consisting of n successive trials by a single player. The outcome of each trial in the sequence is denoted a success or a failure. The outcome at each trial is independent of all others, and there is a probability p of success. A success, or a win, adds an amount a to the player’s account, and a failure, or loss, subtracts an amount b from the player’s account.

(a) Let A_k be the event of a success, or win, on the kth trial. Let X_n() be the net winnings after n trials. Write a suitable expression for X_n(·) in terms of the indicator functions for the events A_k and .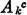

(b) Suppose n = 4, p = 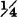, a = 3, and b = 1. Plot the distribution function F_n(·) for X_n(·).

3-11. For each of the six functions F_X(·) listed below

(a) Verify that F_X(·) is a probability distribution function. Sketch the graph of the function.

(b) If the distribution is discrete, determine the probability mass distribution; if the distribution is absolutely continuous, determine the density function f_X(·) and sketch its graph.

Note: Where formulas are given over a finite range, assume F_X(t) = 0 for t to the left of this range and F_X(t) = 1 to the right of this range.

(1)

(2)

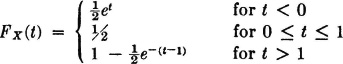
(3)

(4)

(5)

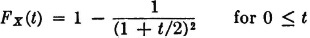
(6)

3-12. A random variable X(·) has a density function f_X(·) described as follows: it is zero for t < 1; it rises linearly between t = 1 and t = 2 to the value 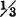; it remains constant for 2 < t < 4; it drops linearly to zero between t = 4 and t = 5.

(a) Plot the distribution function F_X(·).

(b) Determine the probability P(1.5 ≤ X ≤ 3).

ANSWER: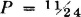

3-13. A random variable X(·) has a density function f_X(·) described as follows: it is zero for t < 1; it has the value 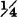for 1 < t < 4; it drops linearly to zero between t = 4 and t = 6.

(a) Plot the distribution function F_X(·).

(b) Determine P(2 < X ≤ 4.5).

ANSWER: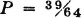

3-14. A random variable X(·) has density function f_X(·) given by

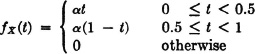
Let A be the event X < 0.5, B be the event X > 0.5, and C be the event 0.25 < X < 0.75.

(a) Find the value of α to make f_X(·) a probability density function.

(b) Find P(A), P(B), P(C), and P(A|B).

(c) Are A and C independent events? Why?

ANSWER: A and C are independent

3-15. The density function of a continuous random variable X(·) is proportional to t(1 − t) for 0 < t < 1 and is zero elsewhere.

(a) Determine f_X(t).

(b) Find the distribution function F_X(t).

(c) Determine P(X < ).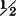

3-16. Let X(·) be a random variable with uniform distribution between 10 and 20. A random sample of size 5 is chosen. From this, a single value is chosen at random. What is the probability that the final choice results in a value between 10 and 12? Interpretative note: Let E_j be the event that exactly j of the five values in the sample lie between 10 and 12. Let C be the event that the final value chosen has the appropriate magnitude. The selection of a random sample means that if X_k(·) is the kth value in the sample, the class {X_k(·): 1 ≤ k ≤ 5} is a class of independent random variables, each with the same distribution as X(·). The selection of one value from the sample of five at random means that P(C|E_j) = j/5.

ANSWER: P(C) = 0.20

3-17. The distribution functions listed below are for mixed probability distributions. For each function

(a) Sketch the graph of the function.

(b) Determine the point mass distribution for the discrete part.

(c) Determine the density function for the absolutely continuous part.

(1)

(2)

(3)

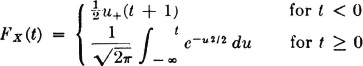
3-18. A recording pen is recording a signal which has the following characteristics. If the signal is observed at a time chosen at random, the observed value is a random variable X(·) which has a gaussian distribution with = 0 and σ = 4. The recorder will follow the signal faithfully if the value lies between −10 and 10. If the signal is more negative than −10, the pen stops at −10; if the signal is more positive than 10, the pen stops at 10. Let Y(·) be the random variable whose value is the position of the recorder pen at the arbitrary time of observation. What is the probability distribution function for Y(·)? Sketch a graph of the function. Determine the point mass distribution and the density for the absolutely continuous part.

3-19. A truck makes a run of 450 miles at an essentially constant speed of 50 miles per hour, except for two stops of 30 minutes each. The first stop is at 200 miles, and the second is at 350 miles. A radio phone call is made to the driver at a time chosen at random in the period 0 to 10 hours. Let X(·) be the distance the truck has traveled at the time of the call. What is the distribution function F_X(·)?

ANSWER: Point masses 0.05 at t = 200, 350. has constant slope 0 < t < 450

3-20. Two random variables X(·) and Y(·) produce a joint mass distribution under the mapping (t, u) − [X, Y]() which is uniform over the rectangle 1 ≤ t ≤ 2, 0 ≤ u ≤ 2.

(a) Describe the marginal mass distributions for X(·) and Y(·).

(b) Determine P(X ≤ 1.5), P(1 < Y ≤ 1.6), P(1.1 ≤ X ≤ 1.2, 0 ≤ Y < 1).

ANSWER: 0.5, 0.3, 0.05

3-21. Two random variables X(·) and Y(·) produce a joint mass distribution under the mapping (t, u) = [X, Y]() which may be described as follows: (1) 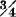of the probability mass is distributed uniformly over the triangle with vertices (0, 0), (2, 0), and (0, 2), and (2) a mass of 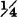is concentrated at the point (1, 1).

(a) Describe the marginal mass distributions.

(b) Determine P(X > 1), P(−3 < Y ≤ 1), P(X = 1, Y ≥ 1), P(X = 1, Y < 1).

ANSWER: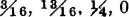

3-22. For two discrete random variables X(·) and Y(·), let

have the following values:

If t₁ = −1, t₂ = 1, t₃ = 2, u₁ = −2, u₂ = 2, plot the joint distribution function F_XY(t, u) by giving the values in each appropriate region of the t, u plane.

3-23. Let X(·) and Y(·) be two discrete random variables. X(·) has range t_i = i − 3, i = 1, 2, 3, 4, 5, and Y(·) has range u_j = j − 1 for j = 1, 2, 3. Values of the joint probabilities p(i, j) are given as follows:

(a) Determine the marginal probabilities, and show the joint and marginal mass distributions on the plane and on the coordinate lines.

(b) Show values of the joint distribution function F_XY(t, u) by indicating values on the appropriate regions of the plane.

3-24. Two random variables X(·) and Y(·) are said to have a joint gaussian (or normal) distribution iffi the joint density function is of the form

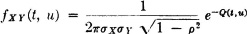
where

and σ_X > 0, σ_Y > 0, |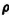| < 1, and _X, _Y are constants which appear as parameters.

Show that X(·) is normal with parameters _X and σ_X. Because of the symmetry of the expression, we may then conclude that Y(·) is normal with parameters _Y and σ_Y. [Suggestion: Let (·) be defined by 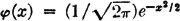. It is known that

Show that

where r depends upon 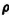, _X, _Y, σ_X, σ_Y, and t. Integrate to obtain f_X(t).]

3-25. Let X(·) and Y(·) be two discrete random variables which are stochastically independent. These variables have the following distributions of possible values:

Determine the mass distribution on the plane produced by the mapping

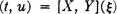
Show the locations and amounts of masses.

3-26. Consider two discrete random variables X(·) and Y(·) which produce a joint mass distribution on the plane. Let p(i, j) = P(X = t_i, Y = u_j), and suppose the values are

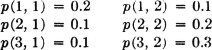
(a) Calculate P(X = t_i), i = 1, 2, 3, and P(Y = u_j), j = 1, 2.

(b) Show whether or not the random variables are independent.

ANSWER: Not independent

3-27. For the random variables in Prob. 3-26, determine the conditional probabilities P(X = t_i|Y = u_j).

3-28. A discrete random variable X(·) has range (1, 2, 5) = (t₁, t₂, t₃), and a discrete random variable Y(·) has range (0, 2) = (u₁, u₂).

Suppose p(i, j) = P(X = t_i, Y = u_j) = α(i + j).

(a) Determine the p(i, j), and show the mass distribution on the plane.

(b) Are the random variables X(·) and Y(·) independent? Justify your answer.

ANSWER: Not independent

3-29. Two independent random variables X(·) and Y(·) are uniformly distributed between 0 and 10. What is the probability that simultaneously 1 ≤ X ≤ 2 and 5 ≤ Y ≤ 10?

3-30. Addition modulo 2 is defined by the following addition table:

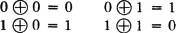
The disjunctive union A ⊕ B of two sets is defined by A ⊕ B = AB^c A^cB.

(a) Show that I_A(·) ⊕ I_B(·) = I_{A ⊕ B}(·), where the ⊕ in the left-hand member indicates addition modulo 2 and in the right-hand member indicates disjunctive union.

(b) Express the function I_A(·) ⊕ 1 in terms of I_A(·) or .

(c) Suppose A and B are independent events with P(A) = 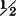. Show that I_B(·) and I_{A ⊕ B}(·) are independent random variables. (Note that it is sufficient to show that B and A ⊕ B are independent events.)

3-31. An experiment consists in observing the values of n points distributed uniformly and independently in the interval [0, 1]. The n points may be considered to be observed values of n independent random variables, each of which is uniformly distributed in the interval [0, 1]. Let a be a number lying between 0 and 1. What is the probability that among the n points, the point farthest to the right lies to the right of point a?

ANSWER: 1 − aⁿ

3-32. The location of 10 points may be considered to be independent random variables, each having the same triangular distribution function. This function rises linearly from t = 1 to t = 2, then decreases linearly to zero at t = 3. The resulting graph is a triangle, symmetric about the value t = 2.

(a) What is the probability that all 10 points lie within a distance 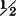of the position t = 2?

ANSWER: P = (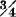)¹⁰

(b) What is the probability that exactly 3 of the 10 points lie within a distance 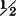of the position t = 2?

3-33. Random variables X(·) and Y(·) have joint probability density function

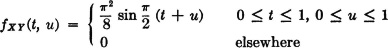
(a) Find the marginal density functions

and show whether or not X(·) and Y(·) are independent.

ANSWER: X(·) and Y(·) are not independent.

(b) Calculate P(X > ).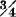

ANSWER: P(X > 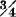) = 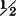[1 − sin (3π/8) + cos (3π/8)] = 0.229

3-34. If X(·) and Y(·) have a joint normal distribution (Prob. 3-24), show that they are independent iffi the parameter 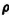= 0.

3-35. Two random variables X(·) and Y(·) produce a joint probability mass distribution which is uniform over the circle of unit radius, center at the origin. Show whether or not the random variables are independent. Justify your answer.

ANSWER: Not independent

3-36. Two random variables X(·) and Y(·) produce a joint probability mass distribution as follows: one-half of the mass is spread uniformly over the rectangle having vertices (0, 0), (1, 0), (1, 1), and (0, 1). A mass of 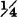is placed at each of the points (0.75, 0.25) and (0.25, 0.75). Show whether or not the random variables are independent. Justify your answer.

3-37. Suppose X(·) and Y(·) have a joint density function f_XY(·, ·).

(a) Show that X(·) and Y(·) are independent iffi it is possible to express the joint density function as

f_XY(t, u) = kg(t)h(u) where k is a nonzero constant

(b) Show that if X(·) and Y(·) are independent, the region of nonzero density must be the rectangle M × N, where M is the set of t for which f_X(t) > 0 and N is the set of u for which f_Y(u) > 0.

3-38. Consider the simple random variable X(·) = −I_A(·) + I_B(·) + 2I_C(·). Let m_i be the ith minterm in the partition generated by {A, B, C), and let p_i = P(m_i).

Values of these probabilities are

(a) Determine the probability mass distribution produced by the mapping t = X(). Show graphically the locations and amounts of masses.

ANSWER: Masses 0.3, 0.3, 0.2, 0.2 at t = 0, 1, 2, 3, respectively

(b) Determine the probability mass distribution produced by the mapping u = X²() + 2.

3-39. The random variable X(·) is uniformly distributed between 0 and 1. Let Z(·) = X²(·).

(a) Sketch the distribution function F_Z(·).

(b) Sketch the density function f_Z(·).

3-40. What is the distribution function F_Y(·) in terms of F_X(·) if Y(·) = −X(·)? In the continuous case, express the density function f_Y(·) in terms of f_X(·).

3-41. Suppose X(·) is any random variable with distribution function F_X(·). Define a quasi-inverse function F_X⁻¹(·) by letting F_X⁻¹(u) be the smallest t such that F_X(t) ≥ u. Show that if X(·) is an absolutely continuous random variable, the new random variable Y(·) = F_X[X(·)] is uniformly distributed on the interval [0, 1]. (Compare these results with Example 3-9-6.)

3-42. Consider the discrete random variables

X(·) with range (−2, 0, 1, 3) = (t₁, t₂, t₃, t₄)

and

Y(·) with range (−1, 0, 1) = (u₁, u₂, u₃)

Let p(i, j) = P(X = t_i, Y = u_j) be given as follows:

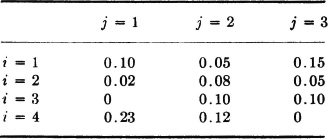
(a) Sketch to scale graphs for F_X(·) and F_Y(·), and show values thereon.

(b) Let Z(·) = Y(·) − X(·). Sketch to scale the graph for F_Z(·), and show values thereon,

ANSWER: F_Z(·) has jumps at v = −4, −3, −1, 0, 1, 2, 3 of magnitudes 0.23, 0.12, 0.12, 0.18, 0.15, 0.05, 0.15, respectively.

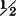3-43. A pair of random variables X(·) and Y(·) produce the joint probability mass distribution under the mapping (t, u) = [X, Y]() as follows: mass of is uniformly distributed on the unit square 0 ≤ t ≤ 1, 0 ≤ u ≤ 1; mass of 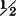is uniformly distributed on the vertical line segment t = 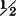, 0 ≤ u ≤ 1. Define the new random variables Z(·) = Y²(·) and W(·) = 2X(·). Determine the distribution functions F_X(·), F_Y(·), F_Z(·), and F_W(·). Sketch graphs of these functions.

3-44. The joint probability mass distribution induced by the mapping

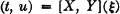
is described as follows: mass of 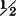is distributed uniformly over a square having vertices (−1, 0), (1, −2), (3, 0), and (1, 2); mass of 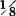is concentrated at each of the points (1, 0), (2, 0), (0, 1), and (2, 1).

(a) Let A = (: X() ≤ 1} and B = {: Y() > 0}. Show that A and B are independent events. However, consider the events A₁ = {: X() < 1) and B₁ = {: Y() ≥ 0} to show that X(·) and Y(·) are not independent random variables.

(b) Let Z(·) = X(·) − Y(·). Determine the distribution function F_Z(·) for the random variable Z(·).

3-45. Random variables X(·) and Y(·) have the joint density functions listed below. For each of these

(a) Obtain the marginal density functions f_X(·) and f_Y(·).

(b) Obtain the density function for the random variable Z(·) = X(·) + Y(·).

(c) Obtain the density function for the random variable W(·) = X(·) − Y(·).

(1) f_XY(t, u) = 4(1 − t)u          for 0 ≤ t ≤ 1, 0 ≤ u ≤ 1

(2) f_XY(t, u) =2t          for 0 ≤ t ≤ 1, 0 ≤ u ≤ 1

(3)

3-46. A pair of random variables X(·) and Y(·) produce a joint mass distribution on the plane which is uniformly distributed over the square whose vertices are at the points (−1, 0), (1, 0), (0, −1), and (0, 1). The mass density is constant over this square and is zero outside. Determine the distribution functions and the density functions for the random variables X(·), Y(·), Z(·) = X(·) + Y(·), and W(·) = X(·) − Y(·).

ANSWER: f_Z(v) = f_w(v) = 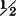        for |v| ≤ 1

3-47. On an assembly line, shafts are fitted with bearings. A bearing fits a shaft satisfactorily if the bearing diameter exceeds the shaft diameter by not less than 0.005 inch and not more than 0.035 inch. If X(·) is the shaft diameter and Y(·) is the bearing diameter, we suppose X(·) and Y(·) are independent random variables. Suppose X(·) is uniformly distributed over the interval [0.74, 0.76] and Y(·) is uniformly distributed over [0.76, 0.78]. What is the probability that a bearing and a shaft chosen at random from these lots will fit satisfactorily?

ANSWER: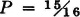

3-48. Suppose X(·) and Y(·) are independent random variables, uniformly distributed in the interval [0, 1]. Determine the distribution function for

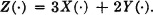
3-49. Random variables X(·) and Y(·) are independent. The variable X(·) is uniformly distributed between (− 2, 0). The variable Y(·) is distributed uniformly between (2, 4). Determine the density function for the variable

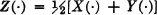
3-50. Let X(·) and Y() be independent random variables. Suppose X(·) is uniformly distributed in the interval [0, 2] and Y(·) is uniformly distributed in the interval [1, 2]. What is the probability that Z(·) = X(·)Y(·) ≤ 1?

ANSWER: 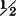loge 2

3-51. Obtain the region Q_v for the function h(t, u) = t/u. Show that, under the appropriate conditions, the density function for the random variable R(·) = X(·)/Y(·) is given by

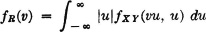
3-52. Suppose A, B are independent events, and suppose A = A₀ [P] and B = B₀ [P]. Show that A₀, B₀ is an independent pair.

3-53. Consider the simple random variable X(·) in canonical form as follows:

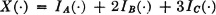
with P(A) = P(B) = 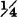and P(C) = 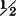. Suppose C = D E with

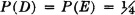
Construct at least three other simple random variables having the same probability distribution but which differ on a set of positive probability.

Selected references

BRUNK [1964], chaps. 3, 4. Cited at the end of our Chap. 2.

FISZ [1963], chap. 2. Cited at the end of our Chap. 2.

GNEDENKO [1962]: “The Theory of Probability,” chap. 4 (transl. from the Russian). Although written primarily for the mathematician, the discussions are generally clear and readable.

GOLDBERG [1960], chap. 4, secs. 1, 2. Cited at the end of our Chap. 1.

LLOYD AND LIPOW [1962]: “Reliability: Management, Methods, and Mathematics,” chaps. 6, 9. Discusses basic mathematical models in reliability engineering in a clear and interesting manner.

McCORD AND MORONEY [1964], chap. 5. Cited at the end of our Chap. 2.

PARZEN [1960], chap. 7. Cited at the end of our Chap. 2.

WADSWORTH AND BRYAN [1960]: “Introduction to Probability and Random Variables,” chaps. 3 through 6. Gives a detailed discussion, with many examples, of a wide variety of useful probability distributions and techniques for handling them.

Handbook

National Bureau of Standards [1964]: “Handbook of Mathematical Functions,” chap. 26. A very useful, moderately priced work which provides an important collection of formulas, properties, relationships, and computing aids and techniques, as well as excellent numerical tables and an extensive bibliography. Much material in other chapters (e.g., combinatorial analysis) adds to the usefulness for the worker in probability.