*See explanations beginning on this page.
1. D
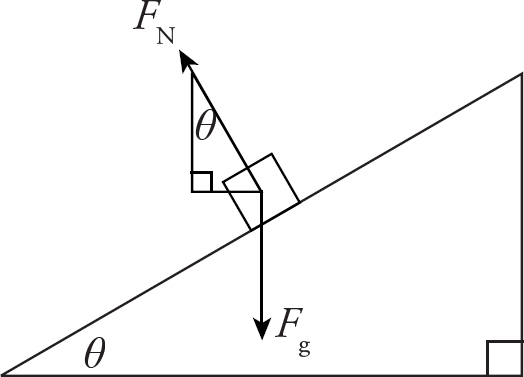
As a ball rolls down an inclined plane, the three forces act on the ball, as shown in the diagram below.
In order for a force to cause an object to rotate, the force must be located off-center, and must not point directly at or away from the object’s center of mass. An object’s weight always acts at its center of mass, so (B) is wrong. The normal force does act at the edge of the ball, but it points directly out of the ramp, which is straight at the center of the ball. Choice (A) is wrong. Friction acts where the ball meets the inclined plane, and it points parallel to the surface, which is tangent to the ball’s surface. So friction is what causes rotation. What kind of friction do we have? The phrase “without slipping” tells us that even though the ball as a whole is moving, the spot on the ball that touches the ramp is at rest with respect to the ramp. That means we have static friction, (D).
2. B
In a velocity-versus-time (also referred to as a v-versus-t) graph, the displacement of an object is the area between the curve and the horizontal axis; area below the t-axis counts as negative. In this case, the area can be broken into multiple rectangles and triangles.
In order of the number labels, each shape has an area of 6, 1, 4, and 12, respectively. The last two, however, are below the t-axis, so their area represents negative displacement. Therefore, the net displacement is 6 m + 1 m − 4 m − 12 m = −9 m. As a check, it looks like most of the area is below the t-axis, so the answer should be negative.
3. B
The formula for centripetal force is Fc = mv2/r, which initially seems to indicate the force is inversely proportional to the radius. However, in the case of circular motion, an object’s linear speed is v = ωr. Substituting this value into the equation gives Fc = m(ωr)2/r = mω2r. So it turns out that the force is directly proportional to r, which means doubling the radius will double the force on the object.
4. D
First, you know Ff = μFN = µ(mg). Second, you know that W = ΔKΕ = KEf − KE0 = −KE0 (since KEf = 0 in this case) = − 
mv02. Plugging in numbers, you get W = − (1000 kg)(5 m/s)2 = −12,500 J. You also know that W = Fdcosθ = [µ(mg)]dcosθ. Solving for μ, you get μ = W/[(mg)dcosθ]. Plugging in the numbers then gives μ = −12,500 J/[(1000 kg)(10 m/s2)(20 m)(cos180°)] = 0.0625.
5. C
The frequency of a spring-block system is f =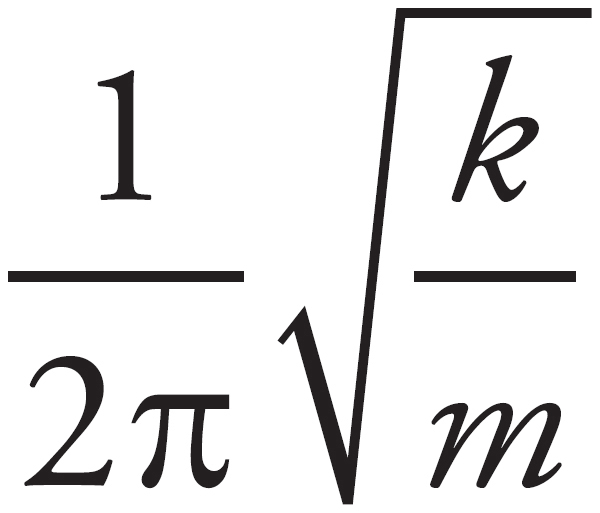 
, so it would be affected by the change in mass. Furthermore, when a spring is at maximum compression or extension, all of its energy is potential energy, which is given by U = kx2. In adding this block, none of the relevant values are changed, so the spring will still extend to the same length, which means the amplitude is unchanged. Finally, maximum speed will be limited by the maximum K of the system (which will be unchanged since the maximum U was unchanged). K = mv2, so the increased mass would have to be balanced by a decrease in speed to leave the K unaltered.
If you want a physical, rather than mathematical, explanation, think about the acceleration of the pair of blocks. The spring exerts the same force as before, but we effectively raised the block’s mass. Thus, the acceleration is less than before. Since the distance from the starting point (maximum compression) to equilibrium is unchanged, the blocks will pick up less speed than the single block did before. Thus, maximum speed decreases.
6. B
The diagram below shows the forces involved.
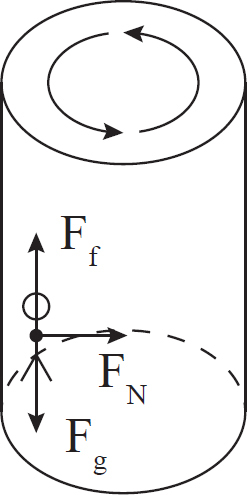
In this case, the person will remain suspended in the air as long as Ff = Fg. Furthermore, because this is an example of uniform circular motion, you know FN = FC = mv2/r. So you can rewrite the first equation as µ(mv2/r) = mg. Thus, the coefficient of friction is an important factor, but the mass of the person is not since it exists on both sides of the equation and will cancel out.
7. D
In any collision, the total momentum of the system must be conserved. Prior to the collision, you see that all of the momentum is horizontal. Therefore, the net momentum after the collision must also be purely horizontal. If one ball is moving up after the collision, the other must be moving down to cancel out that vertical momentum.
8. D
Whenever the ball is in motion, it will be experiencing circular motion, which means there must be a centripetal force. Centripetal force is a net force toward the center, so that means tension must be the greater force whenever the ball is moving. However, the ball is not always moving. At the two extreme edges of its motion, the ball is motionless for an instant as it changes directions. At those times, the net centripetal force is zero, meaning the two given forces are equal.
9. C
In a circuit with multiple paths, the current through each path is inversely proportional to the resistance of that path. If no current passes through the indicated segment of wire, then the ratio (current in top path)/(current in bottom path) is the same before the cross bar as it is after the cross bar. Thus, 
, which means R = 
.
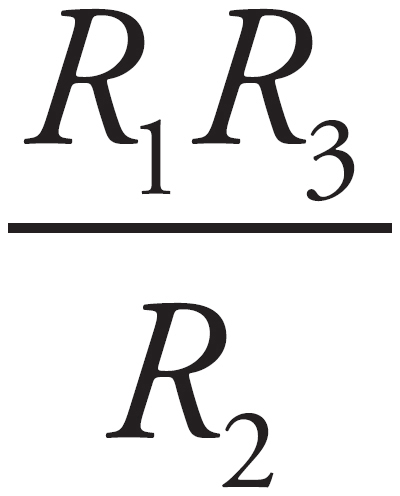10. B
First, note that if the resistance of any resistor increases, the total resistance also increases. Choice (D) is wrong. For resistors in parallel, you know 
, which means RT = 
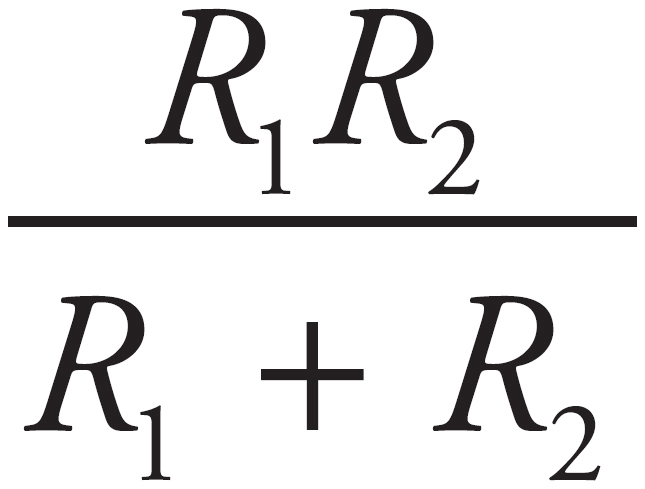. You know R2 = 4 Ω, so plug that in to get RT = 
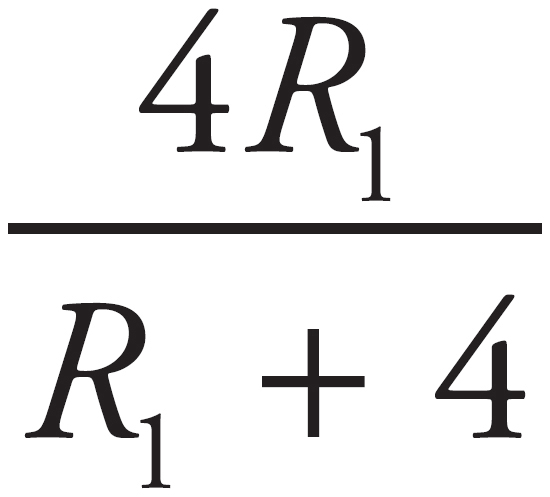. If you don’t know what this graph looks like, plug in a huge number, like 100, for R1. RT = 400/104 = a little less than 4. So the right edge of the graph should approach 4 from below.
11. A
The frequency of a wave can be found using the equation f = v/λ. You also know v =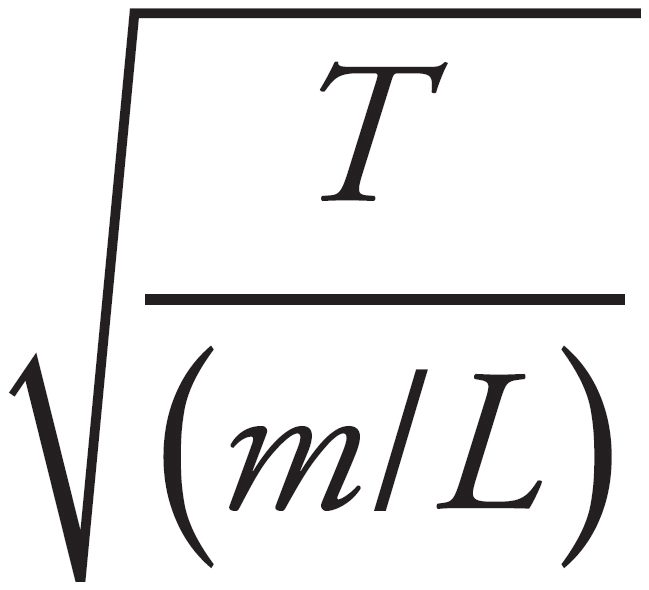 
. Because tension is in the numerator, that means tightening will increase frequency. This eliminates (C) and (D). Finally, because frequency depends on the square root of tension, the tension must be multiplied by 4 to double the frequency.
12. C
Just focus on one end of the rope. Nothing is moving, so the net force must be 0. If a person pulls with a force of 1000 N and nothing moves, then the resulting tension must also be 1000 N. Additionally, tension is a constant magnitude throughout a string. The direction of the tension can change (as in the case of a pulley system), but the magnitude will remain the same.
13. B
The force of static friction will be Ff = µFN = µ(mg). Changing the arrangement of the blocks does not change any of these three quantities, so the force will remain the same. Thus, 10 N will again be required to move them.
14. D
It’s easiest to consider both blocks as one system, calculate the maximum acceleration of the pair of blocks caused by the spring (which occurs at maximum displacement from equilibrium), and determine whether friction between the two block is strong enough to give the top block the necessary acceleration to keep up with the bottom block. Applying Newton’s Second Law to the system of blocks, Fspring = (combined mass) * a → kA = (M + m)a. In order for the top block to accelerate at this rate, static friction must be strong enough that Fsf = ma → µsFN = ma. You don’t need to do any math to see that µs (coefficient of static friction), A (amplitude), and k (spring constant) appear, but average speed doesn’t.
15. B
For Questions 15−17, or any problem that involves an electric circuit with switches, the key is to remember that electricity flows through a closed switch but not an open one. Redraw the circuit, including only the parts that form a closed circuit.
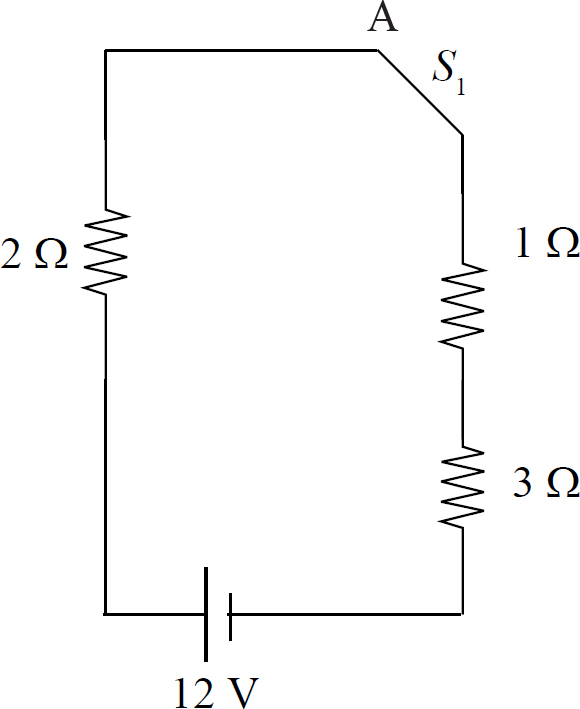
With S1 closed but S2 open, only the left-hand loop is connected. The resistors are in series, so the equivalent resistance is Req = 2 Ω + 1 Ω + 3 Ω = 6 Ω. The current through the circuits including the 1 Ω resistor is Ileft = 
.
16. C
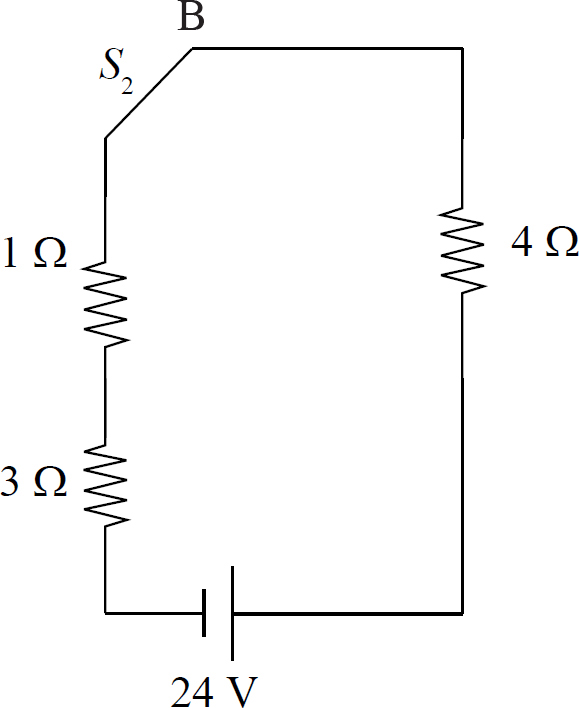
With S1 open but S2 closed, only the right-hand loop is connected. Again, the resistors are in series so the equivalent resistances is Req = 4 Ω + 1 Ω + 3 Ω = 8 Ω. The current through the circuit including the 1 Ω resistor is Iright = 
.
17. A
If neither switch is connected, then no loop can be made, which means no current will flow.
18. A
The forces on the person’s foot are shown in the diagram below:
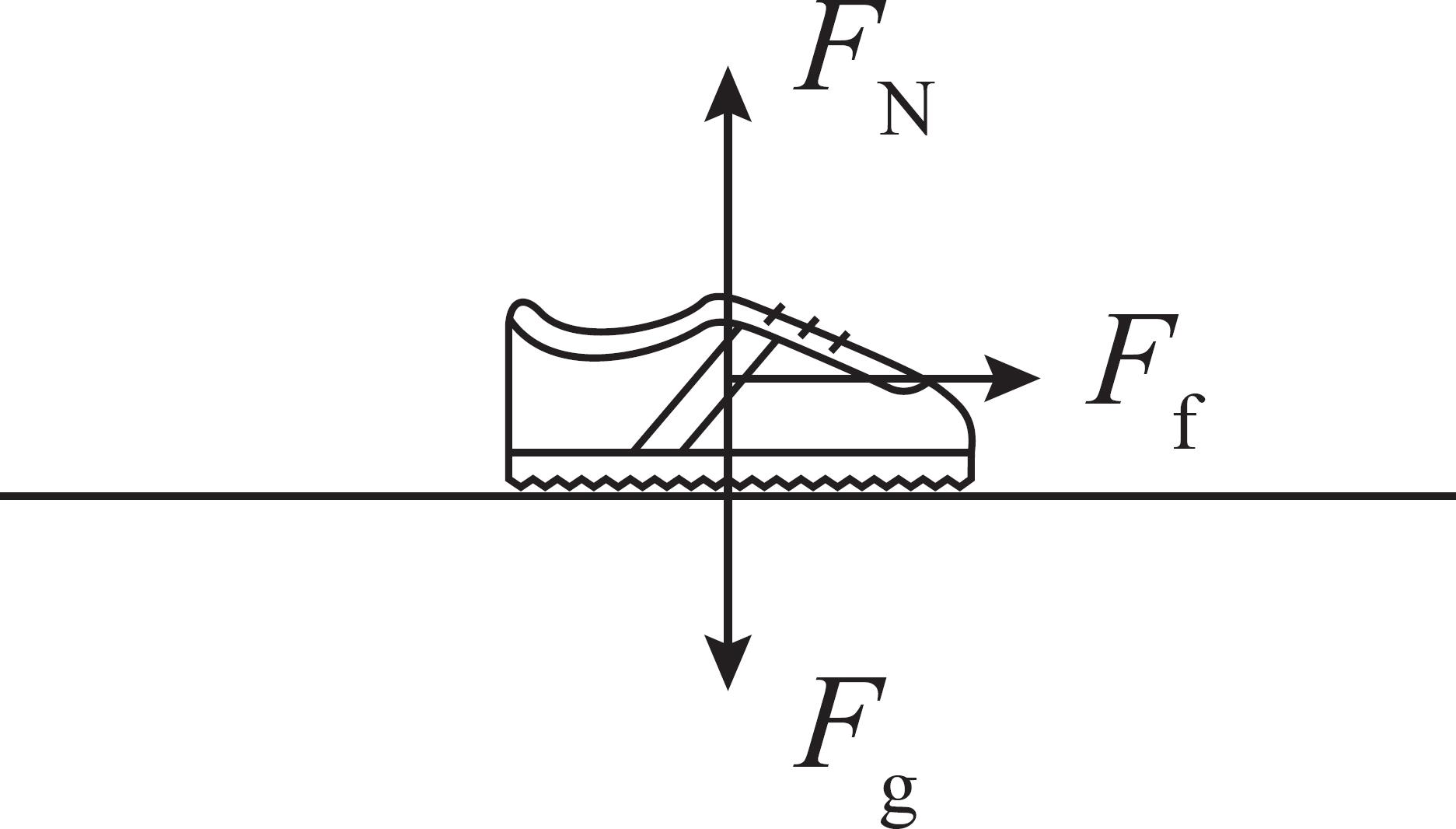
Since the person is accelerating to the right, the net force must be to the right. The interaction causing this force is friction between the ground and the person’s shoe. But the upward normal force also comes from the ground. Thus, the total contact force from the ground points up and to the right.
Of these forces, both the normal force and the friction force ar coming from the ground, so the sum of those vectors is the correct answer.
19. D
Because the lift force is perpendicular to the velocity of the object, lift can have no effect on the magnitude of velocity. The magnitude of velocity is also known as speed, so (D) is correct.
20. C
Remember that in a system with one closed end and one open end, there will be a node at one end and an antinode at the other. From the drawing, you can see that the tube is the length of 1/4 wavelength of this standing wave. That means that this wave is the fundamental standing wave, also called the first harmonic. As you’ll learn on this page, the next harmonic is the third harmonic, and it has 3 times the frequency of the first harmonic.
21. B
An electron is repelled from negative charge and attracted to positive charge, so there are two electric forces on it, both pointing to the right. Thus, as it moves from A to B, the electron’s speed increases. This eliminates (C) and (D). As for potential energy: one way to think about it is to realize that an increase in speed implies an increase in kinetic energy. Where does this energy come from? It comes from the potential energy of the system, which decreases by an equal amount.
22. D
Remember that parallel resistors require you to use the reciprocal sum, while series resistors simply add. For example, the first set of parallel resistors would be combined by doing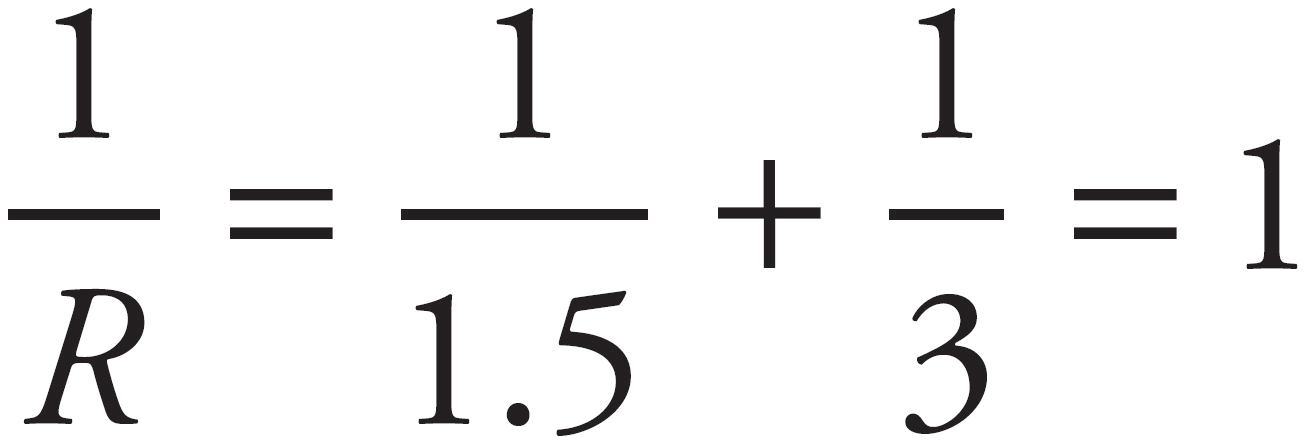 
, which means R = 1 Ω. For the second set of parallel resistors, you would get 
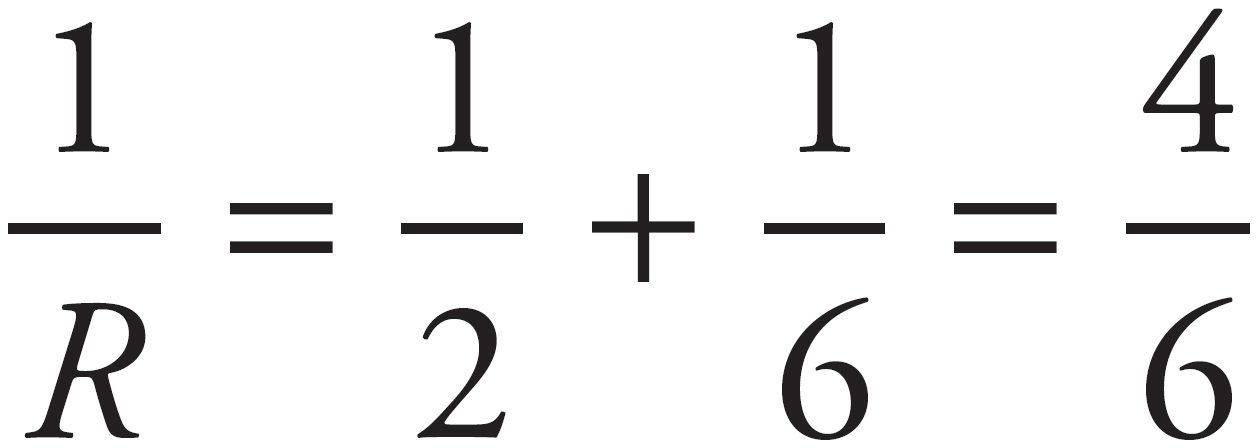, which means R = 1.5 Ω. Adding those two values to the lone series resistor gives RTotal = 2 + 1 + 1.5 = 4.5 Ω.
23. D
If an object leaves a planet at exactly escape velocity, its speed will approach zero as its distance from the planet approaches infinity. Zero speed implies zero KE, and infinite separation implies zero Ug if our reference separation is infinity. Thus, the total mechanical energy of an object traveling at escape velocity is 0 J. That’s why conservation of energy is the relevant concept.
24. A
The intensity of a wave is proportional to 1/r2, so it will increase as the ambulance approaches. This eliminates (B) and (D). The change in pitch will be determined by the Doppler effect. Pitch is simply another term for frequency, and the Doppler effect says that if the source of a wave and the object detecting the wave are growing closer, then the frequency will increase. Thus, (A) is correct.
25. B
The distance from one crest to another is the wavelength. In this case, that distance is 6 m. Furthermore, you know that v = fλ for any wave. Solving for f gives f = v/λ. Plugging in the known values gives f = (600)/(6) = 100 Hz.
26. D
A wave passing along a string with both ends held in place will have a fundamental frequency of f = v/(2l), where v is the speed of the wave and l is the length of the string. Thus, fundamental frequency is inversely proportional to the length of the string, so the first string, which is twice as long as the second, will have a fundamental frequency that is half of the second string’s. Expressed as a ratio, that is 1:2.
27. B
The frequency of a pendulum is f =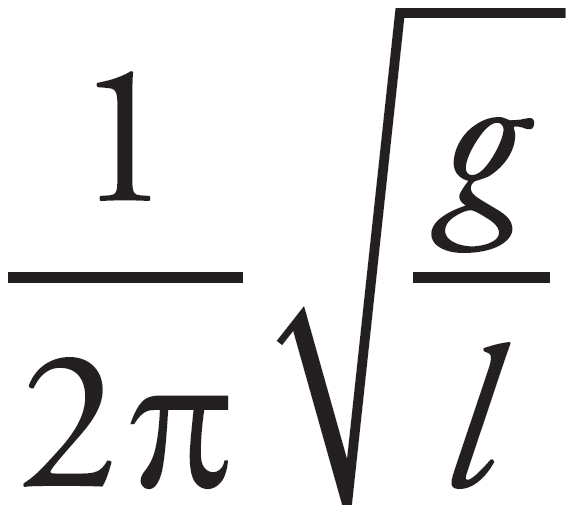 
. Therefore, the change in mass would have no effect on the system, and the others would change the equation to f = 
. Thus, the original frequency f will become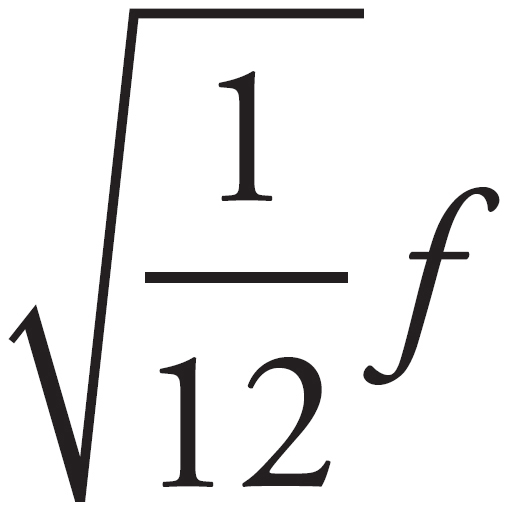 
.
28. D
The net force on each block can be found by using Newton’s Second Law, FNet = ma. The tension in the string can be found by focusing on the hanging mass. You know the net force on it will be FNet = ma = Fg − T = (mg) − T, which means T = (mg) − (ma). Finally, the coefficient of kinetic friction can be found by looking at the top block. For that block, the net force in the horizontal direction will be the same as the overall net force since the two vertical forces (normal and gravity) will cancel out. Thus, you get FNet = ma = T − Ff = T − µFN = T − μmg. The only value in the answers you cannot calculate is the speed of the block when it reaches the edge. In order to compute this value, you would need to know how far from the edge the block is when it begins moving.
29. C
If nothing is moving, then you know that the net force will be 0. Looking first at the forces perpendicular to the plane, you get FN = Fgcosθ = mgcosθ. Next, using Newton’s Second Law and defining “up the ramp” as positive, you can say FNet = T − Fgsinθ − Ff = 0. Solving for tension and plugging in all the variables gives you T = mgsinθ + μmgcosθ.
Next, looking at the hanging block, you can again use Newton’s Second Law to determine that FNet = Fg − T = Mg − (mgsinθ + µmgcosθ) = 0. Thus, solving for μ gives you μ = (Mg − mgsinθ)/(mgcosθ).
30. C
The basic formula for work is W = Fdcosθ, where θ is the angle between the force and the direction of motion. Centripetal force, by definition, is always perpendicular to motion. Therefore, θ will always be 90°, and cos 90° = 0, which means this force cannot do work.
31. B
The force of gravity between two objects is given by Fg = GmM/r2. This comes out to (6.67 × 10−11)(1)(1)/(1)2 = 6.67 × 10−11. Electric force is given by Fe = kqQ/r2. This comes out to (8.99 × 109)(1)(1)/(1)2 = 8.99 × 109. Therefore, in terms of Fg, Fe = [(8.99 × 109)/(6.67 × 10−11)]Fg = (1.35 × 1020)Fg.
32. C
Consider the situation from the perspective of conservation of energy. When it is initially dropped on one end of the planet, the ball has some amount of potential energy and no kinetic energy. When it reaches the center of the Earth, it will have no more potential energy, so all of that energy is now kinetic. Due to inertia, the ball will continue in that direction until the energy has again been converted entirely to potential energy. This would happen just as it reaches the other end of the hole. At that point, it would fall again and the process would repeat infinitely. This is exactly the same motion as an ideal spring system.
33. B
At the top of the ramp, the car will have potential energy PE = mgh. At the bottom, this same amount of energy has been converted into kinetic energy KE = mv2 = mgh. Multiplying both sides by 2 produces mv2 = 2mgh. Finally, divide both sides by r to get mv2/r = 2mgh/r. The first term is the general formula for centripetal force, so the second term must also be equivalent to that force in this situation.
34. B
First, find the net force on the system. Each of the top three blocks will contribute nothing to the net force. The forces on each of the two blocks on the ramp will be the following:
The normal force and the perpendicular component of gravity will cancel out. This leaves just the parallel component of gravity to be a net force. Using Newton’s Second Law, you get FNet = Fg,parallel 2mg sin θ = 5ma. The 2 comes in because there are two blocks on the ramp and each one will contribute the net force discussed earlier. The 5 is necessary because the blocks cannot accelerate individually. Either they all move or none do. Solving for a then gives a = 
gsinθ.
35. A
First, split up v0 into horizontal and vertical components.
vx0 = 20 m/s *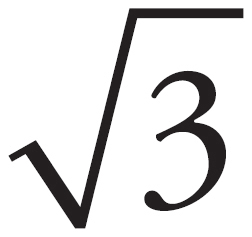 
/2 = 10 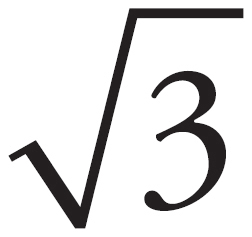m/s, vy0 = 20 m/s * 1/2 = 10 m/s. Then, make a column of vertical values. Take the positive direction to be up.
Vertical
y − y0 = 0 (since it starts and finishes on the ground)
vy0 = 10 m/s
vyf = don’t care
ay = −10 m/s2
t = ?
Plugging these into Big Five #3 gives t = 0 s or 2 s, meaning there are two times at which the elevation of the ball is 0 m. (What is Big Five #3? Or, better yet, what are the 5 Big Five equations that we love so much? We cover them all in Chapter 4: Kinematics. Flip there now to learn more or come back to this page later for further clarification.) Zero seconds corresponds to the instant the ball leaves the ground; 2 seconds corresponds to the time the ball lands on the ground. (Alternatively, you could use Big Five #2 to calculate the time the ball spends traveling up, and then double it to get the total time in flight, as done in Examples 25 and 26 of Chapter 4.)
Finally, make your column of horizontal values.
Horizontal
x − x0 = ?
vx = 10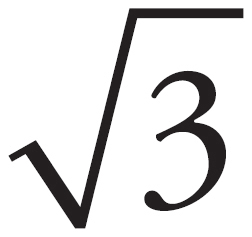 m/s (remember, forward speed is constant for an ideal projectile)
t = 2 s (You just solved for this.)
Solve for the horizontal displacement by using the definition of velocity, x − x0 = vxt, or just d = vxt. This gives d = (10 m/s) * 2 s = 20 m/s.
36. C
For any collision, momentum must be conserved. That means m1v1,0 + m2v2,0 = m1v1,f + m2v2,f. Plugging in known values, that gives (10)(10) + m2(0) = (10)(−2) + m2(8). Solving for m2 gives m2 = 120/8 = 15 kg.
37. A
In a perfectly inelastic collision, the two objects stick together. That is not true in the graph because the objects have different velocities post-collision.
For a perfectly elastic collision, kinetic energy must be conserved. Check this using 
m1v1,02 + m2v2,02 = m1v1,f2 + m2v2,f2. Plugging in the values gives (4)(10)2 + (6)(0)2 = (4)(−2)2 + (6)(8)2. Calculating each side gives 200 + 0 = 8 + 192, which is true. Therefore, kinetic energy is conserved, which makes this a perfectly elastic collision.
38. D
In all of these cases, mechanical energy must be conserved. Thus, the energy required will be mgh for all of them.
39. A
You know TNet = Iα. The torque applied to each is equal, so the sphere with a smaller moment of inertia (I) will experience a greater angular acceleration. Moment of inertia is smaller for an object with its mass concentrated closer to the center, so the solid sphere will have a smaller moment of inertia and thus increase its angular speed more quickly.
40. A
You know Ff = µFN. In both cases, μ will be the same, so you need only concern yourself with FN. There are three vertical forces in this problem: gravity, the normal force, and the vertical component of the applied force. In the first case, that means FN = Fg − mgsinθ = mg − mgsin30 = mg − mg/2 = mg/2.
In the second case, FN = Fg + mgsinθ = mg + mgsin30° = mg + mg/2 = 3mg/2. Therefore, the force in this case will be 3 times what it was in the first case.
41. C
First, the force diagram for this situation would look like the following picture:
The car’s path is horizontal, which means the net force in the vertical direction is zero. Thus, the vertical component of the normal force must be large enough to cancel out weight. This can happen only if the magnitude of the normal force is greater than the gravitational force on the car.
42. B
Using Newton’s Second Law and taking up as the positive direction, you get FNet = ma = T − mg for the first block and FNet = M(−a) = T − Mg for the second block. Subtracting the second equation from the first gives ma + Ma = Mg − mg. Solving for a then gives a =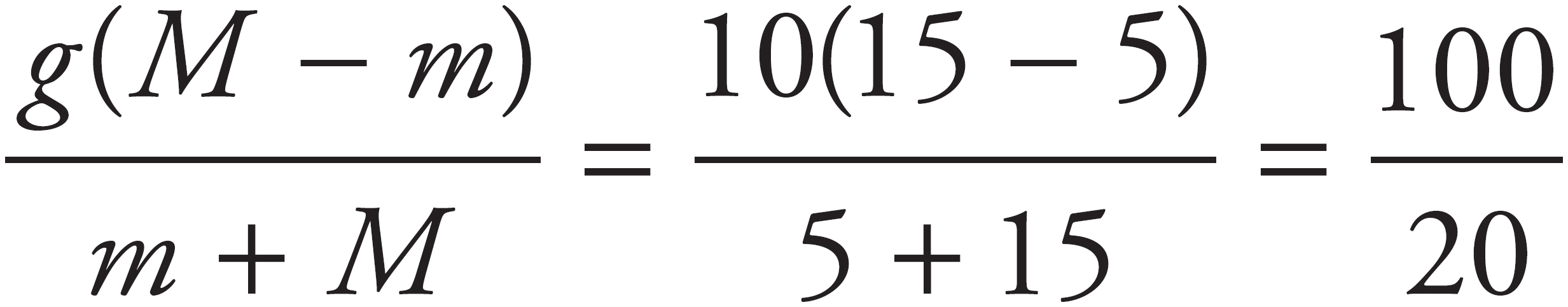 
= 5 m/s2.
From there, the problem is simply a situation of uniform accelerated motion. The blocks need to move a distance of d = 0.5 m each, the starting speed is 0 m/s, and the acceleration is 5 m/s2. Using d = v0t + at2 gives (0.5) = (0)t + (5)t2, so t = 
s.
43. D
The easiest way to solve this is to think qualitatively. A given force stretches each spring by a certain amount. When the springs are connected in series, the increases in length add together, but the tension forces don’t. Thus, the object must move a larger distance to experience the same force from the springs. This is consistent with a reduced spring constant. Choice (D) is the only answer in which the new spring constant is less than the original, k1. If you want to see a proof, consider a situation in which the block is displaced some distance x from the equilibrium position. The first spring would be displaced some amount x1, and the second spring would be displaced some amount x2. Then you can say x = x1 + x2. Knowing that, F = −kx for all springs, you can say x1 = −F/k1 and x2 = −F/k2. Substituting those into the first equation gives x =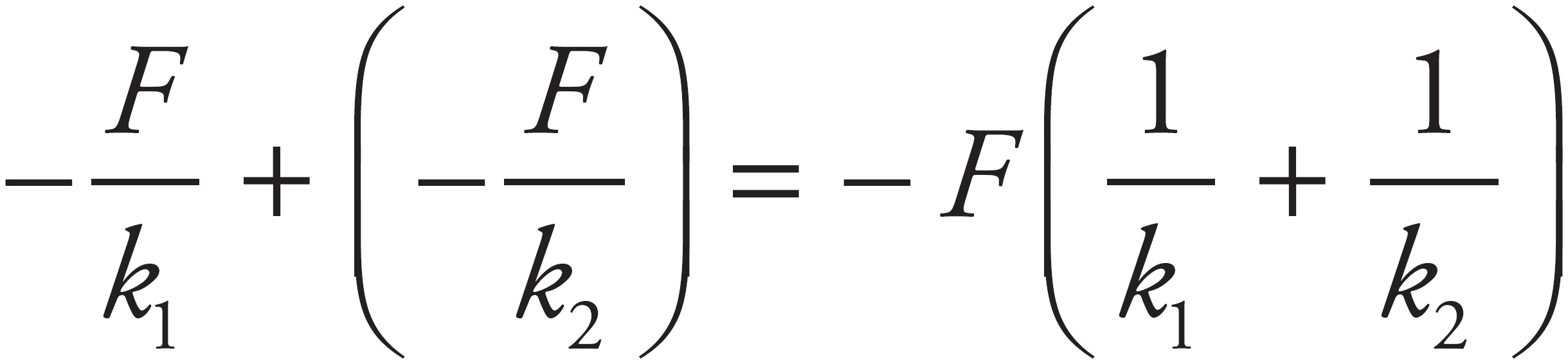 
. Solving for F then gives 
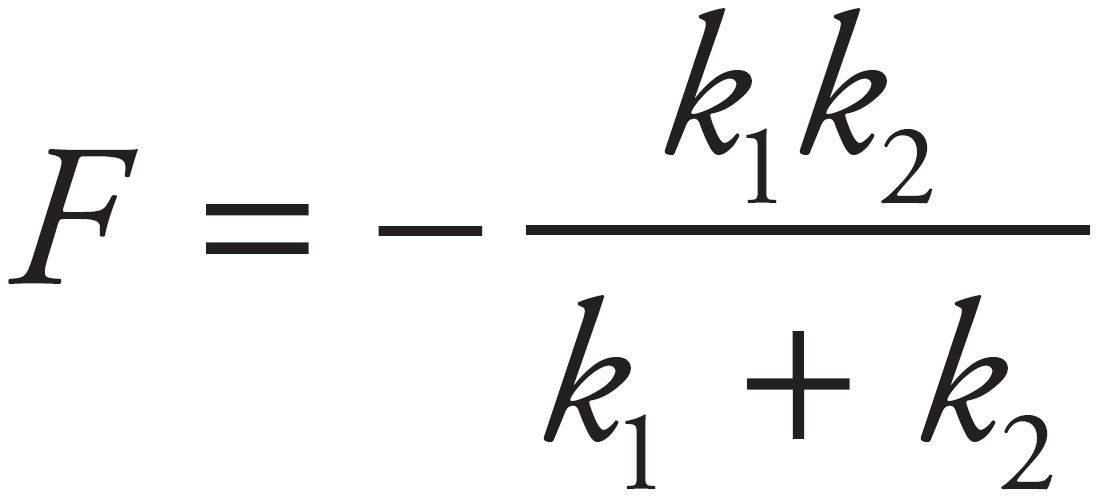. Therefore, the effective spring constant is 
. Plugging in the given values for this problem, you get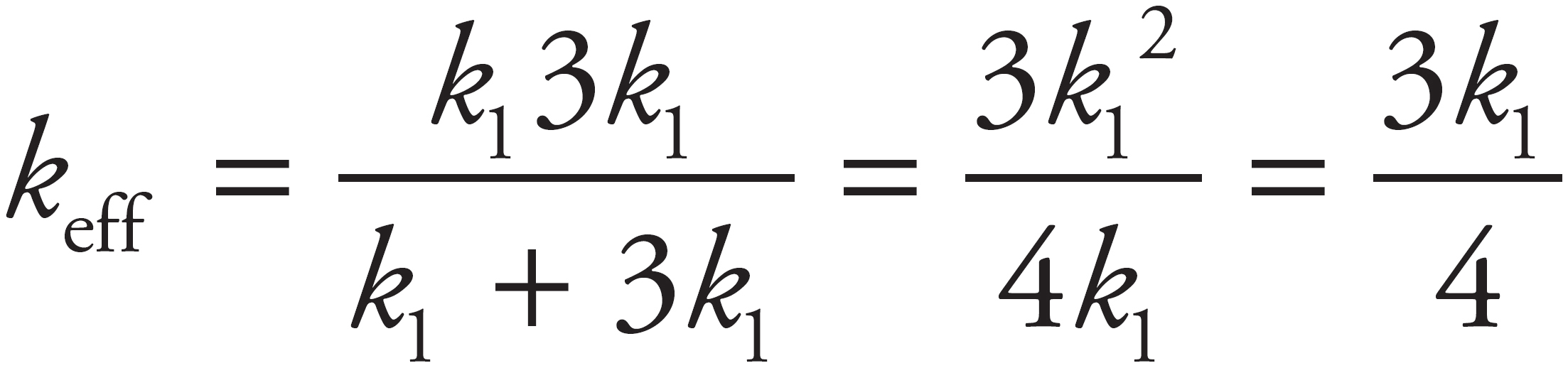 
.
44. A
In this situation, the left-hand block will provide counterclockwise torque, and the right-hand block will provide clockwise torque. Therefore, the two must be equal in magnitude for the system to be balanced. You know that the formula for torque is τ = Frsinθ. In this problem, θ will always be 90 degrees, and sin 90° = 1, so that term will be neglected for the rest of the explanation. Furthermore, the only forces involved in this problem are the forces of gravity on the blocks, and you know Fg = mg.
For (A), the net counterclockwise torque (left side of the system) would be τ = (m2g)(2L) + (m1g)(L) = (2m1g)(2L) + (m1g)(L) = 5m1gL. The clockwise torque (right side of the system) would be τ = (m2g)(L) + (m1g)(2L) = (2m1g)(L) + (m1g)(2L) = 4m1gL. Thus, it would not be balanced. Choice (B) would make both torques 0, so that would be balanced. Choices (C) and (D) both result in the fulcrum being twice as far from m1 as it is from m2, which would counteract the difference in their weights.
45. C
The correct answer is (C). For the left and right sides of the tracks, all three tracks are identical. Looking only at the middle segment of each track, (B) would hold steady throughout. Choice (A) would decrease the speed of the ball as it climbed the hill and then increase the speed back to the original amount as it descended the hill. That means it spends the entire middle segment at a speed less than the initial speed. Choice (C) would be the opposite of (A). The ball gains speed as it descends, and then loses speed as it climbs back up, eventually ending at the original speed. Therefore, it spends the entire middle segment at a speed greater than the initial amount.
46. B, D
On a velocity-versus-time graph, the acceleration at any instant is the slope of the graph at that point. Uniformly accelerated motion means the acceleration is constant, and only straight lines have constant slope. Thus, the correct answers are the two graphs with lines, (B) and (D).
47. A, D
First, the momentum of a system will always be conserved, regardless of the type of collision that takes place. Thus, (D) must be true. You can eliminate (C) because that is true only for perfectly elastic collisions, and this collision is not. Much like linear momentum, angular momentum is always conserved for an entire system. Therefore, (A) is correct, but (B) is not because it does not encompass the entire system.
48. A, D
Choice (B) can eliminated because KE would increase in this situation due to the object’s increasing speed. Choice (C) is also incorrect. In this situation, KE would decrease, but KE = mv2, meaning it would be a linear decrease. Choices (A) and (D) are correct because a graph of a falling object loses more altitude each second than it did the previous second, and gravitational potential energy is proportional to altitude.
49. A, B
First, assume the second charge is positive. If this is the case, both charges will repel the positive test charge. For two repelling forces to cancel out, the test charge must be between the two spheres. Additionally, because Fe = kq1q2/r2, the test charge must be closer to the left-hand sphere to counteract the greater magnitude of charge on the right-hand sphere. Thus, location B would be acceptable for this situation.
Next, assume the second charge is negative. If this is the case, placing the positive test charge anywhere between the two spheres would result in a net force to the right since the electric force from each sphere would be in that direction. That leaves only location A as an acceptable answer in this situation.
50. C, D
Recall that the potential energy of a spring-block system is given by PE = kx2. Using conservation of energy, you can then say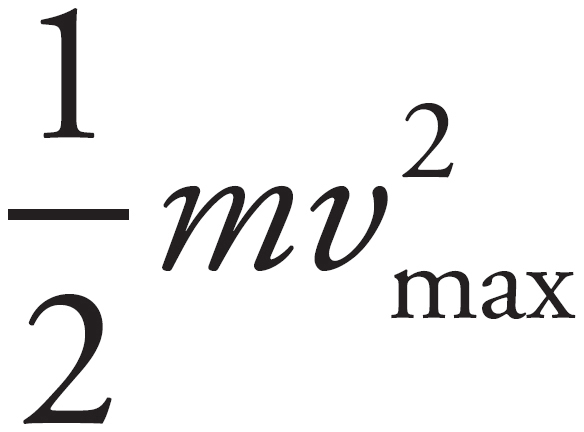 
= kA2, where the left side represents a time when all the energy is kinetic (at equilibrium) and the right side represents when all the energy is potential (at either maximum displacement). Therefore, one of the correct answers is (D). The maximum kinetic energy would give a value for the left side of the equation, and a value for k would leave A as the only variable, which you could then calculate.
Next, recall that the period of a spring system is given by T = 2π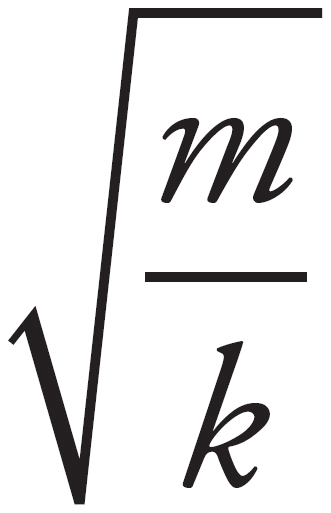
Because m is already known, knowing T would allow you to solve for k. This means (C) is also correct. You could calculate k from the previous equation and then use the maximum kinetic energy in the same way you did in the first paragraph to solve for A.
The defining characteristic of a perfectly elastic collision is that no kinetic energy is lost. Therefore, you must record the speeds of each car before and after the collision. Then, the equation 
+ 
= 
+ 
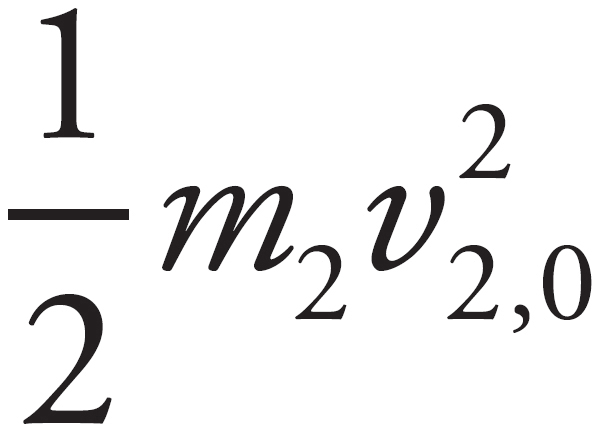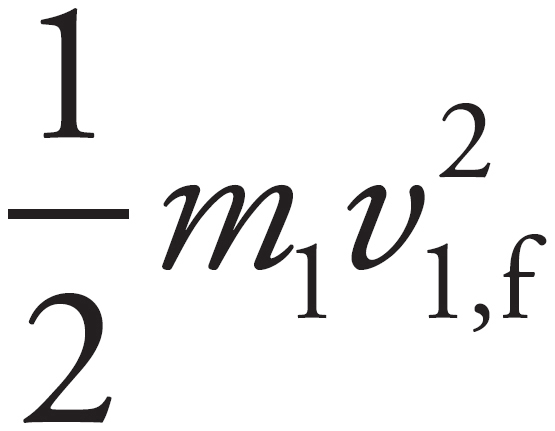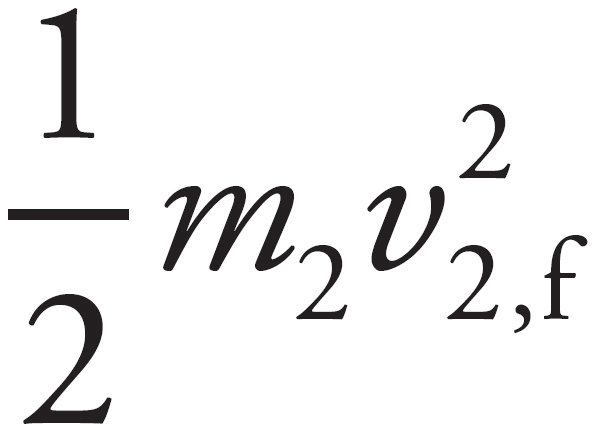can be used to check whether or not it is elastic.
The defining feature of a perfectly inelastic collision is that the objects stick together after the collision. This can be simply observed. If the two cars remain intact post-collision, then the collision is perfectly inelastic.
If neither of the above is true, then it is neither perfectly elastic nor perfectly inelastic.
Finally, a few possible sources of energy loss would be the heat generated as metal is warped, the sound made by the crash, and even the light of any sparks generated.
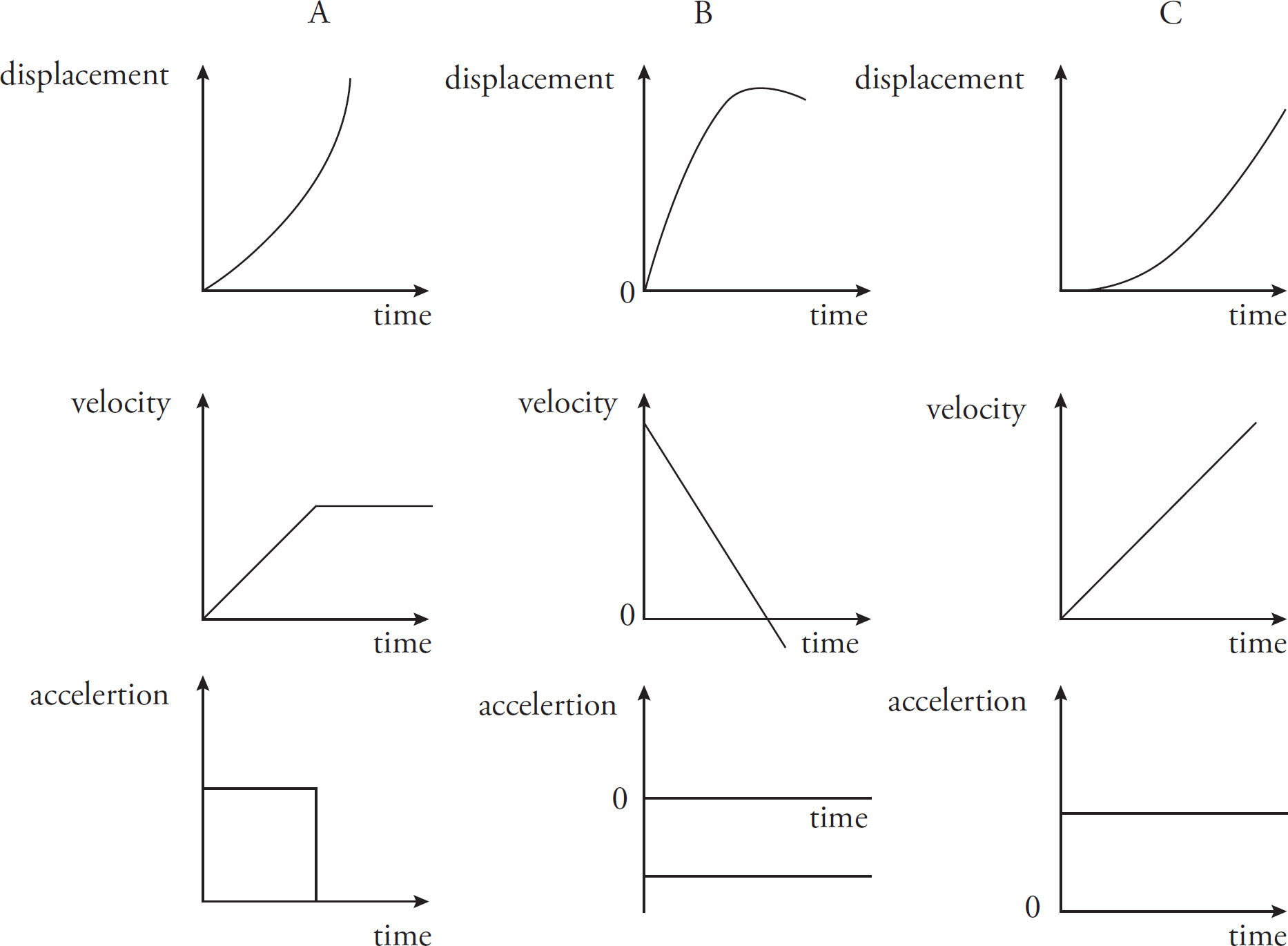
Read the graphs column by column. Object A is on the left, Object B in the middle, and Object C on the right. Memorize the fourth bullet point from the Chapter 4 Summary: the slope of an x versus t graph gives velocity. The slope of a v versus t graph gives acceleration. Object A could be made from a car or plane accelerating up to a certain speed and then maintaining it. Object B could be made from any case of ideal projectile motion where the initial velocity is up. Object C could be anything that uniformly accelerates from a stop.
3. (a)
Your graph should look like this:
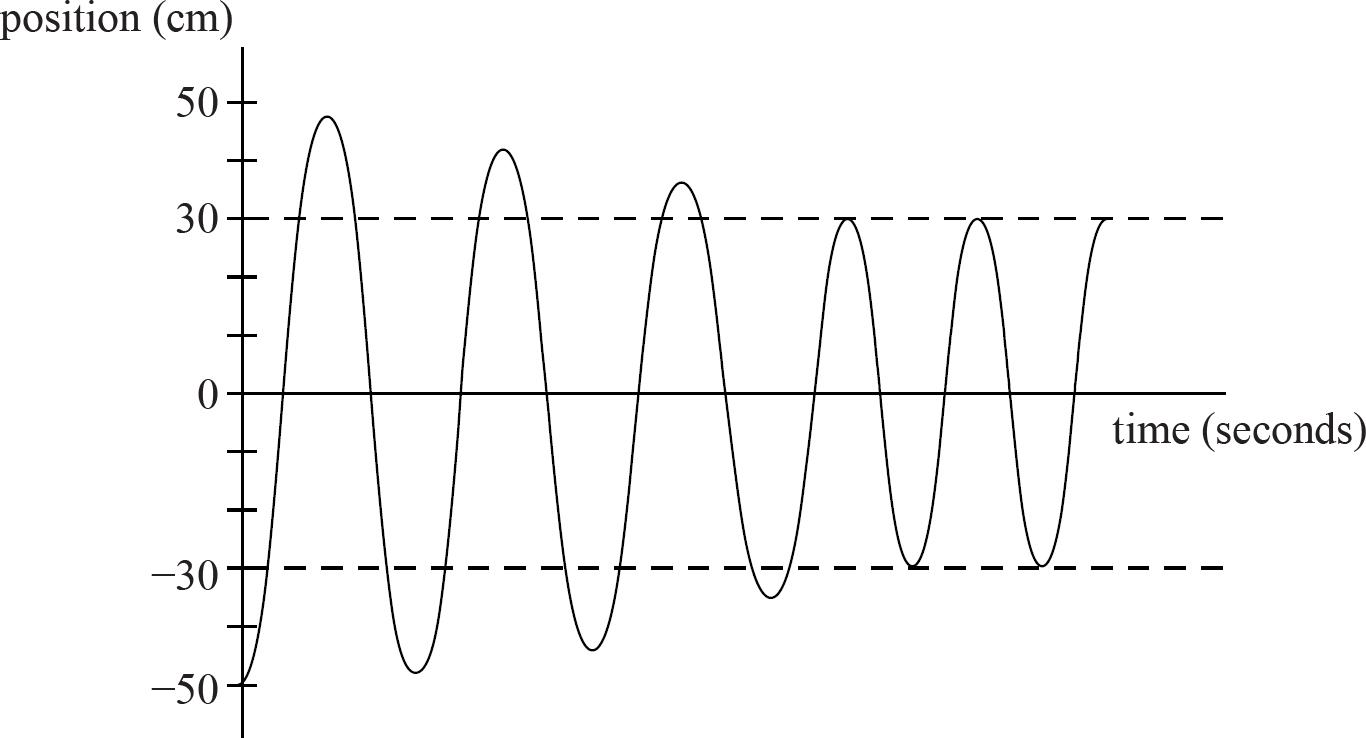
First, it must start at position −50 as the problem indicates. Second, it must go up to a point that is nearly 50 but not quite. This is because the frictional surface will remove some of the energy from the system as the block slides across it. Each time the block swings back to the frictional surface, it will drain a little more of the energy, making the amplitude slowly taper off until it eventually is only on the frictionless surface. Because the frictionless surface extends to 30 cm, it will oscillate between that point and −30 cm indefinitely.
(b)
The energy of a spring system can be found by PE = kA2, where A is the amplitude of the system, so the initial energy of the system will be PE = (100)(0.5)2 = 50(0.25) = 12.5 J. After the oscillations have tapered off, it will have a new energy of PE = (100)(0.3)2 = 50(0.09) = 4.5 J. Therefore, the frictional surface has caused 8 J of energy to be lost.
4. (a)
Using conservation of energy, set the potential energy at the top of the ramp equal to the kinetic energy at the bottom to get mgh = mv2. Solving for v gives v =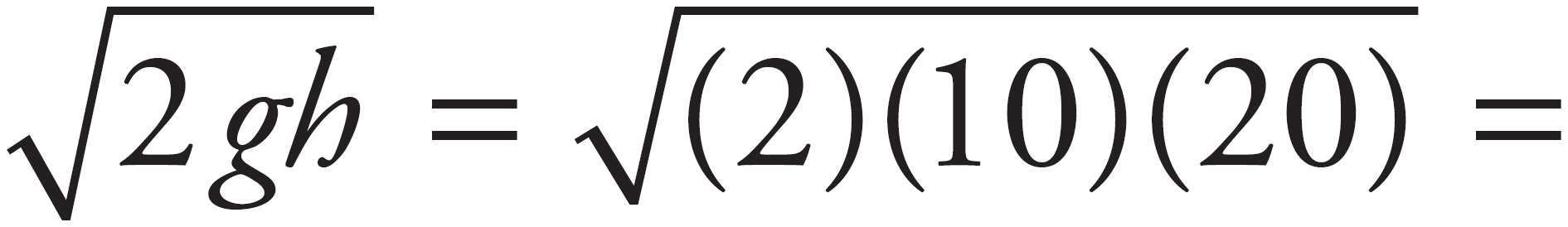 
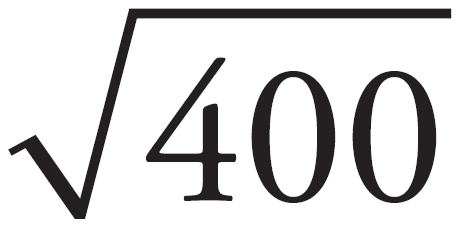= 20 m/s.
(b)
You’re asked to compare a force when the car’s at the bottom of the loop to a force when the car’s at the top of the loop. So start by drawing two force diagrams, one for each situation. The only forces acting on the car are its weight and the normal force from the track. It will be easiest to make the positive direction point toward the center of the loop.
At the bottom, the net force points upward. In terms of vectors, Fnet, bottom = FN, bottom + Fg, but Fg points in the negative direction. So in terms of magnitudes, Fnet, bottom = FN, bottom − Fg. Solving for normal force gives Fnet, bottom + Fg = FN, bottom, or
FN, bottom = Fnet, bottom + mg. (equation 1)
Meanwhile, at the top, net force points downward, and both the normal force and gravitational force point in the positive direction. Thus, Fnet, top = FN, top + Fg → Fnet, top − Fg = FN, top →
FN, top = Fnet, top − mg. (equation 2)
Since mg is positive, this says that at the bottom, normal force is greater than net force, while at the top, normal force is less than net force. It seems like the normal force is greater just after entering the loop than it is at the peak of the loop. However, the net force isn’t the same at both locations, so we don’t know for sure yet.
To prove that your hunch is correct, you need to know the net force at each location. In general, the motion of the car about the loop is not uniform circular motion, because the car’s speed changes. However, at the very bottom and at the very top, the path is momentarily horizontal, so the speed is momentarily constant. Therefore, it’s okay to apply UCM at these two locations only.
At the top, Fnet, top = mvtop2/r; at the bottom, Fnet, bottom = mvbottom2/r. Obviously, the car is going faster at the bottom of the loop than at the top, so vbottom > vtop, so Fnet, bottom > Fnet, top. Therefore, at the bottom, equation (1) says that FN, bottom = (large Fnet) + (positive value). At the top, equation (2) says that FN, top = (small Fnet) − (positive value). Thus, normal force must be greater at the bottom than at the top.
(c)
Mechanical energy will be constant throughout since the track is frictionless, so set the energy at the beginning equal to the energy at the top of the loop. This gives mgh = mg(2r) + mv2, where r is the radius of the circle and v is the speed at the top of the loop.
Next, recall that in order for the car to complete the loop, it must be going fast enough to create some normal force at the top. In general, this equation would look like 
= FN + Fg. If the loop is at its maximum height, FN approaches 0 at the top, so = mg. Moving the r to the other side gives mv2 = mgr.
Substituting this value into the first equation gives mgh = mg(2r) + (mgr). You can cancel out m and g since they appear in every term, so h = 2r + r = 2.5r. The problem shows h = 20, so solving for r gives r = h/(2.5) = (20)/(2.5) = 8 m.
(d)
Conservation of energy can be used to find the speed of the car as it enters the final segment. Set the potential energy of the initial position equal to the potential and kinetic energies as the cart enters the final stretch. This gives mgh1 = mgh2 + mv2. First, realize m can be dropped since it appears in every term. Solving for v then gives v =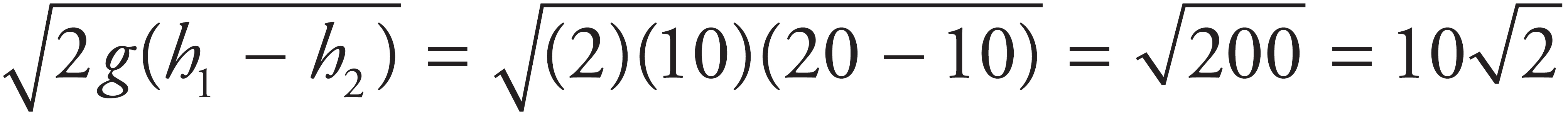 
m/s.
In order for the friction to bring the cart to a stop, it must do work to the cart. You know W = ΔKE, so Fdcosθ = mvf 2 −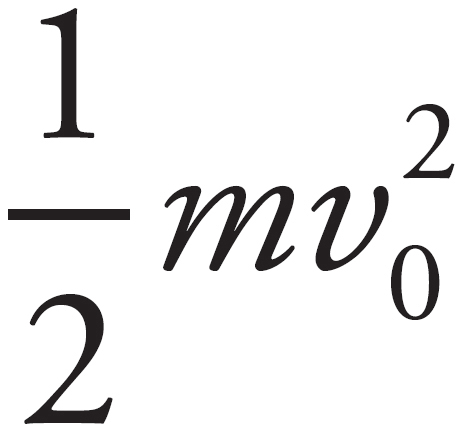 
. The first KE term can be dropped since the final speed will be 0. Substitute Ff = μFN = µmg for F term since friction is the force doing the work. Additionally, θ = 180° because the frictional force will act in a direction opposite the cart’s motion. All of this gives (µmg)dcos180° = −
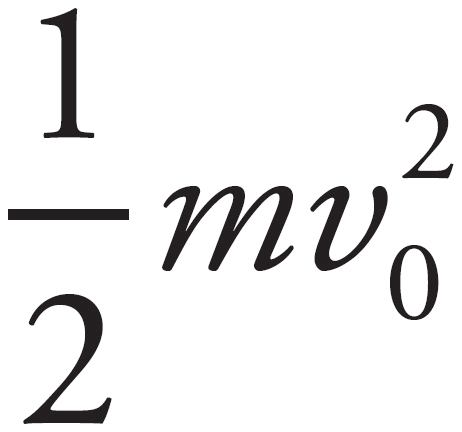. Canceling the m on each side and solving for d then gives d = − v02/(µgcos180°) =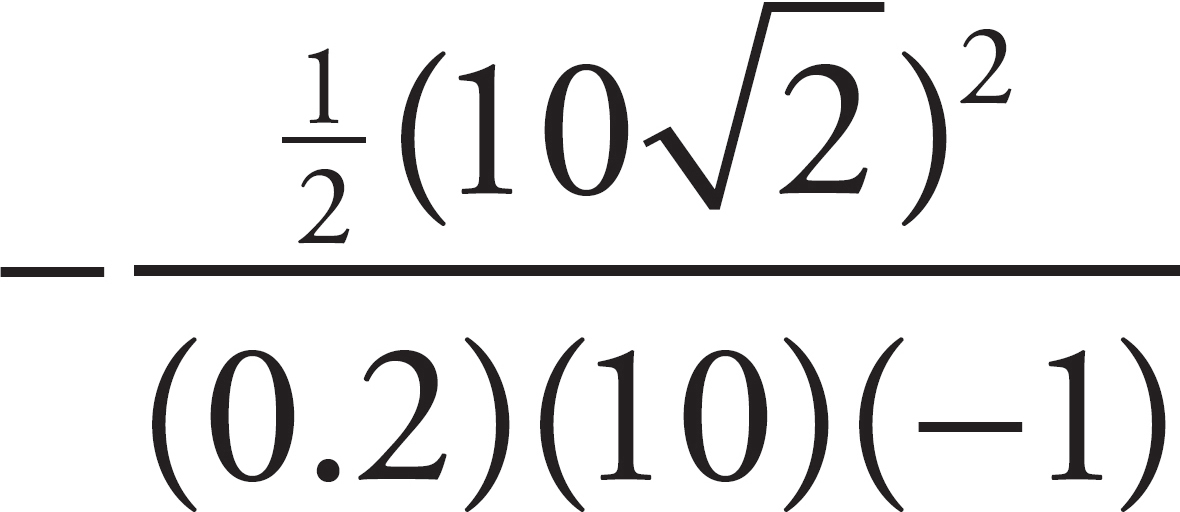 
= 50 m.
5. (a)
First, find the equivalent resistance for the whole circuit. First, the total resistance of the two parallel resistors can be found by using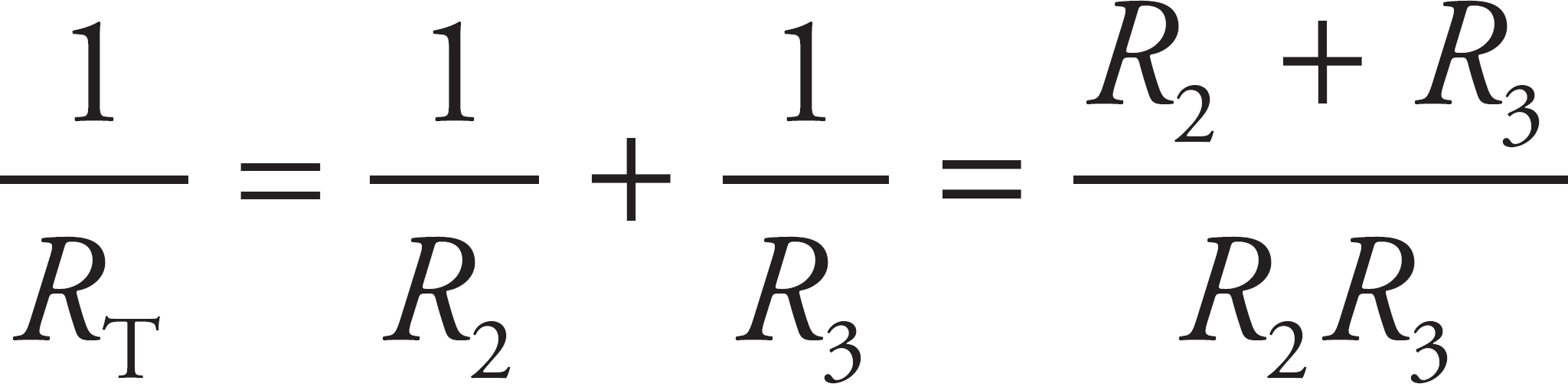 
, which means 
. Then this would be in series with the first resistor, so the equivalent resistance of the whole circuit, Req, would be Req =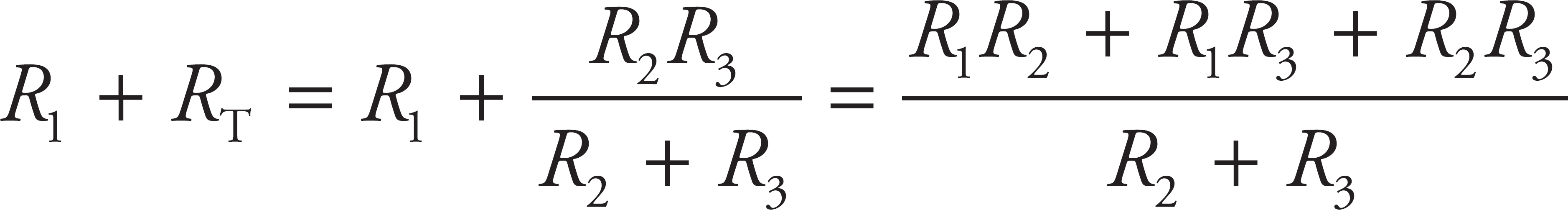 
.
Next, you know from Ohm’s Law that V = IR, so you can say I = V/R =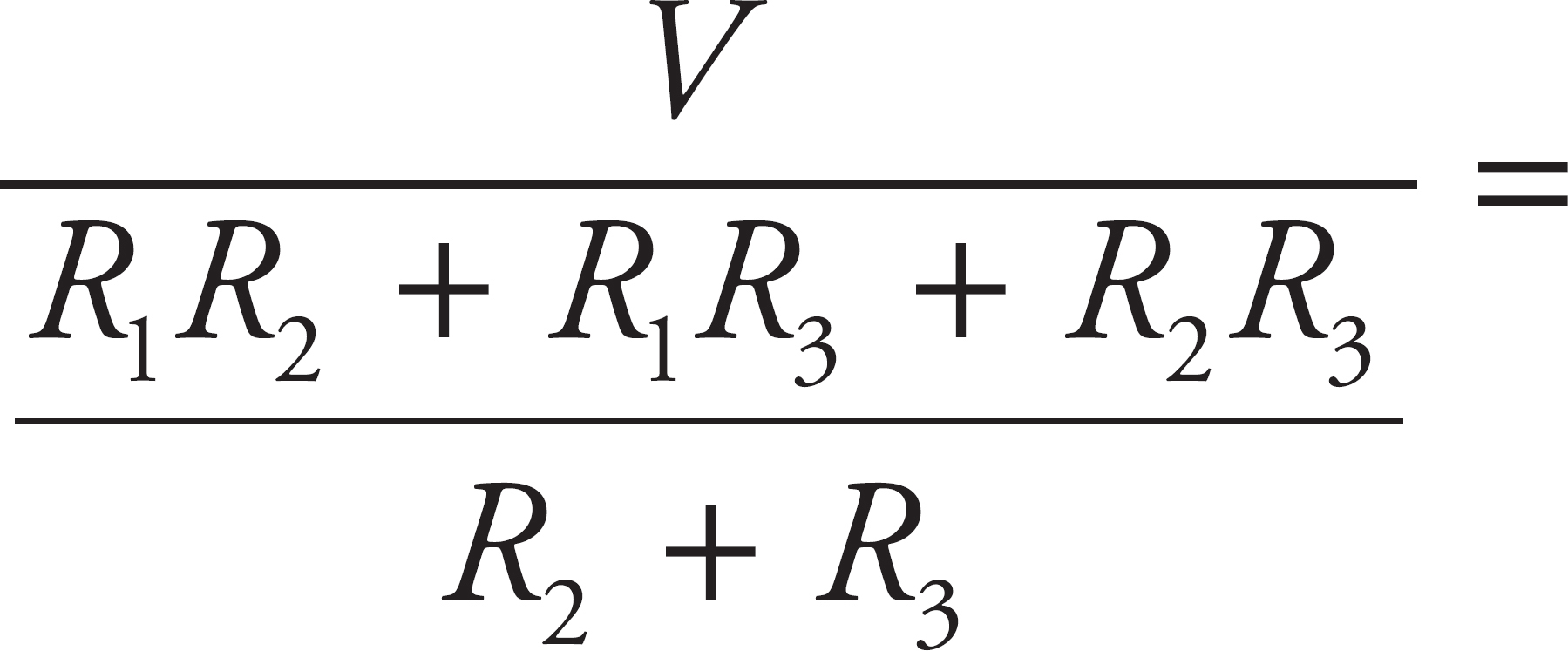 
. This will be the total current of the circuit. Because there are no branches before R1, this will also be the current flowing through that resistor. So the voltage drop of that resistor, V1, can be found by again using Ohm’s Law for that location rather than the whole resistor. This gives V1 = I1R1 = 
.
(b)
The diagram should look like this:
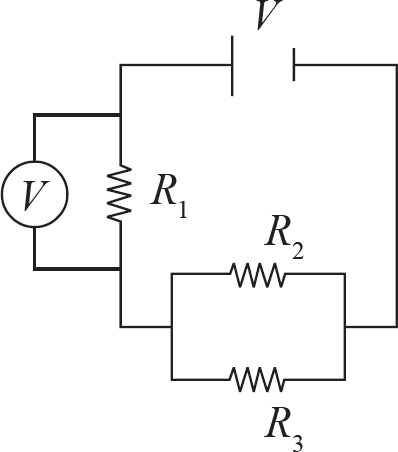
In order to measure the voltage loss of a particular resistor, the voltmeter must be arranged in parallel with that resistor. This is because parallel elements always have equal voltage drops. Thus, whatever voltage drop the device measures will be the same as the voltage drop in the resistor being measured.
(c)
The diagram should look like this:
In order to measure the current passing through a particular resistor, the ammeter must be arranged in series with that resistor. This is because elements in series always have equal currents. Thus, whatever current the device measures will be the same as the current flowing through the resistor being measured.
(d)
For the voltmeter, infinite resistance would be ideal. As in all measurements, you don’t want to disturb the system in any way as you take the measurement. Otherwise, your readings would not be accurate for the original system. Thus, in order to leave the circuit as it was, you need to maintain the flow of current that exists before you started your measurement. Having an infinite resistance would ensure no current flows into the voltmeter, leaving it all on its original path.
For the ammeter, 0 resistance would be ideal. Again, you want to have minimal disturbance on the system. If the ammeter did have resistance, then it would be a source of voltage loss that did not previously exist. In essence, it would be an additional resistor that would need to be considered, forcing you to recalculate everything from the ground up.