IN THIS CHAPTER
Summary: A traveling disturbance in a material is a wave. Waves have observable interference properties.
Key Ideas
The speed of a wave is constant within a given material. When a wave moves from one material to another, its speed and its wavelength change, but its frequency stays the same.
Interference patterns can be observed when a wave goes through two closely spaced slits.
Interference patterns can also be observed when light reflects off of a thin film.
The Doppler effect causes a moving observer to observe a different frequency than a stationary observer.
Relevant Equations
Speed of a wave:
v = λf
Position of bright and dark spots for a double slit:
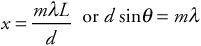
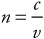
Wavelength of light in a material:
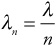
Thin film interference:
2t = mλn
For Physics C Students
Physics C students should have an understanding of the electromagnetic spectrum, electromagnetic waves, and Maxwell’s equations. Wave interference will not be tested on the Physics C exam
What do a flute, a microwave oven, and a radio all have in common? Well, yes, they all would be nice (if unconventional) birthday presents to receive, but more fundamentally, they all rely on waves. Flutes are designed to produce harmonious sound waves, microwaves use electromagnetic waves to cook food, and radios pick up a different frequency of electromagnetic waves and decode those waves into a Top 40 countdown.
This chapter presents information about what waves are and how they interact. Some of this information will seem familiar—for example, waves are characterized by frequency and amplitude, and these are concepts you already know from simple harmonic motion. And for the Physics C students, you’ll see that Maxwell’s equations bring together several ideas you encountered when we discussed electricity and magnetism.
Waves come in two forms: transverse and longitudinal.
Wave: A rhythmic up-and-down or side-to-side motion. Energy is transferred from one particle to another in waves. |
A transverse wave occurs when the particles in the wave move perpendicular to the direction of the wave’s motion. When you jiggle a string up and down, you create a transverse wave. A transverse wave is shown in Figure 23.1.
Figure 23.1 Transverse wave.
Longitudinal waves occur when particles move parallel to the direction of the wave’s motion. Sound waves are examples of longitudinal waves. A good way to visualize how a sound wave propagates is to imagine one of those “telephones” you might have made when you were younger by connecting two cans with a piece of string.1 When you talk into one of the cans, your vocal cords cause air molecules to vibrate back and forth, and those vibrating air molecules hit the bottom of the can, which transfers that back-and-forth vibration to the string. Molecules in the string get squished together or pulled apart, depending on whether the bottom of the can is moving back or forth. So the inside of the string would look like Figure 23.2, in which dark areas represent regions where the molecules are squished together, and light areas represent regions where the molecules are pulled apart.
Figure 23.2 Longitudinal wave.
The terms we use to describe waves can be applied to both transverse and longitudinal waves, but they’re easiest to illustrate with transverse waves. Take a look at Figure 23.3.
Figure 23.3 Wave terminology.
A crest (or a peak) is a high point on a wave, and a trough is a low point on a wave. The distance from peak-to-peak or from trough-to-trough is called the wavelength. This distance is abbreviated with the Greek letter λ (lambda). The distance that a peak or a trough is from the horizontal axis is called the amplitude, abbreviated with the letter A.
The time necessary for one complete wavelength to pass a given point is the period, abbreviated T. The number of wavelengths that pass a given point in one second is the frequency, abbreviated f. The period and frequency of a wave are related with a simple equation, which we first saw when we discussed simple harmonic motion:
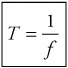
If you take a string and jiggle it just once, so that a single peak travels along the string, you generate a wave pulse. An example of a wave pulse is shown in Figure 23.4.
Figure 23.4 Wave pulse.
A standing wave occurs when you connect one end of a string to a wall and hold the other end in your hand. As you jiggle the string, waves travel along the string, hit the wall, and then reflect off the wall and travel back to you. If you jiggle the string at just the right frequency, you will notice that the string always looks the same, as in Figure 23.5. This is a standing wave.
Figure 23.5 Standing wave.
A wave moves a distance λ in a time T. So the velocity at which a wave travels is just distance over time, or λ/T; more simply, this relation is expressed:
v= λf |
For sound waves moving through air at room temperature, v = 343 m/s; for light waves in a vacuum, v = 3.0 × 108 m/s. Don’t memorize these speeds; just be aware.
When two waves cross each other’s path, they interact with each other. There are two ways they can do this—one is called constructive interference, and the other is called destructive interference.
Constructive interference happens when the peaks of one wave align with the peaks of the other wave. So if we send two wave pulses toward each other as shown in Figure 23.6a,
Figure 23.6a Two wave pulses about to interfere constructively.
then when they meet in the middle of the string they will interfere constructively (Figure 23.6b).
Figure 23.6b Two wave pulses interfering constructively.
The two waves will then continue on their ways (Figure 23.6c).
Figure 23.6c Two wave pulses after interfering constructively.
However, if the peaks of one wave align with the troughs of the other wave, we get destructive interference. For example, if we send the two wave pulses in Figure 23.7a toward each other
Figure 23.7a Two wave pulses about to interfere destructively.
they will interfere destructively (Figure 23.7b),
Figure 23.7b Two wave pulses interfering destructively.
and then they will continue along their ways (Figure 23.7c).
Figure 23.7c Two wave pulses after interfering destructively.
If you play a stringed instrument, you are already familiar with standing waves. Any time you pluck a guitar string or bow on a cello string, you are setting up a standing wave. Standing waves show up a bit on the AP exam, so they’re worth a closer look.
A standing wave occurs when a string is held in place at both ends. When you move the string up and down at certain precise frequencies, you produce a standing wave. Let’s first examine several simple standing waves.
Figure 23.8a shows the simplest standing wave, called the fundamental frequency. The wavelength of this wave, λ1, is twice as long as the distance between the two walls, L.
Figure 23.8a The simplest standing wave.
Notice we labeled our wave with the terms node and antinode.
Node: Point on a standing wave where the string (or whatever the wave is traveling in) does not move at all |
Antinode: Point on a standing wave where the wave oscillates with maximum amplitude |
Figure 23.8b shows the next simplest standing wave.
Figure 23.8b The second simplest standing wave.
Here, the wavelength, λ2, is exactly equal to the distance between the walls, L. The next standing wave in our progression is drawn in Figure 23.8c.
Figure 23.8c The next standing wave in our progression.
Okay, we have a pattern developing here. Notice that the relationship between L, the distance between the walls, and the wavelength of the standing wave is
We can manipulate this equation to say
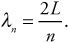
And we know that the velocity of a wave is v = λf. So we can do some more manipulation of variables and come up with this equation:
This equation says that the frequency of the 1st, 2nd, 3rd, or nth standing wave equals n, multiplied by the velocity of the wave, v, divided by two times the distance between the walls, L.
There are two uses of this equation. One is for stringed instruments—the illustrations on the previous pages could be viewed as a guitar string being plucked—and one is for sound in a pipe open at both ends.
If we have sound waves in a pipe that’s closed at one end, the situation looks slightly different. The fundamental frequency is shown in Figure 23.9a.
Figure 23.9a Fundamental frequency in a closed pipe.
And the next simplest standing wave is shown in Figure 23.9b.
Figure 23.9b Next simplest standing wave in a closed pipe.
Notice that we did not have a λ2. When one end of a pipe is closed, we can only have odd values for n. The frequency of the nth standing wave in a closed pipe is
When you have two sound waves of almost, but not quite, equal frequency, you may hear beats.
Beats: Rhythmic interference that occurs when two notes of unequal but close frequencies are played |
If you have a couple of tuning forks of similar—but not identical—frequency to play with, or if you have a couple of tone generators at your disposal, you might enjoy generating some beats of your own. They make a wonderful “wa-wa” sound.
Whenever a fire engine or ambulance races by you with its sirens blaring, you experience the Doppler effect. Similarly, if you enjoy watching auto racing, that “Neeee-yeeeer” you hear as the cars scream past the TV camera is also attributable to the Doppler effect.
Doppler Effect: The apparent change in a wave’s frequency that you observe whenever the source of the wave is moving toward or away from you |
To understand the Doppler effect, let’s look at what happens as a fire truck travels past you (Figures 23.10a and 23.10b).
As the fire truck moves toward you, its sirens are emitting sound waves. Let’s say that the sirens emit one wave pulse when the truck is 50 meters away from you. It then emits another pulse when the truck is 49.99 meters away from you. And so on. Because the truck keeps moving toward you as it emits sound waves, it appears to you that these waves are getting scrunched together.
Figure 23.10a When the fire truck moves toward you, the sound waves get squished together, increasing the frequency you hear.
Then, once the truck passes you and begins to move away from you, it appears as if the waves are stretched out.
Figure 23.10b As the fire truck moves away from you, the sound waves spread apart, and you hear a lower frequency.
Now, imagine that you could record the instant that each sound wave hit you. When the truck was moving toward you, you would observe that the time between when one wave hit and when the next wave hit was very small. However, when the truck was moving away from you, you would have to wait a while between when one wave hit you and when the next one did. In other words, when the truck was moving toward you, you registered that the sirens were making a higher frequency noise; and when the truck was moving away, you registered that the sirens were making a lower frequency noise.
That’s all you really need to know about the Doppler effect. Just remember, the effect is rather small—at normal speeds, the frequency of, say, a 200 Hz note will only change by a few tens of Hz, not hundreds of Hz.
When radio waves are beamed through space, or when X-rays are used to look at your bones, or when visible light travels from a light bulb to your eye, electromagnetic waves are at work. All these types of radiation fall in the electromagnetic spectrum, shown in Figure 23.11.
Figure 23.11 The electromagnetic spectrum.
The unique characteristic about electromagnetic waves is that all of them travel at exactly the same speed through a vacuum—3 × 108 m/s. The more famous name for “3 × 108 m/s” is “the speed of light,” or “c.”
What makes one form of electromagnetic radiation different from another form is simply the frequency of the wave. AM radio waves have a very low frequency and a very long wavelength; whereas, gamma rays have an extremely high frequency and an exceptionally short wavelength. But they’re all just varying forms of light waves.
Long ago, when people still used words like “thence” and “hither,” scientists thought that light was made of particles. About a hundred years ago, at the beginning of the twentieth century, however, scientists began to change their minds. “Light is a wave!” they proclaimed.
Then such physicists as Einstein said, “Actually, light acts as either a particle or a wave, depending on what methods you’re using to detect it.”2 But now, let’s stick to the turn-of-the-twentieth-century notion that light is simply a wave.
The way that physicists showed that light behaves like a wave was through slit experiments. Consider light shining through two very small slits, located very close together— slits separated by tenths or hundredths of millimeters. The light shone through each slit and then hit a screen. But here’s the kicker: rather than seeing two bright patches on the screen (which would be expected if light was made of particles), the physicists saw lots of bright patches. The only way to explain this phenomenon was to conclude that light behaves like a wave.
Look at Figure 23.12a. When the light waves went through each slit, they were diffracted. As a result, the waves that came through the top slit interfered with the waves that came through the bottom slit—everywhere that peaks or troughs crossed paths, either constructive or destructive interference occurred.
Figure 23.12a Light waves interacting in the double-slit experiment.
So when the light waves hit the screen, at some places they constructively interfered with one another and in other places they destructively interfered with one another. That explains why the screen looked like Figure 23.12b.
Figure 23.12b Image on the screen in the double-slit experiment.
The bright areas were where constructive interference occurred, and the dark areas were where destructive interference occurred. Particles can’t interfere with one another—only waves can—so this experiment proved that light behaves like a wave.
When light passes through slits to reach a screen, the equation to find the location of bright spots is as follows.
d sin θ= mλ |
Here, d is the distance between slits, λ is the wavelength of the light, and m is the “order” of the bright spot; we discuss m below. θ is the angle at which an observer has to look to see the bright spot. Usually, the bright spots are pretty close together, and almost directly across from the slits. In this case, the angle θ is small, so we can use the following equation instead. It describe where on the screen you would find patches of constructive or destructive interference.
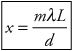
In these equations, x is the distance from the center of the screen wherein you would find the region you’re seeking (either a bright region or a dark region), λ is the wavelength of the light shining through the slits, L is the distance between the slits and the screen, and d is the distance between the slits. The variable m represents the “order” of the bright or dark spot, measured from the central maximum as shown in Figure 23.13. Bright spots get integer values of m; dark spots get half-integer values of m.The central maximum represents m = 0.
Figure 23.13 Variables used in the double-slit equations.
So, for example, if you wanted to find how far from the center of the pattern the first bright spot labeled m = 1 is, you would plug in “1” for m, If you wanted to find the dark region closest to the center of the screen, you would plug in “½” for m.
Single Slits and Diffraction Gratings
Once you understand the double-slit experiment, single slits and diffraction gratings are simple.
A diffraction grating consists of a large number of slits, not just two slits. The locations of bright and dark spots on the screen are the same as for a double slit, but the bright spots produced by a diffraction grating are very sharp dots.
A single slit produces interference patterns, too, because the light that bends around each side of the slit interferes upon hitting the screen. For a single slit, the central maximum is bright and very wide; the other bright spots are regularly spaced, but dim relative to the central maximum.
Light also undergoes interference when it reflects off of thin films of transparent material. Before studying this effect quantitatively, though, we have to examine how light behaves when it passes through different materials.
Light—or any electromagnetic wave—travels at the speed c, or 3 × 108 m/s. But it only travels at this speed through a vacuum, when there aren’t any pesky molecules to get in the way. When it travels through anything other than a vacuum, light slows down. The amount by which light slows down in a material is called the material’s index of refraction.
Index of refraction: A number that describes by how much light slows down when it passes through a certain material, abbreviated n |
The index of refraction can be calculated using this equation.
This says that the index of refraction of a certain material, n, equals the speed of light in a vacuum, c, divided by the speed of light through that material, v.
For example, the index of refraction of glass is about 1.5. This means that light travels 1.5 times faster through a vacuum than it does through glass. The index of refraction of air is approximately 1. Light travels through air at just about the same speed as it travels through a vacuum.
Another thing that happens to light as it passes through a material is that its wavelength changes. When light waves go from a medium with a low index of refraction to one with a high index of refraction, they get squished together. So, if light waves with a wavelength of 500 nm travel through air (nair = 1), enter water (nwater = 1.33), and then emerge back into air again, it would look like Figure 23.14.
Figure 23.14 Light passing through air, into water, and then back into air again. The wavelength of the light changes as it goes from one medium to another.
The equation that goes along with this situation is the following.
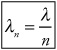
In this equation, λn is the wavelength of the light traveling through the transparent medium (like water, in Figure 23.14), λ is the wavelength in a vacuum, and n is the index of refraction of the transparent medium.
It is important to note that, even though the wavelength of light changes as it goes from one material to another, its frequency remains constant. The frequency of light is a property of the photons that comprise it (more about that in Chapter 25), and the frequency doesn’t change when light slows down or speeds up.
Thin Films
When light hits a thin film of some sort, the interference properties of the light waves are readily apparent. You have likely seen this effect if you’ve ever noticed a puddle in a parking lot. If a bit of oil happens to drop on the puddle, the oil forms a very thin film on top of the water. White light (say, from the sun) reflecting off of the oil undergoes interference, and you see some of the component colors of the light.
Consider a situation where monochromatic light (meaning “light that is all of the same wavelength”) hits a thin film, as shown in Figure 23.15. At the top surface, some light will be reflected, and some will penetrate the film. The same thing will happen at the bottom surface: some light will be reflected back up through the film, and some will keep on traveling out through the bottom surface. Notice that the two reflected light waves overlap; the wave that reflected off the top surface and the wave that traveled through the film and reflected off the bottom surface will interfere.
Figure 23.15 Monochromatic light hitting a thin film.
The important thing to know here is whether the interference is constructive or destructive. The wave that goes through the film travels a distance of 2t before interfering, where t is the thickness of the film. If this extra distance is precisely equal to a wavelength, then the interference is constructive. You also get constructive interference if this extra distance is precisely equal to two, or three, or any whole number of wavelengths.
But be careful what wavelength you use . . . because this extra distance occurs inside the film, we’re talking about the wavelength in the film, which is the wavelength in a vacuum divided by the index of refraction of the film.
The equation for constructive interference turns out to be
2t = mλn |
where m is any whole number, representing how many extra wavelengths the light inside the film went.
So, when does destructive interference occur? When the extra distance in the film precisely equals a half wavelength . . . or one and a half wavelengths, or two and a half wavelengths . . . so for destructive interferences, plug in a half-integer for m.
There’s one more complication. If light reflects off of a surface while going from low to high index of refraction, the light “changes phase.” For example, if light in air reflects off oil (n ~1.2), the light changes phase. If light in water reflects off oil, though, the light does not change phase. For our purposes, a phase change simply means that the conditions for constructive and destructive interference are reversed.
Summary: For thin film problems, go through these steps.
1. Count the phase changes. A phase change occurs for every reflection from low to high index of refraction.
2. The extra distance traveled by the wave in the film is twice the thickness of the film.
3. The wavelength in the film is λn = λ/n, where n is the index of refraction of the film’s material.
4. Use the equation 2t= mn. If the light undergoes zero or two phase changes, then plugging in whole numbers for m gives conditions for constructive interference. (Plugging in half-integers for m gives destructive interference.) If the light undergoes one phase change, conditions are reversed—whole numbers give destructive interference, half-integers, constructive.
Finally, why do you see a rainbow when there’s oil on top of a puddle? White light from the sun, consisting of all wavelengths, hits the oil. The thickness of the oil at each point only allows one wavelength to interfere constructively. So, at one point on the puddle, you just see a certain shade of red. At another point, you just see a certain shade of orange, and so on. The result, over the area of the entire puddle, is a brilliant, swirling rainbow.
Maxwell’s Equations
Okay, we’ll get this out of the way right now: You will not have to solve Maxwell’s equations on the AP Physics exam.These four equations include integrals the likes of which you will not be able to solve until well into college physics, if then. However, you can understand the basic point of each equation, and, most importantly, understand the equations’ greatest consequence.
Accelerating charges produce oscillations of electric and magnetic fields. These oscillations propagate as waves, with speed |
|
Maxwell obtained this wave speed as a mathematical result from the equations. He noticed that, when the experimentally determined constants were plugged in, the speed of his “electromagnetic waves” was identical to the speed of light.3 Maxwell’s conclusion was that light must be an electromagnetic wave.
What are Maxwell’s equations? We’re not even going to write them out, for fear that you might throw down your book in trepidation. If you’re really interested in the integral or differential form of the equations, you will find them in your physics book (or on a rather popular T-shirt). While we won’t write the equations, we’ll gladly summarize what they are and what they mean.
• Maxwell equation 1 is simply Gauss’s law: The net electric flux through a closed surface is proportional to the charge enclosed by that surface.
• Maxwell equation 2 is sometimes called Gauss’s law for magnetism: The net magnetic flux through a closed surface must always be zero. The consequence of this equation is that magnetic poles come in north/south pairs—you cannot have an isolated north magnetic pole.
• Maxwell equation 3 is simply Faraday’s law: A changing magnetic flux through a loop of wire induces an EMF.
• Maxwell equation 4 is partly Ampére’s law, but with an addition called “displacement current” that allows the equation to be valid in all situations. The principal consequence is that just as a changing magnetic field can produce an electric field, a changing electric field can likewise produce a magnetic field.
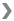Practice Problems
Multiple Choice:
1. A talk show host inhales helium; as a result, the pitch of his voice rises. What happens to the standing waves in his vocal cords to cause this effect?
(A) The wavelength of these waves increases.
(B) The wavelength of these waves decreases.
(C) The speed of these waves increases.
(D) The speed of these waves decreases.
(E) The frequency of these waves decreases.
2. In a pipe closed at one end and filled with air, a 384-Hz tuning fork resonates when the pipe is 22-cm long; this tuning fork does not resonate for any smaller pipes. For which of these closed pipe lengths will this tuning fork also resonate?
(A) 11 cm
(B) 44 cm
(C) 66 cm
(D) 88 cm
(E) 384 cm
3. Monochromatic light passed through a double slit produces an interference pattern on a screen a distance 2.0 m away. The third-order maximum is located 1.5 cm away from the central maximum. Which of the following adjustments would cause the third-order maximum instead to be located 3.0 cm from the central maximum?
(A) doubling the distance between slits
(B) tripling the wavelength of the light
(C) using a screen 1.0 m away from the slits
(D) using a screen 3.0 m away from the slits
(E) halving the distance between slits
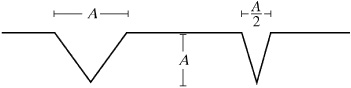
4. The two wave pulses shown above are moving toward each other along a string. When the two pulses interfere, what is the maximum amplitude of the resultant pulse?
(A) (1/2)A
(B) A
(C) (3/2)A
(D) 2A
(E) (5/2)A
5. Laser light is passed through a diffraction grating with 7000 lines per centimeter. Light is projected onto a screen far away. An observer by the diffraction grating observes the first order maximum 25° away from the central maximum.
(a) What is the wavelength of the laser?
(b) If the first order maximum is 40 cm away from the central maximum on the screen, how far away is the screen from the diffraction grating?
(c) How far, measured along the screen, from the central maximum will the second-order maximum be?
Solutions to Practice Problems1. C—The frequency of these waves must go up, because the pitch of a sound is determined by its frequency. The wavelength of the waves in the host’s voice box doesn’t change, though, because the wavelength is dependent on the physical structure of the host’s body. Thus, by v = λf, the speed of the waves in his vocal cords must go up. You can even look it up—the speed of sound in helium is faster than the speed of sound in normal air.
2. C—A wave in a pipe closed at one end has a node at one end and an antinode at the other. 22 cm is the length of the pipe for the fundamental oscillation, which looks like this:
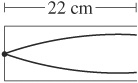
You can see that 1/2 of a “hump” is contained in the pipe, so the total wavelength (two full “humps”) must be 88 cm. The next harmonic oscillation occurs when there is again a node at one end of the pipe and an antinode at the other, like this:
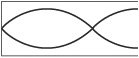
This pipe contains 1½ “humps,” so its length equals three-quarters of the total wavelength. The pipe length is thus 66 cm.
3. E—Use the equation
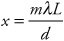
Here m = 3 because we are dealing with the third-order maximum. We want to double the distance to this third-order maximum, which means we want to double x in the equation. To do this, halve the denominator; d in the denominator represents the distance between slits.
4. D—When wave pulses interfere, their amplitudes add algebraically. The question asks for the maximum amplitude, so the widths of the pulses are irrelevant. When both pulses are right on top of one another, each pulse will have amplitude A; these amplitudes will add to a resultant of 2A.
5. (a) Use d sin θ = mλ Here d is not 7000! d represents the distance between slits. Because there are 7000 lines per centimeter, there’s 1/7000 centimeter per line; thus, the distance between lines is 1.4 × 10¯4 cm, or 1.4 × 10¯6 m. θ is 25° for the first-order maximum, where m= 1. Plugging in, you get a wavelength of just about 6 × 10¯7 m, also known as 600 nm. (b) This is a geometry problem.
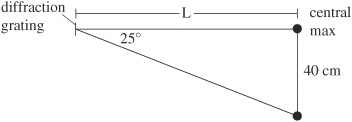
tan 25° = (40 cm)/L; solve for L to get 86 cm, or about 3 feet.
(c) Use d sin θ = mλ; solve for θ using m = 2, and convert everything to meters. We get sin θ= 2(6.0 × 10¯7 m)/(1.4 × 10¯6 m). The angle will be 59°. Now, use the same geometry from part (b) to find the distance along the screen: tan 59° = x/(0.86 m), so x = 143 cm. (Your answer will be counted correct if you rounded differently and just came close to 143 cm.)
Rapid Review• Waves can be either transverse or longitudinal. Transverse waves are up–down waves, like a sine curve. Longitudinal waves are push–pull waves, like a sound wave traveling through the air.
• When two waves cross paths, they can interfere either constructively or destructively. Constructive interference means that the peaks of the waves line up, so when the waves come together, they combine to make a wave with bigger amplitude than either individual wave. Destructive interference means that the peak of one wave lines up with the trough of the other, so when the waves come together, they cancel each other out.
• Standing waves occur when a wave in a confined space (for example, on a violin string or in a pipe) has just the right frequency so that it looks the same at all times. The simplest standing wave possible in a situation is called the fundamental frequency.
• The Doppler effect describes what happens when the source of a wave—such as a fire truck’s siren—is moving relative to you. If the source moves toward you, you perceive the waves to have a higher frequency than they really do, and if the source moves away from you, you perceive the waves to have a lower frequency than they really do.
• All electromagnetic waves travel at a speed of 3 × 108 m/s in a vacuum.
• The double-slit experiment demonstrates that light behaves like a wave.
• When light travels through anything other than a vacuum, it slows down, and its wavelength decreases. The amount by which light slows down as it passes through a medium (such as air or water) is related to that medium’s index of refraction.
• Thin films can cause constructive or destructive interference, depending on the thickness of the film and the wavelength of the light. When solving problems with thin films, remember to watch out for phase changes.
• Maxwell’s equations, which include among them Gauss’s law, Faraday’s law, and a modified version of Ampére’s law, predict that accelerating charges produce electromagnetic waves that travel at a speed equal to 3 × 108 m/s.
