IN THIS CHAPTER
Summary: Atoms and subatomic particles sometimes obey rules that aren’t relevant to larger objects.
Key ideas
Electrons occupy energy levels in atoms. In order to change energy levels, electrons must absorb or emit photons.
The energy of a photon is given by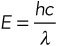 
where hc = 1240 eV·nm.
Draw an energy level diagram with every atomic physics problem.
Three types of nuclear decay can occur: Alpha, Beta, and Gamma.
Charge and momentum are conserved in nuclear decay.
Mass-energy is conserved in nuclear decay. The conversion between energy and mass is E = mc2.
Relevant Equations
Energy of a photon:
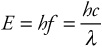
Momentum of a photon:
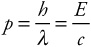
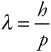
Energy-mass conversion:
E = mc2
Atomic and nuclear physics takes us into the bizarre world of the very, very small. This is the realm where the distinction between waves and particles gets fuzzy, where things without mass can have momentum, and where elements spontaneously break apart.
But even if the phenomena seem bizarre, the physics that describes them, fortunately, isn’t. As far as the AP exam is concerned (and this, again, is a topic that appears exclusively on the Physics B exam), you won’t be writing wacky equations or using lots of cryptic symbols. The math tends to be pretty straightforward, and, as we show you in this chapter, there really are only a few concepts you need to know to answer any question the AP exam could throw at you. So there’s nothing to worry about . . . after all, it’s only nuclear physics, right?
We already introduced the key subatomic particles in Chapter 20, when we first discussed the concept of electric charge. But we review them briefly here.
Atoms, as you know, are the fundamental units that make up matter. An atom is composed of a small, dense core, called the nucleus, along with a larger, diffuse “cloud” of electrons that surrounds the nucleus. The nucleus of an atom is made up of two types of subatomic particles: protons and neutrons. Protons are positively charged particles, neutrons carry no charge, and electrons are negatively charged. For an atom to be electrically neutral, therefore, it must contain an equal number of protons and electrons. When an atom is not electrically neutral, it is called an ion; a positive ion has more protons than electrons, and a negative ion has more electrons than protons.
One particle we didn’t introduce in Chapter 20 is the photon. A photon is a particle of light.1 Photons have no mass, but they can transfer energy to or from electrons.
Table 25.1 summarizes the properties of the four subatomic particles. Note that the mass of a proton (and, similarly, the mass of a neutron) equals one atomic mass unit, abbreviated “1 amu.” This is a convenient unit of mass to use when discussing atomic physics.
Table 25.1 Properties of the Subatomic Particles
The electron-volt, abbreviated eV, is a unit of energy that’s particularly useful for problems involving subatomic particles. One eV is equal to the amount of energy needed to change the potential of an electron by one volt. For example, imagine an electron nearby a positively charged particle, such that the electron’s potential is 4 V. If you were to push the electron away from the positively charged particle until its potential was 5 V, you would need to use 1 eV of energy.
1 eV = 1.6 × 10-19 J |
The conversion to joules shows that an eV is an itty-bitty unit of energy. However, such things as electrons and protons are itty-bitty particles. So the electron-volt is actually a perfectly-sized unit to use when talking about the energy of a subatomic particle.
The electrons in an atom can only have certain, specific amounts of energy. This is an unusual concept—if an electron is whirling around an atom with a given amount of energy, couldn’t you just nudge it slightly to give it a tiny bit more energy? No, you can’t. To understand what we mean, look at Figure 25.1.
Figure 25.1 Energy levels in a hypothetical atom.
In Figure 25.1, we’ve drawn a few of the energy levels of a hypothetical atom. Let’s start by looking at E1. This is the lowest energy level, and it is called the ground state energy of the atom. When an electron is sitting as close to the nucleus as possible, and when it’s completely unexcited, it will have the energy of E1, –10 eV.
To increase the energy of the electron—to move the electron into a higher energy level—energy must somehow be transferred to the electron. This energy transfer is done by a photon. To jump up in energy, an electron absorbs a photon, and to drop down in energy, an electron emits a photon.
The energy diagram in Figure 25.1 tells us that to get to E2 from the ground state, an electron must absorb a photon carrying 3 eV—and only 3 eV!—of energy. If a photon with an energy of 2.9 eV comes along and knocks into the electron, nothing will happen. Similarly, if a photon with an energy of 3.1 eV comes along, nothing will happen. It’s all or nothing; either the electron gets just the right amount of energy to go from one energy level to the next, or it doesn’t.
How does the electron get from the ground state to E3? There are two ways. The electron could first absorb a photon with an energy of 3 eV, taking it from E1 to E2, and then it could absorb another photon with an energy of 1 eV, taking it from E2 to E3. Or, the electron could start in E1 and simply absorb a photon with an energy of 4 eV.
We’ve been talking about photons having certain energies, but we haven’t yet told you how to figure out the energy of a photon. Here’s the formula:
E = hf |
This formula tells us that the energy of a photon is equal to Planck’s constant, h, which is 6.63 × 10-34 J-s (this value is given to you on the constants sheet), multiplied by the frequency of the photon. You should remember from Chapter 23 that the frequency of a wave is related to the wavelength by the formula
v= λf
For light, the velocity is c, or 3 × 108 m/s, so we can instead write
c= λf
This means that we can rewrite the equation for the energy of a photon to read
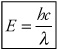
These formulas tell us that a photon with a high frequency, and therefore with a small wavelength, is higher in energy than a photon with a low frequency and long wavelength. So gamma rays, for example, are a lot higher energy than radio waves because gamma rays have a higher frequency.
Okay, let’s try these formulas with a problem.
What wavelength of light must an electron absorb in order to get from E1 to E2 in Figure 25.1? |
This is a simple plug-and-chug problem. Figure 25.1 gives us the energy levels, and we just need to use our formula to find the wavelength of the absorbed photon. But what value do we use for the energy? –10 eV? –7 eV? Wrong . . . the value we use is the energy of the jump, not the energy of one of the states. To get from E1 to E2, an electron must absorb 3 eV of energy, so that’s the value we use in the formula:
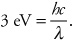
At this point, the problem is simply a matter of converting units and using your calculator. However, solving it is a lot easier if you know that the quantity hc equals 1240 eV-nm. (Check the math yourself, just to be sure.) This value is on the constants sheet, and it is very important to know! Look at how, by knowing this value, we can solve for the photon’s wavelength very quickly.
In other words, for an electron in Figure 25.1 to go from the ground state to E2, it must absorb light with a wavelength of exactly 410 nm, which happens to be a lovely shade of violet.
If you look back at Figure 25.1, you might wonder what’s going on in the gap between E3 and E∞. In fact, this gap is likely filled with lots more energy levels—E4, E5, E6 . . . However, as you go up in energy, the energy levels get squeezed closer and closer together (notice, for example, how the energy gap between E1 and E2 is greater than the gap between E2 and E3). However, we didn’t draw all these energy levels, because our diagram would have become too crowded.
The presence of all these other energy levels, though, raises an interesting question. Clearly, an electron can keep moving from one energy level to the next if it absorbs the appropriate photons, getting closer and closer to E∞. But can it ever get beyond E∞? That is, if an electron in the ground state were to absorb a photon with an energy greater than 10 eV, what would happen?
The answer is that the electron would be ejected from the atom. It takes exactly 10 eV for our electron to escape the electric pull of the atom’s nucleus—this minimum amount of energy needed for an electron to escape an atom is called the ionization energy2—so if the electron absorbed a photon with an energy of, say, 11 eV, then it would use 10 of those eV to escape the atom, and it would have 1 eV of leftover energy. That leftover energy takes the form of kinetic energy.
An electron in the ground state of the atom depicted in Figure 25.1 absorbs a photon with an energy of 11 eV. The electron is ejected from the atom. What is the speed of the ejected electron? |
As we said above, it takes 10 eV for our electron to escape the atom, which leaves 1 eV to be converted to kinetic energy. The formula for kinetic energy requires that we use values in standard units, so we need to convert the energy to joules.
If we plug in the mass of an electron for m, we find that v = 5.9 × 105 m/s. Is that a reasonable answer? It’s certainly quite fast, but electrons generally travel very quickly. And it’s several orders of magnitude slower than the speed of light, which is the fastest anything can travel. So our answer seems to make sense.
The observation that electrons, when given enough energy, can be ejected from atoms was the basis of one of the most important discoveries of twentieth century physics: the photoelectric effect.
Photoelectric Effect: Energy in the form of light can cause an atom to eject one of its electrons, but only if the frequency of the light is above a certain value. |
This discovery was surprising, because physicists in the early twentieth century thought that the brightness of light, and not its frequency, was related to the light’s energy. But no matter how bright the light was that they used in experiments, they couldn’t make atoms eject their electrons unless the light was above a certain frequency. This frequency became known, for obvious reasons, as the cutoff frequency. The cutoff frequency is different for every type of atom.
A metal surface has a work function of 10 eV. What is the cutoff frequency for this metal? |
Remembering that hc equals 1240 eV·nm, we can easily find the wavelength of a photon with an energy of 10 eV:
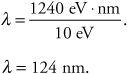
Using the equation c = λf, we find that f = 2.42 × 1015 Hz. So any photon with a frequency equal to or greater than 2.42 × 1015 Hz carries enough energy to eject a photon from the metal surface.
Given that photons can “knock” an electron away from a nucleus, it might seem reasonable to talk about the momentum of a photon. Photons don’t have mass, of course, but the momentum of a photon can nonetheless be found by this equation:
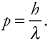
The momentum of a photon equals Planck’s constant divided by the photon’s wavelength. You can rearrange this equation a bit to show that the energy of a photon, which equals hc/λ, also equals the photon’s momentum times c.
We’ve been discussing over the past few pages how light, which acts like a wave, also has the characteristics of particles. As it turns out, things with mass, which we generally treat like particles, also have the characteristics of waves. According to de Broglie, a moving mass behaves like a wave. The wavelength of a moving massive particle, called its de Broglie wavelength, is found by this formula:
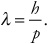
So an object’s de Broglie wavelength equals Planck’s constant divided by the object’s momentum. For a massive particle, momentum p = mv.Note that the formula above is valid even for massless photons — it’s just a rearrangement of the definition of the photon’s momentum. What’s interesting here is that the formula can assign a “wavelength” even to massive particles.
Okay, sure, massive particles behave like waves . . . so how come when you go for a jog, you don’t start diffracting all over the place?
Let’s figure out your de Broglie wavelength. We’ll assume that your mass is approximately 60 kg and that your velocity when jogging is about 5 m/s. Plugging these values into de Broglie’s equation, we find that your wavelength when jogging is about 10-36 m, which is way too small to detect.3
Only subatomic particles have de Broglie wavelengths large enough to actually be detected. Moving neutrons can be diffracted, but you can’t.
When physicists first investigated nuclear decay in the early twentieth century, they didn’t quite know what they were seeing. The subatomic particles (protons, neutrons, electrons, and so forth) had not been definitively discovered and named. But, physicists did notice that certain kinds of particles emerged repeatedly from their experiments. They called these particles alpha, beta, and gamma particles.
Years later, physicists found out what these particles actually are:
• Alpha particle, α: two protons and two neutrons stuck together
• Beta particle, β: an electron or a positron4
• Gamma particle, γ: a photon
Be sure you recall the properties of these particles; if you have to, look in the glossary for a reminder. A couple of observations: The alpha particle is by far the most massive; the gamma particle is both massless and chargeless.
Nuclear Notation
The two properties of a nucleus that are most important are its atomic number and its mass number. The atomic number, Z, tells how many protons are in the nucleus; this number determines what element we’re dealing with because each element has a unique atomic number. The mass number, A, tells the total number of nuclear particles a nucleus contains. It is equal to the atomic number plus the number of neutrons in the nucleus. Isotopes of an element have the same atomic number, but different mass numbers.
A nucleus is usually represented using the following notation:
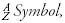
where “symbol” is the symbol for the element we’re dealing with. For example,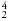 
He represents helium with two protons and two neutrons. A different isotope of helium might be 
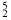He, which contains three neutrons.
Now, you don’t have to memorize the periodic table, nor do you have to remember what element is number 74.5 But you do have to recognize what’s wrong with this nucleus: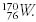 
Since we just told you in the footnote that tungsten is element 74, then an element with atomic number 76 can’t be tungsten!
Alpha decay happens when a nucleus emits an alpha particle. Since an alpha particle has two neutrons and two protons, then the daughter nucleus (the nucleus left over after the decay) must have two fewer protons and two fewer neutrons than it had initially.
|
The answer is found by simple arithmetic. The atomic number decreases by two, to 90. The mass number decreases by four, to 234. (The element formed is thorium, but you don’t have to know that.) This alpha decay can be represented by the equation below:
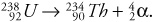
Beta Decay
In beta decay, a nucleus emits either a positron (β+ decay) or an electron (β- decay). Because an electron is not a normal nuclear particle, the total mass number of the nucleus must stay the same after beta decay. But the total charge present must not change— charge is a conserved quantity. So, consider an example of neon (Ne) undergoing β+ decay:
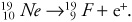
Here e+ indicates the positron. The mass number stayed the same. But look at the total charge present. Before the decay, the neon nucleus has a charge of +10. After the decay, the total charge must still be +10, and it is: +9 for the protons in the Fluorine (F), and +1 for the positron. Effectively, then, in β+ decay, a proton turns into a neutron and emits a positron.
For β¯ decay, a neutron turns into a proton, as in the decay process important for carbon dating:
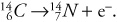
The mass number of the daughter nucleus didn’t change. But the total charge of the carbon nucleus was initially +6. Thus, a total charge of +6 has to exist after the decay, as well. This is accounted for by the electron (charge –1) and the nitrogen (charge +7).
In beta decay, a neutrino or an antineutrino also must be emitted to carry off some extra energy. But that doesn’t affect the products of the decay, just the kinetic energy of the products.
Gamma Decay
A gamma particle is a photon, a particle of light. It has no mass and no charge. So a nucleus undergoing gamma decay does not change its outward appearance:
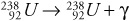
However, the photon carries away some energy and momentum, so the nucleus recoils.
We can imagine that the nuclei in the last few examples are at rest before emitting alpha, beta, or gamma particles. But when the nuclei decay, the alpha, beta, or gamma particles come whizzing out at an appreciable fraction of light speed.6 So, the daughter nucleus must recoil after decay in order to conserve momentum.
But now consider energy conservation. Before decay, no kinetic energy existed. After the decay, both the daughter nucleus and the emitted particle have gobs of kinetic energy.7Where did this energy come from? Amazingly, it comes from mass.
The total mass present before the decay is very slightly greater than the total mass present in both the nucleus and the decay particle after the decay. That slight difference in mass is called the mass defect, often labeled Am. This mass is destroyed and converted into kinetic energy.
How much kinetic energy? Use Einstein’s famous equation to find out. Multiply the mass defect by the speed of light squared:
E = (Δm)c2.
And that is how much energy is produced.
Practice ProblemsMultiple Choice:
1. Which of the following lists types of electromagnetic radiation in order from least to greatest energy per photon?
(A) red, green, violet, ultraviolet, infrared
(B) ultraviolet, infrared, red, green, violet
(C) red, green, violet, infrared, ultraviolet
(D) infrared, red, green, violet, ultraviolet
(E) ultraviolet, violet, green, red, infrared
Questions 2 and 3
In a nuclear reactor, uranium fissions into krypton and barium via the reaction
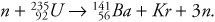
2. What are the mass number A and atomic number Z of the resulting krypton nucleus?
3. How much mass is converted into the kinetic energy of the resulting nuclei?
(A) 1 amu
(B) 2 amu
(C) 3 amu
(D) zero
(E) much less than 1 amu
4. 
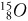decays via β+ emission. Which of the following is the resulting nucleus?
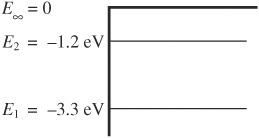
5. A hypothetical atom has two energy levels, as shown above.
(a) What wavelengths of electromagnetic radiation can be absorbed by this atom? Indicate which of these wavelengths, if any, represents visible light.
(b) Now, monochromatic 180-nm ultraviolet radiation is incident on the atom, ejecting an electron from the ground state. What will be
i. the ejected electron’s kinetic energy
ii. the ejected electron’s speed
iii. the incident photon’s speed
For parts (c) and (d), imagine that the 180-nm radiation ejected an electron that, instead of being in the ground state, was initially in the –1.2 eV state.
(c) Would the speed of the ejected electron increase, decrease, or stay the same? Justify your answer briefly.
(d) Would the speed of the incident photon increase, decrease, or stay the same? Justify your answer briefly.
Solutions to Practice Problems1. D—The radiation with the highest frequency (or shortest wavelength) has the highest energy per photon by E= hf. In the visible spectrum, red has the longest wavelength and violet has the shortest. Outside the visible spectrum, infrared radiation has a longer wavelength than anything visible, and ultraviolet has a shorter wavelength than anything visible. So, infrared has the smallest energy per photon, and so on up the spectrum to ultraviolet with the most energy per photon.
2. A—The total number of protons + neutrons is conserved. Before the reaction, we have one free neutron plus 235 protons and neutrons in the uranium, for a total of 236 amu. After the reaction, we have 141 amu in the barium plus 3 free neutrons for a total of 144 amu . . . leaving 92 AMUs for the krypton.
Charge is also conserved. Before the reaction, we have a total charge of +92 from the protons in the uranium. After the reaction, we have 56 protons in the barium. Since a neutron carries no charge, the krypton must account for the remaining 36 protons.
3. E—Einstein’s famous equation is written ΔE = mc2, because it is only the lost mass that is converted into energy. Since we still have a total of 236 amu after the reaction, an entire amu of mass was not converted to energy. Still, the daughter particles have kinetic energy because they move. That energy came from a very small mass difference, probably about a million times less than one amu.
4. C—In β+ emission, a positron is ejected from the nucleus. This does not change the total number of protons + neutrons, so the atomic mass A is still 15. However, charge must be conserved. The original O nucleus had a charge of +8, so the products of the decay must combine to a charge of +8. These products are a positron, charge +1, and the daughter nucleus, which must have charge +7.
5. (a) ΔE = hc/λ, so hc/ΔE = λ. hc= 1240 eV·nm, as found on the equation sheet. ΔE represents the difference in energy levels. An electron in the ground state can make either of two jumps: it could absorb a 2.1-eV photon to get to the middle energy level, or it could absorb a 3.3 eV photon to escape the atom. An electron in the middle state could absorb a 1.2-eV photon to escape the atom. That makes three different energies. Convert these energies to wavelengths using ΔE = hc/λ, so hc/ΔE = λ. hc= 1240 eV·nm, as found on the equation sheet; ΔE represents the energy of the absorbed photon, listed above. These photons thus have wavelengths of 590 nm for the E1 to E2 transition; 380 nm or less for the E1 to E∞ transition; and 1030 nm or less for the E2 to E∞ transition. Only the 590 nm wavelength is visible because the visible spectrum is from about 400-700 nm.
(b) 1. Find the energy of the incident photon using ΔE = hc/λ, getting 6.9 eV. This is the total energy absorbed by the electron, but 3.3 eV of this is used to escape the atom. The remaining 3.6 eV is kinetic energy.
2. To find speed, set kinetic energy equal to ½mv2. However, to use this formula, the kinetic energy must be in standard units of joules. Convert 3.6 eV to joules by multiplying by 1.6 × 10¯19 J/eV (this conversion is on the constant sheet), getting a kinetic energy of 5.8 × 10¯19 J. Now solve the kinetic energy equation for velocity, getting a speed of 1.1 × 106 m/s. This is reasonable—fast, but not faster than the speed of light.
3. A photon is a particle of light. Unless it is in an optically dense material (which the photons here are not), the speed of a photon is always 3.0 × 108 m/s.
(c) The electron absorbs the same amount of energy from the incident photons. However, now it only takes 1.2 eV to get out of the atom, leaving 5.7 eV for kinetic energy. With a larger kinetic energy, the ejected electron’s speed is greater than before.
(d) The speed of the photon is still the speed of light, 3.0 × 108 m/s.
Rapid Review• Atoms contain a nucleus, made of protons and neutrons, and one or more electrons that orbit that nucleus. Protons, neutrons, and electrons all have mass. By contrast, photons are subatomic particles without mass.
• The electron-volt is a unit of energy that’s convenient to use when solving atomic physics problems.
• The electrons that surround an atom can only have certain, specific amounts of energy. To go from a low energy level to a high energy level, an electron absorbs a photon. To go from a high energy level to a low energy level, an electron emits a photon.
• If an electron absorbs a photon that has a higher energy than the electron’s work function, the electron will be expelled from the atom.
• Moving particles have a characteristic wavelength, found by the de Broglie equation.
• Nuclei can undergo three types of decay. In alpha decay, a nucleus emits an alpha particle, which consists of two protons and two neutrons. In beta decay, a nucleus emits either a positron or an electron. In gamma decay, a nucleus emits a photon. When solving nuclear decay problems, remember to conserve both mass and charge.
• During nuclear decay, mass is converted to energy. The relationship between the mass defect and the gained energy is found by Einstein’s famous formula, E = (Δm)c2.
undergoes alpha decay. Give the atomic number and mass number of the nucleus produced by the alpha decay.