9
An Act of Desperation
… what I did can be described simply as an act of desperation …. A theoretical interpretation [of the radiation formula] … had to be found at any cost, not matter how high.
Max Planck1
Einstein’s special and general theories of relativity are triumphs of human intellectual endeavour. They are amazingly powerful, used routinely today by scientists and engineers in applications that are at once both esoteric and mundane, touching many aspects of our everyday lives. But the direct effects of relativity are substantially beyond common experience. We will never travel at speeds approaching the ultimate speed, c. We cannot perceive the local curvature of spacetime caused by the Earth (although we can certainly feel the pull of Earth’s gravity that results). We cannot reach out and touch dark matter, though it must be all around us. And dark energy—the energy of ‘empty’ space—though real, is so dilute as to be virtually beyond imagination.
We believe the special and general theories of relativity because we are able to make scientific observations and perform measurements that take us far beyond common experience. But, as we’ve seen in Part II, these theories serve only further to confuse our understanding of the nature of mass, and thus of material substance itself.
Perhaps this is a good time to turn our gaze away from the large-scale structure of the universe, and look more closely at the small-scale structure of its elementary constituents (well, the elementary constituents of 4.9 per cent of it), in the questing spirit of the early Greek atomists. But let’s at least be prepared. Because the truth will prove to be even more shocking.
Let’s wind the clock back to December 1900. Although considerable momentum for an atomic interpretation of matter had built since the time of Newton, as we saw in Chapter 4, at the turn of the nineteenth century many physicists were still inclined to be rather stubborn about it. It’s perhaps difficult for readers who have lived with the fall-out from the ‘atomic age’ to understand why perfectly competent scientists should have been so reluctant to embrace atomic ideas, but we must remember that in 1900 there was very little evidence for their existence.
The German physicist Max Planck, for one, was not persuaded. He was something of a reactionary, declaring that the atomic theory was nothing less than a ‘dangerous enemy of progress’.2 Matter is continuous, not atomic, he insisted. He had no doubt that atomic ideas would eventually be abandoned ‘ … in favour of the assumption of continuous matter’.3
Planck was a master of classical thermodynamics, a subject that was being pulled inside-out by his arch-rival, Austrian physicist Ludwig Boltzmann. If matter can indeed be reduced to atoms, Boltzmann argued, then thermodynamic quantities such as heat energy and entropy (a measure of the ‘disorder’ of a physical system) result from statistical averaging over the properties and behaviour of billions and billions of individual self-contained atoms or molecules. To take one example from everyday life, the temperature of the water in your kettle represents a statistical average of the random motions (and the kinetic energies) of all its molecules. Heating the water simply increases the speeds of these motions, increasing the temperature.
But statistics have a dark side. They deal with probabilities, not certainties. Classical thermodynamics had by this time established that certain thermodynamic quantities obey certain laws, with certainty. Perhaps the best-known example is the second law of thermodynamics. In a closed system, insulated from all external influences, in any spontaneous change the entropy of whatever is inside always increases. The cables behind your television, set-top box, DVD player, games console, and playbar will become tangled. Disorder will reign. One hundred per cent.
The cocktail glass that in Chapter 3 fell to the floor and shattered (thereby increasing its entropy) follows this second law behaviour. But Boltzmann’s statistics implied that such behaviour is not certain, but simply the most probable outcome for this kind of system. That the shattered glass might spontaneously reassemble, decreasing its entropy (much to the astonishment of party guests), couldn’t be ruled out, although statistically it is very highly unlikely.
This was too much for Planck. He needed to find a way to show that Boltzmann’s statistical approach was wrong, and in 1897 he chose the properties of so-called ‘black-body’ radiation as a battleground. Heat any object to a high temperature and it will emit light. We say that the object is ‘red hot’ or ‘white hot’. Increasing the temperature of the object increases the intensity of the light emitted and shifts it to a higher range of frequencies (shorter wavelengths). As it gets hotter, the object glows first red, then orange-yellow, then bright yellow, then brilliant white.
Theoreticians had simplified the physics somewhat by adopting a model based on the notion of a ‘black body’, a completely non-reflecting object that absorbs and emits light radiation ‘perfectly’. The intensity of radiation a black body emits is then directly related to the amount of energy it contains.
The properties of black-body radiation could be studied in the laboratory using specialized ‘cavities’, empty vessels made of porcelain and platinum with almost perfectly absorbing walls. Such cavities could be heated, and the radiation released and trapped inside could be observed with the aid of a small pinhole, a bit like looking into the glowing interior of an industrial furnace. Such studies provided more than just an interesting test of theoretical principles. Cavity radiation was also useful to the German Bureau of Standards as a reference for rating electric lamps.
This must have seemed like a safe choice. Building on earlier work by Austrian physicist Wilhelm Wien and some new experimental results, in October 1900 Planck deduced a ‘radiation law’ which accounted for all of the available data on the variation in the density of radiation with frequency and temperature. Though the law was elegant, it was in truth no more than a mathematical ‘fit’ to the data. Planck’s challenge now was to find a deeper theoretical interpretation for it.
The law requires two fundamental physical constants, one relating to temperature and a second relating to radiation frequency. The first would gain the label k (or kB) and become known as Boltzmann’s constant. The second would eventually gain the label h and become known as Planck’s constant.
In trying to derive the radiation law from first principles, Planck tried several different approaches. But he found that he was compelled to return to an expression strongly reminiscent of the statistical methods of his rival Boltzmann. The mathematics led him in a direction he really had not wanted to go. He eventually succumbed, in a final act of desperation.
Although the approach Planck took was subtly different from that of Boltzmann, he found that black-body radiation is absorbed and emitted as though it is composed of discrete ‘atoms’, which Planck called quanta. Moreover, he found that each quantum of radiation has an energy given by E = hν, where ν (Greek nu) is the frequency of the radiation. Though much less familiar, this is an expression that is every bit as profound as Einstein’s E = mc2.
Planck’s own voyage of discovery turned him into a willing and enthusiastic convert to the atomist view, and he presented his new derivation of the radiation law to a regular fortnightly meeting of the German Physical Society on 14 December 1900. This date marks the beginning of the quantum revolution.
Planck had used a statistical procedure without giving much thought to its physical significance. If atoms and molecules are real things, something Planck was now ready to accept, then in his own mind the radiation energy itself remained continuous, free to flow uninterrupted back and forth. Planck’s own interpretation of E = hν was that this reflected the ‘quantization’ of matter—matter comes in discrete lumps, but the radiation energy it absorbs or emits is continuous.
But there is another possible interpretation. E = hν could mean that radiation energy is itself quantized. Could radiation, including light, also be ‘lumpy’?
Einstein, for one, was wary of Planck’s derivation, figuring that it had involved rather more sleight-of-hand than was satisfactory. By 1905, the evidence for atoms and molecules was becoming overwhelming and this particulate view of matter was now in the ascendancy, as Einstein’s own paper on Brownian motion suggested. But did it really make sense to adopt a particulate model for matter and a model for radiation based on continuous waves, as demanded by Maxwell’s electromagnetic theory?
Einstein now made a very bold move. In another paper published in his ‘miracle year’ of 1905, he suggested that E = hν should indeed be interpreted to mean that electromagnetic radiation itself consists of ‘energy quanta’.4 This is Einstein’s famous ‘light-quantum hypothesis’. Two hundred years after Newton, Einstein was ready to return to an atomic theory of light.
He was not proposing to abandon the wave theory completely. There was simply too much experimental evidence for the wave properties of light—phenomena such as light diffraction and interference can only be explained in terms of a wave model. And—lest we forget—the equation E = hν connects energy with frequency, hardly a characteristic property of ‘atoms’ in the conventional sense.
Einstein imagined that these two contrasting, or even contradictory, descriptions might eventually be reconciled in a kind of hybrid theory. He believed that what we see and interpret as wave behaviour is actually a kind of statistical behaviour of many individual light-quanta averaged over time.
Whilst special relativity found many advocates in the physics community, the same cannot be said for his light-quantum hypothesis. Most physicists (including Planck) rejected it outright. But this was no idle speculation. Einstein applied the idea to explain some puzzling features associated with a phenomenon known as the photoelectric effect, features that were duly borne out in experiments by American physicist Robert Millikan in 1915, earning Einstein the 1921 Nobel Prize for Physics. The idea of light-quanta—‘particles of light’—eventually became more acceptable, and the American chemist Gilbert Lewis coined the name photon in 1926. It now became possible to draw a few key threads together.
The discovery of the negatively charged electron by Thomson in 1897 implied that atoms, indivisible for more than 2,000 years, now had to be recognized as having some kind of internal structure.* Further secrets were revealed by Rutherford in 1909. Together with his research associates Hans Geiger and Ernest Marsden in Manchester, he had shown that most of the atom’s mass is concentrated in a small central nucleus, with the lighter electrons orbiting the nucleus much like the planets orbit the Sun. According to this model, the atom is largely empty space. As a visual image of the internal structure of the atom, Rutherford’s planetary model remains compelling to this day.
Rutherford and his colleagues discovered the positively charged proton in 1917. Scientists now understood that a hydrogen atom consists of a single proton in a central nucleus, orbited by a single electron.
The planetary model might be compelling, but it was also understood to be quite impossible. Unlike the Sun and planets, electrons and atomic nuclei carry electrical charge. It was known from Maxwell’s theory and countless experiments that electrical charges moving in an electromagnetic field will radiate energy. This is the basis of all radio and television broadcasting. As the ‘planetary’ electrons lost energy they would slow down, leaving them exposed to the irresistible pull of the positively charged nucleus. Atoms built this way would be inherently unstable. They would collapse in on themselves within about 100 millionth of a second.
And there was another problem. The absorption and emission of radiation by material substances could now be traced to the properties of their atoms and, more specifically, to the electrons within these atoms. Now, when we heat a substance, such as water in a kettle, we find that heat energy is transferred to the water in what appears to be a continuous manner.* The temperature of the water increases gradually, it doesn’t suddenly jump from say 40°C to 70°C. Even though radiation energy comes in lumps, we might nevertheless anticipate that it transfers smoothly and continuously to the electrons inside the atoms of a substance. We might imagine that the electrons ‘soak up’ the radiation energy as we increase its frequency, until we cross a threshold at which the electrons have too much energy and are ejected.
But this is not the case. As we saw in Chapter 8, it was discovered that atoms absorb or emit light only at a few very discrete frequencies, forming a spectrum consisting of just a few ‘lines’. We know that if we pass sunlight through a prism, we will get the familiar rainbow spectrum of colours. But if we look very closely we will see that the harmonious flow from red to violet is actually interrupted by a series of dark lines. These lines appear at frequencies that are absorbed by atoms in the outer layers of the Sun.
The frequencies of the lines in the spectra of individual atoms such as hydrogen appear seemingly at random. However, they are not random. In 1885, the Swiss mathematician Johann Jakob Balmer had studied the measurements of one series of hydrogen emission lines and found them to follow a relatively simple pattern which depends on pairs of integer numbers, such as 1, 2, 3, and so on. This behaviour was extraordinary. The absorption and emission spectra of atoms were providing scientists with a window on the atoms’ inner structures. And through this window they glimpsed a baffling regularity.
Balmer’s formula was generalized in 1888 by Swedish physicist Johannes Rydberg, who introduced an empirical constant (called the Rydberg constant) into the formula alongside the integer numbers.5 In themselves, the Balmer and Rydberg formulae are purely empirical—they are mathematical patterns deduced directly from the data. Nobody had any idea how these integer numbers related to the inner structure of the atom.
The orbit of the Earth around the Sun is fixed, to all intents and purposes, with an orbital radius of about 150 million kilometres and an orbital period (the time taken for one complete orbit of the Sun) of a little more than 365 days. In 1913, Danish physicist Niels Bohr wondered if the orbit of an electron around a central proton might be similarly fixed, but instead of only one possible orbit, what if there are several, all of different energy?
In this scenario, absorbing light would pull the electron out of one orbit and shift it out to another, higher-energy orbit, more distant from the nucleus. As the electron returned to the lower-energy inner orbit, it would emit light with a frequency determined by the difference in their energies. If this difference is ΔE, where the Greek symbol Δ (delta) denotes ‘difference’, then the frequency of radiation emitted in the transition from one orbit to the other could be found by rearranging Planck’s relation to ν = ΔE/h.
Bohr found that he needed to impose only one ‘quantum’ condition, one that introduced an integral number, n, characteristic of each electron orbit.6 This was sufficient to enable him to derive the generalized Balmer formula and show that the Rydberg constant is simply a collection of other fundamental physical constants, including the mass and charge of the electron, Planck’s constant, and the speed of light. Bohr used the values available to him from experiment to calculate the Rydberg constant for hydrogen and got a result that was within six per cent of the measured value, a margin well within experimental uncertainty.
This was yet another example of the use of primarily classical concepts into which a few quantum principles had been shoehorned. But it nevertheless represented a significant step forward. The integer number that characterizes the electron orbits would come to be known as a quantum number, and the shifts or ‘transitions’ between different orbits would be called quantum jumps.
The agreement between Bohr’s atomic theory and experiment was obviously much more than just coincidence, but the theory begged a lot more questions. The physical impossibility of an electron moving in an orbit around a central proton hadn’t been forgotten, but it had been temporarily set aside, a problem to be solved later. Likewise, the ‘jumps’ between electron orbits had to happen instantaneously if the same problem was to be avoided. Given that the frequency of the radiation emitted by the electron as it jumps from a higher to a lower orbit must match precisely the energy difference (according to ΔE = hν), the electron somehow had to ‘know’ in advance which orbit it was going to end up in.
And, before we get too carried away with excitement, we should acknowledge that Bohr had introduced the quantum number n by imposing a quantum condition on its structure. He hadn’t answered the question: where do the quantum numbers come from? The outline of an answer came ten years later.
To take this next step we need to think about the energy of a photon according to special relativity. It is reasonably clear how Einstein’s equation E = mc2 applies to objects with mass, but how should we now apply it to photons? We know by now that the relativistic mass is given by m = γm0, but countless measurements suggest that photons have zero rest mass, m0 = 0. Photons also travel at the speed of light, so the Lorentz factor γ is infinite. What is infinity times zero? The fact is, I’ve no idea.
Here’s the curious thing. We know for sure that massless photons carry energy. We also know that radiation possesses momentum because we can measure it in the form of radiation ‘pressure’. To give one example, the pressure of radiation released by nuclear fusion reactions at the Sun’s core balances the gravitational pull at the surface, preventing the Sun from collapsing in on itself.
These facts are reconciled in the expression for the relativistic energy.7 The energy of a photon with zero rest mass is simply equal to its kinetic energy, E = pc, where p is the linear momentum. This might appear to be rather puzzling—isn’t kinetic energy supposed to be equal to ½mv2?—until we realize that this more familiar expression for kinetic energy is an approximation valid for speeds v much less than the speed of light.8
We resist the temptation to equate the linear momentum p with mass times velocity (another perfectly valid approximation for speeds v much less than c), allowing us to duck the difficult question about the relativistic mass of the photon. In any case, we will see in Chapter 10 that the cosily familiar classical concept of momentum takes on a completely different guise in quantum mechanics.
It fell to French physicist Prince Louis de Broglie,* the younger son of Victor, fifth duc de Broglie, to put two and two together. The equation E = pc comes from special relativity. The equation E = hν comes from Planck’s radiation law and Einstein’s light-quantum hypothesis. If these are both expressions for the energy of a photon, then why not put them together?
This is what de Broglie did, in 1923. He simply set pc equal to hν and, since the frequency of a wave is equal to its speed divided by the wavelength (Greek lambda, λ), he was able to deduce the de Broglie relation, λ = h/p. The wavelength of radiation is inversely proportional to its linear momentum.
The de Broglie relation connects a characteristically wave property—wavelength—on the left with a characteristically particle property—momentum—on the right. This suggests that photons are in some curious sense both waves and particles. In itself this was a fairly remarkable conclusion, but it was de Broglie’s next step that was truly breathtaking. He simply asked himself if this strange behaviour could be somehow universal. What if electrons could also be considered to behave like waves?9
Of course, this is all completely counter-intuitive. It is not our experience that objects with mass behave like waves. But in our daily lives we deal with objects with large masses and therefore large momenta, and the value of Planck’s constant is very, very small (it is 6.63 × 10−34 joule-seconds). According to the de Broglie relation, the wavelength of a fast-moving tennis ball is so short as to be well beyond perception.10
De Broglie also had a long-standing interest in chamber music, and this now led him to a major breakthrough. Musical notes produced by string or wind instruments are audible manifestations of so-called standing waves, vibrational wave patterns which ‘fit’ within the stopped length of the string or the length of the pipe. A variety of standing wave patterns is possible provided they meet the requirement that they fit between the string’s secured ends or the ends of the pipe. This simply means that they must have zero amplitude (they must be ‘fastened’) at each end. It turns out that this is possible only for patterns which contain an integral number of half-wavelengths. In other words, the length of the string or pipe must equal n times ½λ, where n is an integer number (1, 2, 3, … ) and λ is the wavelength (Figure 10).
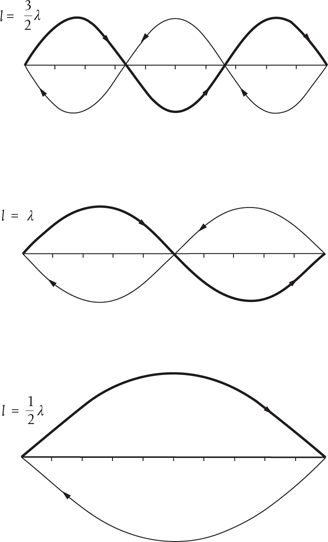
Figure 10. Examples of standing wave patterns. These are characterized by having zero height or amplitude at each end of the stopped string or length of pipe. The arrows give some sense of the direction in which the waves ‘travel’ although, once established, the waves appear to stand still.
If the length of the string or pipe is l, then the longest wavelength standing wave is equal to twice this length, such that l = ½λ (n = 1). Such a wave has no points (called ‘nodes’) where the wave amplitude passes through zero—between the ends. The next wave is characterized by a wavelength equal to l, with one node between the ends, such that l = λ (n = 2). The wave first rises to a peak, falls back down to zero (the node) and falls further to a trough, before rising back up to zero again. The third has one-and-a-half wavelengths and two nodes, l = 3∕2λ (n = 3), and so on.
De Broglie saw that the quantum number n in Bohr’s theory could emerge naturally from a model in which an ‘electron wave’ is confined to a circular orbit around the nucleus. Perhaps, he reasoned, the stable electron orbits of Bohr’s theory represent standing electron waves, just like the standing waves in strings and pipes which generate musical notes. The same kinds of arguments would apply. For a standing wave to be produced in a circular orbit, the electron wavelengths must fit exactly within the orbit circumference.
Although these ideas were very illuminating, they were nothing more than a loose connection between theoretical concepts. De Broglie had not derived a wave theory of the electron from which the quantum numbers could be expected to emerge naturally. And he had no explanation for the quantum jumps.
The existence of atoms was now accepted, and atoms had been revealed to have an internal structure, with a central nucleus and orbiting electrons. But here, inside the atom, was something unexpected and really rather puzzling. The Greek atomists had argued that matter cannot be divided endlessly to nothing. Two-and-a-half thousand years later the scientists had continued to divide matter, discovering smaller and smaller particles, just as the Greeks might have anticipated. But instead of running up against some kind of ultimate indivisible constituents, the scientists had now discovered particles that could also be waves. What on earth was that supposed to mean?