14
The Goddamn Particle
… the publisher wouldn’t let us call it the Goddamn Particle, though that might be a more appropriate title, given its villainous nature and the expense it is causing. And two, there is a connection, of sorts, to another book, a much older one …
Leon Lederman1
Yang and Mills were in pursuit of a quantum field theory of the strong force, but what of the weak force? Like the strong force, the weak force is also short-range, again implying that its force carriers must be massive particles.
In 1941, Schwinger reasoned that if the weak force is imagined to be carried by a single force particle,* and this is assumed to be massive, equal in size to a couple of hundred times the mass of a proton, then its range would indeed become very limited.2 Unlike massless photons, massive particles are very sluggish, moving at speeds substantially slower than light. A force carried by such sluggish particles would also be considerably weaker than electromagnetism.
Schwinger realized that if the mass of such a weak force carrier could be somehow ‘switched off’—if the carrier was imagined to be massless—then the weak force would actually have a range and strength similar in magnitude to electromagnetism. This was nothing more than a bit of numerology, and quite an outrageous speculation, but it was also the first hint that it might be possible to unify the weak and electromagnetic forces into a single, ‘electro-weak’ force.3
The logic runs something like this. Despite the fact that they appear so very different, the electromagnetic and weak forces are in some strange way manifestations of the same, ‘electro-weak’, force. They appear very different because something has happened to the carriers of what we now recognize as the weak force. Unlike the photon, these force particles have somehow become ‘three-dimensional’, their speeds reduced below light-speed, and they have gained a lot of mass. This restricts the range of the force and greatly diminishes its strength relative to electromagnetism.*
We can look at this another way. If we were able to wind the clock back to the very earliest moments of the big bang origin of the universe, then at the energies and temperatures that prevailed at this time all the forces of nature (including gravity, as a ‘force’ exerted by mass-energy on spacetime) are thought to have been fused together and indistinguishable. Gravity was the first to separate, followed by the strong force. At around a trillionth of a second after the big bang, the ‘electro-weak’ force split into two separate forces—the weak force and electromagnetism. By this time, all the four forces of nature were established. The key question is this. What happened to the carriers of the weak force to make them so heavy? Or, equivalently, what happened a trillionth of a second after the big bang to cause the electro-weak force to split apart?
The challenge was taken up by Schwinger’s Harvard graduate student, Sheldon Glashow. After a few false starts, Glashow developed a quantum field theory of weak interactions based, like the Yang–Mills theory, on the SU(2) symmetry group. In this theory the weak force is carried by three particles (remember the number of force carriers involved in an SU(n) structure is determined by n2 – 1). Two of these particles carry electrical charge and are now called the W+ and W– particles. This leaves a third, neutral force carrier called the Z0.
But Glashow now ran into the very same problem that Yang and Mills had experienced. The quantum field theory said that the W and Z particles should all be massless, just like the photon. And if he tried to fudge the equations by adding masses ‘by hand’, the theory couldn’t be renormalized.
So, we know that carriers of the weak force must be massive particles. But the theory says they should be massless. Precisely how then do the carriers of the weak force gain their mass? The solution to this puzzle emerged in the seven-year period spanning 1964 to 1971. The answer was to invoke something called spontaneous symmetry-breaking.
This sounds all rather grand, but spontaneous symmetry-breaking is actually a familiar, everyday kind of phenomenon. Imagine watching a time-lapse video of a large glass jar of water that is being cooled below freezing. What would we expect to see? At some point we would see the first ice crystals form and then slowly spread through the whole volume of water, turning it eventually into a block of ice.
Now, the water molecules in the liquid have a certain symmetry—they look broadly similar in different directions—up, down, left, right, forward, back—by virtue of their random motions within the loose network that forms the liquid, as shown in Figure 19(a). But ice is a crystal lattice, a regular array with planes tiled (or ‘tessellated’) with hexagonal rings of atoms. This structure looks distinctly different in different directions. Look to the left or right and we see a ‘corridor’ formed by the lattice structure. But look up and we see a ‘ceiling’; look down and we see a ‘floor’, as shown in Figure 19(b).

Figure 19. The structure of liquid water is governed by short-range forces between neighbouring molecules, but does not look different in different directions, as we can see in (a). However, ice is a crystal structure, with distinct orientations of the water molecules organized in hexagonal arrays, (b). The ice therefore has a lower overall symmetry compared with the liquid.
Although the crystal is a more regular, repeating structure, in three dimensions the water molecules are organized in a less symmetrical way than in liquid water—they take up different orientations in different directions. So freezing the water ‘breaks’ the higher symmetry of the liquid.
This tells us what spontaneous symmetry-breaking is but not how it works. So let’s rewind the video and watch it again, more closely. We see that the first ice crystals form at a specific—but seemingly quite random—place in the volume of water, most likely adjacent to the wall of the jar. Why? We can see that once the first ice crystals have formed, more crystals ‘nucleate’ around these and the ice expands to fill the jar. So we ask a slightly different question: what causes the first ice crystals to nucleate?
Here’s a clue. Let’s repeat this experiment with ultra-pure water and ensure that the walls of the jar are perfectly smooth. We now cool the jar really slowly. We find that we can reduce the temperature of the water well below its freezing point without forming any ice at all. This is super-cooling. And there’s the answer. The first ice crystals nucleate around impurities in the water or on inhomogeneities in the surface of the jar. So removing the impurities and the inhomogeneities prevents the first ice crystals from forming.
We conclude that the crystals need something to ‘hang on to’ to get them going. To get spontaneous symmetry-breaking we need to add something (impurities or inhomogeneities, in this case) to encourage it to happen.
How does this help? Well, the SU(2) quantum field theories developed by Yang and Mills and by Glashow are much like the example in which the water is ultra-pure and the walls of the jar perfectly smooth. To get the symmetry to break, physicists realized that they needed to add something—a missing ingredient—to the ‘background environment’ of the quantum field.
In a sense, they needed something for the massless force carriers of the field to ‘hang on to’. This ingredient is needed to break the symmetry and drive a distinction between the forces. Now there really aren’t that many options to choose from, so they introduced another, but altogether new, kind of quantum field.
This idea was developed in the early 1960s in connection with the properties of superconducting materials. Japan-born American physicist Yoichiro Nambu realized that spontaneous symmetry-breaking can result in the formation of particles with mass.4
It took a few years to work out a detailed mechanism. There were hints in the work of Nambu, British theorist Jeffrey Goldstone, and remarks by American physicist Philip Anderson. The mechanism was finally detailed in a series of papers which appeared in 1964, published independently by American physicist Robert Brout and Belgian François Englert, English physicist Peter Higgs at Edinburgh University, and Americans Gerald Guralnik and Carl Hagen and British physicist Tom Kibble, all at Imperial College in London. From about 1972, the mechanism has been commonly referred to as the Higgs mechanism and the new quantum field is referred to as the Higgs field.
Once again, it is important to remember that theorists are primarily concerned with getting the structure of the mathematics right. They’re not overly concerned with the physical interpretation (and certainly not the visualization) of what their mathematical equations are telling them. That’s a problem they’ll happily leave to somebody else. It was enough that adding a background Higgs field with certain properties did indeed introduce new terms into the equations of the quantum field theory, terms which can be interpreted as mass terms, related to m2ϕ2. The mechanism works in a mathematical sense, and it’s left to us to try to make sense of it physically. We can but try.
Adding a background Higgs field suggests that, whatever it is, it pervades the entire universe like a modern-day ether (though much, much more tenuous than the ether of nineteenth-century physicists such as Maxwell). In the absence of this field, all particles (as it turns out, both matter and force particles) are by default massless and two-dimensional, and will happily go about their business at the speed of light.
Make no mistake, if this situation were to persist there would be no mass and no material substance. There would be no universe of the kind so familiar to us, no stars or galaxies, planets, life, or Homo sapiens. What happens is that the massless particles interact with the Higgs field, resulting in a number of effects. They gain a third dimension—they swell and become ‘thick’—and they slow down. As a consequence the particles gain mass (terms of the form m2ϕ2 appear in the equations)—see Figure 20. Various analogies have been used to ‘explain’ these effects, the most popular suggesting that the Higgs field behaves rather like molasses, dragging on the particles and slowing them down, their resistance to acceleration manifesting itself as inertial mass. Such analogies are always inadequate (Higgs himself prefers to think of the mechanism as one involving a kind of diffusion), but at least they help us to get our heads around what’s happening.
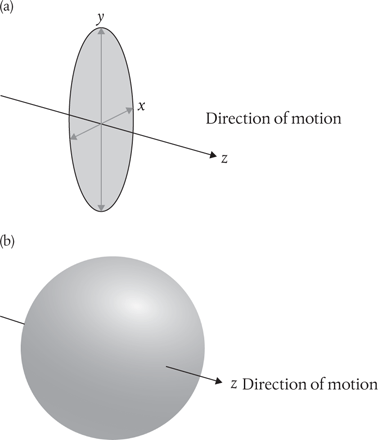
Figure 20. (a) A massless boson moves at the speed of light and has just two directions to ‘point’ in, which are shown here as left/right (x) and up/down (y). It cannot ‘point’ in the direction in which it is moving. (b) On interacting with the Higgs field, the particle gains a third dimension—forward/back (z). The particle gains ‘depth’, slows down, and mass terms appear in the field equations of the form m2ϕ2.
The most important point to remember concerns the ‘origin’ of mass. Ever since the Greek atomists, we have tended to think of mass as an innate, inseparable, ‘primary’ property of the ultimate constituents of matter. Galileo and Newton refined this concept but they did not change it in any essential way. The inertial mass of an object is a measure of its resistance to acceleration, and our instinct is to equate inertial mass with the amount of substance that the object possesses. The more ‘stuff’ it contains, the harder it is to accelerate.
We now interpret the extent to which the motion of an otherwise massless elementary particle is ‘resisted’ by interaction with the Higgs field as the particle’s inertial mass. The concept of mass has vanished in a puff of mathematical logic. It has become a secondary property, the result of interactions between massless particles and the Higgs field.
Looking back, we would now suggest that, a trillionth of a second after the big bang, the temperature of the universe had cooled sufficiently to allow the Higgs field to settle to a fixed value. This provided the background necessary to break the symmetry of the electro-weak force. The W and Z particles found something to ‘hang on to’; they gained a third dimension, they gained mass, and the weak force separated from electromagnetism.
Despite its attractions, the Higgs mechanism did not win converts immediately. Higgs actually had some difficulties getting his paper published. He sent it to the European journal Physics Letters in July 1964, but it was rejected by the editor as unsuitable. He was indignant, but the simple truth is that in the early 1960s quantum field theory had become rather unfashionable, principally because of the problems that Higgs was now showing how to fix.5
Higgs made some amendments to his paper and re-submitted it to the journal Physical Review Letters. It was sent to Nambu for peer review. Nambu asked Higgs to comment on the relationship between his paper and a similar article just published in the same journal by Brout and Englert. Higgs had not been aware of Brout and Englert’s work on the same problem and acknowledged their paper in an added footnote. He also added a final paragraph to the main text in which he drew attention to the possibility of another, massive boson, the quantum particle of the Higgs field. This would come to be known as the Higgs boson.
Physicists now had a mechanism, but not a fully fledged quantum field theory (and certainly not a field theory that could be renormalized). The next step was taken three years later. Steven Weinberg had spent a couple of years puzzling on the effects of spontaneous symmetry-breaking in strong-force interactions when he realized that his approach wasn’t going to work. It was at this moment that he was struck by another idea.6
Weinberg had been applying the Higgs mechanism to the strong force in an attempt to give mass to the strong force carriers. He now realized that the mathematical structures he had been trying to apply to strong-force interactions were precisely what were needed to resolve the problems with weak-force interactions and the massive force carriers these interactions implied. He had been applying the right idea to the wrong problem—this was the answer to the mystery of massive force carriers in weak-force interactions.7
But rather than apply the approach to protons and neutrons, which are also affected by the strong force, Weinberg decided to restrict himself only to particles such as electrons and neutrinos, which are not. Weinberg later confessed his reason. A hesitant Murray Gell-Mann and George Zweig had, a few years earlier, proposed that protons and neutrons are actually composite particles, composed of what would come to be known as quarks (more on this in Chapter 15). Applying the Higgs mechanism to the weak force operating on protons and neutrons would mean involving quarks in the picture, and Weinberg wasn’t at all sure these really did exist.8
Weinberg published a paper detailing a unified electro-weak theory in November 1967. In this theory the Higgs mechanism works like this. Prior to breaking the symmetry, the electro-weak force is carried by four massless particles which, for the sake of simplicity, we will call the W+, W0, W–, and the B0 particles. Interactions with the background Higgs field cause the W+ and W– particles to acquire a third dimension, slow down, and gain mass.
The W0 and B0 particles also gain mass, but it’s a simple fact in quantum mechanics that neutral particles have a tendency to form superpositions and mix together. The W0 and B0 particles mix to produce a massive Z0 particle and the massless photon. We associate the massive W+, W–, and Z0 particles with the weak force and the massless photon with electromagnetism.
Weinberg was able to estimate the mass-scales of the weak-force carriers. He predicted that the masses of the W particles should be about eighty-five times the proton mass (about 80 billion electron volts, or 80 GeV/c2) and that the Z0 should have a mass about ninety-six times that of the proton (about 90 GeV/c2).
In 1964, Higgs had referred to the possibility of the existence of a Higgs boson, but this was not in relation to any specific force. In his electro-weak theory, Weinberg had found it necessary to introduce a Higgs field with four components, implying four fundamental field particles (four Higgs bosons). As a result of the interaction, three Higgs bosons are ‘swallowed’ by the W+, W–, and Z0 particles, adding a third dimension to each and slowing them down.
The fourth appears as a physical particle—a residual Higgs boson.
In the United Kingdom, Abdus Salam had been introduced to the Higgs mechanism by Tom Kibble. He had worked earlier on an electro-weak field theory and immediately saw the possibilities afforded by spontaneous symmetry-breaking. When he saw a preprint of Weinberg’s paper he discovered that both he and Weinberg had independently arrived at precisely the same model. He decided against publishing his own work until he had had an opportunity properly to incorporate protons and neutrons in the picture. Both Weinberg and Salam believed that the electro-weak theory was renormalizable, but neither was able to prove this at the time.
The proof followed a few years later. By sheer coincidence, in 1971 Dutch theorists Martinus Veltman and Gerard ‘t Hooft independently re-discovered the field theory that Weinberg had first developed, but they were now able to show how it could be renormalized. ‘t Hooft had initially thought to apply the theory to the strong force, but when Veltman asked a colleague about other possible applications, he was pointed in the direction of Weinberg’s 1967 paper. Veltman and ‘t Hooft realized that they had developed a fully renormalizable quantum field theory of electro-weak interactions.
What does this mean for the electron? Recall from Chapter 12 that mass renormalization implies that the mass of the electron has two parts. It has a hypothetical ‘bare mass’, or the mass it would have if it could be separated from its own, self-generated electromagnetic field. It also has an ‘electromagnetic mass’, generated by the energy of the interactions between the electron and its electromagnetic field, which ‘dress’ the electron in a covering of virtual photons.
Now we learn that even the ‘bare mass’ is not an intrinsic property of the electron. It is derived from interactions between the electron and the Higgs field. These interactions add a third dimension and slow the electron down, resulting in effects that we interpret as mass.
Experimental high-energy particle physics caught up with the theorists a few years later. Weinberg had predicted the masses of the weak-force carriers. At the time he made these predictions there was no particle collider large enough to observe them. But in the years that followed a new generation of particle colliders was constructed in America and at CERN, near Geneva in Switzerland. The discovery of the W particles at CERN was announced in January 1983, with masses eighty-five times that of the proton, just as Weinberg had predicted. The discovery of the Z0 was announced in June that year, with a mass about 101 times the mass of a proton. (The Z0 mass is now reported to be ninety-seven times the proton mass.)*
And, of course, the electro-weak theory predicts the existence of the Higgs boson. Given that the Higgs mechanism allows the masses of the weak-force carriers to be predicted with such confidence, the existence of a Higgs field—or something very like it—seemed a ‘sure thing’. However, there were alternative theories of symmetry-breaking that did not require a Higgs field and there remained problems with the electro-weak theory which could not be easily resolved. These problems tended to sow seeds of doubt and erode the theorists’ confidence. The Higgs mechanism was far from being proved.
The Higgs mechanism slotted comfortably into the electro-weak theory and rendered it renormalizable. It all seemed to fit together perfectly. But the mechanism demands the existence of a new kind of quantum field which fills all of space. So, it came down to this. If the Higgs field really exists, then so should its fundamental field particle, the Higgs boson.
The obvious next step was to find evidence for the existence of the Higgs boson, and a race began between Fermilab in Chicago and CERN in Geneva. In a book published in 1993, American particle physicist Leon Lederman emphasized (or over-emphasized, depending on your point of view) the fundamental role played by the Higgs boson. He called it the ‘God particle’.
He gave two reasons for this name: ‘One, the publisher wouldn’t let us call it the Goddamn Particle, though that might be a more appropriate title, given its villainous nature and the expense it is causing. And two, there is a connection, of sorts, to another book, a much older one …’.9