15
The Standard Model
… the finder of a new elementary particle used to be rewarded by a Nobel Prize, but such a discovery now ought to be punished by a $10,000 fine.
Willis Lamb1
The decade spanning the late-1960s through to the late 1970s was a golden age for high-energy particle physics. As the details of a unified quantum field theory of the weak force and electromagnetism were being figured out, so too was the nature of the strong force. By 1979, all the theoretical ingredients of what was to become known as the standard model of particle physics were in place. This model accounts for the set of all the known elementary particles and the forces at work inside both the atom and the atomic nucleus. All that was missing was experimental confirmation of a few of the heavier members of the set.
The secrets of the strong force were gradually teased out into the open. Clues were available from studying the pattern of the ‘zoo’ of particles that experimental physics turned up in the thirty-year period from the 1930s to the 1960s. To the physicists of the time, this procession of new particle discoveries was simply bewildering. To the proton, neutron, electron, and neutrino was added a host of new and bizarrely unusual particles. Dirac’s ‘dream of philosophers’ turned into a nightmare.
In 1932, American physicist Carl Anderson had discovered Dirac’s positron in cosmic rays, streams of high-energy particles from outer space that constantly wash over the Earth’s upper atmosphere. Four years later, he and fellow American Seth Neddermeyer identified another new particle. It was initially believed that this was one of the particles predicted by Yukawa in 1935—its mass was in the right ballpark. But it behaved just like an electron, with a mass about 200 times greater than an ordinary electron. This particle has had many names and is today called the muon. At the time of its discovery it simply didn’t fit with any theories or preconceptions of how the building blocks of matter should be organized.
In 1947, another new particle was discovered in cosmic rays by Bristol University physicist Cecil Powell and his team. This was found to have a slightly larger mass than the muon, 273 times that of the electron. But unlike the muon it came in positive, negative and, subsequently, neutral varieties. These were called pi-mesons (or pions). These were the particles that Yukawa had predicted.
As detection techniques became more sophisticated, the floodgates opened. The pion was quickly joined by positive and negative K-mesons (or kaons) and a neutral particle called the lambda. New names proliferated. Responding to a question from one young physicist, Fermi remarked: ‘Young man, if I could remember the names of these particles, I would have been a botanist.’2
The kaons and the lambda in particular behaved very strangely and fit none of the established quantum rules. American physicist Murray Gell-Mann felt he had no alternative but to propose that these particles are governed by some new, hitherto unknown quantum property, which he called strangeness,* paraphrasing Francis Bacon: ‘There is no excellent beauty that hath not some strangeness in the proportion.’3 Whatever this was supposed to be, in strong-force interactions involving particles exhibiting this strange behaviour, their ‘strangeness’ is conserved.
There had to be some kind of underlying pattern. A structure was needed that would bring order to the zoo and explain how all these weird and wonderful particles were related to each other, much as Russian chemist Dmitry Mendeleev had brought order to the array of chemical elements by arranging them in a periodic table.
Physicists had by this time organized the particles into categories based on their broad properties. There are two principal classes, called hadrons (from the Greek hadros, meaning ‘thick’ or ‘heavy’) and leptons (from the Greek leptos, meaning small). Hadrons are affected by the strong force, the weak force, and electromagnetism. Leptons are affected only by the weak force and electromagnetism.
The class of hadrons includes a sub-class of baryons (from the Greek barys, also meaning ‘heavy’). These are heavier particles and include the proton, neutron, lambda, and two further series of particles that had been discovered in the 1950s named sigma and xi. The second sub-class is that of mesons (from the Greek mésos, meaning ‘middle’). These particles experience the strong force but are of intermediate mass. Examples include the pions and the kaons. The class of leptons includes the electron, muon, and the neutrino. Both the baryons and the leptons are fermions, with half-integral spin quantum numbers.
In the early 1960s, Gell-Mann and Israeli Yuval Ne’eman suggested that the only way to make sense of the pattern of hadrons is to assume that they are not, in fact, elementary. This was history repeating itself. A few centuries of scientific endeavour had led to (admittedly indirect) evidence that matter is composed of atoms. But these were not the ultimate, indivisible atoms of Greek philosophy, or of mechanical philosophy. Atoms are divisible. They contain atomic nuclei and electrons, and the nuclei contain protons and neutrons. Now it was suggested that the protons and neutrons are themselves composites, made up of other particles that are even more elementary.
It slowly dawned on the physicists that these new elementary particles could form the basis for a new understanding of the nature and composition of matter. Together with the leptons they would be the new ‘atoms’. They would be the new building blocks from which all the creatures in the particle ‘zoo’—protons, neutrons, pions, kaons, lambda, sigma, xi—are assembled.
The pattern suggested that two new kinds of elementary particle would be needed to make up a proton or a neutron, with each containing three of these. For example, if we called the two different kinds of new particles A and B, then the proton and neutron appeared to require combinations such as AAB and ABB. But these are quite awkward combinations. What do we do about the proton’s electric charge? Do we suppose that one of these new particles carries the positive charge (B+, say), with the other particle neutral? But then simple combinations of these cannot reproduce the electrically neutral neutron. The combination AAB+ gives us a positive proton, but AB+B+ doesn’t give us a neutral neutron. This kind of pattern doesn’t fit.
This problem was highlighted by Gell-Mann himself, when his colleague Robert Serber suggested precisely this three-of-two-kinds solution over lunch at Columbia University in New York in 1963. Gell-Mann was dismissive. ‘It was a crazy idea’, he said. ‘I grabbed the back of a napkin and did the necessary calculations to show that to do this would mean that the particles would have to have fractional electric charges— –1⁄3, +2⁄3, like so—in order to add up to a proton or neutron with a charge of plus [one] or zero.’4
This is the only way the electric charge can be distributed over three particles of two kinds. To make a proton we need two particles with a charge of +2⁄3 and one particle carrying –1⁄3 to get an overall charge of +1. One particle with a charge of +2⁄3 and two carrying –1⁄3 would give a neutron with overall zero charge. To account for other particles in the zoo a third kind of particle, also with a charge of –1⁄3, was needed.
There were certainly no precedents for thinking that particles could possess fractional electric charges, and the whole idea seemed ridiculous. Gell-Mann called them ‘quorks’, a nonsense word deliberately chosen to highlight their absurdity. But despite these worrying implications, there was no doubting that this combination did provide a potentially powerful explanation for the pattern. Maybe if the ‘quorks’ are forever trapped or confined inside the larger hadrons, then this might explain why fractionally charged particles had never been seen in high-energy physics experiments.
As he wrestled with this idea, Gell-Mann happened on a passage from James Joyce’s Finnegan’s Wake: ‘Three quarks for Muster Mark!’5 The word quark didn’t quite rhyme with his original ‘quork’ but it was close enough. Gell-Mann now had a name for these odd new particles.*
The pattern demanded three different kinds of quarks, which Gell-Mann called ‘up’ (u), with a charge of +2⁄3, ‘down’ (d), with a charge of –1⁄3, and strange (s), a heavier version of the down quark also with a charge of –1⁄3. The baryons known at that time could then be formed from various permutations of these three quarks and the mesons from combinations of quarks and anti-quarks.
The properties up, down, and strange are described as types of quark ‘flavour’, which we can think of as a new kind of quantum number.* This is obviously not intended to suggest that quarks actually possess flavour as we experience it. It’s best to think of quark flavour as a property similar to electrical charge. Quarks and leptons possess electrical charge and this comes in two varieties—positive and negative. In addition to electrical charge, quarks also possess flavour, and at the time of these proposals there were three varieties—up, down, and strange. We now know that there are actually six flavours.
In this scheme the proton consists of two up quarks and a down quark (uud), with a total electrical charge that adds up to +1. The neutron consists of an up quark and two down quarks (udd), with a total charge that balances out at zero. Beta radioactivity could now be understood to involve the conversion of a down quark in a neutron into an up quark, turning the neutron into a proton, with the emission of a W– particle.
Incidentally, recall from Chapter 13 that Heisenberg had tried to develop an early quantum field theory based on the idea that the proton and neutron are two different ‘states’ of the same particle. We can now see that this idea contained more than a grain of truth. Protons and neutrons are indeed composed of the same two flavours of quark—up and down—and differ by virtue of the fact that in the neutron an up quark has been replaced by a down quark.
Isospin is now defined as half the number of up quarks minus the number of down quarks.† For the neutron, this gives an isospin of ½ × (1 – 2), or –½. ‘Rotating’ the isospin of the neutron is then equivalent to changing a down quark into an up quark, giving a proton with an isospin of ½ × (2 – 1), or +½.
The kaons and the lambda behave ‘strangely’ because they contain strange quarks. The positive kaon is a meson formed from up and anti-strange quarks, the negative kaon from strange and anti-up quarks, and the neutral kaon is a superposition of down-anti-strange and strange-anti-down (remember, electrically neutral particles have a tendency to mix together). The lambda is a baryon formed from a combination of up, down, and strange quarks. It is a kind of ‘heavy neutron’, in which a down quark in a neutron is replaced with a strange quark.
Hints that there may be a fourth quark emerged in 1970. This is a heavy version of the up quark with charge +2⁄3. It was called the charm quark. Most physicists were sceptical. But when another new particle, called the J/ψ (pronounced ‘jay-psi’), was discovered in the ‘November revolution’ of 1974, simultaneously at Brookhaven National Laboratory in New York and the Stanford Linear Accelerator Center in California, it was realized that this is a meson formed from charm and anti-charm quarks.* The scepticism vanished.
It was now understood that the neutrino is partnered with the electron (and so it is now called the electron-neutrino). The muon-neutrino was discovered in 1962, and for a time it seemed possible that the elementary building blocks of material substance are formed into two ‘generations’ of matter particles. The up and down quarks, and the electron and electron-neutrino form the first generation. The charm and strange quarks, muon and muon-neutrino form a heavier second generation.
When the discovery of another, even heavier, version of the electron—called the tau—was announced in 1977, this caused less consternation than you might imagine. It was quickly assumed that there must be a third generation of matter particles, implying the existence of another pair of heavier quarks and a tau-neutrino. American physicist Leon Lederman found evidence for what came to be known as the bottom quark at Fermilab in Chicago in August 1977. He and his colleagues discovered the upsilon, a meson consisting of a bottom quark and its anti-quark. The bottom quark is an even heavier, third-generation version of the down and strange quarks, with a charge of –1⁄3.
The discoveries of the top quark and the tau-neutrino were announced at Fermilab in March 1995 and July 2000, respectively. Together they complete the heavier third generation of matter particles. Although further generations of particles are not impossible, there are some reasonably compelling arguments from theory and some experimental evidence to suggest that three generations is probably all there is.
The quark model was a great idea, but at the time these particles were proposed there was simply no experimental evidence for their existence. Gell-Mann was himself rather cagey about the status of his invention. He had argued that the quarks are somehow ‘confined’ inside their larger hosts and, wishing to avoid getting bogged down in philosophical debates about the reality or otherwise of particles that could never be seen, he referred to them as ‘mathematical’.
But experiments carried out at the Stanford Linear Accelerator Center in 1968 provided strong hints that the proton is indeed a composite particle containing point-like constituents inside it. It was not clear that these constituents were necessarily quarks and the results suggested that, far from being held tightly inside the proton, they actually rattle around as though they are entirely free. This seemed to contradict the idea that the quarks are never seen because they are forever bound or confined inside protons and neutrons. If they’re free to rattle around, why don’t they ever come out?
The solution to this puzzle is actually breathtakingly simple. Our instinct is to think of a force of nature as something that is centred on a point—typically the centre of a particle or an object which ‘generates’ the force, and which declines in strength the further away we get from it. The obvious examples are Newtonian gravity and electromagnetism, both of which are forces that decline by 1/r2 as the distance r from the centre increases, as shown in Figure 21(a).* Hurl it far enough from the Earth’s centre, and a rocket will escape Earth’s gravitational force. The pull we feel between the north and south poles of two bar magnets gets weaker as we move them apart.
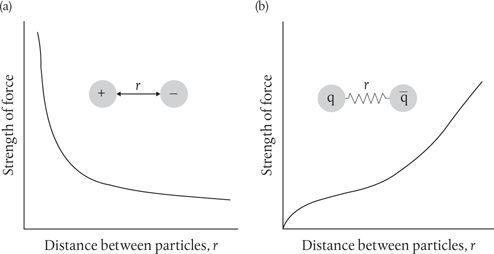
Figure 21. The electromagnetic force between two electrically charged particles increases in strength as the particles move closer together, (a). But the colour force that binds quarks together behaves differently, (b). In the limit of zero separation between a quark and an anti-quark (for example), the force falls to zero. The force increases as the quarks are separated.
But, as Princeton theorists David Gross and Frank Wilczek and Harvard theorist David Politzer showed in 1973, the strong force doesn’t behave this way at all. Instead, it acts as though adjacent quarks are tethered to each other by a piece of strong elastic or a spring—Figure 21(b). As the quarks move close together, the elastic or the spring slackens, and the force between them diminishes. Inside a proton or neutron, the quarks are tethered but close enough together to be free to ‘rattle around’.
But the strong force is like a sleeping tiger. Trying to pull the quarks apart is then like tugging on the tiger’s tail. The strong force awakens,† and we feel its full strength as the elastic or the spring tightens. It resists further separation and the force grows stronger. The strong force works in the opposite sense to Newtonian gravity and electromagnetism.
Gell-Mann, German theorist Harald Fritzsch, and Swiss theorist Heinrich Leutwyler now had all the ingredients to develop a quantum field theory of the strong force. But this is not a strong force acting between protons and neutrons, which had preoccupied Yang and Mills in the early 1950s. It is instead an even stronger force acting between quarks inside protons and neutrons.
The same questions that had confronted Yang and Mills now had to be confronted once again. In the even-stronger strong force interactions between quarks, what property is conserved? And what kind of symmetry is required?
Yang and Mills had fixed on isospin and the SU(2) symmetry group, but their focus had been on interactions between protons and neutrons. Quark flavour was ruled out because the pattern of quarks inside a proton or neutron demand that each hold two quarks of the same flavour (two up quarks in a proton and two down quarks in a neutron). If, as seemed reasonable, the quarks are also spin-½ fermions, then the Pauli exclusion principle applies—a proton or neutron cannot comfortably hold two quarks in the same quantum state.
Yet another new quantum number was needed. Gell-Mann and Fritzsch had earlier fixed on the idea of ‘colour’.6 In this model, each quark possesses one of three different kinds of ‘colour charge’—red, green, or blue. Baryons are formed from three quarks each of different colour, such that their total colour charge balances out to zero (or ‘neutral’) and the resulting particle is ‘white’.* For example, a proton may consist of a blue up quark, a red up quark, and a green down quark. A neutron may consist of a blue up quark, a red down quark, and a green down quark. The mesons, such as pions and kaons, consist of coloured quarks and their anti-coloured anti-quarks, such that the total colour charge is zero or neutral and the particles are also ‘white’.
So, in these even-stronger strong force interactions, it is quark colour that is conserved. The fact that there are three different colours means that the quantum field theory has to be constructed based on the symmetry group SU(3), the special unitary group of transformations of three complex variables. Eight force carriers are required (remember the number of force particles in an SU(n) field theory is given by n2 – 1). These force carriers are called gluons, the particles which ‘glue’ the coloured quarks together inside hadrons.
We can now stop referring to an ‘even stronger’ strong force and simply call it the colour force. Gell-Mann called the resulting field theory quantum chromodynamics, or QCD.
But, hang on. Earlier logic demanded that forces operating over very short distances must be carried by massive particles. So does this mean that the gluons are massive? Actually, no. This logic applies to a short-range force like the weak force, which declines in strength as the distance between particles being acted on increases. But, as we just saw, the colour force operates in a very different way. The gluons are massless particles, like the photon, but unlike photons they cannot ‘leak’ from inside the nucleus of an atom. Like the quarks, they also carry colour charge and are ‘confined’.
So what about Yukawa’s prediction that the strong force should be carried by particles with a mass of around 100 MeV/c2? It turns out he was partly right. Although it stays within the nucleus, the colour force binding quarks together inside protons and neutrons strays beyond the confines of these particles, giving rise to a ‘residual’ strong force. This can then be imagined to act between the protons and neutrons in the nucleus, binding them together. As there are only two particles to be acted on, only three residual force carriers are required. These are, in fact, the pions, with masses of 139.6 MeV/c2 (π+ and π–) and 135.0 MeV/c2 (π0).*
So, this is the standard model of particle physics. It consists of QCD and an electro-weak field theory which is split by the Higgs mechanism into an SU(2) field theory of the weak force (which is sometimes—though rarely—referred to as quantum flavourdynamics, QFD) and the U(1) field theory of quantum electrodynamics, or QED. It consists of three generations of matter particles, a collection of force particles, and the Higgs boson. By 2000, all the particles involved had been discovered experimentally, except for the Higgs.
Fermilab’s Tevatron particle collider promised that hints of the Higgs might be glimpsed, but there were no guarantees and it was clear that the Tevatron couldn’t create sufficiently high collision energies to yield a convincing discovery. In 1986, American physicists embarked on an ambitious project to build the world’s largest particle collider, known as the Superconducting Supercollider. But the project was cancelled by the US Congress in October 1993, with nothing to show for the $2 billion that had already been spent except for a rather large hole beneath the Texas prairie. All hopes transferred to a new collider, commissioned just over a year later, to be built at CERN in Geneva, called the Large Hadron Collider (LHC).
The LHC has two main detectors, called ATLAS and CMS, each of which involves collaborations of about 3,000 physicists from around the world. The first proton–proton collisions were recorded at the LHC on 30 March 2010, at a collision energy of 7 trillion electron volts (7 TeV). This was half the LHC’s design energy, but still the highest energy particle collisions ever engineered on Earth. Excitement built through the next two years as collision data at 7 TeV, then 8 TeV, were accumulated. The discovery of the Higgs boson, with a mass of about 125 GeV/c2 (equivalent to about 133 protons) was announced on 4 July 2012. I watched events unfold in a webcast live from CERN’s main auditorium.*
Further data were collected through to mid-December 2012 and at a conference in March 2013 the results from both detector collaborations confirmed the identity of the new particle. This was definitely a Higgs boson, although the physicists remained deliberately vague about it, declaring ‘ … we still have a long way to go to know what kind of Higgs boson it is’.7 But this was more than enough for the Nobel Prize committee, which awarded the 2013 Physics Prize to Higgs and Englert.*
The physicists’ confidence that this is indeed ‘the’ standard model Higgs boson continued to grow. When the results from both collaborations were combined and evaluated in a paper published in September 2015 it was clear that the new particle is entirely consistent with the predictions of the standard model.8 The standard model of particle physics was now complete (Figure 22).
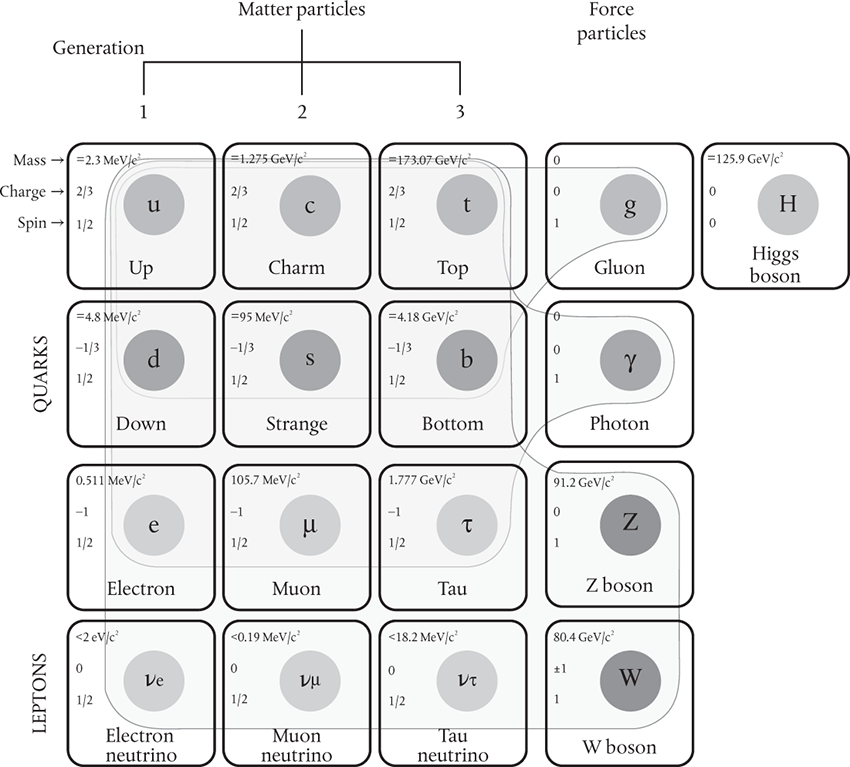
Figure 22. The standard model of particle physics describes the interactions of three generations of matter particles through three kinds of force, mediated by a collection of ‘force carriers’. The masses of the matter and force particles are determined by their interactions with the Higgs field.
In December 2015, the LHC, now operating at a collision energy of 13 TeV, produced tantalizing hints of a new, beyond-standard model particle with a mass of about 750 GeV/c2. This caused quite a buzz and had theorists scrambling to churn out papers at a rate of about ten per week. But as further experimental data were gathered at the LHC in 2016, these ‘hints’ were revealed to be nothing more than rather cruel, misleading statistical fluctuations. At the time of writing, there is no observation or experimental result in high-energy particle physics that cannot be accommodated within the standard model framework.
The loss of the 750 GeV/c2 ‘hint’ caused considerable grief within the particle physics community. This might seem odd, given that the discovery of the Higgs boson proved to be such a triumph. The simple truth is that physicists are desperate for some guidance from experiment on how the standard model might be transcended.
Why so? Put simply, the standard model is full of glaring omissions. As it stands, the model provides no clues about the strengths of the interactions between the elementary matter and force particles and the Higgs field, and so it cannot be used to calculate the masses of these particles from ‘first principles’. The Higgs mechanism tells us that this is where mass comes from, but it cannot tell us how much mass will result. The particle masses (or the strengths of their interaction with the Higgs field) have to be put in ‘by hand’ based on experimental measurements.
All the particles in the standard model have anti-matter counterparts. Anti-particles possess the same masses as their matter equivalents but have opposite electrical charges, such as the positron and electron (neutral particles are their own anti-particles). When they collide, particles and anti-particles will annihilate to produce high-energy photons (gamma rays). But, provided they are kept separate from matter, the anti-particles are perfectly stable.
Anti-hydrogen atoms, consisting of a negatively charged anti-proton and a positively charged positron, have been produced at CERN and trapped for short periods to allow them to be studied. They have physical properties essentially identical to ordinary hydrogen atoms.
So, why is the visible universe made of matter, and not anti-matter (or a mixture)? If equal amounts of matter and anti-matter were produced in the first few moments following the big bang, as seems reasonable, why did it not all annihilate, leaving a universe full of light but empty of matter? The arm-waving explanation is that—by chance or necessity—as the early universe evolved, the balance was tipped ever so slightly in favour of matter particles. The standard model gives no clue as to why this might have happened.
Then there’s the puzzle of dark matter. As we learned in Chapter 8, to explain the large-scale structure of the universe as it appears to us today we need to invoke another form of matter which is detectable by virtue of its gravity but invisible to all forms of electromagnetic radiation. We can’t see it but we know it must be there. None of the elementary building blocks of the standard model meet the requirements of dark matter. We have no idea what it is.
And, finally, there is no room in the standard model for the ‘force’ of gravity, essential for our description of matter on a large scale. Einstein’s general theory of relativity works extraordinarily well, as we’ve seen. But the standard model of particle physics is constructed from a set of quantum field theories. Now, the general theory of relativity handles the large-scale behaviour of mass-energy and curved spacetime. Quantum field theories handle the colour-force, weak-force and electromagnetic interactions of atomic and sub-atomic particles. When we try to put these two theoretical structures together to create some kind of unified theory that could do the work of both, we find that they really don’t get along.
There are differing views about why this might be, but it seems clear that general relativity and quantum field theory treat space and time in ways that are quite different, if not contradictory. In general relativity spacetime is active; it results from interactions involving matter and energy. In quantum field theory spacetime is passive; it merely provides a background in which interactions involving matter and force particles take place. Theorists have been trying to find ways to fix this for more than forty years, and we will take a brief look at their efforts in the epilogue, but it is fair to say that progress has been slow and there is no real consensus on the way forward.
There’s clearly plenty still to do. But, in the meantime, I think we’re now is a position to address the question with which I opened this book. What, exactly, is matter?