13
The Symmetries of Nature
That is not a sufficient excuse.
Wolfgang Pauli1
Even though physicists struggled to come to terms with what quantum theory was telling them about the nature of the material world, there could be no denying the theory’s essential correctness. Today the theory continues to make predictions that defy comprehension, only for these same predictions to be rigorously upheld by experiment.
But the quantum theory we have surveyed in Chapters 9–12 is primarily concerned with the properties and behaviour of electrons and the electromagnetic field. Now, it’s true to say that the behaviour of electrons which surround the nuclei of atoms underpins a lot of physics and pretty much all of chemistry and molecular biology. Yet we know that there is much more to the inner structure of atoms than this. With the problems of quantum electrodynamics (QED) now happily resolved, the attentions of physicists inevitably turned inwards, towards the structure of the atomic nucleus itself.
QED was extraordinarily successful, and it seemed to physicists that they now had a recipe that would allow them to establish theories of other forces at work inside the atom. By the early 1950s, it was understood that there were three of these. Electromagnetism is the force that holds electrically charged nuclei and electrons together. The other two forces work on protons and neutrons inside the atomic nucleus.
The first of these is called the weak nuclear force. As the name implies, it is much weaker than the second kind of force which—for rather obvious reasons—is called the strong nuclear force. The weak nuclear force manifests itself in the form of certain types of radioactivity, such as beta-radioactive decay. This involves a neutron spontaneously converting into a proton, accompanied by the ejection of a fast-moving electron. We can write this as n → p+ + e–, where n represents a neutron, p+ a positively charged proton, and e– a negatively charged electron.
In fact, a free neutron is inherently radioactive and unstable. It has a half-life of about 610 seconds (a little over ten minutes), meaning that within this time we can expect that half of some initial number of neutrons will decay into protons (or, alternatively, there’s a fifty per cent chance that each neutron will have decayed). Neutrons become stabilized when they are bound together with protons in atomic nuclei, so most nuclei are not radioactive. There are a few exceptions, however. For example, the nucleus of an isotope of potassium with nineteen protons and twenty-one neutrons has a little too much energy for its own good. It undergoes beta-radioactive decay with a half-life of about 1.3 billion years, and is the most significant source of naturally occurring radioactivity in all animals (including humans).
The involvement of an electron in beta-radioactivity suggests that the weak nuclear force operates on electrons, too, although it is very different from electromagnetism. For this reason I’ll drop the name ‘nuclear’ and call it the ‘weak force’. There’s actually a little more to this force. Careful analysis of the energies of the particles we start with in beta-radioactive decay compared with the particles we end up with gives a small discrepancy. In 1930, Pauli suggested that another kind of uncharged particle must also be ejected along with the electron, responsible for carrying away some of the energy of the transformation. The mysterious particle was called the neutrino (Italian for ‘small neutral one’) and was discovered in 1956. Like the photon, the neutrino is electrically neutral and for a long time was thought to be massless. Neutrinos are now believed to possess very small masses.
So, to keep the energy bookkeeping above-board, we now writ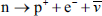e: 
where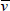 
(pronounced ‘nu-bar’) represents an anti-neutrino, the anti-particle of the neutrino.
Now, if QED is a specific form of quantum field theory, the key question the theorists needed to ask themselves in the early 1950s was this: what kind of quantum field theories do we need to develop to describe the weak and strong forces acting on protons and neutrons?
As they scrambled for clues, theorists reached for what is arguably one of the greatest discoveries in all of physics. It provides us with a deep connection between critically important laws of conservation—of mass-energy, linear, and angular momentum* (and many other things besides, as we will see)—and basic symmetries in nature.
In 1915, German mathematician Emmy Noether deduced that the origin of conservation laws can be traced to the behaviour of physical systems in relation to certain so-called continuous symmetries. Now, we tend to think of symmetry in terms of things like rotations or mirror reflections. In these situations, a symmetry transformation is equivalent to the act of rotating the object around a centre or axis of symmetry, or reflecting an object as though in a mirror.
We claim that an object is symmetrical if it looks the same following such a transformation. So, we would say that a diamond symbol, such as ♦, is symmetrical to 180° rotation around its long axis (top to bottom) or when reflected through its long axis, the point on the left mirroring the point on the right.
These are examples of discrete symmetry transformations. They involve an instantaneous ‘flipping’ from one perspective to another, such as left-to-right or top-to-bottom. But the kinds of symmetry transformations identified with conservation laws are very different. They involve gradual changes, such as continuous rotation in a circle. Rotate a perfect circle through a small angle measured from its centre and the circle obviously appears unchanged. We conclude that the circle is symmetric to continuous rotational transformations around the centre. We find we can’t do the same with a square or a diamond. A square is not continuously symmetric—it is instead symmetric to discrete rotations through 90°, a diamond to discrete rotations through 180° (see Figure 18).
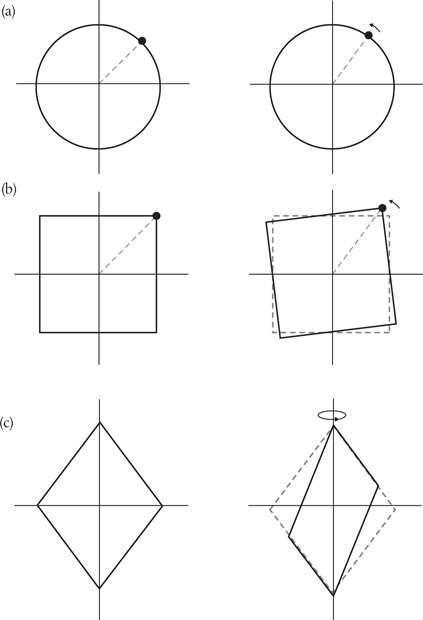
Figure 18. Continuous symmetry transformations involve small, incremental changes to a continuous variable, such as a distance or an angle. When we rotate a circle through a small angle, the circle appears unchanged (or ‘invariant’) and we say that it is symmetric to such transformations, (a). In contrast, a square is not symmetric in this same sense. It is, instead, symmetric to discrete rotations through 90°, (b). A diamond is symmetric to 180° rotations around its long axis, (c).
Noether found that changes in the energy of a physical system are symmetric to continuous changes in time. In other words, the mathematical laws which describe the energy of a system now will be exactly the same a short time later. This means that these relationships do not change with time, which is just as well. Laws that broke down from one moment to the next could hardly be considered as such. We expect such laws to be, if not eternal, then at least the same yesterday, today, and tomorrow. This relationship between energy and time is the reason these are considered to be conjugate properties, their magnitudes governed by an uncertainty relation in quantum theory.
The laws describing changes in linear momentum are symmetric to continuous changes in position. The laws do not depend on where the system is. They are the same here, there, and everywhere, which is why position (in space) and linear momentum are also conjugate properties, governed by an uncertainty relation.
For angular momentum, defined as motion in a circle at a constant speed, the equations are symmetric to continuous changes in the angle measured from the centre of the rotation to points on the circumference. And the answer to your next question is yes, there are uncertainty relations that govern the angular momentum of quantum systems.
Once the connection had been established, the logic of Noether’s theorem could be turned on its head. Suppose there is a physical quantity which appears to be conserved but for which the laws governing its behaviour have yet to be worked out. If the physical quantity is indeed conserved, then the laws—whatever they are—must be symmetric in relation to some specific continuous symmetry. If we can discover what this symmetry is, then we are well on the way to figuring out the mathematical form of the laws themselves. Physicists found that they could use Noether’s theorem to help them find a short cut to a theory, narrowing the search and avoiding a lot of unhelpful speculation.
The symmetry involved in QED is represented by something called the U(1) symmetry group, the unitary group of transformations of one complex variable, also known as the ‘circle group’. A symmetry ‘group’ is a bit like a scoreboard. It represents all the different transformations for which an object is symmetrical. The number in brackets refers to the number of ‘dimensions’ associated with it—in this case, just 1. These are not the familiar dimensions of spacetime. They are abstract mathematical dimensions associated with the properties of the different transformations. It really doesn’t matter too much what the symbol stands for, but we can think of U(1) as describing transformations synonymous with continuous rotations in a circle.2 This symmetry ties the electron and the electromagnetic field together in an intimate embrace. The upshot is that, as a direct result, electric charge is conserved.
The charge of the electron is preserved in all interactions with photons, so the photon is not required to carry a charge of its own. Also, the electromagnetic field acts over long ranges (though the strengths of these interactions fall off with distance). This means that the electromagnetic force can be carried quite happily by neutral, massless particles, able to travel long distances at the speed of light, which we call photons.
Although they are rather abstract, the dimensions of the symmetry groups have important consequences which are reflected in the properties and behaviours of particles and forces in our physical world. At this stage it’s useful just to note that a U(1) quantum field theory describes a force carried by a single force particle, the photon, acting on electrically charged matter particles, such as protons and electrons.
This is all very fine for electromagnetism, but the strong and weak forces clearly act on both positively charged protons and neutral neutrons. In beta-decay, a neutron transforms into a positively charged proton, so although the charge is balanced by the emitted electron, the charge on the particle acted on by the weak force is not conserved.
It is also pretty obvious that the strong and weak forces must be very short-range forces—they appear to act only within the confines of the nucleus, distances of the order of a femtometre (10−15 metres), in stark contrast to electromagnetism. In 1935, Japanese physicist Hideki Yukawa suggested that the carriers of short-range forces should be ‘heavy’ particles. Such force carriers would move rather sluggishly between the matter particles, at speeds much less than light.3 Yukawa went on to predict that the carriers of the strong force ought to have masses of the order of ~100 MeV/c2.4
There was no lack of interest in the weak force, as we will soon see, but the strong force appeared to hold the key to understanding the physics of the nucleus itself. As physicists began to think about the formulation of quantum field theories to describe the strong force, they asked themselves: what physical property is conserved in strong force interactions? The answer wasn’t all that obvious.
The proton and neutron have very similar masses—938.3 and 939.6 MeV/c2, according to the Particle Data Group, a difference of just 0.14 per cent. At the time the neutron was discovered in 1932, it was perhaps natural to imagine that it was some kind of composite, consisting of a proton and an electron.
Adopting this logic, Heisenberg developed an early theory of the strong force by imagining that this is carried by electrons. In this model, protons and neutrons interact and bind together inside the nucleus by exchanging electrons between them, the proton turning into a neutron and the neutron turning into a proton in the process. By the same token, the interaction between two neutrons would involve the exchange of two electrons, one in each ‘direction’.
This suggested that the protons and neutrons inside the nucleus are constantly changing identities, flickering back and forth from one to the other. In such a scenario, it makes more sense to think of the proton and neutron as though they are two different ‘states’ of the same particle, or two sides of the same coin.
Heisenberg introduced a new quantum number to distinguish these states, which he called isospin, or ‘isotopic spin’, in analogy with electron spin. Just like electron spin, he assigned it a fixed value, I = ½. This implies that a nuclear particle with isospin is capable of ‘pointing’ in two different directions, corresponding to +½ and –½. Heisenberg assigned one direction to the proton, the other direction to the neutron. Converting a neutron into a proton would in this picture then be equivalent to ‘rotating’ its isospin.
It was a crude model, but Heisenberg was able to use it to apply non-relativistic quantum mechanics to the nucleus itself. In a series of papers published in 1932, he accounted for many observations in nuclear physics, such as the relative stability of isotopes and alpha particles (helium nuclei, consisting of two protons and two neutrons). But a model in which the force is carried by electrons is too restricting—it does not allow for any kind of interaction between protons. Experiments soon showed that the strength of the force between protons is comparable to that between protons and neutrons.
Heisenberg’s theory didn’t survive, but the idea of isospin was seen to hold some promise and was retained. Now, the origin of this quantum number is quite obscure (and despite the name it is not another type of ‘spin’—it has nothing to do with the proton or neutron spinning like a top). Today we trace a particle’s isospin to the identities of the different kinds of quarks from which it is composed (more on this in Chapter 15).
We can now get back to our main story. So, when in 1953 Chinese physicist Chen Ning Yang and American Robert Mills searched for a quantity which is conserved in interactions involving the strong force, they settled on isospin. They then searched for a corresponding symmetry group on which to construct a quantum field theory.
It’s clear that the symmetry group U(1) will not fit the bill, as this is limited to one dimension and can describe a field with only one force particle. The interactions between protons and neutrons demand at least three force particles, one positively charged (accounting for the conversion of a neutron into a proton), one negatively charged (accounting for the conversion of a proton into a neutron), and one neutral (accounting for proton–proton and neutron–neutron interactions).
Their reasoning led them to the symmetry group SU(2), the special unitary group of transformations of two complex variables. Again, don’t get distracted by this odd label. What’s important to note is that the resulting quantum field theory has the right symmetry properties. It introduced a new quantum field analogous to the electromagnetic field in QED. Yang and Mills called it the ‘B field’.
Generally speaking, a symmetry group SU(n) has n2 – 1 dimensions. In the context of a quantum field theory, the number of dimensions determines the number of force-carrying particles the theory will possess. So, an SU(2) quantum field theory predicts three new force particles (22 – 1), responsible for carrying the force between the protons and neutrons in the nucleus, analogues of the photon in QED. The symmetry group SU(2) thus fits the bill. Yang and Mills referred to the charged force carriers as B+ and B–, and the neutral force carrier as B0 (B-zero). It was found that these carrier particles interact not only with protons and neutrons, but also with each other.
It was here that the problems started. The methods of mass renormalization that had been used so successfully in QED could not be applied to the new theory. Worse still, the zero-interaction term in the perturbation series indicated that the three force particles should all be massless, just like the photon. But this was self-contradictory. The carriers of short-range forces were expected to be heavy particles. Massless force carriers made no sense.
At a seminar delivered at Princeton on 23 February 1954, Yang was confronted by a rather grumpy Pauli. ‘What is the mass of this B field?’, Pauli wanted to know. Yang didn’t have an answer. Pauli persisted. ‘We have investigated that question’, Yang replied, ‘It is a very complex question, and we cannot answer it now.’ ‘That is not a sufficient excuse’, Pauli grumbled.5
It was a problem that simply wouldn’t go away. Without mass, the force carriers of the Yang–Mills field theory did not fit with physical expectations. If they were supposed to be massless, as the theory predicted, then the strong force would reach well beyond the confines of the nucleus and the force particles should be as ubiquitous as photons, yet they had never been observed. Accepted methods of renormalization wouldn’t work. They published a paper describing their results in October 1954. They had made no further progress by this time. Although they understood that the force carriers couldn’t be massless, they had no idea where their masses could come from.6 They turned their attentions elsewhere.
Let’s pause for a moment to reflect on this. The language that had developed and which was in common use among physicists in this period is quite telling. Remember that in a quantum field theory the field is the thing, and particles are simply elementary fluctuations or disturbances of the field. Pauli had demanded to know the mass of Yang and Mills’ B field. So, an elementary disturbance of a field distributed over space and time is associated with a mass.
Whether we can get our heads around a statement like this is actually neither here nor there as far as the physics is concerned. For as long as quantum field theories of various kinds remain valid descriptions of nature, then this is the kind of description we have to learn to live with. In a quantum field theory the terms in the equation that are associated with mass (called—rather obviously—‘mass terms’) vary with the square of the field and contain a coefficient which is also squared. If this coefficient is identified with the particle mass, m, then the mass terms are related to m2ϕ2, where ϕ (Greek, phi) represents the quantum field in question.7 Pauli nagged Yang for the mass of the B field because he knew there were no mass terms in Yang’s equations. He knew that Yang didn’t have a satisfactory answer.
And this was only part of the problem. A particle with a spin quantum number s generally has 2s + 1 ways of aligning (or ‘pointing’) in a magnetic field, corresponding to 2s + 1 different values of the magnetic spin quantum number, ms. Recall that an electron is a fermion with s = ½, and so it has 2 × ½ + 1 = 2 different values of ms (+½ and –½) corresponding to spin-up and spin-down states.
What about the photon? Photons are bosons with a spin quantum number s = 1. So there are 2 × 1 + 1 = 3 possible orientations of the photon spin (three values of ms), right?
To answer this question, let’s play a little game of ‘pretend’. Let’s forget everything we know about photons and pretend that they’re actually tiny, spherical particles or atoms of radiation energy, much as Newton had once envisaged. Let’s also forget that they travel only at the speed of light and pretend that we can accelerate them from rest up to this speed. What would we expect to see?
We know from Einstein’s special theory of relativity that as the speed of an object increases, from the perspective of a stationary observer time dilates and lengths shorten. As we accelerate a spherical photon, we would expect to see the diameter of the sphere moving in the direction of travel contracting and the particle becoming more and more squashed or oblate. The closer we get to the speed of light the flatter the spheroid becomes. What happens when it reaches light-speed?
Recall from Chapter 5 that the relativistic length l is given by l0/γ, where l0 is the ‘proper length’ (in this case, the diameter of the particle when it is at rest) and γ is 1/√(1 − v2/c2). When the velocity, v, of the particle reaches c, then γ becomes infinite and l becomes zero. From the perspective of a stationary observer, the particle flattens to a pancake. One with absolutely no thickness.
Of course, photons only travel at the speed of light and our game of pretend is just that—it’s not physically realistic. But we are nevertheless able to deduce from this that photons are in some odd way ‘two-dimensional’. They are flat. Whatever they are they have no dimension—they’re forbidden by special relativity from having any dimension—in the direction in which they’re moving.
Now we can go back to our question about photon spin. If s = 1, we would indeed be tempted to conclude that the photon spin can point in three different directions. But, as we’ve just seen, the photon spin doesn’t have three directions to point in. By virtue of the simple fact that it is obliged to move at the speed of light, it has only two dimensions. One of the spin directions (one of the possible values of ms) is ‘forbidden’ by special relativity.
There are therefore only two possible spin orientations for the photon, not three. These correspond to the two known types of circular polarization, left-circular (ms = +1, by convention), and right-circular (ms = –1). These properties of light may be unfamiliar, but don’t fret. We can combine the left-circular and right-circular polarization states of light in a certain kind of superposition which yields linearly polarized states—vertical and horizontal. These are much more familiar (though note that there are still only two—there is no ‘back-and-forth’ polarization). Polaroid® sunglasses reduce glare by filtering out horizontally polarized light.
So, all massless bosons (such as photons) travel at the speed of light and are ‘flat’, meaning that they can have only two spin orientations rather than three expected for bosons with s = 1. But if, as Yukawa had suggested, the carriers of short-range forces are massive particles then there is no such restriction. Heavy particles cannot travel at the speed of light so they are expected to be ‘three-dimensional’. If they are also bosons with s = 1, then they would have three spin orientations.
Physicists needed to find a mechanism which would somehow act to slow down the massless force carriers of the Yang–Mills field theory, thereby allowing them to gain ‘depth’, acquiring a third dimension in the direction of travel for the particles’ spin to point in. The mechanism also needed to conjure up mass terms in the equations related to m2ϕ2. Just how was this supposed to happen?