Psychophysics
In this chapter, you will learn how to use MATLAB® to do psychophysics. Once you master these fundamentals, you can use MATLAB to address any psychophysical question that might come to mind. While—in principle—all sensory modalities are open to psychophysical investigation, we will focus on visual psychophysics in this chapter.
Keywords
psychophysics; visual psychophysics; visual stimuli; method of limits; absolute threshold
8.1 Goals of this Chapter
In this chapter, you will learn how to use MATLAB® to do psychophysics. Once you master these fundamentals, you can use MATLAB to address any psychophysical question that might come to mind. While—in principle—all sensory modalities are open to psychophysical investigation, we will focus on visual psychophysics in this chapter.
8.2 Background
Psychophysics deals with the nature of the quantitative relationship between physical and mental qualities. Today, the practice of psychophysics is ubiquitous in all fields of neuroscience that involve the study of behaving organisms, be they man or beast. Curiously enough, the origins of systematic psychophysics can be traced to a single individual: Gustav Theodor Fechner (1801–1887). Fechner’s biography exhibits many telling idiosyncrasies. Born the son of a pastor, he studied medicine at the University of Leipzig, but never practiced it after receiving his degree. Mostly by virtue of translating chemistry and physics textbooks from French into German, he was appointed professor of physics at the University of Leipzig. In the course of studying afterimages by gazing into the sun for extended periods of time—himself being the primary and sole research participant—he almost lost his eyesight and went into deep depression in the early 1840s. This episode lasted for nearly a decade, a time which Fechner spent mostly within a darkened room. Emerging from this secluded state, he was overwhelmed by the sheer brilliant radiance of his surroundings, giving rise to his panpsychist worldview: he was now utterly certain that all things have souls, including inanimate objects such as plants and stones. Determined to share his insights with the rest of humanity, he soon started publishing on the topic, formulating an “identity theory” stating that the physical world and the spiritual world are not separate entities, but actually the same—the apparent differences resulting from different perspectives (first versus third person) onto the same object. In his view, this reconciles the incompatible dominant philosophical worldviews of the 19th century: idealism and materialism. However, his philosophical treatises on subjects such as the soul-life of plants or the transcendence of materialism were poorly received by the scientific community of the day (Fechner, 1848). In order to convince his colleagues of the validity of his philosophical notions, he set out to devise methods that would allow him to empirically link physical and spiritual realms (Fechner, 1851). His rationale being that if it can be shown that mental and physical qualities are in a clear functional relationship, this would lend credence to the notion that they are actually metaphysically identical.
Publishing the results of empirical studies on the topic in his Foundations of Psychophysics in 1860, he showed that this is the case for several mental domains, such as the relationship between physical mass and the perception of heaviness or weight. Fechner formulated several methods to arrive at these results that are still in use today. Importantly, he expressed the results of his investigations in mathematical, functional terms. This allowed for the theoretical interpretation of his findings. Doing so, he introduced notions such as sensory thresholds quantitatively.
Ironically, inventing psychophysics did not help Fechner in convincing his philosophical adversaries of the merits of his identity theory. Few philosophers of the day renounced their idealistic or materialistic positions in favor of identity theory. Most of them simply chose to ignore Fechner, while the others mostly attacked him. Consequently, Fechner spent much of the remainder of his life fighting these real or imaginary adversaries, publishing two follow-up volumes in 1877 and 1882, chiefly focusing on the increasingly bitter struggle against the philosophical establishment of Imperial Germany. Ultimately, these efforts had little tangible or lasting impact. Meanwhile, the first experimental psychologists, particularly the group around Wundt, pragmatically used these very same methods to create a psychology that was both experimental and empirical. It is not too bold to claim that they never stopped and that contemporary psychophysics derives in an unbroken line from these very roots.
The key to visual psychophysics (and psychophysics more generally) is to elicit relatively simple mental phenomena that lend themselves to quantification by presenting physical stimuli that are easily described by just a few parameters such as luminance, contrast, or spatial frequency.
It is imperative that the experimenter has complete control over these parameters. In other words, the visual stimuli that s/he is presenting have to be precise. One way to create these stimuli is to use commercially available graphics editors, most prominently Photoshop®. While this practice is very common, it comes at a cost. For example, the images created by Photoshop have to be imported by the experimental control software. It is more elegant to create the stimuli in the same environment in which they are used. More importantly, the experimenter surrenders some degree of control over the created stimuli, when using commercial graphics editors, because the proprietary algorithms to perform certain image functions are not always completely documented or disclosed. This problem is equally avoided by creating the stimuli in a controlled way within MATLAB.
8.3 Exercises
We need to introduce methods by which to create and present visual stimuli of any kind on the screen. Fortunately, MATLAB includes a large library of adequate functions. We will introduce the most important ones here.
By default, MATLAB visualizes images by triplets in a 256-element RGB space. Each element of the triplet has to be an integral value between 0 and 255. This corresponds to a range of 8 bits. Hence, these elements can be represented by variables of the type uint8. These values correspond to the intensity of red, green, and blue at a particular location in the image. Depending on the physical output device (typically cathode ray tube or LCD displays), these values effectively regulate the voltage of individual ray guns or pixels. Of course, MATLAB also supports much higher bit-depths. For the purposes of our discussion, 8 bit will suffice.
One important caveat is that the relationship between the assigned voltage values of the three individual ray guns in the cathode ray tube (0 to 255) and the perceived luminance of the screen is not necessarily linear. Visual scientists generally calibrate their monitors by “gamma correcting” them. This linearizes the relationship between assigned voltage or intensity values and the perceived luminance.
To be able to linearize the relationship, you need a photometer. Because we assume that those are—due to their generally high price—not readily available, we will forgo this step for the purposes of this book. However, we urge budding visual scientists to properly calibrate their monitors before doing an experiment in which the veracity of the data is crucial—as is the case if they are intended for publication. For more information on the issue of monitor calibration, see for example Carpenter and Robson (1999).
To begin, create a simple matrix with the following command:
This command creates the matrix test_disp, which is a three-dimensional matrix with three elements in each dimension. Importantly, it is of the data type uint8, which MATLAB assumes by default for its imaging routines. Of course, the function image can also image other matrices, but this would require to specify additional parameters. Imaging only matrices of the type uint8 is the most straightforward thing to do for the purposes of this chapter.
The function image compels MATLAB to interpret the values in the matrix as commands for the ray guns of the monitor and to display them on the screen. You should now be looking at a completely and uniformly dark (black) subplot 1.
The structure of the matrix and the function of the image command now become apparent.
The 0 values are interpreted as turning off all ray guns. The 255 values are interpreted as full power. As you maximally engage all three guns (represented by the third dimension of the matrix), the result is an additive mix of spectral information that is interpreted by the visual system as white. Now, try this:
The picture in subplot 2 is devoid of color from the red gun. It should appear cyan. Now try the following:
This code has the opposite effect, yielding a red inner pixel. The result should look something like Figure 8.2.
While it is hard to surpass this example of using just 9 pixels in clarity, it is also somewhat pedestrian. The true power of this approach becomes clear when considering natural stimuli, which are also increasingly used in visual psychophysics. To do this, you need to import an image into MATLAB. For this example, use the imread function:
This command creates a large three-dimensional matrix of the uint8 type (positive integral values from 0 to 255, as can be addressed by 8 bits).
Next, type the following to get a magnificent view of the Harper Library at the University of Chicago:
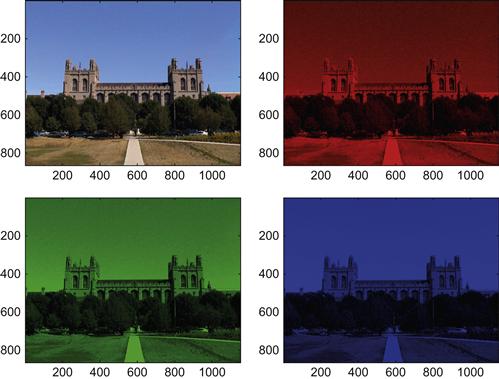
Now, you can manipulate this image in any way, shape, or form. Importantly, you will know exactly what you are doing, since you are the one doing it, which cannot be said for most of the opaque algorithms of image processing software. For example, you can separate the information in different color channels by typing the following:
>> bigmatrix(:,:,:,ii) = zeros(size(temp,1),size(temp,2),3);
>> bigmatrix(:,:,ii,ii) = temp(:,:,ii);
You get the picture shown in Figure 8.3 as a result.
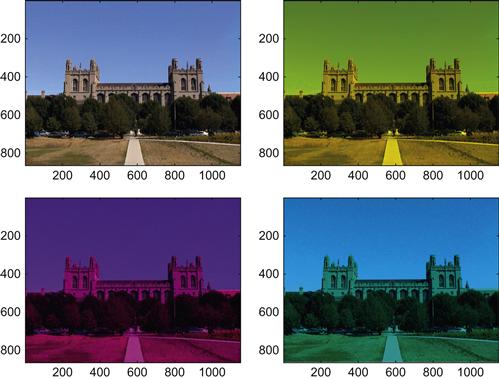
Note the use of the upazila helper variable. You have to use this because MATLAB interprets non-3D-uint8 matrices differently when presenting images. Later you will learn how to make do without the upazila step. The different subplots illustrate the brightness values assigned to an individual ray gun (Upper left: all of them together. Upper right: red. Lower left: green. Lower right: blue). This allows you to assess the contribution of every single channel (red/green/blue) to the image. Another way of judging the impact of a particular channel is to leave it out. To do this, you add the other channels together, as follows:
>> bigmatrix2(:,:,:,1) = bigmatrix(:,:,:,1)+bigmatrix(:,:,:,2)+bigmatrix(:,:,:,3);
>> bigmatrix2(:,:,:,2) = bigmatrix(:,:,:,1)+bigmatrix(:,:,:,2);
>> bigmatrix2(:,:,:,3) = bigmatrix(:,:,:,1)+bigmatrix(:,:,:,3);
>> bigmatrix2(:,:,:,4) = bigmatrix(:,:,:,2)+bigmatrix(:,:,:,3);
Doing so should yield the picture shown in Figure 8.4.
In this figure, the upper left is all channels. In the upper right, the blue channel is missing. In the lower left, the green channel is missing. In the lower right, the red channel is missing. Belaboring this point enhances an understanding of the relationship between the brightness values in the three-dimensional matrix and the appearance of the image.
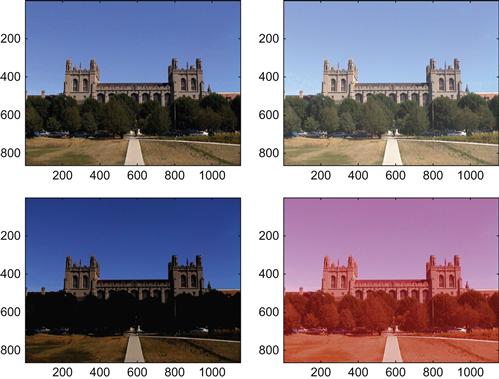
You are now in a position to implement arbitrary changes to the image. For example, you can brighten it, increase the contrast, or selectively change the color balance. To explore this, start by changing the overall brightness by typing the following:
>> image(uint8(bigmatrix2(:,:,:,1)))
>> image(uint8(bigmatrix2(:,:,:,1)+50))
>> image(uint8(bigmatrix2(:,:,:,1)-50))
The result, shown in Figure 8.5, is a picture that has been somewhat brightened (upper right), darkened (lower left), and where the red channel has been turned (way) up in the lower right.
One of the most common image manipulations using image editors is the smoothing or sharpening of the image. The former is often performed to get rid of random noise or granularities in the image. Scientists might do this to simulate and understand the output of the visual system of another species. Importantly, these ends are typically achieved by low- or high-pass filtering of the original image. Unfortunately, most users don’t really understand what is happening behind the scenes when using a commercially available image editor. Of course, this is unacceptable for doing psychophysics in particular or science in general.
Hence, we will now discuss how to perform these operations in MATLAB. First, import another image by typing the following. This image is more suited to making the effects of your manipulations more readily apparent.
Look at the image. So far, so good. Now, slightly blur the image. To do so, you will convolve the image with a filter. Refer to Chapter 16, “Convolution,” to understand precisely the underlying mathematics of the operation. For purposes of this example, it is enough to understand that the convolution operation will allow you to blur the image by blending brightness values of adjacent pixels. To create a small 3×3 filter, you type
to perform the convolution of the image with the 3×3 filter. You might have noted that the values are no longer in the range between 0 and 255. This is due to the multiplying and adding brought about by the convolution. Next, divide by the block size (9) to rectify this situation:
This operation creates floating-point values, so you have to be careful when imaging this:
This code creates a very slightly low-pass filtered version of the image. This result is most readily apparent when you look at the texture of the hat or hair in the image. Now, try a more radical low-pass filtering:
Looking at the image reveals significant blurring. This is the low-frequency component of the image. It is similar to what a typical nocturnal animal with relatively poor spatial acuity might see (sans the color). You arrive at the image by blurring a substantial number of pixels together.
Note that the matrices you created with the convolution operation are slightly larger than the one that represents the initial picture (which had a format of 600×800). This is due to the nature of the convolution operation. It creates an artificial black rim not present in the original picture. You will understand why this happens and why this is a hard problem when reading Chapter 16. For now (we will encounter much more elegant ways in Chapter 16), and to (mostly) get rid of it and cut the image back to size, try the following:
You might also have noted that the execution of the convolution operation took a significant amount of time. This might be important if you want to create your stimuli on the fly, as the observer does the experiment. To assess how your system stacks up against certain known benchmarks, type this command:
Doing so makes MATLAB perform various typical operations and compare the speed of their execution to other benchmark systems. This is particularly crucial when you’re running a time-sensitive program. Don’t be surprised when receiving rather low benchmark values, particularly when running MATLAB over a network, despite basically fast hardware. To evaluate the reliability of the benchmark values, try running bench more than once, e.g. bench(5) runs it 5 times.
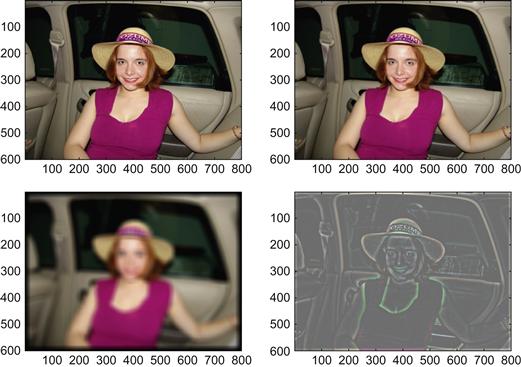
Let’s get back to the filtering problem. The image in the lower left corresponds to what psychophysicists would call the “low spatial frequency” channel. It contains the low spatial frequency information in the image. Notably, it is mostly devoid of sharp edges. This information about edges in the image is contained in the “high spatial frequency” channel. How do you get there? By subtracting the low spatial frequency information from the original image. Try this:
The image in the lower right now contains the high spatial frequency information. It represents most of the textures and sharp edges in the original image.
Unfortunately, it is rather dark (due to the subtraction). To appreciate the full high spatial frequency information, add a neutral brightness level back in:
Much better. The final result should look something like that shown in Figure 8.6.
We have discussed a variety of image manipulations with MATLAB, namely the manipulation of form, color, and spatial frequency. One remaining major issue is the creation of moving stimuli. There are many ways to do this in MATLAB. One of the most straightforward is to use the circshift function in combination with a frame capture function.
To use this function, type the following:
The circshift function shifts all matrix values by the stated amount in the second argument—in this case, 100 in the direction of the first dimension, nothing in the others.
You can use this to create a movie:
There are other ways to create movie frames, for example, using the im2frame function. However, this version lets you preview the movie as you create it. You can play it by typing
This command plays the movie in matrix M three times, at 24 frames per second, in the existing figure. One caveat for movies is size in memory. These frames take up a considerable amount of space. You might get an error message indicating that the frames could not be created if you go beyond the available memory. The available memory depends on the computer and operating system. To assess the memory situation on the machine you are using, type
There are several caveats when making movies with MATLAB. For example, the choppiness will depend on many factors, including machine speed, available memory, step size of the circshift, as well as frame rate. On most systems, it will be hard to avoid trade-offs to create movies that are reasonably smooth.
As the color information is represented in the third dimension of the matrix, you can also use circshift to elegantly swap colors, as in this example:
The result should look something like Figure 8.7.
Often, when creating large numbers of stimuli, you might want to save them on the hard disk to free up some space in available memory. You can easily do this by using the imwrite function. For example, you can save the image in which the RGB values were swapped for BRG by typing imwrite(pic,’BRG.jpg’,’jpg’). This should have created the file BRG.jpg as a .jpg file in your working directory. You can now open it with other image editing software, put it online, etc. Similarly, you can save the movie by typing
which creates an .avi file named upazila at a frame rate of 24 and a quality of 100 in your working directory. From now on, this file will behave like any other movie file you might have on your hard disk.
At this point, we have explored several important image manipulation routines that should really give you a deep appreciation of the way MATLAB represents and displays images. Of course, many more image manipulations are possible in MATLAB. We will leave those for you to discover and return to the task of collecting psychophysical data, using this newfound knowledge. Because MATLAB represents images as brightness values in a three-dimensional matrix, you can manipulate them at will with any number of matrix operations. In principle, you could write your own Photoshop toolbox in MATLAB.
Let’s get back to psychophysics. Fechner formalized three fundamental methods to elicit the relationship between mental and physical qualities and introduced them to a wider audience. These methods are still in use today. You should recognize the method of limits from visits to the ophthalmologist investigating your vision or the otologist investigating your hearing. Basically, the observer is presented with a series of stimuli in increasing (or decreasing) intensity and asked to judge whether or not the stimulus is present. This method is extremely efficient because only a few stimuli are necessary to establish fairly reliable thresholds. Unfortunately, the method suffers from hysteresis; the threshold is path dependent, as participants exhibit a certain inertia (e.g., stating that the stimulus is still present even if they can’t detect it, if coming from the direction of a stimulus being present). This problem can be overcome by counterbalancing (starting from different states). However, a better correction is the method of constant stimuli. In this method, the experimenter presents stimuli to be judged by the observer in random order, from a predetermined set of values. The advantage of this method is that it yields very reliable and mostly unbiased threshold measurements. The drawback is that one needs to sample a relatively large range of stimuli (as one doesn’t a priori know where the threshold will lie) and a large number of repetitions per conditions to reduce error. Hence, this method is usually not used where time is at a premium (such as in a doctor’s office), but rather in research, where the time of undergrad or grad student observers is routinely sacrificed for increases in accuracy.
Finally, the method of adjustment lets the research participant manipulate a test stimulus that is supposed to match a given control. This method is particularly popular in color psychophysics. It is relatively efficient, but suffers from its own set of biases.
8.4 Project
In this project, you will use the method of constant stimuli to determine the absolute threshold of vision, a classic experiment in visual psychophysics (Hecht, Shlaer, and Pirenne, 1942). Obviously, you will be able to do only a crude mock-up of this experiment in the scope of this chapter. The actual experiment was extremely well controlled and took a long time to carry out (not to mention specialized equipment).
Since you are unconcerned with publishing the results (these are extremely well established), you can pull off a “naïve” version in order to highlight certain features and principles of the psychophysical method. If you want to increase experimental control, perform the experiment in a dark room and wait 15 minutes (or better 30 minutes) before data collection. Also, try to keep a fixed distance from the monitor (e.g., 50 cm) throughout the data collection phase of the experiment.
However, before you can collect data, you need to write a stimulus control program utilizing the skills from the previous two chapters and the image manipulation skills introduced in this chapter. Here is a simple program that will do what is needed (make this an M-file). Note the somewhat obsolete use of the modulus function to order the stimuli. We could also do this with randi in the latest versions of MATLAB. On the other hand, the use of the modulus function allows you to have exactly the same number of trials per condition (as opposed to them having random frequencies).
clear all; %Emptying workspace
close all; %Closing all figures
temp = uint8(zeros(400,400,3)); %Create a dark stimulus matrix
temp1 = cell(10,1); %Create a cell that can hold 10 matrices
temp(200,200,:) = 255; %Inserting a fixation point
temp(200,240,:) = (ii-1)*10; %Inserting a test point 40 pixels right
%of it. Brightness range 0 to 90.
temp1{ii} = temp; %Putting the respective modified matrix in cell
h = figure %Creating a figure with a handle h
stimulusorder = randperm(200); %Creating a random order from 1 to 200.
%For the 200 trials. Allows to have
%a precisely equal number per condition.
stimulusorder = mod(stimulusorder,10); %Using the modulus function to
%create a range from 0 to 9. 20 each.
stimulusorder = stimulusorder + 1; %Now, the range is from 1 to 10, as
score = zeros(10,1); %Keeping score. How many stimuli were reported seen
for ii = 1:200 %200 trials, 20 per condition
image(temp1{stimulusorder(1,ii)}) %Image the respective matrix. As
ii %Give observer feedback about which trial we are in. No other feedback.
temp2 = get(h,’CurrentCharacter’); %Get the keypress. “.” for present,
temp3 = strcmp(‘.’, temp2); %Compare strings. If . (present), temp3 = 1,
score(stimulusorder(1,ii)) = score(stimulusorder(1,ii)) + temp3; %Add up.
Note that these are relatively crude steps. In a real experiment, you might want to probe every luminance value and collect more samples per condition (50 or 100 instead of 20). Also, a time limit of exposure and decision time is usually used. But for now, this will do. When running this program yourself, make sure to focus on the central fixation dot. Don’t get frustrated or bored. Psychophysical experiments are extremely intricate affairs, usually operating at the limits of the human sensory apparatus. Hence, they are rarely pleasant. So try to focus the firepower of your cortex on the task at hand. Also note that you will make plenty of errors. Don’t get frustrated. That is the point of psychophysics. In a way, psychophysics amounts to a very sophisticated form of producing and analyzing errors. If you don’t make any errors, there is no variance, and without variance, most of the psychophysical analysis methods fail—hence the large number of trials. Given enough trials, you can count on the statistical notion that truly random errors will average out, while retaining and strengthening the systematic trends in the data, revealing the properties of the system that produced it. As a matter of fact, you might want to throw in a couple of practice runs before deciding to analyze your data for real. Given that you are likely to be what is technically called an untrained observer there will be various dynamics going on during the experiment. At first, practice effects will enhance the quality of your judgments; then fatigue will diminish it. Also note that you are technically not a “naïve” observer, as you are aware of the purpose of the experiment. Don’t let this discourage you for now. Doing so, we obtained the curve shown in Figure 8.8. This figure shows a fairly decent psychometric curve. It is obvious that we did not see the dot on the left tail of the curve (the observed variation represents errors in judgment). Similarly, it is obvious that we did always see the dot on the right of the curve, yet there is some variation in the reported instances seen. In other words, the points on the left are below threshold, whereas the points on the right are already saturated. In a real experiment, we would resample the range between the brightness values 20 and 70 much more densely, as it is clear that the date points outside this range add no information. However, this neatly illustrates one problem of the method of constant stimuli. We didn’t know where the threshold would lie. Hence, we had to sample a broad range—undersampling the crucial range and oversampling regions of no interest. Even limiting the range from 0 to 90 was an educated guess. Strictly speaking, and without any previous knowledge, we would have had to sample the entire range of 0 to 255. Modern “staircase” procedures attempt to solve this problem, but are beyond the scope of this chapter. Psychophysicists like to boil down this entire dataset into one number: the absolute threshold. In this case, you can derive this value by interpolation. It is the x-value that corresponds to the intersection between the curve and the y-value of probability reported seen of 0.5, as shown in Figure 8.9. In other words, this analysis indicates an absolute threshold of a brightness value of 43. If you want to get a precise threshold, you would have to resample the range between 30 and 60 (or even between 40 and 50) very densely. Also note that this value of 43 is not inherently meaningful. Without having the monitor calibrated with a photometer, we don’t know to how much physical light energy this corresponds to. Hence, we can’t relate it to the minimum number of light quanta that can be detected. However, this threshold is meaningful in the context of a behavioral task: a shifted threshold under different conditions can give rise to conjectures about the structure and function of the physiological system producing these thresholds, as you will see when doing the exercises. Moreover, the absolute threshold is a stochastic concept. It is not true that lights below it are never seen. Of course, psychophysicists have very elaborate ways to analyze data like these. Most straightforwardly, they like to fit sigmoidal logistic curves to such data. We will go into the intricacies of psychophysical data analysis in the next chapters. Finally, we chose luminance values that worked on our monitor, yielding a decent psychometric curve, allowing us to determine the threshold. You might have to use a different range when working within your setup. For more background on psychophysical methods, read the classic Elements of Psychophysics by Fechner (1860) or, for a modern treatment of the use of these methods in visual neuroscience, The Psychophysical Measurement of Visual Function by Norton, Corliss, and Bailey (2002). In this project, you should specifically address the following issues: Compare thresholds in the periphery and center. You just did a parafoveal stimulus presentation (if you were honest and fixated the fixation point) or even a foveal presentation (if you looked at the stimulus directly). How does the threshold change in the periphery (putting the stimulus several hundred pixels away from the fixation point)?

Figure 8.8 The psychometric curve reveals below-threshold regions, saturation regions, and a linear range.
Determine the thresholds for brightness values of the red, green, and blue guns individually. Which gun has the lowest threshold (is perceived as brightest)? Which gun has the highest threshold (is perceived as dimmest)? Can you account for the white threshold (as we did above) by adding the individual thresholds?
You just determined absolute thresholds. Another important concept in psychophysics is the relative threshold. To determine the relative threshold, put another test dot to the left of the fixation point. The task is now to indicate if the brightness of the right dot is higher (.) or lower (,). Does the relative threshold depend on the absolute brightness values of the dots? If so, can you characterize the relationship between relative threshold (difference in stimulus brightness values that gives a probability of 0.5) and absolute value of the stimuli?
When determining the relative threshold, can you reason why it makes sense to ask which of the two is brighter, instead of asking if they are the same or different (which might be more intuitive)?