Chapter 13

Wavelets

In this chapter, you will be introduced to the use of wavelets and wavelet transforms as an alternative method of spectral analysis. We will discuss a number of common wavelets and introduce the Wavelet Toolbox of the MATLAB® software.

Keywords

wavelet; continuous wavelet transform; Morlet wavelet; Mexican hat wavelet; scalogram; discrete wavelet transform

13.1 Goals of This Chapter

In this chapter, you will be introduced to the use of wavelets and wavelet transforms as an alternative method of spectral analysis. We will discuss a number of common wavelets and introduce the Wavelet Toolbox of the MATLAB® software.

13.2 Background

In Chapter 12, “Frequency Analysis Part II: Nonstationary Signals and Spectrograms,” introduced the short-time Fourier transform (STFT) to decompose the frequency composition of nonstationary signals. Under certain situations, though, the STFT results in a less-than-optimal breakdown of frequency as a function of time. With increased precision in frequency distribution, localization in time becomes less precise. In other words, there is a time–frequency precision tradeoff. The reverse is also true: better temporal localization reduces the precision of the frequency distribution. This may bring to mind the well-known relationship of position and momentum of the Heisenberg uncertainty principle.

One of the benefits of the STFT is that the transform window can be chosen to optimize the resolution of frequency or localization of that frequency in time. A larger window allows for better frequency resolution, and a smaller window allows for better temporal resolution. However, for the STFT, the window size is constant throughout the algorithm. So, while the STFT can optimize for frequency or time in a given signal, the choice in the time-frequency tradeoff holds for the entire signal. This can pose a problem for some nonstationary signals. The wavelet transform provides an alternative to the STFT that often provides a better frequency/time representation of the signal.

13.2.1 What is a Wavelet?

A wavelet is a function that satisfies at least the following two criteria:

1. The integral of the function ψ(x) over all x is 0.

(13.1)

2. The square of ψ(x) has integral 1. A function adhering to this property is called square-integrable.

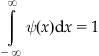(13.2)

Fulfilling the first criterion mandates that the wavelet function has an equal area above and below zero. Fulfilling the second criterion mandates that the function approach zero at positive and negative infinity. Because of this second criterion, the function decays away from the origin, unlike sinusoidal or other infinite waves (thus, wavelet).

13.2.2 The Continuous Wavelet Transform

The continuous wavelet transform (CWT) is analogous to the continuous Fourier transform:

(13.3)

Here, the parameter t is the typical t in the time series x(t). The parameter s is called scale and is analogous to frequency for Fourier transforms. The wavelet function itself varies with both s and t:

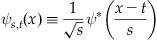(13.4)

The inclusion of t and s allows the function to be scaled and translated (shifted) for different values of s and t. The original wavelet function (untranslated and unscaled) is often termed the mother wavelet, since the set of wavelet functions is generated from that initial function.

The scaling provides a significant benefit over the short-time Fourier transform. The multiple scales of the wavelet transform permit the equivalent of large- or small-scale transform windows in the same time series. The preceding transform can be approximated for a discrete time series.

13.2.3 Choosing a Wavelet

A number of wavelet functions are commonly used in data analysis. Here are two used primarily for spectral analysis.

Morlet wavelet (for large ω₀):

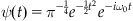(13.5)

The Morlet wavelet was originally developed to analyze signals with short, high-frequency transients and long, low-frequency transients (see Figure 13.1).

Figure 13.1 Morlet wavelet at various scales

Mexican hat wavelet:

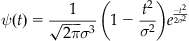(13.6)

The Mexican hat wavelet has poorer frequency resolution than the Morlet wavelet, but often better temporal resolution.

13.2.4 Scalograms

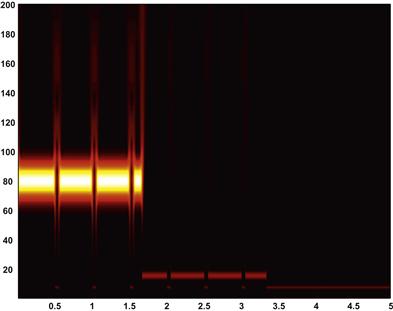
The scalogram depicts the strength of a particular wavelet transform coefficient at a point in time. As such, it is the wavelet analog of the spectrogram.

The scalogram in Figure 13.2 shows the continuous wavelet transform of the following signal with a Morlet wavelet (sigma=10). This code generates a time series with three long blocks of time at 100, 500, and 1000 Hz. At every half second, a 0.05 transient at 1000 Hz is inserted.

Fs = 5000;

total_time = 5;

t = (1/Fs):(1/Fs):(total_time/3);

f = [100 500 1000];

x = [cos(f(1)*2*pi*t) cos(f(2)*2*pi*t) cos(f(3)*2*pi*t)];

t = (1/Fs):(1/Fs):total_time;

%add short transients

trans_time = 0:(1/Fs):0.05;

trans_f = 1000;

for secs = 0.5:0.5:4

trans = cos(trans_f*2*pi*trans_time);

x((secs*Fs):(secs*Fs+length(trans)−1)) = trans;

end

Figure 13.2 Scalogram for sinusoid + transient signal in text.

Be aware that the relationship between scale and frequency is an inverse one and that frequency increases with decreasing scale. Also, note how the frequency resolution improves for the higher frequency band in the later third of the series. This corresponds to the 1000 Hz section of the time series.

The code to generate and plot the CWT follows.

In my_cwt.m:

function coefs = simple_cwt(t, x, mother_wavelet, max_wavelet, scales, params)

% Generates coefs for a continuous wavelet transform

% t, x are time and data points for time series data

% mother_wavelet is a function, taking parameters (t, params),

% where the value of params depends on the specific function used

% max_wavelet is the maximum range of the wavelet function (beyond which

% the wavelet is essentially zero)

% scales is a vector of desired scales

% params is the parameter for the mother wavelet function

max_t = max(t);

dt = t(2)-t(1);

full_t = −(max_t/2):dt:(max_t/2);

coefs = zeros(length(scales), length(x));

points = length(x);

t_scale = linspace(−max_wavelet, max_wavelet, points);

dt = (max_wavelet*2)/(points−1);

mom_wavelet = feval(mother_wavelet, t_scale, params);

row = 1;

for scale = scales

time_scale = [1+floor([0:scale*max_wavelet*2]/(scale*dt))];

wavelet = mom_wavelet(time_scale);

w = conv(x,wavelet)/sqrt(scale);

mid_w = floor(length(w)/2);

mid_x = floor(length(x)/2);

w = w(((−mid_x:mid_x)+mid_w));

scale % print scale to show progress

coefs(row,:) = abs(w);

row = row + 1;

end

In my_morlet.m:

function m=morlet(t, params)

sigma = params(1);

m = pi^{^}−0.25*exp(−i*sigma.*t−0.5*t.^{^}2);

In plot_cwt.m:

function plot_cwt(t, coefs, scales)

imagesc(t, scales, coefs);

colormap(hot);

axis xy;

end

Here, imagesc generates an imagemap from two vectors of data. Given parameters x, y, and c, imagesc generates a colored area of color(n,m) centered at x(n) and y(m). So, here in plot_cwt, at values of t and coefs, the corresponding scales value is used to assign a color.

To generate the scalogram, type:

scales = 1:200;

coefs = my_cwt(t, x, @my_morlet, 10, scales, [10]);

plot_cwt(t, coefs, scales);

13.2.5 The Discrete Wavelet Transform

In addition to the continuous wavelet transform, there is a transformation termed the discrete wavelet transform (DWT). However, the DWT is not merely a discretized continuous wavelet transform. Instead, the discrete wavelet transform calculates only a subset of the possible scales, usually dyadic values (successive values in 2ⁿ, i.e., 1, 2, 4, 8, 16, 32, etc.). Moreover, the DWT is usually calculated using an algorithm called the pyramid algorithm, in which the data series is recursively split in two and reprocessed.

An exploration of the pyramid algorithm is beyond the scope of this chapter. For a thorough discussion, see Percival and Walden (2000). The DWT has been used to denoise signals and to cluster neural spikes for sorting (Quiroga, Nadasdy, and Ben-Shaul, 2004).

13.2.6 Wavelet Toolbox

Wavelet Toolbox provides an implementation of the DWT and a number of appropriate wavelets. Analyses using the discrete wavelet transform use different wavelets than analyses with the continuous transform. The Haar wavelet and the Daubechies wavelet are among the most widely used.

In the following commands, ‘wname’ corresponds to the name of a specific wavelet included in Wavelet Toolbox. Possible choices are ‘dbN’ for Daubechies N, ‘haar’ for Haar, ‘morl’ for Morlet, and ‘mexh’ for the Mexican hat. To view all supported wavelets, use help waveform.

coefs = cwt(S, SCALES, ‘wname’)

The function cwt performs a continuous wavelet transform on the dataset S. The scales given as SCALES are used, and the wavelet is given by ‘wname’. The function cwt will also automatically plot the scalogram if given the parameter ‘plot’ at the end:

coefs = cwt(x, 1:200, ‘morl’, ‘plot’)

[cA. cD] = dwt(X, ‘wname’)

X = idwt(cA, cD, ‘wname’)

The functions dwt and idwt perform a single level decomposition and synthesis given the wavelet name.

[C, L] = wavedec(X, N, ‘wname’)

X = waverec(C, L, ‘wname’)

The functions wavedec and waverec perform multilevel decomposition and synthesis given wavelet name and level N. Note that N cannot be greater than the exponent of the largest power of 2 less than the size of X. The C vector contains the transform, and the L vector contains bookkeeping information used by wavedec and waverec to find the position of the parts of the transform in C.

Here is an example plotting scales 2 through 7 for a Debauches 4 wavelet:

% here size(s) = 128

[C, L] = wavedec(s, 7, ‘db4’);

for scale = 2:7

subplot(7,1,scale)

c_sub = (2^{^}(scale−1)):(2^{^}scale);

t_sub = linspace(1, time, time/size(c_sub));

plot(t_sub, C(c_sub))

end

wavedemo

The wavedemo function opens an automated tour of Wavelet Toolbox, showing various transforms and functions provided by the toolbox.

13.3 Exercises

Exercise 13.1

Which of the following MATLAB functions can be wavelet functions? Why or why not? function x = f_one(t)

x = cos(t);

end

function x = f_two(t)

if (x < 0 or x > pi/2)

x = 0;

else

x = cos(t);

end

end

function x = f_three(t)

x = sqrt(2) * t * exp(−t^{^}2/2) / pi^{^}4;

end

function x = f_four(t)

x = sqrt(2) * t^{^}2 * exp(−t^{^}2/2) / pi^{^}4;

end

function x = f_five(t)

x = (x > −1 && x < 0) * −1 + (x > 0 && x < 1);

end

Exercise 13.2

Generate the scalogram in Figure 13.2. Generate a spectrogram and compare. How clearly does each render the transients? The primary frequencies?

Exercise 13.3

Write a Mexican hat mother wavelet function compatible with the previous continuous wavelet transform code. Generate a scalogram of the sinusoid+transient signal used in Figure 13.2. Compare Mexican hat transform to the Morlet transform.

Exercise 13.4

Download the EEG signal wavelet, eeg, from the companion website. Generate scalograms using the Mexican hat and Morlet wavelet transforms. Compare to a spectrogram generated with spectrogram().

13.4 Project

In Chapter 12, “Frequency Analysis Part II: Nonstationary Signals and Spectrograms,” you used the short-time Fourier transform to look for sleep state transitions. Here, you will be asked to examine the same data files using the continuous wavelet transform and Morlet and Mexican hat wavelets. Compare and contrast your findings with what you found using only the STFT.

MATLAB Functions, Commands, and Operators Covered in This Chapter

cwt

dwt

idwt

wavedec

waverec