Synaptic Transmission

Pascal Wallisch

This chapter will use a number of methods to characterize the processes surrounding synaptic transmission, in particular the release and diffusion of neurotransmitters. This chapter will also introduce handles for graphic objects to update images dynamically. By the end of this chapter, you should have an understanding of different random variables, discrete distributions, finite difference approximations to partial differential equations, and the use of graphic handles for rudimentary animation.

Keywords

synaptic cleft; presynaptic; postsynaptic; neuromuscular junction; Bernoulli random variable

26.2 Background

Chemical synapses use the release of chemical neurotransmitters to propagate signals from one neuron (presynaptic) to another (postsynaptic). The two cells are separated by the synaptic cleft, a gap of approximately 40 nm between the presynaptic and postsynaptic membranes.

On the presynaptic side of the cleft, depolarization from the arrival of the action potential triggers the opening of voltage-sensitive Ca⁺² channels. The subsequent influx of calcium ions causes the fusion of neurotransmitter-containing vesicles with the presynaptic cell membrane, releasing neurotransmitters into the synaptic cleft.

On the postsynaptic side, neurotransmitters diffuse across the cleft and bind to neurotransmitter-specific sites on channels on the postsynaptic terminal. These receptors selectively allow ions to enter the postsynaptic terminal. The influx of positive or negative charge changes the voltage across the postsynaptic membrane, creating a small hyperpolarization or depolarization. Over time, the concentration of the neurotransmitters decreases to a level insufficient to activate the postsynaptic receptors.

Specifically, in this chapter we will focus on the neuromuscular junction, the site of innervation of skeletal muscle. We will also focus on the steps of neurotransmitter release and neurotransmitter diffusion.

26.3 Exercises

26.3.1 Modeling Neurotransmitter Release

In a classic experiment, Fatt and Katz demonstrated at the neuromuscular junction that spontaneous postsynaptic potentials occurred at voltages of 0.5 mV in the absence of presynaptic stimulation. Later work (del Castillo and Katz, 1954) further demonstrated that single acetylcholine channels produced much smaller responses than the 0.5 mV measured by Fatt and Katz. This result implied that the spontaneous results observed by Fatt and Katz not only recruited multiple acetylcholine channels, but also recruited roughly the same number of channels during each spontaneous postsynaptic potential del Castillo and Katz posited that synaptic transmission occurred in discrete units, termed quanta. Additional work (del Castillo and Katz) established that increasing Ca⁺² at the postsynaptic terminal produced postsynaptic responses in increments of the original spontaneous postsynaptic responses. The step-like response implicated neurotransmitter release as a quantized process. In other words, neurotransmitter release occurs in discrete steps rather than a continuous concentration in response to increasing calcium concentration. Synaptic vesicles contain a relatively constant number of neurotransmitter molecules. This fixed number of molecules per vesicle provides for the observed quantization of postsynaptic responses. At the neuromuscular junction, each vesicle contains approximately 5000 acetylcholine (ACh) molecules.

For purposes of this chapter, assume that the release of individual vesicles occurs independently with some probability p. In the presence of low calcium concentration, p is low. After an action potential and subsequent calcium influx, p increases. You can model the release of a single vesicle as a Bernoulli random variable.

26.3.2 Modeling Random Variables

A Bernoulli random variable X takes on a value of 1 with probability p or a value of 0 with probability 1 – p. A coin toss is an excellent example of a Bernoulli process. Take a coin that lands on heads with probability 1/2. A Bernoulli random variable models a single coin flip, or a single trial.

Thus, in the case of the release of a single vesicle, the vesicle is released with probability p or not with probability 1 – p.

Exercise 26.1

Using the rand function in the MATLAB® software, write a function titled my_bernoulli_rnd() to return the result of a Bernoulli trial, given p. You should be able to invoke the function like this:

>> p = 0.5;

>> my_bernoulli_rnd(p)

ans =

You can model the process of multiple vesicles as the sum of multiple Bernoulli variables with probability p. The sum of n Bernoulli trials with probability p of success is termed a binomial random variable with parameters n and p. Such a variable is called binomial because the probability of a certain number of successes in a trial can be calculated with the binomial coefficient:

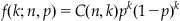(26.1)

where

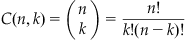(26.2)

The function f(), called a probability mass function, yields the probability of a certain number of successes, k, in a single binomial trial with parameters n and p. A single binomial trial with parameters n and p would model the number of successes for an experiment in which each trial has n coin tosses with probability p of success.

Exercise 26.2

Generate a graph of the probability mass function for a binomial random variable with parameters n=10 and p=0.5.

Under conditions of calcium influx, approximately 150 quanta can be released at the neuromuscular junction in 1–2 milliseconds. In the absence of action potentials, only 1 quantum per second is released by the presynaptic terminal. For this chapter, model the release of multiple vesicles as a binomial random variable in which p is either 0.001 or 150, depending on the state of calcium concentration. Then, the number of successes will be the number of vesicles released into the synaptic cleft.

The following code calculates p for 1 second of time, choosing 10 random 1 ms intervals during which p is high, representing the calcium influx following an action potential:

>> t=0:999;

>> t_slices=length(t);

>> p=ones(t_slices,1)*0.001;

>> x=rand(10,1)*t_slices;

>> p(floor(x)+1)=150;

Note that x holds the set of random intervals. When you evaluate p(floor(x)+1) = 150, each element of x corresponding to one of the random intervals is set to 150. The use of floor() forces the values of x to integer values, the proper type for indices. (The floor() function truncates the decimal portion of a value.) You can see which indices contain large p values with the following command:

>> find(p>1)

Exercise 26.3

Evaluate the preceding code and graph p(t) against time. Write code to generate a binomial random variable at each time slice (use binornd). Graph the number of successes, or released vesicles, as a function of time.

26.3.3 Modeling the Motion of a Single Molecule

Upon release, the neurotransmitter molecules enter the synaptic cleft and diffuse across fairly quickly. On a microscopic level, diffusion is the aggregate effect of many particles moving randomly. As a first step, examine the motion of a single molecule:

xbounds = [0 10];

ybounds = [0 4];

xdata = [mean(xbounds)];

handle = scatter(xdata, ydata, ‘filled’);

dx = ((rand > p) - 0.5) * 2;

dy = ((rand > p) - 0.5) * 2;

xdata = xdata + dx*xgrid;

% these two lines assure the molecule stays in x bounds

xdata(find(xdata < xbounds(1))) = xbounds(1);

xdata(find(xdata > xbounds(2))) = xbounds(2);

ydata = ydata + dy*ygrid;

% these two lines assure the molecule stays within y bounds

ydata(find(ydata < ybounds(1))) = ybounds(1);

ydata(find(ydata > ybounds(2))) = ybounds(2);

set(handle, ‘xdata’, xdata, ‘ydata’, ydata);

drawnow;

end

Some sample screenshots of the resulting animation are shown in Figure 26.1. In the preceding code, the handle of the scatterplot is stored in a variable. Much like matrices or scalar numbers, variables can store other types of information. In this case, you are storing a handle. Most of the graphics functions in MATLAB return a handle when invoked. You can use the handle to modify properties at a later time, as done previously with set.

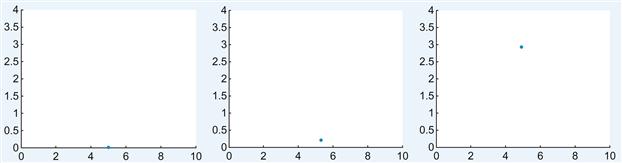
Figure 26.1 Screenshots of the animation for the diffusion of a single neurotransmitter molecule across the synaptic cleft for t=1 (left), t=500 (middle), and t=10,000 (right).

The function set allows specifying properties of a graphics object. The first argument should be the handle. Following this should be a series of property, value pairs, consisting of the name of a property in single quotation marks and the desired value of the property. Here, the x and y data for the scatterplot are changed. Each time the variables xdata and ydata are modified, set is invoked to update the coordinates of the point in the scatterplot.

After set comes the function drawnow. Even though set updates the coordinates of the point in the scatterplot, MATLAB will not redraw the figure without notification. drawnow provides notification that the figure has changed and forces a redraw. Try running the preceding code with drawnow commented out.

Exercise 26.4

Modify the preceding code to model multiple particles (try 100).

As the number of particles increases, modeling the motion of individual particles becomes computationally limiting. Instead, you can model concentrations rather than particle counts.

26.3.4 Modeling Diffusion

To model the process as a concentration, you need to use the diffusion equation:

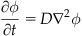(26.3)

Or in two dimensions, you can use:

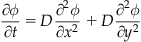(26.4)

where D is the constant of diffusion and ϕ is the concentration of acetylcholine, ACh.

In this chapter, you will use a finite difference approach to estimate the change in the probability distribution over time. The finite difference method estimates the infinitely small derivatives by finite differences. Because this approximates the continuous equation with discrete differences, we should mention that large time steps can produce unstable results.

To approximate ϕ over time and space, assume both are discrete yet partitioned into very small steps. Use the following notation to denote an element of phi in space and time:

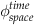(26.5)

Thus, a superscript denotes a time index, and a subscript denotes a space index.

To generate the finite difference equation, replace the derivatives with differences:

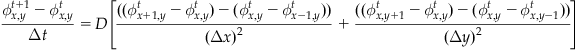(26.6)

With some rearrangement, you get:

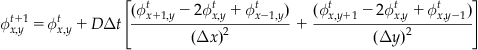(26.7)

which provides an expression for a concentration at a given spatial location and time in terms only of concentrations at previous time steps. If you use the same grid spacing for x and y, you can simplify even further:

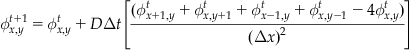(26.8)

You already saw an efficient way to compute this spatial second derivative in MATLAB. As will be further discussed in Chapter 30, “Fitzhugh-Nagumo Model: Traveling Waves,” this is found via a two-dimensional convolution of ϕ with the filter [0 1 0; 1 4 1; 0 1 0]/dx^2. To encode the dynamics of the ACh concentration diffusion in MATLAB, use a three-dimensional array: two spatial dimensions and one temporal dimension.

The following code implements iterations of the previous equation, using a three-dimensional array to track change in concentration. The time steps are in 10 ns increments, and the spatial steps are in 1 nm increments. The diffusion constant here is 4×10⁻⁶ cm²/sec, and free boundary conditions are used:

% phi : 100 x steps (100 nm), 40 y steps (40 nm)

% 100 t steps (1 t = 10 us)

clear all

close all

phi = zeros(100, 40, 100);

dt = 1e-10; % time in steps of 10 ns

dx = 1e-9; % space from 0 to 50

D=4e-6 * (1/100)^2;

phi0=5000/(dx^2);

phi(50,1,1) = phi0; % initial condition

F = [0 1 0; 1 -4 1; 0 1 0]/dx^2;

for t = 1:99

phi(:,:,t+1) = phi(:,:,t) +...

D*dt*conv2(phi(:,:,t),F,‘same’);

end

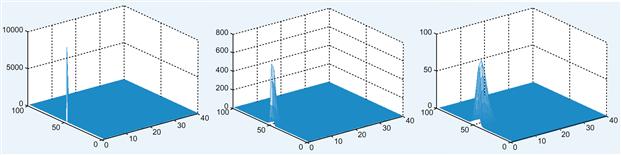
You can plot a time-slice of the concentration using surf(phi(:, :, t)). Sample screenshots of the concentration diffusing in the synaptic cleft using the surf function are shown in Figure 26.2. Similarly, you can visualize this using the command imagesc(phi(:,:,t), [0 phi0]), where the [0 phi0] input to the function ensures that the color scale is the same for all t.

Exercise 26.5

Generate an animated display to show the evolution of the ACh concentration diffusion using surf(). Capture the handle and use set() with the property ‘zdata’.

Exercise 26.6

The algorithm could be changed to save only the current and previous time steps, allowing an unlimited number of time steps to be calculated if so desired without exceeding the memory of MATLAB. Obviously, this approach is less than optimal if all the time step calculations are needed, but, for an animation, only the current time step is necessary. Modify the algorithm to store only the current and previous time step and animate the diffusion.

Figure 26.2 Screenshots of the animation for the diffusion of the concentration of acetylcholine, ACh, in the synaptic cleft for t=10 μs (left), t=250 μs (middle), and t=1000 μs (right).

26.4 Project

At this point you can combine the vesicular release of neurotransmitters with the diffusion of the neurotransmitters across the synaptic cleft. This can be accomplished by combining the neurotransmitter release code with the code for diffusion.

To do so, use a single time loop for both the vesicular release and the diffusion code. At any given time slice, the code will need to determine the number of vesicles released. If vesicles are released during a given time slice, then (1) a location along the presynaptic edge of the diffusion grid needs to be selected, and (2) the concentration of ACh in that square of the finite difference grid needs to be increased. Create an animated display of synaptic transmission by showing the evolution of the ACh concentration diffusion generated by multiple released vesicles over time.

MATLAB Functions, Commands, and Operators Covered in This Chapter