Simplified Model of Spiking Neurons

Keywords

delta rhythms; theta rhythms; alpha rhythms; beta rhythms; gamma rhythms

29.1 Goal of This Chapter

The goal of this chapter is to study a computationally efficient spiking cortical neuron model first introduced by Izhikevich (2003), and to generalize this model to a network of neurons. Ultimately, you will obtain and examine a raster plot of modeled network activity.

29.2 Background

The task of understanding how different areas of the brain interact with each other to perform higher level functions such as motor coordination and speech is a major interest of modern neuroscience, but also an extremely difficult one. Many factors contribute to the global dynamics of neural networks. First, neurons isolated from a network exhibit a variety of patterns and behaviors. Some examples include regular spiking neurons, fast spiking neurons, intrinsic bursting neurons, and subthreshold membrane oscillations, as shown in Figure 29.1. Some of these behaviors are more common than others. For example, under normal conditions there are more regular spiking neurons in the cortex than intrinsic bursting ones. How these different dynamics are manifested at the network level remains an open area of current research. Second, the synaptic coupling between neurons can have a large impact on the network’s dynamics leading to synchronization among the neurons and network oscillations.

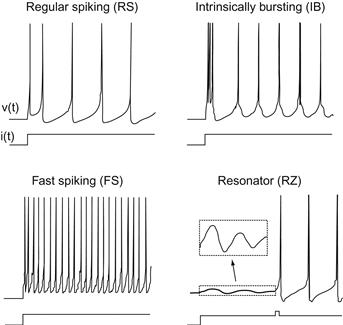
Figure 29.1 Known types of neurons. (An electronic version of the figure and reproduction permissions are freely available at www.izhikevich.org/publications/spikes.htm.)

Network oscillations in the brain are often categorized by their frequency. Oscillations with a frequency less than 4 Hz are called delta rhythms. Oscillations between 4 and 8 Hz are called theta rhythms. Rhythms from 8 to 12 Hz are called alpha rhythms, and rhythms from 12 to 30 Hz are called beta rhythms. Rhythms above 30 Hz are called gamma rhythms.

29.2.1 The Model

The model for this chapter is a two-dimensional system of ordinary differential equations with a reset condition, as shown in Equations 29.1–29.3:

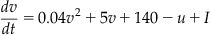(29.1)

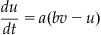(29.2)

The reset condition is:

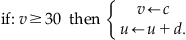(29.3)

The variable v represents the membrane potential of the neuron while u represents a generic recovery variable that feeds back negatively onto v. There are five additional parameters in the model: I, a, b, c, and d. The parameter I represents external input to the neuron. This input could be thought of as external input to the neuron from outside the network or even synaptic input from a neuron within the network. The parameter a controls the rate of recovery of u, and b controls the sensitivity of recovery to subthreshold fluctuations of the membrane potential. The parameters c and d control the after-spike reset values for v and u, respectively. If you choose certain parameter combinations, this simple model can exhibit all the firing patterns and behaviors shown in Figure 29.1.

To model a whole network of neurons, you will have to couple many neurons together where each neuron behaves according to Equations 29.1–29.3. This means that you will have to select a value for each parameter for every neuron you model. Additionally, since the network is coupled (i.e., the neurons are connected to each other), the input I to a particular neuron will depend on other neurons in the network that synapse onto it. Therefore, you will need to model the connectivity of the network. You could choose to make every neuron in the network be connected to every other neuron in the network, or possibly make neurons connect only to neurons that are close. Additionally, you need to choose whether a connection between neurons will be excitatory or inhibitory and how strong the connection will be.

29.3 Exercises

The code for implementing Equations 29.1–29.3 is not very complicated. You can solve the equations using Euler’s method, as introduced in Chapter 25, “Voltage-Gated Ion Channels.” The script for implementing a single neuron is as follows (adapted from Izhikevich, 2003):

%These are some default parameter values

%The initial values for v and u

v=-65;

u=b*v;

%Initialize the vector that will contain the membrane potential time series.

v_tot=zeros(1000, 1);

for t=1:1000

%set v_tot at this time point to the current value of v

v_tot(t)=v;

%Reset v and u if v has crossed threshold. See Eq. 29.3 earlier.

%Use Euler’s method to integrate Eqs. 29.1 and 29.2 from earlier. Here v is

%calculated in 2 steps in order to keep the time step small (0.5 ms step in the

%line below).

v=v+0.5*(0.04*v&circ;2+5*v+140-u+I);

u=u+a*(b*v-u);

end;

%This line uses the function find to locate the indices of v_tot that hold elements

%with values greater than or equal to 30 and then sets these elements to 30.

%This normalizes to heights of the action potential peaks to 30.

v_tot(find(v_tot >= 30))=30;

%Plot the neuron’s membrane potential.

plot(v_tot);

Exercise 29.1

Before going on to generalize this model to a network of neurons, you should explore this model thoroughly. See if you can discover what parameter sets lead to regular spiking, fast spiking, or intrinsically bursting behavior. What kinds of behaviors do the following parameter sets produce?

a. [a, b, c, d]=[0.02, 0.2, −65, 8]

b. [a, b, c, d]=[0.02, 0.2, −55, 4]

c. [a, b, c, d]=[0.1, 0.2, −65, 2]

d. [a, b, c, d]=[0.1, 0.25, −65, 2]

Now consider how to modify this script to model a network of neurons where each neuron is described by the dynamics of Equations 29.1–29.3. First, convert the parameters from numbers to vectors. The vectors will hold the value of each parameter for each neuron in the network. Since you want some neurons in the network to be regular spiking and others to be intrinsically bursting, you will need to have different values for the elements of the vectors. The modified code should begin as follows:

% The number of excitatory neurons in the network. The mammalian cortex has

% about 4 times as many excitatory neurons as inhibitory ones.

Ne=800;

%The number of inhibitory neurons in the network.

%This will set the value of a for all excitatory neurons to 0.02 and the value of a

%for inhibitory neurons to a random number between 0.02 and 0.1

a=[0.02*ones(Ne, 1); 0.02+0.08*ri];

%This will allow b to range from 0.2–0.25

b=[0.2*ones(Ne, 1); 0.25–0.05*ri];

%This will allow the spike reset membrane potential to range between -65 and -50

c=[-65+15*re.^2; -65*ones(Ni,1)];

%This will allow the recovery reset value to range between 2 and 8

d=[8-6*re.^2; 2*ones(Ni, 1)];

Before you continue with the code, it is worthwhile to consider how these definitions of the parameters impact the composition of the network.

Exercise 29.2

What parameter sets are most neurons likely to possess? Is there any correlation between excitatory neurons as represented in this model and regular spiking neurons, for example?

The next line of code should create a weight matrix that holds the strength of the connectivity between every pair of neurons in the network. Since the network has Ne+Ni neurons, then the weight matrix will be a square matrix with these dimensions. The code to implement this is:

S=[0.5*rand(Ne+Ni, Ne), -rand(Ne+Ni, Ni)];

Notice that this definition allows the strength of connections of excitatory neurons onto other neurons to range from 0 to 0.5, whereas inhibitory neurons have a synaptic strength between 0 and −1. According to this definition, a single inhibitory neuron can have, in general, a stronger effect on the neurons it contacts than a single excitatory neuron, which is supported by current experimental research. Also notice that very few elements of S will be exactly 0, so in this model almost every neuron has synaptic contacts with all other neurons in the network. The rest of the code for the network model is:

%The initial values for v and u

v=-65*ones(Ne+Ni,1);

u=b.*v;

%Firings will be a two-column matrix. The first column will indicate the time that a %neuron’s membrane potential crossed 30, and the second column will be a number %between 1 and Ne+Ni that identifies which neuron fired at that time.

%firings=[];

for t=1:1000

%Create some random input external to the network

I=[5*randn(Ne, 1); 2*randn(Ni,1)];

%Determine which neurons crossed threshold at the current time step t.