Chapter 2

REMARKS ON THE FOUNDATIONS OF
AGENT-BASED GENERATIVE SOCIAL SCIENCE

JOSHUA M. EPSTEIN^*

GENERATIVE EXPLANATION

THE SCIENTIFIC ENTERPRISE is, first and foremost, explanatory. While agent-based modeling can change the social sciences in a variety of ways, in my view its central contribution is to facilitate generative explanation (see Epstein 1999). To the generativist, explaining macroscopic social regularities, such as norms, spatial patterns, contagion dynamics, or institutions requires that one answer the following question:

How could the autonomous local interactions of heterogeneous boundedly rational agents generate the given regularity?

Accordingly, to explain macroscopic social patterns, we generate—or “grow”—them in agent models. This represents a departure from prevailing practice. It is fair to say that, overwhelmingly, game theory, mathematical economics, and rational choice political science are concerned with equilibria. In these quarters, “explaining an observed social pattern” is essentially understood to mean “demonstrating that it is the Nash equilibrium (or a distinguished Nash equilibrium) of some game.”

By contrast, to the generativist, it does not suffice to demonstrate that, if a society of rational (homo economicus) agents were placed in the pattern, no individual would unilaterally depart—the Nash equilibrium condition. Rather, to explain a pattern, one must show how a population of cognitively plausible agents, interacting under plausible rules, could actually arrive at the pattern on time scales of interest. The motto, in short, is (Epstein 1999): If you didn't grow it, you didn't explain it. Or, in the notation of first-order logic:

To explain a macroscopic regularity x is to furnish a suitable microspecification that suffices to generate it.¹ The core request is hardly outlandish: To explain a macro-x, please show how it could arise in a plausible society. Demonstrate how a set of recognizable—heterogeneous, autonomous, boundedly rational, locally interacting—agents could actually get there in reasonable time. The agent-based computational model is a new, and especially powerful, instrument for constructing such demonstrations of generative sufficiency.

FEATURES OF AGENT-BASED MODELS

As reviewed in Epstein and Axtell 1996 and Epstein 1999, key features of agent-based models typically include the following:²

HETEROGENEITY

Representative agent methods—common in macroeconomics—are not used in agent-based models. Nor are agents aggregated into a few homogeneous pools. Rather, every individual is explicitly represented. And these individuals may differ from one another in myriad ways: by wealth, preferences, memories, decision rules, social network, locations, genetics, culture, and so forth, some or all of which may adapt or change endogenously over time.

AUTONOMY

There is no central, or “top down,” control over individual behavior in agent-based models. Of course, there will generally be feedback between macrostructures and microstructures, as where newborn agents are conditioned by social norms or institutions that have taken shape endogenously through earlier agent interactions. In this sense, micro and macro will, in general, co-evolve. But as a matter of model specification, no central controllers (e.g., Walrasian auctioneers) or higher authorities are posited ab initio.

EXPLICIT SPACE

Events typically transpire on an explicit space, which may be a landscape of renewable resources, as in Epstein and Axtell 1996, an n-dimensional lattice, a dynamic social network, or any number of other structures. The main desideratum is that the notion of “local” be well-posed.

LOCAL INTERACTIONS

Typically, agents interact with neighbors in this space (and perhaps with sites in their vicinity). Uniform mixing (mass action kinetics) is generically not the rule. Relatedly, many agent-based models, following Herbert Simon, also assume:

BOUNDED RATIONALITY

There are two components of this: bounded information and bounded computing power. Agents have neither global information nor infinite computational capacity. Although they are typically purposive, they are not global optimizers; they use simple rules based on local information.

NON-EQUILIBRIUM DYNAMICS

Non-equilibrium dynamics are of central concern to agent modelers, as are large-scale transitions, “tipping phenomena,” and the emergence of macroscopic regularity from decentralized local interaction. These are sharply distinguished from equilibrium existence theorems and comparative statics, as is discussed below.

RECENT EXPANSION

The literature of agent-based models has grown to include a number of good collections (e.g., The Sackler Colloquium, Proceedings of the National Academy of Sciences, 2002), special issues of scholarly journals (Computational Economics 2001, The Journal of Economic Dynamics and Control, 2004), numerous individual articles in academic journals (such as Computational and Mathematical Organization Theory), the science journals (Nature, Science) and books (e.g., Epstein and Axtell 1996; Axelrod 1997; Cederman 1997). New journals (e.g., The Journal of Artificial Societies and Social Simulation) are emerging, computational platforms are competing (e.g., Ascape, Repast, Swarm, Mason). International societies for agent-based modeling are being formed. Courses on agent-based modeling are being offered at major universities. Conferences in the U.S., Europe, and Asia are frequent, and agent-based modeling is receiving considerable attention in the press. The landscape is very different than it was a decade ago.

EPISTEMOLOGICAL ISSUES

Einstein wrote that, “Science without epistemology is—in so far as it is thinkable at all—primitive and muddled” (Pais 1982). Given the rapid expansion of agent-based modeling, it is an appropriate juncture at which to sort out and address certain epistemological issues surrounding the approach. In particular, and without claiming comprehensiveness, the following issues strike me as fundamentally important, and in need of clarification, both within the agent modeling community and among its detractors.

1. Generative sufficiency vs. explanatory necessity
2. Generative agent-based models vs. explicit mathematical models
3. Generative explanation vs. deductive explanation
4. Generative explanation vs. inductive explanation
5. Generality of agent models

I will attempt to address these and a variety of related issues. At several points, there will be a need to distinguish claims from their converses. The first example of this follows.

Generative Sufficiency

The generativist motto (1) cited above was:

If you didn't grow it, you didn't explain it. It is important to note that we reject the converse claim. Merely to generate is not necessarily to explain (at least not well). A microspecification might generate a macroscopic regularity of interest in a patently absurd—and hence non-explanatory—way. For instance, it might be that Artificial Anasazi (Axtell et al. 2002) arrive in the observed (true Anasazi) settlement pattern stumbling around backward and blindfolded. But one would not adopt that picture of individual behavior as explanatory. In summary, generative sufficiency is a necessary, but not sufficient condition for explanation.

Of course, in principle, there may be competing microspecifications with equal generative sufficiency, none of which can be ruled out so easily. The mapping from the set of microspecifications to the macroscopic explanandum might be many-to-one. In that case, further work is required to adjudicate among the competitors.

For example, if the competing models differ in their rules of individual behavior, appropriate laboratory psychology experiments may be in order to determine the more plausible empirically. In my own experience, given a macroscopic explanandum, it is challenging to devise any rules that suffice to generate it. In principle, however, the search could be mechanized. One would metrize the set of macroscopic patterns, so that the distance from a generated pattern to the target pattern (the pattern to be explained) could be computed. The “fitter” a microspecification, the smaller the distance from its generated macrostructure to the empirical target. Given this definition of fitness, one would then encode the space of permissible micro-rules and search it mechanically—with a genetic algorithm, for example (as in Crutchfield and Mitchell 1995).

In any event, the first point is that the motto (1) is a criterion for explanatory candidacy. There may be multiple candidates and, as in any other science, selection among them will involve further considerations.³

The Indictment: No Equations, Not Deductive, Not General

Plato observed that the doctors would make the best murderers. Likewise, in their heart of hearts, leading practitioners of any approach know themselves to be its most capable detractors. I think it is healthy for experienced proponents of any approach to explicitly formulate its most damaging critique and, if possible, address it. In that spirit, it seems to me that among skeptics toward agent modeling, the central indictment is tripartite: First, that in contrast to mathematical “hard” science, there are no equations for agent-based models. Second, that agent models are not deductive;⁴ and third, that they are ad hoc, not general. I will argue that the first two claims are false and that, at this stage in the field's development, the third is unimportant.

Equations Exist

The oft-claimed distinction between computational agent models, and equation-based models is illusory. Every agent model is, after all, a computer program (typically coded in a structured or object-oriented programming language). As such, each is clearly Turing computable (computable by a Turing machine). But, for every Turing machine, there is a unique corresponding and equivalent partial recursive function (see Hodel 1995).

This is precisely the function class constructible from the zero function, the successor function, and the “pick out” or projection function (the three so-called initial functions) by finite applications of composition (substitution), bounded minimization, and—the really distinctive manipulation—primitive recursion. This, as the defining formula below suggests, can be thought of as a kind of generalized induction.

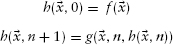
(See Hamilton 1988, Boolos and Jeffrey 1989, Epstein and Carnielli 1989, or Hodel 1995 for a technical definition of this class of functions.) So, in principle, one could cast any agent-based computational model as an explicit set of mathematical formulas (recursive functions). In practice, these formulas might be extremely complex and difficult to interpret. But, speaking technically, they surely exist. Indeed, one might have called the approach “recursive social science,” “effectively computable social science,” “constructive social science,” or any number of other equivalent things. The use of “generative” was inspired by Chomsky's usage (Chomsky 1965). In any case, the issue is not whether equivalent equations exist, but which representation (equations or programs) is most illuminating.

To all but the most adept practitioners, the recursive function representation would be quite unrecognizable as a model of social interaction, while the equivalent agent model is immediately intelligible as such. However, at the dawn of the calculus, the same would doubtless have been true of differential equations. It is worth noting that recursive function theory is still very young, having developed only in the 1930s. And, it is virtually unknown in the social sciences. It is the mathematical formalism directly isomorphic (see Jeffrey 1991) to computer programs, and over time, we may come to feel as comfortable with it as we now do with differential equations. Moreover, it is worth noting that various agent-based models have, in fact, been revealingly mathematized using other, more familiar, techniques. (See Dorofeenko and Shorish 2002; Pollicott and Weiss 2001; Young 1998.)

In sum, the first element of the indictment, that agent models are “just simulations” for which no equations exist, is simply false. Moreover, even if equivalent equations are not in hand, computational agent models have the advantage that they can be run thousands of times to produce large quantities of clean data. These can then be analyzed to produce a robust statistical portrait of model performance over the parameter ranges (and rule variations) of interest.

This critique, moreover, betrays a certain naiveté about contemporary equation-based modeling in many areas of applied science, such as climate modeling. The mathematical models of interest are huge systems of nonlinear reaction diffusion equations. In practice, they are not solved analytically, but are approximated computationally. So, the opposition of analytically soluble mathematical models on the one hand, and computational models on the other, while conceptually enticing, is quite artificial in practice.

Agent Models Deduce

Another misconception is that the explicit equation-based approach is deductive, whereas the agent-based computational approach is not. This, too, is incorrect. Every realization of an agent model is a strict deduction. There are a number of ways to establish this. Perhaps the most direct is to note that it follows from the previous point.

Every program can be expressed in recursive functions. But recursive functions are computed deterministically from initial values. They are mechanically (effectively) computable—in principle by hand with pencil and paper. Given the nth (including the initial) state of the system, the (n+1)st state is computable in a strictly mechanical and deterministic way by recursion. Since this mechanical procedure is obviously deductive, so is each realization of an agent model.

A more sweeping equivalence can be established, in fact. It can be shown that Turing machines, recursive functions, and first-order logic itself (the system of deduction par excellence) are all strictly intertranslatable (see Hodel 1995). So, in a rigorous sense, every state generated in an agent model is literally a theorem. Since, accepting our motto, to explain is to generate (but not conversely), and to generate a state is to deduce it as a theorem, we are led to assert that to explain a pattern is to show it to be theorematic.

A third, slightly less rigorous way to think of it is this. Every agent program begins in some configuration x—a set of initial (agent) states analogous to axioms—and then repeatedly updates by rules of the form; if x then y. But, {x, x ⊃ y} is just modus ponens, so the model as a whole is ultimately one massive inference in a Hilbert-type deductive system. To “grow” a pattern p (and to explain a pattern p) is thus to show that it is one of these terminal y's—in effect, that it is theorematic, very much as in the classic hypothetico-deductive picture of scientific explanation.

What about Randomness?

If every run is a strict deduction, what about stochasticity, a common feature of many agent models? Stochastic realizations are also strict deductions. In a computer, random numbers are in fact produced by strictly deterministic pseudo-random number generators. For example, the famous linear congruential method (Knuth 1998) to generate a series of pseudo-random numbers is as follows:

Define: m, the modulus (m > 0); a, the multiplier (0 ≤ a ≤ m); c, the increment (0 ≤ c ≤ m), and x(0), the seed, or staring value (0 ≤ x(0) ≤ m). Then, the (recursion) scheme for generating the pseudo-random sequence is, for n ≥ 0:

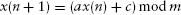
This determinism is why, when we save the seed and re-run the program, we get exactly the same run again.

What Types of Propositions are Deduced?

In principle, the only objects we ever technically deduce are propositions. When we deduce the Fundamental Theorem of Calculus, we deduce the proposition: “The definite integral of a continuous real-valued function on an interval is equal to the difference of an anti-derivative's values at the interval's endpoints.” The result is normally expressed in mathematical notation, but, in principle, it is a proposition statable in English.⁵ In turn, we explain an empirical regularity when that regularity is rendered as a proposition and that proposition is deduced from premises we accept. For example, we explain Galileo's leaning Tower of Pisa observation (i.e., that objects of unequal masses dropped from the same height land simultaneously) by strictly deducing, from Newton's Second Law and the Law of Universal Gravitation, the following proposition: “The acceleration of a freely falling body near the surface of the earth is independent of its mass.”

Well, if agent models explain by generating, and thus deducing, and if, as I have just argued, the only deducible objects are propositions, the question arises: what sorts of propositions are deduced when agent models explain? In many important cases, the answer is: a normal form.

Social Science as the Satisfaction of Normal Forms

We explain a pattern when the pattern is expressed as a proposition and the proposition is deduced from premises we accept. Seen in this light, many of the macroscopic patterns we, as social scientists, are trying to explain are expressible as large disjunctive normal forms, DNFs. In general a DNF, δ has the logical form

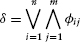
where ø_ij is a statement form (see Hamilton 1988). Clearly, this discussion applies to arbitrarily large, but finite, populations.

EXAMPLE 1. DISTRIBUTIONS

Suppose, then, that we are trying to explain a skewed wealth distribution observed in some finite population of agents. For simplicity's sake, imagine three agents: A, B, and C. And suppose we observe that 6 indivisible wealth units (the country's GNP) are distributed as 3:2:1. That is the empirical target; and our model will be deemed a success if it grows that distribution, regardless of who has what. What that means is that the successful model will generate any one of the six conjunctions in the following DNF, shown in braces (where A3 means “Agent A has 3 units,” and so forth):

The model succeeds if it grows any one of these conjuncts, that is, a conjunction whose truth makes the DNF true.

EXAMPLE 2. SPATIAL PATTERNS

Likewise, suppose we are trying to model segregation in a population composed of two white and two black agents (W1, W2, B1, B2) arranged on a line with four positions: 1, 2, 3, 4. The model works if it generates two contiguous agents of the same color, followed by two contiguous agents of the other color. As above, we don't care who is where so long as we get segregation on the line. The truth of any of the eight conjunctions of the following DNF will therefore suffice (here W12 denotes the proposition: “white agent 1 occupies position 2”):

Again, success in generating “segregation” consists in generating any one of these conjunctions. That suffices to make the DNF true. While this exposition has been couched in terms of wealth distributions and distributions of spatial position, it obviously generalizes to distributions of myriad sorts (e.g., size and power), and with straightforward modification, to sequences of patterns over time. A dynamic sequence of patterns would, in fact, be a Conjunctive Normal Form (CNF), each term of which is a DNF of the sort just discussed.⁶

Generative Implies Deductive, but Not Conversely: Nonconstructive Existence

A generative explanation is a deductive one. Generative implies deductive. The converse, however, does not apply. It is possible to deduce without generating. Not all deductive argument has the constructive character of agent-based modeling. Nonconstructive existence proofs are clear examples. Often, these take the form of reductio ad absurdum⁷ arguments, which work as follows.

Suppose we wish to prove the existence of an x with some property (e.g., that it is an equilibrium). We take as an axiom the so-called Law of the Excluded Middle (LEM), implying that either x exists or x does not exist. Symbolically:

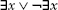
One of those must be true. Next, we assume that x does not exist and derive a contradiction. That is, we show that

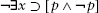
Since contradictions are always False, this has the form:

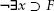
But this implication can be True only if the antecedent, ¬∃x, is False. From this it follows from the LEM that ∃x is True and voila: the x in question must exist!

But we have failed to exhibit x, or specify any algorithm that would generate it, patently violating our generative motto (1). We have failed to show that x is generable at all, much less that it is generable on time scales of interest. But, the existence argument is nonetheless deductive.

Now, there are deductive and nonconstructive existence proofs that do not use reductio ad absurdum. One of my favorites is the beautiful and startling index theoretic proof that, in regular economies, the number of equilibria must be an odd integer (see Mas-Colell et al. 1995; Epstein 1997). This proof gives no clue how to compute the equilibria. Like reductio, it fails to show the equilibria to be generable at all, much less on time scales of interest. But, the existence argument is nonetheless deductive.

Hence, if we insist that explanation requires generability, we are led to the position that deductive arguments can be non-explanatory. Generative explanation is deductive, but deduction is not necessarily explanatory.

We have addressed the first two points of the indictment: that there are no equations, and that agent modeling is not deductive. The third issue was the generality of agent models. I would like to approach this topic by a seemingly circuitous route, extending the preceding points on existence and generability into the areas of incompleteness and computational complexity.

INCOMPLETENESS (ATTAINABILITY AT ALL) AND COMPLEXITY

(ATTAINABILITY ON TIME SCALES OF INTEREST) IN SOCIAL SCIENCE

As background, in mathematical logic, there is a fundamental distinction between a statement's being true and its being provable. I believe that in mathematical social science there is an analogous and equally fundamental distinction between a state of the system (e.g., a strategy distribution) being an equilibrium and its being attainable (generable). I would like to discuss, therefore, the parallel between the following two questions: (1) Is every true statement provable? and (2) Is every equilibrium state attainable?

In general, we are interested in the distinction between satisfaction of some criterion (like being true, or being an equilibrium) and generability (like being provable through repeated application of inference rules, or being attainable through repeated application of agent behavioral rules).

Now, mathematico-logical systems in which every truth is provable are called complete.⁸ The great mathematician David Hilbert, and most mathematicians at the turn of the Twentieth Century, had assumed that all mathematical systems of interest were complete, that all truths statable in those systems were also provable in them (i.e., were deducible from the system's axioms via the system's inference rules). A major objective of the so-called Hilbert Programme for mathematics was to prove precisely this. It came as a tremendous shock when, in 1931, Kurt Gödel proved precisely the opposite: all sufficiently rich⁹ mathematical systems are incomplete. In all such systems, there are true statements that are unprovable! Indeed, he showed that there were true statements that were neither provable nor refutable in the relevant systems—they were undecidable.¹⁰ (See Gödel 1931; Smullyan 1992; Hamilton 1988.)

Now, truth is a special criterion that a logical formula may satisfy. For example, given an arbitrary formula of the sentential calculus, its truth (i.e., its tautologicity) can be evaluated mechanically, using truth tables. Provability, by contrast, is a special type of generability. A formula is provable if, beginning with a distinguished set of “starting statements” called axioms, it can be ground out—attained, if you will—by repeated application of the system's rule(s) of inference.

Equilibrium (Nash equilibrium, for example) is strictly analogous to truth: it too is a criterion that a state (a strategy distribution) may satisfy. And the Nash “equilibriumness” of a strategy configuration (just like the truth of a sentential calculus formula) can be checked mechanically.

I venture to say that most contemporary social scientists—analogous to the Hilbertians of the 1920s—assume that if a social configuration is a Nash equilibrium, then it must also be attainable. In short, the implicit assumption in contemporary social science is that these systems are complete.

However, we are finding that this is not the case. Epstein and Hammond (2002) offer a simple agent-based game almost all of whose equilibria are unattainable outright. This model is presented in the next chapter. More mathematically sophisticated examples of incompleteness include Prasad's result, based on the unsolvability of Hilbert's 10th Problem:

For n-player games with polynomial utility functions and natural number strategy sets the problem of finding an equilibrium is not computable. There does not exist an algorithm which will decide, for any such game, whether it has an equilibrium or not…When the class of games is specified by a finite set of players, whose choice sets are natural numbers, and payoffs are given by polynomial functions, the problem of devising a procedure which computes Nash equilibria is unsolvable. (Prasad 1997)

Other examples of uncomputable (existent) equilibria include Foster and Young 2001; Lewis 1985, 1992a, 1992b; and Nachbar 1997. Some equilibria are unattainable outright.

A separate issue in principle, but one of great practical significance, is whether attainable equilibria can be attained on time scales of interest to humans. Here, too, we are finding models in which the waiting time to (attainable) equilibria scales exponentially in some core variable. In the agent-based model of economic classes of Axtell, Epstein, and Young (2001),¹¹ we find that the waiting time to equilibrium is exponential in both the number of agents and the memory length per agent, and is astronomical when the first exceeds 100 and the latter 10. Likewise, the number of time steps (rounds of play) required to reach the attainable equilibria of the Epstein and Hammond (2002) model was shown to grow exponentially in the number of agents.

One wonders how the core concerns and history of economics would have developed if, instead of being inspired by continuum physics and the work of Lagrange and Hamilton (see Mirowski 1989)—blissfully unconcerned as it is with effective computability—it had been founded on Turing. Finitistic issues of computability, learnability, attainment of equilibrium (rather than mere existence), problem complexity, and undecidability, would then have been central from the start. Their foundational importance is only now being recognized. As Duncan Foley summarizes,

The theory of computability and computational complexity suggests that there are two inherent limitations to the rational choice paradigm. One limitation stems from the possibility that the agent's problem is in fact undecidable, so that no computational procedure exists which for all inputs will give her the needed answer in finite time. A second limitation is posed by computational complexity in that even if her problem is decidable, the computational cost of solving it may in many situations be so large as to overwhelm any possible gains from the optimal choice of action. (See Albin 1998,46)

For fundamental statements, see Simon 1982, 1987; Hahn 1991; and Arrow 1987. Of course, beyond these formal limits on canonical rationality, there is the body of evidence from psychology and laboratory behavioral economics that homo sapiens just doesn't behave (in his decision-making) like homo economicus.

Now, the mere fact that an idealization (e.g., homo economicus) is not accurate in detail is not grounds for its dismissal. To say that a theory should be dismissed because it is “wrong” is vulgar. Theories are idealizations. There are no frictionless planes, ideal gases, or point masses. But these are useful idealizations in physics. However, in social science, it is appropriate to ask whether the idealization of individual rationality in fact illuminates more than it obscures. By empirical lights, that is quite clearly in doubt.

This brings us to the issue of generality. The entire rational choice project, if you will, is challenged by (1) incompleteness and outright uncomputability, by (2) computational complexity (even of computable equilibria), and by (3) powerful psychological evidence of framing effects and myriad other systematic human departures from canonical rationality. Yet, the social science theory that enjoys the greatest formal generality¹² (and mathematical elegance) is precisely the rational choice theory.

Generality Is Quantification over Sets

Now, generality has to do with quantification. Universal gravitation says that for any two masses whatsoever, the attractive gravitational force is inversely proportional to the square of the separation distance. Mechanics quantifies over the set of all masses. Axiomatic general equilibrium theory quantifies over the set of all consumers in the economy, positing constrained utility maximization for every agent in the system. Rational choice theory likewise posits expected utility maximization for all actors.

Clearly, agent modelers do not quantify over sets this big. There is a great deal of experimentation with tags, imitation, evolution, learning, bounded rationality, and zero-intelligence traders, for example. In many cases, however, the experiment is motivated by responsiveness to data. Empirically successful (generatively sufficient) behavioral rules for the Artificial Anasazi of 900 A.D.¹³ probably should not look much like the agent rules in the Axtell-Epstein (1999) model of U.S retirement norms,¹⁴ which in turn may have little relation to the rules governing agents in Axtell's (1999) model of firms, or the Epstein et al. (2004) model of smallpox response,¹⁵ or the zero-intelligence traders of Farmer et al. (1993). Yet, despite their diversity, these models are impressive empirically. If reasonable fidelity to data requires us to be ad hoc (i.e., to quantify over smaller sets), with different rules for different settings, then that is the price of empirical progress.

Truth and Beauty

All of this said, the real reason some mathematical social scientists don't like computational agent-based modeling is not that the approach is empirically weak (in notable areas, it's empirically stronger than the neoclassical approach). It's that it isn't beautiful. When theorists, such as Frank Hahn, lament the demise of “pure theory” in favor of computer simulation (Hahn 1991), they are grieving the loss of mathematical beauty. I would argue that reports of its death are premature. Let us face this aesthetic issue squarely.

On the topic of mathematical beauty, none have written more eloquently than Bertrand Russell (1957):

Mathematics, rightly viewed, possesses not only truth, but supreme beauty—a beauty cold and austere, like that of sculpture, without appeal to any part of our weaker nature, without the gorgeous trappings of painting or music, yet sublimely pure, and capable of a stern perfection such as only the greatest art can show.

Later, in the same essay, Russell writes:

In the most beautiful work, a chain of argument is presented in which every link is important on its own account, in which there is an air of ease and lucidity throughout, and the premises achieve more than would have been thought possible, by means which appear natural and inevitable. (Emphasis added)

Hahn (1991) defines “pure theory” as “the activity of deducing implications from a small number of fundamental axioms.” And when he writes that “with surprising frequency this leads to beauty (Arrow's Theorem, The Core, etc),” it is clear that it is Russell's beauty he has in mind.

Generality (mathematical unification) for its own sake satisfies this fine impulse to beauty and has proven to be highly productive scientifically. Physics is highly general, and so is mathematical equilibrium theory. And, as Mirowski (1989) has documented, “physics envy” was quite explicitly central to its development. This is entirely understandable. Any scientist who doesn't have physics envy is an idiot. I am not advocating that we abandon the quest for elegant generality in favor of a case by case narrative (i.e., purely historical) approach. By comparison to a beautiful (Newton-like) generalization, actual history is just this particular apple bobbling down this particular hill. To me, the mathematical theory of evolution is more beautiful than any particular tiger. One of the most miraculous results of our own evolution is that our search for beauty can lead to truth. But there are different kinds of beauty. An analogy to music history may be apposite.

Just as the German classical composers had the dominant 7th and circle of fifths as harmonic propulsion, so the neoclassical economists have utility maximization to propel their analyses. And it is a style of “composition” subscribed to by an entire school of academic thought. We agent modelers are not of this school. We don't have the Germanic dominant 7th of utility maximization to propel every analysis forward—more like the French impressionists, we must in each case be inventive to solve the problem of social motion, devising unique agent rules model by model. If that makes us ad hoc, then so was Debussy, and we are in good artistic company.

Schelling's (1971) segregation model is important not because it's right in all details (which it doesn't purport to be), and it's beautiful not because it's visually appealing (which it happens to be). It's important because—even though highly idealized—it offers a powerful and counter-intuitive insight. And it's beautiful because it does so with startling Russellian parsimony. The mathematics of chaos is beautiful not because of all the pretty fractal pictures it generates, useful as these are in stimulating popular interest. What's beautiful in Russell's sense is the startlingly compact yet sweepingly general Li-Yorke (1975) theorem that “period three implies chaos.” And when an agent-based model is beautiful in this deep sense, it has nothing to do with the phantasmagorical “eye candy”—Russell's gorgeous trappings—of animated dot worlds. Rather, its beauty resides in the far-reaching generative power of its simple microrules, seemingly remote from the elaborate macro patterns they produce. Precisely as Russell would have it: “the premises achieve more than would have been thought possible, by means which appear natural and inevitable.”

The musical parallels are again irresistible. To be sure, Bach's final work, The Art of the Fugue, is gorgeous music, but to Bach, the game was to explore the generative power of a single fugue theme. Bach wrote nineteen stunningly diverse fugues based on this single theme, this “premise,” if you will.¹⁶ In Bach's hands, it certainly “achieves more than would have been thought possible.” While its musical beauty is clear, the intellectual beauty lies not in the sound, but in its silent unified structure. Perhaps the best agent models unfold as “social fugues” in which the apparent complexity is in fact generated by a few simple individual rules.

In any case, and whatever one's aesthetic leanings, agent modelers are in good scientific company trading away a certain degree of generality for fidelity to data. The issue of induction arises in this connection.

Induction over Theorem Distributions

As noted earlier, one powerful mode of agent-based modeling is to run large numbers of stochastic realizations (each with its own random seed), collect clean data, and build up a robust statistical portrait of model output. One goal of such exercises is to understand one's model when closed form analytical expressions are not in hand (though these exist in principle, as discussed). A second aim of such exercises is to explain observed statistical regularities, such as the distribution of firm sizes in the U.S. economy (Axtell 1999, 2001). In either case, one builds up a large sample of model realizations. But, as emphasized earlier, each realization is a strict deduction. So, while I have no objection to calling such activity inductive, it is induction over a sample distribution of theorems, in fact. And it has quite a different flavor from “inductive” survey research, where one collects real-world data and estimates it by techniques of aggregate regression.

SUMMARY

A number of uses of agent-based models have not been touched on here. These include purely exploratory applications and those related to mechanism design, among others (see Epstein 1999). My focus has been on computational agent models as instruments in the generative explanation of macroscopic social structures. In that connection, the main epistemological points treated are as follows:

1. We distinguish the generative motto from its converse. The position is:
   

   

   
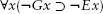
   If you didn't grow it, you didn't explain it. But not conversely. A microspecification that generates the explanandum is a candidate explanation. Generative sufficiency is explanatorily necessary, but not explanatorily sufficient. There may be more than one explanatory candidate, as in any science where theories compete.
2. For every agent model, there exist unique equivalent equations. One can express any Turing machine (and hence any agent model) in partial recursive functions. Many agent models have been revealingly mathematized in other ways, as stochastic dynamical systems, for example.
3. Every realization of an agent model is a strict deduction. So, (Gx⊃ Dx), but not conversely, as in non-constructive (reductio ad absurdum) existence proofs. One can have (Dx∧¬Gx) and hence, by (1), (Dx∧¬Ex). Not all deduction is explanatory.
4. We often generate, and hence deduce, conjuncts satisfying Disjunctive Normal Forms, as when we grow distributions or spatial settlement patterns in finite agent populations.
5. We carefully distinguish between existence and attainability in principle. And we furthermore carefully distinguish between asymptotic attainability and attainability on time scales of interest. In short, we are attentive to questions of incompleteness (à la Gödel) and of computational complexity (as in problems whose time complexity is exponential in key variables). These considerations, when combined with powerful psychological evidence, cast severe doubt on the rational choice picture as the most productive idealization of human decision-making, and serve only to enforce the bounded rationality picture insisted on by Simon (1982).
6. Generality, while a commendable impulse, is not of paramount concern to agent-based modelers at this point. Responsiveness to data often requires that we quantify over smaller sets than physics or neoclassical economics. If that is ad hocism, I readily choose it over what Simon (1987) rightly indicts as an empirically oblivious a priorism in economics.
7. Empirical agent-based modeling can be seen as induction over a sample of realizations, each one of which is a strict deduction, or theorem, and comparison of the generated distribution to statistical data. This differs from inductive survey research where we assemble data and fit it by aggregate regression, for example.

CONCLUSION

As to the core indictment that agent models are non-mathematical, non-deductive, and ad hoc, the first two are false, and the third, I argue, is unimportant. Generative explanation is mathematical in principle; recursive functions could be provided. Ipso facto, generative explanation is deductive. Granted, agent models typically quantify over smaller sets than rational choice models and, as such, are less general. But, in many cases, they are more responsive to data, and in years to come, may achieve greater generality and unification. After all, a fully unified field theory has eluded even that most enviable of fields, physics.

REFERENCES

Albin, Peter S., ed. 1998. Barriers and Bounds to Rationality: Essays on Economic Complexity and Dynamics in Interactive Systems. Princeton: Princeton University Press.

Albin, Peter S., and D. K. Foley. 1990. Decentralized, Dispersed Exchange without an Auctioneer: A Simulation Study. Journal of Economic Behavior and Organization 18(1): 27-51.

Arrow, Kenneth J. 1987. Rationality of Self and Others in an Economic System. In Rational Choice: The Contrast between Economics and Psychology, ed. Robin M. Hogarth and Melvin W. Reder. Chicago: University of Chicago Press.

Axelrod, Robert. 1997. Advancing the Art of Simulation in the Social Sciences. Complexity 3:193-99.

Axtell, Robert L. 1999. The Emergence of Firms in a Population of Agents: Local Increasing Returns, Unstable Nash Equilibria, and Power Law Size Distributions. Santa Fe Institute Working Paper 99-03-019.

_____. 2001. U.S. Firm Sizes Are Zipf Distributed. Science 93:1818-20.

Axtell, Robert L., and Joshua M. Epstein. 1999. Coordination in Transient Social Networks: An Agent-Based Computational Model of the Timing of Retirement. In Behavioral Dimensions of Retirement Economics, ed. Henry Aaron. New York: Russell Sage Foundation.

Axtell, Robert L., Joshua M. Epstein, Jeffrey S. Dean, George J. Gumerman, Alan C. Swedlund, Jason Harburger, Shubha Chakravarty, Ross Hammond, Jon Parker, and Miles T. Parker. 2002. Population Growth and Collapse in a Multiagent Model of the Kayenta Anasazi in Long House Valley. Proceedings of the National Academy of Sciences 99, suppl. 3: 7275-79.

Axtell, Robert L., Joshua M. Epstein, and H. Peyton Young. 2001. The Emergence of Economic Classes in an Agent-Based Bargaining Model. In Social Dynamics, ed. Steven Durlauf and H. Peyton Young. Cambridge: MIT Press.

Berry, Brian J. L., Douglas Kiel, and Evel Elliott, editors. 2002. Adaptive Agents, Intelligence, and Emergent Human Organization: Capturing Complexity Through Agent-Based Modeling. Proceedings of the National Academy of Sciences, 99, suppl. 3: Results from the Arthur M. Sackler Colloquium of the National Academy of Sciences held October 4-6, 2001.

Boolos, George S., and Richard C. Jeffrey. 1989. Computability and Logic. 3rd ed. Cambridge: Cambridge University Press.

Cederman, Lars-Erik. 1997. Emergent Actors in World Politics: How States and Nations Develop and Dissolve. Princeton: Princeton University Press.

Chomsky, Noam. 1965. Aspects of the Theory of Syntax. Cambridge: MIT Press.

Crutchfield, J. P., and M. Mitchell. 1995. The Evolution of Emergent Computation. Proceedings of the National Academy of Sciences 92:10740-46.

Dorofeenko, Victor, and Jamsheed Shorish. 2002. “Dynamical Modeling of the Demographic Prisoner's Dilemma,” Economic Series 124, Institute for Advanced Studies, Vienna, November.

Epstein, Joshua M. 1997. Nonlinear Dynamics, Mathematical Biology, and Social Science. Menlo Park, CA: Addison-Wesley.

_____. 1999. Agent-Based Computational Models and Generative Social Science. Complexity 4(5): 41-60.

Epstein, Joshua M., and Robert L. Axtell. 1996. Growing Artificial Societies: Social Science from the Bottom Up. Washington, DC: Brookings Institution Press; Cambridge: MIT Press.

Epstein, Joshua M., Derek A. T. Cummings, Shubha Chakravarty, Ramesh M. Singha, and Donald S. Burke. 2004. Toward a Containment Strategy for Smallpox Bioterror: An Individual-Based Computational Approach. Washington, D.C.: Brookings Institution.

Epstein, Joshua M., and Ross A. Hammond. 2002. Non-Explanatory Equilibria: An Extremely Simple Game with (Mostly) Unattainable Fixed Points. Complexity 7(4): 18-22.

Epstein, Richard L., and Walter A. Carnielli. 1989. Computability: Computable Functions, Logic, and the Foundations of Mathematics. Belmont, CA: Wadsworth and Brooks.

Epstein, Samuel David, and Norbert Hornstein, eds. 1999. Working Minimalism. Cambridge: MIT Press.

Farmer, J. Doyne, P. Patelli, and I. I. Zovko. 2003. The Predictive Power of Zero Intelligence in Financial Markets. Santa Fe Institute Working Paper 03-09-051.

Foster, Dean P., and H. Peyton Young. 2001. On the Impossibility of Predicting the Behavior of Rational Agents. Proceedings of the National Academy of Sciences 98(22): 12848-53.

Garey, Michael R., and David S. Johnson. 1979. Computers and Intractability: A Guide to the Theory of NP-Completeness. New York: W. H. Freeman.

Gödel, Kurt. 1931. Uber formal unentscheidbare Satze der Principia Mathematica und verwadter Systeme I. Monatshefte fur Mathematik und Physik 38:173-98. For the English version: On Formally Undecidable Propositions of the Principia Mathematica and Related Systems, in Collected Works, vol. 1, ed. Solomon Feferman (Oxford: Oxford University Press, 1986).

Hahn, Frank. 1991. The Next Hundred Years. Economic Journal 101:47-50.

Hamilton, A. G. 1988. Logic for Mathematicians. Cambridge: Cambridge University Press.

Hodel, R. E. 1995. An Introduction to Mathematical Logic. Boston: PWS Publishing.

Jeffrey, Richard. 1991. Formal Logic: Its Scope and Limits. 3rd ed. New York: McGraw-Hill.

Knuth, Donald E. 1998. The Art of Computer Programming. 3rd ed. Vol. 2, Seminumerical Algorithms. Boston: Addison-Wesley.

Krishnamurthy, E. V. 1985. Introductory Theory of Computer Science. New York: Springer-Verlag.

Lewis, A. A. 1985. On Effectively Computable Realizations of Choice Functions. Mathematical Social Sciences 10:43-80.

____. 1992a. Some Aspects of Effectively Constructive Mathematics That Are Relevant to the Foundations of Neoclassical Mathematical Economics and the Theory of Games. Mathematical Social Sciences 24:209-35.

_____. 1992b. On Turing Degrees of Walrasian Models and a General Impossibility Result in the Theory of Decision Making. Mathematical Social Sciences 24: 141-71.

Li, T. Y., and J. A. Yorke. 1975. Period Three Implies Chaos. American Mathematical Monthly 82:985.

Mas-Colell, Andreu, Michael D. Whinston, and Jerry R. Green. 1995. Microeconomic Theory. Oxford: Oxford University Press.

Mirowski, Philip. 1989. More Heat Than Light: Economics as Social Physics, Physics as Nature's Economics. Cambridge: Cambridge University Press.

Nachbar, J. H. 1997. Prediction, Optimization, and Learning in Games. Econometrica 65:75-309.

Pais, Abraham. 1982. Subtle is the Lord: The Science and the Life of Albert Einstein. Oxford: Oxford University Press.

Pollicot, Mark, and Howard Weiss. 2001. The Dynamics of Schelling-Type Segregation Models and a Nonlinear Graph Laplacian Variational Problem. Advances in Applied Mathematics 27:17-40.

Prasad, Kislaya. 1997. On the Compatibility of Nash Equilibria. Journal of Economic Dynamics and Control 21:943-53.

Russell, Bertrand. 1957. Mysticism and Logic. New York: Doubleday Anchor.

Schelling, Thomas C. 1971. Dynamic Models of Segregation. Journal of Mathematical Sociology 1:143-86.

Simon, Herbert A. 1982. Models of Bounded Rationality. Cambridge: MIT Press.

_____. 1987. Rationality in Psychology and Economics. In Rational Choice: The Contrast between Economics and Psychology, ed. Robin M. Hogarth and Melvin W. Reder. Chicago: University of Chicago Press.

Smullyan, Raymond M. 1992. Godel's Incompleteness Theorems. Oxford: Oxford University Press.

Tufillaro, Nicholas B., Tyler Abbott, and Jeremiah Reilly. 1992. An Experimental Approach to Nonlinear Dynamics and Chaos. Boston: Addison-Wesley.

Young, H. Peyton. 1998. Individual Strategy and Social Structure: An Evolutionary Theory of Institutions. Princeton: Princeton University Press.

Young, H. Peyton, and Dean Foster. 1991. Cooperation in the Short and in the Long Run. Games and Economic Behavior 3:145-56.

---

^* Joshua M. Epstein is a Senior Fellow in Economic Studies at The Brookings Institution, a member of The Brookings-Johns Hopkins Center on Social and Economic Dynamics, and an External Faculty member of The Santa Fe Institute.

For thoughtful comments on this chapter, the author thanks Claudio Cioffi-Revilla, Samuel David Epstein, Carol Graham, Ross Hammond, Kislaya Prasad, Brian Skyrms, Leigh Tesfatsion, and Peyton Young. For assistance in preparing the manuscript for publication, he thanks Danielle Feher.

This essay is published simultaneously in Handbook of Computational Economics, Volume 2: Agent-Based Computational Economics, ed. L. Tesfatsion and K. Judd. 2006. North-Holland.

¹ In slightly more detail, if we let M = {i : i is a microspecification} and let G(i, x) denote the proposition that i generates x, then the proposition Gx can be expressed as ∃iG(i, x). Then, longhand, the motto becomes: ∀x(¬∃iG(i, x) ⊃ ¬Ex).

² I do not claim that every agent-based model exhibits all these features. My point is that the explanatory desiderata enumerated (heterogeneity, local interactions, bounded rationality, etc.) are easily arranged in agent-based models.

³ As noted, empirical plausibility is one such. Theoretical economy is another. In generative linguistics, for example, S. D. Epstein and N. Hornstein (1999, ix-xviii) convincingly argue that minimalism should be central in selecting among competing theories.

⁴ Not everyone who asserts that computational agent modeling is non-deductive necessarily regards it as a defect. See, for example, Axelrod 1997.

⁵ In principle, it can be further broken down into statements about limits of sums, and so forth. As a completely worked out simple example, consider the mathematical equation

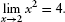
It asserts: “The limit of the square of x, as x approaches two, is four.” In further detail, it is the following claim:

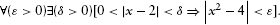
In English, “For every number epsilon greater than zero, there exists a number delta greater than zero such that if the absolute value of the difference between x and 2 is strictly between zero and delta, then the absolute value of the difference between the square of x and four is less than epsilon.” The fact that it is easier to manipulate and compute with mathematical symbols than with words may say something interesting about human psychology, but it does not demonstrate any limit on the precision or expressive power of English.

⁶ The general problem of satisfying an n-term CNF is NP-Complete (Garey and Johnson 1979). Based on this observation, it is tempting to conjecture that nonequilibrium social science—suitably cast as CNF satisfaction—is computationally hard in a rigorous sense.

⁷ Reduction to an absurdity.

⁸ Sometimes the terms adequate or analytical are used.

⁹ For a punctilious characterization of precisely those formal systems to which the theorem applies, see Smullyan 1992.

¹⁰ Importantly, he did so constructively, displaying a (self-referential) true statement that is undecidable; that is, neither it nor its negation are theorems of the relevant system.

¹¹ Chapter 8 of this book.

¹² Here, I mean generality in the theory's formal statement, not in its range of successful empirical application.

¹³ Chapters 4-6 of this book.

¹⁴ Chapter 7 of this book.

¹⁵ Chapter 12 of this book.

¹⁶ Bach died before completing this work, and doubtless could have composed countless further fugues.