The Sixteenth and Seventeenth Centuries. The Founding of the Infinitesimal Calculus

2.1 The Sixteenth Century

From Stevin to Kepler

The early modern period saw the spread of knowledge in Europe of ancient geometry, particularly that of Archimedes , and a loosening of the Aristotelian grip on thinking. In regard to the problem of the continuum, the focus shifted away from metaphysics to technique, from the problem of “what indivisibles were, or whether they composed magnitudes” to “the new marvels one could accomplish with them”¹ through the emerging calculus and mathematical analysis. Indeed, tracing the development of the continuum concept during this period is tantamount to charting the rise of the calculus.

Traditionally, geometry is the branch of mathematics concerned with the continuous and arithmetic (or algebra) with the discrete. The infinitesimal calculus that took form in the sixteenth and seventeenth centuries, which had as its primary subject matter continuous variation , may be seen as a kind of synthesis of the continuous and the discrete, with infinitesimals bridging the gap between the two. The widespread use of indivisibles and infinitesimals in the analysis of continuous variation by the mathematicians of the time testifies to the affirmation of a kind of mathematical atomism which, while logically questionable, made possible the spectacular mathematical advances with which the calculus is associated. It was thus to be the infinitesimal, rather than the infinite, that served as the mathematical stepping stone between the discrete and the continuous.

The “dynamic” as opposed to “static” form this mathematical atomism assumed in the work of Simon Stevin (1548–1620) has been identified by historians of mathematics as an anticipation of the theory of limits.² It is instructive to see how Stevin proved (in his work on statics of 1586) that the centre of gravity of a triangle lies on its median. Here is Boyer’s account (see Fig. 2.1):

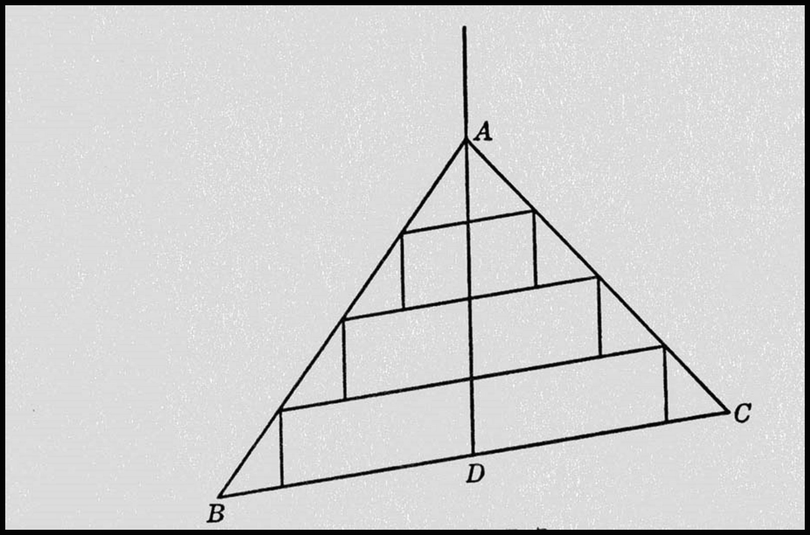
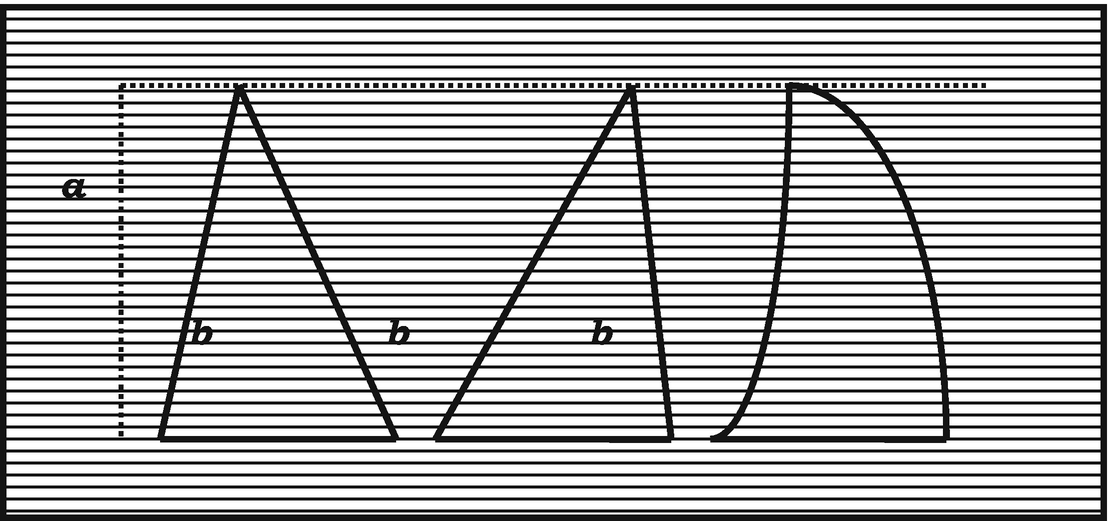
Inscribe in the triangle ABC a number of parallelograms of equal height…The center of gravity of the inscribed figure will lie on the median by the principle that bilaterally symmetrical figures are in equilibrium… . However, we may inscribe in the triangle an infinite number of such parallelograms, for all of which the center of gravity will lie on AD. Moreover, the greater the number of parallelograms thus inscribed, the smaller will be the difference between the inscribed figure and the triangle ABC. If, now, the “weights” of the triangles ABD and ACD are not equal, they will have a certain fixed difference. But there can be no such difference, inasmuch as each of these triangles can be made to differ by less than this from the sums of the parallelograms inscribed within them, which are equal. Therefore the “weights” of ABD and ACD are equal, and hence the centre of gravity of the triangle ABC lies on the median AD. ³

../images/474107_1_En_2_Chapter/474107_1_En_2_Fig1_HTML.png — Fig. 2.1
Caption

Here Stevin implicitly employs the principle that any pair of magnitudes, the difference between which can be shown to be less than any assigned magnitude, are themselves equal.⁴ The “infinity of parallelograms” inscribable in the triangle seems to mean a potential, not an actual infinity, while the parallelograms themselves are varying elements of area—and so of the same dimension as the figure to which their sum approximates—rather than fixed “indivisible” lines of a lower dimension. Stevin applied the same idea to determine the centres of gravity of a number of plane curvilinear figures and solids.

In contrast with Stevin’s cautious approach, Johann Kepler (1571–1630) made abundant use of infinitesimals in his calculations. In his Nova Stereometria of 1615, a work actually written as an aid in calculating the volumes of wine casks, he regards curves as being infinilateral polygons , and solid bodies as being made up of infinitesimal cones or infinitesimally thin discs.⁵ A particularly fetching application of the former idea is Kepler’s determination of the volume of a sphere.⁶ The sphere may be regarded as being made up of infinitesimal cones, each with its base on the sphere’s surface and its apex at the centre (Fig. 2.2). From the fact that the volume of a cone is 1/3 × height × area of base , it follows that the sphere’s volume is 1/3 × radius × surface area.

../images/474107_1_En_2_Chapter/474107_1_En_2_Fig2_HTML.png — Fig. 2.2
Caption

Such uses are in keeping with Kepler’s customary use of infinitesimals of the same dimension as the figures they constitute; but he also used indivisibles on occasion. He spoke, for example, of a cone as being composed of circles,⁷ and in his Astronomia Nova of 1609, the work in which he states his famous laws of planetary motion, he takes the area of an ellipse to be the “sum of the radii” drawn from the focus.

It seems to have been Kepler who first introduced the idea, which was later to become a reigning principle in geometry, of continuous change of a mathematical object, in this case, of a geometric figure.⁸ In his Astronomiae pars Optica of 1604 Kepler notes that all the conic sections are continuously derivable from one another both through focal motion and by variation of the angle with the cone of the cutting plane.

Galileo and Cavalieri

Galileo Galilei (1564–1642) advocated a form of mathematical atomism in which the influence of both the Democritean atomists and the Aristotelian scholastics can be discerned. This emerges when one turns to the First Day of his Dialogues Concerning Two New Sciences (1638), more particularly to the extended discussion therein of the composition of material continua. Salviati, Galileo’s spokesman, proposes an atomic account of matter similar in spirit to that of Democritus : bodies are composed of “infinitely small indivisible particles”,⁹ themselves infinite in number, interspersed with an infinity of infinitesimally small vacua. Salviati, that is, Galileo, also maintains, contrary to Bradwardine and the Aristotelians, that continuous magnitude is made up of indivisibles, indeed an infinite number of them:

Since lines and all continuous quantities are divisible into parts which are themselves divisible without end, I do not see how it is possible to avoid the conclusion that these lines are built up of an infinite number of indivisible quantities because a division and a subdivision which can be carried on indefinitely presupposes that the parts are infinite in number, since otherwise the subdivision would reach an end ¹⁰ ; and if the parts are infinite in number, we must conclude that they are not finite in size, because an infinite number of finite quantities would give an infinite magnitude. And thus we have a continuous quantity built up of an infinite number of indivisibles. ¹¹

Salviati/Galileo recognizes that this infinity of indivisibles will never be produced by successive subdivision, but claims to have a method for generating it all at once, thereby removing it from the realm of the potential into actual realization:

I am willing, Simplicio, at the outset, to grant to the Peripatetics the truth of their opinion that a continuous quantity is divisible only into parts which are still further divisible so that however far the division and subdivision be continued no end will be reached; but I am not so certain that they will concede to me that none of these divisions of theirs can be a final one, as is surely the fact, because there always remains “another”; the final and ultimate division is rather one which resolves a continuous quantity into an infinite number of indivisible quantities, a result I grant can never be reached by successive division into an ever-increasing number of parts. But if they employ the method which I propose for separating and resolving the whole of infinity, at a single stroke… I think that they would be contented to admit that a continuous quantity is built up out of absolutely indivisible atoms , especially since this method, perhaps better than any other, enables us to avoid many intricate labyrinths… ¹²

And what is this “method for separating and resolving, at a single stroke, the whole of infinity”? Simply the act of bending a straight line into a circle:

If now the change which takes place when you bend a line at right angles so as to form now a square, now an octagon, now a polygon of forty, a hundred or a thousand angles, is sufficient to bring into actuality the four, eight, forty, hundred, and thousand parts which, according to you, existed at first only potentially in the straight line, may I not say, with equal right, that, when I have bent the straight line into a polygon having an infinite number of sides, i.e., into a circle, I have reduced to actuality that infinite number of parts which you claimed, while it was straight, were contained in it only potentially. ¹³

Here Galileo finds an ingenious “metaphysical” application of the idea of regarding the circle as an infinilateral polygon . When the straight line has been bent into a circle Galileo seems to take it that that the line has thereby been rendered into indivisible parts, that is, points. But if one considers that these parts are the sides of the infinilateral polygon, they are better characterized not as indivisible points, but rather as unbendable straight lines, each at once part of and tangent to the circle.¹⁴ Galileo does not mention this possibility, but nevertheless it does not seem fanciful to detect the germ here of the idea of considering a curve as an assemblage of infinitesimal “unbendable” straight lines.¹⁵

While Galileo was firm in his conviction that continua are composed of an infinity of indivisibles in an actual sense, he considers that the number of such indivisibles must be regarded as a potential infinity:

…if we consider discrete quantities, I think there is, between finite and infinite quantities, a third intermediate term which corresponds to every assigned number; so that if asked, as in the present case, whether the finite parts of a continuum are finite or infinite in number the best reply is that they are neither finite nor infinite but correspond to every assigned number. ¹⁶

In the last analysis both the infinite and the infinitesimal are essentially beyond the grasp of intuition:

…infinity and indivisibility are in their very nature incomprehensible to us; imagine then what they are when combined. Yet if we wish to build up a line out of indivisible points, we must take an infinite number of them, and are, therefore, bound to understand both the infinite and the indivisible at the same time… ¹⁷

The mysterious “merging of parts into unity”¹⁸ to form a continuum is likened to the liquefaction of a solid:

Having broken up a solid into many parts, having reduced it to the finest of powder and having resolved it into its infinitely small indivisible atoms why may we not say that this solid has been reduced to a single continuum, perhaps a fluid like water or mercury or even a liquefied metal? And do we not see stones melt into glass and the glass itself become under strong heat more fluid than water?

…I am not able to find any better means [than that substances become fluid in virtue of being resolved into their infinitely small indivisible components] of accounting for certain phenomena of which the following is one. When I take a hard substance such as stone or metal and when I reduce it by means of a hammer or hard file to the most minute and impalpable powder, it is clear that its finest particles, although when taken one by one are, on account of their smallness, imperceptible to our sight and touch, are nevertheless finite in size, possess shape, and the capability of being counted. It is also true that when once heaped up they remain in a heap; and if an excavation be made within limits the cavity will remain and the surrounding particles will not rush in to fill it; if shaken the particles come to rest immediately after the external disturbing agent is removed; the same effects are observed in all piles of larger and larger particles, of any shape, even if spherical, as is the case with piles of millet, wheat, lead shot, and every other material. But if we attempt to discover such properties in water we do not find them; for when once heaped up it immediately flattens out unless held up by some vessel or other external retaining body; when hollowed out nit quickly rushes in to fill the cavity; and when disturbed it fluctuates for a long time and sends out its waves through great distances .
Seeing that water has less firmness than the finest of powder, in fact has no consistence whatsoever, we may, it seems to me, very reasonably, conclude that the smallest particles into which it can be resolved are quite different from finite and divisible particles; indeed the only difference I am able to discover is that the former are indivisible. ¹⁹

Despite Galileo’s uncertainty concerning the exact nature of indivisibles, he employed them in analyzing rectilinear motion and the motion of projectiles, in so doing authorizing their use by his successors.

It was Galileo’s pupil and colleague Bonaventura Cavalieri (1598–1647) who refined the use of indivisibles into a reliable mathematical tool; indeed the “method of indivisibles” remains associated with his name down to the present day. Cavalieri nowhere explains precisely what he understands by the word “indivisible”, but it is apparent that he conceived of a surface as composed of a multitude of equispaced parallel lines and of a volume as composed of equispaced parallel planes, these being termed the indivisibles of the surface and the volume respectively.²⁰ While Cavalieri recognized that these “multitudes” of indivisibles must be unboundedly large, indeed was prepared to regard them as being actually infinite, he avoided following Galileo into ensnarement in the coils of infinity by grasping that, for the “method of indivisibles” to work, the precise “number” of indivisibles involved did not matter. Indeed, the essence of Cavalieri’s method was the establishing of a correspondence between the indivisibles of two “similar” configurations,²¹ and in the cases Cavalieri considers it is evident that the correspondence is suggested on solely geometric grounds, rendering it quite independent of number. The very statement of Cavalieri’s principle embodies this idea: if plane figures are included between a pair of parallel lines, and if their intercepts on any line parallel to the including lines are in a fixed ratio, then the areas of the figures are in the same ratio. (An analogous principle holds for solids.) As an application, consider a circle of radius a inscribed in an ellipse with major semi-axis b (see Fig. 2.3). Since the intercepts of the lines parallel to the tangents are in the fixed ratio b: a, Cavalieri’s principle entails that the area of the ellipse is $\raisebox{1ex}{$b$}\!\left/ \!\raisebox{-1ex}{$a$}\right.$ × the area of the circle. Clearly the number of parallel lines is irrelevant to the argument.

../images/474107_1_En_2_Chapter/474107_1_En_2_Fig3_HTML.png — Fig. 2.3
Caption

Cavalieri’s method is in essence that of reduction of dimension : solids are reduced to planes with comparable areas and planes to lines with comparable lengths. While this method suffices for the computation of areas or volumes, it cannot be applied to rectify curves, since the reduction in this case would be to points, and no meaning can be attached to the “ratio” of two points. For rectification a curve has, it was later realized, to be regarded as the sum, not of indivisibles, that is, points, but rather of infinitesimal straight lines, its “microsegments”.

Cavalieri recognized that his method differed from Kepler’s in taking continua to be sums of heterogenea , that is, parts of a lower dimension, rather than homogenea , parts of an unreduced dimension. He was challenged by critics that this feature made his whole approach unsound: for how can a sum of planes without thickness produce a volume, or breadthless lines a surface? Cavalieri failed to provide a convincing answer to this question, sidestepping it with the response that, while the indivisibles are correctly regarded as lacking thickness or breadth, nevertheless one “could substitute for them small elements of area and volume in the manner of Archimedes ”.²² In a number of places Cavalieri suggests that surfaces and volumes could be regarded as being generated by “the flowing of indivisibles”.²³ Although he failed to develop this idea into a geometric method, the suggestion is natural enough, given that continua had from the first been regarded as being generated by motion: a line can be considered as the trace of a moving point, a surface as a moving line, a solid as a moving surface.

2.2 The 17th Century

The Cartesian Philosophy

The mathematical work of René Descartes (1596–1650), though unquestionably of major importance, has been described as “only an episode in his philosophy”.²⁴ He, too, employed infinitesimals in his early mathematical work, and was acquainted with the views concerning them of his predecessors and contemporaries.²⁵ Later, however, he came to avoid infinitesimals, and even to deplore their use. He developed purely algebraic methods for determining tangents to curves, directing some of his sharpest criticism at those such as Fermat who employed infinitesimals for this purpose.

As a philosopher Descartes may be broadly characterized as a synechist. His philosophical system rests on two fundamental principles: the celebrated Cartesian dualism—the division between mind and matter—and the less familiar identification of matter and spatial extension. In the Meditations Descartes distinguishes mind and matter on grounds similar to that of the Indian idealists—that the corporeal, being spatially extended, is divisible, while the mental is partless:

…there is a vast difference between mind and body, in respect that body, from its nature, is always divisible, and that mind is entirely indivisible. For in truth, when I consider the mind, that is, when I consider myself in so far only as I am a thinking thing, I can distinguish no parts, but I very clearly discern that I am somewhat absolutely one and entire; and although the whole mind seems to be united to the whole body, yet, when a foot, an arm, or any other part is cut off, I am conscious that nothing has been taken from my mind; nor can the faculties of willing, perceiving, conceiving, etc., properly be called its parts, for it is the same mind that is exercised [all entire] in willing , in perceiving, and in conceiving, etc. But quite the opposite holds in corporeal or extended things; for I cannot imagine any one of them [however small soever it may be], which I cannot easily sunder in thought, and which, therefore, I do not know to be divisible. This would be sufficient to teach me that the mind or soul of man is entirely different from the body, if I had not already been apprised of it on other grounds. ²⁶

In The Principles of Philosophy Descartes identifies space and matter:

Space or internal place, and the corporeal substance which is comprised in it, are not different in reality, but merely in the mode by which they are wont to be conceived by us. For, in truth, the same extension in length, breadth and depth, which constitutes space, constitutes body; and the difference between them lies only in this, that in body we consider extension as particular; whereas in space we attribute to extension a generic unity…Nothing remains in the idea of body, except that it is something extended in length, breadth and depth; and this something is comprised in our idea of space, not only of that which is full of body, but even of what is called void space. ²⁷

And from this it follows that matter is continuous and divisible without limit:

We likewise discover that there cannot exist any atoms or parts of matter that are of their own nature indivisible. For however small we suppose those parts to be, yet because they are necessarily extended, we are always able in thought to divide any one of them into two or more smaller parts, and may accordingly admit their divisibility. For there is nothing we can divide in thought which we do not recognize to be divisible; and, therefore, were we to judge it indivisible our judgment would not be in harmony with the knowledge we have of the thing; and although we should even suppose that God had reduced any particle of matter to a smallness so extreme that it did not admit of being further divided, it would nevertheless be improperly styled indivisible, for though God had rendered the particle so small that it was not in the power of any creature to divide it, he could not however deprive himself of the ability to do so, since it is absolutely impossible for him to lessen his own omnipotence…Wherefore, absolutely speaking, the smallest extended particle is always divisible, since it is such of its very nature. ²⁸

Since extension is the sole essential property of matter and, conversely, matter always accompanies extension, matter must be ubiquitous. Descartes ’ space is accordingly, as it was for the Stoics , a plenum pervaded by a continuous medium. But Descartes parted from the Stoics in postulating that this medium was primordially divided, in the manner of a Rubik cube, into material corpuscles of equal size. These corpuscles, being themselves divisible, are not atoms. Nor could they be spherical in form, at least initially, because spheres cannot be packed together without leaving some “empty” space. Now Descartes also posited that his corpuscles were originally in continual motion, a motion which, in such a densely packed universe, could only be circular. As a result of this motion certain corpuscles would be ground down, like the pebbles on a beach, into a quasispherical form, the resulting intermediary space becoming filled with the residue left by the process of abrasion. The circular motions of the particles are manifested as whirlpools of material particles varying in size and velocity. This is the basis of Descartes ’ celebrated theory of vortices.

The Cartesian view of the world was firmly endorsed by the authors of the Port-Royal Logic (1662), the philosopher-theologians Antoine Arnauld (1612–94) and Pierre Nicole (1625–95). In that work the Cartesian infinite divisibility of matter, with its worlds within worlds, is described in almost rhapsodic terms:

How to understand that the smallest bit of matter is infinitely divisible and that one can never arrive at a part that is so small that not only does it not contain several others, but it does not contain an infinity of parts; that the smallest grain of wheat contains in itself as many parts, although proportionately smaller, as the entire world; that all the shapes imaginable are actually to be found there; and that it contains in itself a tiny world with all its parts—a sun, heavens, stars, planets, and an earth—with admirably precise proportions; that there are no parts of this of this grain that do not contain yet another proportional world? ²⁹

And yet these marvels must necessarily be realized, since the infinite divisibility of matter has been provided with geometric demonstration, “proofs of it as clear as proofs of any of the truths it reveals to us.”. Three proofs are initially provided. The first draws on the demonstrated existence of incommensurable lines, the second on the theorem that no whole number exists whose square is double that of another whole number. The third pivots on the observation that the unextended cannot generate extension:

Finally, nothing is clearer than this reasoning, that two things having zero extension cannot form an extension, and that every extension has parts. Now taking two of these parts that are supposed to be indivisible, I ask whether they do or do not have any extension. If they have some extension, then they are divisible, and they have several parts. If they do not, they therefore have zero extension, and hence it is impossible for them to form an extension. ³⁰

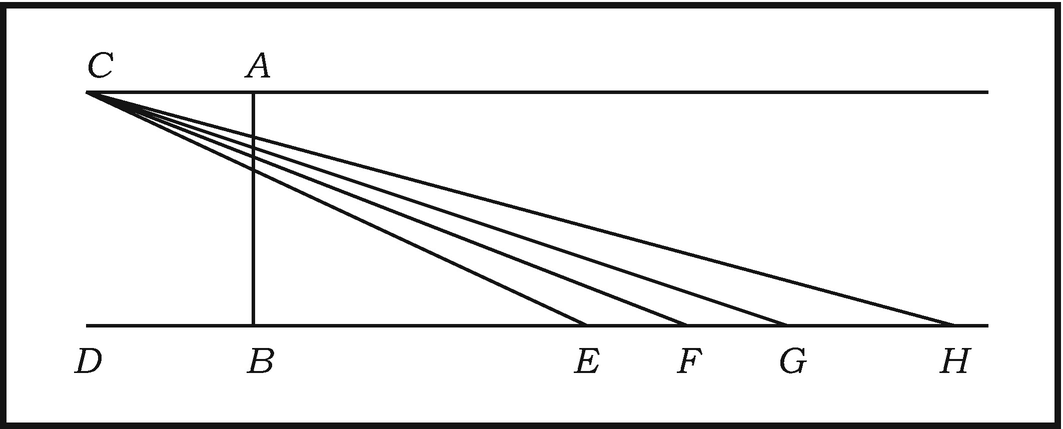
For good measure Arnauld and Nicole throw in another proof of infinite divisibility , this time based on the indefinite extensibility of lines:

Certainly, while we might doubt whether extension can be infinitely divided, at least we cannot doubt that it can be increased to infinity, and that we can join to a surface of a hundred thousand leagues another surface of a hundred thousand leagues, and so on to infinity. Now this infinite increase in extension proves its infinite divisibility . To understand this we have only to imagine a flat sea that is increased infinitely in extent, and a vessel at the shore which leaves the port in a straight line. It is certain that when the bottom of this vessel is viewed from the port through a lens or some other transparent body, the ray that ends at the bottom of this vessel will pass through a certain point of the lens, and the horizontal ray will pass through another point of the lens higher than the first. Now as the vessel goes further away, the point of intersection with the lens of the ray ending at the bottom of the vessel will continue to rise and will divide space infinitely between these two points. The further away the vessel goes, the more slowly it will rise, without ever ceasing to rise. Nor can it reach the point of the horizontal ray, because these two lines that intersect at the eye will never be parallel nor the same line. Thus this example provides at the same time proofs of the infinite divisibility of extension and of an infinite decrease in motion. ³¹

This argument was to turn up in a number of other places, notably in Kant’s Physical Monadology of 1756. Its precise geometric form is the following (see Fig. 2.4). Given two parallel lines CA and CB and suppose that each is extended to infinity. Draw AB perpendicular to CA and DB. A line drawn from C to a point E lying to the right of B will cut the lie AB at some point, and lines drawn from C to points F, G, H, … proceeding still further to the right will cut AB at points closer and closer to A. Since DB extends to infinity, this process may be continued indefinitely, generating points on AB that become ever closer to A, but never actually reach it. Thus AB is infinitely divisible .³²

../images/474107_1_En_2_Chapter/474107_1_En_2_Fig4_HTML.png — Fig. 2.4
Caption

Of Descartes ’ contemporaries, it was the philosopher and mathematician Pierre Gassendi (1592–1665) who mounted the strongest attack on the Cartesian vision of the world. Gassendi was chiefly responsible for the revival of the physical atomism of Democritus ’ and Epicurus ’ view that the physical world consists of indivisible corpuscles moving in empty space . Rejecting Descartes’ identification of matter and extension, Gassendi was enabled to accept that pure extension was infinitely divisible , and at the same time maintain that matter was not. In defending Epicurean atomism he denies that Epicurus claimed that every entity is reducible to points:

Let us now investigate what is usually objected to in Epicurus: it is really a wonder not only that there should have been some in antiquity who attacked Epicurus as if he had believed that the division of magnitude is terminated in certain mathematical points; but also that there have been learned men from more recent times who inveighed against him in whole tomes as if he had said that bodies were constituted from surfaces, surfaces from lines, lines from points, and accordingly bodies and indeed all things, from points, into which, accordingly bodies and all things were resolved. This is a wonder, I say, since if they had been willing to pay the least attention, they would have been able to observe that the indissectibles into which Epicurus held divisions to be terminated are not mathematical points, but the meagerest bodies; since, moreover, he not only gave them magnitude, when it is acknowledged that there is nothing of this kind in a point; but he also gave them incomprehensibly variable shapes, such as cannot be conceived in a point, which lacks magnitude and parts. ³³

Here is Gassendi on continuity of magnitude, in which he maintains that atoms are the only absolutely continuous entities:

… it will be evident that each body must be said to be continuous insofar as its parts are conjoined, cohering with, and unseparated from one another, and are such that, even though they are only contiguous with each other, their joints cannot be distinguished by any of the senses. That is to say, magnitude or as [the Schoolmen] call it, continuous quantity, differs from multiplicity, i.e., discrete quantity , in the fact that the parts of a continuous quantity can indeed be separated , but are not in fact separated, whereas the parts of a discrete quantity are actually or really separated. This is not to say that the parts of a multiplicity are not also contiguous with each other, a, for example, many stones in one pile; but that they do not mutually grip each other, bind together, and hold onto one another by their own angles or little hooks. … Thus in a word, all bodies that may be broken apart by the force of heat, or by something else, have parts which are only in mutual contact, and which separate when this bond is severed and their continuity is broken.

Thus it is that, if we are asked what is so continuous that it does not on any account consist of the contiguous , the only thing we can specify in reply is the Atom. And we should understand Democritus to have been talking about this when, according to Aristotle , he wrote: “And neither can one become two, nor two, one,” since, of course, one atom is not dissectible in such a way that two should emerge, nor are two penetrable by each other in such a way that they might coalesce into one. But this does not prevent every body that is not actually divided into parts from being called continuous, in accordance with common usage, and inasmuch as the senses cannot reach as far as atoms or their joints.

Aristotle, however, says that a continuum is “a thing whose parts are conjoined at a common boundary .” This is physically true, to the extent that it has no two assignable parts which are not conjoined at some intermediate part, either a sensible part—as in a magnitude of three feet, the outermost feet are conjoined by the middle one—or an insensible one—as in a magnitude of two feet, these two feet have an item lying between them that evades the senses … I … declare that it is impossible for any continuous thing to be dissected with such great subtlety that middle-sized conglomerates of innumerable atoms are not expelled from it. ³⁴ Of course, accepting with Aristotle that the common boundary is a mathematical individual (for he asserts that the parts of a line are conjoined by a point, the parts of a surface by a line, and the parts of a body by a surface), this insensible boundary cannot be a physical reality, insofar as there do not exist in the nature of things indissectible things of this kind, which are only imagined or supposed … ³⁵

Gassendi also upheld the Mutakallemim theory that, while motion appears continuous to the senses, it actually occurs in jerks, with alternating periods of movement and rest.

Infinitesimals and Indivisibles

The use of infinitesimals and indivisibles was widespread in seventeenth century mathematics. Grégoire de St.-Vincent (1584–1667), like Kepler , regarded figures as being made up of infinitely many infinitesimal elements of the same dimension as the figure, but, with Stevin , conceived of these elements as being obtained by continuing subdivision.³⁶ Gilles Personne de Roberval (1602–75) upheld the infinite divisibility of matter, and of every mathematical continuum.³⁷ His method of determining areas and volumes, which he termed the “method of infinities”, rested on the conception of figures being built up from small surface or volume elements, but treated as if they were indivisibles. It was Roberval who first, in 1634, determined the area under an arch of the cycloid. Evangelista Torricelli (1608–1647), while not wholly convinced of the logical soundness of the method of indivisibles, was nevertheless virtuosic in its application. The most striking use he made of the method was his discovery, in 1641, that the volume of an infinitely long solid, obtained by revolving a segment of the equilateral hyperbola about its asymptote, is finite.³⁸ André Tacquet (1612–60), who also employed indivisibles in his determinations of areas and volumes, did not regard the method as legitimate, maintaining that a geometrical magnitude is made up only of homogenea , as opposed to heterogenea .³⁹ Blaise Pascal (1623–1662) employed the intuition that addition to a figure of an indivisible of lower dimension had no effect on its size to justify the neglect of terms of lower degree in calculating curvilinear areas. Pascal’s “arithmetical” interpretation of indivisibles was to be a major influence on Leibniz , who “repeatedly states that he was led to the invention of the calculus by a study of the works of Pascal”.⁴⁰

John Wallis (1616–1703) arithmetized Cavalieri’s indivisible methods, using what amounts to limits of sums of integral powers of numbers. He went so far as to introduce the symbol “∞” for the infinitely many lines or parallelograms making up a surface.⁴¹ Unlike Tacquet , Wallis was unconcerned with the question of whether the indivisibles constituting a figure should be taken as homogenea or heterogenea . On the other hand, he insisted that a line, for example, is to be regarded as possessing sufficient thickness so as to enable it, by infinite multiplication, to acquire an altitude equal to that of the figure in which it is inscribed.

Thus, for example, to determine the area of a triangle with base b and altitude a, one writes ∞ for the total number of lines in the triangle (see Fig. 2.5). Taking the lengths of the lines to be in arithmetic progression, the total length of the lines is then ½∞b, that is, the sum of the extreme terms 0 and b multiplied by one half the number of terms. Since the altitude of each inscribed parallelogram is a/∞ = a. 1/∞, the triangle’s area is ½∞b × a/∞ = ½ab.

../images/474107_1_En_2_Chapter/474107_1_En_2_Fig5_HTML.png — Fig. 2.5
Caption

The concept of infinitesimal had arisen with problems of a geometric character and infinitesimals were originally conceived as belonging solely to the realm of continuous magnitude as opposed to that of discrete number. But from the algebra and analytic geometry of the 16th and 17th centuries there issued the concept of infinitesimal number . Wallis , for example, treats 1/∞ as such a number. However, the idea first appears in the work of Pierre de Fermat (1601–65) on the determination of maximum and minimum (extreme) values, published in 1638. Fermat had been struck by the observation, traceable to Pappus, that in a problem which in general has two solutions, an extreme value gives just a single solution.⁴² So, for example, in determining the maximum area of a rectangle of semiperimeter a, it is required to maximize the quantity A = x(a – x). In general, there are two values of x corresponding to each value of A, say x and x + E. In that case,

$\left(\ast \right)\kern5.24em x\left(a-x\right)=\left(x+E\right)\left(a-x-E\right),$

whence

$0= aE-2 xE-{E}^2$

so that, dividing by E and rearranging,

Now by Pappus’ observation, for a maximum value of A, x and x + E must coincide, so that E = 0. It then follows that x = a/2.

There is a glaring logical flaw in this argument (of which Fermat seems to have been aware), namely, that E is initially assumed to differ from 0, and is then finally set equal to 0. Simultaneously equal and unequal to zero: a strange sort of “number” indeed! In answer to criticisms, Fermat later modified his method by observing that at a maximum point the two values of A set equal in (∗) above are not actually equal but “should be” equal.⁴³ He accordingly introduces the relation of “adequalitas” or “near-equality” between the two values, a relation which, on setting E = 0, coincides with genuine equality.⁴⁴ This amounts to treating E as an infinitesimal number , a quantity “nearly equal”, but not necessarily coinciding with, zero. This move does not, of course, do away with the logical difficulties; what it does seem to indicate is that Fermat thought of infinitesimals as formal, algebraic conceptions rather than as variable quantities.

Fermat’s treatment of maxima and minima contains the germ of the fertile technique of “infinitesimal variation ”, that is, the investigation of the behaviour of a function by subjecting its variables to small changes. Fermat applied this method in determining tangents to curves and centres of gravity.

Another of Fermat’s major contributions to infinitesimal analysis is to be found in his work on the rectification of curves. While it had been long known that a curvilinear figure could be equal in area to a rectilinear one (Archimedes , for instance, had shown that the area ofa parabolic segment is $\frac{4}{3}$ times thevarea of the triangle with the same base and vertex), it was by no means clear whether a curved line could be exactly equal in length to a straight one. Aristotle had held a negative view⁴⁵ on the matter, a view which Fermat and most of his contemporaries shared. Nevertheless, shortly before 1660 a number of mathematicians, including Christopher Wren , Heinrich van Heuraet, and John Wallis , produced such rectifications. Fermat’s response was to carry out a rectification of the semicubical parabola ky ² = x ³ by reducing the problem to the quadrature of a parabola.⁴⁶

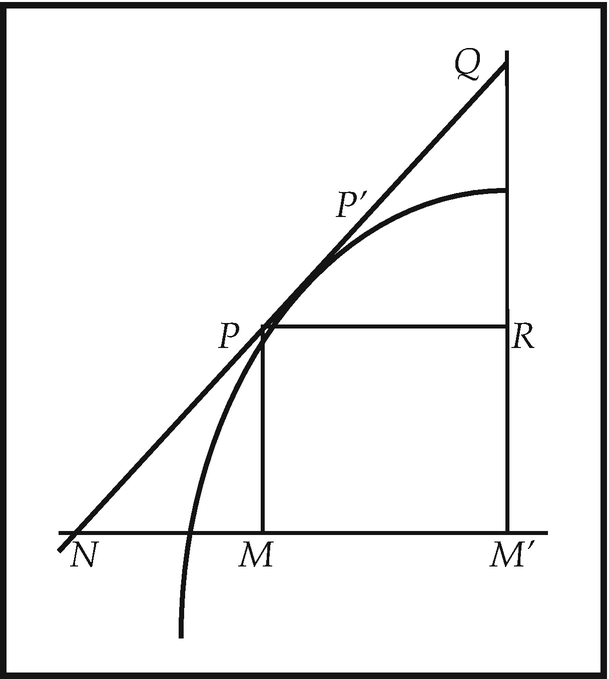
Barrow and the Differential Triangle

It has been claimed that Isaac Barrow (1630–77) was “the first inventor of the Infinitesimal Calculus ”.⁴⁷ While this may be an exaggeration, there is no disputing the importance of his role in its emergence. Barrow was one of the first mathematicians to grasp the reciprocal relation between the problem of quadrature and that of finding tangents to curves—in modern parlance, between integration and differentiation. Indeed, in his Lectiones Geometricae of 1670, Barrow observes, in essence, that if the quadrature of a curve y = f(x) is known, with the area up to x given by F(x), then the subtangent to the curve y = F(x) is measured by the ratio of its ordinate to the ordinate of the original curve.⁴⁸

Barrow’s approach, in 1669, to the problem of finding tangents to curves⁴⁹ is particularly instructive in its use of the characteristic, differential or infinitesimal triangle , a device which played an important role in the early development of the calculus. Starting with the triangle PRQ generated by the increment PR (Fig. 2.6), the fact that this triangle is similar to the triangle PMN enables one to claim that the slope QR/PR of the tangent is equal to PM/MN. Now, Barrow asserts, when the arc PP’ is sufficiently small (which follows upon taking the increment PR sufficiently small, see Fig. 2.7) we may safely identify it with the segment PQ of the tangent at P. (Here Barrow is evidently thinking of the curve as an infinilateral polygon .) The triangle PRP’, in which PP’ is regarded both as an arc of the curve and as part of the tangent, is the characteristic triangle . The characteristic triangle associated with an infinitesimal abscissal increment at a point on a curve thus represents the additional increment in area under the curve over what would have been generated had the curve been straight from that point on.⁵⁰

../images/474107_1_En_2_Chapter/474107_1_En_2_Fig6_HTML.png — Fig. 2.6
Caption

../images/474107_1_En_2_Chapter/474107_1_En_2_Fig7_HTML.png — Fig. 2.7
Caption

Barrow’s explicit determination of tangents proceeds along lines similar to that followed by Fermat .⁵¹ Starting with the equation of a curve, say y ² = px, he replaces x by x + e and y by y + a, obtaining

${y}^2+2 ay+{a}^2= px+ pe.$

Form this y ² = px is subtracted, yielding

$2 ay+{a}^2= pe.$

Then, in a typical move, he discards powers of a and e above the first, which amounts to replacing the first figure above by the second. It then follows that

$\frac{a}{e}=\frac{p}{2y}.$

But a/e = PM/NM, so that

$\frac{PM}{NM}=\frac{p}{2y}.$

Since PM is y, the position of N is determined.

Barrow regarded the conflict between divisionism and atomism as a live issue, as may be inferred from a remark in his Lectiones Mathematicae of 1683:

I am not unaware, for indeed nobody is unaware, that this doctrine of the perpetual divisibility of quantity is admitted by some only reluctantly, and simply rejected by others, and that the controversy over composition of magnitudes (whether it be from indivisibles, or from homogeneous parts) is everywhere conducted with great obstinacy. ⁵²

As presented in the 1683 Lectiones, Barrow’s case against geometric atomism pivots on the fact that it is in contradiction with most of the propositions of Euclidean geometry:

…there is the necessary agreement of all mathematicians [to the thesis of infinite divisibility ]; for although they hardly ever suppose it openly, they often assume it covertly, and if it were not true, many of their demonstrations would fall to the ground. ⁵³

As can be seen from the 1670 Lectiones, Barrow conceived of continuous magnitudes as being generated by motions, and so necessarily dependent on time:

Every magnitude can be either supposed to be produced, or in reality can be produced, in innumerable ways. The most important is that of “local movements”. In motion, the matters chiefly to be considered are the mode of motion and the quantity of the motive force. Since quantity of motion cannot be discussed without Time, it is necessary first to discuss Time. Time denotes not an actual existence, but a certain capacity or possibility for a continuity of existence; just as space denotes a capacity for intervening length. Time does not imply motion, as far as its absolute and intrinsic nature is concerned; not any more than it implies rest; whether things move or are still, whether we sleep or wake, Time pursues the even tenor of its way. Time implies motion to be measurable; without motion we could not perceive the passage of Time… .

Time has many analogies with a line, either straight or circular, and therefore may be conveniently represented by it; for time has length alone, is similar in all its parts, and can be looked upon as constituted from a simple addition of successive instants or as from a continuous flow of one instant; either a straight or a circular line has length alone, is similar in all its parts, and can be looked upon as being made up of an infinite number of points or as the trace of a moving point. ⁵⁴

Barrow followed Cavalieri in regarding figures as being composed of indivisibles, and, like Wallis , was indifferent to the question of whether the indivisibles constituting a figure should be taken as homogenea or heterogenea :

To every instant of time, or indefinitely small particle of time, (I say instant or indefinite particle, for it makes no difference whether we suppose a line to be composed of points or indefinitely small linelets; and so in the same manner, whether we suppose time to be made up of instants or indefinitely minute timelets); to every instant of time, I say, there corresponds some degree of velocity, which the moving body is supposed to possess at the instant; to this degree of velocity there corresponds some length of space described.. Hence, if through all the points of a line representing time are drawn.. parallel lines, the plane surface that results as the aggregate of the parallel straight lines, when each represents the degree of velocity corresponding to the point through which it is drawn, exactly corresponds to the aggregate of the degrees of velocity, and thus most conveniently can be adapted to represent the space traversed also. Indeed, this surface, for the sake of brevity, will be called the aggregate of the velocity or the representative of the space. It may be contended that rightly to represent each separate degree of velocity retained during any timelet, a very narrow rectangle ought to be substituted for the right line and applied to the given interval of time. Quite so, but it comes to the same thing whichever way you take it; but as our method seems to be simpler and clearer, we will in future adhere to it. ⁵⁵

Barrow’s conceptions formed the starting point for the groundbreaking work on the infinitesimal calculus of his illustrious pupil Isaac Newton (1642–1727).

Newton

Newton’s meditations on the subject during the plague year 1665–66 issued in the invention of what he called the “Calculus of Fluxions ”, the principles and methods of which were presented in three tracts published many years after they were written⁵⁶: De analysi per aequationes numero terminorum infinitas; Methodus fluxionum et serierum infinitarum; and De quadratura curvarum. Newton’s approach to the calculus rests, even more firmly than did Barrow’s , on the conception of continua as being generated by motion. In the introductory paragraph to De quadratura curvarum he adopts the kinematic view explicitly, contrasting it with the conception of magnitudes as being composed of infinitesimal parts:

I don’t here consider Mathematical Quantities as composed of Parts extremely small, but as generated by a continual motion. Lines are described, and by describing are generated, not by any apposition of Parts, but by a continual motion of Points. Surfaces are generated by the motion of Lines, Solids by the motion of Surfaces, Angles by the rotation of their Legs, Time by a continual flux, and so in the rest. ⁵⁷

Newton’s exploitation of the kinematic conception went much deeper than had Barrow’s. In De Analysi, for example, Newton introduces a notation for the “momentary increment” (moment)—evidently meant to represent a moment or instant of time—of the abscissa or the area of a curve, with the abscissa itself representing time. This “moment”—effectively the same as the infinitesimal quantity Fermat had denoted by E and Barrow by e—Newton denotes by o in the case of the abscissa, and by ov in the case of the area. From the fact that Newton uses the letter v for the ordinate, it may be inferred that Newton is thinking of the curve as being a graph of velocity against time. By considering the moving line, or ordinate, as the moment of the area Newton established the generality of and reciprocal relationship between the operations of differentiation and integration, a fact that Barrow had grasped but had not put to systematic use. Before Newton, quadrature or integration had rested ultimately “on some process through which elemental triangles or rectangles were added together”,⁵⁸ that is, on the method of indivisibles. Newton’s explicit treatment of integration as inverse differentiation was the key to the integral calculus.

In the Methodus fluxionum Newton makes explicit his conception of variable quantities as generated by motion and introduces his characteristic notation. He calls the quantity generated by a motion a fluent , and its rate of generation a fluxion. The fluxion of a fluent x is denoted by x ^•, and its moment, or “infinitely small increment accruing in an infinitely short time o ”, by x ^• o . The problem of determining a tangent to a curve is transformed into the problem of finding the relationship between the fluxions x ^• and y ^• when presented with an equation representing the relationship between the fluents x and y. (A quadrature is the inverse problem, that of determining the fluents when the fluxions are given.) Thus, for example, in the case of the fluent y = x ⁿ , Newton first forms y + y ^• o = (x + x ^• o)ⁿ , expands the right-hand side using the binomial theorem, subtracts y = x ⁿ, divides through by o, neglects all terms still containing o, and so obtains y ^· = nx ^n-1 x ^•.

Newton later became discontented with the undeniable presence of infinitesimals in his calculus and dissatisfied with the doubtful procedure of “neglecting” them. In the preface to the De quadratura curvarum he remarks that there is no necessity to introduce into the method of fluxions any argument about infinitely small quantities. In their place he proposes to employ what he calls the method of prime and ultimate ratio. This method, in many respects an anticipation of the limit concept, receives a number of allusions in Newton’s celebrated Principia mathematica philosophiae naturalis of 1687. For example, the first section of Book One is entitled “The method of first and last quantities, by the help of which we demonstrate the propositions that follow”; its first Lemma reads:

Quantities, and the ratios of quantities, which in any finite time converge continually to equality, and before the end of that time approach nearer to each other than by any given difference, become ultimately equal ⁵⁹ ;

its third:

…the ultimate ratio of the arc, chord, and tangent, any one to any other, is the ratio of equality. ⁶⁰

Later Newton compares the method of indivisibles with his procedure and attempts to meet any objections to its use.

For demonstrations are shorter by the method of indivisibles; but because the hypothesis of indivisibles seems somewhat harsh, and therefore that method is reckoned less geometrical, I chose rather to reduce the demonstrations of the following Propositions to the first and last sums and ratios of nascent and evanescent quantities, that is, to the limits of those sums and ratios, and so to premise, as short as I could, the demonstrations of those limits. For hereby the same thing is performed as by the method of indivisibles; and now those principles being demonstrated, we may use them with greater safety. Therefore, if hereafter I should happen to consider quantities as made up of particles, or should use little curved lines for right ones, I would not be understood to mean indivisibles, but evanescent divisible quantities; not the sums and ratios of determinate parts, but always the limits of sums and ratios…

Perhaps it may be objected, that there is no ultimate proportion of evanescent quantities; because the proportion, before the quantities have vanished, is not the ultimate, and when they are vanished, is none. But by the same argument it may be alleged that a body arriving at a certain place, and there stopping, has no ultimate velocity; because the velocity, before the body comes to the place, is not its ultimate velocity; when it has arrived, there is none. But the answer is easy; for by the ultimate velocity is meant that with which the body is moved, neither before it arrives at its last place and the motion ceases, nor after, but at the very instant it arrives; that is, that velocity with which the body arrives at its last place, and with which the motion ceases. And in like manner, the by the ultimate ratio of evanescent quantities is to be understood the ratio of the quantities not before they vanish, nor afterwards, but with which they vanish. In like manner the first ratio of nascent quantities is that with which they begin to be.…

It may also be objected, that if the ultimate ratios of evanescent quantities are given, their ultimate magnitudes will also be given; and so all quantities will consist of indivisibles, which is contrary to what Euclid has demonstrated concerning incommensurables, in the tenth Book of his Elements. But this objection is founded on a false supposition. For those ultimate ratios with which quantities vanish are not truly the ratios of ultimate quantities, but limits towards which the ratios of quantities decreasing without limit do always converge; and to which they approach nearer than by any given difference, but never go beyond, nor in effect attain to, till the quantities are diminished in infinitum. … Therefore if in what follows, for the sake of being more easily understood, I should happen to mention quantities as least, or evanescent, or ultimate, you are not to suppose that quantities of any determinate magnitude are meant, but such as are conceived to be always diminished without end. ⁶¹

Here Newton presents, in kinematic dress, the idea of a continuously variable quantity approaching a limit.

Newton thus developed three approaches for his calculus, all of which he regarded as leading to equivalent results, but which varied in their degree of rigour.⁶² The first employed infinitesimal quantities which, while not finite, are at the same time not exactly zero. Finding that these eluded precise formulation, Newton focussed instead on their ratio, which is in general a finite number. If this ratio is known, the infinitesimal quantities forming it may be replaced by any suitable finite magnitudes—such as velocities or fluxions —having the same ratio. This is the method of fluxions. Recognizing that this method itself required a foundation, Newton supplied it with one in the form of the doctrine of prime and ultimate ratios, which is, as we have observed, a kinematic form of the theory of limits.

While Newton the mathematician was unquestionably a synechist, his view of the ultimate constitution of matter inclined towards atomism . At the beginning of Book III of the Principia he observes:

…that the divided but contiguous particles of bodies may be separated from one another, is a matter of observation; and, in the particles that remain undivided, our minds are able to distinguish yet lesser parts, as is mathematically demonstrated. But whether the parts so distinguished, and yet not divided, may, by the powers of Nature, be actually divided and separated from one another, we cannot certainly determine. Yet, had we the proof of but one experiment that any undivided particle, in breaking a hard and solid body, suffered a division, we might conclude by virtue of this rule that the undivided as well as the divided particles may be divided and actually separated to infinity. ⁶³

Newton’s point here is that, while every particle of matter is divisible in theory, only observable particles are known to be physically divisible. Short of an experimentum crucis demonstrating the actual divisibility of all material particles, whether observable or not, the existence of physically indivisible material atoms remains a possibility. Newton defended material atomism with greater vigour in his Opticks, as can be seen from the following celebrated passage:

It seems probable to me, that God in the Beginning form’d Matter in solid, massy, hard, impenetrable, moveable Particles, of such Sizes and Figures, and with such other Properties, and in such proportion to Space, as most conduced to the End for which He formed them. ⁶⁴

These particles, or atoms, are, according to Newton, perfectly solid plena of homogeneous matter. Each is inseparable in itself, but a number may come into contact to form compound bodies. In doing so, however, they

do not conjoin into solidity, but are in mutual contact only at some mathematical point, the remaining spaces being left in each case between them vacant. ⁶⁵

As Andrew Pyle observes,⁶⁶ in replacing Epicurean minimal parts by mathematical points Newton avoids the difficulty arising in the Epicurean theory from the conception of atoms as being composed of a finite number of minimal parts in contact. For if two minimal parts can be physically separated after coming into contact, so can any finite number, leading to the conclusion that the atom is physically fissionable. Newton’s account of the contact of atoms does not lead to this conclusion, because an atom contains, not a finite number of mathematical points (as opposed to minimal parts), but an infinite number; “splitting the atom” would then require the separation of an infinite number of such points, and hence the application of an infinite force.

Leibniz

The philosopher-mathematician G. W. F. Leibniz (1646–1716) was greatly preoccupied with the problem of the composition of the continuum—the “labyrinth of the continuum”, as he called it.⁶⁷ Indeed, we have it on his own testimony that his philosophical system— monadism —grew from his struggle with the problem of just how, or whether, a continuum can be built from indivisible elements. Leibniz asked himself: if we grant that each real entity is either a simple unity or a multiplicity, and that a multiplicity is necessarily an aggregation of unities, then under what head should a geometric continuum such as a line be classified? Now a line is extended and Leibniz held that extension is a form of repetition:

All repetition…is either discrete, as in numbered things are discriminated; or continuous, where the parts are indeterminate and can be assumed in infinite ways. ⁶⁸

Since a line is divisible into parts, it cannot be a (true) unity. It is then a multiplicity, and accordingly an aggregation of unities. But of what sort of unities? Seemingly, the only candidates for geometric unities are points, but points are no more than extremities of the extended, and in any case, as Leibniz knew, solid arguments going back to Aristotle establish that no continuum can be constituted from points. It follows that a continuum is neither a unity nor an aggregation of unities. Leibniz concluded that continua are not real entities at all; as “wholes preceding their parts” they have instead a purely ideal character. In this way he freed the continuum from the requirement that, as something intelligible, it must itself be simple or a compound of simples. Accordingly,

…continuous quantity is something ideal, which belongs to possibles, and to actuals considered as possibles. For the continuum involves indeterminate parts, while in actuals there is nothing indefinite—indeed in them all divisions which are possible are actual…But the science of continua, i.e. of possibles, contains eternal truths, which are never violated by actual phenomena, since the difference is always less than any assignable given difference. ⁶⁹

From the fact that a mathematical solid cannot be resolved into primal elements it follows immediately that it is nothing real but merely an ideal construct designating only a possibility of parts. ⁷⁰

Properly speaking, the number ½ in the abstract is a mere ratio, by no means formed by the composition of other fractions…And we may say as much of the abstract line, composition being only in concretes, or masses of which these abstract lines mark the relations. And it is thus also that mathematical points occur, which are also only modalities, i.e. extremities. And as everything is indefinite in the abstract line, we take notice of it of everything possible, as in the fractions of a number, without concerning ourselves concerning the divisions actually made, which designate these points in a different way. But in substantial actual things, the whole is a result or assemblage of simple substances, or of a multiplicity of real units. And it is the confusion of the ideal and the actual which has embroiled everything and produced the labyrinth concerning the composition of the continuum. Those who compose a line of points have sought first elements in ideal things or relations, otherwise than was proper; and those who have found that relations such as number, and space …cannot be formed of an assemblage of points, have been mistaken in denying, for the most part, the first elements of substantial realities, as if they had no primitive units, or as if there were no simple substances. ⁷¹

Leibniz held that space and time, as continua, are ideal, and anything real, in particular matter, is discrete, compounded of simple unit substances he termed monads :

Matter is not continuous but discrete, and actually infinitely divided, though no assignable part of space is without matter. But space, like time, is something not substantial, but ideal, and consists in possibilities, or in an order of coexistents that is in some way possible. And thus there are no divisions in it but such as are made by the mind, and the part is posterior to the whole. In real things, on the contrary, units are prior to the multitude, and multitudes only exist through units. (The same holds of changes, which are not really continuous.) ⁷²

Space, just like time…is something indefinite, like every continuum whose parts are not actual, but can be taken arbitrarily, like the parts of unity, or fractions… Space is something continuous but ideal, mass is discrete, namely an actual multitude, or being by aggregation, but composed of an infinite number of units. In actuals, single terms are prior to aggregates, in ideals the whole is prior to the part. The neglect of this consideration has brought forth the labyrinth of the continuum. ⁷³

Within the ideal or continuum the whole precedes the parts… The parts are here only potential; among the real [i.e. substantial] things, however, the simple precedes the aggregates, and the parts are given actually and prior to the whole. These considerations dispel the difficulties regarding the continuum—difficulties which arise only when the continuum is looked upon as something real, which possesses real parts before any division as we may devise, and when matter is regarded as a substance.

In actuals there is nothing but discrete quantity, namely the multitude of monads or simple substances. ⁷⁴

Leibniz explains how he came to develop his doctrine:

At first, when I had freed myself from the yoke of Aristotle , I took to the void and the atoms, for that is the view which best satisfies the imagination. But having got over this, I perceived, after much meditation, that it is impossible to find the principles of a real unity in matter alone, or in that which is only passive, since it is nothing but a collection or aggregation of parts ad infinitum. Now a multiplicity can derive its reality only from true unities , which come from elsewhere and are quite other than mathematical points, which are only extremities of the extended… of which it is certain that the continuum cannot be composed. Therefore to find these real unities I was compelled to have recourse to a formal atom, since a material being cannot be both material and perfectly indivisible or endowed with a true unity. It was necessary, hence, to recall and, so to speak, rehabilitate the substantial forms so decried today, but in a way which would make them intelligible and which would separate the use we should make of them from the abuse that has been made of them. I thence found that their nature consists in force, and that from that there ensues something analogous to feeling and appetite; and that accordingly they must be conceived in imitation of the idea we have of Souls. ⁷⁵

That Leibniz had come to abandon atomism sometime before 1675 is attested to by the following passage written at that time, in which he repudiates the existence of minimal parts of continua:

A minimum time (minimum space ) is part of a greater time (space) between whose boundaries it lies—from the notion that we have of whole and part. Therefore a minimum time is a minimum part of time, and a minimum space is a minimum part of space. There is no such thing as a minimum part of space. Because otherwise there would be as many minima in the diagonal as the in the side, and thus the diagonal would equal the side, since two things all of whose parts are equal, are themselves equal. In the same way it is demonstrated that there is no such thing as a minimum of time. If a minimum is a minimum of anything, then it will be a minimum of those things that are in space, or rather of the parts of space, seeing as you distinguish them from bodies. Nor can we speak otherwise about the matter. If, then, we suppose a minimum, both a moment and time will entail a contradiction. Everything greater is composed out of something smaller. Therefore every minimum is part of the greater thing within whose boundaries it lies.

If a continuum is something other than the sum of supposed minima (if there are minima in it), it follows that there is a part that is left over when the sum of the minima has been taken away; therefore this part is greater than a minimum, since it is neither smaller nor equal, therefore there are also minima in it. But this is absurd, since we have already removed all the minima. Therefore if there are minimum parts in the continuum, it follows that the continuum is composed of them. But it is absurd for the continuum to be composed out of minima, as I have demonstrated; therefore it is also absurd for there to be minima in the continuum, or for minima to be parts of the continuum. To be in something (i.e. to be within its boundaries ) and to something which cannot be understood without something else, is to be a part. Therefore there is no such thing [ as a minimum in a continuum]. Hence if there are instants in time, there will be nothing but instants, and time will be but the sum of instants. ⁷⁶

Yet in Leibniz’s philosophy the concept of point, or indivisible, plays a key role. Indeed, despite having thrown off the Aristotelian yoke, Leibniz continued to adhere to the Aristotelian doctrine that mathematical points are extremities or positions and that they can never, by themselves, constitute a continuum. Thus:

A point is not a certain part of matter, nor would an infinite number of points make an extension. ⁷⁷

…The continuum is infinitely divisible . And this appears in the straight line, from the mere fact that its part is similar to the whole. Thus when the whole can be divided, so can the part, and similarly any part of the part. Points are not part of the continuum, but extremities, and there is no more a smallest part of a line than a smallest fraction of unity. ⁷⁸

As to indivisibles, while they are understood as the simple extremities of time or of line, they cannot be conceived as containing new extremities of either actual or potential parts. Whence, points are neither big nor small, and no jump is necessary to pass through them. However, the continuous, though it everywhere has such indivisibles, is definitely not composed of them. ⁷⁹

Extremities of a line and units of matter do not coincide. Three continuous points in the same straight line cannot be conceived. But two are conceivable: the extremity of one straight line and the extremity of another, out of which one whole is formed. As, in time, are the two instants, the last of life and the first of death. ⁸⁰

As Russell observes,⁸¹ Leibniz actually distinguished three kinds of point or indivisible: metaphysical points, or monads , from which actual entities such as bodies are compounded⁸²; mathematical points, or positions in space ; and physical points, which Russell quite plausibly identifies with “an infinitesimal extension of the kind used in the Infinitesimal Calculus.”⁸³ Thus:

Atoms of matter are contrary to reason…only atoms of substance, i.e. unities which are real and absolutely destitute of parts, are sources of actions and the absolute first principles of the composition of things and, as it were, the last elements of the analysis of substances. They might be called metaphysical points; they possess a certain vitality and a kind of perception, and mathematical points are their points of view to express the universe. But when corporeal substances are compressed, all their organs form only a physical point to our sight. Thus physical points are only indivisible in appearance; mathematical points are exact, but they are merely modalities; only metaphysical points [i.e., monads] …are exact and real, and without them there would be nothing real, for without true unities there would be no multiplicity. ⁸⁴

Like William of Ockham , Leibniz held that density of point-distribution was sufficient to ensure continuity :

There is continuous extension whenever points are assumed to be so situated that there are no two between which there is not an intermediate point. ⁸⁵

And like Cusanus , he accepted the existence of the actual infinite:

I am so much for the actual infinite that instead of admitting that nature abhors it, as is commonly said, I hold that it affects nature everywhere in order to indicate the perfections of its Author. So I believe that every part of matter is, I do not say divisible, but actually divided, and consequently the smallest particle should be considered as a world full of an infinity of creatures… ⁸⁶

Among the best known of Leibniz’s doctrines is the Principle or Law of Continuity . In a somewhat nebulous form this principle had been employed on occasion by a number of Leibniz’s predecessors, including Cusanus and Kepler , but it was Leibniz who gave the principle its first clear formulation. In a letter to Bayle of 1687, Leibniz stated the principle as follows:

In any supposed transition, ending in any terminus, it is permissible to institute a general reasoning in which the final terminus may be included. ⁸⁷

This would seem to indicate that Leibniz considered “transitions” of any kind as continuous. Certainly he held this to be the case in geometry and for natural processes, where it appears as the principle Natura non facit saltum (“Nature makes no jump”). It is the Law of Continuity that allows geometry and the evolving methods of the infinitesimal calculus to be applicable in physics:

You ask me for some elucidation of my Principle of Continuity . I certainly think that this principle is a general one and holds good not only in Geometry but also in Physics. Since geometry is but the science of the continuous, it is not surprising that this law is observed everywhere in it, for Geometry by its very nature cannot admit any break in its subject matter. In truth we know that everything in that science is interconnected and that no single instance can be adduced of any property suddenly vanishing or arising without the possibility of our determining the intermediate transition, the points of inflection and singular points, with which to render the change explicable, so that an algebraic equation which represents one state exactly virtually represents all the other states which may properly occur in the same subject ⁸⁸

The Principle of Continuity also furnished the chief grounds for Leibniz’s rejection of material atomism :

My axiom that nature never acts by a leap has a great use in Physics. It destroys atoms, small lapses of motion, globules of the second element, and other similar chimeras…You are right in saying that all magnitudes may be subdivided. There is none so small in which we cannot conceive an inexhaustible infinity of subdivisions. But I see no harm in that or any necessity to exhaust them. A space infinitely divisible is traversed in a time also infinitely divisible. I conceive no physical indivisibles short of a miracle, and I believe nature can reduce bodies to the smallness Geometry can consider. ⁸⁹

Matter, according to my hypothesis, would be divisible everywhere and more or less easily with a variation which would be insensible in passing from pone place to another neighbouring place; whereas, according to the atoms, we make a leap from one extreme to another, and from a perfect incohesion, which is in the place of contact, we pass to an infinite hardness in all other places. And these leaps are without example in nature. ⁹⁰

The Principle of Continuity also played an important underlying role in Leibniz’s mathematical work, especially in his development of the infinitesimal calculus.⁹¹ Leibniz’s essays Nova Methodus of 1684 and De Geometri Recondita of 1686 may be said to represent the official births of the differential and integral calculi, respectively. Characteristically, Leibniz’s approach to the calculus has combinatorial roots, traceable to his early work on derived sequences of numbers. Let us attempt to describe, in modern terms, how he arrived at his conceptions.

Let P = {(x ₀, y ₀), (x ₁, y ₁), …(x _n, y _n)}be a finite sequence of pairs of (real) numbers with x ₀ < x ₁ < … < x _n. (See Fig. 2.8.) For each i = 0, …, n – 1 write dx _i = x _i + 1 – x _i, dy _i = y _i + 1 – y _i. Then the quantity

${\mathrm{D}}_iP=\frac{\mathrm{d}{y}_i}{\mathrm{d}{x}_i}$

represents the slope of the line passing through the points in the plane with coordinates (x _j, y _j) and (x _j + 1, y _j + 1).Also for each j = 0, …, n – 1, the quantity

${\int}^jP=\sum \limits_{i-0}^j{y}_i\mathrm{d}{x}_i$

represents the sum of the areas of the rectangles R ₀, R ₁, …, R _j . Now define ∫P, the integral of P by

$\int P=\left\{\left({x}_0,{\int}^0P\right),\dots \left({x}_{n-1},{\int}^{n-1}P\right)\right\},$

and DP, the derivative or differential of P by

$\mathrm{D}P=\Big\{\left({x}_0,{\mathrm{D}}_0P\right),\dots, \left\{\left({x}_{n-1},{\mathrm{D}}_{n-1}P\right)\right\}.$

An easy calculation then shows that, for each j = 0, …, n – 1,

${\mathrm{D}}_j\int P={y}_j\kern1.00em {\int}^j\mathrm{D}P={y}_j-{y}_0.$

The first of these means that

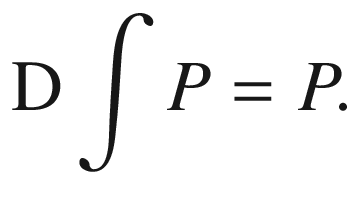
$\mathrm{D}\int P=P.$

(2.1)

Provided we set the “constant of integration” y ₀ to 0, the second means that

$\int \mathrm{D}P=P.$

(2.2)

That is, for finite sequences, differentiation and integration are mutually inverse operations.

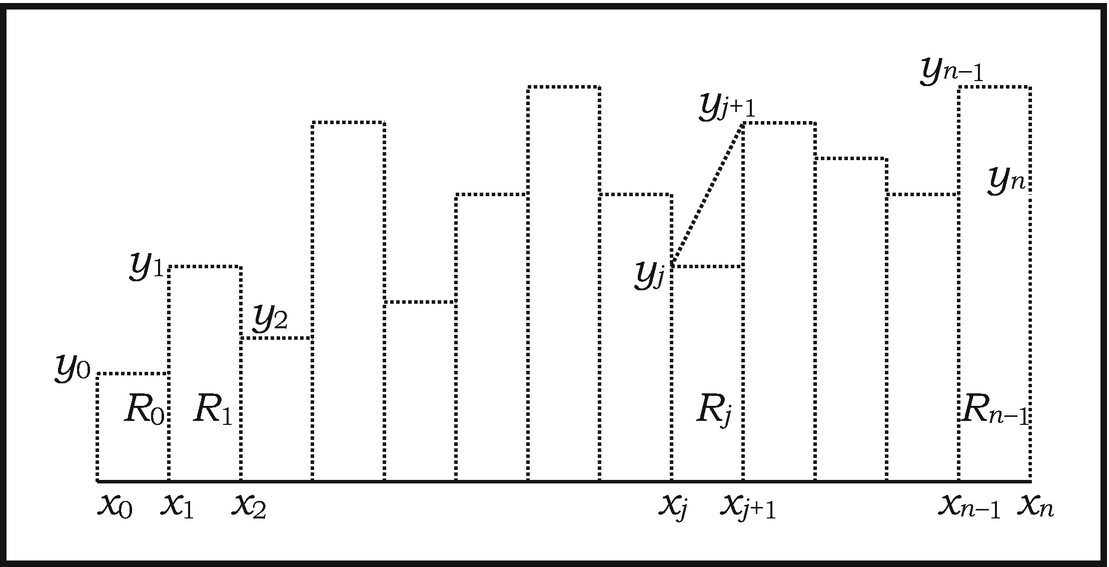
../images/474107_1_En_2_Chapter/474107_1_En_2_Fig8_HTML.png — Fig. 2.8
Caption

Now consider P to be a finite set of points in the plane, and let C be a continuous curve passing through the points of P (Fig. 2.9). Then D_j P is a rough approximation to the slope of the tangent to C at the point (x _j , y _j) and ∫^n − 1 P is a rough approximation to the area under C. Clearly, these approximations improve as the number of points increases and the distance between successive points decreases. Leibniz saw that if the number n of points was permitted to increase to infinity and the differences dx _i and dy _i to become infinitesimal the corresponding “approximations” to tangent slope and area of C could be taken as exact. He wrote dx and dy for such infinitesimal differences, or differentials, and $\frac{\mathrm{d}y}{\mathrm{d}x}$ for the ratio of the two, which he then took to represent the slope of the curve at the corresponding point. This suggestive, if highly formal procedure led Leibniz to evolve rules for calculating with differentials, which was achieved by appropriate modification of the rules of calculation for ordinary numbers. Determining the integral for the curve, however, raised the thorny problem of attempting to sum infinitely many infinitesimal quantities. Leibniz’s way out of this difficulty was to appeal to his Principle of Continuity , which suggested that the Eqs. (2.1) and (2.2) holding in the discrete case would also be preserved in the transition to continuity, with the result that “integration” and “differentiation” remain mutually inverse operations. As a result, it became unnecessary to provide a satisfactory account of the integral : as long as one had some way of calculating derivatives, of “differentiating”, integrals could be determined by mere inversion of the procedure of differentiation.⁹²

../images/474107_1_En_2_Chapter/474107_1_En_2_Fig9_HTML.png — Fig. 2.9
Caption

Although the use of infinitesimals was instrumental in Leibniz’s approach to the calculus, in 1684 he introduced the concept of differential without mentioning infinitely small quantities, almost certainly in order to avoid foundational difficulties. He states without proof the following rules of differentiation:

If a is constant, then da = 0 and d(ax) = adx

$d\left(x+y-z\right)= dx+ dy- dz$

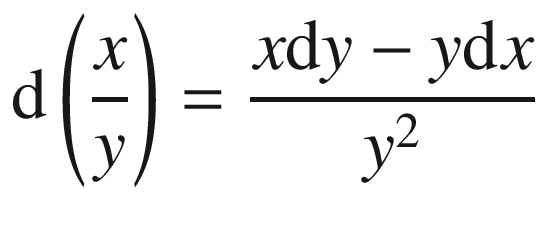
$\mathrm{d}\left(\frac{x}{y}\right)=\frac{x\mathrm{d}y-y\mathrm{d}x}{y^2}$

$d\left({x}^p\right)={px}^{p-1} dx, also\ for\ fractional\ p.$

But behind the formal beauty of these rules—an early manifestation of what was later to flower into differential algebra—the presence of infinitesimals makes itself felt, since Leibniz’s definition of tangent employs both infinitely small distances and the conception of a curve as an infinilateral polygon :

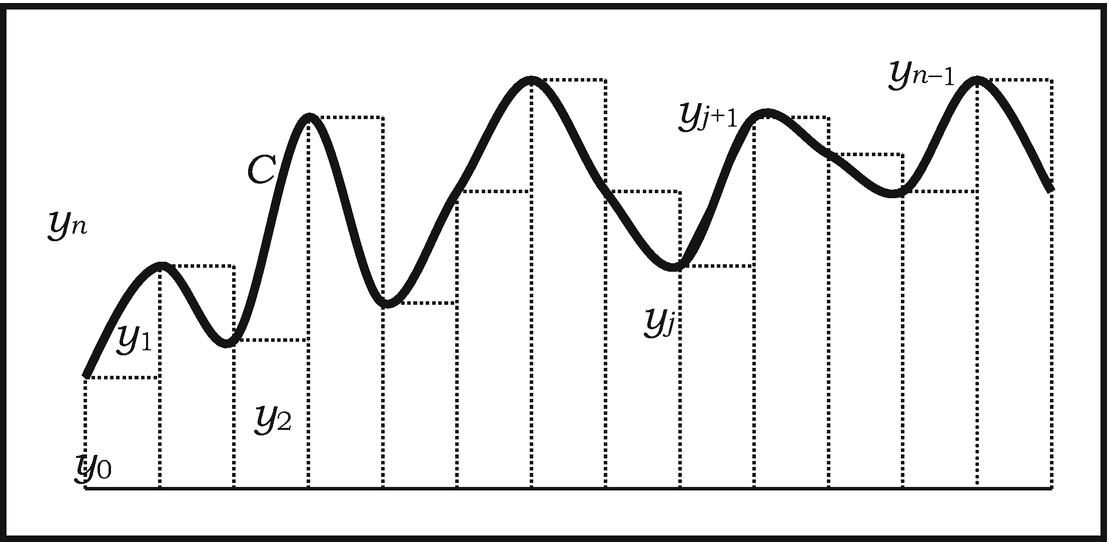
We have to keep in mind that to find a tangent means to draw a line that connects two points of a curve at an infinitely small distance, or the continued side of a polygon with an infinite number of angles, which for us takes the place of a curve. ⁹³

In thinking of a curve as an infinilateral polygon (as in Fig. 2.9), the abscissae x ₀, x ₁, … and the ordinates y ₀, y ₁, are to be regarded as lying infinitesimally close to one another; the symbols x, y are then conceived as variables ranging over sequences of such abscissae or ordinates. Leibniz also conceived the differentials dx, dy as variables ranging over differences. This enabled him to take the important step of regarding the symbol d as an operator acting on variables, so paving the way for the iterated application of d, leading to the higher differentials ddx = d² x, d³ x = dd² x, and in general d^n + 1 x = ddⁿ x. ⁹⁴

Leibniz supposed that the first-order differentials dx, dy, … were incomparably smaller than, or infinitesimal with respect to, the finite quantities x, y, … ., and, in general that an analogous relation obtained between the (n + 1)^th –order differentials d^n + 1 x and the n ^th –order differentials dⁿ x. He also assumed that the n ^th power (dx)ⁿ of a first-order differential was of the same order of magnitude as an n ^th –order differential dⁿ x, in the sense that the quotient dⁿ x/(dx)ⁿ is a finite quantity .

For Leibniz the incomparable smallness of infinitesimals derived from their failure to satisfy Archimedes ’ principle; and quantities differing only by an infinitesimal were to be considered equal:

…only those homogeneous quantities are comparable, of which one can become larger than the other if multiplied by a number, that is, a finite number. I assert that entities, whose difference is not such a quantity, are equal…This is precisely what is meant by saying that the difference is smaller than any given quantity. ⁹⁵

But while infinitesimals were conceived by Leibniz to be incomparably smaller than ordinary numbers, the Law of Continuity ensured that they were governed by the same laws as the latter:

Meanwhile, we conceive of the infinitely small not as a simple and absolute zero, but as a relative zero … that is, as an evanescent quantity which yet retains the character of that which is disappearing. ⁹⁶

Leibniz’s attitude toward infinitesimals and differentials seems to have been that they furnished the elements from which to fashion a formal grammar, an algebra, of the continuous. Since he regarded continua as purely ideal entities, it was then perfectly consistent for him to maintain, as he did, that infinitesimal quantities themselves are no less ideal—simply useful fictions, introduced to shorten arguments and aid insight.

Supporters and Critics of Leibniz

Although Leibniz himself did not credit the infinitesimal or the (mathematical) infinite with objective existence, a number of his followers did not hesitate to do so. Among the most prominent of these was Johann Bernoulli (1667–1748). A letter of his to Leibniz written in 1698 contains the forthright assertion that “inasmuch as the number of terms in nature is infinite, the infinitesimal exists ipso facto.”⁹⁷ One of his arguments for the existence of actual infinitesimals begins with the positing of the infinite sequence $\frac{1}{2},\frac{1}{3},\frac{1}{4},\dots$ . If there are ten terms, one tenth exists; if a hundred, then a hundredth exists, etc.; and so if, as postulated, the number of terms is infinite, then the infinitesimal exists.⁹⁸

Leibniz’s calculus gained a wide audience through the publication in 1696, by Guillaume de L’Hôpital (1661–1704), of the first expository book on the subject, the Analyse des Infiniments Petits Pour L’Intelligence des Lignes Courbes. L’Hôpital begins his exposition by laying down two definitions:

I.
Variable quantities are those that continually increase or decrease; and constant or standing quantities are those that continue the same while others vary.

II.
The infinitely small part whereby a variable quantity is continually increased or decreased is called the differential of that quantity. ⁹⁹

Following Leibniz , L’Hôpital writes dx for the differential of a variable quantity x.

Two postulates are next introduced:

I.
Grant that two quantities, whose difference is an infinitely small quantity , may be taken (or used) indifferently for each other: or (what is the same thing) that a quantity, which is increased or decreased only by an infinitely small quantity, may be considered as remaining the same.

II.
Grant that a curve line may be considered as the assemblage of an infinite number of infinitely small right lines: or (what is the same thing) as a polygon with an infinite number of sides, each of an infinitely small length, which determine the curvature of the line by the angles they make with each other. ¹⁰⁰

L’Hôpital applies Postulate I (and Definition II) in determining the differential of a product xy:

$\mathrm{d}(xy)=\left(x+\mathrm{d}x\right)\left(y+\mathrm{d}y\right)- xy=y\mathrm{d}x+x\mathrm{d}y+\mathrm{d}x\mathrm{d}y=y\mathrm{d}x+x\mathrm{d}y.$

Here the last step is justified by Postulate I, since dxdy is infinitely small in comparison to ydx + xdy.

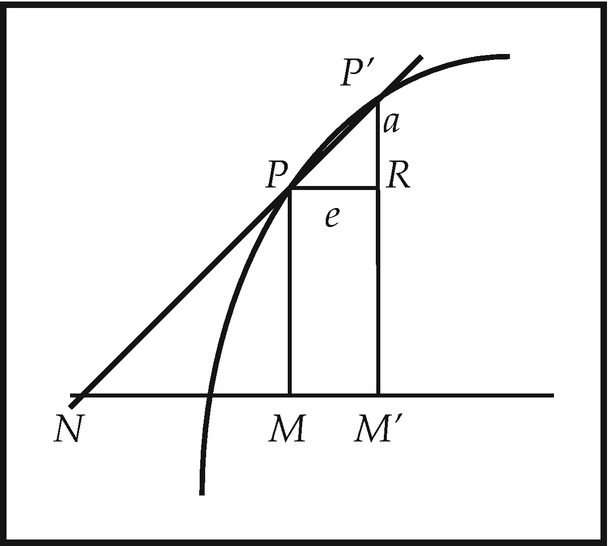
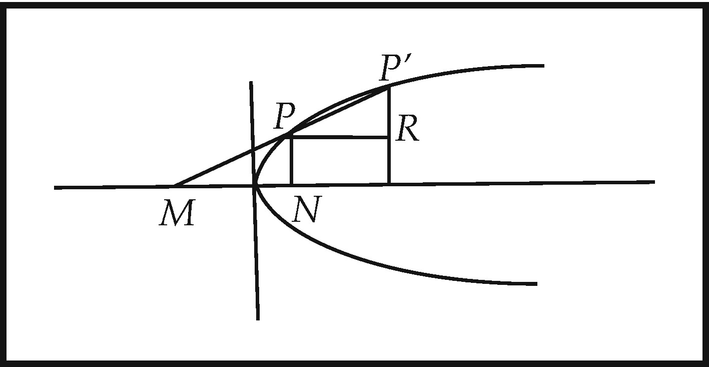
A typical application of Postulate II is in determining the length of the subtangent to the parabola x = y ². In Fig. 2.7 above, the infinitesimal abscissal increment e is dx and the corresponding increment in the ordinate, a, is dy. The triangles PNM and the infinitesimal triangle (which, by postulate II, is a triangle) PRP’ are similar, so that NM = ydx/dy. Now the differential equation of the parabola is dx = d(y ²) = 2ydy, which yields NM = 2y ² = 2x.

Leibniz’s calculus of differentials, resting as it did on somewhat insecure foundations, soon attracted criticism. The attack mounted by the Dutch physician Bernard Nieuwentijdt (1654–1718) in works of 1694–6 is of particular interest, since Nieuwentijdt offered his own account of infinitesimals which conflicts with that of Leibniz and has striking features of its own.¹⁰¹ Nieuwentijdt postulates a domain of quantities, or numbers, subject to an ordering relation of greater or less. This domain includes the ordinary finite quantities, but it is also presumed to contain infinitesimal and infinite quantities—a quantity being infinitesimal, or infinite, when it is smaller, or, respectively, greater, than any arbitrarily given finite quantity. The whole domain is governed by a version of the Archimedean principle to the effect that zero is the only quantity incapable of being multiplied by some quantity to equal any given quantity. Infinitesimal quantities may be characterized as quotients b/m of a finite quantity b by an infinite quantity m. In contrast with Leibniz’s differentials, Nieuwentijdt’s infinitesimals have the property that the product of any pair of them vanishes; in particular squares and all higher powers of infinitesimals are zero. This fact enables Nieuwentijdt to show that, for any curve given by an algebraic equation, the hypotenuse of the differential triangle generated by an infinitesimal abscissal increment e coincides with the segment of the curve between x and x + e. That is, a curve truly is an infinilateral polygon .¹⁰²

It is instructive to see how Nieuwentijdt’s calculus worked in practice.¹⁰³ For example, consider again the determination of the subtangent to the parabola x = y ² (Fig. 2.10). Let e be an infinitesimal abscissal increment and a the corresponding increment in the ordinate. Thus PN = y, PR = e, RP’ = a. Then the triangles PNM and the infinitesimal triangle PRP’ are similar, so that a = ey/NM. Since the point (x + e, y + a) lies on the curve, it follows that x + e = (y + a)² = y ² + 2ay + a ². Since a is infinitesimal, a ² = 0, so subtracting the original equation gives e = 2ya, whence a = e/2y. Accordingly e/2y = ey/NM, so that NM = ey/(e/2y) = 2y ² = 2x.

../images/474107_1_En_2_Chapter/474107_1_En_2_Fig10_HTML.png — Fig. 2.10
Caption

The major differences between Nieuwentijdt’s and Leibniz’s calculi of infinitesimals are summed up in the following table:

Leibniz	Nieuwentijdt
Infinitesimals are variables	Infinitesimals are constants
Higher-order infinitesimals exist	Higher-order infinitesimals do not exist
Products of infinitesimals are not absolute zeros	Products of infinitesimals are absolute zeros
Infinitesimals can be neglected when infinitely small with respect to other quantities	(first-order) infinitesimals can never be neglected

In responding to Nieuwentijdt’s assertion that squares and higher powers of infinitesimals vanish, Leibniz remarked that “it is rather strange to posit that a segment dx is different from zero and at the same time that the area of a square with side dx is equal to zero.”¹⁰⁴. Yet this oddity is in fact a consequence—apparently unremarked by Leibniz —of one of his own key principles, namely that curves may be considered as infinilateral polygons (L’Hôpital’s Postulate II).¹⁰⁵ For consider the curve y = x ² (Fig. 2.11). Given that the curve is an infinilateral polygon, an infinitesimal stretch of the curve between the abscissae 0 and dx must coincide with the tangent to the curve at the origin—in this case, the axis of abscissae—between those two points. But then the point (dx, dx ²) must lie on the axis of abscissae, which means that dx ² = 0.

../images/474107_1_En_2_Chapter/474107_1_En_2_Fig11_HTML.png — Fig. 2.11
Caption

A related argument surfaces in the debate concerning the infinitesimal calculus that flared up at the start of the eighteenth century among the mathematical luminaries of the Paris Academy of Sciences.¹⁰⁶ The algebraist Michel Rolle (1652–1719) raised a number of objections to the calculus, among which was the claim that talk of differentials was nonsense, since “it could be proved that differentials were absolute zeros”. Rolle later used the following argument to back up his claim.¹⁰⁷ Starting with the parabola y ² = ax, L’Hôpital’s rules yield the differential equation adx = 2ydy. Assuming that the point (x + dx, y + dy) lies on the parabola, one obtains ax + adx = y ² + 2ydy + dy ², whence dy ² = (ax – y ²) + (adx – 2ydy) = 0 + 0 = 0. Since dy ² = 0, Rolle infers that dy = 0, from which it also follows that dx = 0. Here the crucial step is from dy ² = 0 to dy = 0, a step that Nieuwentijdt , who accepted the first assertion but not the second, would not have taken.

Nevertheless, a number of the Paris academicians embraced the infinitesimal (and the infinite) with enthusiasm. One such was the polymath Bernard de Fontenelle (1657–1757), who put the fact on record with the publication of his Éléments de la Géométrie de l’Infini in 1727. Dismissing the notion that the infinite is in any way mysterious,¹⁰⁸ Like Wallis he writes ∞ as the last term of the infinite sequence 0, 1, 2, 3, … and proceeds to treat this symbol with great latitude, allowing it to be raised not merely to integral but even to fractional and infinite powers as in ${\infty}^{\frac{3}{4}}$ and ${\infty}^{\infty^3}$ . Infinitesimals of various orders are obtained as reciprocals of powers of ∞.

The insistence that infinitesimals obey precisely the same algebraic rules as finite quantities forced Leibniz and the defenders of his differential calculus into treating infinitesimals, in the presence of finite quantities, as if they were zeros, so that, for example, x + dx is treated as if it were the same as x. This was justified on the grounds that differentials are to be taken as variable, not fixed quantities, decreasing continually until reaching zero. Considered only in the “moment of their evanescence”,¹⁰⁹ they were accordingly neither something nor absolute zeros.

Thus differentials (or infinitesimals) dx were ascribed variously the four following properties:

$1.\mathrm{d}x\approx 0\kern1em 2. neither\ \mathrm{d}x=0\ nor\ \mathrm{d}x\ne 0\kern0.75em 3.\mathrm{d}{x}^2=0\kern0.75em 4.\mathrm{d}x\to 0$

where “≈ “” stands for “indistinguishable from ”, and “→ 0″ stands for “becomes vanishingly small”. Of these properties only the last, in which a differential is considered to be a variable quantity tending to 0, survived the nineteenth century refounding of the calculus in terms of the limit concept.¹¹⁰

Bayle

Finally, the sceptical views of the philosopher Pierre Bayle (1647–1706) concerning the continuous should be noted. In his Dictionnaire article on Zeno of Elea ,¹¹¹ Bayle argues that the idea of extension is incoherent whatever its mode of composition. It cannot be composed of unextended mathematical points, since extension cannot be produced by compounding the extensionless. Nor can it consist of Epicurean atoms, extended but indivisible corpuscles, since anything extended is divisible. The sole remaining possibility is that extension is composed of parts that are themselves divisible to infinity. To refute this Bayle provides a number of arguments, among the most interesting of which are that extension conceived as infinitely divisible would make it impossible for parts of extended substances to touch one another, and at the same time necessary that they penetrate one another. Bayle’s conclusions in regard to the existence of extended substance are similar to those of Leibniz :

We must acknowledge with respect to bodies what mathematicians acknowledge with respect to lines and surfaces…They frankly admit that a length and breadth without depth is something that cannot exist outside of our minds. Let us say the same of the three dimensions . They can exist only in our minds. They can exist only ideally. ¹¹²

While Bayle, like Leibniz, held that extension is a purely ideal notion, he viewed time quite differently. He affirmed its reality and, further, claimed that it was atomic in composition, with successive “nows” as atoms:

Time is not divisible ad infinitum. … I will make it more obvious by an example. Thus I say that what suits Monday and Tuesday with regard to succession suits every part of time whatsoever. Since it thus impossible that Monday and Tuesday exist together, and since it must be the case necessarily that Monday cease before Tuesday begins to exist, there is no other part of time, whatever it may be, that can coexist with another. Every one has to exist alone. Every one must begin to exist, when the other ceases to do so. Every one must cease to exist, before the following one begins to be. From which it follows that time is not divisible to infinity, and that successive durations of things are composed of moments properly so called, of which each is simple and indivisible, perfectly distinct from the past and future, and contains only the present time. ¹¹³

Bayle’s views later had a significant influence on Hume’s philosophy of space , time, and mathematics.

Bibliography

Aristotle. 1980. Physics, 2 vols. Trans. Cornford and Wickstead. Loeb Classical Library, Harvard University Press and Heinemann.
Arnauld, A., and P. Nicole. 1996. Logic or the Art of Thinking. Trans. Buroker. Cambridge: Cambridge University Press.
Baron, M.E. 1987. The Origins of the Infinitesimal Calculus. New York: Dover.
Bayle, P. 1965. Historical and Critical Dictionary; Selections. Trans. Popkin. Bobbs-Merrill.
Bell, J.L. 1998. A Primer of Infinitesimal Analysis. Cambridge: Cambridge University Press. Second edition 2oo8.
Bos, H. 1974. Differentials, higher order differentials and the derivative in the Leibnizian calculus. Archive for History of Exact Sciences 14: 1–90.Crossref
Boyer, C. 1959. The History of the Calculus and Its Conceptual Development. New York: Dover.
Child, J. 1916. The Geometrical Lectures of Isaac Barrow. Chicago: Open Court.
Descartes, R. 1927. Discourse on method, meditations, and principles of philosophy. In Everyman’s Library. London: Dent.
Galilei, G. 1954. Dialogues Concerning Two New Sciences. Trans. Crew and De Salvio. Dover.
Heath, T. 1949. Mathematics in Aristotle. Oxford: Oxford University Press.
Jesseph, D. 1993. Berkeley’s Philosophy of Mathematics. Chicago: Chicago University Press.Crossref
Kline, M. 1972. Mathematical Thought from Ancient to Modern Times. Vol. 3 volumes. Oxford: Oxford University Press.
Leibniz, G. 1951. In Selections, ed. P. Wiener. New York: Scribners.
———. 2001. The Labyrinth of the Continuum : Writings on the Continuum Problem, 1672–1686. Trans. Arthur. Yale University Press.
Mancosu, P. 1996. Philosophy of Mathematics and Mathematical Practice in the Seventeenth Century. New York/Oxford: Oxford University Press.
Murdoch, J. 1957. Geometry and the Continuum in the 14th Century: A Philosophical Analysis of Th. Bradwardinne’s Tractatus de Continuo. Ph.D. thesis, University of Wisconsin.
Newton, I. 1952. Opticks (1730). New York: Dover.
———. 1962. Principia, Vols, I, II. Trans. Motte, revsd. Cajori. University of California Press.
Pyle, A. 1997. Atomism and Its Critics. Bristol: Thoemmes Press.
Russell, B. 1958. A Critical Exposition of the Philosophy of Leibniz. 2nd ed. London: Allen & Unwin.
Walker, E. 1932. A Study of the Traité des Indivisibles of Gilles Personne de Roberval. New york: Bureau of Publications, Teachers College, Columbia Unversity.
Weyl, H. 1949. Philosophy of Mathematics and Natural Science. Princeton: Princeton University Press. (An expanded Engish version of Philosophie der Mathematik und Naturwissenschaft, Leibniz Verlag, 1927.).Crossref
Wilson, C. 2015. Leibniz’s Metaphysics: A Historical and Comparative Study. Princeton: Princeton University Press.Crossref

Footnotes

Murdoch (1957), p. 325.

A similar, but independent approach was taken by Luca Valerio (1552–1618).

Boyer (1959), pp. 99–100.

Baron (1987), p. 97

Ibid., pp. 108–116; Boyer (1969), pp. 106–110.

Baron (1987), p. 110.

Boyer (1959), p. 107.

Kline (1972) p. 299.

Galilei (1954), p. 55.

Here Galileo is giving expression to the conviction, which he shares with Cantor , that no potential infinity is unaccompanied by an actual one.

Galilei (1954), pp. 33–34

Ibid., p. 48

Ibid., p. 47.

Hermann Weyl makes a similar suggestion in connection with Galileo’s “bending” procedure:

If a curve consists of infinitely many straight “line elements”, then a tangent can simply be conceived as indicating the direction of the individual line segment; it joins two “consecutive” points on the curve. (Weyl 1949, p. 44.)

This conception was to prove fruitful in the later development of the calculus and to achieve fully rigorous formulation in the synthetic differential geometry of the later twentieth century. See Chap. 10 below.

Galilei (1954), p. 37

Ibid., p. 30.

Boyer (1959), p. 116

Galilei (1954), pp. 39–40.

Boyer (1969), p. 117.

Ibid., p. 118.

Ibid., p. 121.

Ibid., p. 122.

Ibid., p. 166.

Ibid., p. 165

Descartes (1927), p. 139.

Ibid., pp. 203–4.

Ibid., p. 209.

Arnauld and Nicole (1996), p. 230.

Ibid., p. 232.

Ibid.

It is interesting to note that this argument fails for geometries in which lines are not indefinitely extensible, for instance in elliptic geometries.

Quoted in Leibniz (2001), p. 361.

In this connection see the discussion at the end of Appendix A,

Ibid., pp. 361–2.

Boyer (1959), p. 137.

Walker (1932), p. 34.

Boyer (1959), pp. 125–6.

Ibid., p. 139.

Baron (1987), p. 205n.

Ibid., pp. 206–7. Baron reports (p. 213) that in Wallis’s A Treatise of Algebra of 1685 he lists the stages in the development of infinitesimal methods as follows: 1. Method of Exhaustion (Archimedes ); 2. Method of Indivisibles (Cavalieri ); 3. Arithmetick of Infinites (Wallis ); 4. Method of Infinite Series (Newton ).

Boyer (1959), p. 155.

Here Fermat seems to recognize that the function f(x) = x(a – x) is locally one-one.

Boyer (1959), p. 156.

Aristotle (1980), VII, 4. See also Heath (1949), pp. 140–142.

Boyer (1959), pp. 162–163.

Child (1916), p. viii. The quotation continues:

Newton got the main idea of it from Barrow by personal communication; and Leibniz also was in some measure indebted to Barrow’s work, obtaining confirmation of his own original ideas, and suggestions for their further development, from the copy of Barrow’s book he purchased in 1673.

Article “Infinitesimal Calculus”, Encyclopedia Britannica, 11th edition. But, while Barrow recognized the fact, he failed to put it to systematic use.

Kline (1972), p. 346.

In smooth infinitesimal analysis, the area of a characteristic triangle always reduces to 0. See Chap. 10 below.

Kline (1972), pp. 346–7.

Quoted in Jesseph (1993), p. 63n.

Quoted ibid, p. 63.

Child (1916), pp. 35–7.

Ibid., pp. 38–9.

De analysi, written 1666, published 1711; Methodus fluxionum, written 1671, published 1736; Quadratura, written c. 1676, published 1704.

Quoted in Jesseph (1993), p. 144.

Baron (1987), p. 268.

Newton (1962), p. 29.

Ibid., p. 32.

Ibid., pp. 38–9.

Boyer (1959), p. 200.

Newton (1962), p. 399,

Newton (1952), p. 400.

Quoted from Pyle (1997), p.415.

Ibid.

Actually, as pointed out in Wilson (2015), the metaphor of the labyrinth was a familiar one in seventeenth century writing. In connection with the continuum it had already been employed, for example, by Galileo in Two New Sciences.

Russell (1958), p. 245.

Ibid., p. 246.

Quoted in Weyl (1949) p.41.

Russell (1958), p. 246.

Ibid., p. 245.

Ibid.

Ibid., pp. 245–6.

Leibniz (1951), pp. 107–108.

Quoted in Leibniz (2001), pp. 37, 39.

Russell (1958), p. 242.

Ibid., p. 248.

Leibniz (1951), p. 99.

Russell (1958), p. 247.

Ibid., p. 104.

Strictly speaking, for Leibniz , as Russell points out (p. 106), matter or extended mass is nothing more than “a well-founded phenomenon”, not a substantial unity but a plurality engendered by indifferent monadic aggregation. Monads are not parts of phenomena but rather constitute their foundation. The monads themselves are the sole substantial realities: with the Eleatics Leibniz avers (Russell , p. 242) “What is not truly one being is also not truly a being.”

Russell (1958), p. 105.

Ibid., p. 105.

Ibid.,, p. 247.

Reply to Foucher, 1693, Leibniz (1951), p. 99.

Quoted in Boyer (1959), p. 217.

Letter to Varignon, 1702, Leibniz (1951), pp. 184–5.

Letter to Foucher, 1692, Leibniz (1951), p. 71.

Quoted in Russell (1958), p. 235.

Leibniz’s abilities as a mathematician have been memorably characterized by E. T. Bell:

The union in one mind of the highest ability in the two broad, antithetical domains of mathematical thought, the analytical and the combinatorial, or the continuous and the discrete, was without precedent before Leibniz and without sequent after him. He is the one man in the history of mathematics to have both qualities of thought in a superlative degree. (Bell, E.T. 1965, p. 128).

Indeed, Jakob and Johann Bernoulli , who made many contributions to the Leibnizian calculus and who introduced the term “integral ”, actually defined the operation of integration as the inverse of differentiation.

Quoted in Mancosu (1996), p. 156.

Ibid., p. 156.

Quoted from Bos (1974), p. 14.

Quoted in Boyer (1959), p. 219.

Ibid., p. 239.

Ibid.

Quoted in Mancosu (1996), p. 151.

100

Quoted ibid., p. 152.

101

Ibid., p. 159 et seq.

Ibid., p. 159.

Ibid., pp. 153–4.

Ibid., p. 161.

Bell (1998), p. 9. In fact the “nilsquare” property of infinitesimals and L’Hôpital’s Postulate II (for algebraic curves) are equivalent. As remarked above, Nieuwentijdt saw that the first assertion implies the second.

106

Mancosu (1996), pp. 165 et seq.

107

Ibid., p. 167.

108

Boyer (1959), p. 242.

109

Mancosu (1996), p. 167.

110

But the other properties have resurfaced in the theories of infinitesimals which have emerged over the past several decades. Appropriately defining the relation, ≈, property 1 holds of the differentials in nonstandard analysis , while properties 1, 2 and 3 hold of the differentials in smooth infinitesimal analysis. See Chaps. 8 and 10 below.

111

Bayle (1965), pp. 350–94.

112

Bayle (1965), p. 363.

113

Op. cit.

2. The Sixteenth and Seventeenth Centuries. The Founding of the Infinitesimal Calculus

2.1 The Sixteenth Century

From Stevin to Kepler

Galileo and Cavalieri

2.2 The 17th Century

The Cartesian Philosophy

Infinitesimals and Indivisibles

Barrow and the Differential Triangle

Newton

Leibniz

Supporters and Critics of Leibniz

Bayle