Category/Topos Theory

7.1 Categories and Functors

Category theory is a framework for the investigation of mathematical form and structure in their most general manifestations. Central to it is the concept of structure-preserving map , or transformation. While the importance of this notion was long recognized in geometry (witness, for example, Klein’s Erlanger Programm of 1872),¹ its pervasiveness in mathematics did not really begin to be appreciated until the rise of abstract algebra in the 1920s and 30s,² where, in the form of homomorphism, the idea had been central from the beginning. So emerged the view that the essence of a mathematical structure lies not in its internal constitution as a set-theoretical construct, but rather in the nature of its relationship with other structures of the same kind through the network of transformations between them.

This idea achieved its fullest expression in the theory of categories introduced in 1945 by S. Eilenberg (1913–1998) and S. Mac Lane (1909–2005).³ They created an axiomatic framework within which the notion of map and preservation of structure are primitive, that is, are not defined in terms of anything else. As in biology, the viewpoint of category theory is that mathematical structures fall naturally into species or categories. But a category is specified not just by identifying the species of mathematical structure which constitute its objects; one must also specify the transformations linking these objects.

Formally, then, a category consists of two collections of entities called objects and maps. Each map f is assigned an object A called its domain and an object B called its codomain : this fact is indicated by writing f: A → B. Each object A is assigned a map 1_A: A → A called the identity map on A. For any pair of maps f: A → B, g: B → C (i.e., such that the domain of g coincides with the codomain of f; such pairs of maps are called composable), there is defined a composite map g ° f: A → C. These prescriptions are subject to the associative and identity laws, viz., given three maps f: A → B, g: B → C, h: C → D, the composites h ∘ (g ∘ f) and (h ∘ g) ∘ f coincide; and for any map f: A → B the composites f ∘ 1_A and 1_B ∘ f both coincide with f.

There are a number of ways of envisioning categories. They may, for instance, be considered as frameworks for the analysis of variation . Thus we suppose given.

domains of variation or types A, B, C, …
transformations or correlations f: A → B or $A\overset{f}{\to }B$ between such domains: A and B are said to be correlated by f; A is the domain, B the codomain of f.

As concrete examples we may consider:

Space → Time	Analogue clocks
Natural numbers → Time	Digital clocks
Time → Space	Motions
Space → Rational/ Real numbers	Thermometers, barometers, speedometers

A correlation A → B may be thought of as a B-valued quantity varying over A. As such, correlations may be composed:

$\frac{A\overset{f}{\to }B\overset{g}{\to }C}{A\overset{g\circ f}{\to }C}$

E.g. the use of a digital stopwatch amounts to the composite correlation.

$Natural\ numbers\to Time\to Space$

Composition of correlations is associative in the evident sense.

Associated with each domain A is an identity correlation $A\overset{1_A}{\to }A$ satisfying f ∘ 1_A = f, g ∘ 1_A = g for any $A\overset{f}{\to }B$ , $C\overset{g}{\to }A.$

These specifications are just the basic data of a category.

A category may also be thought of as the objective presentation of a mathematical form (or idea), with objects as structures manifesting the associated form, and maps as form-preserving transformations between structures. Now topological spaces and continuous functions constitute the objects and maps, respectively, of a category, the category Top of topological spaces. Top may be thought of as the objective presentation of the form of continuity. Other important examples of categories include the category Set of sets, with (arbitrary) sets as objects and (arbitrary) functions as maps; the category Grp of groups, with groups as objects and group homomorphisms as maps ; and the category Man of manifolds, with differentiable manifolds as objects and smooth functions between them as maps. For Set, the associated form is pure discreteness ; for Grp, it is composition-inversion, and for Man, it is smoothness.

A concept central to category theory is that of functor. A functor F: C → D from a category C to a category D is an assignment, to each object A of C, of an object FA of D and to each map f: A → B of C a map Ff: FA → FB of D such a way that composites and identities are preserved, i.e. F(g ∘ f) = Fg ∘ Ff for composable f, g, and F(1_A) = 1_FA for any object A. As examples of functors we have the so-called “forgetful” functors Top → Set , Grp → Set, and Man → Set that assign to each space, group, or manifold its underlying set of points (i.e., “forgets” the structure); the functor Top → Grp that assigns to each topological space its homology group⁴ of a prescribed dimension ; and the functor Man → Man that assigns to each manifold its tangent bundle .

If categories are associated with mathematical forms, then functors may be conceived of as devices for effecting a change of form. ⁵ Thus, for example, the three “forgetful” functors just mentioned take the forms of continuity, composition-inversion and smoothness, respectively, to the form of pure discreteness . Observe that functors, or “changes of form” can be composed in the evident way. This gives rise to the “meta-category Cat with categories as objects and functors as maps. Cat may be regarded as the category-theoretic embodiment of the idea of mathematical form, and its maps, the functors between categories, as vehicles for inducing morphological variation .

7.2 Pointless Topology

Another way of presenting topology in category-theoretic terms is through the development of what has become known as pointless topology . ⁶ Here the idea is to deal directly with the topology of a space , bypassing the underlying set which supports that topology: the approach may be seen as a way of investigating the continuous (topologies) without reduction to the discrete (sets of points). Pointless topology originates with the observation that, under the partial order of inclusion, a topology is a certain kind of complete lattice, that is, a partially ordered structure (L, ≤) possessing a largest element 1, and in which each subset X has a least upper bound, or join, ∨X, and a greatest lower bound, or meet, ∧X. (In the case of a topology on a set X, 1 is X, joins are set-theoretic unions and the meet of a family ../images/474107_1_En_7_Chapter/474107_1_En_7_Figa_HTML.gif

of open sets is the interior of the intersection of ../images/474107_1_En_7_Chapter/474107_1_En_7_Figa_HTML.gif

, that is, the union of all the open sets included in the intersection of ../images/474107_1_En_7_Chapter/474107_1_En_7_Figa_HTML.gif

.) Additionally, in a topology meets distribute over joins in the sense that ⁷

$a\wedge \mathbf{\bigvee}X=\mathbf{\bigvee}\left\{a\wedge x:x\in X\right\}.$

A complete lattice satisfying this condition is called a locale . A locale may be regarded as a topology not built on an underlying set of points.⁸ Pointless topology is obtained by enlarging attention from topologies to locales.

We note that an implication operation ⇒ may be introduced in a locale L by defining

$x\Rightarrow y=\vee \left\{z:x\wedge z\le y\right\}.$

It is then not hard to show that x ⇒ y is the largest element z for which x ∧ z ≤ y. A complete lattice in which an implication operation is so definable is called a complete Heyting algebra ; thus any locale is one.

What are the counterparts, for locales, of continuous functions between topological spaces ? Recall that a continuous function f: X → Y between topological spaces is characterized by the property that the inverse image f ⁻¹[U] of any open set U in Y is open in X. The inverse image operation can accordingly be seen as a function from the topology on Y to that on X. Now the inverse image operation also preserves 1, arbitrary unions and pairwise intersections of subsets. So it is natural to take a continuous map f between locales to be one satisfying the analogous conditions:

$f\left(\mathbf{1}\right)=\mathbf{1};\kern1.5em f\left(x\wedge y\right)=f(x)\wedge f(y);\kern1.5em f\left(\vee X\right)=f\left(\vee X\right).$

Because inverse images and functions “run in opposite directions” we agree that, given two locales L and L’, a continuous map L → L’ will be a function f: L’ → L— in the opposite direction— satisfying the above conditions.

Locales and continuous functions in the sense just defined can now be regarded as constituting the objects and maps of Loc, the category of locales. Associating each topological space with its topology and each continuous map between spaces with its inverse image operation now gives rise to a functor Top → Loc which embeds the former in the latter. If Top can be seen as an embodiment of the idea of continuity but still dependent on the point concept, Loc can be seen as a more general embodiment of the idea of continuity, now freed of all dependence on the point concept.

7.3 Sheaves and Toposes

The most far-reaching generalization of the concept of topological space , and hence the most general embodiment of the idea of continuity, is the category-theoretic concept of topos. The idea of a topos developed from the concept of a sheaf on a topological space. Mac Lane and Moerdijk present the idea underlying the latter in the following terms:

A sheaf [on a space X] is a way of describing a class of functions on X—especially classes of “good” functions, such as the functions on ( parts of) X which are continuous or differentiable. The description tells the way in which a function f defined on an open subset U of X can be restricted to functions f|_V on open subsets V ⊆ U and then can be recovered by piecing together (collating) the restrictions to the open subsets V _i of a covering of U. The restriction-collation description applies not just to functions, but to other mathematical structures defined “locally” on a space X. ⁹

Here is the formal definition. We first define a presheaf ¹⁰ on a topological space X to be an assignment to each open set U of a set F(U) and to each pair of open sets U, V such that V ⊆ U of a “restriction” map F _UV: F(U) → F(V) such that, whenever W ⊆ U ⊆ V, F _UW = F _{VW °} F _UV and F _UU is the identity map on F(U). If s ∈ F(U), write s|_V for F _UV(s)—the restriction of s to V. A presheaf F is a sheaf if it satisfies the following “covering” condition: whenever $U=\underset{i\in I}{\cup }{U}_i$ and we are given a set {s _i: i ∈ I} such that s _i ∈ F(U _i) for all i ∈ I and s _i | _{Ui ∩Uj} = s _j| _{Ui ∩Uj} for all i, j ∈ I, then there is a unique s ∈ F(U) such that s|_Ui = s _i for all i ∈ I. For example, C(U) = set of continuous real-valued functions on U, and s|_V = restriction of s to V defines the sheaf of continuous real-valued functions on X.

Given two presheaves F, G on X, a natural transformation η: F → G is an assignment, to each open set U, of a map η_U: F(U) → G(U) which is compatible with restrictions, i.e. satisfies for V ⊆ U, η_V ∘ F _UV = G _UV ∘ η_U. Presheaves, or sheaves, on X, together with natural transformations, form categories Pshv(X), Shv( X )—the category of presheaves, or sheaves, ¹¹ respectively. on X. Shv(X) may be regarded as a category-theoretic embodiment of X: it encodes all the information about locally defined structures on X.

A sheaf on a topological space arises by the imposition of a covering condition on a presheaf. In the early 1960s Alexandre Grothendieck (1928–2014) extended the notion of covering, and so also the concept of sheaf to arbitrary categories, thus conferring on both concepts a vast new generality.

To see how this was effected, we require the notion of a set varying over a category C (or C- variable set) , which is defined simply to be a functor from C to the category Set , and the notion of a natural transformation between variable sets. A natural transformation between two C- variable sets F and G is a function assigning to each object A of C a map η_A: FA → GA in such a way that, for each map f: A → B, we have Gf _° η_A = η_{B °} Ff. The category Set ^C of sets varying over C then has as objects C-variable sets and as arrows natural transformations between them.

Now we can define a presheaf on C to be a set varying over the category C ^op—the opposite category to C in which all maps are “reversed”^. ¹² The category ${\mathbf{Set}}^{{\mathbf{C}}^{\mathbf{op}}}$ is called the category of preheaves on C. There is a natural embedding¹³—the Yoneda embedding —of C into ${\mathbf{Set}}^{{\mathbf{C}}^{\mathbf{op}}}$ whose action on objects is defined as follows. For any object C of C, YC is the presheaf on C which assigns, to each object X of C, the set Hom(X, C) of maps X → C in C. YC—the Yoneda presheaf of C—is the natural presheaf representative of C; the two are usually identified.

To see how the notion of covering may be extended to arbitrary categories, we re-examine the concept in the case of a topological space X. Given an open set U, we define a sieve on U to be a family S of open subsets of U such that any open subset of a member of S is itself a member of S; if ⋃ S = U, the sieve S is called a covering sieve on U. We write J(U) for the set of all covering sieves on U . It is easily seen that J(U) satisfies the following conditions:

(1)
the maximal sieve consisting of all open subsets of U is a member of J(U);

(2)
if S ∈ J(U) and V is open in X, then the sieve V∗S = {W: W ∈ S and W ⊆ V} is a member of J(V); that is, the restriction of a covering sieve to a smaller open set is a covering sieve;

(3)
if S ∈ J(U) and R is a sieve on U such that, for each V ∈ S we have V∗S ∈ J(V), then R ∈ J(U); that is, if the restriction of a sieve R to each member of a covering sieve S is a covering sieve, then R is a covering sieve.

These three conditions were taken by Grothendieck as being characteristic of the notion of covering; they can be generalized to an arbitrary category C in the following way, giving rise to what has become known as a Grothendieck topology .

First, by analogy with the above definition of sieve , we define a sieve on an object C of C to be a family S of maps in C, each with codomain C, ¹⁴ closed under composition on the right, that is, satisfying f ∈ S ⇒ f _° g ∈ S for any map g composable with f on the right. Equivalently, a sieve on C may be defined as a subfunctor¹⁵ of C’s Yoneda presheaf YC. Note that, if S is a sieve on C and h: D → C is any map with codomain C, then the set

h ^∗(S) = {g : codomain(g) = D & h ∘ g ∈ S}

is a sieve on D. A Grothendieck topology, or covering system , on C is a function J which assigns to each object C a collection J (C) of sieves—called J-covering sieves—on C in such a way that the following conditions (i), (ii), (iii) are satisfied:

(i)
for any C, the maximal sieve {h: codomain (h) = C} is a member of J(C);

(ii)
if S ∈ J(C) and h: D → C, then the sieve h∗S is a member of J(D);

(iii)
if S ∈ J(C) and R is a sieve on U such that, for each member h: D → C of S we have h∗R ∈ J(D), then R ∈ J(C).

Clearly these conditions are immediate generalizations of (1), (2), (3) to the category C. The Grothendieck topology Trv on C in which only the maximal sieves on an object are covering sieves is called the trivial topology.

A category equipped with a covering system was termed by Grothendieck a site . ¹⁶ If X is a topological space , and J is defined on the category O(X) of open sets by taking J(U) to be the family of all sieves S on U in the above sense such that ⋃ S = U, then O(X), equipped with the Grothendieck topology J, is a site. It is called the site canonically associated with X. In view of this a site may be regarded as a “generalized topological space”, or indeed as a new embodiment of the idea of a pointless space.

Now we can sketch how Grothendieck went on to extend the concept of sheaf to arbitrary sites.¹⁷ Recall that any sieve S on an object C of C may be regarded as a subfunctor of C’s Yoneda functor YC. Now suppose we are given an object F of ${\mathbf{Set}}^{{\mathbf{C}}^{\mathbf{op}}}$ —a presheaf on C—and a map f: S → F in ${\mathbf{Set}}^{{\mathbf{C}}^{\mathbf{op}}}$ —a natural transformation from S to F. A map g: YC → F is called an extension of f to YC if its restriction (in the evident sense) to the subfunctor S coincides with f. The presheaf F is then a (J-)sheaf if, for any object C and any J-covering sieve S on C, each map f: S → F in ${\mathbf{Set}}^{{\mathbf{C}}^{\mathbf{op}}}$ has a unique extension to YC. Speaking figuratively, a J-sheaf is a presheaf which “believes” that (the Yoneda presheaf of) any object C is “really covered” by any of its J-covering sieves, in the sense that, in ${\mathbf{Set}}^{{\mathbf{C}}^{\mathbf{op}}}$ is, any map from a J-covering sieve to F fully determines a map from YC to F. Note that every presheaf is a Trv-sheaf.

Now the category Shv _J(C) of sheaves on a site (C, J) has objects all sheaves and as maps all natural transformations between them. So in particular Shv _Trv(C) is just the category of presheaves on C. There is a natural functor L: ${\mathbf{Set}}^{{\mathbf{C}}^{\mathbf{op}}}\to {\mathbf{Shv}}_J\left(\mathrm{C}\right)$ called the associated sheaf functor which sends each presheaf F to the to the sheaf LF which “best approximates” it in an appropriate sense.¹⁸

Grothendieck assigned the term “topos”¹⁹ to any category of sheaves associated with a site . So in particular all categories of presheaves, or variable sets , are toposes. Grothendieck saw the topos concept as uniting the continuous and the discrete:

This idea encapsulates, in a single topological intuition, both the traditional topological spaces , incarnation of the world of the continuous quantity … and a huge number of other sorts of structures which … had appeared to belong irrevocably to the “arithmetic world” of “discontinuous” or “discrete” aggregates. ²⁰

F. William Lawvere and Myles Tierney later formulated a simple and decisive list of axioms satisfied by Grothendieck’s toposes. These turned out to be the same as certain key axioms satisfied by the category of sets: aremarkable instance of the unity of the Continuous and the Discrete. Lawvere and Tierney introduced the term elementary topos (subsequently just “topos”) for a category E possessing the following properties, each of which, suitably expressed in category-theoretic language, is clearly possessed by Set :

(a)
E has a “terminal” object 1 such that, for any object A, there is a unique map A → 1. (In Set, 1 may be taken to be any singleton, in particular {0}. Note that elements of a set A correspond to maps 1 → A.)²¹
(b)
Any pair of objects A, B of E has a (Cartesian) product A × B in E.
(c)
For any pair of objects A, B in E one can form in E the ‘exponential” object B ^A of all maps A → B.
(d)
E has a “truth-value” object Ω containing a distinguished element true such that for each object A there is a natural correspondence between subobjects of A and maps A → Ω. (In Set , Ω may be taken to be the set 2 = {0, 1}, and true the element 1; maps A →Ω are then characteristic functions on A and the exponential Ω^A corresponds to the power set of X.)
(e)
E has a “natural numbers” system, that is, a triple (N, s, o) consisting of an object N and maps s: N → N, o: 1 → N. These are subject to the Peano-Lawvere axiom

For any diagram $1\overset{a}{\to }X\overset{g}{\to }X$ in E, there is a unique map $N\overset{f}{\to }X$ for which the diagram
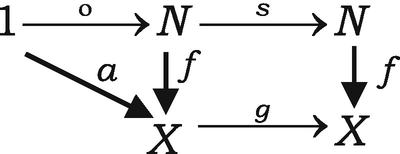
commutes.

Thus Set and all categories of “sets undergoing variation ” such as sheaves and presheaves are toposes.

Toposes can also arise as categories of sets with a generalized equality relation‖, with arrows preserving that relation in an appropriate sense. Some of the most important examples in this regard are the categories of Heyting algebra-valued sets. Given a complete Heyting algebra H, an H-valued set is a pair (I, δ) consisting of a set I and a map δ: I × I → H (the generalized equality relation on I) satisfying the following conditions, in which we write δ_ii’ for δ(i, I′) (and similarly below):

${\updelta}_{i{i}^{\prime }}={\updelta}_{i^{\prime }i}\kern1em \left(\mathrm{symmetry}\right)$

${\updelta}_{i{i}^{\prime }}\wedge {\updelta}_{i^{\prime }{i}^{{\prime\prime} }}\le {\updelta}_{i{i}^{{\prime\prime} }}\kern1em \left(\mathrm{substitutivity}\right)$ The category Set _H of H-valued sets has as objects all H-valued sets. A Set _H -arrow f: (I, δ) → (J, ε) is a map f: I × J → H such that

${\updelta}_{i{i}^{\prime }}\wedge fij\le {f}_{i^{\prime }j}\ {f}_{ij}\wedge {\upvarepsilon}_{j{j}^{\prime }}\le {f}_{i{j}^{\prime }}\kern1em \left(\mathrm{preservation}\ \mathrm{of}\ \mathrm{identity}\right)$

${f}_{ij}\wedge {f}_{i{j}^{\prime }}\le {\upvarepsilon}_{j{j}^{\prime }}\kern1em \left(\mathrm{single}\hbox{-} \mathrm{valuedness}\right)$

${\vee}_{i\in I}{f}_{ij}={\updelta}_{ii}\kern0.24em \left(\mathrm{denined}\;\mathrm{on}\;\mathrm{I}\right)$

The composite g _° f of two arrows f: (I, δ) → (J, ε) and g: (J, ε) → (K, η) is given by(g ∘ f)_ik = ∨_j ∈ J(f _ij ∧ g _jk).Then Set _H is a topos in which the subobject classifier is the H-valued set (H, ⇔).

There are three principal types of topos:

Type I: categories of “sets undergoing variation These include sheaves and presheaves.
Type II: categories of sets with a generalized equality relation.
Type III: categories arising as models of intuitionistic many- sorted theories (see below)

Lawvere and Tierney established a striking connection between topos theory and logic . This originates with the observation that in the category of sets we have the usual logical operations ∧ (conjunction), ∨ (disjunction), ¬ (negation), → (implication), ∀ (universal quantification), ∃ (existential quantification) defined on the object 2 = {0, 1} of truth values. The richness of a topos E’s internal structure enables analogous “logical operations” to be defined on its object Ω of truth values. The remarkable thing is that the body of laws satisfied by the logical operations in a topos—its “internal logic”—does not, in general, correspond to classical logic, but rather to the intuitionistic or constructive logic of Brouwer and Heyting in which the law of excluded middle is not affirmed.²²

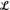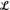To be precise, to each topos E can be associated a certain formal language ../images/474107_1_En_7_Chapter/474107_1_En_7_Figc_HTML.gif (E)—its internal language ²³ —which resembles the usual language of set theory in that included among its primitive signs are equality (=), membership (∈) and the set formation operator ({:}). ../images/474107_1_En_7_Chapter/474107_1_En_7_Figc_HTML.gif (E) is a many-sorted language—let us call it a topos language— with each of its sorts corresponding to an object of E. Thus, in particular, for each object A of E, 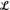(E) contains a list of variables of sort A. Each term t of 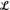(E) with free variables x ₁, …, x _n, of sorts A ₁, …, A _n is then assigned an object B as a sort in such a way as to enable a map 〚t〛 : A ₁ × … × A _n → B —the interpretation of t in E—to be defined. Terms of sort Ω are called formulas, or propositions. A formula φ is said to be true, or to hold, in E if its interpretation 〚φ〛 : A ₁ × … × A _n → Ω has constant value true. 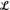It can be shown then that all the axioms and rules of inference of (free) intuitionistic logic ²⁴ formulated in ../images/474107_1_En_7_Chapter/474107_1_En_7_Figc_HTML.gif (E) are true in E. It is in this sense that the “internal logic” of a topos is intuitionistic or constructive.²⁵

The set of all sentences of 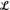../images/474107_1_En_7_Chapter/474107_1_En_7_Figc_HTML.gif (E) which are true in E is called the (internal) theory Th (E) of E. Th (E) is an intuitioistic many-sorted theory. A topos E is then, in a natural sense, a model of Th (E). Within the internal language and the associated theory of a topos mathematical concepts can be formulated, arguments carried out and constructions performed much as one does in “ordinary” set theory, only observing the rules of intuitionistic logic . In fact, any topos may be regarded as a model of intuitionistic set theory IST.²⁶ This means that, within a topos, mathematical constructions can be carried out as if within IST. In particular, the rational numbers can be defined as usual and the real numbers oconstructed by employing either Dedekind ’s procedure of making cuts in the rationals or Cantor’s procedure employing equivalence classes of Cauchy sequences of rationals. While classically these two constructions lead to isomorphic results, this is not true in constructive logic : indeed, a number of toposes have been constructed in which (in the topos’s internal logic), the ordered rings of Dedekind and Cantor reals fail to be isomorphic.²⁷

Accordingly, in a topos-theoretic or constructive universe there is more than one candidate²⁸ for the role of the mathematical continuum. The classical view that the linear continuum is a uniquely determined entity is replaced by a pluralistic conception under which the continuum has a number of realizations with essentially different properties. And even if one decides, for example, to choose the Dedekind reals as one’s continuum, its properties may fall far short of those possessed by its classical counterpart. For example, in constructive logic it cannot be proved that the Dedekind reals satisfy the least upper bound property. It can be shown, in fact,²⁹ that, in a topos’s internal theory, the Dedekind reals possess this property exactly when the logical law³⁰ ¬(α ∧ β) → (¬α ∨ ¬β) holds there. This is an arresting instance of the connection between logic and the properties of the mathematical continuum made visible by the shift from classical to constructive logic .

We have mentioned that in 1924 Brouwer proved from his intuitionistic principles that every real-valued function on a closed interval of the real numbers is uniformly continuous. A number of toposes have been constructed in which the corresponding statement for Dedekind reals holds. One such³¹ is the topos of sheaves on the space of irrational numbers. In any topos in which Brouwer’s theorem holds all closed intervals are cohesive .³²

Topos theory thus allows a remarkable flexibility in the handling of the continuum. In Chap. 10 we shall describe a still more remarkable representation of the continuum made possible by topos theory, one in which the infinitesimal plays a key role.

Bibliography

Bell, E.T. 1945. The Development of Mathematics. 2nd ed. New York/London: McGraw-Hill.
Bell, J.L. 1988. Toposes and Local Set Theories: An Introduction, Oxford Logic Guides 14. Oxford: Clarendon Press. Reprinted by Dove, 2008.
———. 1998. A Primer of Infinitesimal Analysis. Cambridge: Cambridge University Press. Second edition 2oo8.
———. 2014. Intuitionistic Set Theory. London: College Publications.
Fourman, M., C. Mulvey, and D. Scott., eds. 1979. Applications of Sheaves. Proc. L.M.S. Durham Symposium 1977. Springer Lecture Notes in Mathematics 753.
Grothendieck, A. 1986. Récoltes et Semailles. Trans. Lisker. http: // www. fermentmagazine.org/rands/recoltes1.html
Johnstone, P.T. 1982. Stone Spaces, Cambridge Studies in Advanced Mathematics 3. Cambridge: Cambridge University Press.
———. 1983. The point of pointless topology. Bulletin of American Mathematical Society (N.S.) 8 (1): 41–53.Crossref
———. 2002. Sketches of an Elephant: A Topos Theory Compendium, Vols. I and II, Oxford Logic Guides Vols. 43 and 44. Oxford: Clarendon Press.
Kline, M. 1972. Mathematical Thought from Ancient to Modern Times. Vol. 3 volumes. Oxford: Oxford University Press.
Mac Lane, S., I. Moerdijk, and I. 1992. Sheaves in Geometry and Logic: A First Introduction to Topos Theory. New York: Springer.

Footnotes

The kernel of Klein’s Erlanger Programm was the characterization of geometry as the study of those properties of figures that remain invariant under a particular group of transformations, See, e.g. E.T. Bell (1945), pp. 443–9.

See, e.g., Kline (1972), Ch. 49

Eilenberg , S. and Mac Lane , S., General Theory of Natural Equivalences, Transactions of the American Mathematical Society 58, 1945, pp. 231–294.

It was the attempt to create a tractable theory of homology groups that first led Eilenberg and Mac Lane to formulate the idea of a functor , and then of a category.

At the same time, functors embody a version of the Principle of Continuity in that composites and identities are preserved.

See Johnstone (1983).

Here we write x ∧ y for {x, y}.

It should be mentioned, however, that the concept of a point can be defined for locales and locales arising as topologies characterized in terms of that notion. See Johnstone (1982), Ch. 2.

Mac Lane and Moerdijk (1992), p. 64. Grothendieck describes a sheaf on a space as a “ruler that can be used for taking measurements on it.” (1986, Promenade 13).

A presheaf on X may be seen as a functor of a certain kind. Any partially ordered set (P, ≤) can be regarded as a category in which the members of P constitute the objects and, for each p, q ∈ P, there is given exactly one map p → q just when p ≤ q. In particular the family O(X) of open sets of a topological space X, partially ordered by inclusion, may be regarded as a category. The same family, partially ordered by reverse inclusion, yields the “opposite” category O(X)^op. Functors from the latter to Set are just the presheaves on X.

Grothendieck sees the category of sheaves on a space as a “superstructure of measurement”, which may be “taken to incorporate all that is most essential about that space.” (1986 , Promenade 13).

To be precise, C ^op has the same objects as C; and in C ^op the maps from an object A to an object B correspond precisely to the maps B → A in C, with composites and identity maps defined analogously.

A functor F: C → D is an embedding if, for any objects A, B of C, any map FA → FB in D is of the form Ff for a unique f: A → B in C.

Here we view a map f: D → C as an “inclusion” of D in C.

If F and G are two functors C ^op → Set , F is called a subfunctor of G if FX ⊆ GX for any object X of C.

Strictly speaking, in defining a site one should specify that the underling category C be small, that is, its collections of objects and maps should both be sets rather than proper classes in the sense of Gödel-Bernays set theory.

For a detailed account, see Mac Lane and Moerdijk (1992), Ch. III.

See, e.g., Mac Lane and Moerdijk (1992), p. 87.

The term is a back-formation from the word “topology” to its original Greek source “topos”, “place”.

Grothendieck (1986), Promenade 13. He goes on:

As is often the case in mathematics, we’ve succeeded … in expressing a certain idea—that of a “space ” in this instance—in terms of another one—that of a “category”. Each time the discovery of such a translation from one notion (representing one kind of situation) to another (which corresponds to a different situation) enriches our understanding of both notions, owing to the unanticipated confluence of specific intuitions which relate first to one and then to the other. Thus we see that a situation said to have a “topological” character (embodied in some given space) has been translated into a situation whose character is “algebraic” (embodied in the category); or, if you wish, “continuity” (as present in the space) finds itself “translated” or “expressed by a categorical structure of an algebraic character, which until then had been understood in terms of something “discrete” or “discontinuous”.

More generally, elements or points of an object A of a category are maps from the terminal object to A.

See Chap. 9.

See Bell (1988).

For these see, e.g., Bell (1998), Ch. 8.

Of course, many important toposes such as the topos of sets have an internal logic that is classical. These are exceptions, however.

By intuitionistic set theory IST we mean the theory in intuitionistic first-order logic whose axioms are the “usual” axioms of Zermelo set theory (without the axiom of choice ), namely: Extensionality, Pairing, Union, Power set, Infinity and Separation. For an exposition of IST, see Bell (2014).

In fact, this is the case for the topos Shv (ℝ) of sheaves on the usual (classical) topological space ℝ of real numbers . For an account see Johnstone (2002), §D4.7.

Others are mentioned in Johnstone, op. cit.

Op. cit., Thm. 4.7.11.

This is the only one of De Morgan’s laws which does not generally hold in constructive logic . It fails, in particular, in Shv(ℝ).

As shown by Dana Scott in his paper Extending the topological interpretation to intuitionistic analysis II, pp. 235–255 of Buffalo Conference in Proof Theory and Intuitionism , North-Holland, 1970. Scott’s result was extended by Martin Hyland in Continuity and spatial toposes, in Fourman, Mulvey and Scott (1979), pp. 440–465. In Mac Lane and Moerdijk (1992), Ch. VI, §9 a topos is constructed in which all real-valued functions defined on the whole real line are continuous. See Appendix C for further discussion.

See Appendix A.

7. Category/Topos Theory

7.1 Categories and Functors

7.2 Pointless Topology

7.3 Sheaves and Toposes