1.4 The Marginal Principle

Learning Objective The Marginal Principle: Decisions about quantities are best made incrementally. You should break “how many” decisions down into a series of smaller, or marginal, decisions.

Applying the Marginal Principle: Once you have broken a problem into a series of marginal choices, apply the cost-benefit principle. The marginal principle is useful for “how many” decisions, but not for “either/or” choices.

Let’s revisit Nerida, a few years after business school. She has decided to combine her entrepreneurial savvy with her love of food by opening an Italian restaurant. She has already chosen a location and remodeled it. Next she needs to decide how many workers to hire. The benefit of hiring a larger staff is that she’ll serve more meals leading to higher revenue. But this also means higher costs—because more staff means a higher wage bill and selling more meals means buying more fresh produce. As with so many things, there’s a trade-off. So, Nerida wonders just how many workers she should hire.

The marginal principle says that decisions about quantities are best made incrementally. Whenever you face a decision about how many of something to choose (such as, “How many workers should I hire?”), it is always easier to break it into a series of smaller, or marginal, decisions (such as, “Should I hire one more worker?”).

marginal principle

Decisions about quantities are best made incrementally. You should break “how many” questions into a series of smaller, or marginal decisions, weighing marginal benefits and marginal costs.

The marginal principle suggests that you evaluate whether the extra benefit from hiring one more worker exceeds the extra cost of that extra worker. We call the extra benefit you get from one more worker the marginal benefit; the extra cost of that worker is called the marginal cost. Applying the cost-benefit principle to this marginal choice, you should hire one more worker only if the marginal benefit exceeds the marginal cost.

marginal benefit

The extra benefit from one extra unit (of goods purchased, hours studied, etc.).

marginal cost

The extra cost from one extra unit.

As Figure 5 illustrates, this is a process that you should apply iteratively: After you’ve decided to hire that extra worker, you should compare the marginal cost and benefit of hiring another worker. Again, if the marginal benefit exceeds the marginal cost, you should hire that person, too. Then you should ask whether it is worth hiring yet another worker. And so it continues, as you work your way through a series of straightforward “either/or” choices, until eventually you decide against hiring any more workers.

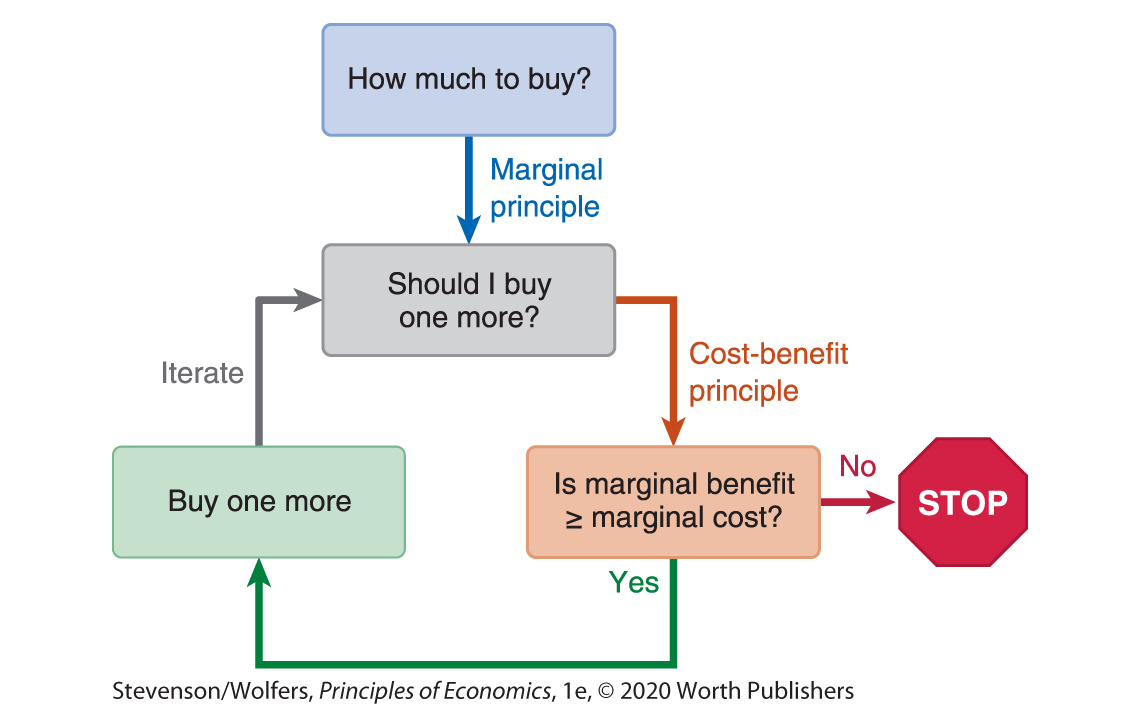
Figure 5 | Applying the Marginal Principle

The starting component reads, How much to buy? An arrow labeled marginal principal points from the starting component to the next that reads, Should I buy one more? An arrow labeled cost-benefit-principle points to the next component that reads, Is marginal benefit greater than or equal to marginal cost? The first arrow from this component, labeled No, leads to a component that reads, Stop. The second arrow labeled Yes leads to the component that reads, Buy one more. An arrow labeled Iterate points back to the component, Should I buy one more?

When Is the Marginal Principle Useful?

Whenever you have to decide “how many” of something to choose, you should use the marginal principle to break your decision into a series of smaller marginal choices. However, there are some decisions that are not “how many” questions, but rather “either/or” questions. For instance, when Nerida was deciding whether to open her restaurant, she faced an “either/or” decision, so the marginal principle was not relevant. But sometimes we’ll find that even choices that seem like “either/or” choices have “how many” questions lurking within. For instance, Nerida wasn’t just deciding whether to open a restaurant, but also how big it should be, and so she found the marginal principle useful when she decided how many square feet of retail space to lease.

The bottom line: First determine what type of choice you face. If you face a “how many” choice, you should break it down into a series of smaller marginal decisions. You know that you have broken a decision into its smallest components when you are left with only “either/or” choices to make. Then, apply the cost-benefit principle and the opportunity cost principle to each of these simpler “either/or” choices.

Do the Economics

Can you apply the marginal principle to simplify the following decisions?

• How many workers should I hire?

  Simplifies to: Should I hire one more worker?

• How many pairs of shoes should I buy?

  Simplifies to: Should I buy one more pair of shoes?

• How many classes should I take?

  Simplifies to: Should I take one more class this semester?

• How many children should I have?

  Simplifies to: Should I have one more child?

• Should I marry my current boyfriend/girlfriend?

  This is an either-or question, and so can’t be further simplified.

• How many hours per week should I work?

  If you are in a job where you can change your hours of work, then you should ask: Should I work one more hour?

  If you can’t change the number of hours you work, then this is an either-or question (should I get a second job?), and can’t be further simplified.

Now we have figured out how to restate any “how many” choice as an “either/or” marginal choice. But remember, deciding “how many” actually requires answering a series of these marginal “either/or” questions. Every time you ask one of these marginal questions and the answer is yes, you should ask it again. And if the answer is yes, ask it yet again. You should keep asking until the answer is no. In fact, that is the essence of the most powerful application of the marginal principle, called the Rational Rule.

Using the Rational Rule to Maximize Your Economic Surplus

The marginal principle provides a simple rule of thumb that will help you maximize your economic surplus (the difference between your total benefits and total costs). Here’s the rule:

The Rational Rule: If something is worth doing, keep doing it until your marginal benefits equal your marginal costs.

Rational Rule

If something is worth doing, keep doing it until your marginal benefits equal your marginal costs.

The logic of this rule is straightforward. You know from the cost-benefit principle that whenever the benefits of a choice exceed the costs, it is a good choice. And when you apply the marginal principle, you don’t analyze the “how many” choice all at once (“How many workers should I hire?”). Instead, you analyze a series of simpler “either/or” choices (“Should I hire one more worker?”). And so the marginal principle tells you to keep hiring, as long as the marginal benefit of each worker exceeds the marginal cost. But you should stop hiring just before the marginal cost becomes larger than the marginal benefit. When does this occur? In most cases, this crossing point occurs right when the marginal benefit is equal to the marginal cost. (In the remaining cases—when the marginal benefit and marginal cost are never exactly equal—you should keep hiring as long as the marginal benefit exceeds the marginal cost.)

The Rational Rule says to keep going until marginal benefit equals marginal cost.

Let’s apply this reasoning to a decision you face at the start of each semester: how many classes to take. The marginal principle says to break up this “how many” choice into a series of “either/or” choices. Should you take one class? The benefit of the first class is surely greater than the cost. So you should definitely take that class. Given that you are taking one class this semester, should you take a second? If the marginal benefit of this extra class exceeds the marginal cost, you should. And the same logic holds for a third class and a fourth (and possibly more). In fact, you should keep increasing your course load as long as the marginal benefit of each extra class is at least as large as the marginal cost. But at some point—usually when you are thinking about whether to take a fifth or a sixth class—the marginal benefit of an extra class will be too low or the marginal cost is just too high (perhaps because the opportunity cost of one more class is constant sleep deprivation). And if the marginal cost of that extra class is greater than the marginal benefit, you shouldn’t take that extra class.

Following the Rational Rule leads to good decisions.

Some people find the Rational Rule confusing—why would you want to set your marginal benefits equal to your marginal costs? After all, don’t you simply want to maximize your economic surplus—the difference between the benefits you enjoy and the costs you incur? It turns out that if you follow the Rational Rule, your choices will maximize your economic surplus. Why? Let’s try to provide Nerida with some insight as she tries to figure out how many workers to hire.

If the marginal benefit of hiring one more worker exceeds the marginal cost, then hiring an additional worker will increase your economic surplus.

Since the marginal benefit of this extra worker exceeds their marginal cost, hiring them will boost your total benefit by more than it boosts your total cost. Thus, hiring this extra worker will raise your economic surplus (which is the difference between the total benefits you enjoy and the total costs you incur). If you always hire more workers when the marginal benefits are greater than the marginal costs, you will increase your economic surplus, which moves you ever closer to the point at which your economic surplus is at its highest possible level.

If the marginal benefit of hiring one more worker is less than the marginal cost, then hiring an additional worker will lower your economic surplus.

If you did hire this worker, they would raise your total costs by more than they would raise your total benefits, and so hiring them would lower your economic surplus. Hiring (or keeping) a worker whose marginal benefit is less than their marginal cost will move you further away from the point at which your economic surplus is maximized.

You maximize your economic surplus right at the point where the marginal cost of hiring the last worker equals the marginal benefit.

So, hiring more workers will increase your economic surplus as long as the marginal benefit exceeds the marginal cost. But at some point, the marginal benefit of an additional worker will be less than the marginal cost. When this happens, hiring that worker would reduce your economic surplus. So, at what point do you stop hiring? Right when the marginal benefit equals the marginal cost. At this point, you have increased your economic surplus as much as possible, right up to the point where hiring another worker would reduce your economic surplus.

Do the Economics

Let’s now apply the Rational Rule to helping Nerida figure out the number of workers to hire. In each row of Figure 6, she has written down her projections of her total costs and total benefits, according to the different staffing levels she is considering. She considers as few as two staff (in the first row), to as many as seven (in the final row). Each staffing level is noted in the first column. The second column shows the number of meals that Nerida anticipates selling, and this increases as she hires more staff.

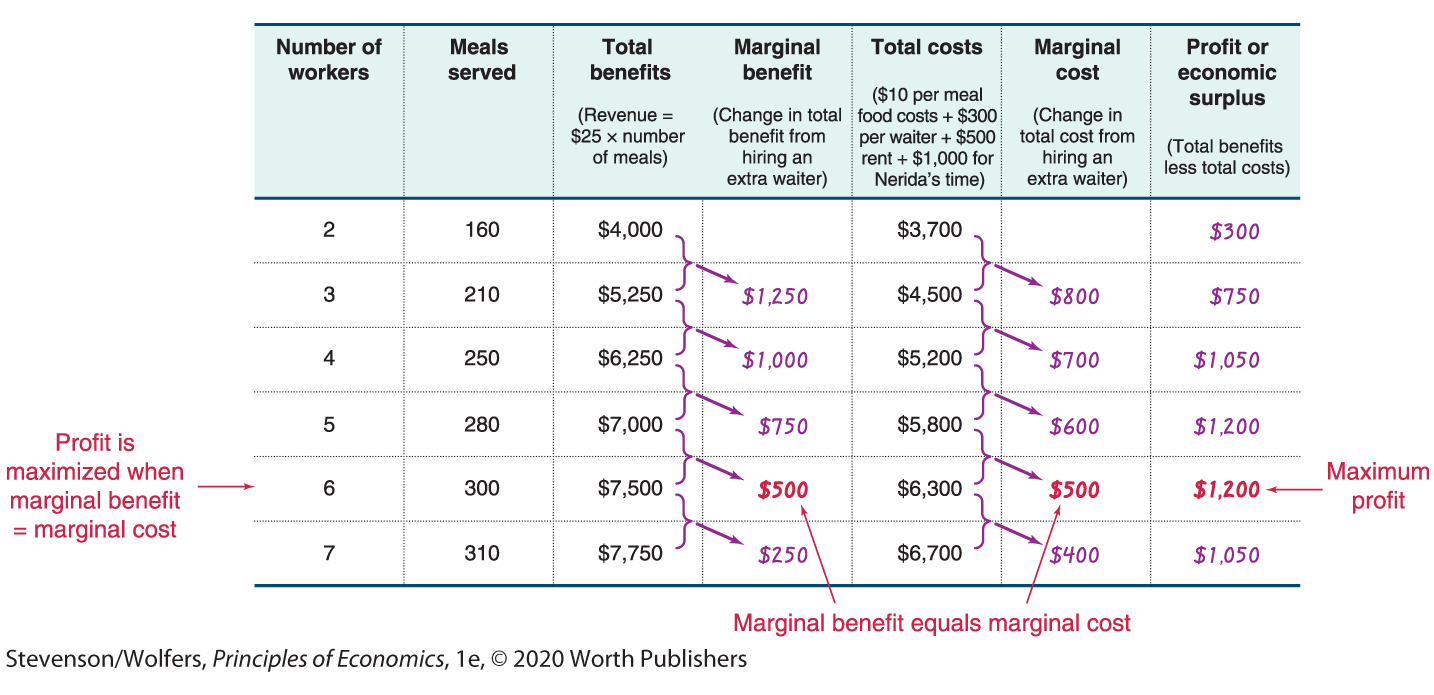
Figure 6 | Nerida’s Weekly Costs and Benefits Depend on the Number of Staff

The table has six rows and seven columns. The column headers are as follows: Number of workers, Meals Served, Total benefits (Revenue minus 25 dollars multiplied by number of meals), Marginal benefit (Change in total benefit from hiring and extra waiter), Total costs (10 dollars per normal food costs plus 300 dollars per water plus 500 dollars rent plus 1000 dollars for Nerida’s time), Marginal cost (Change in total cost from hiring an extra wallet), and Profit or economic surplus (Total benefits less total costs).

Row 1: Number of workers, 2; Meals Served, 160; Total benefits, 4,000 dollars; Marginal benefit, blank; Total costs, 3,700 dollars; Marginal cost, blank; Profit or economic surplus, 500 dollars.

Row 2: Number of workers, 3; Meals Served, 210; Total benefits, 5,250 dollars; Marginal benefit, 1,250 dollars; Total costs, 4,250 dollars; Marginal cost, 800 dollars; Profit or economic surplus, 750 dollars.

Row 3: Number of workers, 4; Meals Served, 250; Total benefits, 6,250 dollars; Marginal benefit, 1,000; Total costs, 5,200 dollars; Marginal cost, 700 dollars; Profit or economic surplus, 1,050 dollars.

Row 4: Number of workers, 5; Meals Served, 280; Total benefits, 7,000; Marginal benefit, 750 dollars; Total costs, 5,800 dollars; Marginal cost, 600 dollars; Profit or economic surplus, 1,200 dollars.

Row 5: Number of workers, 6; Meals Served, 300; Total benefits, 7,500 dollars; Marginal benefit, 500 dollars; Total costs, 6,300 dollars; Marginal cost, 500 dollars; Profit or economic surplus: 1,200 dollars. A callout pointing to this row reads, Profit is maximized when marginal benefit equals marginal cost. A callout pointing to 500 dollars in marginal benefit and marginal cost reads, Marginal benefit equals marginal cost. A callout pointing to profit surplus of 1,200 dollars reads, Maximum profit.

Row 6: Number of workers, 7; Meals Served, 310; Total benefits, 7,750 dollars; Marginal benefit, dollar 250; Total costs, 6,700 dollars; Marginal cost, 400 dollars; Profit or economic surplus, 1,050 dollars.

What are the implications of this? On the benefit side, the more meals she sells each week, the greater the revenue she earns. On average, each meal sells for about $25, and so her weekly revenue will be $25, multiplied by the number of meals served. This total revenue, which is her total benefit, is shown in the third column. On the cost side, running a restaurant is an expensive business. She pays $500 per week in rent. Also, as an entrepreneur, she has to consider the opportunity cost of her own time, which is $1,000 per week. Each waiter she hires costs $300 per week, and each extra meal that is prepared costs $10 in raw ingredients. The sum of these costs is her total cost, and the total costs associated with each staffing level are shown in the fifth column.

While Nerida has worked out her total costs and benefits, the marginal principle suggests that we focus on her marginal benefits, rather than her total benefits. The marginal benefit to Nerida of hiring an additional worker, shown in the fourth column, is the extra revenue that she will earn from that worker. For example, the marginal benefit of hiring the third worker is simply the total benefit from hiring three workers, minus the total benefit from hiring two workers, or $5,250 – $4,000 = $1,250 per week. We can do similar calculations for each extra staff member, and these marginal benefit calculations are shown in the fourth column. We also need to work out Nerida’s marginal costs, which are the extra costs that come with hiring each extra worker (and from making the extra meals they serve). For instance, adding a third worker and increasing the number of meals Nerida serves causes her total costs to rise from $3,700 per week in the first row, to $4,500 per week in the next row, for a marginal cost of $800. When we do similar marginal cost calculations for each additional staff member, we arrive at the numbers shown in the sixth column.

Now, let’s apply the Rational Rule. Notice that hiring that third worker brings an additional (or marginal) benefit of $1,250 per week, and an additional (or marginal) cost of $800 per week. Because the marginal benefits exceed the marginal costs, Nerida is definitely better off hiring that third worker. But should she also hire a fourth worker? And what about a fifth worker after that? The Rational Rule is useful: Keep hiring workers until the marginal benefits are equal to the marginal costs. In this case, Nerida’s marginal benefits and costs are equal when she hires six workers. And so the rule says: Hire six workers.

Does this make sense? You can check the final column, which calculates her economic surplus, which in this case is her economic profit—her total benefits less total costs. Looking down this column, the highest profit Nerida can earn is $1,200. She can earn this profit if she hires either five or six workers. The Rational Rule led Nerida to hire six workers, which is the choice that yields the (equal) highest profits. Great news!

You might notice that the Rational Rule recommends that you keep hiring until the marginal benefit is equal to the marginal cost, which occurred when she hired six workers. But hiring that sixth worker whose marginal benefit was exactly equal to their marginal cost neither raised nor lowered her economic surplus. So while the rule told Nerida to hire six workers, she would have earned the same profit had she hired only five people. In practice, the important point is to stop hiring just before your marginal cost becomes larger than your marginal benefit.

Applying the Rational Rule

The marginal principle is particularly useful precisely because it is so practical. As you study economics, you will see that the Rational Rule is applicable to just about every choice you make. Indeed, it describes how people like Nerida actually run their businesses. The problem is that most people don’t know in advance exactly what the costs and benefits will be for each alternative they face. So how do they make decisions?

Businesses experiment at the margin to learn their marginal costs and benefits.

Nerida needs to decide how many workers to hire, but in reality, she isn’t sure whether she would be better off hiring two workers or three. So she experiments with different business decisions. She starts by hiring two workers. And then, as an experiment, she tries hiring one more person, to figure out whether that boosts her benefits by more than it boosts her costs. If it does—that is, if the marginal benefit exceeds the marginal cost—she’ll declare that experiment a success, and keep that extra person on payroll permanently. If the costs exceed the benefits, she’ll eventually let that person go or fail to replace a worker who quits.

For Nerida, hiring the third worker yields $1,250 extra revenue, which more than offsets the $800 in extra costs. She then continues her experimenting, hiring a fourth person; when that also raises her profits, she’ll experiment further, hiring a fifth and sixth person, and then a seventh. With each experiment, she focuses on the changes in costs and benefits that occur; these are her marginal costs and marginal benefits. When she tries adding a seventh worker, she finds that her costs rise by $400, but her revenue only rises by $250. Because this experiment reveals that her marginal cost exceeds the marginal benefit (and hence that the seventh person reduces her total profit), she declares that experiment a failure, and won’t keep a seventh worker on permanently.

Notice that in this process of judging her experiments as successes or failures, Nerida is following the Rational Rule: If hiring additional staff is worth doing, she’ll keep doing it until her marginal benefits equal her marginal costs. And by using this rule, she experiments her way to the point where her profits are maximized.

Do the Economics

Now, it’s your turn to apply the Rational Rule to make decisions. Remember to think about the relevant marginal costs and marginal benefits. Consider yourself in the following roles:

• As a consumer: How many cups of coffee should you buy today?

  Keep buying coffee until the marginal benefit (your willingness to pay for that last cup of coffee) is equal to the marginal cost (the price and, if it’s late, how much it would stand in the way of getting a good night’s rest).

• As a producer: How many tons of coffee should you produce?

  Keep producing coffee until the marginal benefit of producing an extra ton (the wholesale price you can sell it for) is equal to the marginal cost of producing another ton.

• As a worker: How many hours should you work as a barista?

  Keep working until the marginal benefit (your hourly wage) is equal to the marginal cost of working (the value of the marginal hour of leisure time that you are missing).

• As an investor: How much should you invest in a new chain of specialty coffee shops?

  Keep investing until the marginal benefit (your return on the last dollar invested) is equal to the marginal cost. (This includes the opportunity cost of that last dollar: How else could you invest that dollar, and how could you spend it now?)

• As an export company: How many tons of coffee should you export?

  Keep exporting until the marginal benefit (the price you can get for the coffee overseas) is equal to the marginal cost (the price at which domestic producers will sell you one more ton, plus the price of shipping it overseas).

• As a job-seeker: How many coffee shops should you send your résumé to?

  Keep sending job applications until the marginal benefit (the value of the increased chance of finding a job) is equal to the marginal cost of an application (the time and hassle of filling out one more application).

• As an employer: How many workers should you hire?

  Keep hiring until the marginal benefit of an extra worker (the rise in revenues you get from selling more coffee) is equal to the marginal cost (the wages of that last worker and the cost of that extra coffee).

They may all look the same, but that doesn’t mean that the marginal benefit of each bean is the same.

-

Recap: The marginal principle creates a structure to simplify complicated “how many” questions.

Each of these examples involves thinking about making decisions in very different economic roles. Yet all of the answers follow a parallel structure. The power of the marginal principle is that it creates a common structure in all decisions in which you choose “how many,” and it simplifies an otherwise complicated decision. The best choices—the ones that maximize your economic surplus—all follow the same pattern, as described by the Rational Rule: Choose the quantity where the marginal benefit equals the marginal cost. That way, you will maximize your economic surplus.

By now, we’ve come a long way in developing the skills you need to think like an economist. It’s all about learning to identify the key issues underpinning any choice. The cost-benefit principle asks you to identify the relevant costs and benefits of a decision. The opportunity cost principle asks you to identify your true opportunity costs. And the marginal principle asks you to identify the marginal choices that make up any “how many” decision. Now, let’s turn to the final principle, which is all about identifying the many different ways that your decisions affect and are affected by other decisions.