18.2 The Prisoner’s Dilemma and the Challenge of Cooperation
In a typical quarter, Coca-Cola spends nearly a billion dollars on marketing. Pepsi also spends a roughly similar amount. Coca-Cola recently did some market research, and learned that advertising helps it earn market share from Pepsi, but Pepsi then regains that lost market share with its own advertising. The billions of dollars spent on advertising don’t do much to convince people to drink more cola overall.
Armed with this insight, the CEO of Coke asks you for strategic advice. You arrive at his office and find him pacing, excited by his new idea. He speaks quickly as he explains his radical thought: “Why don’t we just abolish our advertising budget altogether?” He explains his thinking: “If Pepsi does the same thing, then both firms will earn higher profits, because both will sell roughly the same amount of cola, with neither of us wasting billions of dollars on useless advertising.” Of course, this plan only works if Pepsi’s CEO chooses to cooperate. If instead she defects from the plan and keeps advertising, then Coke’s decision to stop advertising will result in losing customers to Pepsi. It’s tricky, because you’ll have to make a decision about next quarter’s ad buy before you know if Pepsi will play along. What’s your advice?
Understanding the Prisoner’s Dilemma
As you start to answer, you note that Coke’s payoffs from pursuing this plan depend on whether Pepsi will cooperate with it. Likewise, Pepsi’s payoffs depend on Coke’s choice. Immediately you recognize this as a strategic interaction—the sort of setting where you should apply game theory. Time to work through our four-step recipe.
Step one: Consider all the possible outcomes and construct the payoff table.
Let’s start with step one of a game theoretic analysis: Consider all the possible outcomes. You can construct a payoff table that shows all the possible outcomes by listing each of Coke’s possible actions as rows, and each of Pepsi’s possible actions as columns, as in Figure 2. We’ll describe each company’s choice as either cooperating with the plan to quit advertising, or defecting from it. Each of the four cells in this table describes a possible outcome.
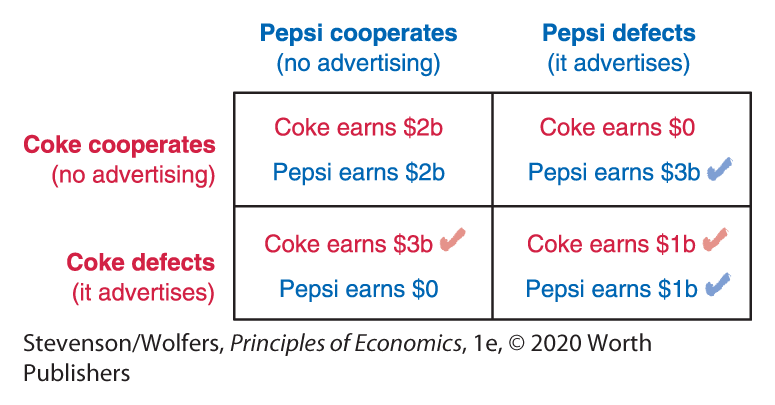
Figure 2 | The Prisoner’s Dilemma
For each possible outcome, you need to consider the payoffs to both Coke and Pepsi. You turn to your market research division for some help, and here’s what they tell you:
- Currently both Pepsi and Coke advertise, and they each make around $1 billion in profits each quarter. (This is the defect–defect cell at the bottom right.)
- If the CEO of Pepsi cooperates with Coke’s plan to stop advertising, then both companies will each save $1 billion per quarter, boosting the quarterly profits of each firm to $2 billion. (This is the cooperate–cooperate cell at the top left.)
- There’s a risk: If Coke cooperates and stops advertising, but Pepsi defects from the plan and continues to advertise, then Pepsi will win over a lot of Coke’s customers. This will boost Pepsi’s quarterly profits to $3 billion, while Coke earns $0 profits. (Top right.)
- Pepsi faces a similar risk: If Pepsi cooperates with the plan but Coke defects, then Coke’s quarterly profits will rise to $3 billion, while Pepsi’s will fall to $0. (Bottom left.)
Next, translate all of this information into the payoff table shown in Figure 2, which summarizes all the possible outcomes and lists the payoffs to each player for each outcome.
The payoff table shows explicitly how your payoffs depend on the choices that others make, and likewise, how their payoffs vary with your choices.
Step two: Think in terms of “what ifs” and Step three: Play your best response.
Okay, what should you do? Coke’s best choice depends on what Pepsi does, while Pepsi’s best choice depends on what Coke does. Step two tells you to think separately about the different “what ifs.” So Coke needs to separately assess what to do if Pepsi cooperates, and what to do if Pepsi defects. In each of these scenarios, step three says that you want to play your best response.
Applying steps two and three together, you need to think about your best response to any choice that Pepsi might make:
- If Pepsi cooperates: Coke can either cooperate and make $2 billion, or defect and earn $3 billion. If Pepsi cooperates, Coke’s best response is to defect.
- If Pepsi defects: Coke can cooperate and make $0, or defect and earn $1 billion. If Pepsi defects, Coke’s best response is to defect.
No matter what Pepsi chooses, you should advise Coke’s CEO that his best response is to defect. Notice one more thing: In Figure 2, I put a red check mark next to each of these best responses; this is something you should get in the habit of doing, and it will turn out to be helpful in just a moment.
Step four: Put yourself in the other player’s shoes and figure out their best response.
To figure out what Pepsi will do, move to step four of our analysis and put yourself in the other player’s shoes. Pepsi will evaluate its best response to any choice that Coke might make:
- If Coke cooperates: Pepsi can either cooperate and make $2 billion, or defect from the plan and earn $3 billion. If Coke cooperates, Pepsi’s best response is to defect.
- If Coke defects: Pepsi can cooperate and make $0, or defect and earn $1 billion. If Coke defects, Pepsi’s best response is to defect.
Putting it together, we see that no matter what Coke chooses, it looks like Pepsi will choose to defect. (And you’ll also notice that I put a blue check mark next to each of these best responses in Figure 2.)
Nash Equilibrium
Okay, so what’s going to happen in this game? In this situation, neither Pepsi nor Coke can benefit by changing its strategy unless it expects the other to change. As a result the likely outcome is simply that each person plays their best response to their opponent’s best response.
A Nash equilibrium occurs when you both choose your best response.
When everyone is playing their best response to the choices that other players are making, we call the resulting equilibrium outcome a Nash equilibrium. In a Nash equilibrium all of the players choose their best responses—they’re each making their best choice, given the choices that others are making. It’s an equilibrium because no one can do better by changing their choice alone.
Use the check mark method to find a Nash equilibrium.
Remember that whenever we found a player’s best response, I suggested that you put a check mark next to it? That’s because it makes finding a Nash equilibrium really easy: Just look for an outcome with two check marks and you’ve found a Nash equilibrium. After all, a Nash equilibrium occurs whenever both players choose their best response, and so if you mark each player’s best response with a check mark, then an outcome with a check mark from each player is a Nash equilibrium. This simple trick, called the check mark method, is so useful that we’ll keep using it throughout the rest of this chapter.
The Prisoner’s Dilemma yields a failure to cooperate.
Let’s use the check mark method to figure out the Nash equilibrium to the Prisoner’s Dilemma. Figure 2 shows that there are two check marks in the cell in which both Pepsi and Coke defect, and so this is the Nash equilibrium.
Thus, the most likely outcome of this game is that neither company will cooperate with the plan to quit advertising. Even though both companies are better off if they both quit wasteful advertising, Coke and Pepsi each continue advertising. The logic behind this forecast is this: If Coke expects Pepsi to defect, then its best response is to defect; likewise, if Pepsi expects Coke to defect, then its best response is to defect. And so in equilibrium, each set of executives expects the other to defect, and this in turn leads each of them to choose to defect.
Notice that in a Nash equilibrium two things are true:
- Best responses: Each player’s choice is their best response to what they expect the other to choose.
- Correct expectations: Each player’s expectation about what the other player will choose is also correct.
The Prisoner’s Dilemma and the Failure of Cooperation
Let’s take a step back to put this into a broader context. Both Coke and Pepsi understand that they would be jointly better off if they would cooperate and agree to quit advertising, yet they both continue to spend billions of dollars on wasteful advertising. Even though this isn’t the best outcome for either company, it’s likely to be the actual outcome because each is making the best choice it can, given the choice the other will make.
Agreements to cooperate are not credible.
You might wonder why Pepsi and Coke can’t figure out a way to cooperate to both eliminate wasteful advertising. The CEO of Coke could call the CEO of Pepsi, to say “I’ll cooperate with this no-advertising plan if you do.” The problem is that the CEO of Pepsi understands that if she cooperates, then Coke’s best response will be to defect. (Check the payoffs: A $3 billion payoff beats $2 billion.) Moreover, the Pepsi CEO knows that billions of dollars are more persuasive than mere talk, so she doesn’t find the Coke CEO’s promise to be credible. Similar logic suggests that the Coke CEO would never believe a promise from Pepsi’s CEO to cooperate. The problem is that neither can credibly commit to cooperating, and so neither expects the other to actually cooperate, and this makes defecting the best response. (It’s just as well: An agreement to eliminate advertising may be illegal collusion because it limits competition.)
The Prisoner’s Dilemma shows how markets can deliver bad outcomes.
We’ve just discovered what may be the most important insight of game theory. It’s the juxtaposition of two facts:
- The best outcome would be for Pepsi and Coke to both cooperate and quit advertising. They would earn the highest possible joint profit ($4 billion, or $2 billion each) under this outcome.
- But this was not the equilibrium outcome. Instead, when both Pepsi and Coke follow their self-interest and play their best responses, they both choose to defect from the plan. The result makes them both worse off, as they each earn a $1 billion profit instead of $2 billion.
That is, the equilibrium outcome is not the best outcome. Indeed, in the Prisoner’s Dilemma, the equilibrium outcome need not even be a good outcome. The Prisoner’s Dilemma is a striking counterpoint to the idea that free markets deliver the best outcomes. Indeed, the Prisoner’s Dilemma yields the opposite result, as Coke and Pepsi each pursued their own self-interest but ended up reaching an equilibrium that’s worse for both of them.
The temptation to take advantage undermines cooperation.
The Prisoner’s Dilemma is best read as a parable—an example that applies far more broadly than to just the Coke and Pepsi case. In particular, the big insight is that people often fail to cooperate even when there’s a project that could make them all better off. (In this example, that project was to quit advertising.) Even though the benefits of cooperation exceed the benefits of defecting in the Prisoner’s Dilemma, defecting to take advantage of a cooperative rival yields an even bigger and more tempting payoff. That temptation can cause cooperation to fail.
How do we reconcile the failure of self-interest to reach the best outcome with our analysis in Chapter 7, which suggested that competitive markets generally yield efficient outcomes? The answer is that our earlier analysis focused on the case of perfect competition, when all buyers and all sellers were so small that the choices made by one business didn’t much affect the payoffs of others. That is, our earlier analysis didn’t involve strategic interactions. But Pepsi and Coke are both big firms, and Pepsi’s choices affect Coke’s payoffs, and this creates strategic interactions. These interactions can lead people to make strategic choices that lead to inefficient outcomes. And so in a world full of strategic interactions, there’s no reason to assume that free markets will yield good outcomes.
Why is it called the Prisoner’s Dilemma?
Okay, so if the real problem here is getting people to cooperate, why do we call this the Prisoner’s Dilemma, rather than the Cooperation Dilemma? It’s because the clearest illustration of a cooperation dilemma involves a scenario in which the police are trying to extract a confession from a pair of bank robbers.

The real-life Bonnie and Clyde never got a chance to confess.
Following a bank heist, the police took two suspects—we’ll call them Bonnie and Clyde—in for questioning. If the police can’t extract a confession, they can only charge Bonnie and Clyde for speeding away from the scene, which will result in jail terms of only one year. And so realizing that this minor charge is their best joint outcome, Bonnie and Clyde hatch a plan to both deny the crime.
But the police are savvy game theorists, and so they put Bonnie and Clyde in separate interview rooms and offered each of them a deal that they thought might be tempting: “I can cut you a sweet deal: If your friend persists in denying the crime and you help me make the case against them, you’ll avoid jail altogether.” But, the police add, “If your friend confesses and you don’t, we’ll throw the book at you, and you’ll get three years.” Finally, the police add that “in the unlikely event that you both confess, you’ll each get two years.”
What would you do if you were in Bonnie’s shoes? And what’s likely to happen here? It’s time to use your newfound skills as a game theorist.
Do the Economics
It’s your turn to solve the Prisoner’s Dilemma. Put yourself in Bonnie’s shoes and work through the four steps for analyzing strategic interactions:
First, consider all the outcomes by drawing up the payoff table.

Second, think about the “what ifs” separately. And third, for each of these alternatives, play your best response.
What if Clyde denies the crime? Bonnie’s best response is to confess so that she gets zero years instead of three. Go ahead, put a check mark in the bottom-left cell of the table. And what if Clyde confesses? Bonnie’s best response is to confess (so she gets two years instead of three), and so you should also put a check mark in the bottom-right cell.
Fourth, apply the other people’s shoes technique.
It’s time for Bonnie to think about what Clyde will do. As Clyde considers the possible outcomes, thinking about each “what if” separately, he’ll ask: What if Bonnie denies the crime? Then Clyde’s best response is to confess and get zero years rather than denying and getting one year. This says that you should put a check mark in the top-right cell. And what if Bonnie confesses? Then Clyde’s best response is to confess and get two years, rather than denying and getting three years. Add a check mark to the bottom-right cell.
Make sure you avoid this mistake: Double check that you’re making the relevant comparisons. When you’re thinking about the player who has to choose their best row (in this case, Bonnie), you’re trying to find your best response to each choice your opponent might make, and so you should compare outcomes within each column. Don’t make the mistake of comparing two cells in the same row! And the player who is choosing among columns (Clyde) needs to compare outcomes within each row (and he should not compare two cells in the same column!).
The equilibrium: OK, now it’s time to look for the Nash equilibrium: Look for a cell with two check marks. It’s the bottom-right cell, where both Bonnie and Clyde confess to the crime.
This is a rather remarkable use of game theory. The police set a trap that led both Bonnie and Clyde to confess, despite the fact that if they both persisted in denying the crime, they’d get away with it. By offering each criminal a sweet deal for ratting the other out, they elicited two confessions. That sweet deal was so tempting that Bonnie realized she couldn’t trust Clyde to cooperate with their plan to deny their crime, just as Clyde realized he couldn’t trust Bonnie to cooperate with their plan. This failure to cooperate led to a worse outcome for both of them. The police are the real winners here, and because their strategy got both Bonnie and Clyde to confess, they didn’t end up giving either of them the sweet deal. Clearly being a savvy game theorist can confer a strategic advantage.
Examples of the Prisoner’s Dilemma
The Prisoner’s Dilemma highlights the difficulty of getting people to cooperate. The tension that it highlights extends well beyond the Pepsi versus Coke advertising wars or the story of Bonnie versus Clyde. As you start thinking like a game theorist, you’ll come to see Prisoner’s Dilemma’s everywhere.
The tragedy of commons leads shared resources to be overused.

Recall from Chapter 10 that the “tragedy of the commons” is a story that shows how shared resources tend to be overused in a way that makes everyone worse off. It’s an insight usually told as a story about two farmers who are both allowed to graze their sheep on the grassy town square, which is called the commons. The best outcome involves both farmers grazing their sheep on the commons only every few days, so that there’s plenty of time for the grass to grow back. But there’s a temptation to graze your sheep on the commons every day, so that your sheep get more grass, even if this means that there’s nothing left for the other farmer’s flock. The tragedy is that this temptation yields a Nash equilibrium in which both farmers graze their sheep on the commons every day, and this overgrazing kills the grass, with the unfortunate result that the commons yield little grass for either flock.
This story is an illustration of the Prisoner’s Dilemma, and it’s a metaphor for problems that often arise when there are shared resources, as in many environmental problems. Just as farmers are tempted to overgraze the town commons, the oceans are depleted by fishermen who overfish, and the atmosphere is destroyed by factories that emit too much pollution. Beyond the environment, drivers who overuse public roads create traffic jams, politicians who care about special interests overspend, and your friends who overorder when you are splitting the bill are the reason that your group’s restaurant bill is so large. In each case, the tragedy of the overuse of common resources is due to a failure to cooperate and only take your fair share.
EVERYDAY Economics
Can game theory help get money out of politics?
One reason why there’s been so little effort to reduce the role of money in politics is that incumbent politicians get most of the donations, and so few members of Congress actually want to pass a reform that would limit campaign contributions.
Suppose that an eccentric billionaire wants to see a campaign finance reform bill pass. He could simply promise that if this bill didn’t pass then he would donate a billion dollars to fight whichever party delivered the fewest votes. The result is that Democrats couldn’t afford to be the minority responsible for the bill failing, and so they would all vote for the bill. Similarly, Republicans couldn’t afford to be the minority responsible for the bill failing, so they would also vote for it. The result is that the reform bill would pass. And the best part for that billionaire: It costs him nothing. He only promised to make a big donation if the bill failed, and game theory suggests his bill will pass.
You may have noticed a similarity across all of these games—the Nash equilibrium involves both players defecting. Don’t let that fool you into thinking that you should always defect in all strategic interactions. Rather, each of these examples are variants of exactly the same game, the Prisoner’s Dilemma. As we turn to examining other games, you’ll see many different outcomes emerge.

