19.1 Risk Aversion
When you finish college, should you work for a large, stable company that will pay you a reliable salary? Or launch a start-up, which could either succeed wildly or fail dismally? It’s a tough choice. But it’s just one of the many risky decisions that you’re going to have to make.
Life is risky, and whether you’re skiing, investing, or just trying to cross the street without getting run over, you never really know what’s going to happen. You’re going to need to make good decisions even when the consequences of each choice are uncertain. And so our next task is to figure out how to extend the cost-benefit principle so that it can provide useful guidance even when you don’t know the exact consequences of each choice.
Understanding Risk
There’s risk whenever you don’t know what the outcome will be with certainty. And you can’t eliminate risk from your life. Rather, the smart thing to do is to make the best decisions you can, taking account of those risks.
Risk is a set of probabilities and payoffs.
While every risk is different, you can always strip it down to two essential elements: probabilities and payoffs. You should look at the probability of each outcome occurring, and the payoff you’ll get from each of these outcomes if they do occur.
For instance, perhaps you have the opportunity to invest in a new, promising tech company—SharkField. However, it’s still in its early stages, so success isn’t guaranteed. If you invest in this company, your wealth could be $20,000 higher. But, it’s a risky business and there’s uncertainty involved. If SharkField fails, your wealth would be $20,000 lower. You do some analysis and you decide that SharkField has a 50% chance of success. Should you invest?
If your winnings offset your losses on average, it’s a fair bet.
Whether you should invest in SharkField depends on how you feel about uncertainty. Making this investment is like making a bet: Heads, your wealth is $20,000 higher; tails, your wealth is $20,000 lower. In fact, this is an example of a fair bet—a gamble that, on average, will leave you with the same amount of money. In any particular instance, your wealth will change. Half the time, it’ll be $20,000 higher; the other half, it’ll be $20,000 lower. But on average, these gains and losses will cancel out, leaving your wealth unchanged.
Risk-averse people reject fair bets.
Here’s the thing about risk: You’re better off avoiding it. Most people are risk averse, which means that they dislike uncertainty. A risk-averse person will never take a fair bet, because the fair bet simply takes your current level of wealth and adds further uncertainty. In fact, risk-averse people will often pay good money to avoid risk—that’s what insurance markets are all about.
Let’s look at their risk aversion through the lens of the cost-benefit principle. You should refuse a fair bet if the costs exceed the benefits. What’s the cost of taking this bet? It’s a 50% chance that your wealth will be $20,000 lower. And the benefit? It’s a 50% chance that your wealth will be $20,000 higher. The probabilities are the same in both cases, and so are the sums of money. Yet risk-averse people find that the cost—the decline in their well-being when their wealth level is $20,000 lower—exceeds the benefit, which is the gain in their well-being when their wealth level is $20,000 higher. Why is that?
What’s happening here is that you’re not just looking at financial costs and benefits; you’re thinking about the costs and benefits for your well-being. Let’s turn to figuring out how and why the marginal decrease in your well-being from your wealth level being $20,000 lower outweighs the marginal increase in your well-being from your wealth level being $20,000 higher.
Diminishing Marginal Utility
To evaluate a risky choice, you need to be able to think in terms of the marginal benefits, and not just focus on the dollar amounts involved. After all, money is just a means to an end—a way to enjoy a better life. The marginal benefit of a dollar is how much that dollar helps you enjoy a better life or, put another way, how much it improves your well-being. Economists use the word utility to describe your level of well-being. If your ultimate objective is to live the best possible life, you should make utility—rather than money—central to how you evaluate your choices.
Marginal utility is highest when you are poor and declines as your wealth grows.
Your utility is closely related to your wealth. After all, greater wealth enables you to make choices that will make you happier and enjoy more utility, whether it’s due to buying more stuff, working less, helping those you love, or donating to charity. As a result, more wealth leads to more utility. But your utility probably doesn’t rise one-for-one with your wealth. After all, when you’re poor, an extra $20,000 would make a big difference in your quality of life and hence utility. But when you’re doing well, an extra $20,000 doesn’t help as much. Figure 1 shows a typical utility function, which embodies this idea. The utility function starts off steep—each extra dollar raises utility by a lot—and then flattens out, because at high levels of wealth, more money doesn’t make as much of a difference as it does at lower levels of wealth.
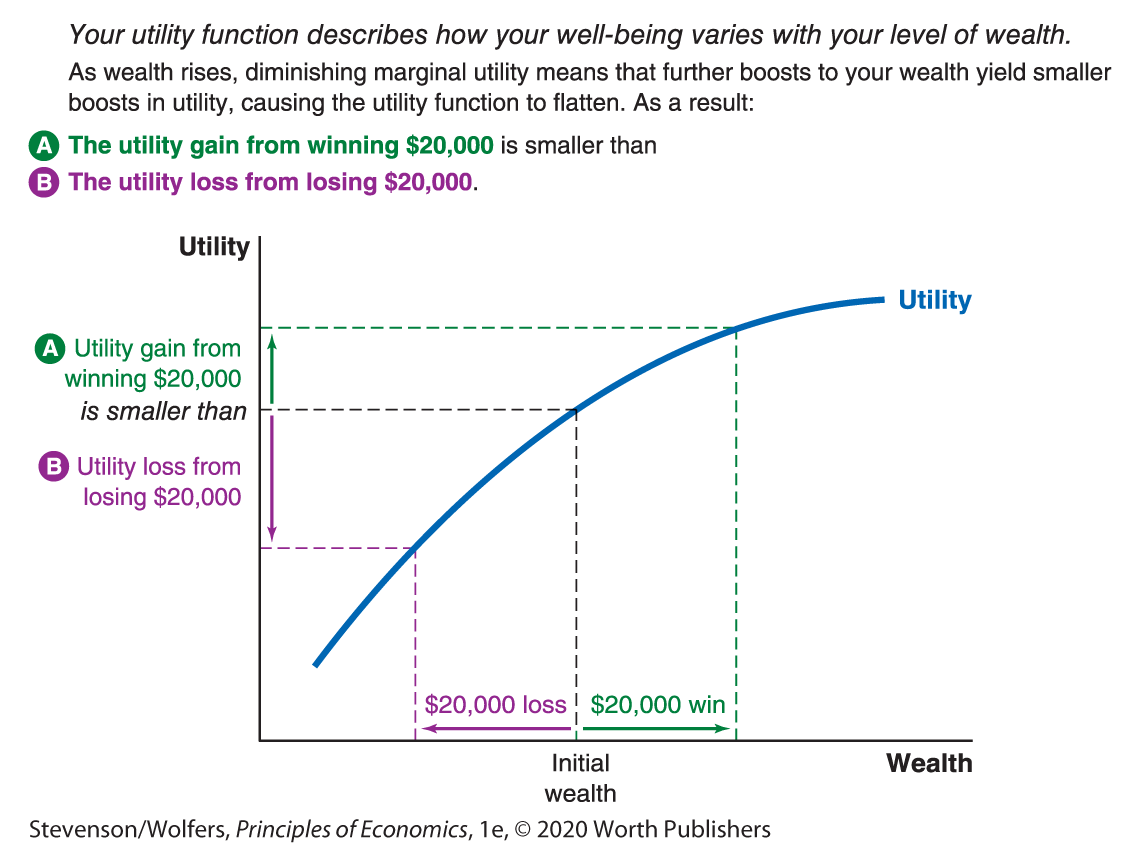
Figure 1 | Your Utility Function
The marginal principle reminds you to think at the margin, and there’s diminishing marginal benefit from each extra dollar. Just as your third pair of jeans yields a smaller marginal benefit to you than your second pair, your 30,000th dollar is less useful than your 20,000th. To be precise, marginal utility is the boost to utility you get from one more dollar. And because each additional dollar yields a smaller boost to your well-being, you have diminishing marginal utility. This means that your marginal utility may be large when you are poor, but it gets smaller as you get richer. Diminishing marginal utility is the reason that the utility function gets flatter at each higher level of wealth.
Diminishing marginal utility makes you risk averse.
Diminishing marginal utility explains why you’re risk averse. Again, consider your opportunity to invest in SharkField. But now focus on the payoffs in terms of what they mean for your utility, rather than your level of wealth.
Figure 1 illustrates that the gain in utility from a $20,000 higher level of wealth is smaller than the loss in utility from a $20,000 lower level of wealth. And so if you apply the cost-benefit principle and evaluate the costs and benefits in terms of utility, the costs of a fair bet exceed the benefits. When you look at utility rather than money, the potential upside isn’t large enough to compensate for the potential downside.
Notice the central role of diminishing marginal utility in making you risk averse. You dislike risk because you stand to gain money that has a low marginal utility, while you stand to lose money that is more valuable to you because it has a higher marginal utility.
The Risk-Reward Trade-off
Risk aversion should not lead you to avoid all risks. Rather, you should take risks when the benefits exceed the costs—again, making sure to measure benefits and costs in terms of utility. That’s more likely to happen when greater risk is also coupled with greater reward.

It all involves risk.
You don’t want to eliminate all risk.

It all involves risk.
Let me tell you a story about I.M. Scared, who went on a mission to eliminate risk from her life. She never gambled in Las Vegas, never invested in risky stocks, and never went skydiving. Beyond that, she never ate eggs for breakfast because of the risk that her eggs were contaminated with Salmonella. Come to think of it, she never ate because she didn’t want to risk choking on her food. She didn’t drink water because she was worried about the risk of contaminants. She didn’t get a job because she didn’t want to risk getting fired. In fact, she never left the house because she didn’t want to risk getting exposed to cancer-causing sunrays or getting run over by a car. And she never fell in love because she wanted to avoid the risk of heartbreak.
You know how this story ends. When you’ve eliminated all risk from your life, you’re only left with certainty: the certainty of a quick and lonely death.
There’s a trade-off between risk and reward.
While you want to avoid some risks, you shouldn’t try to eliminate all risk. Indeed, it’s often worth taking calculated risks. The question is simply whether the rewards outweigh the risk. That is, you should think in terms of a risk-reward trade-off, where you’re better off taking a risky choice if it comes with a sufficiently high reward.
We’ve already seen that risk aversion will lead you not to make an investment in SharkField if its upside potential is equal to its downside potential. That lesson, which we first saw in Figure 1, is now illustrated in the left panel of Figure 2. Now let’s reevaluate the investment when SharkField has better prospects than you originally thought. If it succeeds, your wealth will increase by $30,000; if it fails your wealth will only decrease by $10,000. It still has only a 50% chance of succeeding. But now you are comparing the utility gain from your wealth level being $30,000 higher to the utility loss of your wealth level being $10,000 lower.

Figure 2 | The Risk-Reward Trade-off
This investment is just as risky as before—the difference in your wealth between the good and bad outcome is still $40,000—but the reward is now $10,000 higher. Now that it’s a more rewarding investment, you might just find it a bet worth making. Indeed, the right panel of Figure 2 illustrates an example of someone whose utility gain from their wealth being $30,000 higher exceeds their utility loss from their wealth being $10,000 lower. The cost-benefit principle says they should make this risky investment.
The big idea here is that the greater the reward, the more willing you should be to make a risky investment.
Interpreting the DATA
The risk-reward trade-off
The risk-reward trade-off has an obvious implication: People will only be willing to make risky investments if the potential returns are high enough. And sure enough, the history of investment returns bears this out.
Figure 3 shows the average historical risk and reward associated with several major types of investments. The vertical axis shows the reward, which is the average annual return—the yearly increase in your wealth—from a $100 investment. The horizontal axis shows how risky each investment is. (The standard deviation is a measure of how much the value of an investment typically rises or falls each year.) The least risky investment is to buy U.S. Treasury bills, which are effectively a loan to the U.S. government for a few weeks. There’s virtually no chance of the government going bust and not paying back the loan. So when you invest in Treasury bills, you have little chance of losing your investment. That’s why people are willing to invest in Treasury bills despite the low average annual return. By contrast, buying stocks in newly emerging economies, or stocks in small companies, is very risky. So while lots of people lose their investment, when it works out there’s a high return. That’s because investors will only take on this much risk if they expect a high return on average.
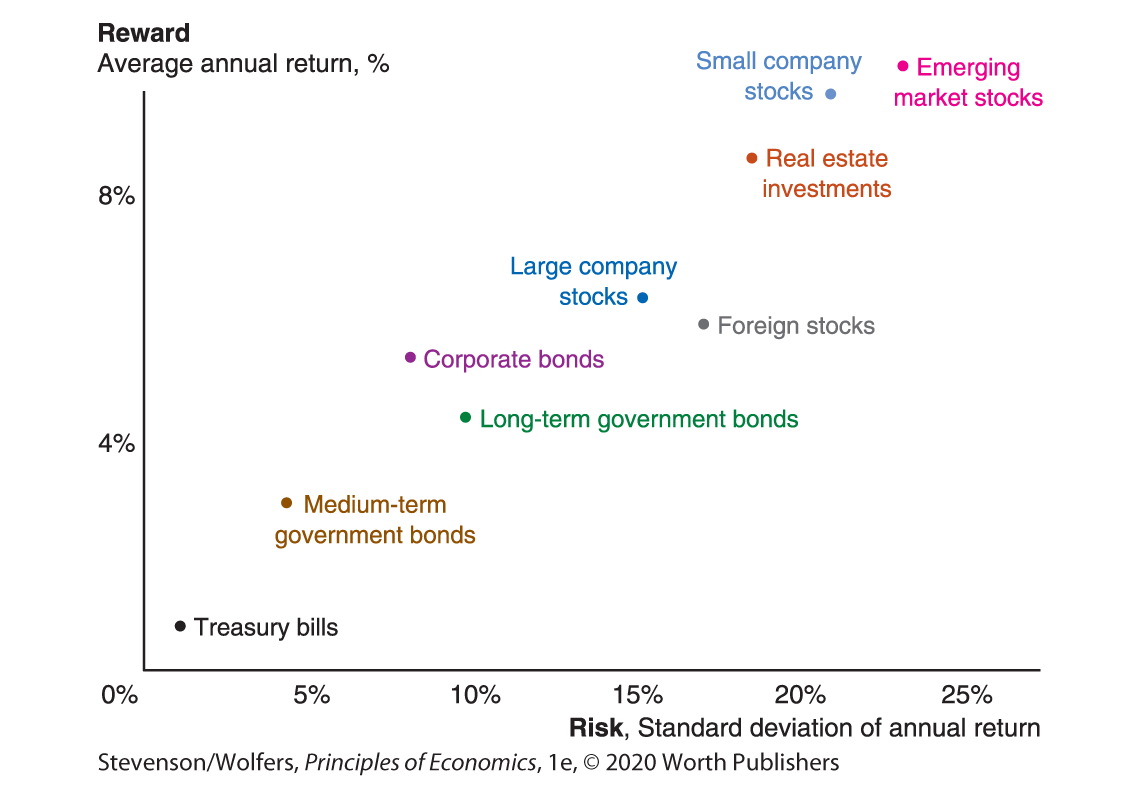
Figure 3 | The Risk-Reward Trade-off for Investments
Realize that each of us has different degrees of risk aversion. And so as you think about your own investment strategy, you’ll need to think about whether the reward associated with riskier investments is high enough to make it a good deal for you.
More risk-averse people will accept fewer risks.

Who is more likely to make a risky investment?
Your willingness to accept a given risk-reward combination reflects your level of risk aversion, which in turn depends on your temperament and your life situation. Let’s return to SharkField with its more favorable assessment—a fifty-fifty chance of a $30,000 increase in your wealth or a $10,000 decrease in your wealth. This time, however, we’ll look at the choice through the eyes of two people in different circumstances and see why they might make different decisions.
Imani works as a nonprofit executive, has no debt, and rents an affordable one-bedroom apartment. She’s been diligent about saving and has a $20,000 nest egg built up. She’s a happy-go-lucky type who says she has a bit of a Tigger-like personality. She’s excited about the idea of investing in a new tech company, and she doesn’t feel that she has a lot to lose. If she loses $10,000, she would have to cut back on some expenses like eating out, but she won’t have to make any big changes in her spending habits. If the business succeeds, she’ll probably move to a nicer apartment and take an international vacation. All of this means that while she has diminishing marginal utility, it’s not diminishing very rapidly—her marginal utility at low levels of wealth is only a little bit higher than at high levels of wealth. This means that she’s not very risk averse, and the left panel of Figure 4 shows that her utility function doesn’t flatten out much. As a result, Imani’s utility gain from winning $30,000 exceeds the utility loss from losing $10,000. The cost-benefit principle tells her that investing in this new business is a risk worth taking.

Figure 4 | Your Willingness to Take on Risk Depends on Your Level of Risk Aversion
Now, meet Lucas. He’s a regional manager for a large corporation, and as a single dad, he’s responsible for providing for his two kids. He has worked hard to save despite the expenses associated with raising kids, and he’s succeeded in building up a $20,000 nest egg. Lucas knows how important the nest egg is in case he ever loses his job. He’s a bit of an Eeyore, perpetually worried that the worst will happen. His job pays as well as Imani’s, but his family has a lot of expenses. His kids go to the public school, but as a single parent he has a babysitter who picks them up in the afternoon and takes care of them until he gets home from work. He has a larger apartment than Imani so that his kids have their own room. Even though he’s doing as well financially as Imani, he spends more on necessities like food, housing, and work-related expenses like commuting and child care. That means that his family could face real hardship if he faces a decrease in his wealth. All of this means that he’s very risk averse. His utility function, shown in the right panel of Figure 4, is initially very steep. This indicates how hard it would be to absorb a $10,000 loss. Then his utility function flattens out quickly because he has rapidly declining marginal utility. For Lucas, the utility gained from a $30,000 increase in his wealth just isn’t big enough to offset the utility sacrificed from a $10,000 decrease in his wealth. The cost-benefit principle tells him not to make this risky investment.
Are you more like Imani or Lucas—more of a Tigger or an Eeyore? The more risk averse you are, the less willing you are to take on risk. As you evaluate risky choices, it’s important to do so with an awareness of your level of risk aversion, which reflects both your temperament and your circumstances.
EVERYDAY Economics
How risk averse are you?
Here’s a simple quiz to assess how risk averse you are, compared to other people:

Risk aversion motivates many choices you make.
Risk aversion doesn’t just guide your financial choices; it should also guide the many risky decisions you face across different domains of your life. Indeed, studies have found that the more risk averse someone is, the less likely they are to take risks with their health by smoking, binge drinking, being overweight, or failing to wear a seatbelt. Risk averse people are less likely to start their own businesses and less likely to invest in stocks. They’re less likely to change jobs, move to another state, or immigrate. They’re more likely to buy insurance and they’re more likely to own their own home. They are more likely to work in steady public-sector jobs that offer a reliable wage and little risk of being fired. The logic in each case is the same: If you’re sufficiently risk averse, the lower utility associated with the downside outweighs the potentially higher utility from the upside.
Expected Utility
Let’s summarize what we’ve learned so far. Whenever you’re deciding whether to take a risk, your decision should depend on three factors: the size of the risk relative to the reward, whether the stakes are high or low, and your degree of risk aversion. A choice that’s good for me might be bad for you since your level of risk aversion likely differs from mine.
This means that you can’t rely on someone else to tell you how to invest, what career to pursue, or whether to start a new business. No outside expert can judge whether you should take a particular risk without knowing your utility function. And if you can’t rely on experts, you’ll need a systematic approach so that you can evaluate risky choices for yourself. That’s our next task.
Expected utility is just your average utility.
When you’re comparing choices that involve no risk—do you want a Pepsi or a Coke?—you’ll choose whichever makes you happiest. That is, you’ll make the choice that yields the most utility.
But when you’re choosing among risky alternatives, you don’t know what the outcome will be. For instance, if you start your own business, your utility might be quite high (if your business succeeds), or it might be low (if it fails). Even though you don’t know what your utility will be in any specific instance, you can calculate what it will be on average.
Your expected utility measures what your utility will be, on average, if you make a particular choice. You calculate your expected utility as a weighted average of the different utility levels associated with each possible outcome, weighted by the probability that outcome occurs. For instance, if there are two possible outcomes from starting a new business, your expected utility is:

Do the Economics
You currently have a wealth of $50,000 and are offered a chance to invest in a risky company. If you invest, there’s a 50% chance that you’ll gain $30,000 next year, raising your wealth to $80,000, and a 50% chance the company fails and you’ll lose $10,000, bringing your wealth down to $40,000.
Your expected utility is:

Note: U($80,000) means “Your utility when your wealth is $80,000.”
The answer will depend on your utility function. There isn’t a natural unit for measuring utility, so we’ll measure it in terms of how you feel about your life, on a 0 to 10 scale. Let’s say that with $80,000 in wealth, you’d rate your utility as being 8 out of 10. And if you only had $40,000, you’d rate your utility as being 6 out of 10. Therefore:

By comparison, with your current wealth of $50,000, you rate your utility at 6½ out of 10. As a result, your expected utility if you invest in this company is higher than your current utility, so you should make the investment.
What should you do if there’s only a 20% chance your investment will pan out?
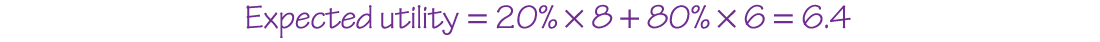
Since your current wealth yields a utility level of 6½, you’ll be happier if you don’t invest in that company.
As an exercise, show that you’ll be better off investing in this company as long as the probability of success is at least 25%.
In other words, you should choose the options with the largest expected utility. If you follow this rule, your decisions will, on average, yield a higher level of well-being.
Why do people gamble?
Risk aversion is a powerful concept that explains why it’s a good idea to try to avoid unnecessary risk. But some people seem to seek out risk through gambling or buying lottery tickets. Why do people do this? Some people speculate that gamblers are risk loving, which means that they actually prefer uncertainty. Someone who is risk loving is not only comfortable with uncertainty; they like it so much that they’re willing to lose money in order to experience it. (And people lose money on average when gambling.)

Part of the fun is that if he wins, you win.
But I don’t find this to be a convincing explanation for gambling. Most people who spend a few dollars on lottery tickets also spend money insuring their houses against burning down, insuring their car against theft, and buying health insurance—all ways in which they pay to reduce risk. So most people who gamble don’t seem to like risk in their daily lives. A better answer for why people gamble is that it is a form of entertainment. A night at the casino can be fun, just as you might enjoy a night at a concert. A few bets at the racetrack is part of how some people cheer on some extraordinary athletes, just as you cheer on your favorite players at a baseball game. A lottery ticket offers you the fantasy that you might one day be rich, just as a sci-fi novel can offer you the fantasy of a better future. By this view, it’s fun, not love of risk, that drives many people to gamble.

