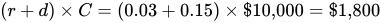26.3 Making Investment Decisions
Now that you’ve got these tools in your analytic toolkit, it’s time to put them to work. They’ll be essential for our next task, which is to develop the framework that top managers use to evaluate investment opportunities.
How to Evaluate an Investment Opportunity
There’s no better way to illustrate this framework than to work through a real-world problem, so put yourself in Valentina’s shoes as we work through her assignment. She has gathered all the relevant information and now needs to put it together to figure out whether to invest in another wind turbine.
Compare the present value of costs and benefits.
An investment is like any other choice—the cost-benefit principle says it’s worth doing if the benefits exceed the costs. The wrinkle is that the costs and benefits accrue at different points in time. The opportunity cost principle reminds you that revenues you receive in the future are less valuable because you’ll forgo the opportunity to earn interest on those funds. That’s why you should focus on the present value of the costs and benefits associated with an investment, which account for this opportunity cost. Computing the present value of both your costs and benefits puts them in similar units—today’s dollars—which makes them comparable. The difference between the present value of your revenues and the present value of your costs tells you how much an investment opportunity will boost your profits relative to investing those funds in your next best alternative.
All of this yields clear advice that should guide your analysis: Invest in new capital if the present value of the benefits exceeds the present value of the costs.
The present value of an up-front cost is simply the up-front cost.

Turbines depreciate.
Valentina sets to work, making a few calculations. The cost of this investment is the easy part: Buying a wind turbine costs $4 million. Because this cost is incurred in the present, it has a present value of $4 million. (If the costs accrued over many years, then you would evaluate the total of the present value of each of those future costs.) As we’re about to see, the real work of evaluating most investment projects comes in valuing the stream of future benefits.
Take account of depreciation when projecting future revenue.
To figure out the benefits, Valentina needs to forecast the future annual revenues one extra turbine will generate, and then calculate their corresponding present values. Her company’s engineers have provided Valentina with data summarizing their expectations for the extra energy the new turbine will generate each year; and she has translated those gains into revenue forecasts.
This year: Installing the turbine will take all year, so it will generate no revenue.
First year revenue: The turbine will generate revenue of $600,000.
Revenue in following years: As the turbine ages, it won’t be as productive due to depreciation. It’ll break down more often and spend more days out of service being repaired. The engineers report that, on average, a wind turbine will produce 4% less output each year than it did in the previous year. They’re describing the depreciation rate, which is the proportion of an investment’s remaining productive capacity you lose each year due to depreciation. We’ll use the letter d to denote the depreciation rate.
Valentina makes sure her revenue forecasts account for this depreciation rate. She expects the price she’ll get for the electricity the turbine generates will keep up with inflation, and so depreciation is the only reason her real revenues will change over time. That’s why she forecasts that the real revenue the turbine generates will decline from $600,000 in the first year, to be 4% lower at $576,000 in the second year, and then another 4% lower at $552,960 in the third year. As you read down each row of Figure 9, you’ll see that in each subsequent year, she forecasts that the turbine will generate 4% less revenue than it did the previous year.

Figure 9 | Calculating the Stream of Revenues in Present Value
Convert future revenues into their present values.
Having forecast the turbine’s future revenues, Valentina needs to account for the fact that the value of this money depends on when she receives it. She does this by calculating the present value of each year’s revenue forecast. She applies a 6% real interest rate to the discounting formula, because that’s what the folks in her company’s treasury department say they could earn if they invested the $4 million elsewhere.
The final column of Figure 9 shows the present value of each year’s revenue forecast. The turbine generates no revenue while it’s being installed. After one year, it creates $600,000 in revenue. But it’ll take a year to get that revenue, so Valentina needs to discount it, multiplying $600,000 by 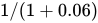
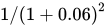
A good wind turbine can last a long time, so Valentina’s actual spreadsheet goes on for dozens more rows showing the present value of the revenue she forecasts it’ll generate each year over many future decades. I can’t show you the whole thing here, but Figure 10 shows the column that matters most to Valentina—the present value of the additional revenue she forecasts the turbine will generate in each year. Add it all up, and you get 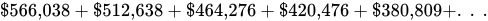
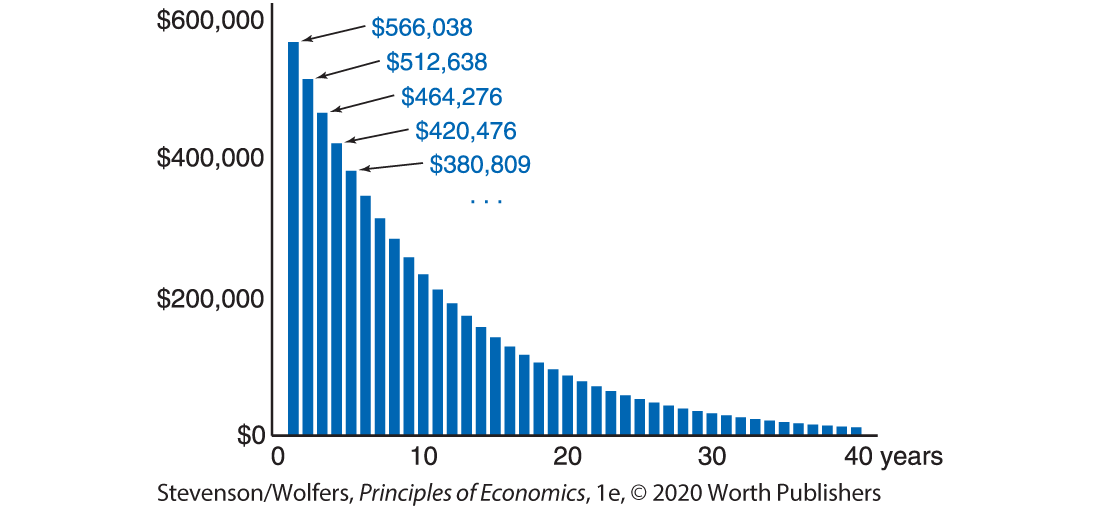
Figure 10 | Present Value of Each Year’s Future Revenue
A shortcut: Use the valuation formula to calculate the present value of a stream of future revenues.
It might appear that calculating the present value of a stream of future revenues takes a lot of spreadsheet work. But there’s a shortcut that makes it a lot easier. The valuation formula says that the present value of a stream of payments that starts with next year’s revenue and subsequent payments decline or depreciate each year by d percent is:

It’s called the valuation formula because it tells you how much you would value this future stream of revenue in today’s dollars. (This bit is in parentheses, so you can skip it. If you want some intuition for where this formula comes from, notice in the last column of Figure 9 that the present value of each year’s revenue is 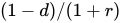
Top executives know how to use this formula, even if they’ve forgotten the math that leads to it. Most importantly, they know when it applies, which is anytime you’re evaluating the expected value of a long-lasting stream of future revenues that start next year and then decline at a constant proportional rate over time.
Do the Economics
Let’s apply the valuation formula to Valentina’s investment decision. Her turbine will generate $600,000 revenue in its first year, the real interest rate is 6%, the depreciation rate is 4%, and it’ll keep generating revenues for many decades:

This shortcut worked perfectly, producing exactly the same answer as when we calculated each year’s revenues and calculated their present values.
Invest if the present value of benefits exceeds the present value of costs.
At this point, Valentina has all the information she needs. Having assessed both the costs and benefits in present value terms, she can return to the cost-benefit principle. The total benefits of purchasing the turbine—many years of future revenue that add up to a present value of $6 million—exceed the up-front cost of $4 million. This looks like an extremely profitable investment, so she advises her company’s CEO to purchase that extra wind turbine. It’s a smart decision that will add $2 million to her company’s value.
The Rational Rule for Investors
You’ll boost your company’s long-run profitability any time you invest in an opportunity where the present value of your future revenues exceeds the up-front cost. It’s profitable because the benefits exceed the costs. We focus on present values to put these costs and benefits in comparable terms, accounting for the opportunity cost of having to wait to receive those future revenues.
At this point, you’ve uncovered a powerful rule you can apply to your company’s investment decisions:
The Rational Rule for Investors: Pursue an investment opportunity if the present value of future revenues exceeds the up-front cost, C. This means you should invest when:
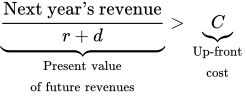
Follow this rule, and every investment will boost your long-run profits. The Rational Rule for Investors puts together the advice from three of the four core principles in one sentence. It takes the big question facing managers about how much to invest, and applies the marginal principle, focusing on the simpler question of whether you should invest in one more turbine. The cost-benefit principle suggests that yes, you should, if the benefits—which are the future revenues you’ll receive—exceed the up-front cost. To compare these, you should focus on present values that embed the opportunity cost principle, evaluating future revenues in terms of what you would have to give up to get them.
The Rational Rule for Investors provides good advice because it’ll lead you to invest only when it’ll boost your long-run profitability. Let’s apply it to the most important investment decision you may ever make.
EVERYDAY Economics
Your decision to invest in education

An incredibly important investment.
Your education is a lot like a wind turbine: It involves a big up-front cost (which you’re incurring now), and it’ll yield a stream of benefits that will accrue over the rest of your life. Indeed, you can evaluate the benefits of investing in your intellectual machinery using the same ideas that managers use to evaluate investments in any other kind of machinery.
One of the biggest benefits of education is the higher salary you’ll earn as a result of having more education. Let’s take a stab at valuing these higher earnings using the valuation formula. We’ll need three inputs: the extra revenue you get from your college degree, the depreciation rate of your degree, and the real interest rate you could earn investing in your next best alternative.
Measuring the extra revenue: The median earnings of someone with a bachelor’s degree (but no graduate degree) in 2017 was $53,900, while those with only a high school degree earned $32,300. The difference is roughly $22,000 dollars per year. (An associate’s degree boosts your earnings by about half this amount.)
Measuring the depreciation rate: College graduates continue to outearn high school graduates throughout their lives, suggesting that whatever you learn in college sticks with you throughout your career. But your degree still depreciates because as you age you’re less likely to work, and economists estimate the depreciation rate to be around 2% a year.
The real interest rate: We’ll plug in a value for the real interest rate of 3%, which is roughly the rate at which college graduates can borrow and lend. (You can experiment with other values.)
Put it all together, and we get:

Let that sink in. A four-year college degree is so valuable that it’s worth nearly half a million dollars in present value. (And it follows that an associate’s degree provides around half this boost and is worth nearly a quarter of a million dollars.) To evaluate the relevant costs, apply the opportunity cost principle and ask “or what?” Don’t just count the costs of tuition; you also need to factor in the opportunity cost of the income you could otherwise have earned if you were in the workforce instead of college. It’s a good bet that the present discounted value of your degree will be much higher than the present value of tuition plus the wages you’re giving up to be in school.
In short, it’s unlikely that the up-front cost of college is as large as the present value of the benefit, suggesting that college is a very profitable investment. Given how profitable it is, I would urge you to invest in reading the rest of this chapter about investment!
An Alternative Perspective: The User Cost of Capital
So far, we’ve analyzed Valentina’s investment decision as if she’s deciding whether to buy a wind turbine that her company will keep forever—or at least until it breaks down. That required assessing the full set of costs and benefits that accrue over the turbine’s entire lifetime. You can gain an alternative perspective on the Rational Rule for Investors by pushing the marginal principle even further. Instead of asking whether to buy a machine you’ll keep for many decades, you might ask: Should I buy one more machine for one more year? That is, should you buy a machine even if you plan on selling it in a year’s time?
The cost-benefit principle says your answer should be yes, if the marginal benefits exceed the marginal costs. And so this alternative perspective focuses on the marginal benefit and marginal cost of using that extra machine for one more year. (And at the end of that year, you can evaluate what to do the following year.)
The marginal benefit is fairly straightforward: That extra machine will generate extra revenue, and we’ll describe this extra revenue you’ll earn next year as being next year’s revenue.
The user cost of capital is forgone interest plus depreciation.
What is the marginal cost of buying one more wind turbine at the start of the year, and then selling it at the end? There are two costs to consider:
Depreciation: The turbine will be worth less at the end of the year because of depreciation. If the depreciation rate is 4%, then a $4 million turbine will sell for 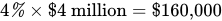
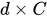
Forgone interest: The opportunity cost principle reminds you that there’s another cost to consider, because you’re tying up your funds for a year. To assess this cost, ask yourself: I could invest in this machine, or what? The opportunity cost for Valentina of investing $4 million in the wind turbine for a year is that her company could earn a 6% return on those funds, which means that she’s forgoing 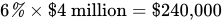

Putting these two pieces together yields the user cost of capital, which is the extra cost associated with using one more machine next year. It’s called the user cost—or sometimes the rental cost—because it’s what you’re effectively paying to “use” or “rent” the turbine for a year. The user cost of employing one more machine for a year is equal to the depreciation cost 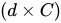
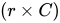
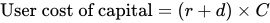
Do the Economics
The engineers tell Valentina that if she spends $4 million buying a new wind turbine to use next year, at the end of the year it’ll be worth 4% less. The real interest rate is 6% per year. Calculate the user cost of owning this turbine for one year.

Compare the user cost of capital with next year’s additional revenue.

Invest if next year’s revenue exceeds the user cost of capital.
The user cost of capital represents the marginal cost of adding one more machine for a year. You should compare it to the corresponding marginal benefit of adding that extra turbine, which is the extra revenue you’ll earn next year. Comparing these suggests that it’ll be profitable to invest in an additional turbine for next year if:

Let’s apply this logic to Valentina’s company. The marginal benefit of investing in a turbine for a year is the extra revenue it’ll generate next year. If she’s looking at a new turbine, that’ll be the first-year revenue, which you may recall is $600,000. That marginal benefit exceeds the user cost of capital we just calculated to be $400,000, so this alternative perspective also concludes that she should invest in buying the turbine.
Both perspectives yield the same advice.
You can re-arrange this formula by dividing both sides by 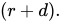
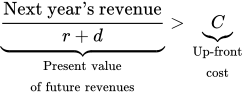
This is exactly the same as the Rational Rule for Investors! That means you’ll come to the same decision by evaluating:
- Whether the present value of all future revenues over the life of the machine exceeds the up-front cost (as we did a few pages back); or
- Whether next year’s marginal revenue exceeds the user cost of buying a machine for just one year (as we just did).
This equivalence is useful because it means you can apply whichever approach you find most intuitive in the context of the investment opportunity you’re evaluating. In some settings, it’ll be easiest to evaluate the present value of future revenues, while in others it’ll be more natural to analyze the user cost of capital.
EVERYDAY Economics
The true cost of car ownership

Depreciation is costly.
Most people who buy a car do so because it’s convenient. But before you invest in a car, it’s worth evaluating how much you’re paying each year for that convenience. Try asking your friends what they think the annual cost of car ownership is. Chances are they’ll focus on the out-of-pocket costs, like gas, insurance, repairs, and registration.
But too often, people miss the most important expense: The user cost of capital. Cars depreciate rapidly: If you buy a new car you’ll lose 20% almost right away, and beyond the first year, cars typically lose around 15% of their remaining value each year after that. That means that if you buy a used car, it will lose 15% of its value each year that you own it. If you buy a used car worth about $10,000, a year later, it’ll only be worth $8,500. And you won’t earn any interest on the money tied up in that car, so if the real interest rate is 3%, you’ll forgo $300 in interest. Add it up, and the user cost of capital is