Population Ecotoxicology
Exposure and Effects of Environmental Chemicals
Abstract
Just as organisms are affected by environmental contaminants, so too can populations. Instead of looking for cellular or chemical changes in organisms, biologists interested in population ecotoxicology look for changes in reproductive rate, mortality rate, or similar signs in a population. As we increase the scale of our concerns, going from organisms to populations, and then eventually to communities and ecosystems, stochasticity or randomness tends to increase. It becomes increasingly important, therefore, to identify the possible sources of this randomness. For example, we define demographic stochasticity as that which occurs due to age, sex, or reproductive status and environmental stochasticity is that which is due to randomness in the environment.
Keywords
Ecological scale; population ecotoxicology; mesocosm; additive mortality; compensatory mortality; demographic stochasticity; environmental stochasticity
[E]ach level (of biological integration) offers unique problems and insights, and … each level finds its explanations of mechanisms in the levels below, and its significance in the levels above.
Introduction: Working Beyond Individual Organisms
The study of the effects of chemicals on individual organisms is most often encountered in the guise of toxicity assessment, as summarized in Chapter 2. Yet, many ecotoxicologists are primarily interested in answering questions that focus on outcomes linked to effects observed in the field and not necessarily constrained to a single species, such as when working with an endangered species. Thus, an understanding of the principles of population ecology is necessary for ecotoxicologists to pursue knowledge of adverse effects in the field. Describing cause and effect relationships between chemicals released to the environment and their effects on populations—or as we will encounter in the next chapter, their effects on communities and ecosystems—is frequently a conundrum for ecotoxicologists to solve.
Although often observed and noted, large or scale differences enter our analysis of exposure and effects perhaps because a scale difference related to shifts from organism to population levels of biological organization, or due to a realization that exposures in the field capture spatiotemporal (space and time) scales inadequately considered in laboratory toxicity tests. Indeed, the simple observation of scale differences serves as a source of confounding factors linked to multiple stressors co-occurring with chemicals in the environment. Multiple stressors present even more challenges in characterizing exposure and effects relationships at any level of biological organization, particularly if chemicals occur at low levels for long time periods over large spatial scales. However, when we leave the realm of individual organisms—for example, exposing 10 organisms in each concentration of a laboratory toxicity test, or estimating species-specific effects in resident species based on the outcomes of these tests—we enter a larger range of possibilities in populations or communities and ecosystems where ecotoxicologists use various analytical approaches and deploy a wide range of tools to characterize these scale-dependent interactions. In other words, the larger the scale of investigation, the greater number of confounding factors to deal with.
We collectively discover conceptual frameworks, some of which are presented in published literature, while others are unique to the specific questions for the population, habitats, or landscapes at hand. Biological and ecological systems exist as hierarchical structures, wherein interactions among different levels within a system can be functionally linked and regulated “control systems” similar to the banners of physiology, endocrinology, molecular biology, or biochemistry seen at the individual scale. Such functional or process-oriented interplay also occurs at differing spatiotemporal scales, running the spectrum from events that occur relatively slowly (eg, geological events accompanied by ecological events) to more rapidly occurring events (eg, cellular levels of biological organization). Indeed, as agents responding to these contrasting spatiotemporal scales, organisms operate in a region of overlap between biology and ecology (Fig. 10.1).
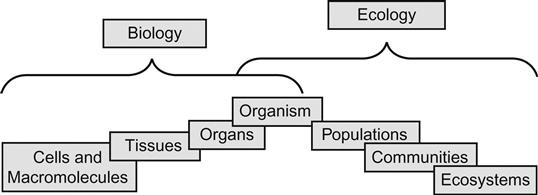
For example, scientists may focus on one of two broad classifications in ecological studies—autecology or the study of an organism and its environment, and synecology, which looks at entire populations or communities. In either case, however, scientists must be aware of the overlap of both the ecological and biological requirements of the organisms under study. Indeed, autecology and synecology may be considered complementary terms distinguished by their interpretive context; for autecology, it is just a matter of scale focusing on the spatiotemporal dynamics of species, whereas synecology encompasses studies focused on distribution, abundance, demography, and interactions between coexisting groups of organisms or species (Cain et al., 2014; Gimme and Hengeveld, 2014). As such, population ecology easily captures the transition between autecology and synecology frames of reference, a transition that affords ecotoxicologists an opportunity to consider chemical effects at a species-specific level of organization. This often includes the study of biological effects for chemical exposures through single-species toxicity tests in the laboratory, followed by estimating responses in field settings by considering relevant endpoint, such as reproductive effects potentially linked to population-level changes in abundance or population dynamics. However, before diving into our overview of population-level studies and tools that an ecotoxicologist commonly deploys in such studies, a brief sojourn would benefit this chapter and the next. Both this chapter and the next anticipate our integrating of a species-specific population focus, largely within an autecological frame of reference, that builds toward a synecological interpretative context pertinent to moving beyond a strictly species-specific, at best an organism-centric view of ecotoxicology.
Spatiotemporal Scales in Ecology and Ecotoxicology
Regardless of the level of biological organization, responses and their relevance within biological and toxicological, or ecological and ecotoxicological contexts cannot be characterized in the absence of spatiotemporal scale (Fig. 10.2). Biological systems are complex, highly interwoven, and, in many respects, entangled systems that are typically characterized by linear rather than nonlinear interactions among their many components. These components can be considered along hierarchical levels of organization. Understanding how changes at one level of biological organization alter emergent patterns or mechanisms at another level of biological organization may be an intractable problem at this time, yet such problems must be considered if we aim to improve the understanding of how contaminants may affect these levels or scales of ecotoxicology. Indeed, ecology—and, to a lesser extent, ecotoxicology as most often practiced today—explicitly or implicitly focuses on landscapes in time and space, landscapes wherein individuals of a species collectively became populations, and populations of various species with all of their various life histories and niches subsequently assembled into communities. All are parts of highly adaptive, dynamic systems of interacting biological and physicochemical components distributed across a wide array of habitats.
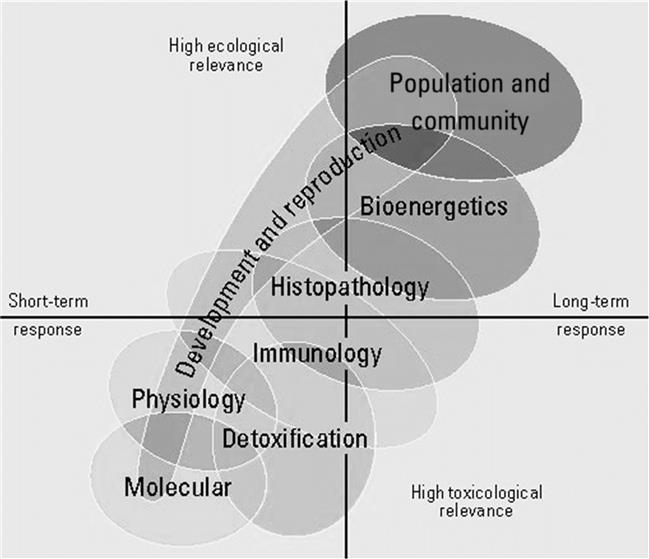
This chapter and the next focus on scale-dependent networks, some simple, others much more complex. Some may be characterized by interactions that involve chemicals as one of many stressors affecting organisms in field settings. Within such field settings and populations, the important endpoints are often those that relate to abundance or actual reproduction. In contrast, laboratory studies often emphasize finer molecular or physiological responses that are of less concern to population ecologists. Within the context of ecological or ecotoxicological relevance, some populations may be more highly valued than others. For example, populations of some species may have greater economic, recreational, aesthetic, or biological significance to resource managers. In general, population dynamics are often more well-defined and predictable than community and ecosystem responses to perturbations.
Population Ecotoxicology
Before we forge onward for an overview of population ecotoxicology, it would be helpful to review some elements of population ecology. For our purposes, population ecology focuses on microbial, plant, or animal populations and how these populations change over time and space, and perhaps more importantly, how these changes may be influenced by interactions with their environment. A simple definition of population is ‘a collection of individuals of the same species living in the same area at the same time.’ As such, populations are generally characterized based on attributes of population size, which is generally measured by counting individuals in a specific area; population density, which refers to how many individuals live in a given area; and population growth, which is most often considered as a change in population size through time. Conditioned on this brief characterization of population ecology, we focus on the responses that populations present when field exposures to environmental chemicals occur. Few monographs have been published strictly on population ecotoxicology (see Albers et al., 2000; Newman, 2001), yet we can find lengthy discussions of the topic in larger compendiums of related articles (Linder et al., 2003; Shugart et al., 2003) or within some monographs that include sections that have populations as their frame of reference (eg, Newman and Clements, 2007).
Population-level effects displayed by biota exposed to environmental chemicals range from dramatic to subtle. The most drastic of population-level effects is extirpation or extinction. In general parlance, extirpation refers to the complete loss of a local population whereas extinction is the loss of an entire species; extirpation may be temporary but extinction is permanent. Both effects are well defined and potentially have biological significance well beyond the immediate loss of biodiversity consequent to the loss of a population. Within the context of time, however, both might be expressed as a catastrophic outcome to a global calamity. More likely, however, the loss of an entire species will be the outcome of subtle processes, with exposure to environmental chemicals being only one of many stressors that will contribute to a series of local extirpations that cumulatively express themselves as an extinction event. The rate at which these subtler processes occur may reflect combinations of stressors acting jointly or serially. For example, habitat loss coupled with chronic or subchronic exposures to environmental chemicals may be as detrimental to long-term sustainability of a species as a release of chemicals at high concentrations that produce acute toxicity and increased mortality in exposed populations. Rapidly progressing extinction processes, such as those linked to acute exposures, can be monitored without great effort, especially if the species is relatively easy to observe in the field.
In general, local extirpations are relatively common, often directly resulting from toxic effects linked to intentional or accidental releases of chemicals to the environment, but they more commonly result from a combination of factors, such as habitat degradation or loss of competitive advantage when challenged by a species with increased tolerance to the released chemicals (see Chapter 11). In contrast, diminished population numbers or fewer areas of occupation are subtle changes in populations that may be more difficult to monitor than total extirpations.
Yield, abundance, and production are each expressions of a population’s capacity to fulfill its biological role within a community or ecosystem. Depending on the species’ role in the environment, these and other attributes of populations may characterize a species’ biological significance within a community or ecosystem. However, such characterizations require that we understand the species’ natural history with sufficient detail to distinguish natural variability in population numbers from negative responses to contaminants over the course of time. Thus, natural fluctuations in population numbers must first be understood before assigning cause and effect relationships between population fluctuations and environmental stressors, including released chemicals. Similarly, the effects of habitat modification on wildlife may adversely affect populations, and habitat evaluations would need to be completed prior to characterizing linkages between chemical exposure and population effects. Indeed, information on the response of organisms to chemicals derived from toxicity tests can be critical for identifying responses to contaminants under field conditions. As such, characterizing adverse effects based on observations of populations in the field can be very important to the evaluation process. Population-level endpoints are frequently used to evaluate chemical exposures and are most appropriate for the assessment process when (1) habitats are similar between the affected and study areas; (2) chemical exposures to individuals are well characterized; and (3) adverse effects exhibited by individuals of a species may be causally linked to significant effects on the population as a whole.
Field Surveys
Conventional population parameters (ie, occurrence, abundance, age structure, birth and death rates, and yield) are poor subjects for laboratory tests, yet should still be considered as key components of field studies, given that they are directly interpretable with respect to potentially exposed populations. Some characteristics of populations such as birth rates, death rates, and yield require long-term studies, sometimes extending over a period of years depending on the longevity of the population’s individuals. Age and sex structure can usually be assessed through studies of intermediate length, perhaps a year or less, again depending on the nature of the species. With some exceptions, these population characteristics are more easily measured for annual plants and small animals than for perennials and larger animals, but there are substantial differences among species, regardless of size. The easiest data to obtain typically include estimates of population size at a given time; if only approximations are necessary, often a few statistically designed surveys are sufficient. Spatiotemporal scale will critically influence what we measure to evaluate population responses to chemical exposure. For example, are life-history attributes such as home range of sufficient size to notice a reduction due to chemical influences or do we have data on population density prior to a chemical incident that can be used for comparison? Otherwise, movement of individuals on or off of areas of concern will potentially confound empirical data gathered during field surveys.
While we could not easily find a study that actually proved chemical aversion influences population density or site usage, Kristensen et al. (2000) presented some data suggesting it could be a possibility. Ammonia gas is one of the most abundant aerial pollutants of modern poultry buildings. The authors, therefore, conducted an experiment to test domestic chickens’ aversion to ammonia. They set up six groups of six laying hens, where each group was given one of three concentrations of ammonia (0–45 ppm in air) in a preference chamber over a period of 6 days and recorded their location and behavior throughout the day. The authors found significant differences in some key behaviors: hens foraged (p =0.018), preened (p =0.009), and rested (p =0.029) significantly more in fresh air than in ammonia-polluted environments. The differences occurred between the 0 and 25 ppm levels (p >0.05), but not between 25 and 45 ppm, which suggested that ammonia may aggravate hens at levels ≤25 ppm. Other species could express an aversion to other contaminants in the field and reject areas that have concentrations higher than a specified threshold value.
Sometimes areas suspected of receiving chemical releases potentially serve as adversely impacted habitat islands with distinct exposed populations that can be compared with reference populations over time to assess the effects of acute or chronic exposures. Although methods for population surveys are not as standardized as toxicity tests, there are well published and widely used methods applicable to reconnaissance survey needs (eg, Sutherland, 2006; US EPA, 2007, 2011).
The frequency of mass mortalities, and the frequency and nature of overt signs of toxicity correspond to assessment endpoints. Overt signs might be readily measured in the field for most vertebrates through adequate sampling designs. However, mass mortalities are unlikely to occur during a field survey, so local residents or agencies may have to suffice as sources of data. Frequencies of overt signs are quite variable and care must be taken in the diagnosis of lesions and tumors to distinguish effects of toxicants from those of parasites or mechanical injury. These endpoints are not standardized and, with the possible exception of fish kills and a few signs in birds and mammals, are unlikely to be interpreted through the use of existing data. A significant problem in surveying a population of animals for signs or mortality is that animals frequently seek shelter when feeling ill. Thus, sick animals or carcasses may be concealed from investigators, which may severely reduce the observed impact of contaminant exposure relative to the real effect.
Field surveys potentially call for measurements of structural and functional characteristics of populations and communities. Recommended methods for field surveys are many: for aquatic ecosystems—freshwater, estuarine, or marine—(eg, Flotemersch et al., 2006; Peck et al., 2007; US EPA, 2002); terrestrial vegetation (eg, Elzinga et al., 1998; USDA, USFS, 2005; Bonham, 2013); terrestrial vertebrates (eg, Gregory et al., 2004; Silvy, 2012); and terrestrial invertebrates (eg, Hodkinson and Jackson, 2005). Methods are readily available from many different sources, but likely require case-specific implementation depending on the habitats and biota of concern. For example, are reptiles, small mammals, or both of interest in evaluating effects from chemical releases? Methods may differ substantially depending on the type of questions asked and the organisms under investigation. The advantages and limitations of using field surveys in assessing ecological effects are briefly summarized in Table 10.1, yet integrated field and laboratory approaches tend to offset or at least diminish the downsides of either method when used alone and well-designed studies will employ both. On the one hand, without at least some field validation, results of toxicity tests only infer potential population- and community-level effects; thus, field surveys and monitoring activities provide a means for empirical verification of actual larger-scale effects. On the other hand, survey data may be used to identify problem areas, but without knowing what signs denote exposure, an investigator may miss or fail to sample for important evidence. Organisms are exposed in real-world settings and measured effects represent an integrated response to the temporal and spatial variations in exposure and contaminant concentrations in the field. As noted in other chapters and in published case studies, causality is best established through a combination of approaches, including chemical sampling, toxicity testing, biomarkers, and field surveys.
Table 10.1
Advantages and Limitations of Field Surveys in Ecological Assessments
Field surveys often result in data that contain a high degree of variability that reflects the high degree of stochasticity (both spatial and temporal) inherent in populations or communities (see Chapter 11). For instance, sampling of animals is influenced by the biota of interest to the study and their responses to trap type, seasonal variation in occurrence, habitat heterogeneity, and other factors. As a result, background variability may be relatively high, and extensive sampling may be needed to measure the ecological characteristics of interest with a sufficient level of precision to detect the effects clearly linked to chemical releases. In addition, particular attention to sampling plans helps optimize survey and monitoring designs. Procedures for quality assurance/quality control exist for field surveys, but are not nearly as well-established or clear-cut as the protocols for toxicity testing.
Integration of Toxicity Tests With Field Surveys
Toxicity assessments are usually derived from laboratory-generated data, but in situ toxicity assessments, while not as well-standardized as laboratory toxicity tests, are becoming more prominent in the ecological assessment process. In situ methods more closely approximate the complexities of real-life situations and reduce the problems associated with extrapolating lab data to field conditions. Ecological effects assessments also rely upon field methods that measure ecological endpoints, either at onsite or at reference sites, and yield survey data relevant to the estimates of adverse ecological effects associated with contamination. Integration of toxicity assessments (be those in situ or laboratory-generated) and field assessments requires a well-designed sample plan to establish linkages among toxicity, site-sample chemistry, and adverse ecological effects if they are apparent.
Instead of conducting tests on amphibian responses to chemicals in a small aquarium located within a controlled environmental chamber that contains only tadpoles, purified water, and the test chemical, many scientists are now using cattle tanks or other larger units located outside that may contain sediment, vegetation, and even other animals to more closely mimic real-life situations. Relyea et al. (2005) conducted a three-way factorial outdoor mesocosm experiment using 1200 L cattle tanks filled with 1000 L well water, an example of which can be seen in Fig. 10.3. All tanks contained tadpoles of gray treefrogs (Hyla versicolor), American toads (Bufo [Anaxyrus] americanus), and northern leopard frogs (Rana [Lithobates] pipiens), as well as zooplankton and algae. Some tanks also had predators, such as newts or larval diving beetles (Dytiscus sp.), and some had the insecticide malathion or Roundup (the active ingredient was the herbicide glyphosate). With these microecosystems, the authors determined that Roundup had substantial direct negative effects on the tadpoles by reducing the total tadpole survival and biomass by 40%, compared with controls. They also found that Roundup had no indirect effects on the amphibian community, such as affecting predator survival or the abundance of algae. In contrast, malathion had few direct effects on the tadpoles and actually had a positive influence on tadpoles by killing the beetles (but not the newts). Simple laboratory chronic-exposure tests might have revealed some interactions, but not under the more natural presentations of the mesocosms. These results make it clear that pesticides can have both direct and indirect effects in natural communities and that these effects critically depend upon the composition of the community.
In another study, Boone and James (2003) tested the effects of the insecticide carbaryl and the herbicide atrazine on an amphibian community composed of southern leopard frogs (R. [Lithobates] sphenocephala), American toads, spotted salamanders (Ambystoma maculatum), and small-mouthed salamanders (Ambystoma texanum) under mesocosms conditions. Salamanders were virtually eliminated in carbaryl treatments, indicating that at realistic levels, this insecticide might cause population declines for salamanders in contaminated habitats. Carbaryl also negatively affected toad survival. Atrazine had negative effects on body size, development, and time to metamorphoses in the frog and toad species and these effects were associated with the chlorophyll measurements in water. Chlorophyll was produced by algae and its decrease suggested a decrease in food availability for these species. The authors also observed a significant atrazine-by-carbaryl interaction for spotted salamanders, resulting in smaller and less-developed spotted salamander larvae than in control ponds.
Field surveys can identify adversely affected populations and can provide information for assessing adverse ecological effects potentially caused by chemical stressors. However, field surveys alone cannot identify the specific causes of effects. Cause and effect can be more clearly established when field studies are accompanied by toxicity tests with appropriate chemicals. This is more easily done with mesocosms than in natural situations. The actual causes mediating adverse effects observed in the field may be chemical stressors, but these effects could also be caused or exacerbated by habitat alteration, offsite sources of toxic chemicals, and natural variability that spuriously suggests linkages between contaminant and ecological effects.
Yet it may be practically intractable to determine which chemical or chemicals are causing toxicity, and ecological endpoints (eg, reduced population abundance) may be signs that indicate cumulative effects associated with exposure to a complex chemical mixture. In part, outcomes of integrated field and laboratory investigations then gain interpretative context by our assessment of population-level effects, which is reliant on our observations and measures taken in the field.
Population Models in the Ecotoxicologist’s Toolbox
As will be discussed in Chapter 12, we frequently rely on quantitative-modeling tools to characterize existing populations and develop population forecasts based on empirical data (eg, census data for individuals garnered from field studies). Published studies (eg, Snider and Brimlow, 2013) provide a variety of technical materials as background information for using modeling tools that can be used to estimate population-level effects potentially affected by chemical exposures. As such, models for evaluating population growth can become components of integrated field and laboratory approaches that contribute to our understanding of population-level effects.
Descriptions of population growth require consideration of mathematical models ranging from the simple to the complex. Yet, our interest here lies simply in introducing the concepts related to both population growth and the regulation of that growth through time. For example, a simple model may be posited to describe population growth as a simple algorithm Eq. (10.1):
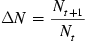(10.1)
wherein growth was considered at two times, Nt and Nt+1.
Then, from census data, we could simply describe how the population changed during the interval ΔN between these two points. We do not really know what events contributed to the difference between population size at these two periods—perhaps it was simply a matter of births and deaths, but emigration and immigration could also be factors. We also do not know how changes in survivorship occurred during the interval—exposures to disease agents, physical, or chemical hazards may have contributed to population declines if deaths exceeded reproduction or immigration during the interval between census data collections. If we simply count individuals without garnering additional data for attributes linked to those counts—for example, what sex and how old are the individuals we count at each census event—we also do not have data sufficient to say much about the change we observe in calculating ΔN; thus, population numbers are incompletely considered with respect to population growth.
Early recognition of this insufficiency or data gap encouraged development of models that captured population growth in age-structured populations (Leslie, 1945; Akçakaya et al., 1999; Caswell, 2001). Here, adults and offspring were assumed to coexist and age-specific contributions to population growth were shown with respect to recruitment and mortality. Thus, the projected population size was described as Eq. (10.2):
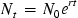(10.2)
wherein t is time, Nt is the population size at time t, N0 is the initial size of the population, r is the relative and invariant rate of growth (expressed as a proportion of the population through time t), and e is the base of the natural logarithm (2.7182).
Although this equation is an improvement over the relatively simple difference equation that yielded ΔN, this model presents a different challenge with respect to forecasting population growth through time. Simply said, under these conditions, population growth (positive or negative) just never stops! Thus, our brief introduction to population modeling introduces the exponential growth model (Leslie, 1945; Vandermeer and Goldberg, 2013).
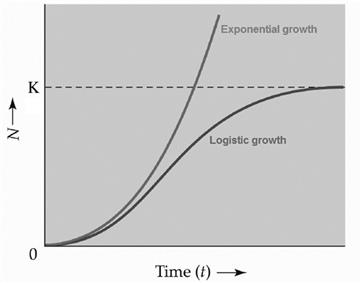
A population that experiences exponential growth increases as illustrated in Fig. 10.4. Yet, the possibility of such population growth over long time periods does not follow outcomes observed in the field or in the laboratory. Indeed, depending on the organism being considered, exponential growth may occur over small time intervals. For instance, when population size is very small and resources are abundant, such as when an invasive species enters into previously unoccupied habitats or in early growth phases in laboratory cultures of bacteria, populations may undergo rapid growth. Such growth in the absence of limited or no competition from other biota or physicochemical processes that affect the availability of otherwise abundant resources is characteristic of density-independent systems, but such system behavior cannot continue indefinitely. Instead, as time passes either the population consumes all of the available nutrients and crashes, or the systems fall under density-dependent mechanisms with respect to population growth and receive some regulation.
In general, factors that enhance or diminish population growth may be either density-dependent or density-independent, yet the literature suggests that hard and fast rules for assigning these descriptors vary from species to species. For example, competitive interactions with other species encountered in a shared habitat may strongly influence the extent to which populations might attain their maximum population levels. Other factors that tend to be density-dependent are predation and disease agents that change in strength with population density and can eventually limit population size (see Chapter 11). Other factors, including exposure to chemicals released to the environment and physical hazards, such as those linked to seasonal weather extremes and natural disasters, usually affect populations irrespective of their density and can limit population growth by severely reducing the number of individuals in the population.
In 1838, Pierre François Verhulst first posited that uninhibited exponential growth would eventually become limited with respect to resource availability and the growth of human populations. Mathematically, Verhulst (1838) described a logistic equation that limited exponential growth as the size of the population increased toward the carrying capacity, K, of its environment (Fig. 10.4) Eq. (10.3).
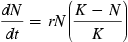(10.3)
wherein dN is the change in numbers, dt is the change in time, dN/dt is the rate of growth, r is the intrinsic rate of natural increase, N is the population size at a given time, and K is a measure of environmental resistance known as carrying capacity.
As with exponential growth, logistic growth is commonly observed in laboratory studies. However, populations under more natural conditions often fluctuate in ways not predicted by simple logistic growth models. Such fluctuation is often ascribed to seasonal or other environmental cycles (eg, daily, lunar cycles). At other times, fluctuating population levels appear to be linked to density-dependent population growth factors or interactions among density-independent factors (eg, changing seasonal conditions linked to increased temperatures, decreased precipitation) and density-dependent factors (eg, exposure to disease agents that may be more abundant under certain weather conditions than in others). Populations may also display marked decreases in numbers if changing environmental conditions (including chemical releases that result in acutely lethal exposures) cause increased death rates that greatly exceed birth rates, which would place any population on a downward trend (see Beissinger and McCullough, 2002 for a discussion of evaluation of vulnerabilities and population viability analysis).
We’re going out on a limb here, realizing that some exceptions will be found, but the effects of contaminants are almost always going to be density-independent. The severity of their effects will be largely determined by the average sensitivity of the population to the range of concentrations present in the exposure. The effects of the contaminant in and of itself should not be related to the density of the population being exposed. Given that, there may be mitigating factors such as “safe zones” where contaminant concentrations are lower and can hold only a certain number of animals, but those type of situations should be rare. We would expect that toxic levels of a pesticide or other chemical would claim a relatively constant percentage of organisms, regardless of population density. Since only density-dependent factors can actually regulate population numbers in animals (Lack, 1954) and plants, contaminants can increase population declines but cannot regulate them.
Given the strengths and weaknesses of exponential and logistic population models as tools applicable to understanding the effects of chemicals released in the environment, alternative models that leverage this modeling experience are available for the ecotoxicologist and amenable to exposure-effects analysis. Many of these alternative models are well-developed and used by population ecologists, but their application within the regulatory context is limited. Perhaps one of the most useful tools, and one widely applied to resource-management issues, is life-table analysis, which is implemented in its various forms.
Additive Versus Compensatory Mortality and Ecotoxicology
As we have stated, in population ecology it is important to identify how stressors affect a population’s dynamics. Broadly, there are two ways a stressor can affect a population’s growth (Nichols et al., 1984; Williams et al., 2002). The stressor can be additive, in which case it contributes to population loss in addition to all other factors and can have a real influence on the population. Alternatively, the stressor can be compensatory if other stressors would result in the same population loss even if the stressor of interest was not present. Take, for example, the case where a field investigator found a die-off of 200 mallards in a farmer’s field and determines that the birds were killed by the pesticide malathion. If the malathion had an additive effect, those 200 mallards would have survived all other stressors including predation, hunting, food scarcity, disease, and the like. Thus, the loss of 200 birds was a true loss. If, however, those birds had not been poisoned and had died from any of the other stressors, then there is not a true loss to the population and the malathion could have been a compensatory stressor. Fig. 10.5 shows this graphically. In additive mortality, Factor X (eg, malathion) exerts mortality on the population regardless of how many individuals survive. In compensatory mortality, however, the factor has no influence on the population until some hypothetical point or threshold (T), when the concentration of malathion becomes sufficiently high to have an overwhelming effect on the population. In reality, that threshold may never be reached under field conditions.
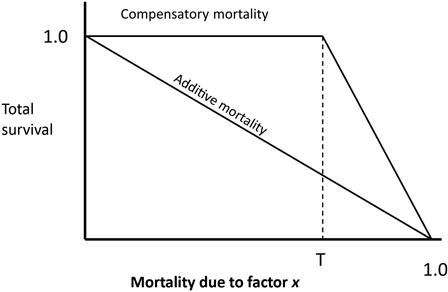
It is extremely difficult to determine if a contaminant (or almost any other stressor for that matter) is actually having an effect on a population in and of itself. This simple model is made more complex because a factor can be compensatory at some point and additive at another unknown point, and multiple factors can interact to enhance mortality or ameliorate each other’s effects. As discussed in Chapter 8, for example, the concentration of calcium or even zinc may alter the toxicity of other metals in an aquatic environment.
Life Table Analysis
For the ecotoxicologist focused on characterizing exposure and effect relationships at the population level, life table analysis yields quantitative results that describe: (1) population age structure, including characterization of fecundity and reproductive endpoints; (2) population growth rate; and (3) patterns in population survivorship patterns. Life tables are built from empirical data garnered from field studies and provide a model of the age distribution of a population. Life tables consider the number of individuals of a given age or stage of development, let’s call that n, at various times (t) during a sampling period, for example, during a long-term study or monitoring program. Among other population attributes, life tables allow us to characterize population growth, including an idea of how its structure changes with time. Whereas population ecology is keenly interested in understanding factors and processes that govern population growth, ecotoxicologists may extend the application of life table analysis to characterize chemical effects on populations based, in part, on observed results from laboratory toxicity tests. Perturbations, such as those linked to chemical exposure, become one of many environmental stressors at play in field settings, and serve as contributing factors influencing density-independent or density-dependent processes affecting individual survival and population growth to varying extents. Alternative methods, such as the Kaplan–Meier product-limit method (Skalski et al., 2005), are also widely reported in the literature as techniques for survival analysis. Life table models have long been available and may be deployed in integrated field and laboratory studies given empirical data likely gleaned from such investigations.
Completed life table models yield estimates of population abundance based on data assembled as a schedule of births and deaths for a population, or, more often than not, some portion of a population. Life table analysis frequently relies on models built on empirical data wherein year-class or stage-class cohorts—referred to as cohort life tables or dynamic life tables—are followed from birth to death. Such dynamic life tables are most often applied to short-lived organisms or long-lived biota amenable to longitudinal studies. As an alternative to cohort life table analysis, static life table or time-specific table analysis focuses on count data for all individuals entering a study during the same time interval and subsequently followed as a cross-section data. Static life table analysis is less frequently followed in field surveys than cohort tables.
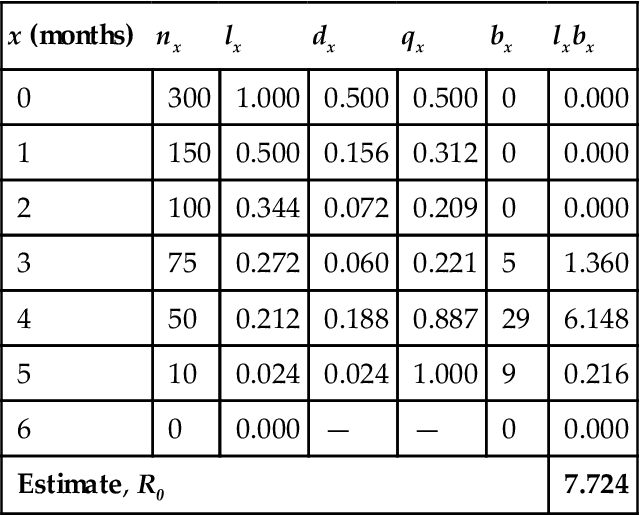
As an illustration of cohort life table analysis, Table 10.2 summarizes the arithmetic derivation of typical life table outputs derived from empirical data used to develop such an analysis. Although life tables may vary with respect to empirical data used for the analysis, most follow a convention used for the following variables:
x =age (eg, 0, 1, 2, 3 years old) or stage (eg, egg, larvae, nymph, adult) class
nx =number of individuals in each age or stage x
lx =percent of the original cohort that survives to age or stage x (=nx/n0)
dx =probability of dying during age or stage x (=lx – lx+1)
qx =percent of dying between age or stage x and age or stage x+1 (=dx/lx)
bx =number of offspring produced per individual in age/stage x
Table 10.2
Illustration of Data Assembled for Cohort Life Table Analysis
| x (months) | nx | lx | dx | qx | bx | lxbx |
| 0 | 300 | 1.000 | 0.500 | 0.500 | 0 | 0.000 |
| 1 | 150 | 0.500 | 0.156 | 0.312 | 0 | 0.000 |
| 2 | 100 | 0.344 | 0.072 | 0.209 | 0 | 0.000 |
| 3 | 75 | 0.272 | 0.060 | 0.221 | 5 | 1.360 |
| 4 | 50 | 0.212 | 0.188 | 0.887 | 29 | 6.148 |
| 5 | 10 | 0.024 | 0.024 | 1.000 | 9 | 0.216 |
| 6 | 0 | 0.000 | — | — | 0 | 0.000 |
| Estimate, R0 | 7.724 | |||||
With data derived from literature or when integrated field and laboratory studies are available, summary information derived from cohort life table analysis includes estimates of several other important population variables:
R0, or net reproductive rate (a measure of the change in population size), where R0 = Σ(lxbx)
T, the generation time (the time between the birth of one cohort and the birth of their offspring) where: T = (Σxlxbx)/R0
r, the per capita rate of increase (as is R0, r is a measure of the change in population size) and is calculated as: r = ln R0/T
Note that R0 and r do not estimate the same population parameter; r tells us whether a population is experiencing more births than deaths, but R0 tells us if the population is increasing or decreasing relative to some fixed point defined as 1. In other words:
An example of using life tables to predict population effects of contaminants can be found in Sha et al. (2015), who sought to assess the relative toxicity effects of two polybrominated diphenyl ethers (PBDEs), BDE-47 and BDE-209 congeners, on the marine rotifer Brachionus plicatilis. They calculated rotifer population demographic parameters into life tables, including age-specific survivorship (lx), age-specific fecundity (mx), net reproductive rate (R0), intrinsic rate of increase (r), finite rate of increase (λ), life expectancy (E0), and generation time (T), and used them as measures of treatment effects. Though this was a laboratory study, rotifers are so small that they do not require large chambers or lakes to show population changes. Results from this study revealed increasingly intense negative effects on many of the rotifer demographic parameters with elevated PBDE concentrations. The population growth curves of control B. plicatilis showed almost instantaneous growth and reached peak abundances within 11 days, whereas B. plicatilis exposed to BDE-209 did not increase in numbers until after 5 days. PBDE exposure also reduced population abundances and peak population densities of the rotifer. The PBDEs suppressed carrying capacity (K) of the habitats in a dose-dependent fashion. The study also showed that the time for population growth to level off was shortened by PBDEs compared with controls. The authors concluded that life table demography and the population growth curve can be used to evaluate PBDE effects.
Another example might better demonstrate the value of life table parameters. Martinez-Jeronimo et al. (2013) exposed recently hatched Daphnia schoedleri to three sublethal concentrations of the pyrethroid α-cypermethrin (0.54, 5.4, and 54 ng/L) plus a control for 21 days. Daphnia schoedleri is another species that can be easily maintained in the laboratory for many generations. Effects were measured through a life table analysis for fecundity (mx) and survivorship (lx). In addition, the intrinsic rate of population growth (r), net reproductive rate (R0), life expectancy at birth (ex), generation time (G), and the average lifespan were also calculated for survivorship and fecundity values recorded during 21 days in each cohort. Survivorship curves showed substantial loss to the populations at 0.54 ng/L α-cypermethrin. Moreover, significant differences were found in all life table parameters. The α-cypermethrin negatively affected average life span, life expectancy at hatching (ex), net reproductive rate (R0), intrinsic rate of population growth (r), and, at the highest concentrations, generation time (G).
Regardless of our selection of tools and analytical models, as ecotoxicologists, the central question should be “How do exposure and effects findings derived from individual-based toxicity tests work with respect to our forecasting ecological effects from chemical releases in the field?” In this chapter and the next, we focus on extrapolations from toxicity tests commonly completed on individual organisms under controlled conditions to demographic endpoints characteristic of groups of individuals of the same species in a given place at a given time. In short, from a population ecologist’s perspective, ecotoxicologists most often focus on acute exposures to reliably predict natality (specifically, birth rates) and mortality (specifically, death rates). Thus, they forecast population-level effects, perhaps gleaned from census data collected in the field with little, if any, empirical data collected that characterizes effects on other elements of population dynamics such as immigration and emigration and how those processes might influence interpretation of chemical effects on age distribution, genetic composition, or spatial distribution patterns of biota directly or indirectly exposed to chemical releases in field settings (see the section “Focus—Almost, But Still Not There: The Story of Contaminants and Population Status of California Amphibians,” later in this chapter). As with other analytical methods, life table analysis can be a powerful tool, however these methods have their limits. One limitation is that there are few long-term studies available that follow cohorts through a lifetime. As such, our inability to conduct empirical “lifetime studies” generally precludes completion of a comprehensive cohort analysis. Our assumption of a stable-age distribution, though critical to the underlying analysis, is also difficult to fully characterize (Anderson et al., 1985; Skalski et al., 2005). However, as one of the tools available to ecotoxicologists focused on characterizing exposure and effects relationships in field settings, life table analysis serves to link empirical data derived from field or laboratory studies with modeling efforts intended to forecast alternative futures involving questions of resource management and releases of environmental chemicals.
Stochasticity and Uncertainty
Given our brief overview of population growth and models built to project population growth through time, and density-independent and density-dependent factors potentially influencing population growth, we next briefly consider factors that promote caution in our interpretations of adverse effects from exposures to environmental chemicals in the field. In short, we focus on how stochastic (random) events occurring in the field might influence population growth and long-term viability (Beissinger and McCullough, 2002). Whether or not chemical exposures are likely stressors encountered in the field, stochastic events threaten the persistence of any population; the smaller the population, the greater the threat. Four general classes of threats may influence population growth and its long-term viability: demographic stochasticity, environmental stochasticity, natural catastrophes, and genetic stochasticity.
Demographic stochasticity accounts for variability in population growth rates linked to random differences in survival and reproduction among individuals within given time periods. As a process affecting any population, demographic stochasticity is usually more apt to influence relatively small populations—for example, with endangered species—and when jointly occurring with releases of chemicals to the environment, outcomes could be problematic, particularly when a catastrophic release of chemicals to habitats identified as critical to endangered species would represent an extreme event of significant consequence. In contrast to demographic stochasticity, environmental stochasticity includes abnormal events such as extremes in weather, such as prolonged winters characterized by unusually low temperatures or by cycles in drought or flooding that may affect populations of any size, even those of large populations.
Natural catastrophes might be considered an extreme case of environmental stochasticity. These catastrophes are usually unpredictable and may include local extirpation events such as major floods, volcanic eruptions, tsunamis, earthquakes, or flash fires that quickly consume acres of land. Perhaps the only defense that a population has against these events is a wide distribution, so that survivors can reinhabit an area, and the often-slim possibility of finding refugees from the event.
Genetic stochasticity refers to genetic drift; that is, changes in the genetic composition of a population unrelated to organism-level processes driving population growth, such as emigration, immigration, and other systematic events. Such stochasticity influences genetic structure of populations, reducing genetic diversity and population viability by adversely affecting the reproductive capacity of individuals. Genetic stochasticity becomes particularly problematic when initial population size is small, say, fewer than 100–300 individuals in the population. As with demographic stochasticity, genetic stochasticity is less likely to be a problem in populations large enough to buffer environmental stochasticity (eg, Lande, 1993; Dunham et al., 1999). Often, the species most vulnerable to these forms of stochasticity are those most often encountered on lists of sensitive species or species of concern to resource management organizations, such as threatened or endangered species. Among even these species, vertebrates with generally lower fecundity, may be more at risk than invertebrates or plants. Life-history attributes are critical to the evaluation of a population’s growth and its long-term viability, with the most critical stages of an organism’s life cycle likely yielding the greatest impact on its population dynamics.
As this chapter’s preamble, courtesy of Bartholomew (1964), suggested, bridging the data and knowledge gaps inherent to extrapolation from individual-based models, such as those yielding toxicity data, to population, community, and ecosystem levels of biological organization continue to offer research challenges for ecotoxicologists and applied ecologists. In many respects, design and implementation of integrated field and laboratory studies addresses these scale-related issues given their focus on multiple stressors and the characterization of cause and effect relationships linked to the chemical exposures to biota under field conditions. In preparation for our focus on communities and ecosystems in the next chapter, and in recognition of the roles that humans play in releasing chemicals to the environment and the effects of these chemicals on human populations, integrated field and laboratory studies mirror the efforts of field epidemiologists whose primary focus lies with exposure and effects of multiple stressors, originally disease agents, on human health. Indeed, the process is identical; only the names of the stressors may have changed. Indeed, exposure is the common thread that ties together all receptors, particularly within exposure networks encountered in field settings.
Segue
Here, we begin our overview of integrative processes, building from individual-based studies, such as toxicity testing and assessment introduced in Chapter 2 and setting the stage for our focus on populations in this chapter. In future chapters, we will subsequently extend our overview to “populations of populations,” more commonly called communities and ecosystems (see Chapter 11). In essence, we will become more aware of the inter-relationships among individuals, populations, and communities, all part of larger ecosystems. As such, human health becomes entangled in our overview of ecotoxicology as an issue in which we discover dependencies throughout the larger “system of systems” through the discipline of field epidemiology. Although beyond the scope of our overview, field epidemiology captures disciplines in social sciences, such as medical sociology or psychology and other biological sciences (microbiology, pathology, or nutrition). Although we leave those disciplines to their own devices, we have so far presented brief overviews focused on essentials of ecotoxicology and also provided a brief overview of selected chemicals released to the environment. In addition, the principal focus of this chapter has been on introducing spatiotemporal scale as an underlying ecological principle that we will consider next in our snapshot of communities and ecosystems, and the effects of chemical exposures in highly networked populations whose individuals serve as receptors and transfer agents.
Focus—Almost, But Still Not There: The Story of Contaminants and Population Status of California Amphibians
Populations of several species of amphibians in the Sierra Mountains of California have been declining at alarming rates. For example, among 16 sites in Lassen National Park that had recent records of the Cascades frog (Rana cascadae), only one site had frogs, and even there only two individuals were found (Fellers and Drost, 1993). Farther south at Yosemite National Park, five of seven species of frogs and toads had suffered serious declines (Drost and Fellers, 1996). One of the most common species had shrunk to a few remnant populations. Even attempts to repopulate areas that had depleted populations of amphibians failed (Fellers et al., 2007). Although these studies occurred 20 years ago, the status of most California anurans has not improved in recent years (Brown et al., 2014). At the start of concern for amphibian species, several factors including drought, habitat loss, and introduced fish were thought to be the causes for the declines. Eventually, introduced trout were shown to be important in some lakes, but not in much of the areas of decline (Knapp and Matthews, 2000). What was causing these widespread declines in California anurans? Salamander populations did not seem to be at risk, so what was particular to frogs and toads?
Eventually, two possible causes came to the forefront of attention: contaminants and disease. We’ll review some of the data supporting contaminants first, then return to disease. First, a little bit of geography: California has four principal national parks in the Sierra Nevada Mountains, from north to south, they are Lassen Volcanoes National Park, Yosemite National Park, and Sequoia/Kings Canyons National Park. West of the Sierra Nevada is the Central Valley, a huge agricultural region that uses thousands of tons of active-ingredient pesticides each year, although the amount of pesticide used has declined over the past decade or more (California Department of Pesticide Regulation, 2013). Prevailing winds from the coast carry volatilized pesticides into the foothills and mountains with concentrations of contaminants in general decreasing with distance from the coast and elevation—the two measures being highly related (Bradford et al., 2010). These winds also tend to blow in a southerly direction and circulate the lower end of the Valley or the San Joaquin Valley around Sequoia/Kings Canyon National Parks, carrying heavier loads of pesticides. In contrast, coastal and more northern populations are declining less precipitously. Using the still abundant Pacific treefrog (Pseudacris regilla) as a sentinel species, Sparling et al. (2001) found that cholinesterase (ChE) activity in tadpoles was depressed in mountainous areas east of the Central Valley compared with sites along the coast or north of the Valley. Cholinesterase was also lower in areas where ranid population status was poor or moderate compared with areas that had good ranid status. Up to 50% of the sampled population in areas with reduced ChE had detectable organophosphorus pesticide residues, mostly diazinon, malathion, and chlorpyrifos with concentrations as high as 190 ppb wet weight. In addition, nearly 90% of some populations had measurable endosulfan concentrations and 40% had detectable p,p′-DDT and o,p′-DDT residues. Angermann et al. (2002) found polychlorinated biphenyls (PCBs), PBDEs, and other persistant organic pollutants (POPs) in the tissues of P. regilla in a pattern consistent with wind-blown contaminants.
Laboratory experiments showed that some California frogs could be very sensitive to pesticides. H. regilla was less sensitive to chlorpyrifos (LC50 365 μg/L) than the more threatened mountain yellow leg frog (Rana boylii, LC50 65.5 μg/L) (Sparling and Fellers, 2009). Treefrogs were also less sensitive to endosulfan (LC50 15.6 μg/L) than R. boylii (LC50 0.55 μg/L). However, by the time contaminant studies had begun on Californian frogs, field residues of these pesticides were in the ng/L range. Recall from Chapter 5 that many organophosphorus pesticides are chemically altered to their oxon or sulfon forms which have half-lives of a few days in the environment. Oxon forms of diazinon and malathion were one to two orders of magnitude more toxic than parent forms and chloroxon (degradate of chlorpyrifos) was at least three orders of magnitude more toxic (Sparling and Fellers, 2007). Thus, at the very least, endosulfan and chloroxon were determined to be lethal in the laboratory at concentrations found in the environment.
An extensive 2-year study was led by Dr Deborah Cowman in 2001 and 2002 that raised P. regilla in Teflon-net structures in situ within Lassen Volcanoes, Yosemite, and Sequoia National Parks (Sparling et al., 2015). Twenty contaminants were identified in tadpoles with an average of 1.3–5.9 and a maximum of 10 different contaminants per animal. In line with the prevailing wind patterns, Sequoia tadpoles had the greatest variety and concentrations of contaminants in 2001. They also experienced the greatest mortality and the slowest developmental rates in both years and the lowest cholinesterase activities of all three parks in 2001. In addition, Yosemite and Sequoia tadpoles had greater genotoxicity than those in Lassen during 2001. In 2001, tadpoles at Yosemite showed a high rate of hind limb malformations. Although concentrations of most contaminants were below known lethal concentrations, simultaneous exposure to multiple chemicals and other stressors could have resulted in lethal and sublethal effects. Unfortunately, we do not know much about the interactive effects of chemicals.
Despite all of these and other studies and data on chemicals and amphibians’ sensitivity to them, we still cannot claim that we have shown a population effect. Recall the difference between additive and compensatory mortality. Whereas we have seen mortality in the field that would appear to be related to contaminants, we have not studied other stressors such as predation or disease simultaneously with contaminants. We also cannot distinguish if the mortality was additive or compensatory. Furthermore, there is doubt because the field concentrations tended to be much lower than what were found to be lethal in the laboratory. Perhaps the combination of chemicals are more toxic than any one alone. It is likely that because the use of organochlorine pesticides ceased in the Central Valley 40 years ago, concentrations were much higher in the past and these and other POPs may have historically devastated populations of frogs. However, we do not have data from back then. Perhaps (there is that word again) the current-use pesticides do not last sufficiently long in the environment and field collections failed to catch their peak concentrations. The bottom line is that the hypothesis that contaminants have caused the long-term population declines seen in several species of California frogs still has not been scientifically proven.
Another cause for some population declines has been found. The fungus Batrachochytrium dendrobatidis infects anurans and feeds on keratin in the skin, causing the disease chytridiomycosis (chytrid). This disease infiltrates the dermis of the frogs and toads, reducing dermal respiration and water transport, resulting in die-offs. The fungus is global in distribution and is reportedly widespread throughout much of California (Fellers et al., 2011). No doubt chytrid has been responsible for some die-offs. Unfortunately, there is a difference between the way chytrid and contaminants affect amphibians that plays a major role in attracting interest. Chytrid kills relatively quickly, resulting in many dead bodies of frogs strewn along shores or shallow waters of a wetland and making a very conspicuous display. Contaminants, on the other hand, seldom produce acute mortality. Rather they work quietly by reducing reproductive rates, altering endocrine systems, producing slow-acting cancers, and possibly even facilitating death by conspicuous diseases resulting from impaired immune systems.
Study Questions
1. Did you notice any differences between the study of population ecotoxicology and population ecology while reading this chapter?
2. Discuss in your own words what is meant by spatiotemporal scales.
3. Are contaminants more likely to cause an extirpation or an extinction? Why?
4. How can controlled laboratory experiments on cause and effect with a single chemical and a single species help in understanding possible population effects under more natural conditions? Can they?
5. In this chapter, we mentioned that aversion to contaminants may affect population size or density, but that we could not find any specific examples in a scan of the scientific literature. Can you imagine a way in which chemical aversion could have population effects? Provide details.
6. What problems might occur if you conducted field surveys without having run laboratory tests or access to studies that did run tests with the chemicals and species of concern?
7. What are your thoughts on mesocosm experiments? Can mesocosms completely mimic a natural environment? What are some of the advantages and disadvantages of using mesocosms for testing chemicals in an aquatic environment?
8. Do you imagine that a contaminant could be a density-dependent regulating factor for a population? If so, what conditions would have to exist for that to happen?
9. In cooperation with your class, design a study to determine if a contaminant has an additive or compensatory effect on a population. For simplicity’s sake, you can use a mesocosms design.
10. Have you used or built life tables in any other course you have taken, such as an ecology course? What do you think of the idea of using life table techniques to determine if a contaminant is exerting a population effect?
11. We will discuss stochasticity in greater detail when we get to risk assessment and we’ll see that randomness can be a major factor in making good decisions. How can stochasticity affect the interpretations of a scientific study?
12. What did you learn from the story in the “Focus” section? What more would have to be done to show that contaminants are having a true population effect?