In the preceding chapters, we presented four different styles of garbage collection. In this chapter, we compare them in more detail. We examine the collectors in two different ways. First, we consider criteria by which we may assess the algorithms and the strengths and weaknesses of the different approaches in different circumstances. We then present abstractions of tracing and reference counting algorithms due to Bacon et al [2004]. These abstractions reveal that while the algorithms exhibit superficial differences they also bear a deep and remarkable similarity.
It is common to ask: which is the best garbage collector to use? However, the temptation to provide a simple answer needs to be resisted. First, what does ‘best’ mean? Do we want the collector that provides the application with the best throughput, or do we want the shortest pause times? Is space utilisation important? Or is a compromise that combines these desirable properties required? Second, it is clear that, even if a single metric is chosen, the ranking of different collectors will vary between different applications. For example, in a study of twenty Java benchmarks and six different collectors, Fitzgerald and Tarditi [2000] found that for each collector there was at least one benchmark that would have been at least 15% faster with a more appropriate collector. And furthermore, not only do programs tend to run faster given larger heaps, but also the relative performance of collectors varies according the amount of heap space available. To complicate matters yet further, excessively large heaps may disperse temporally related objects, leading to worsened locality that may slow down applications.
The first item on many users’ wish lists is likely to be overall application throughput. This might be the primary goal for a ‘batch’ application or for a web server where pauses might be tolerable or obscured by aspects of the system such as network delays. Although it is important that garbage collector actions be performed as quickly as possible, employing a faster collector does not necessarily mean that a computation will necessarily execute faster. In a well configured system, garbage collection should account for only a small fraction of overall execution time. If the price to be paid for faster collection is a larger tax on mutator operations, then it is quite possible for the application’s execution time to become longer rather than shorter. The cost to the mutator may be explicit or implicit. Explicit actions include read and write barrier actions, such as those that reference counting requires. However, the performance of the mutator may also be affected implicitly, for example because a copying collector has rearranged objects in such a way as to affect cache behaviour adversely, or because a reference count decrement has touched a cold object. It is also important to avoid wherever possible any need to synchronise operations. Unfortunately, reference count modifications must be synchronised in order not to miss updates. Deferred and coalesced reference counting can eliminate much of these synchronisation costs.
One can consider the algorithmic complexity of different algorithms. For mark-sweep collection, we would need to include the cost of the tracing (mark) and the sweep phases, whereas the cost of copying collection depends only on tracing. Tracing requires visiting every live object whereas sweeping requires visiting every object (live and dead). It is tempting to assume that the cost of mark-sweep collection must therefore necessarily be greater than copying collection. However, the number of instructions executed to visit an object for mark-sweep tracing are fewer than those for copying tracing. Locality plays a significant part here as well. We saw in Section 2.6 how prefetching techniques could be used to hide cache misses. However, it is an open question as to whether such techniques can be applied to copying collection without losing the benefits to the mutator of depth-first copying. In either of these tracing collectors, the cost of chasing pointers is likely to dominate. Furthermore, if marking is combined with lazy sweeping, we obtain greatest benefit in the same circumstances that copying performs best: when the proportion of live data in the heap is small.
The next item for many users is the extent to which garbage collection interrupts program execution. Low pause times are important not only for interactive applications but also for others such as transaction processors for which delays may cause backlogs of work to build up. The tracing collectors considered so far have all been stop-the-world: all mutator threads must be brought to a halt before the collector runs to completion. Garbage collection pause times in early systems were legendary but, even on modern hardware, stop-the-world collectors may pause very large applications for over a second. The immediate attraction of reference counting is that it should avoid such pauses, instead distributing the costs of memory management throughout the program. However, as we have seen, this benefit is not realised in high performance reference counting systems. First, the removal of the last reference to a large pointer structure leads to recursive reference count modifications and freeing of components. Fortunately, reference count modifications on garbage objects are not contended, though they may cause contention on the cache lines containing the objects. More importantly, we saw that deferred and coalesced reference counting, the most effective ways to improve reference counting performance, both reintroduce a stop-the-world pause to reconcile reference counts and reclaim garbage objects in the zero count table. As we shall see in Section 6.6, high performance reference counting and tracing schemes are not so different as they might first appear.
Memory footprint is important if there are tight physical constraints on memory, if applications are very large, or in order to allow applications to scale well. All garbage collection algorithms incur space overheads. Several factors contribute to this overhead. Algorithms may pay a per-object penalty, for example for reference count fields. Semispace copying collectors need additional heap space for a copy reserve; to be safe, this needs to be as large as the volume of data currently allocated, unless a fall-back mechanism is used (for example, mark-compact collection). Non-moving collectors face the problem of fragmentation, reducing the amount of heap usable to the application. It is important not to ignore the costs of non-heap, metadata space. Tracing collectors may require marking stacks, mark bitmaps or other auxiliary data structures. Any non-compacting memory manager, including explicit managers, will use space for their own data structures, such as segregated free-lists and so on. Finally, if a tracing or a deferred reference counting collector is not to thrash by collecting too frequently, it requires sufficient room for garbage in the heap. Systems are typically configured to use a heap anything from 30% to 200% or 300% larger than the minimum required by the program. Many systems also allow the heap to expand when necessary, for example in order to avoid thrashing the collector. Hertz and Berger [2005] suggest that a garbage collected heap three to six times larger than that required by explicitly managed heaps is needed to achieve comparable application performance.
In contrast, simple reference counting frees objects as soon as they become unlinked from the graph of live objects. Apart from the obvious advantage of preventing the accumulation of garbage in the heap, this may offer other potential benefits. Space is likely to be reused shortly after it is freed, which may improve cache performance. It may also be possible in some circumstances for the compiler to detect when an object becomes free, and to reuse it immediately, without recycling it through the memory manager.
It is desirable for collectors to be not only complete (to reclaim all dead objects eventually) but also to be prompt, that is, to reclaim all dead objects at each collection cycle. The basic tracing collectors presented in earlier chapters achieve this, but at the cost of tracing all live objects at every collection. However, modern high-performance collectors typically trade immediacy for performance, allowing some garbage to float in the heap from one collection to a subsequent one. Reference counting faces the additional problem of being incomplete; specifically, it is unable to reclaim cyclic garbage structures without recourse to tracing.
Garbage collection algorithms are difficult to implement correctly, and concurrent algorithms notoriously so. The interface between the collector and the compiler is critical. Errors made by the collector often manifest themselves long afterwards (maybe many collections afterwards), and then typically as a mutator attempts to follow a reference that is no longer valid. It is important, therefore, that garbage collectors be constructed to be robust as well as fast. Blackburn et al [2004a] have shown that this performance-critical system component can be designed with respect for good software engineering practices of modularity and composability, leading to maintainable code.
One advantage of simple tracing collectors is that the interface between the collector and the mutator is simple: when the allocator exhausts memory, the collector is called. The chief source of complexity in this interface is determining the roots of collection, including global variables, and references held in registers and stack slots. We discuss this in more detail in Chapter 11. However, we note here that the task facing copying and compacting collectors is more complex than that facing non-moving collectors. A moving collector must identify every root and update the reference accordingly, whereas a non-moving collector need only identify at least one reference to each live object, and never needs to change the value of a pointer. So-called conservative collectors [Boehm and Weiser, 1988] can reclaim memory without accurate knowledge of mutator stack or indeed object layouts. Instead they make intelligent (but safe, conservative) guesses about whether a value really is a reference. Because non-moving collectors do not update references, the risk of misidentifying a value as a heap pointer is confined to introducing a space leak: the value itself will not be corrupted. A full discussion of conservative garbage collection can be found in Jones [1996, Chapters 9 and 10].
Reference counting has both the advantages and disadvantages of being tightly coupled to the mutator. The advantages are that reference counting can be implemented in a library, making it possible for the programmer to decide selectively which objects should be managed by reference counting and which should be managed explicitly. The disadvantages are that this coupling introduces the processing overheads discussed above and that it is essential that all reference count manipulations are correct.
The performance of any modern language that makes heavy use of dynamically allocated data is heavily dependent on the memory manager. The critical actions typically include allocation, mutator updates including barriers, and the garbage collector’s inner loops. Wherever possible, the code sequences for these critical actions needs to be inlined but this has to be done carefully to avoid exploding the size of the generated code. If the processor’s instruction cache is sufficiently large and the code expansion is sufficiently small (in older systems with much smaller caches, Steenkiste [1989] suggested less than 30%), this blowup may have negligible effect on performance. Otherwise, it will be necessary to distinguish in these actions the common case which needs to be small enough to be inlined (the ‘fast path’), whilst calling out to a procedure for the less common ‘slow path’ [Blackburn and McKinley, 2002]. There are two lessons to be learnt here. The output from the compiler matters and it is essential to examine the assembler code produced. The effect on the caches also has a major impact on performance.
Commercial systems often offer the user a choice of garbage collectors, each of which comes with a large number of tuning options. To complicate matters further, the tuning levers provided with these collectors tend not to be independent of one another. A number of researchers have suggested having systems adapt to the environment at hand. The Java run-time developed by Soman et al [2004] adapts dynamically by switching collectors at run time, according to heap size available. Their system either requires off-line profiling runs to annotate programs with the best collector/heap-size combination, or it can switch based on comparing the current space usage of the program with the maximum heap available. Singer et al [2007a], in contrast, apply machine learning techniques to predict the best collector from static properties of the program (and thus require only a single training run). Sun’s Ergonomic tuning1 attempts to tune their HotSpot collector’s performance against user-supplied throughput and maximum pause time goals, adjusting the size of spaces within the heap accordingly.
The best, and possibly the only, advice that we can offer to developers is, know your application. Measure its behaviour, and the size and lifetime distributions of the objects it uses. Then experiment with the different collector configurations on offer. Unfortunately this needs to be done with real data sets. Synthetic and toy benchmarks are likely to mislead.
6.6 A unified theory of garbage collection
In the preceding chapters, we considered two styles of collection: direct, reference counting and indirect, tracing collection. Bacon et al [2004] show that these collectors share remarkable similarities. Their abstract framework allows us to express a wide variety of different collectors in a way that highlights precisely where they are similar and where they differ.
In place of concrete data structures, the following abstract framework makes use of simple abstract data structures whose implementations can vary. We start by observing that garbage collection can be expressed as a fixed-point computation that assigns reference counts ρ(n) to nodes n ∈ Nodes. Reference counts include contributions from the root set and incoming edges from nodes with non-zero reference counts:
Having assigned reference counts, nodes with a non-zero count are retained and the rest should be reclaimed. Reference counts need not be precise, but may simply be a safe approximation of the true value. Abstract garbage collection algorithms compute such fixed-points using a work list W of objects to be processed. When W is empty these algorithms terminate. In the following, W is a multiset, since every entry in W represents a distinct source for each reference.
The abstraction casts tracing collection as a form of reference counting. Abstract tracing collection is illustrated by Algorithm 6.1, which starts with the reference counts of all nodes being zero. At the end of each collection cycle sweepTracing resets the count of all nodes to zero, and New initialises new nodes with a zero reference count. The collectTracing procedure accumulates all non-null root pointers using rootsTracing and passes them to scanTracing as the work list W.
Collection proceeds as we would expect by tracing the object graph to discover all the nodes reachable from the roots. The procedure scanTracing accomplishes this by tracing elements from the work list, reconstructing the reference count of each node, by incrementing its reference count each time it is encountered (recall how we suggested in Section 5.6 that a tracing collector could be used to correct sticky reference counts). When a reachable node src is discovered for the first time (when ρ(src) is set to 1, line 10), the collector recurses through all the out-edges of src by scanning its fields and adding the (pointers to) child nodes found in those fields to the work list W.2
Termination of the while loop yields all the live nodes, each of which has a non-zero reference count equal to the number of its in-edges. The sweepTracing procedure then frees unused nodes, and resets the reference counts for the next round of collection. Note that a practical implementation of tracing can use a single-bit value for each node’s reference count, in other words a mark bit rather than a full-sized reference count, to record whether the node has already been visited. The mark bit is thus a coarse approximation of the true reference count.
The tracing collector computes the least fixed-point solution to Equation 6.1: the reference counts on the nodes are the lowest counts that satisfy it.
We can interpret garbage collection algorithms in terms of the tricolour abstraction discussed in Section 2.2. In Algorithm 6.1, nodes with reference count 0 are white, while nodes with non-zero reference count are black. The transition of a node from white via grey to black occurs as that node is first traced and then scanned. Thus, we can re-cast the abstract tracing algorithm as partitioning the nodes into two sets, black being reachable and white being garbage.
Algorithm 6.1: Abstract tracing garbage collection
1 atomic collectTracing() :
2 rootsTracing(W)
3 scanTracing(W)
4 sweepTracing ()
5
6 scanTracing(W):
7 while not isEmpty(W)
8 src ← remove(W)
9 ρ(src) ← ρ(src) + 1 | /* shade |
10 if ρ(src) = 1 | /* |
11 for each fld in Pointers(src)
12 ref ← *fld
13 if ref ≠ null
14 W ← W + [ref]
15
16 sweepTracing():
17 for each node in Nodes
18 if p(node) = 0 | /* |
19 free(node)
20 else | /* |
21 ρ(node) ← 0 | /* reset |
22
23 New() :
24 ref ← allocate()
25 if ref = null
26 collectTracing()
27 ref ← allocate()
28 if ref = null
29 error “Out of memory”
30 ρ(ref) ← 0 | /* node is white */ |
31 return ref
32
33 rootsTracing(R):
34 for each fld in Roots
35 ref ← *fld
36 if ref ≠ null
37 R ← R + [ref]
Reference counting garbage collection
The abstract reference counting collection Algorithm 6.2 shows reference count operations being buffered by the mutator’s inc and dec procedures rather than performed immediately, in order to highlight the similarity with tracing. This buffering technique turns out to be very practical for multithreaded applications; we consider it further in Chapter 18. This logging of actions also shares similarities with coalesced reference counting, discussed in Section 5.4. The garbage collector, collectCounting, performs the deferred increments I with applyIncrements and the deferred decrements D with scanCounting.
Algorithm 6.2: Abstract reference counting garbage collection
1 atomic collectCounting(I,D):
2 applyIncrements(I)
3 scanCounting(D)
4 sweepCounting()
5
6 scanCounting (W):
7 while not isEmpty(W)
8 src ← remove(W)
9 ρ(src) ← ρ(src) −1
10 if ρ(src) = 0
11 for each fld in Pointers(src)
12 ref ← *fld
13 if ref ≠ null
14 W ← W + [ref]
15
16 sweepCounting():
17 for each node in Nodes
18 if ρ(node) = 0
19 free(node)
20
21
22
23 New() :
24 ref ← allocate()
25 if ref = null
26 collectCounting(I,D)
27 ref ← allocate()
28 if ref = null
29 error “Out of memory”
30 ρ(ref) ← 0
31 return ref
32
33 dec(ref):
34 if ref ≠ null
35 D ← D + [ref]
36
37 inc(ref):
38 if ref ≠ null
39 I ← I + [ref]
40
41 atomic Write(src, i, dst) :
42 inc(dst)
43 dec(src[i])
44 src[i] ← dst
45
46 applyIncrements(I):
47 while not isEmpty(I)
48 ref remove(I)
49 ρ(ref) ← p(ref) + 1
Algorithm 6.3: Abstract deferred reference counting garbage collection
1 atomic collectDrc(I,D):
2 rootsTracing(I)
3 applyIncrements(I)
4 scanCounting(D)
5 sweepCounting()
6 rootsTracing(D)
7 applyDecrements(D)
8
9 New():
10 ref ← allocate()
11 if ref = null
12 collectDrc(I, D)
13 ref ← allocate()
14 if ref = null
15 error “Out of memory”
16 ρ(ref) ← 0
17 return ref
18
19 atomic Write(src, i, dst):
20 if src ≠ Roots
21 inc(dst)
22 dec(src[i])
23 src[i] ← dst
24
25 applyDecrements (D):
26 while not isEmpty(D)
27 ref ← remove(D)
28 ρ(ref) ← ρ(ref) – 1
Mutation, using the Write procedure, stores a new destination reference dst into a field src[i]. In doing so, it buffers an increment for the new destination, inc(dst), and buffers a decrement for the old referent, dec(src[i]), before storing the new destination to the field, src[i]←dst.
Each collection begins by applying all deferred increments to bring them up to date. The deferred decrements are applied in the next phase. The scanCounting procedure begins with reference counts that over-estimate the true counts. Thus, it must decrement the counts of nodes in the work list as it encounters them. Any source node whose count, ρ(src), is decremented to zero in this phase is treated as garbage, and its child nodes are added to the work list. Finally, the procedure sweepCounting frees the garbage nodes.
The tracing and reference counting algorithms are identical but for minor differences. Each has a scan procedure: the scanTracing collector uses reference count increments whereas the scanCounting collector uses decrements. In both cases the recursion condition checks for a zero reference count. Each has a sweep procedure that frees the space occupied by garbage nodes. In fact, the outline structures of the first 31 lines in Algorithm 6.1 and Algorithm 6.2 are identical. Deferred reference counting, which defers counting references from the roots, is similarly captured by this framework (see Algorithm 6.3).
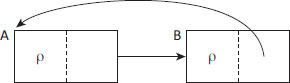
Figure 6.1:
A simple cycle
Finally, we noted earlier that computing reference counts is tricky when it comes to cycles in the object graph. The trivial object graph in Figure 6.1 shows a simple isolated cycle, where assuming A has reference count zero allows B also to have reference count zero (since only source nodes with a non-zero count contribute to the reference counts of their destinations). But there is a chicken-and-egg problem here, since the reference counts of A and B are mutually dependent. It is just as feasible for us to claim that A has reference count 1, because of its reference from B, leading us to claim that B also has reference count 1.
This seeming anomaly arises generally for fixed-point computations, where there may be several different feasible solutions. In Figure 6.1 we have the case that Nodes = {A, B} and Roots = {}. There are two fixed-point solutions of Equation 6.1 for this simple graph: a least fixed-point ρ(A) = ρ(B) = 0 and a greatest fixed-point ρ(A) = ρ(B) = 1. Tracing collectors compute the least fixed-point, whereas reference counting collectors compute the greatest, so they cannot (by themselves) reclaim cyclic garbage. The difference between these two solutions is precisely the set of objects reachable only from garbage cycles. We saw in Section 5.5 that reference counting algorithms can use partial tracing to reclaim garbage cycles. They do so by starting from the greatest fixed-point solution and contracting the set of unreclaimed objects to the least fixed-point solution.
1http://java.sun.com/docs/hotspot/gc5.0/ergo5.html.
2Alternatively, the object could be added to the log in order to trade the size of the log for improved cache performance in the tracing loop (see Section 2.6) but this does not match so well the reference counting abstraction of Algorithm 6.2.