All garbage collection schemes are based on one of four fundamental approaches: mark-sweep collection, copying collection, mark-compact collection or reference counting. Different collectors may combine these approaches in different ways, for example, by collecting one region of the heap with one method and another part of the heap with a second method. The next four chapters focus on these four basic styles of collection. In Chapter 6 we compare their characteristics.
For now we shall assume that the mutator is running one or more threads, but that there is a single collector thread. All mutator threads are stopped while the collector thread runs. This stop-the-world approach simplifies the construction of collectors considerably. From the perspective of the mutator threads, collection appears to execute atomically: no mutator thread will see any intermediate state of the collector, and the collector will not see interference with its task by the mutator threads. We can assume that each mutator thread is stopped at a point where it is safe to examine its roots: we look at the details of the run-time interface in Chapter 11. Stopping the world provides a snapshot of the heap, so we do not have to worry about mutators rearranging the topology of objects in the heap while the collector is trying to determine which objects are live. This also means that there is no need to synchronise the collector thread as it returns free space with other collector threads or with the allocator as it tries to acquire space. We avoid the question of how multiple mutator threads can acquire fresh memory until Chapter 7. There are more complex run-time systems that employ parallel collector threads or allow mutator and collector threads to execute concurrently; we discuss them in later chapters.
We encourage readers to familiarise themselves with the collectors in the next four chapters before progressing to the more advanced collectors covered in later chapters. Experienced readers may wish to skip the descriptions of the basic algorithms, although we hope that the accounts of more sophisticated ways to implement these collectors will prove of interest. We refer readers who find some of the material in these four chapters rather too compressed to Chapters 2 to 6 of Jones [1996], where the classical algorithms are covered in greater detail with more examples.
The goal of an ideal garbage collector is to reclaim the space used by every object that will no longer be used by the program. Any automatic memory management system has three tasks:
1. to allocate space for new objects;
2. to identify live objects; and
3. to reclaim the space occupied by dead objects.
Algorithm 2.1: Mark-sweep: allocation
1 New():
2 ref ← allocate()
3 if ref = null | /* Heap is full */ |
4 collect()
5 ref ← allocate()
6 if ref = null | /* Heap is still full */ |
7 error "Out of memory"
8 return ref
9
10 atomic collect():
11 markFromRoots()
12 sweep(HeapStart, HeapEnd)
These tasks are not independent. In particular, the way space is reclaimed affects how fresh space is allocated. As we noted in Chapter 1, true liveness is an undecidable problem. Instead, we turn to an over-approximation of the set of live objects: pointer reachability (defined on page 13). We accept an object as live if and only if it can be reached by following a chain of references from a set of known roots. By extension, an object is dead, and its space can be reclaimed, if it cannot be reached though any such chain of pointers. This is a safe estimate. Although some objects in the live set may never be accessed again, all those in the dead set are certainly dead.
The first algorithm that we look at is mark-sweep collection [McCarthy, 1960]. It is a straightforward embodiment of the recursive definition of pointer reachability. Collection operates in two phases. First, the collector traverses the graph of objects, starting from the roots (registers, thread stacks, global variables) through which the program might immediately access objects and then following pointers and marking each object that it finds. Such a traversal is called tracing. In the second, sweeping phase, the collector examines every object in the heap: any unmarked object is deemed to be garbage and its space reclaimed.
Mark-sweep is an indirect collection algorithm. It does not detect garbage per se, but rather identifies all the live objects and then concludes that anything else must be garbage. Note that it needs to recalculate its estimate of the set of live objects at each invocation. Not all garbage collection algorithms behave like this. Chapter 5 examines a direct collection method, reference counting. Unlike indirect methods, direct algorithms determine the liveness of an object from the object alone, without recourse to tracing.
From the viewpoint of the garbage collector, mutator threads perform just three operations of interest, New, Read and Write, which each collection algorithm must redefine appropriately (the default definitions were given in Chapter 1 on page 15). The mark-sweep interface with the mutator is very simple. If a thread is unable to allocate a new object, the collector is called and the allocation request is retried (Algorithm 2.1). To emphasise that the collector operates in stop-the-world mode, without concurrent execution of the mutator threads, we mark the collect routine with the atomic keyword. If there is still insufficient memory available to meet the allocation request, then heap memory is exhausted. Often this is a fatal error. However, in some languages, New may raise an exception in this circumstance that the programmer may be able to catch. If memory can be released by deleting references (for example, to cached data structures which could be recreated later if necessary), then the allocation request could be repeated.
Algorithm 2.2: Mark-sweep: marking
1 markFromRoots():
2 initialise(worklist)
3 for each fld in Roots
4 ref ← *fld
5 if ref ≠ null && not isMarked(ref)
6 setMarked(ref)
7 add(worklist, ref)
8 mark()
9
10 initialise(worklist):
11 worklist ← empty
12
13 mark():
14 while not isEmpty(worklist)
15 ref ← remove(worklist) | /* |
16 for each fld in Pointers (ref)
17 child ← *fld
18 if child ≠ null && not isMarked(child)
19 setMarked(child)
20 add(worklist, child)
Before traversing the object graph, the collector must first prime the marker’s work list with starting points for the traversal (markFromRoots in Algorithm 2.2). Each root object is marked and then added to the work list (we defer discussion of how to find roots to Chapter 11). An object can be marked by setting a bit (or a byte), either in the object’s header or in a side table. If an object cannot contain pointers, then because it has no children there is no need to add it to the work list. Of course the object itself must still be marked. In order to minimise the size of the work list, markFromRoots calls mark immediately. Alternatively, it may be desirable to complete scanning the roots of each thread as quickly as possible. For instance, a concurrent collector might wish to stop each thread only briefly to scan its stack and then traverse the graph while the mutator is running. In this case mark (line 8) could be moved outside the loop.
For a single-threaded collector, the work list could be implemented as a stack. This leads to a depth-first traversal of the graph. If mark bits are co-located with objects, it has the advantage that the elements that are processed next are those that have been marked most recently, and hence are likely to still be in the hardware cache. As we shall see repeatedly, it is essential to pay attention to cache behaviour if the collector is not to sacrifice performance. Later we discuss techniques for improving locality.
Marking the graph of live objects is straightforward. References are removed from the work list, and the targets of their fields marked, until the work list is empty. Note that in this version of mark, every item in the work list has its mark bit set. If a field contains a null pointer or a pointer to an object that has already been marked, there is no work to do; otherwise the target is marked and added to the work list.
Termination of the marking phase is enforced by not adding already marked objects to the work list, so that eventually the list will become empty. At this point, every object reachable from the roots will have been visited and its mark bit will have been set. Any unmarked object is therefore garbage.
Algorithm 2.3: Mark-sweep: sweeping
1 sweep(start, end):
2 scan ← start
3 while scan < end
4 if isMarked(scan)
5 unsetMarked(scan)
6 else free(scan)
7 scan ← nextObject(scan)
The sweep phase returns unmarked nodes to the allocator (Algorithm 2.3). Typically, the collector sweeps the heap linearly, starting from the bottom, freeing unmarked nodes and resetting the mark bits of marked nodes in preparation for the next collection cycle. Note that we can avoid the cost of resetting the mark bit of live objects if the sense of the bit is switched between one collection and the next.
We will not discuss the implementation of allocate and free until Chapter 7, but note that the mark-sweep collector imposes constraints upon the heap layout. First, this collector does not move objects. The memory manager must therefore be careful to try to reduce the chance that the heap becomes so fragmented that the allocator finds it difficult to meet new requests, which would lead to the collector being called too frequently, or in the worst case, preventing the allocation of new memory at all. Second, the sweeper must be able to find each node in the heap. In practice, given a node, sweep must be able to find the next node even in the presence of padding introduced between objects in order to observe alignment requirements. Thus, nextObject may have to parse the heap instead of simply adding the size of the object to its address (line 7 in Algorithm 2.3); we also discuss heap parsability in Chapter 7.
It is very convenient to have a concise way to describe the state of objects during a collection (have they been marked, are they in the work list, and so on). The tricolour abstraction [Dijkstra et al, 1976, 1978] is a useful characterisation of tracing collectors that permits reasoning about collector correctness in terms of invariants that the collector must preserve. Under the tricolour abstraction, tracing collection partitions the object graph into black (presumed live) and white (possibly dead) objects. Initially, every node is white; when a node is first encountered during tracing it is coloured grey; when it has been scanned and its children identified, it is shaded black. Conceptually, an object is black if the collector has finished processing it, and grey if the collector knows about it but has not yet finished processing it (or needs to process it again). By analogy with object colour, fields can also be given a colour: grey when the collector first encounters them, and black once traced by the collector. This analogy also allows reasoning about the mutator roots as if the mutator were an object [Pirinen, 1998]. A grey mutator has roots that have not yet been scanned by the collector. A black mutator has roots that have already been scanned by the collector (and do not need to be scanned again). Tracing makes progress through the heap by moving the collector wavefront (the grey objects) separating black objects from white objects until all reachable objects have been traced black.
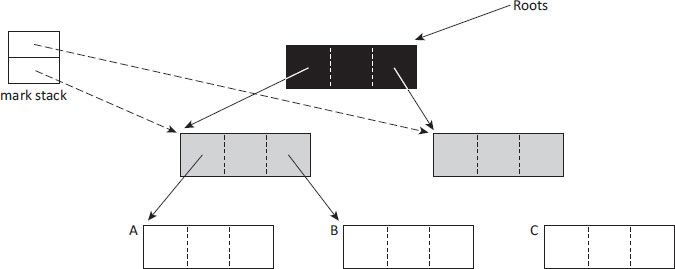
Figure 2.1: Marking with the tricolour abstraction. Black objects and their children have been processed by the collector. The collector knows of grey objects but has not finished processing them. White objects have not yet been visited by the collector (and some will never be).
Objects are coloured by mark-sweep collection as follows. Figure 2.1 shows a simple object graph and a mark stack (implementing the work list), mid-way through the mark phase. Any objects held on the mark stack will be visited again, and so are grey. Any object that has been marked, and is not on the stack, is black (the root of the graph in the figure). All other objects are white (currently, A, B and C). However, once mark has completed its traversal of the graph, the mark stack will be empty (no grey nodes), only C will remain white (garbage), and all other nodes will have been marked (black).
The algorithm preserves an important invariant: at the end of each iteration of the marking loop, there are no references from black to white objects. Thus any white object that is reachable must be reachable from a grey object. If this invariant were to be broken, then a live descendant of a black object might not be marked (and hence would be freed incorrectly) since the collector does not process black nodes further. The tricolour view of the state of garbage collection is particularly useful when algorithms for concurrent garbage collection are considered, where mutator threads run concurrently with the collector.
It is not uncommon for an application’s performance to be dominated by its cache behaviour. The latency to load a value from main memory is possibly hundreds of clock cycles whereas the latency for Level 1 caches may only be three or four cycles. Caches improve performance because applications typically exhibit good temporal locality: if a memory location has been accessed recently, it is very likely that it will be accessed again soon, and so it is worth caching its value. Applications may also exhibit good spatial locality: if a location is accessed, it is likely adjacent locations will also be accessed soon. Modern hardware can take advantage of this property in two ways. Rather than transferring single words between a cache and lower levels of memory, each entry in the cache (the cache line or cache block) holds a fixed number of bytes, typically 32–128 bytes. Secondly, processors may use hardware prefetching. For example, the Intel Core micro-architecture can detect a regular stride in the memory access pattern and fetch streams of data in advance. Explicit prefetching instructions are also commonly available for program-directed prefetching.
Unfortunately, garbage collectors do not behave like typical applications. The temporal locality of mark-sweep collection is poor. In the mark phase, the collector typically reads and writes an object’s header just once, since most objects are not shared (that is, they are referenced by just one pointer), although a small number of objects may be very popular [Printezis and Garthwaite, 2002]. The mark bit is read, and set if the object has not already been marked: it is unlikely to be accessed again in this phase. Typically, the header also contains a pointer to type information (possibly also an object itself), needed so that the collector can find the reference fields in this object. This information may contain either a descriptor identifying these fields, or it may be code that will mark and push the object’s descendants onto the mark stack. Because programs use only a limited number of types, and their frequency distribution is heavily skewed in favour of a small number of heavily used types, type information may be a good candidate for caching. But, otherwise, objects tend to be touched just once in this phase. Hardware prefetching is not tuned for this kind of pointer chasing.
We now consider ways in which the performance of a mark-sweep collector can be improved.
Space for a mark bit can usually be found in an object header word. Alternatively, mark bits can be stored in a separate bitmap table to the side of the heap, with a bit associated with every address at which an object might be allocated. The space needed for the bitmap depends on the object alignment requirements of the virtual machine. Either a single bitmap can be used or, in a block structured heap, a separate bitmap can be used for each block. The latter organisation has the advantage that no space is wasted if the heap is not contiguous. Per-block bitmaps might be stored in the blocks. However, placing the bitmap at a fixed position in each block risks degrading performance. This is because the bitmaps will contend for the same sets in a set-associative cache. Also, accessing the bitmap implies touching the page. Thus it may be better to use more instructions to access the bit rather than to incur locality overheads due to paging and cache associativity. To avoid the cache associativity issue, the position of the bitmap in the block can be varied by computing some simple hash of the block’s address to determine an offset for the bit map. Alternatively, the bitmap can be stored to the side [Boehm and Weiser, 1988], but using a table that is somehow indexed by block, perhaps by hashing. This avoids both paging and cache conflicts.
Bitmaps suffice if there is only a single marking thread. Otherwise, setting a bit in a bitmap is vulnerable to losing updates to races whereas setting a bit in an object header only risks setting the same bit twice: the operation is idempotent. Instead of a bitmap, byte maps are commonly used (at the cost of an 8-fold increase in space), thereby making marking races benign. Alternatively, a bitmap must use a synchronised operation to set a bit. In practice, matters are often more complicated for header bits in systems that allow marking concurrently with mutators, since header words are typically shared with mutator data such as locks or hash codes. With care, it may be possible to place this data and mark bits in different bytes of a header word. Otherwise, even mark bits in headers must be set atomically.
Mark bitmaps have a number of potential advantages. We identify these now, and then examine whether they materialise in practice on modern hardware. A bitmap stores marks much more densely than if they are stored in object headers. Consider how mark-sweep behaves with a mark bitmap. With a bitmap, marking will not modify any object, but will only read pointer fields of live objects. Other than loading the type descriptor field, no other part of pointer-free objects will be accessed. Sweeping will not read or write to any live object although it may overwrite fields of garbage objects as part of freeing them (for example to link them into a free-list). Thus bitmap marking is likely to modify fewer words, and to dirty fewer cache lines so less data needs to be written back to memory.
Bitmap marking dates to at least Lisp 1.5 but was adopted for a conservative collector designed to provide automatic memory management for uncooperative languages like C and C++ [Boehm and Weiser, 1988]. Type-accurate systems can precisely identify every slot that contains a pointer, whether it is in an object, the stack frame of a thread or another root. Conservative collectors, on the other hand, do not receive this level of support from the compiler or run-time system and so have to make conservative decisions on pointer identity. If the value held in a slot looks sufficiently like an object reference, it is assumed to be one. We discuss the problems of pointer finding in more detail in Chapter 11. Conservative collection may interpret a slot as a pointer when it is not; this has two consequences for safety. First, the collector must not alter the value stored in any location owned by the mutator (including objects and roots). This rules out all algorithms that move objects since this would require updating every reference to a moved object. It also rules out storing mark bits in object headers since the ‘object’ in question might not be an object if it was reached by following a false pointer. Setting or clearing a bit might destroy user data. Second, it is very useful to minimise the chance of the mutator interfering with the collector’s data. Adding a header word for the collector’s use, contiguous to every object, is riskier than keeping collector metadata such as mark bits in a separate data structure.
Bitmap marking was also motivated by the concern to minimise the amount of paging caused by the collector [Boehm, 2000]. However, in modern systems, any paging at all due to the collector is generally considered unacceptable. The question for today is whether bitmap marking can improve cache performance. There is considerable evidence that objects tend to live and die in clusters [Hayes, 1991; Jones and Ryder, 2008]. Many allocators will tend to allocate these objects close to each other. Sweeping with a bitmap has two advantages. It allows the mark bits of clusters of objects to be tested and cleared in groups as the common case will be that either every bit/byte is set or every bit/byte is clear in a map word. A corollary is that it is simple from the bitmap to determine whether a complete block of objects is garbage, thus allowing the whole block to be returned to the allocator.
Many memory managers use a block structured heap (for example, Boehm and Weiser [1988]). A straightforward implementation might reserve a prefix of each block for its bitmap. As previously discussed this leads to unnecessary cache conflicts and page accesses, so collectors tend to store bitmaps separately from user data blocks.
Garner et al [2007] adopt a hybrid approach, associating each block in a segregated fits allocator’s data structure with a byte in a map, as well as marking a bit in object headers. The byte is set if and only if the corresponding block contains at least one object. The byte map of used/unused blocks thus allows the sweeper to determine easily which blocks are completely empty (of live objects) and can be recycled as a whole. This has two advantages. Both the bit in the object header and the byte in the byte map, corresponding to the block in which the object resides, can be set without using synchronised operations. Furthermore, there are no data dependencies on either write (which might lead to cache stalls), and writing the byte in the byte map is unconditional.
Printezis and Detlefs [2000] use bitmaps to reduce the amount of space used for mark stacks in a mostly-concurrent, generational collector. First, as usual, mutator roots are marked by setting a bit in the map. Then, the marking thread linearly searches this bitmap, looking for live objects. Algorithm 2.4 strives to maintain the invariant that marked objects below the current ‘finger’, cur in the mark routine, are black and those above it are grey. When the next live (marked) object cur is found, it is pushed onto the stack and we enter the usual marking loop to restore the invariant: objects are popped from the stack and their children marked recursively until the mark stack is empty. If an item is below cur in the heap, it is pushed onto the mark stack; otherwise its processing is deferred to later in the linear search. The main difference between this algorithm and Algorithm 2.1 is its conditional insertion of children onto the stack at line 15. Objects are only marked recursively (thus consuming mark stack space) if they are behind the black wavefront which moves linearly through the heap. Although the complexity of this algorithm is proportional to the size of the space being collected, in practice searching a bitmap is cheap.
Algorithm 2.4: Printezis and Detlefs’s bitmap marking
1 mark () :
2 cur ← nextInBitmap()
3 while cur < HeapEnd | /* marked |
4 add(worklist, cur)
5 markStep(cur)
6 cur ← nextInBitmap()
7
8 markStep(start):
9 while not isEmpty(worklist)
10 ref ← remove(worklist) | /* |
11 for each fld in Pointers (ref)
12 child ← *fld
13 if child ≠ null && not isMarked(child)
14 setMarked(child)
15 if child < start
16 add(worklist, child)
A similar approach can be used to deal with mark stack overflow. When the stack overflows, this is noted and the object is marked but not pushed onto the stack. Marking continues until the stack is exhausted. Now we must find those marked objects that could not be added to the stack. The collector searches the heap, looking for any marked objects with one or more unmarked children and continues the trace from these children. The most straightforward way to do this is with a linear sweep of the heap. Sweeping a bitmap will be more efficient than examining a bit in the header of each object in the heap.
The complexity of the mark phase is O(L), where L is the size of the live data in the heap; the complexity of the sweep phase is O(H) where H is the size of the heap. Since H > L, at first sight it might seem that the mark-sweep algorithm is dominated by the cost of sweeping. However, in practice, this is not the case. Chasing pointers in the mark phase leads to unpredictable memory access patterns, whereas sweep behaviour is more predictable. Further, the cost of sweeping an object tends to be much less than the cost of tracing it. One way to improve the cache behaviour of the sweep phase is to prefetch objects. In order to avoid fragmentation, allocators supporting mark-sweep collectors typically lay out objects of the same size consecutively (see Chapter 7 on page 93) leading to a fixed stride as a block of same-sized objects is swept. Not only does this pattern allow software prefetching, but it is also ideal for the hardware prefetching mechanisms found in modern processors.
Algorithm 2.5: Lazy sweeping with a block structured heap
1 atomic collect():
2 markFromRoots ()
3 for each block in Blocks
4 if not isMarked(block) | /* no objects marked in this block? */ |
5 add(blockAllocator, block) | /* return block to block allocator */ |
6 else
7 add(reclaimList, block) | /* queue block for lazy sweeping */ |
8
9 atomic allocate(sz):
10 result ← remove(sz) | /* allocate from size class for |
11 if result = null | /* if no free slots for this size… */ |
12 lazySweep(sz) | /* sweep a little */ |
13 result ← remove(sz)
14 return result | /* if still null, collect */ |
15
16 lazySweep(sz):
17 repeat
18 block ← nextBlock(reclaimList, sz)
19 if block ≠ null
20 sweep(start(block), end(block))
21 if spaceFound(block)
22 return
23 until block = null | /* reclaim list for this size class is empty */ |
24 allocSlow(sz) | /* get an empty block */ |
25
26 allocSlow(sz): | /* allocation slow path */ |
27 block ← allocateBlock() | /* from the block allocator */ |
28 if block ≠ null
29 initialise(block, sz)
Can the time for which the mutators are stopped during the sweep phase be reduced or even eliminated? We observe two properties of objects and their mark bits. First, once an object is garbage, it remains garbage: it can neither be seen nor be resurrected by a mutator. Second, mutators cannot access mark bits. Thus, the sweeper can be executed in parallel with mutator threads, modifying mark bits and even overwriting fields of garbage objects to link them into allocator structures. The sweeper (or sweepers) could be executed as separate threads, running concurrently with the mutator threads, but a simple solution is to use lazy sweeping [Hughes, 1982]. Lazy sweeping amortises the cost of sweeping by having the allocator perform the sweep. Rather than a separate sweep phase, the responsibility for finding free space is devolved to allocate. At its simplest, allocate advances the sweep pointer until it finds sufficient space in a sequence of unmarked objects. However, it is more practical to sweep a block of several objects at a time.
Algorithm 2.5 shows a lazy sweeper that operates on a block of memory at a time. It is common for allocators to place objects of the same size class into a block (we discuss this in detail in Chapter 7). Each size class will have one or more current blocks from which it can allocate and a reclaim list of blocks not yet swept. As usual the collector will mark all live objects in the heap, but instead of eagerly sweeping the whole heap, collect will simply return any completely empty blocks to the block level allocator (line 5). All other blocks are added to the reclaim queue for their size class. Once the stop-the-world phase of the collection cycle is complete, the mutators are restarted. The allocate method first attempts to acquire a free slot of the required size from an appropriate size class (in the same way as Algorithm 7.7 would). If that fails, the lazy sweeper is called to sweep one or more remaining blocks of this size class, but only until the request can be satisfied (line 12). However, it may be the case that no blocks remain to be swept or that none of the blocks swept contained any free slots. In this case, the sweeper attempts to acquire a whole fresh block from a lower level, block allocator. This fresh block is initialised by setting up its metadata — for example, threading a free-list through its slots or creating a mark byte map. However, if no fresh blocks are available, the collector must be called.
There is a subtle issue that arises from lazy sweeping a block structured heap such as one that allocates from different size classes. Hughes [1982] worked with a contiguous heap and thus guaranteed that the allocator would sweep every node before it ran out of space and invoked the garbage collector again. However, lazily sweeping separate size classes does not make this guarantee since it is almost certain that the allocator will exhaust one size class (and all the empty blocks) before it has swept every block in every other size class. This leads to two problems. First, garbage objects in unswept blocks will not be reclaimed, leading to a memory leak. If the block also contains a truly live object, this leak is harmless since these slots would not have been recycled anyway until the mutator made a request for an object of this size class. Second, if all the objects in the unswept block subsequently become garbage, we have lost the opportunity to reclaim the whole block and recycle it to more heavily used size classes.
The simplest solution is to complete sweeping all blocks in the heap before starting to mark. However, it might be preferable to give a block more opportunities to be lazily swept. Garner et al [2007] trade some leakage for avoiding any sweeps. They achieve this for Jikes RVM/MMTk [Blackburn et al, 2004b] by marking objects with a bounded integer rather than a bit. This does not usually add space costs since there is often room to use more than one bit if marks are stored in object headers, and separate mark tables often mark with bytes rather than bits. Each collection cycle increments modulo 2K the value used as the mark representing ‘live’, where K is the number of mark bits used, thus rolling the mark back to zero on overflow. In this way, the collector can distinguish between an object marked in this cycle and one marked in a previous cycle. Only marks equal to the current mark value are considered to be set. Marking value wrap-around is safe because, immediately before the wrap-around, any live object in the heap is either unmarked (allocated since the last collection) or has the maximum mark bit value. Any object with a mark equal to the next value to be used must have been marked last some multiple of 2K collections ago. Therefore it must be floating garbage and will not be visited by the marker. This potential leak is addressed somewhat by block marking. Whenever the MMTk collector marks an object, it also marks its block. If none of the objects in a block has been marked with the current value, then the block will not have been marked either and so will be reclaimed as a whole at line 5 in Algorithm 2.5. Given the tendency for objects to live and die in clumps, this is an effective tactic.
Lazy sweeping offers a number of benefits. It has good locality: object slots tend to be used soon after they are swept. It reduces the algorithmic complexity of mark-sweep to be proportional to the size of the live data in the heap, the same as semispace copying collection, which we discuss in Chapter 4. In particular, Boehm [1995] suggests that mark and lazy sweep will perform best in the same circumstance that copying performs best: when most of the heap is empty, as the lazy sweep’s search for unmarked objects will terminate quickly. In practice, the mutator’s cost of initialising objects is likely to dominate the cost of sweeping and allocation.
Figure 2.2: Marking with a FIFO prefetch buffer. As usual, references are added to the work list by being pushed onto the mark stack. However, to remove an item from the work list, the oldest item is removed from the FIFO buffer and the entry at the top of the stack is inserted into it. The object to which this entry refers is prefetched so that it should be in the cache by the time this entry leaves the buffer.
2.6 Cache misses in the marking loop
We have seen how prefetching can improve the performance of the sweep phase. We now examine how it can also be employed to advantage in the mark phase. For example, by densely packing mark bits into a bitmap, the number of cache misses incurred by testing and setting marks can be reduced. However, cache misses will be incurred as the fields of an unmarked object are read as part of the traversal. Thus, much of the potential cache advantage of using mark bitmaps in the mark phase will be lost as object fields are loaded.
If an object is pointer-free, it is not necessary to load any of its fields. Although matters will vary by language and by application, it is likely that the heap may contain a significant volume of objects with no user-defined pointer fields. Whether or not an object contains pointers is an aspect of its type. One way that this can be determined is from the type information slot in an object’s header. However, it is also possible to obtain information about an object from its address, for example if objects with similar characteristics are located together. Lisp systems have often used a big bag of pages allocation (BiBoP) technique, allocating objects of only one type (such as cons cells) on a page, thus allowing type information to be compactly associated with the page rather than each object [Foderaro et al, 1985]. Similarly, pointer-full and pointer-free objects could be segregated. Pointers themselves can also encode type information [Steenkiste, 1987; Steenkiste and Hennessy, 1988].
Boehm [2000] observes that marking dominates collection time, with the cost of fetching the first pointer from an object accounting for a third of the time spent marking on an Intel Pentium III system. He suggests prefetching on grey: fetching the first cache line of an object as that object is greyed (added to the mark stack, line 20 of Algorithm 2.2), and prefetching a modest number of cache lines ahead as very large objects are scanned. However, this technique relies on the timing of the prefetch. If the cache line is prefetched too soon, it may be evicted from the cache before it is used. If it is fetched too late, then the cache miss will occur anyway.
Algorithm 2.6: Marking with a FIFO prefetch buffer
1 add(worklist, item):
2 markStack ← getStack(worklist)
3 push(markStack, item)
4
5 remove(worklist) :
6 markStack ← getStack(worklist)
7 addr ← pop(markStack)
8 prefetch(addr)
9 fifo ← getFifo(worklist)
10 prepend(fifo, addr)
11 return remove(fifo)
Algorithm 2.7: Marking graph edges rather than nodes
1 mark():
2 while not isEmpty(worklist)
3 obj ← remove(worklist)
4 if not isMarked(obj)
5 setMarked(obj)
6 for each fld in Pointers(obj)
7 child ← *fld
8 if child ≠ null
9 add(worklist, child)
Cher et al [2004] observe that the fundamental problem is that cache lines are fetched in a breadth-first, first-in, first-out (FIFO), order but the mark-sweep algorithm traverses the graph depth-first, last-in, first-out (LIFO). Their solution is to insert a first-in, first-out queue in front of the mark stack (Figure 2.2 and Algorithm 2.6). As usual, when mark adds an object to its work list, a reference to the object is pushed onto a mark stack. However, when mark wants to acquire an object from the work list, a reference is popped from the mark stack but inserted into the queue, and the oldest item in the queue is returned to mark. The reference popped from the stack is also prefetched, the length of the queue determining the prefetch distance. Prefetching a few lines beyond the popped reference will help to ensure that sufficient fields of the object to be scanned are loaded without cache misses.
Prefetching the object to be marked through the first-in, first-out queue enables mark to load the object to be scanned without cache misses (lines 16–17 in Algorithm 2.2). However, testing and setting the mark of the child nodes will incur a cache miss (line 18). Garner et al [2007] realised that mark’s tracing loop can be restructured to offer greater opportunities for prefetching. Algorithm 2.2 added each node of the live object graph to the work list exactly once; an alternative would be to traverse and add each edge exactly once. Instead of adding children to the work list only if they are unmarked, this algorithm inserts the children of unmarked objects unconditionally (Algorithm 2.7). Edge enqueuing requires more instructions to be executed and leads to larger work lists than node enqueuing since graphs must contain more edges than nodes (Garner et al suggest that typical Java applications have about 40% more edges than nodes). However, if the cost of adding and removing these additional work list entries is sufficiently small then the gains from reducing cache misses will outweigh the cost of this extra work. Algorithm 2.7 hoists marking out of the inner loop. The actions that might lead to cache misses, isMarked and Pointers, now operate on the same object obj, which has been prefetched through the first-in, first-out queue, rather than on different objects, obj and its children, as previously. Garner et al observe that tracing edges rather than nodes can improve performance even without software prefetching, speculating that the structure of the loop and the first-in, first-out queue enables more aggressive hardware speculation through more predictable access patterns.
Despite its antiquity as the first algorithm developed for garbage collection [McCarthy, 1960], there are many reasons why mark-sweep collection remains an attractive option for developers and users.
Mark-sweep in its simplest form imposes no overhead on mutator read and write operations. In contrast, reference counting (which we introduce in Chapter 5) imposes a significant overhead on the mutator. However, note that mark-sweep is also commonly used as a base algorithm for more sophisticated collectors which do require some synchronisation between mutator and collector. Both generational collectors (Chapter 9), and concurrent and incremental collectors (Chapter 15), require the mutator to inform the collector when they modify pointers. However, the overhead of doing so is typically small, a few percent of overall execution time.
Combined with lazy sweeping, mark-sweep offers good throughput. The mark phase is comparatively cheap, and dominated by the cost of pointer chasing. It simply needs to set a bit or byte for each live object discovered, in contrast to algorithms like semispace copying collection (Chapter 4) or mark-compact (Chapter 3) which must copy or move objects. On the other hand, like all the tracing collectors in these initial chapters, mark-sweep requires that all mutators be stopped while the collector runs. The pause time for collection depends on the program being run and its input, but can easily extend to several seconds or worse for large systems.
Mark-sweep has significantly better space usage than approaches based on semispace copying. It also potentially has better space usage than reference counting algorithms. mark bits can often be stored at no cost in spare bits in object headers. Alternatively, if a side bitmap table is used, the space overhead depend on object alignment requirements; it will be no worse than 1/alignment of the heap ( or of the heap, depending on architecture), and possibly better depending on alignment restrictions. Reference counting, on the other hand, requires a full slot in each object header to store counts (although this can be reduced if a limit is placed on the maximum reference count stored). Copying collectors make even worse use of available memory, dividing the available heap into two equally sized semispaces, only one of which is used by the mutator at any time. On the debit side, non-compacting collectors, like mark-sweep and reference counting, require more complex allocators, such as segregated fits free-lists. The structures needed to support such collectors impose a further, non-negligible overhead. Furthermore, non-compacting collectors can suffer from fragmentation, thus increasing their effective space usage.
However, mark-sweep is a tracing algorithm. Like other tracing algorithms, it must identify all live objects in a space before it can reclaim the memory used by any dead objects. This is an expensive operation and so should be done infrequently. This means that tracing collectors must be given some headroom in which to operate in the heap. If the live objects occupy too large a proportion of the heap, and the allocators allocate too fast, then a mark-sweep collector will be called too often: it will thrash. For moderate to large heaps, the headroom necessary may be between 20% and 50% of the heap [Jones, 1996] though Hertz and Berger [2005] show that, in order to provide the same throughput, Java programs managed by mark-sweep collection may need a heap several times larger than if it were to be managed by explicit deallocation.
Not moving objects has both advantages and disadvantages. Its benefit is that it makes mark-sweep a suitable candidate for use in uncooperative environments where there is no communication between language compiler and garbage collector (see Chapter 11). Without type-accurate information about the mutators’ roots and the fields of objects, they cannot be updated with the new locations of moved objects — the putative ‘root’ might not be a pointer but other user data. In some cases, hybrid mostly-copying collection is possible [Bartlett, 1988a; Hosking, 2006]. Here, a program’s roots must be treated conservatively (if it looks like a pointer, assume it is a pointer), so the collector cannot move their referents. However, type-accurate information about the layout of objects is available to the collector so it can move others that are not otherwise pinned to their location.
Safety in uncooperative systems managed by a conservative collector precludes the collector’s modifying user data, including object headers. It also encourages placing collector metadata separate from user or other run-time system data, to reduce the risk of modification by the mutator. For both reasons, it is desirable to store mark bits in bitmaps rather than object headers.
The problem with not moving objects is that, in long running applications, the heap tends to become fragmented. Non-moving memory allocators require space larger than the minimum possible, where min and max are the smallest and largest possible object sizes [Robson, 1971, 1974]. Thus a non-compacting collector may have to be called more frequently than one that compacts. Note that all tracing collectors need sufficient headroom (say, 20–50%) in the heap in order to avoid thrashing the collector.
To avoid having performance suffer due to excessive fragmentation, many production collectors that use mark-sweep to manage a region of the heap also periodically use another algorithm such as mark-compact to defragment it. This is particularly true if the application does not maintain fairly constant ratios of object sizes or allocates many very large objects. If the application allocates more large objects than it previously did, the result may be many small holes in the heap no longer being reused for new allocations of objects of the same size. Conversely, if the application begins to allocate smaller objects than before, these smaller objects might be allocated in gaps previously occupied by larger objects, with the remaining space in each gap being wasted. However, careful heap management can reduce the tendency to fragment by taking advantage of objects’ tendency to live and die in clumps [Dimpsey et al, 2000; Blackburn and McKinley, 2008]. Allocation with segregated-fits can also reduce the need to compact.