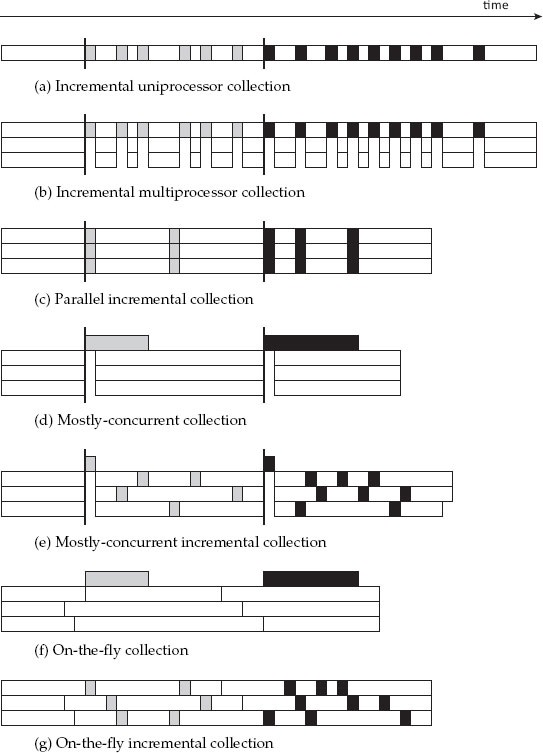
The basic principles of concurrent collection were initially devised as a means to reduce pause times for garbage collection on uniprocessors. Early papers used terms such as ‘concurrent’, ‘parallel’, ‘on-the-fly’ and ‘real-time’ interchangeably or inconsistently. In Chapter 14 we defined the modern usage of ‘parallel’. Here, we define the remaining terms. So far, we have assumed that the mutator is suspended while garbage collection proceeds, and that each collection cycle terminates before the mutator can continue. As before, Figure 14.1a illustrates different collection styles by one or more horizontal bars, with time proceeding from left to right, and shows mutator execution in white while each collection cycle is represented as a distinct non-white shade. Thus, grey boxes represent actions of one garbage collection cycle, and black boxes those of the next.
We have already seen one way to reduce pause times on a multiprocessor in Chapter 14: run a full garbage collection cycle in parallel while all the mutators are stopped, as illustrated in Figure 14.1c.
Another way to reduce pause times on a uniprocessor is to interleave mutator execution with collector execution, as illustrated in Figure 15.1a. Interleaving mutator and collector execution in this way is called incremental collection, since the collection cycle is broken down into multiple finer-grained increments. However, incremental collection is not as straightforward as it might first seem, since the collection cycle is no longer atomic with respect to mutation of the object graph, so the reachability of objects can change from one increment to the next. Thus, incremental collectors must have some way of keeping track of changes to the graph of reachable objects, perhaps re-scanning objects or fields in the face of those changes. There are many different ways to cope with this problem.
Although interleaving provides the illusion of concurrency between mutator and collector, incremental collection assumes that the mutator and collector do not execute in parallel — that is, that the mutator is stopped for each increment of the collector cycle. It is possible to maintain this property on a multiprocessor by making sure that all parallel mutators are stopped for each increment, as illustrated in Figure 15.1b. The increments can also be parallelised, as in Figure 15.1c.
It is a conceptually simple step to go from interleaving of the mutator with the collector on a uniprocessor to concurrent execution of (multiple) mutators in parallel with the collector on a multiprocessor. The main added difficulty is ensuring that the collector and mutators synchronise properly to maintain a consistent view of the heap, and not just for reachability. For example, inconsistency can occur when a mutator attempts to manipulate partially scanned or copied objects, or to access metadata, concurrently with the collector.
The degree and granularity of this synchronisation necessarily impacts application throughput (that is, end-to-end execution time including both mutator and collector work), and synchronisation is more easily maintained in some phases of collection than others. Thus, mostly-concurrent collection avoids some synchronisation overhead by assuming that the mutators are all stopped together for a brief period during each collector cycle, often at the beginning of the cycle, which may include obtaining stack roots from the stopped mutators. This is true whether the collection cycle is monolithic (Figure 15.1d) or incremental (Figure 15.1e). The (hopefully brief) global stop-the-world phase ensures that all the mutators are simultaneously aware that a collection cycle has begun.
Figure 15.1: Incremental and concurrent garbage collection. Each bar represents an execution on a single processor. The coloured regions represent different garbage collection cycles.
Relaxing the need for a global stop-the-world phase yields purely concurrent on-the-fly collection, which executes in parallel with the mutators (Figure 15.1f), possibly incrementally (Figure 15.1g). The vertical lines indicate that each mutator may need to synchronise with the collector prior to each collection cycle, even though there is no global stop-the-world phase.1
15.1 Correctness of concurrent collection
A correct concurrent collector must satisfy two properties:
• safety requires the collector to retain at least all reachable objects;
• liveness requires the collector eventually to complete its collection cycle.
Concurrent collectors are correct only insofar as they are able to control mutator and collector interleavings. As we shall soon see, concurrent mutator and collector operations will be specified as operating atomically, allowing us to interpret a sequence of interleaved operations as being generated by a single mutator (and single collector), without loss of generality. Any concurrent schedule for executing these atomic operations that preserves their appearance of atomicity will be permitted, leaving the actual implementation of the concurrency control for these operations to the discretion of the implementer. Perhaps the easiest way to preserve atomicity of these operations is to alternate collector and mutator work by running the collector incrementally, stopping all the mutator threads while each collector increment runs. Other approaches permit finer-grained synchronisation. Techniques for doing so have been reviewed in Chapter 13.
The tricolour abstraction, revisited
Correctness of concurrent collectors is often most easily reasoned about by considering invariants based on the tricolour abstraction that the collector and mutator must preserve. All concurrent collectors preserve some realisation of these invariants, but they must retain at least all the reachable objects (safety) even as the mutator modifies objects. Recall that:
White objects have not yet been reached by the collector; this includes all objects at the beginning of the collection cycle. Those left white at the end of the cycle will be treated as unreachable garbage.
Grey objects have been reached by the collector, but one or more of their fields still need to be scanned (they may still point to white objects).
Black objects have been reached by the collector, and all their fields have been scanned; thus, immediately after scanning none of the outgoing pointers were to white objects. Black objects will not be rescanned unless their colour changes.
The garbage collector can be thought of as advancing a grey wavefront, the boundary between black (was reachable at some time and scanned) and white (not yet visited) objects. When the collector cycle can complete without mutators concurrently modifying the heap there is no problem. The key problem with concurrent mutation is that the collector’s and the mutator’s views of the world may become inconsistent, and that the grey wavefront no longer represents a proper boundary between black and white.
Let us reconsider the earlier definition of the mutator Write operation, which we can recast as follows by introducing a redundant load from the field right before the store:
atomic Write(src, i, new):
old ← src[i]
src[i] ← new
The Write operation inserts the pointer src→new into the field src[i] of object src. As a side-effect it deletes the pointer src→old from src[i]. We characterise the operation as atomic to emphasise that the old and new pointers are exchanged instantaneously without any other interleaving of mutator/collector operations. Of course, on most hardware the store is naturally atomic so no explicit synchronisation is required.
When the mutator runs concurrently with the collector and modifies objects ahead of the wavefront — grey objects (whose fields still need to be scanned) or white objects (as yet unreached) — correctness ensues since the collector will still visit those objects at some point (if they are still reachable). There is also no problem if the mutator modifies objects behind the wavefront — black objects (whose fields have already been scanned) — so long as it inserts or deletes a pointer to only a black or grey object (which the collector has already decided is reachable). However, other pointer updates may lead to the mutator’s and the collector’s view of the set of live objects becoming incoherent [Wilson, 1994], and thus live objects being freed incorrectly. Let us consider an example.
We illustrate the two scenarios under which a white pointer can be inserted behind the wavefront in Figure 15.2. The first scenario in Figure 15.2a illustrates how the mutator can hide a white object initially directly reachable from a grey object by inserting its pointer behind the wavefront and then deleting its link from the grey object. The initial state of the heap shows a black object X and grey object Y, having been marked reachable from the roots. White object Z is directly reachable from Y. In step D1 the mutator inserts pointer b from X to Z by copying pointer a from grey object Y. In step D2 the mutator deletes unscanned pointer a from the only unscanned object Y that refers to Z. In step D3 the collector scans the object Y to make it black, and terminates its marking phase. In the sweep phase, white object Z will be erroneously reclaimed, even though it is reachable via pointer b.
The second scenario in Figure 15.2b shows how the mutator can hide a white object transitively reachable via a chain of pointers from a grey object by inserting its pointer behind the wavefront and then deleting some other link in the chain. In this scenario no pointer to the lost object itself is deleted, unlike the direct case which does delete a pointer to the lost object. The initial state of the heap shows a black object P and grey object Q, having been marked reachable from the roots. White object R is directly reachable from Q, while white object S is transitively reachable from Q via R. In step T1 the mutator inserts pointer e from P to S by copying pointer d from white object R. In step T2 the mutator deletes pointer c to R, destroying the path from the only unscanned object Q that leads to S. In step T3 the collector scans the object Q to make it black, and terminates its marking phase. In the sweep phase, white object S will be erroneously reclaimed, even though it is reachable via pointer e.
Figure 15.2: The lost object problem: a reachable white object is hidden from the collector by making it unreachable from any grey object.
With kind permission from Springer Science+Business Media: Vechev et al [2005], figures 3–4, pages 584–5.
Wilson [1994] observes that objects can become lost only if two conditions hold at some point during tracing:
Condition 1: the mutator stores a pointer to a white object into a black object, and
Condition 2: all paths from any grey objects to that white object are destroyed.
Inserting a white pointer (that is, a pointer to a white object) into a black object will cause problems if the collector never encounters another pointer to the white object. It would mean that the white object is reachable (from the black object, Condition 1), but the collector will never notice since it does not revisit black objects. The collector could only discover the white object by following a path of unvisited (that is, white) objects starting from an object that the collector has noticed but not finished with (that is, a grey object). But Condition 2 states that there is no such path.
The strong and weak tricolour invariants
To prevent live objects from being reclaimed incorrectly, we must ensure that both conditions cannot hold simultaneously. To guarantee that the collector will not miss any reachable objects it must be sure to find every white object that is pointed to by black objects. So long as any white object pointed to by black objects is also protected from deletion it will not be missed. It is sufficient for such an object to be directly reachable from some grey object, or transitively reachable from some grey object through a chain of white objects. In this case Condition 2 never holds. We say that such an object is grey protected. Thus, we must preserve:
The weak tricolour invariant: All white objects pointed to by a black object are grey protected (that is, reachable from some grey object, either directly or through a chain of white objects).
Non-copying collectors have the advantage that all white pointers automatically turn into grey/black pointers when their target object is shaded grey or black. Thus, white pointers in black objects are not a problem because their grey protected white targets are eventually shaded by the collector — all white pointers in black objects eventually become black before the collection cycle can terminate.
In contrast, concurrent copying collectors are more restricted because they explicitly have two copies of every live object at the end of the collection cycle (the fromspace white copy, and the tospace black copy), at which point the white copies are discarded along with the garbage. By definition, black objects are never revisited by the collector. Thus, a correct concurrent copying collector must never allow a white fromspace pointer (to a white fromspace object) to be stored in a black tospace object. Otherwise, the collector will complete its cycle while leaving dangling white pointers from black tospace into the discarded white fromspace. That is, they must preserve:
The strong tricolour invariant: There are no pointers from black objects to white objects.
Clearly, the strong invariant implies the weak invariant, but not the other way round. Because problems can occur only when the mutator inserts a white pointer into a black object it is sufficient simply to prohibit that. Preserving the strong tricolour invariant is a strategy equally suited to both copying and non-copying collectors.
In both the scenarios in the example, the mutator first wrote a pointer to a white object into a black object (D1/T1), breaking the strong invariant. It then destroyed all paths to that white object from grey objects (D2/T2), breaking the weak invariant. The result was that a (reachable) black object ended up pointing to a (presumed garbage) white object, violating correctness. Solutions to the lost object problem operate at either the step that writes the pointer to the white object (D1/T1) or the step that deletes a remaining path to that object (D2/T2).
Different collector algorithms, which achieve safety and liveness in different ways, will have varying degrees of precision (as determined by the set of objects they retain at the end of the collection cycle), efficiency (throughput), and atomicity (degree of concurrency). Varying precision means that they may retain some varying superset of the reachable objects, and hence affects the promptness of reclamation of dead objects. A stop-the-world collector obtains maximal precision (all unreachable objects are collected) at the expense of any concurrency with the mutator. Finer grained atomicity permits increased concurrency with the mutator at the expense of possibly retaining more unreachable objects and the overhead to ensure atomicity of key operations. It is difficult to identify the minimal yet sufficient set of critical sections to place in tracing. Vechev et al [2007] shows how this search can be semi-automated. Unreachable objects that are nevertheless retained at the end of the collection cycle are called floating garbage. It is usually desirable, though not strictly necessary for correctness, that a concurrent collector also ensure completeness in collecting floating garbage at some later collection cycle.
In classifying algorithms it is also useful to talk about the colour of the mutator roots as if the mutator itself were an object. A grey mutator either has not yet been scanned by the collector so its roots are still to be traced, or its roots have been scanned but need to be rescanned. This means that the grey mutator roots may refer to objects that are white, grey or black. A black mutator has been scanned by the collector so its roots have been traced, and will not be scanned again. Under the strong invariant this means that a black mutator’s roots can refer only to objects that are grey or black but not white. Under the weak invariant, a black mutator can hold white references so long as their targets are protected from deletion.
The colour of the mutator has implications for termination of a collection cycle. By definition, concurrent collection algorithms that permit a grey mutator need to rescan its roots. This will lead to more tracing work if a reference to a non-black object is found. When this trace is complete, the roots must be scanned again, in case the mutator has added to the roots yet another non-black reference, and so on. In the worst case, it may be necessary for grey mutator algorithms to halt all mutator threads for a final scan of their roots.
As mentioned earlier, our simplifying assumption for now is that there is only a single mutator. However, on-the-fly collectors distinguish among multiple mutator threads because they do not suspend them all at once to sample their roots. These collectors must operate with mutator threads of different colours, both grey (unscanned) and black (scanned). Moreover, some collectors may separate a single mutator thread’s roots into scanned (black) and unscanned (grey) portions. For example, the top frame of a thread’s stack may be scanned to make it black, while the remaining stack frames are left unscanned (grey). Returning or unwinding into the grey portion of the stack forces the new top stack frame to be scanned.
Mutator colour also influences the colour objects receive when they are allocated, since allocation results in the mutator holding the pointer to the newly allocated object, which must satisfy whichever invariant applies given the colour of the mutator. But the allocation colour also affects how quickly a new object can be freed once it becomes unreachable. If an object is allocated black or grey then it will not be freed during the current collection cycle (since black and grey objects are considered to be live), even if the mutator drops its reference without storing it into the heap. A grey mutator can allocate objects white and so avoid unnecessarily retaining new objects. A black mutator cannot allocate white (whether the strong or weak invariant applies), unless (under the weak invariant) there is a guarantee that the white reference will be stored to a live object ahead of the wavefront so the collector will retain it. Otherwise, there is nothing to prevent the collector from reclaiming the object even though the black mutator retains a pointer to it. Note also that, initially, a new object contains no outgoing references so allocating black is always safe.
Wilson [1994] calls solutions that address D1/T1 mutations incremental update techniques because they inform the collector of incremental changes made by the mutator to the set of objects known to be live, and hence of additional objects that need to be (re)scanned. Incremental update solutions conservatively treat an object as live (non-white) if a pointer to it is ever inserted behind the wavefront (into a black object), speculating that the mutator may yet delete all other paths to the object ahead of the wavefront. Thus, incremental update techniques preserve the strong invariant. They use a write barrier to protect against insertion of white pointers in black objects. In the example above, the write barrier would re-colour the source or destination of pointer b so that the pointer is no longer black to white.
When a black mutator loads a reference from the heap it is effectively inserting a pointer in a black object (itself). Incremental update techniques can use a mutator read barrier to protect from insertion of white pointers in a black mutator.
Snapshot-at-the-beginning solutions
Wilson calls solutions that address D2/T2 mutations snapshot-at-the-beginning techniques since they preserve the set of objects that were live at the start of the collection. They inform the collector when the mutator deletes a white pointer from a grey or white object (ahead of the wavefront). Snapshot-at-the-beginning solutions conservatively treat an object as live (non-white) if a pointer to it ever existed ahead of the wavefront, speculating that the mutator may have also inserted that pointer behind the wavefront. This maintains the weak invariant, because there is no way to delete every path from some grey object to any object that was live at the beginning of the collection cycle. Snapshot-at-the-beginning techniques use a write barrier to protect against deletion of grey or white pointers from grey or white objects.
Snapshotting the mutator means scanning its roots, making it black. We must snapshot the mutator at the beginning of the collection cycle to ensure it holds no white pointers. Otherwise, if the mutator held a white pointer that was the only pointer to its referent, it could write that pointer into a black object and then drop the pointer, breaking the weak invariant. A write barrier on black could catch such insertions, but degenerates to maintaining the strong invariant. Thus, snapshot collectors operate only with a black mutator.
15.2 Barrier techniques for concurrent collection
Following Pirinen [1998], barrier techniques that maintain one of the two tricolour invariants rely on a number of actions to cope with insertion or deletion of pointers. They can:
• Add to the wavefront by shading an object grey, if it was white. Shading an already grey or black object has no effect.
• Advance the wavefront by scanning an object to make it black.
• Retreat the wavefront by reverting an object from black back to grey.
The only other actions — reverting an object to white or shading an object black without scanning — would break the invariants. Algorithms 15.1 to 15.2 enumerate the range of classical barrier techniques for concurrent collection.
We first consider approaches that operate with a grey mutator. All these techniques preserve the strong invariant by using an insertion barrier2 when writing references into the heap to protect from storing white pointers into black objects. Because the mutator is grey they do not need a read barrier. They are incremental update techniques.
• Steele [1975, 1976] devised the barrier illustrated in Algorithm 15.1a. It yields the most precision of all the techniques because it simply notes the source object being modified. It does not change any decision about reachability of any object, but retreats the wavefront by changing the modified source object from black back to grey. It defers deciding reachability of the target white object until the source object can be rescanned (the inserted pointer might be deleted before rescanning). This precision comes at the cost of progress, since the wavefront is retreated.
• Boehm et al [1991] implemented a variant of the Steele [1975, 1976] barrier which ignores the colour of the inserted pointer, as shown in Algorithm 15.1b. They originally implemented this barrier using virtual memory dirty bits to record pages modified by the mutator without having to mediate the heap writes in software, which meant a less precise barrier that did not originally have the conditional test that the reverted source object is actually black. Boehm et al use a stop-the-world phase to terminate collection at which time the dirty pages are rescanned.
• Dijkstra et al [1976, 1978] designed a barrier (Algorithm 15.1c) that yields less precision than Steele’s since it commits to shading the target of the inserted pointer reachable (non-white), even if the inserted pointer is subsequently deleted. This loss of precision aids progress by advancing the wavefront. The original formulation of this barrier shaded the target without regard for the colour of the source, with a further loss of precision. Omitting this extra check allows atomicity to be relaxed, so long as the store and the shade operations are separately atomic. The store must still be performed ahead of the shade operation so as to avoid a subtle race when the collector transitions from one collector cycle to the next in the middle. If the operations are inverted then a collector cycle transition right after shading the stored ref grey can revert it to white and scan the src to black before the store, which then creates a black to white pointer violating the strong invariant [Stenning, 1976].
Algorithm 15.1: Grey mutator barriers.
(a) Steele [1975, 1976] barrier
1 atomic Write(src, i, ref):
2 src[i] ← ref
3 if isBlack(src)
4 if isWhite(ref)
5 revert(src)
(b) Boehm et al [1991] barrier
1 atomic Write(src, i, ref):
2 src[i] ← ref
3 if isBlack(src)
4 revert(src)
(c) Dijkstra et al [1976, 1978] barrier
1 atomic Write(src, i, ref):
2 src[i] ← ref
3 if isBlack(src)
4 shade(ref)
Algorithm 15.2: Black mutator barriers.
1 atomic Read(src, i):
2 ref ← src[i]
3 if isGrey(src)
4 ref ← shade(ref)
5 return ref
(b) Appel et al [1988] barrier
1 atomic Read(src, i):
2 if isGrey(src)
3 scan(src)
4 return src[i]
(c) Abraham and Patel [1987] / Yuasa barrier
1 atomic Write(src, i, ref):
2 if isGrey(src) || isWhite(src)
3 shade(src[i])
4 src[i] ← ref
Hellyer et al [2010], doi: 10.1145/1806651.1806666.
© 2010 Association for Computing Machinery, Inc. Reprinted by permission.
Algorithm 15.3: Pirinen [1998] black mutator hybrid barrier
1 atomic Read(src, i):
2 ref ← src[i]
3 if isWhite(src)
4 shade(ref)
5 return ref
6
7 atomic Write(src, i, ref):
8 if isGrey(src)
9 shade(src[i])
10 src[i] ← ref
The first two black mutator approaches apply incremental update to maintain the strong invariant using a read barrier to prevent the mutator from acquiring white pointers (that is, to protect from inserting a white pointer in a black mutator). The third, a snapshot technique, uses a deletion barrier on pointer writes into the heap to preserve the weak invariant (that is, to protect from deleting the last pointer keeping an object live that was reachable at the time of the snapshot). Under the weak invariant a black mutator can still hold white references; it is black because its roots do not need to be rescanned, even if it has since loaded pointers to white objects, because those white objects are protected from deletion by the write barrier.
• Baker [1978] used the read (mutator insertion) barrier shown in Algorithm 15.2a. This approach has less precision than Dijkstra et al, since it retains otherwise white objects whose references are loaded by the mutator at some time during the collection cycle, as opposed to those actually inserted behind the wavefront. Note that Baker’s read barrier was designed originally for a copying collector, where the act of shading copies the object from fromspace to tospace, so the shade routine returns the tospace pointer.
• Appel et al [1988] implemented a coarse-grained (less precise) variant of Baker’s read barrier (Algorithm 15.2b), using virtual memory page protection primitives of the operating system to trap accesses by the mutator to grey pages of the heap without having to mediate those reads in software. Having scanned (and unprotected) the page the trapped access is allowed to proceed. This barrier can also be used with a copying collector since scanning will forward any fromspace pointers held in the source object, including that in the field being loaded.
• Abraham and Patel [1987] and Yuasa [1990] independently devised the deletion barrier of Algorithm 15.2c. At D2 it directly shades Z grey. At T2 it shades R grey so that S can eventually be shaded. This deletion barrier offers the least precision of all the techniques, since it retains any unreachable object to which the last pointer was deleted during the collection cycle. With an insertion barrier at least we know that the mutator has had some interest in objects retained by the barrier (whether to acquire or store its reference), whereas the deletion barrier retains objects regardless of whether the mutator manipulated them. This is evident in that shading R retains it as floating garbage — it is not otherwise reachable — solely to preserve S. In its original form, this snapshot barrier was unconditional: it simply shaded the target of the overwritten pointer, regardless of the colour of the source. Abraham and Patel exploited this to drive their snapshot barrier using virtual memory copy-on-write mechanisms.
Completeness of barrier techniques
Pirinen [1998] argues that these barrier techniques cover the complete range of all possible approaches, with the addition of the read and write barrier combination illustrated in Algorithm 15.3. This combines an insertion read barrier on a black mutator with a deletion barrier on the heap. The combination preserves a weak invariant: all black-to-white pointers have a copy in some grey object (this is slightly stronger than the basic weak invariant that requires only a chain of white references from grey to white). The black mutator can safely acquire a white pointer from some grey source object since the target object will eventually be shaded grey when the grey source is scanned, or the write barrier will shade the target grey if the source field is modified. The read barrier makes sure that the mutator never acquires a white pointer from a white object. Thus, every reachable white object has a grey object directly keeping it alive throughout the collection cycle.
Variations on the listed techniques can be obtained in various ways by short-circuiting or coarsening some steps, including:
• Shading an object grey can be short-circuited by immediately scanning the object to make it black.
• A deletion barrier that shades the target of the deleted pointer grey can instead (and more coarsely) scan the source object containing the deleted pointer to black before the store.
• A read barrier that shades the target of the loaded pointer grey can instead (and more coarsely) scan the source object to black before the read. Thus, the read barrier of Appel et al coarsens that of Baker.
• An insertion barrier that shades the target of the inserted pointer grey can instead revert the source to grey. This is how the barriers of Steele and Boehm et al gain precision over that of Dijkstra et al.
Clearly, all strong invariant (incremental update) techniques must at least protect from a grey mutator inserting white pointers into black, or protect a black mutator from acquiring or using white pointers. The strong techniques all do one of these two things and need not do any more.
We have already argued that weak invariant (snapshot) techniques must operate with a black mutator. Under the weak invariant, a grey object does not merely capture a single path to reachable white objects. It may also be a placeholder for a pointer from a black object to some white object on that path. Thus, the snapshot barrier must preserve any white object directly pointed to from grey. The least it can do is to shade the white object when its pointer is deleted from grey.
To deal with white objects transitively reachable via a white path from a grey object (which may also be pointed to from black) we can either prevent the mutator from obtaining pointers to white objects on such paths so it can never modify the path [Pirinen, 1998], or make sure that deleting a pointer from a white object (which may be on such a path) at least makes the target of the pointer grey [Abraham and Patel, 1987; Yuasa, 1990].
Thus, all of the barrier techniques enumerated here cover the minimal requirements to maintain their invariants, but variations on these techniques can be obtained by short-circuiting or coarsening.
Concurrent write barrier mechanisms
In order to preserve either the strong or the weak invariant, write barriers must detect all writes to object fields of interesting pointers and record either their source, their target or the target originally stored in the field. References to these grey objects must be recorded in some data structure. However, concurrently with mutators adding references to the structure, the collector will remove and trace them. It is essential that insertions and removals be efficient and correct in the face of mutator-mutator and mutator-collector races.
One way to record grey objects is to add them to a log. We considered a variety of concurrent data structures and efficient ways to manage them in Chapter 13. In this section, we consider a popular and alternative mechanism: card tables. The basic operation of card tables for stop-the-world collectors was described in Chapter 11. Here we extend that discussion to examine how mutator-collector concurrency complicates their operation and how this can be resolved.
Recall that remembered sets can be implemented by associating a byte in a card table with each small (say, 512 bytes) contiguous area of the heap. Card tables can be used by both generational and concurrent collectors. A write barrier records the location of a grey object by dirtying the byte in the card table that corresponds to the card containing the object. Concurrently, the collector scans the card table for dirty cards. The collector must then search any dirty cards, trace grey objects, and clean the card. Clearly, this presents a race between mutators and collector that raises questions of correctness.
What constitutes an grey entity depends on the style of collector and its write barrier. In a generational collector, object fields are grey if the object is in an older generation and the field holds a reference to an object in a younger generation. In a concurrent collector that uses a Steele-style retreating barrier, an object is grey if it has already been marked (that is, was once black) but now holds a reference to an unmarked child. With a Dijkstra-style advancing barrier or a Yuasa-style deletion barrier, all objects in a dirty card must be considered grey. While this barrier may seem very imprecise since it will preserve garbage neighbours of live objects, note that Abuaiadh et al [2004] found that compacting small blocks rather than individual objects led to an increase in memory footprint of only a few percent.
The card table is the concurrent collector’s work list. The collector must scan it looking for dirty cards and cleaning them until all cards are clean. Since mutators may dirty cards after the collector has cleaned them, the collector must repeatedly scan the card table. An alternative might be to delay processing the card table until a final stop-the-world phase, but this is likely to cause the concurrent part of the tracing phase to terminate too soon [Barabash et al, 2003, 2005].
The simplest organisation is a one-level card table, as described above. Here, a card may be in one of three states: dirty, refining or clean. Mutator write barriers will set the state to be dirty using a simple store instruction rather than an atomic primitive such as CompareAndSwap [Detlefs et al, 2002a]. The collector thread sets the status to refining before searching the card for interesting pointers and determining a new status for the card. The simplest would be dirty but Detlefs et al can also ‘summarise’ cards (see Chapter 11). The collector now attempts to write the new status back to the card. First, it checks that the card’s status is still refining and that no mutator has dirtied the card while the collector was searching it. If the status is still refining, the collector must try to change the value atomically to the new status, for example with a CompareAndSwap. If this fails, then a mutator must have dirtied the card concurrently, meaning that it may contain an unprocessed grey object. Detlefs et al simply leave this card dirty and proceed to the next dirty card, but one might also try to clean the card again.
Because the overwhelming majority of cards are likely to be clean, two-level card tables reduce the cost of searching the card table for dirty cards. Each entry in a second, coarse-grain card table records the state of 2n fine grained cards. Cleaning a two-level card table proceeds similarly to cleaning a one-level table. When a dirty coarse-grain card is found, its status is set to refining and the corresponding fine-grained cards are searched. Once all the fine-grain cards are clean, the collector attempts atomically to set the state of the coarse-grain card to clean. However, there is a subtle concurrency issue here. Because write barrier actions are not atomic with respect to the card-cleaning thread, the write barrier must dirty the fine-grained card before dirtying the corresponding coarse-grained card, while the collector reads them in the opposite order. We note that obtaining the proper order may have extra cost on machines that require a memory fence to force it.
One solution that reduces the amount of redundant work done by the collector is to try to avoid scanning any object more than once [Barabash et al, 2003, 2005]. Here, the authors defer cleaning cards for as long as there is other tracing work for the collector to do. Their mostly-concurrent collector uses a Steele-style retreating insertion barrier. Such collectors must scan marked objects on dirty cards and trace all their unmarked children. The first technique for reducing the amount of redundant scanning is not to trace through an object on a dirty card: it suffices to mark the object as it will be traced through when the card is cleaned. Although objects that are traced through before their card is dirtied will still be scanned twice, this eliminates rescanning objects that are marked after their card is dirtied. Barabash et al observe that this can improve the collector’s performance and reduce the number of cache misses it incurs. Note that although changes in the order of memory accesses on a weakly consistent platform may cause this optimisation to be missed, the technique is still safe.
Their second approach is to reduce the number of dirty cards. Recall that it is necessary for a Steele-style barrier to dirty a card only if the modified object has already been traced by the collector. If it has not, then the collector will notice it eventually so there is no need to dirty the card. In other words, there is no need to shade a white object grey. Card marking is used by collectors because it is a fast, unconditional operation. The question, therefore, is how this check can be made efficient.
One solution is to mark the card dirty unconditionally but maintain a second table indicating whether a card contains an object that has been traced. Periodically the dirty card table can be undirtied as follows, without need for atomic operations assuming the tables hold bytes rather than bits:
for each dirty card C
if not isTraced(C) | $ |
setClean(C)
if isTraced(C)
setDirty(C)
Their second solution rests on the observation that for many programs most pointer writes are made to young objects and that these typically reside in local allocation buffers. Instead of keeping a second card table, a bit is used for each object to indicate whether it is part of an active local allocation buffer. If this bit is set, the collector defers tracing the object to a later time, instead adding the object to a deferred list. When the buffer overflows — the allocation slow path — the mutator sets all the cards in the buffer to be clean and clears all the defer bits for all objects in the buffer. One reason that this is effective is that Barabash et al found that the collector rarely reaches objects in an active local allocation buffer.
Some care is needed with this solution on weakly consistent platforms. The simplest approach is to have the collector run a fence after marking a card traced and before tracing an object and have the undirtying procedure run a fence between checking whether each card is dirty and checking whether it is traced (as above). Note that in both cases only the collector threads execute the fence. An alternative method is to have the undirtying procedure start by scanning the card table, and cleaning and recording (in a list or an additional card table) all cards that are dirty but have not yet been traced. Next, the undirtying procedure handshakes with the collector, requesting the concurrent collector to run a synchronisation barrier. When both have run the handshake, the undirtying procedure rescans all the cards whose dirty bit was cleared and marks them dirty again if the card has been traced.
Garbage collectors that are incremental (mutator interleaved with collector) or concurrent (mutator and collector in parallel) have one primary purpose: minimising the collector pauses observed by the mutator. Whether the pause is due to an increment of collection work needing to be performed by the mutator, or caused by the mutator having to synchronise with (and possibly wait for) the collector to finish some work, incremental/concurrent techniques usually trade increased elapsed time (mutator throughput) for reduced disruption by the collector. In an ideal world, concurrent collectors may be able to reduce elapsed time by running collector work completely in parallel with the mutator. Unfortunately, there is no free lunch. As we have already seen, concurrent collectors require some level of communication and synchronisation between the mutator and the collector, in the form of mutator barriers. Moreover, contention between the mutator and collector for processor time or for memory (including disturbance of the caches by the collector) can also slow the mutator down.
Conversely, incremental or concurrent collection can improve throughput for some applications. The collectors impose overhead on individual mutator actions (loads or stores) in order to reduce the pauses observed by the application’s users. However, an application’s user may be another program, and this client may be very sensitive to delays. Ossia et al [2004] offer three-tier transaction processing systems as an example. They point out that delays for stop-the-world collections may cause transactions to time out and to be retried. By doing a little extra work (executing write barriers), much more extra work (reprocessing transactions that timed out) can be avoided.
The concurrent collection techniques that we consider in subsequent chapters each have their own particular impact on these costs. Concurrent reference counting collectors impose a particularly high overhead on pointer loads and stores. Concurrent mark-sweep collectors, which don’t move objects, have relatively low overhead for pointer access (varying with the barrier), but they may suffer from fragmentation. Concurrent collectors that relocate objects require additional synchronisation to protect the mutator from, or inform the mutator about, objects that the collector moves. Copying collectors also impose additional space overhead that adds to memory pressure. In all concurrent collectors, whether a read barrier or write barrier is used will affect throughput differently, based on the relative frequency of reads and writes, and the amount of work the barrier performs.
Concurrent mark-sweep collectors typically use a write barrier to notify the marker of an object to mark from. Concurrent copying and compacting collectors typically use a read barrier, to protect the mutator from accessing stale objects that have been copied elsewhere. There is a trade-off between the frequency of barrier execution and the amount of work it must do. A barrier that triggers copying and scanning will be more expensive than one that simply copies, which will be more expensive than one that simply redirects the source pointer. Similarly, performing more work early may result in fewer later barriers needing to do much work. All of these factors depend on the granularity of work performed, across a scale from references through objects to pages.
The amount of floating garbage is another factor in the costs of concurrent collection. Not having to collect floating garbage will allow faster termination of the current collection cycle, at the expense of additional memory pressure.
Whether the mutator (threads) must be stopped at the beginning of the collection cycle (to make sure the collector has seen all the roots) or at the end (to check for termination) also has an impact on throughput. Termination criteria also affect the amount of floating garbage.
A further consideration is that most concurrent collectors offer only loose assurances on pauses and space overhead. Providing the hard bounds on space and time needed for realtime applications means making well-defined progress guarantees for mutator operations that interact with the heap, and space guarantees that derive solely from knowledge of the memory allocation footprint of the application.
Incremental or concurrent collection can be particularly desirable when the volume of live data is expected to be very large. In this case, even stop-the-world parallel collection using every processor available would lead to unacceptable pause times. However, one drawback of incremental and concurrent collectors is that they cannot recycle any memory until the collection cycle is complete; we must provide sufficient headroom in the heap or give the collector a sufficiently generous share of processor resources (at the expense of the mutator) to ensure that the mutator does not run out of memory before the collection cycle completes. We consider garbage collector scheduling when we address the problem of real-time collection in Chapter 19; there, the problem is particularly acute.
An alternative approach is to use a hybrid generational/concurrent collection. The young generation is managed in the usual generational way, stopping the world for each minor collection. The old generation is managed by a concurrent collector. This has several advantages. Nursery collections are usually short enough (a few milliseconds) not to be disruptive. Since most objects tend to die young — the weak generational hypothesis — we can expect memory to be recycled promptly for further allocation, thus reducing the space overhead required to avoid running out of memory. There is no need to apply the concurrent write barrier to objects in the young generation as it is collected stop-the-world: the generational write barrier in the slow path suffices. Concurrent collectors typically allocate new objects black, guaranteeing that they will survive a collection even though most objects will not live that long. However, by allocating new objects generationally, this problem disappears. Finally, old objects have much lower mutation rates than young ones [Blackburn and McKinley, 2003]. This is the ideal scenario for an incremental or concurrent collector since their write barrier is less frequently invoked.
1Historically, concurrent collection in general was referred to as ‘on-the-fly’ [Dijkstra et al, 1976, 1978; Ben-Ari, 1984]. However, on-the-fly has since come to mean more specifically never stopping all the mutator threads simultaneously.
2We believe that insertion barrier is a clearer term for the mechanism than incremental update barrier. Likewise, we prefer the term deletion barrier to snapshot barrier.