Concurrent collection algorithms have been studied for a long time, going back at least to the 1970s [Steele, 1975]. For a long time, though, they were relevant to a small minority of users. Now, multiprocessors enjoy widespread commercial availability — even the laptop on which this text is being written has a dual-core processor. Moreover, programmers need to deploy multiple cores to cooperate on the same task since that has become the only way to get a job done faster: clock speed increases can no longer deliver the regular performance boost they used to. Therefore, language implementations need to support concurrent programming, and their run-time systems, and their garbage collectors in particular, need to support the concurrent world well. Later chapters explore parallel, concurrent and real-time collection in depth. Here we consider concepts, algorithms and data structures fundamental to collection in presence of logical and physical parallelism, including an introduction to the relevant aspects of hardware, memory consistency models, atomic update primitives, progress guarantees, mutual exclusion algorithms, work sharing and termination detection, concurrent data structures and the emerging model called transactional memory.
In order to understand both the correctness and the performance of parallel and concurrent collection, it is necessary first to understand relevant properties of multiprocessor hardware. This section offers definitions and overviews of several key concepts: processors and threads, including the various ‘multis’, multiprocessor, multicore, multiprogrammed, and multithreaded; interconnect; and memory and caches.1
A processor is a unit of hardware that executes instructions. A thread is a sequential program, that is, an execution of a piece of software. A thread can be running (also called scheduled), ready to run, or blocked awaiting some condition such as arrival of a message, completion of input/output, or for a particular time to arrive. A scheduler, which is usually an operating system component, chooses which threads to schedule onto which processors at any given time. In general, if a thread is descheduled (moved from running to ready or blocked), when it is next scheduled it may run on a different processor than the one on which it ran previously, though the scheduler may recognise and offer some degree of affinity of a thread to a particular processor.
A slight complication in these definitions is that some processor hardware supports more than one logical processor using a single execution pipeline. This is called simultaneous multithreading (SMT) or hyperthreading, and unfortunately for our terminology, the logical processors are often called threads. Here thread will always mean the software entity and SMTs will be viewed as providing multiple (logical) processors, since the logical processors are individually schedulable, and so on.
A multiprocessor is a computer that provides more than one processor. A chip multiprocessor (CMP), also called a multicore or even many-core processor, is a multiprocessor that has more than one processor on a single integrated circuit chip. Except in the case of SMT, multithreaded refers to software that uses multiple threads, which may run concurrently on a multiprocessor. Multiprogrammed refers to software executing multiple processes or threads on a single processor.
What distinguishes a multiprocessor from the general case of cluster, cloud or distributed computing is that it involves shared memory, accessible to each of the processors. This access is mediated by an interconnection network of some kind. The simplest interconnect is a single shared bus, through which all messages pass between processors and memory. It is helpful to think of memory accesses as like the sending of messages between a processor and a memory unit, given how long the accesses take in terms of processor cycles — now in the hundreds of cycles. A single bus can be reasonably fast in terms of its raw speed, but it can obviously be a bottleneck if multiple processors request service at the same time. The highest bandwidth interconnect would provide a private channel between each processor and each memory, but the hardware resources required grow as the product of the number of processor and number of memory units. Note that for better overall bandwidth (number of memory accesses per second across the entire system), splitting the memory into multiple units is a good idea. Also, transfers between processors and memories are usually in terms of whole cache lines (see page 231) rather than single bytes or words.
In larger CMPs a memory request may need to traverse multiple nodes in an interconnection network, such as a grid, ring or torus connection arrangement. Details lie beyond our scope, but the point is that access time is long and can vary according to where a processor is in the network and where the target memory unit is. Concurrent traffic along the same interconnect paths can introduce more delay.
Note that the bus in single-bus systems generally becomes a bottleneck when the system has more than about eight to sixteen processors. However, buses are generally simpler and cheaper to implement than other interconnects, and they allow each unit to listen to all of the bus traffic (sometimes called snooping), which simplifies supporting cache coherence (see page 232).
If the memory units are separate from the processors, the system is called a symmetric multiprocessor (SMP), because processors have equal access times to each memory. It is also possible to associate memory with each processor, giving that processor more rapid access to that portion of the memory, and slower access to other memory. This is called nonuniform memory access (NUMA). A system may have both global SMP-style memory and NUMA memory, and processors may also have private memory, though it is the shared-access memory that is most relevant to garbage collection.2
The most relevant properties of interconnect are that memory takes a long time to access, that interconnect can be a bottleneck, and that different portions of memory may take relatively longer times to access from different processors.
From the standpoint of garbage collection, shared memory appears as a single address space of words or bytes, even though it may be physically spread out across multiple memory units or processors. Because memory consists of multiple units accessed concurrently, it is not necessarily possible to describe it as having a single definite global state at any given moment. However, each unit, and thus each word, has a well-defined state at each moment.
Because memory accesses take so long, modern processors typically add one or more layers of cache to hold recently accessed data and thus statistically reduce the number of memory accesses a program requires as it runs. Caches generally operate in terms of cache lines (also called cache blocks), typically 32 or 64 bytes in size. If an access finds its containing line in the cache, that is a cache hit, otherwise the access is a cache miss, which requires accessing the next higher level of cache, or memory if this was the highest level. In CMPs it is typical for some processors to share some higher levels of cache. For example, each processor might have its own Level One (L1) cache but share its L2 cache with a neighbour. The line sizes of different levels need not be the same.
When there is a cache miss and there is not room for the new line in the cache, then a line currently in the cache, chosen according to the cache’s replacement policy, must be evicted before loading the new line. The evicted line is called the victim. Some caches are write-through, meaning that updates to lines in the cache are passed on to the next level as soon as practicable, while some caches are write-back, meaning that a modified line (also called a dirty line) is not written to the next higher level until it is evicted, explicitly flushed (which requires using a special instruction) or explicitly written back (which also requires a special instruction).
A cache’s replacement policy depends substantially on the cache’s internal organisation. A fully-associative cache allows any set of lines, up to the cache size, to reside in the cache together. Its replacement policy can choose to evict any line. At the opposite end of the spectrum are direct-mapped caches, where each line must reside in a particular place in the cache, so there is only one possible victim. In between these extremes are k-way set-associative caches, where each line is mapped to a set of k lines of cache memory, and the replacement policy can choose any of the k lines as its victim. A variety of other organisations occur, such as victim caches, whereby a small number of recent victims are held in a fully-associative table on the side of the primary cache, with the primary usually being direct mapped. This gives the hit rate of higher associativity with lower hardware cost.
Another aspect of cache design concerns the relationship between different levels of cache. A design of two adjacent levels of cache is called (strictly) inclusive if every line in the lower level must be held by the higher level. Conversely, a design is exclusive if a line can be held in at most one of the two levels. A design need be neither: it may allow a line to reside in both caches, but not require it.
Caches hold copies of memory data that is potentially shared. Because not all copies are updated at the same moment, particularly with write-back caches, the various copies in general do not contain the same value for each address. Thus, it may be possible for two processors to disagree on the value at a particular location. This is undesirable, so the underlying hardware generally supports some degree of cache coherence. One of the common coherence protocols is MESI, from the initial letters of the names it gives to the possible states of a given line of memory in each cache.
Modified: This cache is the only one holding a copy of the line, and its value has been updated but not yet written back to memory.
Exclusive: This cache is the only one holding a copy of the line, but its value corresponds with that in memory.
Shared: Other caches may hold a copy of this line, but they all have the same value as in memory.
Invalid: This cache does not hold a copy of this line.
To satisfy a processor read, the processor’s cache must hold the line in the M, E, or S state. To satisfy a write, however, the cache must hold it in either the M or the E state, and after the write its new state will be M. How the system satisfies a read in the I state depends on how the line is held elsewhere. If it is held in the M state, that processor must write the line back to memory and drop to the S (or I) state. If it is held in the E state, it just needs to drop to the S (or I) state. If it is held only in the S or I state, then the requesting processor can simply load the line, which might be supplied by an S-state holder or else by memory. To satisfy a write when in I state, the requirements are similar to satisfying a read except that other holders must end up in the I state. To satisfy a write from the S state, other S holders must drop to the I state. Refinements include: supporting read-with-intention-to write, where other holders end in the I state; write-back, where a line drops from the M to the E state; and invalidate, where a line is written back if it is in the M state and in any case drops to the I state.
The point of the protocol is that there can be only one writer at a time for any given line, and that two caches never hold disagreeing values for the same lines. The difficulty with this algorithm, and indeed with any hardware supported cache coherence protocol, is that it does not scale well to large numbers of processors. Therefore larger CMPs are starting to emerge that do not have coherence built in and for which the software manages the coherence according to whatever protocol it desires. This may still not scale, but at least the programmer has a better shot at tuning to the specific algorithm versus relying on one fixed hardware algorithm.
Cache coherence introduces an issue called false sharing. If two processors access and update different data that happen to lie in the same cache line, then they will tend to cause a lot of coherence traffic on the interconnect and possibly extra reads from memory, as the line ‘ping-pongs’ between the two processors, since each must acquire it in an exclusive state before updating it.
Cache coherence performance example: spin locks
A typical mutual exclusion lock can be implemented with an AtomicExchange primitive, as shown in Algorithm 13.1. We distinguish primitive atomic instructions by starting their name with an upper case letter. We also denote low-level read and write operations by load and store respectively in order to avoid any confusion with the interface between the user program and the mutator. The initial value of the lock should be zero, meaning ‘unlocked’. This is called a spin lock because the processor is said to ‘spin’ in the while loop. Each invocation of the atomic read-modify-write operation will try to acquire the lock’s cache line exclusively. If multiple processors contend for the lock, then the line will ping-pong, even while some other processor holds the lock. And even that processor will need to contend for the line just to unlock! This form of lock is also called a test-and-set lock, even though it does not use the TestAndSet primitive, discussed a little later.
Algorithm 13.1: AtomicExchange spin lock
1 exchangeLock(x):
2 while AtomicExchange(x, 1) = 1
3 /* do nothing */
4
5 exchangeUnlock(x):
6 *x ← 0
7
8 AtomicExchange(x, v):
9 atomic
10 old ← *x
11 *x ← v
12 return old
Algorithm 13.2: Test-and-Test-and-Set AtomicExchange spin lock
1 testAndTestAndSetExchangeLock(x):
2 while testAndExchange(x) = 1
3 /* do nothing */
4
5 testAndTestAndSetExchangeUnlock(x):
6 *x ← 0
7
8 testAndExchange(x):
9 while *x = 1
10 /* do nothing */
11 return AtomicExchange(x, 1)
Because the code of Algorithm 13.1 can cause extreme cache contention, many programs use a more subtle version that has the same semantics, called a test-and-test-and-set lock, shown in Algorithm 13.2. The important difference is in line 9, which does ordinary read accesses outside the AtomicExchange. This spins accessing the processor’s (coherent) cache, without going to the bus. If the lock is not in cacheable memory, then a thread might want to delay between tests using an idle loop or a hardware idle instruction, possibly using exponential back-off or some similar algorithm so as to consume fewer resources in longer waits. For even longer waits the thread might involve the operating system scheduler, by giving up the rest of its quantum, or moving to wait on an explicit signal, in which case things must be arranged so that the lock holder will send the signal when the lock is released.
Algorithm 13.3: Spin locks implemented with the TestAndSet primitive
1 testAndSetLock(x):
2 while TestAndSet(x) = 1
3 /* do nothing */
4
5 testAndSetUnlock(x):
6 *x ← 0
7
8 TestAndSet(x):
9 atomic
10 old ← *x
11 if old = 0
12 *x ← 1
13 return 0
14 return 1
15
16 testAndTestAndSetLock(x):
17 while testAndTestAndSet(x) = 1
18 /* do nothing */
19
20 testAndTestAndSet(x):
21 while *x = 1
22 /* do nothing */
23 return TestAndSet(x)
24
25 testAndTestAndSetUnlock(x)
26 testAndSetUnlock(x)
While Section 13.3 covers the range of most frequently available atomic hardware primitives, it is edifying to consider test-and-set and test-and-test-and-set locks implemented with a TestAndSet primitive, as shown in Algorithm 13.3. A possible advantage of the TestAndSet primitive is that the overall intent and use of the values 0 and 1 are implicit in its semantics. This implies that a processor can avoid a bus access and avoid requesting the cache line for exclusive access if the value of the lock is 1 in the cache. In principle hardware could do that same thing for AtomicExchange, but it would require detecting that the old and new values are the same as opposed to looking for the specific value 1.
13.2 Hardware memory consistency
We assume that shared memory provides coherence as discussed above: in the absence of pending incomplete writes, if two processors read the same memory location, they will obtain the same value. Most hardware further guarantees that if two processors write to the same location, one of the writes will happen before the other, and the later write’s value is what every processor will see subsequently. Furthermore, no processor will observe the final value and later see the value change without another write.3 In other words, writes to any particular memory location are totally ordered, and each processor’s view of that location is consistent with that order.
However, a program’s view of the order of writes (and reads) to more than one location does not necessarily correspond with the order of those actions at caches or memories, and thus as perceived by other processors. That is, program order is not necessarily consistent with memory order. This raises two questions: why, and what are the implications? To answer the ‘why’ question, it is a matter of both hardware and software. Broadly, the reasons are tied up with performance: strict consistency requires either more hardware resources, or reduces performance, or both. One hardware reason is that many processors contain a write buffer (also called a store buffer), that receives pending writes to memory. A write buffer is basically a queue of ⟨address, data⟩ pairs. Normally these writes may be performed in order, but if a later write is to an address already in the write buffer, the hardware may combine it with the previous pending write. This means the later write can effectively pass an earlier write to a different location and appear in memory sooner. Designers are careful to provide each processor with a consistent view of its own actions. Thus a read of a location that has a pending write in the write buffer will ultimately produce the value in the write buffer, either with a direct hardware path (faster but more costly) or by waiting for the write buffer to empty and then reading the value from cache. Another reason program actions can be reordered at the memory is cache misses. Many processors will continue executing later instructions past a (data) cache miss, and thus reads can pass reads and writes (and so can writes). Further, write-back caches present writes to memory only when dirty lines are evicted or flushed, so writes to different lines can be drastically reordered. This summary of hardware reasons is illustrative but not exhaustive.
Software reasons for reordering mostly come from compilers. For example, if two memory references are known to go to the same location and there are no intervening writes that can affect that location, the compiler may just use the value originally fetched. More generally, if the compiler can show that variables are not aliased (do not refer to the same memory location), it can freely reorder reads and writes of the locations, since the same overall result will obtain (on a uniprocessor in the absence of thread switches). Languages allow such reordering and reuse of the results of previous accesses because it leads to more efficient code, and much of the time it does not affect the semantics.
Obviously, from a programmer’s standpoint lack of consistency between program and memory order is potentially problematic — but from an implementation perspective it can boost performance and reduce cost.
What are the implications of looser consistency? First, it should be obvious that it can be easy for programmers’ intuitions to go completely wrong and for code that works under total consistency to fail in confusing ways — though perhaps only rarely — under more relaxed models. Second, for techniques such as locks to work, there needs to be some way to guarantee particular ordering between accesses to two different locations when ordering is needed. There are three primary kinds of accesses that an ordering model distinguishes: reads, writes, and atomic operations.4 Atomic operations apply an atomic read-modify-write primitive, often conditionally, such as TestAndSet. It can also be useful to consider dependent loads, where the program issues a load from address x and then later issues a load from address y where y depends on the value returned by loading x. An example is following a pointer chain. There are many different kinds of memory access orderings weaker than total consistency; we consider the more common ones here.
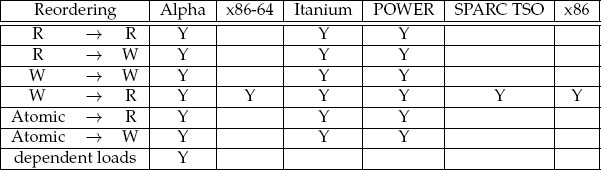
Table 13.1: Memory consistency models and possible reorderings. A Y means that the indicated happens-before order is not necessarily enforced.
A memory fence is an operation on a processor that prevents certain reorderings of memory accesses. In particular it can prevent certain accesses issued before the fence, or certain accesses issued after the fence, or both, from being performed in an order that places them on the other side of the fence. For example, a total read fence requires all reads before the fence to happen before all reads issued after the fence.
This notion of happens-before can be formalised, and refers to requirements on the order in which operations occur on memory. Thus, the total read fence imposes a happens-before relationship between each previous read and each later read. Typically, atomic operations imply a total fence on all operations: every earlier read, write, and atomic operation must happen-before each later read, write, and atomic operation. However, other models are possible, such as acquire-release. In that model, an acquiring operation (think of it as being like acquiring a lock) prevents later operations from being performed before the acquire, but earlier reads and writes can happen after the acquire. A releasing operation is symmetrical: it prevents earlier operations from happening after the release, but later reads and writes may happen before the release. In short, operations outside an acquire-release pair may move inside it, but ones inside it may not move out. This is suitable for implementing critical sections.
The strongest consistency model is strict consistency, where every read, write and atomic operation occurs in the same order everywhere in the system.5 Strict consistency implies that happens-before is a total order, with the order defined by some global clock. This is the easiest model to understand, and probably the way most programmers think, but it is prohibitive to implement efficiently.6 A slightly weaker model is sequential consistency, in which the global happens-before order is any partial order consistent with every processor’s program order. Small scale multiprocessors usually aim for sequential consistency or something close to it, because it is easier to program to than more relaxed models. Weak consistency is the model resulting from treating all atomic operations as total fences. The acquire-release model, mentioned above is usually called release consistency. Intermediate in strength between sequential and weak consistency is causal consistency. This enforces happens-before between previous reads by a program and its subsequent writes, since the reads may causally influence the value written, and it enforces happens-before between a read and the write that stored the value obtained by the read. The term relaxed consistency applies to any model weaker than sequential consistency.
Algorithm 13.4: The CompareAndSwap and CompareAndSet primitives
1 CompareAndSwap(x, old, new):
2 atomic
3 curr ← *x
4 if curr = old
5 *x ← new
6 return curr
7
8 CompareAndSet(x, old, new):
9 atomic
10 curr ← *x
11 if curr = old
12 *x ← new
13 return true
14 return false
While allowed reorderings depend to some extent on the interconnect and memory system, that is they may lie outside total control by the processor, Table 13.1 shows the reorderings allowed by some well-known processor families. All the processors implement at least weak or release consistency. For more background on memory consistency models see Adve and Gharachorloo [1995, 1996].
From some of the earliest computers onwards, processors have supported atomic read-modify-write primitives for locking and synchronisation. Section 13.1 introduced two primitives. AtomicExchange is perhaps the simplest in that it involves no computation or conditional action — it simply writes a new value to a memory location and returns the old value atomically, implying that no other write (atomic or otherwise) can interleave. TestAndSet is also quite simple in that it sets a single bit to 1 and returns the bit’s previous value. However, it can be viewed as a conditional primitive that sets the bit only if its current value is zero. The other widely known and used atomic primitives include: compare-and-swap, also called compare-and-exchange; load-linked/store-conditionally, also called load-and-reserve/store-conditional; and various atomic increment, decrement and add primitives, notably fetch-and-add, also called exchange-and-add. We consider these in turn below.
The CompareAndSwap primitive and its close relation, CompareAndSet, are presented in Algorithm 13.4. CompareAndSet compares a memory location to an expected value old, and if the location’s value equals old, it sets the value to new. In either case it indicates whether or not it updated the memory location. CompareAndSwap differs only in that it returns the value of the memory location observed by the primitive before any update, rather than returning a boolean truth value. The utility of the two primitives is essentially the same, although their semantics are not strictly equivalent.
Algorithm 13.5: Trying to advance state atomically with compare-and-swap
1 compareThenCompareAndSwap(x):
2 if *x = interesting
3 z ← value for the desired next state
4 CompareAndSwap(x, interesting, z)
Algorithm 13.6: Semantics of load-linked/store-conditionally
1 LoadLinked(address):
2 atomic
3 reservation ← address | /* |
4 reserved true | /* |
5 return *address
6
7 StoreConditionally(address, value):
8 atomic
9 if reserved
10 store(address, value)
11 return true
12 return false
13
14 store(address, value): | /* at all processors, not necessarily simultaneously */ |
15 if address = reservation | /* granularity may be same cache line, and so on */ |
16 reserved ← false
17 *address value
CompareAndSwap is often used to advance a location from one state to another, such as ‘locked by thread t1′ to ‘unlocked’ to ‘locked by thread t2′. It is common to examine the current state and then try to advance it atomically, following the pattern of Algorithm 13.5, sometimes called compare-then-compare-and-swap. There is a lurking trap in this approach, namely that it is possible that at the CompareAndSwap the state has changed multiple times, and is now again equal to the value sampled before. In some situations this may be all right, but in others it could be that the bit pattern, while equal, actually has a different meaning. This can happen in garbage collection if, for example, two semispace collections occur, and along the way a pointer was updated to refer to a different object that by coincidence lies where the original object was two collections ago. This inability of CompareAndSwap to detect whether a value has changed and then changed back is called the ABA problem.
Load-linked/store-conditionally
LoadLinked and StoreConditionally solve the ABA problem by having the processor remember the location read by the LoadLinked and use the processor’s coherence mechanism to detect any update to that location. Assuming that the processor applies the semantics of the store function, Algorithm 13.6 describes LoadLinked/StoreConditionally more precisely. It still falls short, though, because the reservation is cleared not only by writes by the same processor, but also by writes coming from other processors. Because any write to the reserved location resets the reserved flag, the compare-then-compare-and-swap code can be rewritten to avoid the possible ABA problem, as shown in Algorithm 13.7.7 LoadLinked/StoreConditionally is thus strictly more powerful than CompareAndSwap. In fact, it should be clear that the LoadLinked/StoreConditionally primitives allow a programmer to implement any atomic read-modify-write operation that acts on a single memory word. Algorithm 13.8 shows how to implement compare-and-swap with LoadLinked/StoreConditionally, and also an implementation of compare-and-set. One more behaviour of LoadLinked/StoreConditionally is worth mentioning: it is legal for a StoreConditionally to fail ‘spuriously’, that is, even if no processor wrote the location in question. There might be a variety of low-level hardware situations that can cause spurious failures, but notable is the occurrence of interrupts, including such things as page and overflow traps, and timer or I/O interrupts, all of which induce kernel activity. This is not usually a problem, but if some code between LoadLinked and StoreConditionally causes a trap every time, then the StoreConditionally will always fail.
Algorithm 13.7: Atomic state transition with load-linked/store-conditionally
1 observed ← LoadLinked(x)
2 compute desired new value z, using observed
3 if not StoreConditionally(x, z)
4 go back and recompute or otherwise handle interference
Algorithm 13.8: Implementing compare-and-swap with load-linked/store-conditionally
1 compareAndSwapByLLSC(x, old, new):
2 previous ← LoadLinked(x)
3 if previous = old
4 StoreConditionally(x, new)
5 return previous
6
7 compareAndSetByLLSC(x, old, new):
8 previous ← LoadLinked(x)
9 if previous = old
10 return StoreConditionally(x, new)
11 return false
Because LoadLinked/StoreConditionally solves ABA problems so neatly, code presented here will most generally prefer LoadLinked/StoreConditionally where CompareAndSwap would exhibit an ABA problem. It would typically be straightforward to convert such instances to use CompareAndSwap with an associated counter.
Strictly speaking, StoreConditionally’s effect may be undefined if it writes to an address other than the one reserved. Some processor designs allow that, however, giving an occasionally useful atomic primitive that acts across two arbitrary memory locations.
For completeness, Algorithm 13.9 defines several atomic arithmetic primitives. It is also easy to offer versions of AtomicIncrement and AtomicDecrement that return either the old or the new value using AtomicAdd or FetchAndAdd. Furthermore, processors often set condition codes when executing these primitives, which can reveal whether the value is (or was) zero, and so on. In the realm of garbage collection, FetchAndAdd might be used to implement sequential allocation (that is, with a ‘bump pointer’) in a concurrent setting — though usually it is preferable to set up local allocation buffers as described in Section 7.7. FetchAndAdd could similarly be used to add or remove items from a queue, though wrap-around in a circular buffer requires care (see Section 13.8).
It has been shown that these atomic arithmetic primitives are strictly less powerful than CompareAndSwap, and thus also less powerful than LoadLinked/StoreConditionally (see Herlihy and Shavit [2008]). In particular, each primitive has what is a called a consensus number. If the consensus number of a primitive is k, then it can be used to solve the consensus problem among k threads, but not more than k. The consensus problem is a multiprocessor algorithm where (a) each thread proposes a value, (b) all threads agree on the result, (c) the result is one of the values proposed, and (d) all threads always complete in a finite number of steps, that is, the algorithm is wait-free (see Section 13.4). Primitives that either set a value unconditionally, such as AtomicExchange, or that when commuted result in the same value for the variable being updated, such as AtomicIncrement and FetchAndAdd, have consensus number 2. On the other hand, CompareAndSwap and LoadLinked/StoreConditionally have consensus number ∞, that is, they can solve consensus in a wait-free manner for any number of threads, as will be illustrated presently in Algorithm 13.13.
One potential advantage to unconditional arithmetic primitives is that they will always succeed, whereas an emulation of these primitives with LoadLinked/StoreConditionally or CompareAndSwap can starve in the face of contention.8
The ‘test then test-and-set’ pattern was illustrated in function testAndTestAndSet (see Algorithm 13.3). Because of the way that algorithm iterates, it is correct. Programmers should avoid two fallacious attempts at the same semantics, here called test-then-test-and-set and test-then-test-then-set, illustrated in Algorithm 13.10. Test-then-test-and-set is fallacious because it does not iterate, yet the TestAndSet could fail if x is updated between the if and the TestAndSet. Test-then-test-then-set is even worse: it fails to use any atomic primitive, and thus anything can happen in between the first and second read of x and the second read and the write. Notice that making x volatile does not solve the problem. There are similar patterns that might be called compare-then-compare-and-set or compare-then-compare-then-set that are equally fallacious. These traps illustrate the difficulty programmers have in thinking concurrently.
As mentioned above, LoadLinked/StoreConditionally is fully general, and hence the most powerful among single-word atomic update primitives. However, primitives that allow updating multiple independent words are even more powerful. In addition to single-word primitives, some processors include double-word primitives such as double-word compare-and-swap, here called CompareAndSwapWide/CompareAndSetWide, in addition to single-word CompareAndSwap (see Algorithm 13.11). These are not of greater theoretical power. However, a wide double-word CompareAndSwap can solve the ABA problem of single-word CompareAndSwap by using the second word for a counter of the number of times the first word has been updated. It would take so long — 232 updates for a 32-bit word — for the counter to wrap around that it may be safe to ignore the possibility. The same would hold even more strongly for updating two adjacent 64-bit words. Thus CompareAndSwapWide can be more convenient and efficient even if it has the same theoretical power as a regular CompareAndSwap.
Algorithm 13.9: Atomic arithmetic primitives
1 AtomicIncrement(x) :
2 atomic
3 *x ← *x + 1
4
5 AtomicDecrement(x) :
6 atomic
7 *x ← *x — 1
8
9 AtomicAdd(x, v) :
10 atomic
11 new ← *x + v
12 *x ← new
13 return new
l4
15 FetchAndAdd(x, v) :
16 atomic
17 old ← *x
18 *x ← old + v
19 return old
Algorithm 13.10: Fallacious test and set patterns
1 testThenTestAndSetLock(x) : | /* fallacious! */ |
2 if *x = 0
3 TestAndSet(x)
4
5 testThenTestThenSetLock(x) : | /* fallacious! */ |
6 if *x = 0
7 other work
8 if *x = 0
9 *x ← 1
But while double-word atomic primitives are useful, it is even more useful to be able to update two arbitrary (not necessarily adjacent) words in memory atomically. The Motorola 88000, and Sun’s Rock design, offered a compare-and-swap-two instruction (also called double-compare-and-swap). Algorithm 13.12 illustrates this CompareAndSwap2 primitive. CompareAndSwap2 is complex to implement in hardware, so it is not surprising that no commercially produced machines presently support it. CompareAndSwap2 can be generalised to compare-and-swap-n, also called n-way compare-and-swap. It was the inspiration for transactional memory, which is to LoadLinked/StoreConditionally what n-way compare-and-swap is to CompareAndSwap. See Section 13.9 for further discussion of transactional memory.
Algorithm 13.11: CompareAndSwapWide
1 CompareAndSwapWide(x, old0, old1, new0, new1):
2 atomic
3 curr0, curr1 ← 1x[0], x[1]
4 if curr0 = old0 && curr1 = old1
5 x[0], x[1] ← new0, new1
6 return curr0 , curr1
7
8 CompareAndSetWide(x, old0, old1, new0, new1):
9 atomic
10 curr0, curr1 ← x[0], x[1]
11 if curr0 = old0 && curr1 = old1
12 x[0], x[1] ← new0, new1
13 return true
14 return false
Algorithm 13.12: CompareAndSwap2
1 CompareAndSwap2(x0, x1, old0, old1, new0, new1):
2 atomic
3 curr0, curr1 ← *x0, *x1
4 if curr0 = old0 && curr1 = old1
5 *x0, *x1 ← new0, new1
6 return curr0 , curr1
7
8 CompareAndSet2(x0, x1, old0, old1, new0, new1):
9 atomic
10 curr0, curr1 ← *x0, *x1
11 if curr0 = old0 && curr1 = old1
12 *x0, *x1 ← new0, new1
13 return true
14 return false
Overheads of atomic primitives
One reason programmers fall into the traps just mentioned is that they know atomic primitives are expensive, so they try to avoid them. Another reason may be that they improperly replicate the pattern of testAndTestAndSet. The primitives tend to be expensive for the two reasons previously mentioned, but it is helpful to distinguish them. One reason is the cost of cache coherence: an atomic read-modify-write primitive must acquire exclusive access to the relevant cache line. Also, it must do that, read the contents, compute the new value and write it, before the instruction is complete. While modern processors may overlap multiple instructions, often there are few instructions available in the pipeline since the next thing to do often depends strongly on the result of the atomic operation. Because of the need for coherence, an atomic update primitive often includes a bus or memory access, which consumes many cycles.
Algorithm 13.13: Wait-free consensus using compare-and-swap
1 shared proposals[N] | /* one entry per thread */ |
2 shared winner ← −1 | /* indicates which thread got here first */ |
3 me ← myThreadId
4
5 decide(v):
6 proposals[me] ← v | /* 0 ≤ threadid < |
7 CompareAndSwap(&winner, −1, me)
8 return proposals[winner]
The other reason atomic primitives tend to be slow is that they either include memory fence semantics, or else, by the way they are used, the programmer will need to insert fences manually, typically on both sides of the atomic operation. This undermines the performance advantage of overlapped and pipelined processing, and makes it difficult for the processor to hide the cost of any bus or memory access the primitive requires.
It is important to guarantee progress among threads that may be contending on the same data structure, such as a shared collected heap, or collector data structures. This is especially true in real-time programming. It is also helpful to know the relative power of the various atomic hardware primitives in supporting progress guarantees. From strongest to weakest, useful progress guarantees include: wait-freedom, lock-freedom and obstruction-freedom. A concurrent algorithm is wait-free if every thread can always make progress, regardless of the actions of other threads. A concurrent algorithm is lock-free if, infinitely often, some thread finishes within a finite number of steps. A concurrent algorithm is obstruction-free if, given a long enough period of isolated execution, any thread will finish in a finite number of steps. Progress guarantees are almost always conditional in real systems. For example, an algorithm might be wait-free as long as it does not exhaust free storage. See Herlihy and Shavit [2008] for a thorough discussion of these concepts, how to implement them, and so on.
A wait-free algorithm typically involves the notion of threads helping each other along. That is, if thread t2 is about to undertake an action that would undermine thread t1 that is somehow judged to be ahead of t2, t2 will help advance the work of t1 and then do its own work. Assuming a fixed bound on the number of threads, there is a bound on helping to accomplish one work unit or operation on the data structure, and thus the total time for any work unit or operation can be bounded. However, not only is the bound large, but the typical time for an operation is rather higher than for weaker progress guarantees because of the additional data structures and work required. For the simple case of consensus, it is fairly easy to devise a wait-free algorithm with low time overhead, as illustrated in Algorithm 13.13. It is fairly easy to see that this meets all of the criteria to be a solution to the consensus problem for N threads, but it does have space overhead proportional to N.
Lock-freedom is easier to achieve. It requires only that at least one contender make progress on any occasion, though any particular individual can ‘starve’ indefinitely.
Obstruction-freedom is easier to achieve than lock-freedom, but may require scheduler cooperation. If threads can see that they are contending, they can use random increasing back-off so as to allow some thread to win. That is, each time they detect contention, they compute a longer possible back-off period T and randomly choose an amount of time between zero and T to wait before trying again. In a pool of contending threads, each will eventually succeed, probabilistically speaking.
Progress guarantees and concurrent collection
Parallel collectors use multiple threads simultaneously in the collector, but stop all mutator threads during collection. Concurrent collectors perform at least some parts of collection while mutators threads are still running, and generally using multiple collector threads too. Both parallel and concurrent collection algorithms typically have a number of phases, such as marking, scanning, copying, forwarding or sweeping, and concurrent collection also has mutator work trying to proceed at the same time. Multiple collector threads may aim to cooperate, yet sometimes interfere with one another and with mutator threads. In such a complex situation, how can collector correctness be described? Certainly the collector must do nothing blatantly wrong — at the least it must preserve the reachable parts of the object graph and support the mutations being performed by the mutators. Next, provided that an invocation of the collector eventually terminates, it should generally return some unreachable memory for reuse. However, the specific expectations vary by collector algorithm. A conservative (ambiguous roots) collector may over-estimate reachability and thus fail to reclaim some unreachable objects. Likewise, generational and other partial-heap collectors intentionally forgo reclaiming unreachable objects from some parts of the heap on any given invocation. A complete collection algorithm gives a stronger guarantee: eventually, if invoked enough times, it will reclaim any given piece of garbage.
Concurrent collectors bring additional interesting issues. One is what can happen to objects allocated during collection that then become unreachable, or objects previously allocated that become unreachable during collection. A given collector might or might not reclaim those during the current invocation.
But there is a more subtle issue and risk that arises with concurrent and parallel collection. Sequential algorithms have more obvious termination properties. For example, marking a reachable object graph maintains some representation of marked-and-scanned, marked-but-not-yet-scanned, and unmarked object sets, and obeys rules where the first set grows, eventually to contain the entire graph of reachable objects. Correctness may sometimes be tricky to prove, but it is relatively easy to see that the algorithm terminates. It is less obvious with concurrent collection, because the object graph can grow because of allocation of new objects, and it can change during a collection cycle. If each mutator change forces more collector work, how can we know that the collector will ever catch up? Mutators may need to be throttled back or stopped completely for a time. Even if a proof deals with the issues of more collector work being created during collection, there remains a further difficulty: unless the algorithm uses wait-free techniques, interference can prevent progress indefinitely. For example, in a lock-free algorithm, one thread can continually fail in its attempts to accomplish a work step. In fact, two competing threads can even each prevent progress of the other indefinitely, an occurrence called livelock.
Different phases of collection may offer different progress guarantees — one phase might be lock-free, another wait-free. However, practical implementations, even of theoretically entirely wait-free algorithms, may have some (it is hoped small) portions that are stop-the-world. Given the code complexity and increased possibility of bugs when trying to implement stronger progress guarantees, it may not be worth the engineering effort to make every last corner wait-free. Further, notice that an overall collection algorithm can be judged wait-free from the standpoint of the mutators only if it can reclaim memory fast enough to ensure that a mutator will not block in allocation waiting for collection to complete. Put another way, the heap must not run out before the collector is done. This requires more than a wait-free guarantee for each phase — it requires overall balance between heap size, maximum live size, allocation rate and collection rate. Enough resources need to be devoted to collection — memory and processing time — for the collector to keep up. This may be required for critical real-time systems, and Chapter 19 discusses it in more detail. Most of the algorithms presented in succeeding chapters make weaker guarantees, such as lock-freedom, possibly only in certain phases. They are easier to implement and their guarantees are acceptable in many less stringent settings.
13.5 Notation used for concurrent algorithms
Given the considerations discussed previously, particularly atomicity, coherence and consistency, what a programmer writes is not always executed in the exact order presented — hardware and compilers can reorder and even eliminate some operations. Exactly what can occur depends strongly on the programming language, its compiler and run-time system, and the hardware. Yet here it is best to present algorithms in pseudocode independently of any particular hardware-software platform. In an algorithm, the relative order of some operations is typically important to correctness, but it is not generally necessary that all operations occur, and be perceived everywhere, in the order presented. Therefore, the code offered here for algorithms that may execute concurrently follows certain conventions. This makes it easier to translate the pseudocode into a working implementation in a given environment. Here are the conventions used.
Meaning of atomic: The actions within an atomic must be perceived by all processors as if they happened instantaneously — no other shared memory read or write can appear to happen in the middle. Moreover, atomic actions must be perceived as happening in the same order everywhere if they conflict (one writes and the other reads or writes the same shared variable), and in program execution order for the thread that executes them. Furthermore, atomic blocks act as fences for all other shared memory accesses. Since not all hardware includes fence semantics with atomic primitives, the programmer may need to add them. The code here may work with acquire-release fence semantics, but is designed assuming total fences.
Ordering effects of load-linked and store-conditionally: Both the load-linked and store-conditionally instructions act as total fences with respect to shared memory accesses.
Marking variables: We explicitly mark shared variables; all other variables are private to each thread.
Arrays: Where we use arrays, we give the number of elements within brackets, such as proposals[N]. Declarations of arrays use shared or private explicitly, so as not to look like uses of the arrays, and may be initialised with a tuple, such as shared pair [2]←[0,1], including tuples extended to the specified length, such as shared level[N]←[−1,…].
References to shared variables: Each reference to a shared variable is assumed to result in an actual memory read or write, though not necessarily in the order presented.
Causality obeyed: Code assumes that if, subject to the sequential semantics of the pseudocode language, an action x causally precedes an action y, then x happens-before y in the actual system. An example is a dependent memory reference. If code accesses a shared pointer variable p then a field f of the structure that p references, namely (*p) .f, then reading p causally preceded reading the field f. Similar remarks apply to accessing a shared index variable i then a shared array element a[i].
Obeying causality also implies obeying control dependence: the evaluation of an if, while, or similar expression that determines control flow causally precedes execution of the code it guards. The programmer must be careful not to allow speculative evaluation of conditional code so as to reorder accesses to shared variables. However, unconditional code following an if is not causally dependent on evaluation of the if expression. Similar remarks apply to moving code across loops.
Explicit fence points: Even with the conventions listed above, many operations may be freely reordered — but sometimes an algorithm requires a particular order for its correctness. Therefore, our conventions include the possibility of marking a line of code with a $, which indicates operations that must occur in the order presented. Furthermore, lines so marked also indicate total fences for shared memory accesses. It is convenient that pseudocode presented thus far in this chapter has not needed these markings. Notice that a line marked with $ may, for some processor architectures, need a fence of some kind before the line, after the line, or both before and after. Usually it is a particular action of the line that is important not to reorder, that is, one store or one load. While the markers do not offer complete guidance on how to translate pseudocode into working code for a given platform, they do serve to indicate where caution is necessary.
One of the most basic problems in concurrent computing is mutual exclusion, by which it is desired to guarantee that at most one thread at a time can be executing certain code, called a critical section. While atomic primitives can sometimes achieve a necessary state transition using one instruction, and techniques with stronger progress guarantees might be applied — though perhaps at greatest cost and almost certainly greater complexity — mutual exclusion remains convenient and appropriate in many cases. Atomic read-modify-write primitives make it fairly easy to construct lock/unlock functions, as shown in Algorithms 13.1 to 13.3. It is less obvious, but nevertheless true, that mutual exclusion can be achieved using only (suitably ordered) reads and writes of shared memory without stronger atomic update primitives. One of the classic techniques is Peterson’s Algorithm for mutual exclusion between two threads, shown in Algorithm 13.14. Not only does this algorithm guarantee mutual exclusion, it also guarantees progress — if two threads are competing to enter the critical section, one will succeed — and that waits are bounded, that is, the number of turns taken by other processes before a requester gets its turn is bounded.9 In this case the bound is one turn by the other thread.
It is not too hard to generalise Peterson’s Algorithm to N threads, as shown in Algorithm 13.15, which highlights its similarity to the two-thread case. How the while loop works is a bit subtle. The basic idea is that a requesting thread can advance a level in the competition to enter the critical section if it sees no other thread at the same or higher level. However, if another thread enters its current level, that thread will change victim and the earlier arrival can advance. Put another way, the latest arrival at a given level waits for threads at all higher levels plus earlier arrivals at its own level. Meanwhile, later arrivals at the same and lower levels will come strictly later. It does not matter that the while loop’s condition is not evaluated atomically. Peterson’s algorithm is illustrative of what is possible and of techniques for reasoning about concurrent programs, but atomic locking primitives are more convenient and practical.
Algorithm 13.14: Peterson’s algorithm for mutual exclusion
1 shared interested[2] ← [false, false]
2 me ← myThreadId
3
4 petersonLock() :
5 other ← 1 - me | /* thread id must be 0 or 1 */ |
6 interested[me] ← true
7 victim me | $ |
8 while victim = me && interested[other] | $ |
9 /* do nothing: wait */
10
11 petersonUnlock() :
12 interested[me] ← false
Algorithm 13.15: Peterson’s algorithm for N threads
1 shared level [N] ← [-1,…]
2 shared victim[N]
3 me ← myThreadId
4
5 petersonLockN() :
6 for lev ← 0 to N – 1
7 level [me] ← lev | /* 0 ≤ thread id < |
8 victim[lev] me | $ |
9 while victim[lev] = me && (∃i = me)(level[i] ≥ lev) | $ |
10 /* do nothing: wait */
11
12 petersonUnlockN() :
13 level[me] ← −1
Algorithm 13.16: Consensus via mutual exclusion
1 shared winner ← −1
2 shared value | /* does not need to be initialised */ |
3 me ← myThreadId
4
5 decideWithLock(v) : | /* simple, but no strong progress guarantee */ |
6 lock()
7 if winner = -1
8 winner ← me
9 value ← v
10 unlock()
11 return value
The previous discussion of consensus in Section 13.3 described the wait-free version of the consensus problem. Mutual exclusion can solve consensus quite easily if stronger progress guarantees are not needed, as shown in Algorithm 13.16. Since Peterson’s mutual exclusion algorithm implements mutual exclusion, it can also support this kind of consensus. However, if CompareAndSwap is available it is usually a more appropriate solution (see Algorithm 13.13).
13.7 Work sharing and termination detection
It is common in parallel or concurrent collection algorithms to need a way to detect termination of a parallel algorithm. Note that this is quite distinct from demonstrating that a parallel algorithm will terminate; it concerns having the program detect that termination has actually been achieved in a specific instance. In particular, consider a generic situation in which threads consume work, and as they process work units, they may generate more work. If each thread is concerned only with its own work, detecting termination is simple — just have each thread set a done flag and when all the flags are set, the algorithm has terminated. However, parallel algorithms generally involve some sort of sharing of work items so as to try to balance the amount of work done by each thread and gain maximum speedup from the available processors. This balancing can take two forms: threads with a relatively large amount of work can push work to more lightly loaded threads, or lightly loaded threads can pull work from more heavily loaded threads. Work pulling is also called work stealing.
Work movement must be atomic, or at least must guarantee that no work unit is lost.10 Here, though, the concern is detecting termination of a work sharing algorithm. It is relatively easy to detect termination using a single shared counter of work units updated atomically by each thread, but such counters may become bottlenecks to performance if the threads update them frequently.11 Therefore a number of termination detection algorithms avoid atomic update primitives and rely on single word reads and writes. It is simplest to consider first algorithms in which detection is the responsibility of a separate thread whose only job is detection.
Algorithm 13.17 shows a simplified version of the shared-memory work sharing termination algorithm of Leung and Ting [1997].12 It is designed for the push model. The basic idea is that workers indicate whether or not they are busy with their busy flags, which the detector scans. Notice that an idle worker will become busy again only if another worker pushes a job to it. However, the pusher can then finish processing and go idle. Since the detector’s scan is not atomic, it might first see the job receiver as idle (because the job has not been sent yet) and then find the pusher idle (after it sends the job). In this situation the detector would falsely indicate termination. Hence the algorithm includes the jobsMoved flag, which indicates whether any jobs have moved recently. The detector restarts detection in that case. It is also important that sendJobs waits until busy[j] is true to guarantee that before, during and immediately after the transfer at least one of the busy[i] is true: the only way that all busy[i] can be false is if there is no work in the system.
Algorithm 13.17: Simplified αβγ shared-memory termination [Leung and Ting, 1997]
1 shared jobs[N] ← initial work assignments
2 shared busy[N] ← [true,…]
3 shared jobsMoved ← false
4 shared allDone ← false
5 me ← myThreadId
6
7 worker():
8 loop
9 while not isEmpty(jobs[me])
10 if the job set of some thread j appears relatively smaller than mine
11 some ← chooseAndDequeueJobs()
12 sendJobs(some, j) | $ |
13 else
14 job ← dequeue(jobs[me])
15 perform job
16 busy[me] ← false | $ |
17 while isEmpty(jobs[me]) && not allDone | $ |
18 /* do nothing: wait for work or termination */
19 if allDone return | $ |
20 busy [me] ← true | $ |
21
22 sendJobs(some, j): | /* push jobs to more lightly loaded thread */ |
23 enqueue(jobs[j ], some) | $ |
24 while (not busy[j]) && (not isEmpty(jobs[j])) | $ |
25 /* do nothing: wait for j to wake up */
26 /* indicate that some work moved */
27 jobsMoved ← true | $ |
28
29 detect():
30 anyActive ← true
31 while anyActive
32 anyActive ← (∃i)(busy[i])
33 anyActive ← anyActive | | jobsMoved | $ |
34 jobsMoved ← false | $ |
35 allDone ← true | $ |
Algorithm 13.18 shows the similar algorithm for a work stealing (pull) model of sharing work. For example, Endo et al [1997] uses essentially this algorithm to detect termination in their parallel collector. Also, while the lock-free collector of Herlihy and Moss [1992] is not based on work sharing, its termination algorithm at its heart uses the same logic as the busy and jobsMoved flags.
Algorithm 13.18: An αβγ-style work stealing termination algorithm
1 me ← myThreadId
2
3 worker():
4 loop
5 while not isEmpty(jobs[me])
6 job ← dequeue(jobs[me])
7 perform job | $ |
8 if another thread j exists whose jobs set appears relatively large
9 some ← stealJobs(j) | $ |
10 enqueue(jobs [me], some)
11 continue
12 busy[me] ← false | $ |
13 while no thread has jobs to steal && not allDone | $ |
14 /* do nothing: wait for work or termination */
15 if allDone return | $ |
16 busy[me] ← true | $ |
17
18 stealJobs(j) :
19 some ← atomicallyRemoveSomeJobs(jobs[j])
20 if not isEmpty(some)
21 jobsMoved ← true | /* indicate that some work moved */ |
22 return some
Algorithm 13.19: Delaying scans until useful
1 shared anyIdle ← false
2 me ← myThreadId
3
4 worker():
5 …
6 busy[me] ← false | $ |
7 anyIdle ← true | $ |
8 …
9
10 detect():
11 anyActive ← true
12 while anyActive
13 anyActive ← false
14 while not anyIdle | $ |
15 /* do nothing: wait until a scan might be useful */
16 anyIdle ← false | $ |
17 anyActive ← (∃i)(busy[i]) | $ |
18 anyActive ← anyActive || jobsMoved | $ |
19 jobsMoved ← false | $ |
20 allDone ← true | $ |
Algorithm 13.20: Delaying idle workers
1 shared anyLarge ← false
2 me ← myThreadId
3
4 worker():
5 loop
6 while not isEmpty(jobs[me])
7 job ← dequeue(jobs[me])
8 perform(job) | $ |
9 if my job set is large
10 anyLarge ← true | $ |
11 if anyLarge
12 anyLarge ← false | /* set false before looking */ $ |
13 if another thread j has a relatively large jobs set | $ |
14 anyLarge ← true | /* could be more stealable work */ |
15 some ← stealJobs(j) | $ |
16 enqueue(jobs[me], some)
17 continue
18 busy[me] ← false | $ |
19 while (not anyLarge) && (not allDone) | $ |
20 /* do nothing: wait for work or termination */
21 if allDone return | $ |
22 busy[me] ← true | $ |
It is straightforward to refine these detection algorithms so that they wait on a single variable anyIdle until a scan might be useful, as shown in Algorithm 13.19. Likewise, in the work stealing case there is a similar refinement so that workers wait on a single anyLarge flag (in addition to allDone), as shown in Algorithm 13.20.
The algorithms presented so far assume a separate detection thread. It is tempting to use idle threads to check termination, as shown in Algorithm 13.21. The problem is that this algorithm does not work. For example, suppose thread A finishes its work, sees no thread to steal from and starts detection. In its detection scan, it now sees that thread B has extra work, so A will give up on detection, and may be just about to set its busy flag. In the meantime, B finishes all of its work, enters detection, sees that all threads are done and declares termination. A simple approach to fix this is to apply mutual exclusion to detection as shown in Algorithm 13.22.
For completeness, Algorithm 13.23 shows termination detection using an atomically updated shared counter. For discussion of a lock-free data structure to support work sharing implemented as a concurrent double-ended queue (deque), see Section 13.8.
Another common synchronisation mechanism in parallel and concurrent collectors is the need for all participants to reach the same point in the algorithm — essentially a point of termination of a phase of collection — and then to move on. In the general case one of the previously presented termination algorithms may be most appropriate. Another common case occurs when the phase does not involve work sharing or balancing, but it is required only to wait for all threads to reach a given point, called the rendezvous barrier. This can use a simplified version of termination detection with a counter (Algorithm 13.23), shown in Algorithm 13.24. Since a collector is usually invoked more than once as a program runs, these counters must be reset as the algorithm starts, or in any case before the phase is run again, and the resetting should be done with care to ensure that no thread can be depending on the value of the rendezvous counter at the time it is reset. Algorithm 13.25 shows such a resetting barrier.
Algorithm 13.21: Symmetric termination detection
1 work() :
2 …
3 while I have no work && not allDone | $ |
4 /* this version is broken! */
5 detectSymmetric()
6 …
7
8 detectSymmetric() :
9 while not allDone | $ |
10 while (not anyIdle) && (not anyLarge) | $ |
11 /* do nothing: wait until a scan might be useful */
12 if anyLarge return | $ |
13 anyIdle ← false
14 anyActive ← (∃i)(busy[i]) | $ |
15 anyActive ← anyActive || jobsMoved | $ |
16 jobsMoved ← false | $ |
17 allDone ← not anyActive | $ |
Algorithm 13.22: Symmetric termination detection repaired
1 shared detector ← −1
2 me ← myThreadId
3
4 work() :
5 …
6 while I have no work && not allDone | $ |
7 if detector ≥ 0
8 continue | /* wait for previous detector to finish before trying */ |
9 if CompareAndSet(&detector, −1, me)
10 detectSymmetric() | $ |
11 detector ← −1 | $ |
12 …
Algorithm 13.23: Termination via a counter
1 shared numBusy ← N
2 worker():
3 loop
4 while work remaining
5 perform(work)
6 if AtomicAdd(&numBusy, −1) = 0
7 return
8 while nothing to steal && (numBusy > 0) | $ |
9 /* do nothing: wait for work or termination */
10 if numBusy = 0
11 return
12 AtomicAdd(&numBusy, 1)
Algorithm 13.24: Rendezvous via a counter
1 shared numBusy ← N
2
3 barrier():
4 AtomicAdd(&numBusy, −1)
5 while numBusy > 0
6 /* do nothing: wait for others to catch up */
Algorithm 13.25: Rendezvous with reset
1 shared numBusy ← N
2 shared numPast ← 0
3
4 barrier():
5 AtomicAdd(&numBusy, −1)
6 while numBusy > 0
7 /* do nothing: wait for others to catch up */
8 if AtomicAdd(&numPast, 1) = N | /* one winner does the reset */ |
9 numPast ← 0 | $ |
10 numBusy ← N | $ |
11 else
12 while numBusy = 0 | /* the others wait (but not for long) */ |
13 /* do nothing: wait for reset to complete */
13.8 Concurrent data structures
There are particular data structures commonly used in parallel and concurrent allocators and collectors, so it is helpful to review some of the relevant implementation techniques. It should be plain that data structure implementations for sequential programs are not suitable as is for parallel and concurrent systems — they will generally break. If a data structure is accessed rarely enough then it may suffice to apply mutual exclusion to an otherwise sequential implementation by adding a lock variable to each instance of the data structure and have each operation acquire the lock before the operation and release it after. If operations can be nested or recursive, then a ‘counting lock’ is appropriate, as shown in Algorithm 13.26.
Some data structures have high enough traffic that applying simple mutual exclusion leads to bottlenecks. Therefore a number of concurrent data structures have been devised that allow greater overlap between concurrent operations. If concurrent operations are overlapped, the result must still be safe and correct. An implementation of a concurrent data structure is said to be linearisable if any pair of overlapping operations produces state changes on the data structure and responses to the operations consistent with executing the two operations in a non-overlapped way in one order or the other [Herlihy and Wing, 1990]. Furthermore, if two operations do not overlap in time, they must appear to happen in the order in which they were invoked. For each operation there is a point in time at which the operation can be viewed as having taken place. This is called its linearisation point. Often an operation has many points in time that might be viewed as its linearisation point, but the relative order of the linearisation points of operations that affect each other will always be consistent with the logical order of the operations. If operations do not affect each other then they can linearise in either order. Many memory manager actions, such as allocation and changes to work lists, must be linearisable.
Algorithm 13.26: Counting lock
1 /* the lock packs into one word a thread id and a count */
2 shared lock ← ⟨thread: −1, count: 0⟩int
3 me ← myThreadId
4
5 countingLock():
6 old ← lock
7 if old.thread = me && old.count > 0
8 /* just increment the count; assume no overflow */
9 lock ← ⟨old.thread, old.count + 1⟩
10 return
11 loop
12 if old.count = 0
13 if CompareAndSet(&lock, old, (thread: me, count: 1))
14 return
15 old ← lock
16
17 countingUnlock():
18 /* leaves thread id, but no harm even when count becomes 0 */
19 old ← lock
20 lock ← ⟨old.thread, old.count — 1⟩
There is a range of generic strategies a programmer can employ in building a concurrent data structure. In order from lower to higher concurrency, and typically from simplest to most complex, they are:13
Coarse-grained locking: One ‘large’ lock is applied to the whole data structure (already mentioned).
Fine-grained locking: In this approach an operation locks individual elements of a larger data structures, such as the individual nodes of a linked list or tree. This can increase concurrency if the locales of access and update are spread around enough. A general concern to keep in mind is that if an operation locks multiple elements, it must ensure that no other invocation of the same operation, or of any other operation, will attempt to lock the same two elements in the opposite order — in that case the operations can deadlock. A common technique on a data structure accessed only in a single direction, such as a singly linked list or a tree, is lock coupling. This locks a node A and then a node B pointed to by A. Then it releases the lock on A and acquires a lock on a node C pointed to by B, and so on. This ‘hand-over-hand’ walking of locks through a data structure guarantees that later-arriving threads cannot pass the current thread in the data structure, and supports safe execution of operations such as inserting or removing an item from a list or tree. A potential drawback of finegrained locking is that the overhead of going to a shared bus or memory multiple times to lock individual elements may swamp the benefit of avoiding a coarser lock.
Optimistic locking: This refines fine-grained locking by doing any searching of the data structure without locks, then locking what appear to be the proper elements for the operation. However, in general, concurrent updates can have changed things, so after locking, the operation validates that it has locked the correct elements for its intended action. If the validation fails, it releases the locks and starts over. Avoiding locking until the latest time necessary reduces overhead and improves concurrency. Optimism is often a good strategy, but can result in poorer performance in the presence of frequent conflicting updates.
Lazy update: Even with optimistic locking, read-only operations may still need to lock a data structure. This can result in a concurrency bottleneck, and also has the effect that a read-only operation performs writes (of locks). It is often possible to design a data structure so that read-only operations need no locking — but of course the updating operations are a bit more complex. Generally speaking, they make some change that logically accomplishes the operation, but may need further steps to complete it and get the data structure into a normalised form. An example may help in understanding this. For lazy update of a linked list representation of a set, the remove operation will first mark an element as being (logically) removed, by setting a boolean flag deleted in the element. After that it will unchain the deleted element by redirecting the predecessor’s pointer. All this happens while holding locks in the appropriate elements, so as to prevent problems with concurrent updaters. The two steps are necessary so that readers can proceed without locking. Adding an element needs to modify only one next pointer in the data structure and therefore needs only one update (again, with appropriate locks held).
Non-blocking: There are strategies that avoid locking altogether and rely on atomic update primitives to accomplish changes to the state of data structures. Typically a state-changing operation has some particular atomic update event that is its linearisation point. This is in contrast to lock based methods, where some critical section marks the linearisation ‘point’.14 As previously mentioned, these can be characterised according to their progress guarantees, in order from easiest to implement to hardest. Lock-free implementations may allow starvation of individual threads; obstruction-free implementations may require long enough periods in which a single thread can make progress without interference; and wait-free implementations guarantee progress of all threads. Some lock-free implementations are sketched below; for wait-free implementation, see Herlihy and Shavit [2008].
For data structures most relevant to implementing parallel and concurrent collection, implementation descriptions and code sketches are offered below. The implementation strategies generally follow those suggested by Herlihy and Shavit.
First, we sketch ways to implement a concurrent stack using a singly linked list. Since there is only one locus of mutation for a stack, the performance of the various approaches to locking will be about the same. The code is obvious, so not illustrated. Algorithm 13.27 shows a lock-free implementation of a stack. It is easy to make push lock-free; pop is a little harder. The popABA routine is a simple CompareAndSet implementation of pop that is lock-free — but that also has an ABA problem. Algorithm 13.27 also shows LoadLinked/Store-Conditionally and CompareAndSetWide solutions that avoid the ABA problem, as concrete examples of how to do that. The problem occurs when some other thread(s) pop the node referred to by currTop, and that node is pushed later with its next different from the currTop.next read by this popping thread.
A concurrent stack based on an array is best implemented using a lock. However, concurrent stacks tend to be a bottleneck not just because of cache and memory issues, but because all the operations must serialise. However it is possible to do better. Blelloch and Cheng [1999] provide a lock-free solution by requiring all threads accessing a shared stack either to be popping from it or all to be pushing onto it, thus allowing the stack pointer to be controlled by a FetchAndAdd instruction rather than a lock. We discuss this in detail in Chapter 14. Chapter 11 of Herlihy and Shavit discusses a concurrent lock-free stack implementation where threads that encounter high contention try to find matching operations in a side buffer. When a pop finds a waiting push, or a push finds a waiting pop, that push instantly satisfies that pop: the pair of operations eliminate each other. They linearise at that moment (push before pop, of course), regardless of what is happening at the ‘main’ stack.
Concurrent queue implemented with singly linked list
A concurrent queue is a more interesting example of concurrency than a concurrent stack, since it has two loci of modification, the head, where items are removed, and the tail, where they are added. It is convenient to include a ‘dummy’ node, before the next element to be removed from the queue. The head pointer refers to the dummy node, while the tail pointer refers to the node most recently added to the queue, or the dummy node if the queue is empty.
Algorithm 13.28 shows an implementation that does fine-grained locking. It has one lock for each locus. Notice that remove changes head to refer to the next node; thus, after the first successful remove, the original dummy node will be free, and the node with the value just removed becomes the new head. This version of queue is unbounded. Algorithm 13.29 shows a similar implementation for a bounded queue. To avoid update contention on a single size field, it maintains counts of the number of items added and the number removed. It is fine if these counts wrap around — the fields storing them just need to be able to store all max + 1 values from zero through max. Of course if these counts lie on the same cache line, this ‘optimisation’ may perform no better than using a single size field.
There is an important special case of this implementation: if either adding or removing or both is limited to one thread, then that end does not need a lock. In particular, if there is one adder and one remover, then this data structure needs no locks at all. A common case in collection is multiple adders and one remover, which is still an improvement over the general case.
Other locking approaches (such as optimistic or lazy update) offer no real advantage over fine-grained locking for this data structure.
Algorithm 13.27: Lock-free implementation of a single-linked-list stack
1 shared topCnt[2] ← [null, any value]
2 shared topAddr ← &topCnt[0] | /* |
3 shared cntAddr ← &topCnt[1] | /* |
4
5 push(val):
6 node ← new Node(value: val, next: null)
7 loop
8 currTop ← *topAddr
9 node.next ← currTop
10 if CompareAndSet (topAddr, currTop, node)
11 return
12
13 popABA():
14 loop
15 currTop ← *topAddr
16 if currTop = null
17 return null
18 /* code below can have an ABA problem if node is reused */
19 next ← currTop.next
20 if CompareAndSet(topAddr, currTop, next)
21 return currTop.value
22
23 pop():
24 loop
25 currTop ← LoadLinked(topAddr)
26 if currTop = null
27 return null
28 next ← currTop.next
29 if StoreConditionally(topAddr, next)
30 return currTop.value
31
32 popCount():
33 loop
34 currTop ← *topAddr
35 if currTop = null
36 return null
37 currCnt ← *cntAddr | $ |
38 nextTop ← currTop.next
39 if CompareAndSetWide(&topCnt, currTop, currCnt,
40 nextTop, currCnt + 1)
41 return currTop.value
Algorithm 13.28: Fine-grained locking for a single-linked-list queue
1 shared head ← new Node(value: dontCare, next: null)
2 shared tail ← head
3 shared addLock ← UNLOCKED
4 shared removeLock ← UNLOCKED
5
6 add(val):
7 node ← new Node(value: val, next: null)
8 lock(&addLock)
9 tail.next ← node
10 tail ← node
11 unlock(&addLock)
12
13 remove():
14 lock(&removeLock)
15 node ← head.next
16 if node = null
17 unlock(&removeLock)
18 return EMPTY | /* or otherwise indicate emptiness */ |
19 val ← node.value
20 head ← node
21 unlock(&removeLock)
22 return val
Algorithm 13.29: Fine-grained locking for a single-linked-list bounded queue
1 shared head ← new Node(value: dontCare, next: null)
2 shared tail ← head
3 shared addLock ← UNLOCKED
4 shared removeLock ← UNLOCKED
5 shared numAdded ← 0
6 shared numRemoved ← 0
7
8 add(val):
9 node ← new Node(value: val, next: null)
10 lock(&addLock)
11 if numAdded – numRemoved = MAX
12 unlock(&addLock)
13 return false | /* or otherwise indicate full */ |
14 tail.next ← node
15 tail ← node
16 numAdded ← numAdded + 1 | /* numeric wrap around is ok */ |
17 unlock(&addLock)
18 return true | /* or otherwise indicate success */ |
19
20 remove () :
21 lock(&removeLock)
22 node ← head.next
23 if numAdded – numRemoved = 0
24 unlock(&removeLock)
25 return EMPTY | /* or otherwise indicate emptiness */ |
26 val ← node.value
27 head ← node
28 numRemoved ← numRemoved + 1 | /* numeric wrap around is ok */ |
29 unlock(&removeLock)
30 return val
Algorithm 13.30: Lock-free implementation of a single-linked-list queue
1 shared head ← new Node(value: dontCare, next: null)
2 shared tail ← head
3
4 add(val):
5 node ← new Node(value: val, next: null)
6 loop
7 currTail ← LoadLinked(&tail)
8 currNext ← currTail.next
9 if currNext ≠ null
10 /* tail appears to be out of sync: try to help */
11 StoreConditionally(&tail, currNext)
12 continue | /* start over after attempt to sync */ |
13 if CompareAndSet(&currTail.next, null, node)
14 /* added to end of chain; try to update tail */
15 StoreConditionally(&tail, node)
16 /* ok if failed: someone else brought tail into sync, or will in the future */
17 return
18
19 remove():
20 loop
21 currHead ← LoadLinked(&head)
22 next ← currHead.next
23 if next = null
24 if StoreConditionally(&head, currHead)
25 /* head has not changed, so truly empty */
26 return EMPTY | /* or otherwise indicate emptiness */ |
27 continue | /* head may have changed so try again */ |
28
29 currTail ← tail
30 if currHead = currTail
31 /* not empty; appears to be out of sync; try to help */
32 currTail ← LoadLinked(&tail)
33 next ← currTail.next
34 if next ≠ null
35 StoreConditionally(&tail, next)
36 continue
37
38 /* appears non–empty and in sync enough; try to remove first node */
39 val ← next.value
40 if StoreConditionally(&head, next)
41 return val
42 /* on failure, start over */
Algorithm 13.31: Fine-grained locking of a circular buffer
1 shared buffer [MAX]
2 shared head ← 0
3 shared tail ← 0
4 shared numAdded ← 0
5 shared numRemoved ← 0
6 shared addLock ← UNLOCKED
7 shared removeLock ← UNLOCKED
8
9 add(val):
10 lock(&addLock)
11 if numAdded – numRemoved = MAX
12 unlock(&addLock)
13 return false | /* indicate failure */ |
14 buffer[tail] ← val
15 tail ← (tail + 1) % MAX
16 numAdded ← numAdded + 1
17 unlock(&addLock)
18
19 remove():
20 lock(&removeLock)
21 if numAdded – numRemoved = 0
22 unlock(&removeLock)
23 return EMPTY | /* indicate failure */ |
24 val ← buffer[head]
25 head ← (head + 1) % MAX
26 numRemoved ← numRemoved + 1
27 unlock(&removeLock)
28 return val
Algorithm 13.30 shows a lock-free implementation. A tricky thing here is that adding a node happens in two steps. First, the current tail node is updated to point to the new node, and then tail is updated to refer to the new node. A lock-free implementation must provide for the possibility that other adders — and also removers — may see the intermediate state. This implementation addresses the issue by having any thread update tail if it notices that tail is ‘out of sync’. This ensures that tail comes into sync without any thread waiting for another one to do it. This is a case of the helping typical of wait-free algorithms, even though this algorithm is not wait-free.
Concurrent queue implemented with array
A queue implemented with an array has higher storage density than one implemented with a linked list, and it does not require on the fly allocation of nodes from a pool. A bounded queue can be implemented with a circular buffer. Algorithm 13.31 shows a finegrained locking version of that, which can be improved by folding together head and numRemoved, and also tail and numAdded, using modular arithmetic, shown in Algorithm 13.32. This is particularly attractive if MAX is a power of two, since then the modulus function can be performed with bit masking. The reason for MODULUS is that we need to distinguish the MAX+1 possible values for the difference between tail and head, that is, the number of elements in the buffer. Thus our modulus for the modular arithmetic needs to be greater than MAX. At the same time, it must be a multiple of MAX so that we can reduce head and tail modulo MAX when indexing into the buffer. The value MAX*2 is the smallest modulus that will work, and has the added virtue of being a power of two when MAX is. In the code we add MODULUS to tail–head to ensure we are taking the modulus of a positive number, which is not necessary if using masking or if the implementation language does a proper modulus (toward −∞ as opposed to toward zero).
Algorithm 13.32: Circular buffer with fewer variables
1 shared buffer [MAX]
2 MODULUS = MAX * 2 | /* see text for explanation */ |
3 shared head ← 0 | /* 0 ≤ |
4 shared tail ← 0 | /* 0 ≤ |
5 shared addLock ← UNLOCKED
6 shared removeLock ← UNLOCKED
7
8 add(val):
9 lock(&addLock)
10 if (tail − head + MODULUS) % MODULUS = MAX
11 unlock(&addLock)
12 return false | /* indicate failure */ |
13 buffer[tail % MAX] ← val
14 tail ← (tail + 1) % MODULUS
15 unlock(&addLock)
16 return true | /* indicate success */ |
17
18 remove():
19 lock(&removeLock)
20 if (tail − head + MODULUS) % MODULUS = 0
21 unlock(&removeLock)
22 return EMPTY | /* indicate failure */ |
23 local val ← buffer[head % MAX]
24 head ← (head + 1) % MODULUS
25 unlock(&removeLock)
26 return val
If there is a distinguished value that can mark empty slots in the buffer, then the code can be further simplified as shown in Algorithm 13.33.
It is often the case that the buffer has just a single reader and a single writer (for example, the channels used by Oancea et al [2009]). In this case, the code for a circular buffer is much simpler; it appears in Algorithm 13.34. This algorithm is a good example for mentioning the adjustments a programmer needs to make to realise the algorithm on different platforms. The algorithm works as is on Intel x86 processors because they are strict about the order of stores to memory as perceived by other processors.
However, on the PowerPC the lines we mark with $ for ordering require attention. One approach is to insert fences, as indicated by Oancea et al. In add we insert an lwsync instruction between the stores to buffer[tail] and tail, to serve as a store-store memory fence.15 This will guarantee that if the remover orders its load instructions properly, it will not perceive the change to tail until after it can perceive the change to buffer. Likewise we add an isync instruction, which serves as a load-store memory fence, before the store to buffer, to ensure that the processor does not speculatively begin the store before the load of head and thus possibly overwrite a value being read by the remover.16
Algorithm 13.33: Circular buffer with distinguishable empty slots
1 shared buffer[MAX] ← [EMPTY,…]
2 shared head ← 0
3 shared tail ← 0
4 shared addLock ← UNLOCKED
5 shared removeLock ← UNLOCKED
6
7 add(val):
8 lock(&addLock)
9 if buffer[tail] ≠ EMPTY
10 unlock(&addLock)
11 return false | /* indicate failure */ |
12 buffer[tail] ← val
13 tail ← (tail + 1) % MAX
14 unlock(&addLock)
15 return true | /* indicate success */ |
16
17 remove():
18 lock(&removeLock)
19 if buffer[head] = EMPTY
20 unlock(&removeLock)
21 return EMPTY | /* indicate failure */ |
22 val ← buffer[head]
23 head ← (head + 1) % MAX
24 unlock(&removeLock)
25 return val
Algorithm 13.34: Single reader/single writer lock-free buffer [Oancea et al, 2009]
1 shared buffer[MAX]
2 shared head ← 0 | /* next slot from which to try removing */ |
3 shared tail ← 0 | /* next slot into which to add */ |
4
5 add(val):
6 newTail ← (tail + 1) % MAX
7 if newTail = head
8 return false
9 buffer[tail] ← val | $ |
10 tail ← newTail
11 return true
12
13 remove():
14 if head = tail
15 return EMPTY | /* or otherwise indicate emptiness */ |
16 value ← buffer[head] | $ |
17 head ← (head + 1) % MAX | $ |
18 return value
Algorithm 13.35: Unbounded lock-free buffer implemented with an array
1 shared buffer[ ] ← [EMPTY,… ] | /* unrealisable unbounded buffer */ |
2 shared head ← 0–0 | /* next slot to fill */ |
3
4 add(val):
5 pos ← FetchAndAdd(&head, 1)
6 buffer[pos] ← val
7
8 remove():
9 limit ← head
10 pos ← −1
11 loop
12 pos ← pos + 1
13 if pos = limit
14 return null | /* found nothing */ |
15 val ← LoadLinked(&buffer[pos])
16 if val ≠ EMPTY
17 if StoreConditionally(&buffer[pos], EMPTY)
18 return val
Similarly we insert an lwsync in remove between loading buffer[head] and updating head, and an isync before loading from buffer, to serve as a load-load memory barrier between loading tail and loading from buffer.
Oancea et al proposed a solution that includes writing null in remove as an explicit EMPTY value, and having both add (remove) watch its intended buffer slot until the slot appears suitably empty (non-empty), before writing its new value (EMPTY). Because there is only one reader and only one writer, one only thread writes EMPTY values, and only one writes non-EMPTY values, and each delays its write until it sees the other thread’s previous write, accesses to the buffer cannot incorrectly pass each other. Likewise, only one thread writes each of head and tail, so at worst the other thread may have a stale view. This solution avoids fences, but the buffer writes by the remover may cause more cache ping-ponging than fences would. Oancea et al actually combine both solutions, but as we just argued, each seems adequate on its own. This all shows the care needed to obtain a correctly working implementation of concurrent algorithms under relaxed memory orders.
Algorithm 13.36: Unbounded lock-free array buffer with increasing scan start
1 shared buffer[ ] ← [EMPTY,…] | /* unrealisable unbounded buffer */ |
2 shared head ← 0 | /* next slot to fill */ |
3 shared lower ← 0 | /* position to look at first */ |
4
5 add(val):
6 pos ← FetchAndAdd(&head, 1)
7 buffer[pos] ← val
8
9 remove():
10 limit ← head
11 currLower ← lower
12 pos ← currLower – 1
13 loop
14 pos ← pos + 1
15 if pos = limit
16 return null | /* found nothing */ |
17 val ← LoadLinked(&buffer[pos])
18 if val = EMPTY
19 continue
20 if val = USED
21 if pos = currLower
22 /* try to advance lower */
23 currLower ← LoadLinked(&lower)
24 if pos = currLower
25 StoreConditionally(&lower, pos+1)
26 continue
27 /* try to grab */
28 if StoreConditionally(&buffer[pos], USED)
29 return val
If the queue is being used as a buffer, that is, if the order in which things are removed need not match exactly the order in which they were added, then it is not too hard to devise a lock-free buffer. First assume an array large enough that wrap around will never occur. Algorithm 13.35 implements a lock-free buffer. It assumes that initially all entries are EMPTY.
This algorithm does a lot of repeated scanning. Algorithm 13.36 adds an index lower from which to start scans. It requires distinguishing not just empty slots, but also ones that have been filled and then emptied, indicated by USED in the code.
Further refinement is needed to produce a lock-free circular buffer implementation along these lines. In particular there needs to be code in the add routine that carefully converts USED slots to EMPTY ones before advancing the head index. It also helps to use index values that cycle through twice MAX as in Algorithm 13.32. The resulting code appears in Algorithm 13.37.
Algorithm 13.37: Bounded lock-free buffer implemented with an array
1 shared buffer[MAX] ← [EMPTY,…]
2 MODULUS = 2 * MAX
3 shared head ← 0 | /* refers to next slot to fill */ |
4 shared lower ← 0 | /* slots from |
5
6 add(val):
7 loop
8 currHead ← head
9 /* could peek before using atomic operator */
10 oldVal ← LoadLinked(&buffer[currHead % MAX])
11 if oldVal = USED
12 currLower ← lower
13 if (currHead % MAX) = (currLower % MAX)
14 && (currHead ≠ currLower)
15 advanceLower() | /* lower is a buffer behind */ |
16 continue
17 /* try to clean entry; ensure head has not changed */
18 if currHead = head
19 StoreConditionally(&buffer[currHead % MAX], EMPTY)
20 continue
21 if oldVal ≠ EMPTY
22 if currHead ≠ head
23 continue | /* things changed: try again */ |
24 return false | /* indicate failure: buffer is full */ |
25 currHead ← LoadLinked(&head) | /* try to claim slot */ |
26 /* recheck inside LL/SC */
27 if buffer[currHead % MAX] = EMPTY
28 if StoreConditionally(&head, (currHead + 1) % MODULUS)
29 buffer[currHead] ← val
30 return true | /* indicate success */ |
31
32 remove():
33 advanceLower()
34 limit ← head
35 scan ← lower – 1
36 loop
37 scan ← (scan + 1) % MODULUS
38 if scan = limit
39 return null | /* found nothing */ |
40 /* could peek at value first before using atomic operator */
41 val ← LoadLinked(&buffer[scan % MAX])
42 if val = EMPTY || val = USED
43 continue
44 /* try to grab */
45 if StoreConditionally(&buffer[scan % MAX], USED)
46 /* Note: always safe to grab entry that is not USED and not EMPTY */
47 return val
1 advanceLower():
2 if buffer[lower % MAX] ≠ USED
3 return | /* quick return without using atomic operation */ |
4 loop
5 currLower ← LoadLinked(&lower)
6 if buffer[currLower % MAX] = USED
7 if StoreConditionally(&lower, (lower + 1) % MODULUS)
8 continue
9 return
A concurrent deque for work stealing
To support work stealing, Arora et al [1998] designed a lock-free implementation of a double-ended queue. The local worker thread can push and pop work items, while other threads can remove (steal) items. The design has the local worker push and pop at one end of the deque, while other threads remove from the opposite end (the deque is input-restricted). Algorithm 13.38 shows an implementation that uses LL/SC to avoid an ABA problem.17 It is straightforward to pack a counter with the tail index to derive a safe implementation in terms of CompareAndSwap.
Pushing a value is simple and involves no synchronisation. Popping checks to see if it trying to get the last value remaining. If it is, it may be in a race with a non-local remover. Both threads will try to update tail; the winner ‘gets’ the value. In any case, the popper sets tail to zero. This will not confuse a contending remover. Either the remover lost the race, in which case it does not return a value, or it won and it already has the value and will leave tail alone. It is also important that pop sets top to zero first, before setting tail to zero — this keeps the top ≤ tail test working in remove. Notice that the conventions for top and tail ensure that top–tail is the number of items in the queue (except in the middle of resetting them both to zero, where the difference may be negative).
First it may be helpful to describe transactional memory further, and after that to proceed to consider its relationship to garbage collection.
A transaction consists of a collection of reads and writes that should appear to execute atomically. That is, the effect should be as if no other reads or writes interleave with those of a transaction. LoadLinked/StoreConditionally achieves this semantics for transactions involving a single word, but the point is to allow transactions over multiple independent words. A suitable mechanism will generally include means to indicate:
• The start of a transaction.
• Each read that is part of the current transaction.
Algorithm 13.38: Lock-free work stealing deque [Arora et al, 1998]
1 shared deque [MAX]
2 shared top ← 0 | /* index one beyond the last used entry */ |
3 shared tail ← 0 | /* index of the first used entry */ |
4
5 push (val) : | /* local worker function to push (enqueue) a value */ |
6 currTop ← top
7 if currTop ≥ MAX
8 return false | /* indicate overflow */ |
9 deque[currTop] ← val
10 top ← currTop + 1
11 return true | /* indicate success */ |
12
13 pop() : | /* local worker function to pop a value from the local end */ |
14 currTop ← top – 1
15 if currTop < 0
16 return null | /* empty */ |
17 top ← currTop
18 val ← deque[currTop]
19 currTail ← LoadLinked(&tail)
20 if currTop > currTail
21 return val | /* cannot be contending with other removers */ |
22 /* might be contending, and deque will be empty */
23 top ← 0
24 if StoreConditionally(&tail, 0)
25 return val | /* I won on changing tail, so I get the value */ |
26 tail ← 0
27 return null
28
29 remove(): | /* steal a value from another thread’s deque */ |
30 loop
31 currTail ← LoadLinked(&tail)
32 currTop ← top
33 if currTop ≤ currTail
34 return null | /* deque is empty */ |
35 val ← deque[currTail]
36 if StoreConditionally(&tail, currTail+1)
37 return val | /* won on setting tail, so can return the value */ |
38 /* contended with another remover, or pop that emptied the deque */
39 /* if stealing is optional, could indicate failure instead of looping */
• Each write that is part of the current transaction.
• The end of a transaction.
The end is usually called the (attempted) commit of the transaction. If it succeeds, then the transaction’s effects appear; if it fails then the writes are discarded and the software may respond by trying again, trying some other action, and so on. Thus, transactions may be executed speculatively. It is necessary to mark their end so that speculation can be resolved and the transaction accepted, with its writes installed, and so on, or rejected and the software notified so that it can retry or take some other action.
Similar to the ACID properties of database transactions, transactional memory transactions ensure:
• Atomicity: All effects (writes) of a transaction appear or none do.
• Consistency: A transaction appears to execute at a single instant.
• Isolation: No other thread can perceive an intermediate state of a transaction, only a state before or a state after the transaction.
The durability property of database transactions, which ensures to very high probability that the results of a successful transaction will not be lost, is omitted from the requirements on transactional memory.
The actual reads and writes of a transaction will be spread out over time. Thus, as transactions run, they may interfere with each other if they access the same locations. Specifically, transactions A and B conflict if one of them writes an item that the other reads or writes. Conflicting transactions must be ordered. In some cases, given the reads and writes a transaction has already performed, this is not possible. For example, if A and B have both read x, and then they both try to write to x, there is no way to complete both transactions so as to satisfy transactional semantics. In that case one or both of A and B must be aborted (discarded), and the situation made to appear as if the aborted transaction had not run. Generally the software will try it again, which will likely force a suitable ordering.
Transactional memory can be implemented in hardware, software or a hybrid combination. Any implementation strategy must provide for: atomicity of writes, detection of conflicts and visibility control (for isolation). Visibility control may be part of conflict detection.
Atomicity of writes can be achieved either by buffering or by undoing. The buffering approach accumulates writes in some kind of scratch memory separate from the memory locations written, and updates those memory location only if the transaction commits. Hardware buffering may be achieved by augmenting caches or using some other side buffer; software buffering might work at the level of words, object fields or whole objects. With buffering, a transaction commit installs the buffered writes, while an abort discards the buffer. This typically requires more work for commits, usually the more common case, and less work for aborts. Undoing works in a converse way: it updates modified data as a transaction runs, but saves in a side data structure called the undo log the previous value of each item it writes. If the transaction commits, it simply discards the undo log, but if the transaction aborts, it uses the undo log to restore the previous values. Undo logs can be implemented in hardware, software, or a combination, just as buffering can.
Conflict detection may be implemented eagerly or lazily. Eager conflict checking checks each new access against the currently running transactions to see if it conflicts. If necessary it will cause one of the conflicting transactions to abort. Lazy conflict checking does the checks when a transaction attempts to commit. Some mechanisms also allow a transaction to request as it runs validation that there are no conflicts so far in the transaction. Software schemes may set flags in object headers or maintain a side table recording accesses. These are checked by transactional accesses to accomplish conflict detection. Hardware will typically associate flags with cache lines or words to the same end.
For purposes of presentation let us discuss a simple hardware transactional memory interface consisting of these primitives, as introduced by Herlihy and Moss [1993]:
TStart() indicates the beginning of a transaction.
TCommit() indicates that the transaction wants to commit. It returns a boolean that is true if and only if the commit succeeded.
TAbort() indicates that the transaction wants to abort, which is sometimes useful to request programmatically.
TLoad(addr) marks a transactional load from the indicated address. This adds that address to the transaction’s read set and returns the current value in that memory location.
TStore(addr, value) marks a transactional store of the indicated value to the indicated address. This adds the address to the transaction’s write set and performs the write transactionally, that is, in a way in which the effect of the write disappears if the transaction aborts, and so on.
These primitives can simplify the implementation of a variety of concurrent data structures. For example, Algorithm 13.30 simplifies to Algorithm 13.39. The add function is simpler because it can write two locations atomically, and remove is simpler because it can read two and even three values atomically. More importantly, it is easier to see that the transactional implementation is correct; verifying the other version requires more subtle arguments about orders of reads and writes.
Using transactional memory to help implement collection
There are two main relationships that transactional memory can have with garbage collection. Transactional memory can help implement the collector [McGachey et al, 2008], or transactions may be part of the managed language semantics that the collector must play with nicely. This section considers transactional memory in support of garbage collection; the next section looks at garbage collection for a language that support transactions.
It should be clear that transactional memory, because of the way it can simplify the programming of concurrent data structures, can make it easier to implement parallel and concurrent allocation and collection. In particular it can simplify concurrent allocators, mutator and collector read and write barriers, and concurrent collector data structures. Given that there are no current hardware standards and an increasing variety of software packages available, it is not possible to be specific, but using transactional memory to support automatic memory management involves these caveats:
• Software transactional memory tends to involve significant overheads, even after optimisation. Given the desire for low overheads in most parts of automatic storage management, the scope for applying software transactional memory may be small. Still, coding of low traffic data structures might be simplified while continuing to avoid the difficulties with locks.
• Hardware transactional memory will likely have idiosyncrasies. For example, it may handle conflict detection, access and updating all in terms of physical units such as cache lines. It will also likely have an upper limit on the number of data items involved in a transaction, because of hardware capacity limitations such as the number of lines per cache set in a set-associative cache, for some approaches to implementing hardware transactional memory. Because the mapping from what a programmer writes to the cache lines actually used may not be obvious, implementers must still be careful with low level details.
Algorithm 13.39: Transactional memory version of a single-linked-list queue
1 shared head ← new Node(value: dontCare, next: null)
2 shared tail ← head
3
4 add(val):
5 node ← new Node(value: val, next: null)
6 loop
7 currTail ← TLoad(&tail)
8 TStore(&currTail.next, node)
9 TStore(&tail, node)
10 if TCommit()
11 return
12
13 remove():
14 loop
15 currHead ← TLoad(&head)
16 next ← TLoad(&currHead.next)
17 if next = null
18 if TCommit() | /* the commit ensures we got a consistent view */ |
19 return EMPTY | /* or otherwise indicate emptiness */ |
20 continue
21
22 /* appears non–empty; try to remove first node */
23 val ← TLoad(snext.value)
24 TStore(&head, next)
25 if TCommit()
26 return val
27 /* on failure, start over */
• Transactional memory can, at most, guarantee lock-freedom, though it does that fairly easily. Even if the underlying commit mechanism of transactional memory is wait-free, transactions can conflict, leading to aborts and retries. Programming wait-free data structures will remain complex and subtle.
• Transactional memory can require careful performance tuning. One concern is inherent conflicts between transactions because they access the same data. An example is a concurrent stack: transactional memory will not solve the bottleneck caused by the need for every push and pop to update the stack pointer. Furthermore, exactly where in a transaction various reads and writes occur — nearer to the beginning or nearer to the end — can significantly affect conflicts and the overhead of retrying transactions.
All that said, a hardware transactional memory facility such as that designed at Advanced Micro Devices, the Advanced Synchronisation Facility [Christie et al, 2010], and similar to that described in the previous section, could be quite useful. That hardware transactional memory design supports reading and writing at least four completely independent cache lines in a transaction, which is enough to simplify the implementation of most of the concurrent data structures presented here. Whether the performance would be comparable, or even better, with hardware transactional memory remains an open question. The simpler model of the world that transactional memory presents may result in fewer bugs and reduce development effort.
Supporting transactional memory in the presence of garbage collection
Consider now the quite different problem of implementing a language that offers both automatic memory management and transactions built using some form of transactional memory [Harris and Fraser, 2003; Welc et al, 2004, 2005]. The key issue is the ways in which these two complex mechanisms — transactions and automatic memory management — may interfere, particularly in a highly concurrent implementation.
One kind of interference is that actions of the storage manager may cause transaction conflicts that result in higher overhead because of more retries, as well as making progress problematic for either a mutator, the collector or both. For example, if the mutator is attempting a long transaction, and collector actions conflict, the mutator transaction may be continually aborted by actions of the collector, or the collector may effectively block for a long time. The issue is particularly severe if the implementation exploits hardware transactional memory. For example, attempts by a concurrent collector to mark, forward or copy an object may cause mutator transactions to abort just because they touched the same memory word — even though the operations are carefully coded not to disturb each other’s semantics. This would be harder to avoid with hardware transactional memory, since it is oblivious to the semantics of the data being managed, whereas a software transactional memory built for a particular language might give special treatment to object headers, as opposed to data fields.
Transactions can become involved in the semantics of memory reclamation. For example, if a transactional memory systems uses a log of old values to support aborting transactions in an update-in-place implementation, then it is possible for the log to contain the only reference to an object. While the transaction remains in doubt, the referent object must be considered still to be reachable. Thus, transaction logs need to be included in the root set for collection. Furthermore, in the case of copying collection, pointers in the logs must not only be provided to the collector for tracing, they must also be updated to reflect the new locations of objects that have moved.
An interesting issue is how to handle allocation in a transactional language. In particular, it would seem logical that if a transaction allocates some objects and then aborts, it should somehow unallocate those objects. However, if the allocation data structures are shared, maintaining ability to rollback values exactly as they were would mean that transactions accessing free-lists or bump pointers effectively lock them until the transaction completes. This is probably undesirable. Therefore allocation should be more a logical action than a physical one, when we consider how to undo it. A free-list system might go back through an aborting transaction’s log and free the objects it allocated. This may put them in a different position on a free-list, and if a block had been split, it might not be recombined, and so forth. It is also possible that the semantics of the language may admit some non-transactional activity within a transaction. In that case an object allocated by the transaction might be revealed, so it can be unsafe to free the object. The implementation must further take care that if an object might be revealed in this way, the initialisation of its crucial contents, such as setting up the object header, is not undone. Concepts such as open nesting [Ni et al, 2007] may help here. A generic strategy is to consider all automatic memory management actions of a transactional mutator to be open nested actions.
Finally, some transactional memory systems do significant allocation as part of how they function, and that has impact on allocators and collectors. In particular many software transactional memory systems work by allocating a new version of an object for a writing transaction, which is installed only if the transaction commits. There may not be anything new here semantically for a collector to deal with, but the load may be a bit different. There is also a bit of a sibling relationship between transactional memory and collection in the sense that they may both need efficient concurrent data structures with adequate progress guarantees. For example, transaction commit is in part a consensus algorithm that ideally is wait-free.
A first consideration cannot be overstated: getting concurrent algorithms correct is hard! Therefore, unless concurrency is absolutely necessary, it should be avoided. That said, concurrency has become more necessary than it was and so we offer these additional considerations.
What is the range of platforms on which the system will run? What are the memory consistency properties and the fence and synchronisation primitives they offer? It is necessary to code to the weakest ordering to be supported, but it may be possible to elide some fences or other primitives on some platforms, as we discussed relative to Algorithm 13.34 in Section 13.8. What orderings will need fences?
What atomic update primitives are available? Although LoadLinked/StoreConditionally is convenient and more powerful, many popular systems offer only Compare-AndSwap or equivalent. Without LoadLinked/StoreConditionally, ABA problems can crop up, which can be addressed as we showed in Algorithm 13.27. Perhaps in the future transactional memory will be of use.
What progress guarantees are needed? Weaker guarantees are much easier to implement and to reason about. For low-traffic data structures, straightforward locking may be appropriate — it is much easier to code and to code correctly than lock-free or stronger guarantees. Further, even deployed systems that are wait-free for most cases may use simpler techniques for corner cases or for some short steps where the implementation effort to make them wait-free is not worth the benefit.
Does the system exhibit true concurrency (more than one thread running at once in hardware) or is it only multiprogrammed? Multiprogrammed concurrent algorithms are easier to deal with.
In the following chapters, we build on the ideas introduced here to construct parallel, incremental, concurrent and real-time collectors.
1We are indebted to Herlihy and Shavit [2008] for the organisation of our discussion, and recommend that book for additional study.
2Private memory is suitable for thread-local heaps if the threads can be bound to processors (allowed to run only on the specific processor where their heap resides). It is also suitable for local copies of immutable data.
3The Java memory model is even looser: if two writes are not otherwise synchronised, then a processor can observe either value on any future read, and thus the value may oscillate.
4Some authors use the word ‘synchronising’ where we use ‘atomic’, but this conflates the atomicity of these operations with their usual influence on ordering, which is a strictly different notion.
5By ‘occurs’ we mean ‘appears to occur’ — a program cannot tell the difference.
6Given relativistic effects, a total order may not even be well-defined in modern systems.
7A thread also loses its reservation on a context-switch.
8Of course if contention is that high, there may be the possibility of starvation at the hardware level, in trying to gain exclusive access to the relevant cache line.
9The time before this happens is not bounded unless a requesting thread whose turn it is enters and then leaves within bounded time.
10Sometimes work is idempotent, so if it is done two or more times, the algorithm is still correct, though possibly wasteful of computing resources.
11Flood et al [2001] use essentially this technique in their parallel collector, but with a single word that has one ‘active’ bit per thread. The termination condition is the same: the algorithm terminates when the status word becomes zero.
12The version shown eliminates the β flags of Leung and Ting [1997], which have to do with operating system sleeping and wakeup, which we elide here for simplicity. Here, we give their α and γ flags the more memorable names busy and jobsMoved. Leung and Ting also give a variant that detects termination a little faster by checking the jobsMoved flag every iterations of the detector’s scanning loop. Given the time needed to perform work in a collection algorithm, it is doubtful that such a refinement is worthwhile.
13See Herlihy and Shavit [2008] Chapter 9 for details of each of these approaches applied to a set implemented as a linked list.
14Because of mutual exclusion, it is a point as far as any other operations are concerned. However, lazy update methods also tend to have a single linearisation point.
15The lwsync instruction ensures that memory accesses by the issuing processor for instructions before the lwsync complete before any memory accesses for instructions after the lwsync, as viewed by all processors. It stands for ‘light-weight sync’ and is a version of the sync, where the ‘heavy-weight’ version, written just sync, deals with input/output device memory in addition to ordinary cached memory. Both lwsync and sync are somewhat expensive since their implementation typically involves waiting for the write buffer to drain before allowing future memory accessing instructions to issue. This implies waiting for inter-processor cache synchronisation to complete.
16The isync instruction ensures that all instructions previously issued by this processor complete before any future instruction of this processor. It is suitable for separating previous loads from future memory accesses. It does not guarantee that previous and future stores will be perceived by other processors in the locally issued order — that requires one of the sync instructions. One reason isync may be more efficient is that it involves only processor-local waiting, for the instruction pipeline to empty sufficiently; it does not itself require cache coherence activity.
17The names of variables are different from Arora et al [1998], and the algorithm here calls the local end’s index top and the opposite end’s index tail, so as to correspond better with the view that the local end of the deque is a stack and the other end is the tail (removal point) of a queue.