The heart of an automatic memory management system is the collector and allocator, their algorithms and data structures, but these are of little use without suitable means to access them from a program or if they themselves cannot appropriately access the underlying platform. Furthermore, some algorithms impose requirements on the programming language implementation, for example to provide certain information or to enforce particular invariants. The interfaces between the collector (and allocator) and the rest of the system, both the language and compiler above and the operating system and libraries beneath, are the focus of this chapter.
We consider in turn allocating new objects; finding and adjusting pointers in objects, global areas and stacks; actions when accessing or updating pointers or objects (barriers); synchronisation between mutators and the collector; managing address space; and using virtual memory.
From the point of view of a programming language, a request for a new object returns an object that is not only allocated, but also initialised to whatever extent the language and its implementation require. Different languages span a large range of requirements. At one end of the spectrum is C, which requires only a freshly allocated cell of storage of the requested size — the values in that cell are arbitrary and initialising the cell is entirely the programmer’s responsibility. At the other end of the spectrum lie pure functional languages such as Haskell, where at the language level one must provide values for all the fields of a new object, and it is not possible to perceive an uninitialised object. Languages more concerned with type safety require proper initialisation of all fields, either by requiring the programmer to provide (or assign) values, or by using safe defaults for each type or through some combination of these techniques.
For our purposes we break allocation and initialisation down into three steps, not all of which apply in every language or case.
1. Allocate a cell of the proper size and alignment. This is the job of the allocation subsystem of the memory manager.
2. System initialisation. By this we mean the initialisation of fields that must be properly set before the object is usable in any way. For example, in object-oriented languages this might include setting the method dispatch vector in the new object. It generally also includes setting up any header fields required by either the language, the memory manager or both. For Java objects this might include space for a hash code or synchronisation information, and for Java arrays we clearly need to record their length somewhere.
3. Secondary initialisation. By this we mean to set (or update) fields of the new object after the new object reference has ‘escaped’ from the allocation subsystem and has become potentially visible to the rest of the program, other threads and so on.
Consider the three example languages again.
• C: All the work happens in Step 1; the language neither requires nor offers any system or secondary initialisation — the programmer does all the work (or fails to). Notice, though, that allocation may include setting up or modifying a header, outside of the cell returned, used to assist in freeing the object later.
• Java: Steps 1 and 2 together provide an object whose method dispatch vector, hash code and synchronisation information are initialised, and all fields set to a default value (typically all zeroes). For arrays, the length field is also filled in. At this point the object is type safe but ‘blank’. This is what the new bytecode returns. Step 3 in Java happens in code provided inside a constructor or static initialiser, or even afterwards, to set fields to non-zero values. Even initialisation of final fields happens in Step 3, so it can be tricky to ensure that other threads do not see those fields change if the object is made public too soon.
• Haskell: The programmer provides the constructor with values for all fields of the requested object, and the compiler and memory manager together guarantee complete initialisation before the new object becomes available to the program. That is, everything happens in Steps 1 and 2, and Step 3 is disallowed. ML works the same way for object creation, even though it offers mutable objects as a special case, and Lisp is likewise biased towards functional creation of objects even though it also supports mutation.
If a language requires complete initialisation, like Haskell and ML, then there is a bit of a problem defining the interface to allocation: there is an essentially infinite variety of signatures for allocating, depending on the number of fields and their types. The implementers of Modula-3, which allows functional-style initialisation of new objects but does not require it, solved the problem by passing an initialising closure to the allocation subroutine. Allocation then acquires the necessary storage and invokes the initialising closure to fill in the new object. The closure has access to the values to insert and code to copy those values into the object. Given the static scoping of Modula-3, such closures do not themselves require heap allocation, but only a static chain pointer (reference to the enclosing environment’s variables) — a good thing, since otherwise there might be an infinite regress. However, if the compiler generates the initialisation code for these languages, whether the initialisation happens ‘inside’ the allocation routine or outside does not matter.
The Glasgow Haskell Compiler solves the problem a different way: it inlines all of Steps 1 and 2, calling the collector if memory is exhausted. It uses sequential allocation so obtaining the cell is simple, and initialisation proceeds by setting the header word and the object’s fields, whose values were already calculated. This is an example of tight integration of a compiler and a particular approach to allocation (and collection).
Note that functional initialisation has two strong advantages: it helps ensure complete initialisation of objects and, provided that the initialisation code is effectively atomic with respect to possible garbage collection, it allows the initialising stores to avoid some write barriers. In particular one can omit generational write barriers in the functional initialisation case because the object being initialised must be younger than any objects to which it refers. In contrast, this is not generally true in Java constructors [Zee and Rinard, 2002].
A language-level request for a new object will eventually translate into a call to an allocation routine, which may sometimes be inlined by a compiler, to accomplish Step 1 and possibly some or all of Step 2. The key property that allocation needs to satisfy is that Steps 1 and 2 are effectively atomic with respect to other threads and to collection. This guarantees that no other component of the system will perceive an object that lacks its system initialisation. However, if we consider the interface to the allocator (Step 1), there remains a range of possibilities depending on the division of labour between Steps 1, 2 and 3. Arguments to an allocation request may include:
The size requested, generally in bytes, but possibly in words or some other granule size. When requesting an array, the interface may present the element size and the number of elements separately.
An alignment constraint. Typically there is a default alignment and a way to request an alignment that is more strict. These constraints may consist of only a power of two indication (word, double-word, quad-word alignment, and so on) or a power of two and an offset within that modulus (such as aligned on word two of a quad-word).
The kind of object to allocate. For example, managed run-time languages such as Java typically distinguish between array and non-array objects. Some systems distinguish between objects that contain no pointers and ones that may contain pointers [Boehm and Weiser, 1988]; objects containing executable code may also be special. In short, any distinction that requires attention by the allocator needs to appear at the interface.
The specific type of object to allocate, in the sense of programming language types. This is different from ‘kind’ in that it may not of itself be interesting to the allocator. Rather, the allocator may use it in initialising the object, and so forth. Passing this value in may simplify making Step 2 atomic (by moving the burden to Step 1) and may also reduce code size by avoiding one or more extra instructions at each allocation site.
Which of these arguments we need depends somewhat on the language we are supporting. Furthermore, we may present information somewhat redundantly at the interface to avoid forcing additional computation at run time. While it is possible to provide a single rich allocation function that takes many arguments and handles all cases, for speed and compactness we might provide a number of allocation functions, tailored to different kinds of object. Considering Java as an example, we might break it down into: scalar objects (non-arrays), arrays of byte/boolean (one-byte elements), arrays of short/char (two-byte elements), arrays of int/float (four-byte elements), arrays of references and arrays of long/double (eight-byte elements). Beyond this there may be internal things such as the objects that represent classes, method dispatch tables, method code and so on, depending on whether they are held in the collected heap. Even if they are not part of the collected, one still needs an interface to the explicit-free allocator that creates them.
Here are some of the possibilities for the post-condition that the allocator guarantees at the end of Step 1 if it succeeds.
• The referenced cell has the requested size and alignment — but is not otherwise prepared for use.
• Beyond having correct size and alignment, the cell is zeroed. Zeroing helps to guarantee that the program cannot treat old pointers — or non-pointer bit patterns for that matter — as valid references. Zero is a good value because it typically represents the null pointer and is otherwise a bland and legal value for most types. Some languages, such as Java, require zeroing or something similar for their security and type-safety guarantees. It can also be helpful in debugging a system if non-allocated memory has a specific non-zero bit pattern, such as 0xdeadbeef or 0xcafebabe, which are values we have actually seen.
• The allocated cell appears to be an object of the requested type. This is a case where we present the type to the allocator. The difference between this and the weakest post-condition (the first one in this list) is that the allocator fills in the object header.
• The allocator guarantees a fully type-safe object of the requested type. This involves both zeroing and filling in the object header. This is not quite the same as a fully initialised object in that zeroing provides a safe, but bland, default value, while a program will generally initialise at least one field to a non-default value.
• The allocator guarantees a fully initialised object. This may be less common, since the interface must provide for passing the initial value(s). A good example is the cons function in Lisp, which we might provide as a separate allocation function because calls to it are so common and need to be fast and simple from the program’s side.
What is the most desirable post-condition? Some aspects, such as zeroing, may be dictated by the language semantics. Likewise, some may be dictated by the level of concurrency in the environment and whether and how objects might ‘leak’ from an allocating thread and become visible to other threads or the collector. Generally, the more concurrent or leaky the setting, the stronger the post-condition we need.
What happens if the allocator cannot immediately satisfy the request? In most systems we want to trigger collection internally and avoid revealing this case to the caller. There is generally little that a caller can do, and it is wasteful to insert retry loops everywhere the program tries to allocate an object.1 However, especially in the presence of inlining, we might inline the common (successful) case and call a collect-and-retry function out of line. Of course if we inline Step 1, then there remains little distinction between Steps 1 and 2 — the overall code sequence must be effectively atomic. Later on we discuss handshaking between mutators and collectors, so as to achieve such atomicity. We note that for purposes of atomicity it is generally more appropriate to view allocation as a mutator activity.
Since many systems and applications tend to allocate at a high rate relative to the rest of their computation, it is important to tune allocation to be fast. A key technique is to inline the common case code (the ‘fast path’) and call out to ‘slow path’ code that handles the rarer, more complex cases. Making good choices here requires careful comparative measurements under suitable workloads.
An apparent virtue of sequential allocation is its simplicity, which leads to a short code sequence for the common case. This is especially true if the target processor provides enough registers to dedicate one to hold the bump pointer, and possibly one more to hold the heap limit. In that case the typical code sequence might be: move the bump pointer to the result register; add-immediate the needed size to the bump pointer; compare the bump pointer against the limit; conditionally branch to a slow path call. Notice that putting the bump pointer into a register assumes per-thread sequential allocation areas. Some ML and Haskell implementations further combine multiple allocations in a straight line (basic block) of code into one larger allocation, resulting in just one limit test and branch. The same technique can work for code sequences that are single-entry but multiple-exit by allocating the maximum required along any of the paths, or at least using that as the basis for one limit test on entry to the code sequence.
It might seem that sequential allocation is necessarily faster than free-list techniques, but segregated-fits can also be quite efficient if partially inlined and optimised. If we know the desired size class statically, and we keep the base pointer to the array of free-list pointers in a dedicated register, the sequence is: load the desired list pointer; compare it with zero; branch if zero to a slow path call; load the next pointer; store the next pointer back to the list head. In a multithreaded system the last step may need to be atomic, say a CompareAndSwap with branch back to retry on failure, or we can provide each thread with a separate collection of free-list heads.
Some system designs require that free space contain a distinguished value, often zero, for safety, or perhaps some other value (generally for debugging). Systems offering a weak allocation guarantee, such as C, may not do this, or may do it only as an option for debugging. Systems with a strong guarantee, such as functional languages with complete initialisation, do not need zeroing — though optionally setting free space to a special value may aid in system debugging. Java is the typical example of a language that requires zeroing.
How and when might a system zero memory? We could zero each object as we allocate it, but experience suggests that bulk zeroing is more efficient. Also, zeroing with explicit memory writes at that time may cause a number of cache misses, and on some architectures, reads may block until the zeroing writes drain from a hardware write buffer/store queue. Some ML implementations, and also Sun’s HotSpot Java virtual machine, prefetch ahead of the (optimised) bump pointer precisely to try to hide the latency of fetching newly allocated words into the cache [Appel, 1994; Gonçalves and Appel, 1995]. Modern processors may also detect this pattern and perform the prefetching in hardware. Diwan et al [1994] found that write-allocate caches that can allocate on a per-word basis offered the best performance, but these do not seem to be common in practice.
From the standpoint of writing an allocator, it is often best to zero whole chunks using a call to a library routine such as bzero. These routines are typically well optimised for the target system, and may even use special instructions that zero directly in the cache without fetching from memory, such as dcbz (Data Cache Block Zero) on the PowerPC. Notice that direct use of such instructions may be tricky since the cache line size is a model-specific parameter. In any case, a system is likely to obtain best performance if it zeroes large chunks that are power-of-two aligned.
Another technique is to use demand-zero pages in virtual memory. While these are fine for start up, the overhead of the calls to remap freed pages that we are going to reuse, and of the traps to obtain freshly zeroed real memory from the operating system, may be higher than zeroing pages ourselves. In any case, we should probably remap pages in bulk if we are going to use this technique, to amortise some of the cost of the call.
Another question is when to zero. We might zero immediately after collection. This has the obvious disadvantage of lengthening the collection pause, and the less obvious disadvantage of dirtying memory long before it will be used. Such freshly zeroed words will likely be flushed from the cache, causing write-backs, and then will need to be reloaded during allocation. Anecdotal experience suggests the best time to zero from the standpoint of performance is somewhat ahead of the allocator, so that the processor has time to fetch the words into the cache before the allocator reads or writes them, but not so far ahead of the allocator that the zeroed words are likely to be flushed. Given modern cache miss times, it is not clear that the prefetching technique that Appel described will work; at least it may need tuning to determine the proper distance ahead of the allocator that we should prefetch. For purposes of debugging, zeroing or writing a special value into memory should be done as soon as we free cells, to maximise the range of time during which we will catch errors.
Collectors need to find pointers in order to determine reachability. Some algorithmic tactics require precise knowledge of pointers. In particular, safely moving an object at location x to a new location x′ and reusing its original cell requires us to update all pointers to x to refer to x′. However, safely reclaiming an object demands certainty that the program will no longer use it, but the converse is not true: it is safe to retain an object that the program will never use again, although it is space-inefficient (which admittedly could cause a program to fail for lack of available heap). Thus a collector can estimate references to non-moving objects, as long as its estimates are conservative — it may only over-estimate the references to an object, not under-estimate them. Reference counting without cycle collection is conservative, but another way conservatism arises in some schemes is because they lack precise knowledge of pointers. Thus they may treat a non-pointer value as if it is a pointer, particularly if it appears to refer to an allocated object. We consider first techniques for conservative pointer finding, and then ones for accurately finding pointers in various locations.
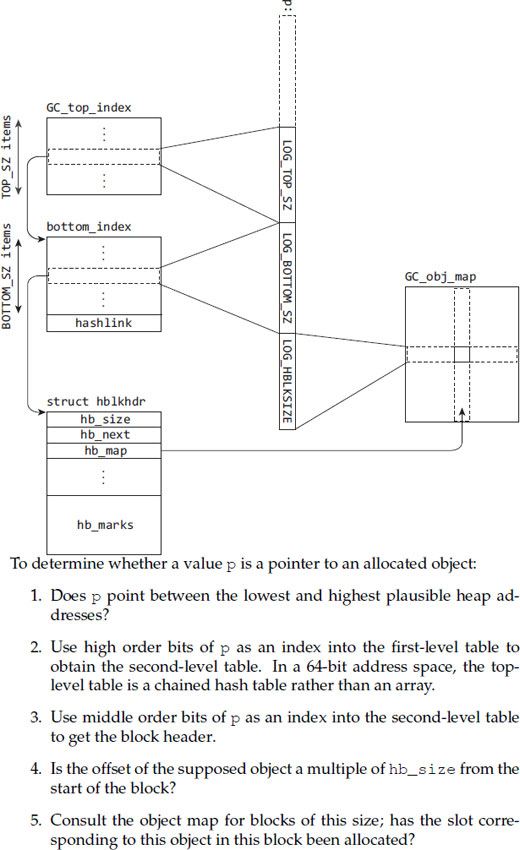
The foundational technique for conservative pointer finding is to treat each contiguous pointer-sized and aligned sequence of bytes as a possible pointer value, called an ambiguous pointer. Since the collector knows what memory regions compose the heap, and even which parts of those regions are allocated, it can discriminate possible pointers from values that cannot be pointers. For speed the collector’s algorithm for testing a pointer value’s ‘pointer-ness’ needs to be efficient. A typical approach works in two steps. First it filters out values that do not refer to any heap area in memory. It might do this with a range test if the heap is one contiguous area, or by taking the value’s upper bits, obtaining a chunk number and looking in a table of heap chunks. The second step is to see if the referenced storage in the heap is actually allocated. It might check that by consulting a bitmap of allocated words. For example, the Boehm-Demers-Weiser conservative collector [Boehm and Weiser, 1988] works in terms of blocks, with each block dedicated to cells of a particular size. A block has associated metadata giving the cell size, and also a bitmap indicating allocated versus free cells. After doing a range check using the heap bounds, this algorithm next checks to see of the referenced block is allocated at all, and if the block is allocated it checks whether the particular object is allocated. Only then will it set a mark bit in its marking phase. The whole process, illustrated in Figure 11.1, has a typical path length of about 30 RISC instructions.
Some languages require that pointers refer to the first word of their referent object, or some standard offset into the object, such as after some header words (see Figure 7.2). This allows a conservative collector to ignore possible interior pointer values as opposed to their canonical reference pointer. It is fairly easy to build conservative pointer finding algorithms in both cases; the Boehm-Demers-Weiser collector can be configured either way.2 One caution concerning conservative collection for C is that it is legal for an ‘interior’ reference to an array to point one element beyond the end of the array. Therefore, conservative collectors for C may need to retain two objects in that case, or else over-allocate arrays by one word to avoid possible ambiguity. An explicit-free system may interpose a header between objects, which also solves the problem. In the presence of compiler optimisations, pointers may be even further ‘mangled’; see page 183 for a discussion of this topic.
Figure 11.1: Conservative pointer finding. The two-level search tree, block header and map of allocated blocks in the Boehm-Demers-Weiser conservative collector.
Jones [1996]. Reprinted by permission.
Since a non-pointer bit pattern may cause the collector to retain an object that is in fact not reachable, Boehm [1993] devised a mechanism called black-listing, which tries to avoid using regions of virtual address space as heap when their addresses correspond to these kinds of non-pointer values. In particular, if the collector encounters a possible pointer that refers to memory in a non-allocated block, it black-lists the block, meaning it will not allocate the block. Were it to allocate the block (and an object at that address), future traces would mistakenly recognise the false pointer as a true pointer. The collector also supports blocks used for strictly non-pointer objects, such as bitmaps. Distinguishing this data not only speeds the collector (since it does not need to scan the contents of these objects), but it also prevents excessive black-listing that can result from the bit patterns of the non-pointer data. The collector further refines its black-listing by discriminating between invalid pointers that may be interior, and those that cannot be interior, because they are from the heap in the configuration that disallows heap-stored interior pointers. In the possibly-interior case, the referenced block is black-listed from any use, while in the other case the collector allows the block to be used for small non-pointer objects (this cannot cause much waste). To initialise the black-list, the collector does a collection immediately before the first heap allocation. It also avoids using blocks whose address ends in many zeroes, since non-pointer data in the stack often results in such values.
Accurate pointer finding using tagged values
Some systems, particularly ones based more on dynamic typing, include a tag with each value that indicates its type. There are two basic approaches to tagging: bit stealing and big bags of pages. Bit stealing reserves one or more bits, generally at the low or high end of each word, and lays out objects that can contain pointers in a word-oriented fashion. For example, on a byte-addressed machine with a word size of four bytes, we might steal two bits for tags. We force objects to start on a word boundary, so pointers always have their low two bits zero. We choose some other value(s) to indicate (say) integers. Supposing that we give integers word values with a low bit of one, we end up with 31-bit integers — bit-stealing in this way does reduce the range of numbers we can represent easily. We might use a pattern of 10 in the low bits to indicate the start of an object in the heap, for parsability (Section 7.6). Table 11.1 illustrates the sample tag encoding, which is similar to one used in actual Smalltalk implementations.
Dealing with tagged integers efficiently is a bit of a challenge, though arguably the common case on modern pipelined processors might not be that bad — one cache miss might swamp it. Still, in order to support dynamically typed language implementations that use tagged integers, the SPARC architecture includes instructions for adding and subtracting tagged integers. These instructions indicate overflow, and there are versions that trap as well, on overflow of the operation or if either operand’s two lowest bits are not zero. For this architecture we might use the tag encoding shown in Table 11.2. This encoding does require that we adjust references made from pointers, though in most cases that adjustment can be included in an offset field of a load or store instruction. The exception is in dealing with accesses to arrays, which then require the pointer to the array, the offset computed from the index and this additional adjustment. Still, given the hardware support for arithmetic on tagged integers, it seemed a reasonable trade-off. This encoding was previously used with the Motorola MC68000, which has a load instruction that adds an immediate constant, a base register and another register, all to form the effective address, so on the MC68000 there was no big penalty to using the encoding.
Tag |
Encoded value |
|
Pointer |
|
Object header |
|
Integer |
Table 11.1: An example of pointer tag encoding
Tag |
Encoded value |
|
Integer |
|
Pointer |
|
Other Primitive Value |
|
Object header |
Table 11.2: Tag encoding for the SPARC architecture
The big bag of pages approach to tagging associates the tag/type information with an entire block. This association is therefore typically dynamic and involves a table lookup. The need for memory references is a disadvantage, but the corresponding advantage is that numeric and other primitive values have their full native length. This tagging approach dedicates whole blocks to hold integers, other blocks to floating point numbers, and so on. Since these are pure values and do not change,3 when allocating new ones we might use hashing to avoid making new copies of the values already in the table. This technique, also called hash consing (from the Lisp cons function for allocating new pairs) is quite venerable [Ershov, 1958; Goto, 1974]. In hash consing Lisp pairs, the allocator maintains a hash table of immutable pairs and can avoid allocating a new pair if the requested pair is already in the table. This extends in the obvious way to any immutable heap-allocated objects, such as those of class Integer in Java. Notice that this is a case where it might be good to use weak references (Section 12.2) from the hash table to the objects it contains.
Accurate pointer finding in objects
Assuming we are not using tagged values, finding pointers in objects generally requires knowing each object’s type — at least in the sense of which fields of the object are pointers. In object-oriented languages, that is, those with dynamic method dispatch, where the actual run-time type of an object is not entirely determined by the type of the referring pointer variable or slot, we need type information associated with the particular object. Systems usually accomplish this by adding a header to each object that includes type information. Since object-oriented languages generally have a method dispatch vector for each type, and they generally store a pointer to that vector in the header of each object of that type, they typically store information about the type in, or pointed to by, the dispatch vector. Thus the collector, or any other part of the run-time that uses type information (such as the reflection mechanism in Java), can find the type information quite readily. What the collector needs is a table that indicates where pointer fields lie in objects of the given type. Two typical organisations are a bit vector, similar to a bitmap of mark bits, and a vector of offsets of pointer fields. Huang et al [2004] used a vector of offsets to particular advantage by permuting the order of the entries to obtain different tracing orders, and thus different orders of objects in a copying collector, improving cache performance. With care, they did this while the system was running (in a stop-the-world collector).
A way to identify pointers in objects that is simpler in some respects than using a table is to partition the pointer and non-pointer data. This is straightforward for some languages and system designs4 but problematic for others. For example, in ML objects can be polymorphic. If the system generates a single piece of code for all polymorphic versions, and the objects need to use the same field for a pointer in some cases and a non-pointer in others, then segregation fails. In object-oriented systems that desire to apply superclass code to subclass objects, fields added in subclasses need to come after those of superclasses, again leading to mixing of pointer and non-pointer fields. One way around that is to place pointer fields in one direction from the reference point in the object (say at negative offsets) and non-pointer fields in the other direction (positive offsets), which has been called bidirectional object layout. On byte-addressed machines with word-aligned objects, the system can maintain heap parsability by ensuring that the first header word has its low bit set — preceding words contain pointers, whose two low bits will always be zero (see US Patent 5,900,001). In practice the tabular approach does not seem to be a problem, and as Huang et al [2004] showed, it can actually be advantageous.
Some systems actually generate object-oriented style methods for tracing, copying and so on [Thomas, 1993; Thomas and Jones, 1994; Thomas, 1995a,b]. One can view the table approach as being like an interpreter and the method approach as the corresponding compiled code strategy. An interesting idea in Thomas’s line of work is the system’s ability, when copying a closure, to create a tailored version of the closure’s environment that omits elements of the environment that the particular function does not use. This saves space in copied environment objects, and perhaps more significantly, avoids copying unused parts of the environment. Cheadle et al [2004] also developed collection code specialised for each type of closure. Bartlett [1989a] applied the idea of methods for collection to C++ by requiring the user to write a pointer-enumerating method for each collected C++ class.
A managed language can use object-oriented indirect function calls in other ways related to collection. In particular, Cheadle et al [2008] dynamically change an object’s function pointer so as to offer a self-erasing read barrier in a copying collector, similar to the approach Cheadle et al [2000] used for the Glasgow Haskell Compiler (GHC). That system also used a version of stack barriers, implemented in a similar way, and it used the same trick again to provide a generational write barrier when updating thunks. A fine point of systems that update closure environments is that since they can shrink an existing object, in order to maintain heap parsability they may need to insert a ‘fake’ object in the heap after the one that shrank. Conversely, they may also need to expand an object: here the old version is overwritten with an indirection node, holding a reference to the new version. Later collections can short-circuit the indirection node. Collectors can also perform other computation on behalf of the mutator such as eager evaluation of applications of ‘well-known’ functions to arguments already partially evaluated: a common example is the function that returns the head of a list.
In principle, statically typed languages can avoid object headers and save space. Appel [1989b] and Goldberg [1991] explain how to do this for ML, starting from type information provided only for roots (we have to start some place). Later, Goldberg and Gloger [1992] observe that this might require full type inference during collection, depending on how the program uses polymorphic types; see also [Goldberg, 1992].
Accurate pointer finding in global roots
Finding pointers in global roots is relatively easy by applying almost any of the techniques mentioned for finding pointers in objects. Languages differ primarily in whether the set of global roots is entirely static or whether it can grow dynamically. Such dynamic growth can result from dynamic code loading. Some systems start with a base collection of objects. For example, Smalltalk, and some Lisp and some Java systems start with a base system ‘image’, also called the boot image, that includes a number of classes/functions and instances, particularly if they start with an interactive programming environment. A running program might modify parts of the system image — usually tables of one kind or another — causing image objects to refer to newer objects. A system might therefore treat pointer fields in the image as roots. Notice, though, that image objects can become garbage, so it may be a good idea sometimes to trace through the image to find what remains actually reachable. This is all tied into whether we are using generational collection, in which case we may treat the image as a particularly old generation.
Accurate pointer finding in stacks and registers
One way to deal with call stacks is to heap allocate activation records, as advocated by Appel [1987], for example. See also [Appel and Shao, 1994, 1996] and a counter-argument by Miller and Rozas [1994]. Some language implementations manage to make stack frames look like heap objects and thus kill two birds with one stone. Examples include the Glasgow Haskell Compiler [Cheadle et al, 2000] and Non-Stop Haskell [Cheadle et al, 2004]. It is also possible to give the collector specific guidance about the contents of the stack, for example as Henderson [2002] does with custom-generated C code for implementing the Mercury language, and which Baker et al [2009] improved upon for a real-time Java implementation.
However, most languages give stack frames special treatment because of the need for a variety of efficiencies in order to obtain best performance. There are three issues we consider:
1. Finding frames (activation records) within the stack.
2. Finding pointers within each frame.
3. Dealing with conventions concerning passing as arguments, returning, saving and restoring values in registers.
In most systems it is not just the collector that needs to find frames in the stack. Mechanisms such as exception handling and continuations may need to ‘parse’ the stack, not to mention the tremendous value of stack examination in debugging and its requirement in some systems, such as Smalltalk. Of course the view given to the programmer may be one very cleaned up from the typically more optimised and ‘raw’ layout in the actual frames. Because stack parsing is generally useful, frame layout conventions generally provide for it. For example, many designs include a dynamic chain field in each frame, which points to the previous frame. Various other fields generally lie at fixed offsets from the reference point of the frame (the address to which the frame pointer or dynamic chain refers). These might include the return address, the static chain and so on. Systems also generally provide a map to determine from a return address the function within which the address lies. In non-collected systems this might occur only in debugger symbol tables, but many managed systems access this table from the program, so it may be part of the loaded or generated information about code, rather than just in auxiliary debugger tables.
To find pointers within a frame, a system might explicitly add stack map information to each frame to help the collector. This metadata might consist of a bitmap indicating which frame fields contain pointers, or the system might partition a frame into pointer-containing and non-pointer portions, with metadata giving the size of each. Notice that there are likely to be some initial instructions of each function during which the new frame exists but is not yet entirely initialised. Collecting during this time might be problematic; see our later discussion of garbage collection safe points and mutator handshaking in Section 11.6. Alternatively we might get by with careful collector analysis of the initial code sequence, with careful use of push instructions on a machine that supports them or some other custom-designed approach. Obviously frame scanning is simpler if the compiler uses any given frame field always as a pointer or always as a non-pointer. That way the whole function needs only one map.
However, the single-map approach is not always possible. For example, at least two language features make it difficult:
• Generic/polymorphic functions.
• The Java Virtual Machine jsr instruction.
We previously observed that a polymorphic function may use the same code for pointer and non-pointer arguments. Since a straightforward stack map cannot distinguish the cases, the system needs some additional source of information. Fortunately the caller ‘knows’ more about the specific call, but it too may be a polymorphic function. So the caller may need to ‘pass the buck’ to its caller. However, this is guaranteed to bottom out, at the main function invocation in the worst case. The situation is analogous to typing objects from roots [Appel, 1989b; Goldberg, 1991; Goldberg and Gloger, 1992].
In the Java Virtual Machine, the jsr instruction performs a local call, which does not create a new frame but rather has access to the same local variables as the caller. It was designed to be used to implement the try-finally feature of the Java language, using a single piece of code to implement the finally block by calling it using jsr in both the normal and the exceptional case. The problem is that during the jsr call, some local variables’ types are ambiguous, in the sense that, depending on which jsr called the finally block, a particular variable, not used in the finally block but used later, might contain a pointer from one call site and a non-pointer from another. There are two solution approaches to this problem. One is to refer these cases to the calling site for disambiguation. In this approach rather than have each stack map entry be just ‘pointer’ or ‘non-pointer’ (that is, a single bit), we need an additional case that means ‘refer to jsr caller’. In addition we need to be able to find the jsr return address, which requires some analysis of the Java bytecode to track where it stored that value. An alternative, more popular in modern systems, is to transform the bytecode, or dynamically compile code, simply to duplicate the finally block. Whilst in pathological cases that might cause exponential blowup in code size, it substantially simplifies this part of the system. Anecdotal evidence suggests that generating Java stack maps for dynamically compiled code has been a significant source of subtle bugs, so managing system complexity here may be important. We note that some systems defer generating a stack map until the collector needs it, saving space and time in the normal case but perhaps increasing collector pause time.
Another reason that a system might choose not to use a single map per frame is that it further restricts the register allocator: it must use a given register consistently as a pointer or non-pointer. This is particularly undesirable on machines that have few registers in the first place.
Notice that whether we have one map per function, or different ones for different parts of a function, the compiler must propagate type information far through the back end. This may not be overly difficult if we understand the requirement before we write the compiler, but revising existing compilers to do it can be quite difficult.
Finding pointers in registers.
To this point we have ignored the issue of pointers in machine registers. There are several reasons why handling registers is more difficult than dealing with stack contents.
• As we pointed out previously, even if each stack frame field is fixed as a pointer or a non-pointer for a whole function, it is less convenient to impose that rule on registers — or to be even further restrictive and require that pointers, and only pointers, reside in a particular subset of the registers. It is probably practical only on machines that provide a large number of registers. Thus most systems will have more than one register map per function.
• Even when guaranteeing that no pointer stored in a global root, heap object or local variable is an interior (page 182) or derived (page 183) pointer, efficient local code sequences may result in a register holding such an ‘untidy’ pointer.
• Calling conventions often provide that some registers follow a caller-save protocol, in which the caller must save and restore a register if it wants the value to survive across a call, and that some other registers follow a callee-save protocol, in which the callee must save and restore a register, on behalf of callers deeper in the stack, before the callee can use the register. Caller-save registers are not a problem since the caller knows what kind of value is in them, but callee-save registers have contents known only to some caller up the stack (if any). Thus a callee cannot indicate in a register map whether or not an unsaved callee-save register contains a pointer. Likewise, if a callee saves a callee-save register to a frame field, the callee cannot say whether that field contains a pointer.
A number of systems require a callee-save stack unwinding mechanism as a matter of course, in order to reconstruct the frame structure of the stack and call chain, especially for systems that do not designate a ‘previous frame’ register and the like.
We now introduce an approach to the callee-save registers problem. First, we add metadata that indicates for each function which callee-save registers it saves, and where in its frame it saves them. We assume the more common design where a function saves in one go, near the beginning of the function, all callee-save registers that it will use. If the compiler is more sophisticated and this information varies from place to place within a function, then the compiler will need to emit per-location callee-save information.
Starting with the top frame, we reconstruct the register state for each frame by ‘unsaving’ a callee’s saved callee-save registers to obtain the register state of the caller at the point of call. As we go, we record which registers we ‘unsaved’ and the value that the callee had in them, for use as we come back up the stack. When we reach the base of the stack, we can ignore any saved callee-save register contents since there is no caller. Therefore, for that frame we can produce any pointers for the collector, and allow it to update them.
As we walk back up the stack, we re-save the callee-save registers. Notice that if the collector updated a pointer, then this will update the saved value appropriately. We get from our side memory the value that the callee had in the register. Once we have done this for all callee-save registers saved by the callee, we produce pointers for the callee, and allow the collector to update them as necessary. However, we should skip any registers whose contents we processed in the caller, to avoid processing them a second time. In some collectors, processing the same root more than once is not harmful; mark-sweep is an example since marking twice is not a problem. However, in a copying collector it is natural to assume that any unforwarded referent is in fromspace. If the collector processes the same root twice (not two different roots referring to the same object) then it would make an extra copy of the tospace copy of the object, which would be bad.
We offer details of this process in Algorithm 11.1, and now proceed to describe the example illustrated in Figure 11.2. In the algorithm, func is the function applied to each frame slot and register, for example the body of the for each loop in markFromRoots of Algorithm 2.2 (Mark-Sweep, Mark-Compact) or the body of the root scanning loop in collect of Algorithm 4.2 (Copying).
Considering Figure 11.2a, notice first the call stack, which appears shaded on the right. The sequence of actions leading to that stack is as follows.
1. Execution begins at main with r1 containing 155 and r2 containing 784. Whatever effectively called main is outside the scope of the collected system, so it cannot refer to heap allocated objects and those register contents therefore cannot be references. Likewise we are not interested in the return address oldlP. As it executed, main saved r1 in slot 1 and set local 2 to refer to object p and local 3 to hold 75. It then called f with r1 containing p, r2 containing 784 and a return address of main + 52.
2. Function f saved the return address, saved r2 in slot 1 and r1 in slot 2, and set local 3 to -13 and local 4 to refer to object q. It then called g with r1 containing a reference to object r, r2 holding 17 and a return address of f + 178.
3. Function g saved the return address, saved r2 in slot 1, and set local 2 to refer to object r, local 3 to hold -7 and local 4 to refer to object s.
The register contents above each frame’s box indicate the values as execution entered the function in question, and the contents below the frame’s box the values when that frame suspended execution. These are the values that our unwinding procedure should attempt to recover.
We now assume that a garbage collection occurs in the middle of g.
4. Garbage collection occurs at location g + 36 in g, when register r1 contains a reference to object r and r2 a reference to object t. One can think of the IP and register values as being stored in a suspended thread data structure or perhaps in an actual frame for the garbage collection routine.
At some point garbage collection calls processStack on this thread stack, with func being the copy function of a copying collector. This is the most interesting case, since a copying collector will generally update object references because the target object moved. The boxes to the left in Figure 11.2a show the values of Regs and Restore as we proceed to examine the frames in the order g, f, main. We show numbered snapshots of Restore and Regs on the left in the figure, labelled with the numbers corresponding to these comments:
5. Here processStack has retrieved registers from the thread state into Regs and initialised Restore. Execution is at line 15 in Algorithm 11.1 for the frame for g.
Algorithm 11.1: Callee-save stack walking
1 processStack(thread, func):
2 Regs ← getRegisters(thread) | /* register contents thread would see */ |
3 Done ← empty | /* no registers processed yet */ |
4 Top topFrame(thread)
5 processFrame(Top, Regs, Done, func)
6 setRegisters(thread, Regs) | /* get corrected register contents back to thread */ |
7
8 processFrame(Frame, Regs, Done, func):
9 IP ← getip(Frame) | /* current instruction pointer (IP) */ |
10 Caller ← getCallerFrame(Frame)
11
12 if Caller ≠ null
13 Restore ← empty | /* holds info to restore after doing caller */ |
14
15 /* Update Regs to Caller’s view at point of call */
16 for each 〈reg,slot〉 in calleeSavedRegs(lP)
17 add(Restore, 〈reg, Regs[reg]〉)
18 Regs[reg] getSlotContents(Frame, slot)
19 processFrame(Caller, Regs, Done, func)
20
21 /* Write updated saved callee-save register value back to slots */
22 for each 〈reg, slot〉 in calleeSavedRegs(IP)
23 setSlotContents(Frame, slot, Regs[reg])
24
25 /* Update Regs to our view, adjusting Done */
26 for each 〈reg, value〉 in Restore
27 Regs[reg] ← value
28 remove(Done, reg)
29
30 /* process our frame’s pointer slots */
31 for each slot in pointerSlots(lP)
32 func(getSlotAddress(Frame, slot))
33
34 /* process our frame’s pointers in registers */
35 for each reg in pointerRegs(lP)
36 if reg ∉ Done
37 func(getAddress(Regs[reg]))
38 add(Done, reg)
6. Here we have updated Regs, and saved information into Restore for later use. Execution is at line 19 for g’s frame. Since g had saved r2 into slot 1, the proper value for f to see is 17. We save into Restore the fact that g’s view of r2 should be t, when we get back to handling g after the recursive call of processFrame. We show the pairs returned by calleeSavedRegs for g’s IP value in a box to the left of g’s frame.
7. Execution is at line 19 for f’s frame. We ‘un-saved’ both r1 and r2 in this case, from slots 2 and 1 respectively.
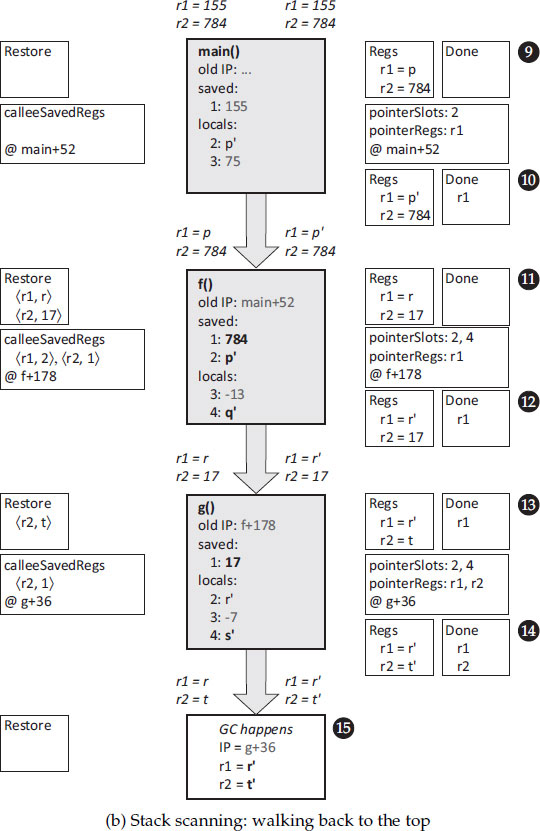
Figure 11.2: Stack scanning
8. Execution is at line 19 for main’s frame. Here we assume that Caller is null, so we do not ‘un-save’ any callee-saved registers — they cannot contain pointers since their values come from outside the managed universe.
Having reconstructed the register contents that held just as main called f, we can proceed to process the frame and registers for main, and likewise handle f and g. Turning to Figure 11.2b, we illustrate two states for each frame: first the state at line 35 of Algorithm 11.1 and then the state after line 38. The frames themselves show the state at line 35. Those values that are written, though their value is not necessarily changed, are in boldface; those not written are grey.
9. Regs holds the register values at the point main called f; as yet, Done is empty.
10. Register r1 was updated by func (because r1 is in pointerRegs for main + 52). Done indicates that r1 refers to a (possibly) new location of its referent object.
11. Regs holds the register values at the point where f called g. Notice that the values of r1 and r2 are saved into slots 2 and 1 of f’s frame and their values in Regs have been set from Restore.
12. Register r1 was updated by func and added to Done.
13. Regs holds the register values at the point garbage collection occurred in g. Specifically, the value in r2 is saved into slot 1 of g’s frame and its value in Regs has been set from Restore. Since r1 has not been set from Restore, r1 remains listed in Done.
Algorithm 11.2: Stack walking for non-modifying func
1 processStack(thread, func):
2 Top ← topFrame(thread)
3 processFrame(Top, func)
4 Regs ← getRegisters(thread) | /* register contents thread would see */ |
5 for each reg in pointerRegs(IP) | /* trace from registers at GC point */ |
6 func(getAddress(Regs[reg]))
7
8 processFrame(Frame, func):
9 Done ← empty
10 loop
11 IP ← getiP(Frame) | /* current instruction pointer (IP) */ |
12
13 /* process our frame’s pointer slots */
14 for each slot in pointerSlots(IP)
15 func(getSlotAddress(Frame, slot))
16
17 /* process our frame’s pointers in registers */
18 for each reg in pointerRegs(lP)
19 if reg ∉ Done
20 func(getAddress(Regs [reg]))
21 add(Done, reg)
22
23 Caller getCallerFrame(Frame)
24 if Caller = null
25 return
26
27 /* Update Regs to Caller’ s view at point of call */
28 for each (reg,slot) in calleeSavedRegs(IP)
29 Regs[reg] ← getSlotContents(Frame, slot)
30 remove(Done, reg)
31
32 Frame ← Caller
14. Register r1 was skipped (because it was in Done), but r2 was updated by func and added to Done
Finally, in step 15 processStack stores the values in Regs back to the thread state.
Variations on Algorithm 11.1. There are a number of reasonable variations on Algorithm 11.1. Here are some of particular interest:
• If func will not update its argument then one can omit the Done data structure, the statements that update it, and the conditional test on line 36, invoking func unconditionally on line 37. This simplification applies for non-moving collectors and non-moving phases of moving collectors. It also applies if a moving collector’s implementation of func works correctly if invoked on the same slot more than once.
• Rather than calling func late in processFrame, one can move the two for loops at the end upwards, inserting them after line 9. If combined with variation one, the resulting algorithm needs to process the stack only in one direction, which allows an iterative implementation as opposed to a recursive one, as shown in Algorithm 11.2.
Algorithm 11.3: No callee-save stack walking
1 processStack(thread, func):
2 Top ← topFrame(thread)
3 processFrame(Top, func)
4 Regs ← getRegisters(thread) | /* register contents thread would see */ |
5 for each reg in pointerRegs(IP) | /* trace from registers at GC point */ |
6 func(getAddress(Regs[reg]))
7 setRegisters(thread, Regs) | /* get corrected reg contents back to thread */ |
8
9 processFrame(Frame, func):
10 repeat
11 IP ← getiP(Frame) | /* current instruction pointer */ |
12 for each slot in pointerSlots(IP) | /* processframe’ s pointer slots */ |
13 func(getSlotAddress(Frame, slot))
14 Frame ← getCallerFrame(Frame)
15 until Frame = null
• If the system does not support callee save registers, and a function desires a register’s contents to be preserved across a call, then the function must save and restore the register itself (caller-save). A saved caller-save register value will have a type known in the caller, so one can treat it just like a local or temporary variable. This results in the substantially simplified Algorithm 11.3, which is also iterative.
Compressing stack maps. Experience shows that the space needed to store stack maps can be a considerable fraction of the size of the code in a system. For example, Diwan et al [1992] found their tables for Modula-3 for the VAX to be 16% of the size of code, and Stichnoth et al [1999] reported their tables for Java to be 20% of the size of x86 code. Tarditi [2000] describes techniques for compressing these tables, and applies them in the Marmot Java compiler, achieving a compression ratio of four to five and final table sizes averaging 3.6% of code size. The approach exploits two empirical observations.
• While there may be many garbage collection points (GC-points) needing maps, many of those maps are the same. Thus a system can save space if multiple GC-points share the same map. In the Marmot system this is particularly true of call sites, which tend to have few pointers live across them. Tarditi [2000] found that this technique cut table space in half.
• If the compiler works to group pointers close together in stack frames, then even more maps tend to be the same. Using live variable analysis and colouring to place pointer variables with disjoint lifetimes into the same slot also increases the number of identical maps. Tarditi [2000] found this to be important for large programs.
The overall flow of Tarditi’s scheme is as follows.
1. Map the (sparse) set of return addresses to a (smaller, denser) set of GC-point numbers.5 In this mapping, if table entry t[i] equals return address ra, then ra maps to GC-point i.
2. Map the set of GC-point numbers to a (small dense) set of map numbers. This is useful because multiple GC-points often have the same map. Given the GC-point i above, this can be written as map number mn=mapnum[i].
3. Index into a map array using the map number to get the map information. Given mn from the previous step, this can be written as info=map[mn].
In Tarditi’s scheme the map information is a 32-bit word. If the information fits in 31 bits, then that word is adequate and its low bit is set to 0; otherwise, the low bit is set to 1 and the remaining bits point to a variable-length record giving the full map. The details probably need to be retuned for different platforms (language, compiler, and target architecture), so refer to the paper for the exact encoding.
Tarditi also explored several organisations for mapping IP (instruction pointer) values to GC-point numbers.
• Using the same number for adjacent GC-points whose stack maps are the same, a technique also used by Diwan et al [1992]. This records only the first GC-point, and subsequent ones whose address is less than the next address in the table are treated as being equivalent.
• Using a two-level table to represent what is conceptually a large array of GC-point addresses. This builds a separate table for each 64 kilobyte chunk of code space. Since all GC-points in the chunk have the same upper bits, it needs to record only the low 16 bits in each table entry. In a 32-bit address space this saves essentially half the table space. We also need to know the GC-point number for the first GC-point in a chunk; simply adding this to the index of a return address within the chunk’s table will get the GC-point number for the matching IP.
• Using a sparse array of GC-points and interpolating by examining the code near the IP value. This chooses points roughly k bytes apart in the code, indicating where these places are, their GC-point number and their map number. It starts from the highest location preceding the IP value, and disassembles code forward. As it finds calls (or other garbage collection points), it updates the GC-point number and map number. Notice that it must be able to recognise GC-points by inspection. Tarditi found that even for the x86 the disassembly process for these purposes was not overly complex or slow, though the scheme includes a 16 element cache to reduce repeated computation for the same return address values. It was the most compact of the schemes examined and the disassembly overhead was small.
Stichnoth et al [1999] described a different stack map compression technique, oriented towards being able to produce a map for every instruction. Similar to the sparse array of Tarditi [2000], this uses a scheme that records full information for certain reference points in the code, and then disassembles forward from the nearest preceding point to the IP value of interest. In Stichnoth et al, though, it is the actual map they compute, as opposed to the GC-point number. The reference points at which it starts are (roughly) the beginning of basic blocks in the code. However, if the map at the end of one block is the same as the map at the beginning of the next one — that is, there was no flow merge that affected the map — then they treat the two blocks as one large block. Working forward from each reference point, they encode the length of the instruction at that point (because the x86 has variable length instructions) and the delta to the map caused by the instruction. For example, the instruction might push or pop a value on the stack, load a pointer into a register, and so on. They Huffman code the delta stream to obtain additional compression. Across a suite of benchmarks they get an average map size of about 22% of code size. They argue that, as a fraction of code size, the situation should not be worse for machines with larger register sets — the instructions increase in size too. Also, the overall space used might be somewhat better for machines with fixed-length instructions, since there is still a noticeable overhead for recording instruction lengths, even though (like Tarditi [2000]) they use a disassembler in most cases to avoid recording instruction lengths. They still need a fraction of a bit to mark those places where they cannot legally allow garbage collection, such as in the middle of the sequence for a write barrier. Given that a fixed-length instruction machine probably uses something like four bytes for each instruction, and the average instruction length for the x86 may be half that or less, the table size for a fixed-length instruction machine using the techniques of Stichnoth et al may be more in the range of 5–10% of code size.
Accurate pointer finding in code
Code may contain embedded references to heap allocated objects, particularly in managed run-time systems that load or generate code dynamically. Even code compiled ahead of time may refer to static/global data, that might lie in an initially loaded heap. There are several difficulties around pointers within code:
• It is not always easy, or even possible, to distinguish code from any data embedded within it.
• As in the case of uncooperative compilers, it is not generally possible to tell embedded pointers from non-pointer data that happen to have a value that looks as if it refers to a location in the heap.
• When embedded in instructions, a pointer may be broken into smaller pieces. For example, on the MIPS processor, loading a 32-bit static pointer value into a register would typically require a load-upper-immediate instruction, which loads a 16-bit immediate field into the upper half of a 32-bit register and zeroes the low 16-bits, and then an or-immediate of another 16-bit value into the lower half of the register. Similar code sequences occur for other instruction sets. This is a particular case of derived pointers (page 183).
• An embedded pointer value may not refer directly to its target object; see our discussions of interior (page 182) and derived (page 183) pointers.
In some cases one may be able to disassemble code to find embedded pointers, but going through all the code each time the collector needs to process the roots may have a large overhead. Of course, the program cannot update such embedded pointers, so caching their locations would be effective.
The more general solution is to arrange for the compiler to generate a side table that indicates where embedded pointers lie in the code.
Some systems simply rule out embedded pointers to avoid the issues altogether. The impact on code performance will vary according to target architecture, compilation strategy, and statistics of programs’ accesses.
Target objects that move. If the target of an embedded reference moves, then the collector must update the embedded reference. One possible difficulty is that for safety or security reasons code areas may be read-only. Thus the collector must either change the permissions temporarily (if possible), which might involve expensive system calls, or the system must disallow embedded references to moving objects. Another difficulty is that updating code in main memory generally does not force updates or invalidations of copies of that code residing in instruction caches. The solution is to require all processors to invalidate the affected instruction cache lines. Some machines may need to follow this by a special synchronisation instruction that guarantees that future instruction fetches occur logically after the invalidations. Furthermore, before invalidating instruction cache lines, one may need to force modified lines in the data cache (holding the bytes of code that were updated) to main memory, and synchronise to make sure that the writes are complete. The details are architecture specific.
Code that moves. A particular case of targets that move is code that a collector moves. Not only must this take into account the concerns that we just considered, but it must also fix up return addresses that lie in the stack and registers since they might refer to code that the collector is moving. Further, it must invalidate all instruction cache lines corresponding to the new location of the code and perform the careful code writing steps we enumerated above. Clearly it would be more deeply problematic if the code of the collector itself could move. Finally, moving code is particularly difficult in the case of concurrent collectors. Either the collector must stop the world, or arrange that threads can use either the old or the new copy of the code, move them to the new code over a period of time, and reclaim the space of the old code only after it knows all the threads have moved over.
An interior pointer is a pointer that refers to some location inside an object, but not necessarily using the standard reference to the object. More precisely, we consider each object to occupy a set of memory locations (addresses), disjoint from those of any other object. An interior pointer to an object refers to one of the object’s locations. If we consider Figure 7.2 we see that an object’s standard reference may not correspond to any of its interior pointers! Also, the set of locations an object occupies may be larger than just the locations holding its programmer-visible data. For example C allows pointers one location beyond the end of an array and that reference is still a legal interior pointer to the array.
While it is possible that a system might break a language-level object up into multiple pieces (as done by, for example, Siebert [1999]), for the purpose of handling interior (and derived) pointers we use the term ‘object’ to mean a contiguous range of locations devoted to representing a particular (language-level) object.
The key problem the collector faces with an interior pointer is determining the object to which the pointer refers, that is, how to compute the standard reference to the object from the value of the interior pointer. Several approaches are possible.
• Provide a table that records the start of each object. A system might maintain an array of object start addresses, perhaps in two-level form as done by Tarditi [2000] for recording GC-point addresses in code (see Section 11.2). Another way is to use a bitmap with one bit per granule (unit of allocation), setting the corresponding bit for granules that are the first granules of objects. This might be useful for the allocator and collector in any case.
• If the system supports heap parsability (Section 7.6), then one can scan the heap to find the object whose locations contain the target of the interior pointer. It would be prohibitively expensive to search from the beginning of the heap every time, so typically a system records the first (or last) object-start position within each k-byte chunk of the heap, where k is usually a power of two for convenient and efficient calculation. This allows parsing to start in the chunk to which the interior pointer refers, or the previous chunk as necessary. There is a trade-off between the space used for this side table and the overhead of parsing. For a more detailed discussion see Section 11.8.
• A big bag of pages organisation can determine object size by looking up the target block’s metadata. It can compute the offset of the target within the block (simply mask so as to keep the appropriate lower bits of the address), and round that down using the object size to determine the first location of the object.
We do assume that given knowledge of the set of locations occupied by the target object, the collector can determine the standard reference and work from there. Notice that if the object moves, as in a copying collector, then we need to update the interior pointer, moving it by the same amount, that is, causing it to refer to the same relative position in the moved object as it did in the old copy. Alternatively, the system might support pinning of objects, as discussed in Section 11.4.
The primary objection to dealing with interior pointers is the space and time overhead they can add to processing. If interior pointers are relatively rare and distinguished from tidy pointers (those that refer to an object’s standard reference point), then the time overhead of dealing with the interior pointers themselves may not be great. However, making provision for them at all may add space cost for tables — though the particular collector design may include the necessary tables or metadata anyway — and add time cost for maintaining the tables.
Return addresses are a particular case of interior pointers into code. They present no special difficulty, though for a variety of reasons the tables for looking up the function containing a particular return address may be distinct from the tables the collector uses for other objects.
Diwan et al [1992] identified what they call derived pointers, that is, values that are derived from one or more pointers via an arithmetic expression. Interior pointers are a special case where the expression has the simple form p + i or possibly p + c where p is a pointer, i is a dynamically computed integer offset and c is a statically known constant. However, for an interior pointer the resulting expression value must be an address within the set of locations of object p, which leads to the simpler solutions already discussed. Derived pointers can be much more general, for example:
• upperk(p) or lowerk(p), the upper or lower k bits of the pointer p.
• p ± c such that the resulting address lies outside of the locations of p.
• p − q, the distance between two objects.
In some cases we can reconstruct a tidy pointer — one that points to the referent’s standard reference address — from the derived pointer. An example is p + c where c is a compile-time known constant. In the general case we must have access to the base expression from which the derived pointer was derived. That expression might itself be a derived pointer, but eventually gets back to tidy pointers.
In a non-moving collector, just having the tidy pointers available as roots is enough. Notice, though, that at a GC-point the tidy pointer may no longer be live in the sense of compiler live variable analysis, even though the derived pointer is live. Thus the compiler must keep at least one copy of the tidy pointer(s) for each live derived pointer. An exception to this rule is the p ± c case since adjusting with a compile-time known value produces the tidy pointer without reference to other run-time data.
For a moving collector we need additional compiler support: the compiler needs to produce extended stack maps that give, for each derived pointer, the locations of the expressions from which it was derived and the operations needed to reconstruct the derived pointer. Diwan et al [1992] give details on handling derived quantities of the form where the pi and qj are pointers or derived values and E is an expression not involving pointers (and thus not affected if any of the pi or qj move). The advantage of this form is that it can subtract out the pi and add in qj, forming E before moving any objects; do any moving; then add back the new and subtract off the new to produce the correct adjusted derived pointer.
Diwan et al [1992] point out several issues that arise in optimising compilers when trying to handle derived pointers, including dead base variables (which we mentioned above), multiple derivations reaching the same point in code (for which they add more variables to record the path that actually pertains), and indirect references (where they record the value in an intermediate location along the chain of references). Supporting derived pointers sometimes required producing less optimal code, but the impact was slight. They achieved table sizes about 15% the size of code for Modula-3 on the VAX.
For reasons of mutator speed and space consumption, many systems have represented object references as direct pointers to their referent objects. A more general approach is to give each object a unique identifier and to locate its contents via some mapping mechanism. This has been of particular interest when the space of objects is large, and possibly persistent, but the hardware’s underlying address space is small in comparison. The focus here is on heaps that fit into the address space. Even in that case, however, some systems have found it helpful to use object tables. An object table is a generally dense array of small records, which refer to objects. An object table entry may contain only a pointer to the object’s data, or it may also contain additional status information. For speed, an object reference is typically either a direct index into the object table or else a pointer to an object table entry. Using an index makes it easier to relocate the table, but requires adding the object table base in order to access an entry — which may not cost additional instructions provided that the system dedicates a register to point to the base of the table.
A significant advantage of object tables is that they permit straightforward compaction, or indeed moving of any object, by simply moving the object(s) and then updating its object table entry to reflect its new location. To simplify this, each object should have a hidden self-reference field (or back pointer to its object table entry), to make it possible to find the table entry from the object’s data. Given that information, a mark-compact collector can proceed by marking as usual (modulo the level of indirection imposed by the object table) and then doing a simple sliding compaction of the object data. Free object table entries can simply be chained into a free-list. Notice that in marking it may be advantageous to keep mark bits in object table entries, so as to save a memory reference when checking or setting the mark bit. A side mark bitmap has similar benefits. It can also be advantageous to keep other metadata in the object table entry, such as a reference to class and size information.
It is also possible to compact the object table itself, for example using the Two-Finger algorithm of Section 3.1. This can be done together with compacting the object data, requiring only one pass over the data in order to compact both the data and the object table.
Object tables may be problematic, or simply unhelpful, if the language allows interior or derived pointers. Note also the similarity of object table entries to handles as used to support references from external code to heap objects, as discussed in Section 11.4. If a language disallows interior pointers, then whether or not the implementation uses an object table should not affect semantics of the implementation. However, there is one language feature that more or less assumes an object table for its efficient implementation: the Smalltalk become: primitive. This operator causes two objects to swap their roles in the object universe. This is easy to do with object tables: the system merely swaps the contents of two table entries. Without an object table a become: may require a sweep over the entire heap. If used sparingly (Smalltalk typically uses become: to install a new version of something) this may remain acceptable, particularly because direct object reference implementations are generally faster than object table ones.
11.4 References from external code
Some languages and systems support use of heap allocated objects from outside of the managed environment. A typical example is the Java Native Interface, which allows code written in C, C++ or possibly other languages to access objects in the Java heap. More generally, just about every system needs to support input/output, which must somehow move data between the operating system and heap objects. Two difficulties arise in supporting references from external code and data to objects in a managed heap. The first issue is ensuring that the collector continues to treat an object as reachable while external code possesses a reference to the object. This is necessary to prevent the object from being reclaimed before the external code is done with it. Often we need the guarantee only for the duration of a call to external code. We can make that guarantee by ensuring that there is a live reference to the object in the stack of the calling thread.
However, sometimes the object will be used by external code for a period of time that extends beyond an initial call. In that case the usual solution is for the collector to maintain a table of registered objects. The external code is required to register an object if the code will use the object after the current call. The external code must also explicitly deregister the object when the code no longer needs the object and will not attempt further use of it. The collector simply treats entries in the registered-object table as additional roots.
The second issue is ensuring that external code knows where an object is. This is relevant only to moving collectors. Some interfaces keep external code at arms length by requiring all accesses to heap objects to go through collector-provided access routines. This makes it easier to support collectors that move objects. Typically the collector provides to external code a pointer to a handle. The handle contains a reference to the actual heap object, and possibly some other management data. Handles act as registered-object table entries, and thus are roots for collection. The Java Native Interface works this way. Notice that handles are similar to entries in object tables.
While handles offer a clean separation of the managed heap from the unmanaged world, and they more easily admit collection techniques that move objects, not all external code is prepared to follow the access protocols, notably operating system calls. Thus it may be necessary to prevent externally referenced objects from moving. To support this, a pinning interface may offer pin and unpin operations, with the meaning that an object cannot be moved while it is pinned, and the further implication that pinned objects are reachable and will not be reclaimed.
If we know when allocating an object that it may need to be pinned, then we can allocate the object directly into a non-moving space. This may work for buffers for file stream I/O if the buffered-stream code allocates the buffers itself. However, in general it is difficult to determine in advance which objects will need to be pinned. Thus, some languages support pin and unpin functions that the programmer can invoke on any object.
Pinning is not a problem for non-moving collectors, but is inconvenient for ones that normally move an object. There are several solutions, each with its strengths and weaknesses.
• Defer collection, at least of a pinned object’s region, while it is pinned. This is simple, but there is no guarantee that it will be unpinned before running out of memory.
• If the application requests pinning an object, and the object is not in a non-moving region, we can immediately collect the object’s containing region (and any others required to be collected at the same time) and move the object to a non-moving region. This might be acceptable if pinning is not frequent, and the collector is of a design such as a generational collector with a nursery whose survivors are copied to a non-moving mature space.
• We can extend our collector to tolerate not moving pinned objects, which complicates the collector and may introduce new inefficiencies.
As a simple example of extending a moving collector to support pinning, consider a basic non-generational copying collector. Extending it to support pinned objects requires first of all that the collector can distinguish pinned from unpinned objects. It can copy and forward unpinned objects as usual. It will trace through pinned objects, updating pointers from the pinned object to objects that move, but leaving pinned objects where they are. The collector should also record in a table the pinned objects it encounters. When all survivors have been copied, the collector reclaims only the holes between pinned objects rather than reclaiming all of fromspace. Thus, rather than obtaining a single, large, free region, it may obtain an arbitrary number of smaller ones. The allocator can use each one as a sequential allocation space. This can lead to a degree of fragmentation, but that is unavoidable in the presence of pinning. Notice that a future collection may find that a previously pinned object is no longer pinned, so the fragmentation need not persist. As we saw in Section 10.3, some mostly non-moving collectors take a similar approach, also sequentially allocating in the gaps between surviving objects [Dimpsey et al, 2000; Blackburn and McKinley, 2008].
Another possible difficulty is that, even though an object is pinned, the collector is examining and updating it, which may lead to races with external code that accesses the object at the same time. Thus, we may need to pin not only a given object but also some of the objects to which it refers. Likewise, if, starting from a given object, external code traces through to other objects, or even just examines or copies references to them without examining the objects’ contents, those other objects also need to be pinned.
Features of a programming language itself, and its implementation, may require pinning. In particular, if the language allows passing object fields by reference, then there may be stack references to the interior of objects. The implementation can apply the interior pointer techniques described on page 182 in order to support moving the object containing the referent field. However, such support can be complex and the code for handling interior pointers correctly may thus be difficult to maintain. Therefore an implementation might choose simply to pin such objects. This requires being able to determine fairly easily and efficiently which object contains a given referent. Hence it most readily allows interior pointers but not more general cases of derived pointers (see page 183).
Earlier we described techniques for finding pointers in stacks, but assumed it was acceptable to scan the whole stack of a thread at once, that is, that the system could pause the thread long enough to process its entire stack. It is not safe to scan a frame in which a thread is actively running, so we must either pause the thread for some period of time or get the thread to scan for us (that is, call a scanning routine, essentially pausing itself) — see Section 11.6 for more discussion of when it is appropriate to scan a thread’s registers and stack. It is possible to scan a stack incrementally, however, and also mostly-concurrently, using a technique called stack barriers. The idea is to arrange for a thread to be diverted if it tries to return (or throw) beyond a given frame in its stack. Suppose we have placed a barrier in frame F. Then we can asynchronously process the caller of F, its caller, and so on, confident that the running thread will not cut the stack back from under our scanning.
The key step to introduce a stack barrier is to hijack the return address of the frame. In place of the actual return address we write the address of the stack barrier handler we wish to install. We put the original return address in some standard place that the stack barrier handler can find, such as a thread-local variable. The handler can then remove the barrier as appropriate. Naturally it must be careful not to disturb any register contents that the caller may examine.
For incremental stack scanning by the thread itself, when it encounters the barrier the handler scans some number of frames up the stack and sets a new barrier at the limit of its scanning (unless it finished scanning the whole stack). We call this synchronous incremental scanning. For asynchronous scanning by another thread, the barrier serves to stop the running thread before it overtakes the scanning thread. For its part, the scanning thread can move the barrier down after it scans some number of frames. That way it is possible that the running thread will never hit the barrier. If it does hit the barrier, then it merely has to wait for the scanning thread to advance and unset that barrier; then it can continue.
Cheng and Blelloch [2001] introduced stack barriers in order to bound the collection work done in one increment and to support asynchronous stack scanning. Their design breaks each stack into a collection of fixed size stacklets that can be scanned one at a time. That is, returning from one stacklet to another is the possible location of what we call a stack barrier. But the idea does not require discontiguous stacklets or predetermination of which frames can have a barrier placed on them.
Stack barriers can also be used in the opposite way from that described above: they can mark the portion of the stack that has not changed, and thus that the collector does not need to reprocess to find new pointers. In collectors that are mostly-concurrent this approach can shorten the ‘flip’ time at the end of a collection cycle.
Another use for stack barriers is in handling dynamic changes to code, particularly optimised code. For example, consider the situation where routine A calls B, which calls C, and there is a frame on the stack for an optimised version of A that inlined B but did not further inline C. In this situation there is a frame for A + B and another one for C. If the user now edits B, future calls of B should go to the new version. Therefore, when returning from C, the system should deoptimise A + B and create frames for unoptimised versions of A and B, so that when B also returns, the frame for A supports calling the new version of B. It might also be possible to re-optimise and build a new A + B. The point here is that returning to A + B triggers the deoptimisation, and the stack barrier is the mechanism that supports the triggering.
11.6 GC-safe points and mutator suspension
In Section 11.2 we mentioned that a collector needs information about which stack frame slots and which registers contain pointers. We also mentioned that this information can vary according to the specific code location (we will say IP, for instruction pointer) at which garbage collection happens in a function. There are two issues of concern about where garbage collection can happen: whether a given IP is safe for garbage collection, and the size of the stack map tables (see Section 11.2 for details on compressing maps), which tend to be large if more IPs are legal for garbage collection.
What might make a given IP unsafe for garbage collection? Most systems have occasional short sequences of code that must be run in their entirety in order to preserve invariants relied on by garbage collection. For example, a typical write barrier needs to do both the underlying write and some recording. If a garbage collection happens between the two steps, some object may be missed by the collector or some pointer not properly updated by it. Systems usually have a number of such short sequences that need to be atomic with respect to garbage collection (though not necessarily atomic with respect to true concurrency). In addition to write barriers other examples include setting up a new stack frame and initialising a new object.
A system is simpler in one way if it can allow garbage collection at any IP — there is no concern about whether a thread is suspended at a point safe for garbage collection, a GC-safe point or GC-point for short. However, such a system is more complex in that it must support stack maps for every IP, or else employ techniques that do not require them, as for uncooperative C and C++ compilers. If a system allows garbage collection at most IPs, then if it needs to collect and a thread is suspended at an unsafe point, it can either interpret instructions ahead for the suspended thread until it is at a safe point, or it can wake the thread up for a short time to get it to advance (probabilistically) to a safe point. Interpretation risks rarely exercised bugs, while nudging a thread gives only a probabilistic guarantee. Such systems may also pay the cost of larger maps [Stichnoth et al, 1999].
Many systems make the opposite choice and allow garbage collection only at certain restricted safe points, and produce maps only for those points. The minimal set of safe points needed for correctness includes each allocation (since garbage collection is always a possibility there)6 and each call of a routine in which there may be allocation or which may cause the thread to suspend in a wait (since if the thread suspends, some other thread may cause garbage collection).
Beyond the minimal points needed for correctness, a system may wish to allow garbage collection at more locations so as to guarantee that garbage collection can proceed without an unbounded wait for the thread to reach its next safe point. To make this stronger guarantee there needs to be a safe point in each loop; a simple rule is to place a safe point at each backwards branch in a function. In addition there needs to be a safe point in each function entry or each return, since otherwise functions, especially recursive ones, could perform many calls and returns before encountering a safe point. Since these additional safe points do not do anything that actually can trigger a garbage collection, they need to have an added check for whether garbage collection is needed/requested, so we call them GC-check points. This checking adds overhead to normal operation of mutators, though perhaps not very much, particularly if the compiler takes some simple measures to reduce the overhead. For example, it might omit the checks in methods that are quite short or have no loops or calls. Also, by inserting an additional level of looping it can avoid checking on every iteration of a loop and check only every nth iteration. If the check itself is cheap then these measures will not be necessary. In any case there is a clear trade-off between the overhead of frequent checks and the latency of infrequent ones.
Agesen [1998] compared two ways of causing a thread to suspend at a GC-point. One is polling, alluded to above, where the thread checks a flag that indicates that a collection has been requested. The other technique is patching, and involves modifying the code at the next GC-point(s) of the thread so that when the suspended thread is restarted, it will stop at the next GC-point. This is similar to placing temporary breakpoints in a debugger. Agesen found that patching has much lower overhead than polling, but of course it is more difficult to implement, and more problematic in a concurrent system.
In bringing up the idea of GC-check points, notice that we have introduced the notion of a handshake mechanism between the collector and a mutator thread. Such handshakes may be necessary even if a system does not include true concurrency but merely multiplexes several mutator threads on one processor — the collector may need to indicate the need for garbage collection and then wake up any suspended thread that is not at a safe point so that the thread can advance to a safe point. Some systems allow threads to suspend only at safe points so as to avoid this additional complexity, but for other reasons a system may not control all aspects of thread scheduling, and so may need this handshake.
For concreteness we mention some particular mechanisms for the handshake. Each thread can maintain a thread-local variable that indicates whether the rest of the system needs that thread’s attention at a safe point. This mechanism can be used for things other than signalling for a garbage collection. At a GC-check point, the thread checks that thread-local variable, and if it is non-zero (say) it calls a system routine that uses the exact value of the variable to determine what action to take. One particular value will indicate ‘time to garbage collect’. When the thread notices the request, it sets another thread-local variable to indicate it has noticed, or perhaps decrements a global variable on which a collector thread is waiting. Systems typically arrange for thread-local variables to be cheap to access, so this may be a good approach.
Another possibility is to set a processor condition code in the saved thread state of the suspended thread. A GC-check point can then consist of a very cheap conditional branch over a call to the system routine for responding to the request. This approach works only if the processor has multiple condition code sets (as for the PowerPC) and can be guaranteed not to be in external code when awakened. If the machine has enough registers that one can be dedicated to the signalling, a register can be used almost as cheaply as a condition code flag. If a thread is in external code, the system needs an alternate method of getting attention when the thread comes out of that code (unless it is suspended as a safe point already). Hijacking the return address (see also Section 11.5) is a way to get attention as the external code completes.
As an alternative to flag setting and return address hijacking, in some cases an operating system-level inter-thread signal, such as those offered by some implementations of POSIX threads, may be a viable alternative. This may be problematic for wide portability, and it may not be very efficient. It can be slow in part because of the relatively long path through the operating system kernel to set up and deliver a signal to a user-level handler. It can also be slow because of the need not only for a low-level processor interrupt but because of the effect on caches and translation lookaside buffers.
In sum, there are two basic approaches: synchronous notification, also appropriately called polling, and asynchronous notification via some kind of signal or interrupt. Each approach has its own overheads, which vary across platforms. Polling may also require a degree of compiler cooperation, depending on the specific technique. Further, asynchronous notification will usually need to be turned into synchronous, since scanning the stack, or whatever action is being requested, may not be possible at every moment. Thus, the signal handler’s main goal may be to set a flag local to its thread where the thread is guaranteed to notice the flag soon and act on it.
We further note that in implementing synchronisation between threads to direct scanning of stacks, considerations of concurrent hardware and software crop up, for which we offer general background in Chapter 13. Of particular relevance may be Section 13.7, which discussed coordinating threads to move from phase to phase of collection, which mutator threads may need to do as collection begins and ends.
While many systems statically compile all code in advance, garbage collection has its roots in implementations of languages like Lisp, which can build and execute code on the fly — originally interpretively but also compiled to native code since early days. Systems that load or construct code dynamically, and that optimise it at run time, are if anything more common now. Loading and generating code dynamically leads logically enough to the desire to reclaim the memory consumed by that code when the code is no longer needed. Straightforward tracing or reference counting techniques often will not work, because code for many functions is accessible through global variables or symbol tables that will never be cleared. In some languages little can be done if the program does not explicitly remove such entries — and the language may provide no approved way to do that.
Two specific cases deserve further mention. First, closures consist of a function and an environment of bindings to use when the function runs. Naive construction of a closure, say for function g nested within function f, provides g with the full environment of f, possibly sharing a common environment object. Thomas and Jones [1994] described a system that, upon collection, can specialise the environment to just those items that g uses. This may ultimately make some other closure unreachable and thus reclaimable.
The other case is class-based systems, such as Java. One consideration is that in such systems object instances generally refer to their class. It is common to place classes, and the code for their methods, in a non-moving, non-collected area. In that way the collector can ignore the class pointer in every object. But to reclaim classes, the collector will need to trace the class pointer fields — possibly a significant cost in the normal case. It might avoid that cost by tracing through class pointers only when invoked in a special mode.
For Java in particular, a run-time class is actually determined by both the class’s code and its class loader. Since loading a Java class has side-effects such as initialising static variables, unloading a class is not transparent if the class might be reloaded by the same class loader. The only way to guarantee that a class will not be reloaded by a given class loader is for the class loader itself to be reclaimable. A class loader has a table of the classes it has loaded (to avoid reloading them, reinitialising them, and so on) and a run-time class needs also to mention its class loader (as part of its identity). So, to reclaim a class, there must be no references to its class loader, any class loaded by that class loader, or any instance of one of those classes, from existing threads or global variables (of classes loaded by other class loaders). Furthermore, since the bootstrap class loader is never reclaimed, no class that it loads can be reclaimed. While Java class unloading is something of a special case, certain kinds of programs rely on it or else servers will run out of space.
In addition to user-visible code elements such as methods, functions and closures, a system may generate multiple versions of code to be interpreted or run natively, for example optimised and unoptimised code, or specialised versions of functions. Generating a new version of a function may make old versions unreachable for future invocations of the function. However, invocations still in process may need the old versions. Thus return addresses embedded in the stack or closures may retain old code. In any case, the system may need tracing or reference counting rather than immediately reclaiming old versions. A related technique is on-stack replacement, in which a system replaces an in-process invocation’s code with new code. While this is commonly done more in order to improve the performance of the still-running invocation, it also helps make old versions reclaimable. See Fink and Qian [2003] and Soman and Krintz [2006] for examples of on-stack replacement approaches and applications for Java. While on-stack replacement is most often directed at optimising code, some applications, such as debugging, requires deoptimised code, which can have the same effect of helping to make old versions of code reclaimable.
Several classes of garbage collection algorithm require ‘interesting’ pointers to be detected as mutators run. If a collector collects only part of the heap, then any reference to an object in that region from outside it is of interest to the collector: in the absence of further knowledge, the collector must treat that reference as a root. For example, generational collectors must detect any reference to a younger generation object written into an object in an older generation. As we shall see in Chapter 15, interleaving mutation and collection (whether or not the collector runs in its own thread) presents ample opportunities for the mutator to hide pointers from the collector. If these references are not detected and passed to the collector, then live objects may be reclaimed prematurely. All these cases require the mutator to add references on the fly to the collector’s work list. This is achieved through read or write barriers.
Other chapters on specific algorithms address the particular content of read and write barriers as needed by those algorithms. However, we offer here some general observations about how to implement barriers. To abstract from particular needs of a collection algorithm, such as generational or concurrent collectors, we concern ourselves with the detection and recording of ‘interesting’ pointers. Detection is the determination that a particular pointer is ‘interesting’ while recording is noting that fact for later use by the collector. To some extent detection and recording are orthogonal, though some detection methods may lend themselves more to particular recording methods. For example, detection via page protection violations lends itself more to recording the location being modified.
A typical barrier involves one or more checks that guard an action. Typical checks include whether a pointer being stored is null and the relationship between the generations of the referring object and its referent, and a typical action is to record an object in a remembered set. The full code for all the checks and the action may be too large to inline entirely, depending on implementation. Even a fairly modest sequence of instructions would create very large compiled code and also risk poor instruction cache performance since much of the code executes only rarely. Therefore designers often separate the code into what is commonly called ‘fast path’ and ‘slow path’ portions. The fast path is inlined for speed, and it calls the slow path part only if necessary; there is one copy of the slow path in order to conserve space and improve instruction cache performance. It is critical that the fast path code include the most common cases and that the slow path part be less common. However, it sometimes helps to apply the same principle to the slow path code. If the barrier involves multiple tests — and they usually do — then it is important to order those tests so that the first one filters out the most cases, the second the next larger set of cases, and so on, modulo the cost of performing the test. In doing this tuning there is no substitute for trying various arrangements and measuring performance on a range of programs, because so many factors come into play on modern hardware that simple analytical models fail to give good enough guidance.
Another significant factor in barrier performance is speed in accessing any required data structures, such as card tables. It may be a good trade-off to dedicate a machine register to hold a data structure pointer, such as the base of the card table, but this can vary considerably by machine and algorithm.
Also of concern is the software engineering and maintenance of those aspects of the garbage collection algorithm — mostly barriers, GC-checks and allocation sequences — they are built into the compiler(s) of a system. If possible it seems best to arrange for the compiler to inline a routine in which the designer codes the fast path portion of a sequence. That way the compiler does not need to know the details and the designer can change them freely. However, as we noted before these code sequences may have constraints, such as no garbage collection in the middle of them, that require care on the compiler’s part. The compiler may also have to disable some optimisations on these code sequences, such as leaving apparently dead stores that save something useful for the collector and not reordering barrier code or interspersing it with surrounding code. To that end the compiler might support special pragmas or markers for the designer to use to indicate special properties such as uninterruptible code sequences.
In the remainder of this section we discuss write barriers. We defer the discussion of read barriers to later chapters where we discuss incremental and concurrent collection since this is the context in which they are used. Write barriers are more complex than read barriers since they not only have to detect ‘interesting’ writes but must also record some information for the garbage collector’s later use. In contrast, read barriers typically cause an immediate action, such as copying to tospace the target of the reference just loaded.
Interesting pointers can be remembered using different policies and mechanisms. Policies dictate the precision with which the location of an interesting pointer is recorded in the remembered set. The choice of policy is a trade-off between adding overheads to the mutator or to the collector. In general it is better to favour adding overhead to relatively infrequent collector actions (such as discovering roots) than to very frequent mutator actions (such as heap stores). Without a barrier, pointer stores are normally very fast (although null pointer or array bounds checks are often required by managed languages). Adding a write barrier can increase the instruction count for a pointer write by a factor of two or more, though some of this cost may be masked if the cache locality of the barrier is better than that of the mutator itself (for example, it is probably unnecessary to stall the user code while the write barrier records an interesting pointer). Typically, more precise recording of interesting pointers in the remembered set means less work for the collector to do to find the pointer but more work for the mutator to filter and log it. At one extreme, in a generational collector, not logging any pointer stores transfers all overheads from the mutator to the collector which must scan all other spaces in the heap looking for references to the condemned generation. While this is unlikely to be a generally successful policy, linear scanning has better locality than tracing, and this may be the only way to collect generationally if there is no support for detecting pointer stores from the compiler or operating system [Bartlett, 1989a]. Swanson [1986] and Shaw [1988] have suggested that this can reduce garbage collection costs by two-thirds compared with simple semispace copying.
There are three dimensions to remembered set policy. First, how accurately should pointer writes be recorded? Not all pointers are interesting to a collector, but unconditional logging may impose less overhead on the mutator than filtering out uninteresting pointers. The implementation of the remembered set is key to this cost. Remembered sets with cheap mechanisms for adding an entry, such as simply writing a byte in a fixed-size table, will favour unconditional logging, especially if addition is idempotent. On the other hand, if adding an entry is more expensive or the size of the remembered set is a concern, then it is more likely to be worthwhile to filter out uninteresting pointers. Filtering is essential for concurrent or incremental collectors to ensure that their work lists do eventually empty. For a particular filtering scheme, there is a trade-off between how much filtering to do inline and when to call an out-of-line routine to complete the filtering and possibly add the pointer to a remembered set. The more filtering that is done inline, the fewer instructions that may be executed, but the code size will increase and the larger instruction cache footprint may undermine any performance gains. This requires careful tuning of the order of filter tests and which are done inline.
Second, at what granularity is the location of the pointer to be recorded? The most accurate is to record the address of the field into which the pointer was written. However, this will increase the size of the remembered set if many fields of an object, such as an array, are updated. An alternative is to record the address of the object containing the field: this also permits duplicates to be filtered, which field remembering does not (since there is generally no room in the field to record that it has been remembered). Object remembering requires the collector to scan every pointer in the object at scavenge time in order to discover those that refer to objects that need to be traced. A hybrid solution might be to object-record arrays and field-record scalars on the assumption that if one slot of an array is updated then many are likely to be. Conversely, it might be sensible to field-record arrays (to avoid scanning the whole thing) and object-record scalars (since they tend to be smaller). For arrays it may make sense to record only a portion of the array. This is analogous to card marking, but specific to arrays and aligned with the array indices rather than with the addresses of the array’s fields in virtual memory. Whether to store the object or one of its slots may also depend on what information the mutator has at hand. If the write action knows the address of the object as well as the field, the barrier can choose to remember either; if only the address of the field is passed to the barrier, then computing the address of the object will incur further overhead. Hosking et al [1992] resolve this dilemma by storing the addresses of both the object and the slot in their sequential store buffer for an interpreted Smalltalk system.
Card table techniques (which we discuss below) divide the heap logically into small, fixed size cards. Pointer modifications are recorded at the granularity of a card, typically by setting a byte in a card table. Note that the card marked can correspond to either the updated field or object (these may reside on different cards). At scavenge time, the collector must first find any dirty cards corresponding to the condemned generation and then find all the interesting pointers held in that card. The choice of object or field card marking will affect how this search is performed. Coarser than cards, pointer stores can be logged at the granularity of a virtual memory page. With help from the hardware and operating system, this may impose no direct overhead on the mutator but, like cards, increases work for the collector. Unlike cards, marked pages will always correspond to the updated slot not to its containing object since the operating system is oblivious to object layout.
Third, should the remembered set be allowed to contain duplicate entries? The case for duplicates is that not checking eases the burden on the mutator; the case against is that duplicates increase the size of the remembered set and move the cost of handling duplicates to the collector. Card and page marking eliminate duplicates since they typically simply set a bit or a byte in a table. Object recording can also eliminate most duplicates by marking objects as logged, for example by using a bit in their header, regardless of the implementation of the remembered set itself, whereas duplicate elimination is unlikely to be so simple if word-sized fields are recorded. The cost to the mutator is that this is an additional check which may or may not be absorbed by the reduction in remembered set entries added, and that an additional write is performed. Otherwise, remembered sets must be implemented as true sets rather than multisets if they are not to contain duplicates.
In summary, if a card or page based scheme is used then the collector’s scanning cost will depend on the number of dirty cards or pages. Otherwise, the cost will depend on the number of pointer writes if a scheme without duplicate elimination is used. With duplicate elimination, it will depend on the number of different objects modified. In all cases, uninteresting pointer filtering will reduce the collector’s root scanning cost. Mechanisms for implementing remembered sets include hash sets, sequential store buffers, card tables, virtual memory mechanisms and hardware support. We consider each of these in turn.
The remembered set must truly implement a set if it is to remember slots without duplicating entries. Equally, a set is required for object remembering if there is no room in object headers to mark an object as remembered. A further requirement for a remembered set is that adding entries must be a fast, and preferably constant time, operation. Hash tables meet these requirements.
Hosking et al [1992] implement a remembered set with a circular hash table, using linear hashing in their multiple generation memory management toolkit, for a Smalltalk interpreter that stores stack frames in generation 0, step 0 in the heap. More specifically, a separate remembered set is maintained for each generation. Their remembered sets can store either objects or fields. The tables are implemented as arrays of 2i + k entries (they use k = 2). Hence addresses are hashed to obtain i bits (from the middle bits of the address), and the hash is used to index the array. If that entry is empty, the address of the object or field is stored at that index, otherwise the next k entries are searched (this is not done circularly, which is why the array size is 2i + k). If this also fails to find an empty entry, the table is searched circularly.
In order not to increase further the work that must be done by the remembering code, the write barrier filters out all writes to generation 0 objects and all young-young writes. In addition, it adds all interesting pointers to a single scratch remembered set rather than to the remembered set for the target generation. Not deciding at mutator time the generation to whose remembered set it should be added might be even more apposite in a multithreaded environment; there per-processor scratch remembered sets could be used to avoid contention as thread-safe hash tables would be too expensive. In all, Hosking et al used 17 inlined MIPS instructions in the fast path of the write barrier, including the call to update the remembered set, making it comparatively expensive even on the MIPS, a register-rich architecture. At scavenge time, the roots for a given generation may reside either in that generation’s remembered set or in the scratch remembered set. Duplicates between the remembered sets are removed by hashing the generation’s remembered set into the scratch remembered set, and the scratch remembered set is processed: any interesting pointers encountered are added to the appropriate remembered sets.
Garthwaite uses hash tables in his implementation of the Train algorithm. The common operations on his hash tables are insertion and iteration, so he uses open addressing. Because it is common to map adjacent addresses, he eschews linear addressing (address modulo N where N is the size of the hash table) which would tend to map these addresses to neighbouring slots in the table. Instead he uses a universal hashing function. He chose a 58-bit prime p and assigns to each remembered set hash table two parameters, a and b, generated by repeated use of a pseudo-random function [Park and Miller, 1988] so that 0 < a, b < p. An address r is hashed by the function ((ar + b) mod p) mod N. Open-addressing requires a tactic for probing alternative slots when a collision occurs. Linear and quadratic probing (in which the current slot’s index is incremented by an amount d and d is incremented by a constant i) suffer from clustering as subsequent insertions follow the same probing sequence, so Garthwaite uses double hashing in which the increment used in quadratic probing is a function of the key. Given a hash table whose size is a power of 2, quadratic probing with any odd increment i applied to the probing step d ensures that the entire table will be visited. This scheme doubles the available set of probing sequences by checking whether d is odd. If so, i is set to zero (linear probing). Otherwise, both d and i are set to d + 1. Finally, a hash table may need to be expanded when its load becomes too high. An alternative may be to rebalance the table by modifying the insertion process. At each collision, we must decide whether to continue probing with the item being inserted or whether to place it in the current slot and probe with the contents of that slot. Garthwaite et al uses robin hood hashing [Celis et al, 1985]. Each entry is stored in its slot along with its depth in the probing sequence, taking advantage of the fact that the least significant bits of an item (such as the address of a card) will be zero. If a slot already contains an item, its depth is compared with the depth of the new item: we leave which either value is deeper in its probing sequence and continue with the other.
Algorithm 11.4: Recording stored pointers with a sequential store buffer
1 Write(src, i, ref):
2 add %src, %i, %fld
3 st %ref, [%fld] ; src[i] ← ref
4 st %fld, [%next] ; SSB[next] ← fld
5 add %next, 4, %next ; next next + 1
Pointer recording can be made faster by using a simpler sequential store buffer (SSB), such as a chain of blocks of slots. A buffer per thread might be used for all generations to save the mutator write barrier from having to select the appropriate one and to eliminate contention between threads.
In the common case, adding an entry requires very few instructions: it is simply necessary to compare a next pointer against a limit, store to the next location in the buffer and bump the next pointer. The MMTk [Blackburn et al, 2004b] implements a sequential store buffer as a chain of blocks. Each block is power-of-two sized and aligned, and filled from high addresses to low. This allows a simple overflow test by comparing the low order bits of the next pointer with zero (which is often a fast operation).
A number of tricks can be used to eliminate the explicit overflow check, in which case the cost of adding an entry to the sequential store buffer can be as low as one or two instructions if a register can be reserved for the next pointer, as in Algorithm 11.4. With a dedicated register this might be as low as one instruction on the PowerPC: stwu fld,4(next).
Appel [1989a], Hudson and Diwan [1990] and Hosking et al [1992] use a write-protected guard page. When the write barrier attempts to add an entry on this page, the trap handler performs the necessary overflow action, which we discuss later. Raising and handling a page protection exception is very expensive, costing hundreds of thousands of instructions. This technique is therefore effective only if traps are very infrequent: the trap cost must be less than the cost of the (large number of) software tests that would otherwise be performed:
Appel ensures that his guard page trap is triggered precisely once per collection by storing the sequential store buffer as a list in the young generation. The guard page is placed at the end of the space reserved for the young generation, thus any allocation — for objects or remembered set entries — may spring the trap and invoke the collector. This technique relies on the young generation’s area being contiguous. It might appear that a system can simply place the heap at the end of the data area of the address and use the brk system call to grow (or shrink) the heap. However, protecting the page beyond the end of the heap interferes with use of brk by malloc, as noted by Reppy [1993], so it may be better to use a higher region of address space and manage it with mmap.
Algorithm 11.5: Misaligned access boundary check
1 atomic insert(fld):
2 *(next – 4) ← fld | /* add the entry in the previous slot */ |
3 tmp ← next >> (n − 1)
4 tmp tmp & 6 | /* |
5 next next + tmp
Example: n = 4 (4 word buffers):
insert at 32: next=40, next>>(n–1)=4, tmp=4
insert at 36: next=44, next>>(n–1)=5, tmp=4
insert at 40: next=48, next>>(n–1)=5, tmp=4
insert at 44: next=54, next>>(n–1)=6, tmp=6
insert at 50: UTRAP!
Architecture-specific mechanisms can also be used to eliminate the overflow check. One example is the Solaris UTRAP fault, which is designed to handle misaligned accesses and is about a hundred times faster than the Unix signal handling mechanism. Detlefs et al [2002a] implement their sequential store buffer as a list of 2n-byte buffers, aligned on 2n+1 boundaries but not 2n+2 ones, which sacrifices some space. The insertion algorithm is shown in Algorithm 11.5. The next register normally points to four bytes beyond the next entry, except when the buffer is full (that is, when next points at the slot before a 2n+2-aligned boundary), in which case the increment on line 5 adds six, causing a UTRAP on the next access.
Sequential store buffers may be used directly as remembered sets or as a fast logging front-end to hash tables. A simple, two-generation configuration with en masse promotion can discard the remembered set at each minor collection since the nursery is emptied: there is no need for more complex remembered set structures (provided the sequential store buffer does not overflow before a collection). However, other configurations require remembered sets to be preserved between collections. If multiple generations are used, the records of pointers spanning older generations must be preserved regardless of whether survivors of the condemned generations are promoted en masse. If the generations being collected have steps or other mechanisms for delaying promotion (Section 9.4), then the record of older generation pointers to surviving, but not promoted objects, must be kept.
One solution might be simply to remove entries that are no longer needed from the sequential store buffer. An entry for a field will not be needed if the value of the field is null, or refers to an object that is only considered at full heap collections (or never). By extension, an entry for an object can be deleted if the object similarly does not contain any interesting pointers. However this solution encourages unrestrained growth of the remembered set and leads to the collector processing the same long-lived entries from one collection to the next. A better solution is to move entries that need to be preserved to the remembered set of the appropriate generation. These remembered sets might also be sequential store buffers or the information might be more concisely transferred into a hash table as we saw above.
Hash tables and sequential store buffers may overflow: this can be handled in different ways. The MMTk acquires and links a fresh block into the sequential store buffer [Black-burn et al, 2004b]. Hosking et al [1992] fix the size of their sequential store buffer by emptying it into hash tables whenever it overflows. In order to keep their hash tables relatively sparse, they grow a table whenever a pointer cannot be remembered to its natural location in the table or one of the k following slots, or when the occupancy of the table exceeds a threshold (for example, 60%). Tables are grown by incrementing the size of the hash key, effectively doubling the table’s size; a corollary is that the key size cannot be a compile-time constant, which may increase the size and cost of the write barrier. As Appel [1989a] stores his sequential store buffer in the heap, overflow triggers garbage collection. The MMTk also invokes the collector whenever the size of its metadata (such as the sequential store buffer) grows too large.
Card table (card marking) schemes divide the heap conceptually into fixed size, contiguous areas called cards [Sobalvarro, 1988; Wilson and Moher, 1989a,b]. Cards are typically small, between 128 and 512 bytes. The simplest way to implement the card table is as an array of bytes, indexed by the cards. Whenever a pointer is written, the write barrier dirties an entry in the card table corresponding to the card containing the source of the pointer (for example, see Figure 11.3). The card’s index can be obtained by shifting the address of the updated field. The motivation behind card tables is to permit a small and fast write barrier that can be inlined into mutator code. In addition, card tables cannot overflow, unlike hash tables or sequential store buffers. As always, the trade-off is that more overhead is transferred to the collector. In this case, the collector must search dirtied cards for fields that have been modified and may contain an interesting pointer: the cost to the collector is proportional to the number of cards marked (and to card size) rather than the number of (interesting) stores made.
Because they are designed to minimise impact on mutator performance, card marking schemes are most often used with an unconditional write barrier. This means that the card table is sufficiently large that all locations that might be modified by Write can be mapped to a slot in the table. The size of the table could be reduced if it were guaranteed that no interesting pointers would ever be written to some region of the heap and a conditional test was used to filter out such dull pointers. For example, if the area of the heap above some fixed virtual address boundary was reserved for the nursery (which is scavenged at every collection), then it is only necessary to map the area below that boundary.
While the most compact implementation of a card table is an array of bits, this is not the best choice for several reasons. Modern processor instruction sets are not designed to write single bits. Therefore bit manipulations require more instructions than primitive operations: read a byte, apply a logical operator to set or clear the bit, write the byte back. Worse, this sequence of operations is not atomic: card updates may be lost if threads race to update the same card table entry even though they may not be modifying the same field or object in the heap. For this reason, card tables generally use arrays of bytes. Because processors often have fast instructions for clearing memory, ‘dirty’ is often represented by 0. Using a byte array, the card can be dirtied in just two SPARC instructions [Detlefs et al, 2002a] (other architectures may require a few more instructions), as shown in Algorithm 11.6. For clarity, we write ZERO to represent the SPARC register %g0 which always holds 0. A BASE register needs to be set up so that it holds the higher order bits of CT1–(H>>LOG_CARD_SIZE) where CT1 and H are the starting addresses of the card table and the heap respectively, and both are aligned on a card-size boundary, say 512 bytes. Detlefs et al [2002a] use a SPARC local register for that, which is set up once on entry to a method that might perform a write, and is preserved across calls by the register window mechanism.
Algorithm 11.6: Recording stored pointers with a card table on SPARC
1 Write(src, i, ref):
2 add %src, %i, %fld
3 st %ref, [%fld] ; src[i] ← ref
4 srl %fld, LOG_CARD_SIZE, %idx ; idx ← fld >> LOG_CARD_SIZE
5 stb ZERO, [%BASE + %idx] ; CT[idx] ← DIRTY
Algorithm 11.7: Recording stored pointers with Hölzle’s card table on SPARC
1 Write(src, i, ref): |
|
2 st %ref, [%src + %i] |
|
3 srl %src, LOG_CARD_SIZE, %idx |
/* calculate approximate byte index */ |
4 clrb [%BASE + %idx] |
/* clear byte in byte map */ |
Algorithm 11.8: Two-level card tables on SPARC
1 Write(src, i, ref): |
|
2 add %src, %i, %fld |
|
3 st %ref, [%fld] |
/* do the write */ |
4 srl %fld, LOG_CARD_SIZE, %idx |
/* get the level 1 index */ |
5 stb ZERO, [%BASE+%idx] |
/* mark the level 1 card dirty */ |
6 srl %fld, LOG_SUPERCARD_SIZE, %idx |
/* get the level 2 index */ |
7 stb ZERO, [%BASE+%idx] |
/* mark the level 2 card dirty */ |
Hölzle [1993] further reduced the cost of the write barrier in most cases by reducing the precision with which the modified field is recorded, as in Algorithm 11.7. Suppose that marking byte i in the card table indicated that any card in the range i … i + L may be dirty. Provided that the offset of the updated word is less than L cards from the beginning of the object, the byte corresponding to the object’s address can be marked instead. A leeway of one (L = 1) is likely to be sufficient to cover most stores except those into array elements: these must be marked exactly in the usual way. With a 128-byte card, any field of a 32-word object can be handled.
Ambiguity arises only when the last object on a card extends into the next card, and in that case the collector also scans that object or the necessary initial portion of it.
The space required for the card table is usually modest, even for small card sizes. For example, a byte array for 128-byte cards occupies less than 1% of the heap in a 32-bit architecture. Card size is a compromise between space usage and the collector’s root scanning time, since larger cards indicate the locations of modified fields less precisely but occupy smaller tables.
At collection time, the collector must search all dirty cards for interesting pointers. There are two aspects to the search. First, the collector must scan the card table, looking for dirty cards. The search can be speeded up by observing that mutator updates tend to have good locality, thus clean and dirty cards will tend to occur in clumps. If bytes are used in the card table, four or eight cards can be checked by comparing whole words in the table.
If a generational collector does not promote all survivors en masse, some objects will be retained in the younger generation, while others are promoted. If a promoted object refers to an object not promoted, then the older-to-younger reference leads unavoidably to a dirty card. However, when a promoted object is first copied into the older generation, it may refer to objects in the younger generation, all of which end up being promoted. In that case it would be better not to dirty the promoted object’s card(s), since doing so will cause needless card scanning during the next collection. Hosking et al [1992] take care to promote objects to clean cards, which are updated as necessary as the cards are scanned using a filtering copy barrier.
Figure 11.3: Crossing map with slot-remembering card table. One card has been dirtied (shown in black). The updated field is shown in grey. The crossing map shows offsets (in words) to the last object in a card.
Even so, a collector may spend significant time in a very large heap skipping clean cards. Detlefs et al [2002a] observe that the overwhelming majority of cards are clean whilst cards with more than 16 cross-generational pointers are quite rare. The cost of searching the card table for dirty cards can be reduced at the expense of some additional space for a two-level card table. The second, smaller card table uses more coarsely grained cards, each of which corresponds to 2n fine-grained cards, thus speeding up scanning of clean cards by the same factor. The write barrier can be made very similar to that of Algorithm 11.6 (just two more instructions are needed) by sacrificing some space in order to ensure that the start of the second level card table CT2 is aligned with the first such that CT1–(H>>LOG_CARD_SIZE)=CT2–(H>>LOG_SUPERCARD_SIZE), as in Algorithm 11.8.
As a card table is searched, each dirty card discovered must be processed, which requires finding the modified objects and slots somewhere in the card. This is not straightforward since the start of the card is not necessarily aligned with the start of an object but in order to scan fields we must start at an object. Worse, the field that caused the card to be dirtied may belong to a large object whose header is several cards earlier (this is another reason for storing large objects separately). In order to be able to find the start of an object, we need a crossing map that decodes how objects span cards.
The crossing map holds as many entries as cards. Each entry in the crossing map indicates the offset from the start of the corresponding card to an object starting in that card. Entries in the crossing map corresponding to old generation cards are set by the collector as it promotes objects, or by the allocator in the case of cards for spaces outside the generational world. Notice that the nursery space does not need cards since objects there cannot point to other object that are still younger — they are the youngest objects in the system. Promotion also requires that the crossing map be updated. The design of the crossing map depends on whether the card table records objects or slots.
Used with a slot-recording write barrier, the crossing map must record the offset to the last object in each card, or a negative value if no object starts in a card. Because objects can span cards, the start of the modified object may be several cards earlier than the dirty one. For example, in Figure 11.3, objects are shown as white rectangles in the heap. We assume a 32-bit architecture and 512 byte cards. The last object in the first card starts at an offset of 408 bytes (102 words) from the start of the card, indicated by the entry in the crossing map. This object spans four cards so the next two crossing map entries are negative. A field in the fifth object has been updated (shown as grey) so the corresponding card (card 4) is marked (shown as black). To find the start of this object, the collector consults the crossing map, moving backwards from the dirtied card (to the left) until it finds a non-negative offset (Algorithm 11.9). Note that the negative value indicates a distance to go back — a process that may need to be repeated a number of times if the preceding object is quite large. Alternatively, the system can reserve a single value, such as -1, to mean ‘back up,’ making backing up slower over a large object.
Algorithm 11.9: Search a crossing map for a slot-recording card table; trace is the collector’s marking or copying procedure.
1 search(card):
2 start ← H + (card << LOG_CARD_SIZE)
3 end ← start + CARD_SIZE | /* start of next card */ |
4 card ← card − 1
5 offset ← crossingMap[card]
6 while offset < 0
7 card ← card + offset | /* |
8 offset ← crossingMap[card]
9 next ← H + (card << LOG_CARD_SIZE) + offset
10 repeat
11 trace(next, start, end) | /* trace the object at |
12 next ← nextObject(next)
13 until next ≥ end
Old generations are commonly managed by a non-moving collector which mixes used and free blocks in the heap. Parallel collectors are especially likely to create islands of promoted data separated by large areas of free space, as each collector thread will promote to its own heap area in order to avoid contention. To aid heap parsability, each free area can be filled with a self-describing pseudo-object. However, slot-based crossing map algorithms are predicated on the assumption that heap usage is dense. If a very large, say ten megabyte, free chunk protrudes into a dirty card, the first loop of the search algorithm in Algorithm 11.9 will iterate tens of thousands of times to discover the head of the pseudo-object describing this free chunk. One way to reduce this search is to store logarithmic backup values when no object starts in the card. Thus, an entry −k would indicate ‘go back 2k−1 cards and then do what it says there’ (and similarly for a linear backup scheme). Note also that if future allocation starts from the beginning of this free block, then only logarithmically many entries (up the ‘spine’ of this list) have to be changed to restore the crossing table to the correct state.
However, Garthwaite et al [2006] show that a clever encoding of the crossing map can usually eliminate the search loop. The simplest way to consider their scheme is to assume that each crossing map entry v is a 16-bit unsigned integer (two bytes). Table 11.3 shows their scheme. If the value υ of a crossing map entry is zero, then no objects in the corresponding card contain any references. A value for υ less than 128 indicates the number of words between the start of the first object and the end of the card. Notice that this is different from the scheme above which gives the offset to the last word in a card. Finding the first word eliminates the need to search back possibly many cards. Large objects, such as arrays, may span cards. The second encoding deals with the case that such an object spans two or more cards, and that the first υ – 256 words of the second card are all references and that this sequence terminates the object. The benefit of this encoding is that the references can be found directly, without accessing the object’s type information. However, this encoding would not work if the portion of the object overlapping this card contains both references and non-references. In this case, the crossing map entry should be set to a value greater than 384 to indicate that collector should consult the entry υ – 384 entries earlier. Garthwaite et al also include a scheme in which, if an object completely spans two crossing map slots, then the four bytes of these slots should be treated as the address of the object. In this discussion, we have assumed that a crossing map entry should be two bytes long. However, a single byte suffices if, for example, we use 512 byte cards and 64-bit alignment.
Table 11.3: The crossing map encoding of Garthwaite et al
Entry υ |
Encoded meaning |
υ = 0 |
The corresponding card contains no references. |
0 < υ ≤ 128 |
The first object starts v words before the end of this card. |
256 < υ ≤ 384 |
The first υ − 256 words of this card are a sequence of references at the end of an object. |
υ > 384 |
Consult the card υ − 384 entries before. |
Some generational collectors do not promote objects en masse. Whenever the collector scans a dirty card and finds an interesting pointer but does not promote its referent, the card must be left dirty so that it is found at the next collection and scanned again. It would be preferable to discover interesting pointers directly rather than by searching through cards. Fortunately, it is common for very few dirty cards to contain more than a small number. Hosking and Hudson [1993] suggest moving interesting pointers to a hash table as a card is cleaned in the same way as Hosking et al [1992] did with sequential store buffers.
Sun’s Java virtual machines optimise card rescanning by having the scavenger summarise dirty cards that retain interesting pointers, taking advantage of card map entries being bytes not bits [Detlefs et al, 2002a]. The state of a card may now be ‘clean’, ‘modified’ or ‘summarised’. If the scavenger finds up to k interesting pointers in a ‘modified’ card, it marks the card as ‘summarised’ and records the offsets of these pointer locations in the corresponding entry of a summary table. If the card contains more than k interesting pointers (for example, k = 2), it is left ‘modified’ and the summary entry is recorded as ‘overflowed’. The k interesting fields can therefore be processed directly at the next collection (unless the card is dirtied again) rather having to search the card using the crossing map. Alternatively, if cards are reasonably small, each byte-sized entry in the card table itself can store a small number of offsets directly.
Reppy [1993] encodes additional generational information in the card table to save scanning effort. As it cleans cards, his multi-generational collector summarises a dirty card with the lowest generation number of any referent found on it (0 being the nursery). In future, when collecting generation n, cards in the table with values larger than n need not be processed. Used with 256-byte cards, this gave an 80% improvement in garbage collection times in a five-generation Standard ML heap.
Hardware and virtual memory techniques
Some of the earliest generational garbage collectors relied on operating system and hardware support. Tagged pointer architectures allowed pointers and non-pointers to be discriminated, and hardware write barriers could set bits in a page table [Moon, 1984]. However, it is possible to use operating system support to track writes without special purpose hardware. Shaw [1988] modified the HP-UX operating system to use its paging system for this purpose. The virtual memory manager must always record which pages are dirty so that it knows whether to write them back to the swap file when they are evicted. Shaw modified the virtual memory manager to intercept a page’s eviction and remember the state of its dirty bit, and added system calls to clear a set of page bits and to return a map of pages modified since the last collection. The benefit of this scheme is that it imposes no normal-case cost on the mutator. A disadvantage is that it overestimates the remembered set since the operating system does not distinguish pages dirtied by writing a pointer or a non-pointer, plus there are the overheads of the traps and operating systems calls.
Boehm et al [1991] avoided the need to modify the operating system by write-protecting pages after a collection. The first write to a page since it was protected leads to a fault; the trap handler sets the dirty bit for the page before unprotecting it to prevent further faults in this collection cycle. Clearly, pages to which objects are promoted should be presumed dirty during collection to avoid incurring traps. Page protection does impose overhead on the mutator but, as for card tables, the cost of the barrier is proportional to the number of pages written rather than the number of writes. However, these schemes incur further expense. Reading dirty page information from the operating system is expensive. Page protection mechanisms are known to incur ‘trap storms’ as many protection faults are triggered immediately after a collection to unprotect the program’s working set [Kermany and Petrank, 2006]. Page protection faults are expensive, particularly if they are referred to user-space handlers. Operating system pages are much larger than cards, so efficient methods of scanning them will be important (perhaps summarising them in the same way that we summarised cards above).
Write barrier mechanisms: in summary
Studies by Hosking et al [1992] and Fitzgerald and Tarditi [2000] found no clear winner amongst the different remembered set mechanisms for generational garbage collectors, although neither study explored Sun-style card summarising. Page-based schemes performed worst but, if a compiler is uncooperative, they do provide a way to track where pointers are written. In general, for card table remembered sets, card sizes around 512 bytes performed better than much larger or much smaller cards.
Blackburn and Hosking [2004] examined the overheads of executing different generational barriers alone on a range of platforms. Card marking and four partial barrier mechanisms were studied: a boundary test, a logging test, a frame comparison and a hybrid barrier. They excluded the costs of inserting an entry into remembered set for the partial barriers. The boundary test checked whether the pointer crossed a space boundary (a compile-time constant). The logging test checked a ‘logged’ field in the source of the pointer’s header. The frame barrier compared whether a pointer spanned two 2n- sized and aligned areas of the heap by xoring the addresses of its source and target: such barriers can allow more flexibility in the choice of space to be collected [Hudson and Moss, 1992; Blackburn et al, 2002]. Finally, a hybrid test chose statically between the boundary test for arrays and the logging test for scalars.
They concluded that the costs of the barrier (excluding the remembered set insertion in the case of the partial techniques) was generally small, less than 2%. Even where a write barrier’s overhead was much higher, the cost can be more than balanced by improvements in overall execution time offered by generational collection [Blackburn et al, 2004a]. However, there was substantial architectural variation between the platforms used (Intel Pentium 4, AMD Athlon XP and PowerPC 970), especially for the frame and card barriers. For example, the frame barrier was significantly more expensive than the others on x86 but among the cheapest on PowerPC; Blackburn and Hosking observed that xor is required to use the eax register on x86 which may increase register pressure. On the other hand, card marking on the PowerPC (their compiler generated a longer instruction sequence than the ones shown above) was very much more expensive than the partial techniques. We conclude that, as always, design decisions must be informed by careful experimentation with realistic benchmarks on a range of hardware platforms, and for each platform a different technique may be best.
Figure 11.4: A stack implemented as a chunked list. Shaded slots contain data. Each chunk is aligned on a 2k byte boundary.
It is common to find list-like data structures in collectors where an array is attractive because it does not require a linked list pointer or object header for each element, and it achieves good cache locality, but where the unused part of large arrays, and the possible need to move and reallocate a growing array, are problematic. A remembered set in a generational collector is such an example. A chunked list offers the advantage of high storage density but without the need to reallocate, and with relatively small waste and overhead. This data structure consists of a linked-list, possibly linked in both directions for a general deque, of chunks, where a chunk consists of an array of slots for holding data, plus the one or two chaining pointers. This is illustrated in Figure 11.4.
A useful refinement of this data structure is to make the size of the chunks a power of two, say 2k, and align them on 2k boundaries in the address space. Then logical pointers into a chunk used for scanning, inserting, or removing, do not need a separate ‘current chunk’ pointer and an index, but can use a single pointer. Algorithm 11.10 shows code for traversing a bidirectional chunked list in either direction, as a sample of the technique. The modular arithmetic can be performed with shifting and masking.
An important additional motivation for chunking is related to parallelism. If a chunked list or deque represents a work queue, then individual threads can grab chunks instead of individual items. If the chunk size is large enough, this greatly reduces contention on obtaining work from the queue. Conversely, provided that the chunk size is small enough, this approach still admits good load balancing. Another application for chunking is for local allocation buffers (Section 7.7), though in that case the chunks are just free memory, not a dense representation of a list data structure.
In other chapters we have described a variety of algorithms and heap layouts, some of which have implications for how a system uses available address space. Some algorithms require, or at least are simpler with, large contiguous regions. In a 32-bit address space it can be difficult to lay out the various spaces statically and have them be large enough for all applications. If that were not problematic enough, on many systems we face the added difficulty that the operating system may have the right to place dynamic link libraries (also called shared object files) anywhere it likes within large swaths of the address space. Furthermore, these libraries may not end up in the same place on each run — for security purposes the operating system may randomise their placement. Of course one solution is the larger address space of a 64-bit machine. However, the wider pointers needed in a 64-bit system end up increasing the real memory requirements of applications.
Algorithm 11.10: Traversing chunked lists
1 /* Assume chunk is of size 2k bytes and aligned on a 2k byte boundary */ |
|
2 /* Assume pointer size and slot size is 4 here */ |
|
3 NEXT = 0 /* byte offset in a chunk of pointer to data of next chunk */ |
|
4 PREV = 4 /* byte offset in a chunk of pointer to end of data of previous chunk */ |
|
5 DATA = 8 /* byte offset in a chunk of first data item */ |
|
6 |
|
7 bumpToNext(ptr): |
|
8 ptr ← ptr + 4 |
|
9 if (ptr % 2k) = 0 |
/* went off the end… */ |
10 ptr ← (ptr - 2k + NEXT) |
/*…back up to start of chunk and chain */ |
11 return ptr |
|
12 |
|
13 bumpToPrev(ptr): |
|
14 ptr ← ptr – 4 |
|
15 if (ptr % 2k) < DATA |
/* went off the beginning of the data… */ |
16 ptr ← *ptr |
/*…chain */ |
17 return ptr |
|
One of the key reasons for using certain large-space layouts of the address space is to make address-oriented write barriers efficient, that is, to enable a write barrier to work by comparing a pointer to a fixed address or to another pointer rather than requiring a table lookup. For example, if the nursery of a generational system is placed at one end of the address space used for the heap, a single check against a boundary value suffices to distinguish writes of pointers referring to objects in the nursery from other writes.
In building new systems, it may be best not to insist on large contiguous regions of address space for the heap, but to work more on the basis of frames, or at least to allow ‘holes’ in the middle of otherwise contiguous regions. Unfortunately this may then require table lookup for write barriers.
Assuming table lookup costs that are acceptable, the system can manage a large logical address space by mapping it down to the available virtual address space. This does not allow larger heaps, but it does give flexibility in that it removes some of the contiguity requirements. To do this, the system deals with memory in power-of-two sized and aligned frames, generally somewhat larger than a virtual memory page. The system maintains a table indexed by frame number (upper bits of virtual address) that gives each frame’s logical address. This table then supports the address comparisons used in a variety of address-oriented write barriers. It may lead to even better code to associate a generation number (for a generational write barrier) with each frame. Algorithm 11.11 gives pseudocode for such a write barrier. Each line can correspond to one instruction on a typical processor, particularly if entries in the frame table are a single byte each, simplifying the array indexing operation. Notice also that the algorithm works even if ref is null — we simply ensure that the entry for null’s frame has the highest generation number so the code will always skip the call to remember.
Algorithm 11.11: Frame-based generational write barrier
1 Write(src, i, ref):
2 ct ← frameTableBase
3 srcFrame ← src >>> LOG_FRAME_SIZE
4 refFrame ← ref >>> LOG_FRAME_SIZE
5 srcGen ← ct[srcFrame]
6 refGen ← ct[refFrame]
7 if srcGen > refGen
8 remember(src, &src[i], ref)
9 src[i] ← ref
It is further possible to arrange true multiplexing of a large address space into a smaller one — after all, that is what operating systems do in providing virtual memory. One approach would be to use wide addresses and do a check on every access, mimicking in software what the virtual memory hardware accomplishes. This could use the software equivalent of translation lookaside buffers, and so on. The performance penalty might be high. It is possible to avoid that penalty by leveraging the virtual memory hardware, which we discuss in more detail in Section 11.10.
It is good to build into systems from the start the capability to relocate the heap. Many systems have a starting heap or system image that they load as the system initialises. That image assumes it will reside at a particular location in the address space — but what if a dynamic link library lies right in the middle of it? If the image includes a table indicating which words need adjusting when the image is moved, not unlike many code segments, then it is relatively straightforward for the image loader to relocate the image to another place in the address space. Likewise it might be desirable to support relocating the entire heap, or segments of it, during system operation.
In actually managing virtual memory, we can distinguish between the managed system’s notion of address space dedicated to particular uses, which we call reserving the space, and actual allocation of pages via a call to the operating system. If the operating system might map new dynamic link libraries into the address space on the fly, to guarantee a reservation that the managed system has in mind it must actually allocate the pages — typically as demand-zero pages. This has relatively low cost, but may involve the operating system in reserving resources such as swap space, and all virtual memory mapping calls tend to be expensive. Allocating pages in advance can also determine earlier that there are not adequate resources for a larger heap. However, operating systems do not always ‘charge’ for demand-zero pages until they are used, so simply allocating may not give an early failure indication.
11.10 Applications of virtual memory page protection
There are a variety of checks that a system can arrange to happen as part of virtual memory protection checking. Implemented in this way the checks have little or no normal case overhead and furthermore require no explicit conditional branches. A general consideration is that the overhead of fielding the trap, all the way through the operating system to the collector software and back again, can be quite high. Also, changing page protections can be costly, especially in a multiprocessor system where the operating system may need to stop processes currently executing and update and flush their page mapping information. So sometimes an explicit check is cheaper even when the system could use protection traps [Hosking et al, 1992]. Traps are also useful in dealing with uncooperative code, in which it is not possible to cause barriers or checks in any other way.
A consideration, especially in the future, is that there are hardware performance reasons to increase page size. In particular, programs use more memory now than when these techniques were first developed, and systems tend to have more main memory available to map. At the same time, translation lookaside buffer size is not likely to grow because of speed and power concerns. But given that translation lookaside buffer size is more or less fixed, staying with a small page size while programs’ memory use increases implies more translation lookaside buffer misses. With larger pages some of the virtual memory ‘tricks’ may not be as desirable.
We assume a model in which data pages can have their protection set for read-write access, read-only access, and no-access. We are not concerned about execute privileges since we are unaware of garbage collection-related exploitation of no-execute protection; it is also less well supported across platforms.
Before considering specific applications we describe a general technique called double mapping, by which the system maps the same page at two different addresses with different protections. Consider for example an incremental copying collector with a tospace invariant. To prevent mutators from seeing fromspace pointers in pages not yet processed, the collector can set those pages to no-access, effectively creating a hardware supported read barrier. But how is the collector to process the pages? If the system is concurrent and the collector unprotects the page, some other mutator may see the contents before the collector processes them. However, if the page is mapped a second time in another place, with read-write access, then the collector can process the contents via that second mapping, then unprotect the page and wake up any mutator waiting for it.
In a smaller address space (even 32 bits is often small now) it may be difficult to double map. A solution to that problem is to fork a child process that holds the second version of the address space with same pages but different protections. The collector can communicate with the child, requesting the child to process a page, and so forth.
Note also that double mapping is problematic on some systems. One problem arises when caches are indexed by virtual address. In the presence of double mapping, the cache could potentially become incoherent. Typically the hardware avoids that by preventing aliased entries from residing in the cache at the same time. This can cause extra cache misses. However, in the case at hand it applies only to accesses by the mutator and collector near in time on the same processor. Another problem arises if the system uses inverted page tables. In this scheme, each physical page can have only one virtual address at a time. The operating system can support double mapping by effectively invalidating one of the virtual addresses and then connecting the other one. This may involve cache flushing.
Applications of no-access pages
In describing double mapping we have already given one example of using no-access pages: for an unconditional read barrier. There are at least two more applications for no-access pages in common use. One is to detect dereferences of null pointers, which we assume to be represented by the value 0. This works by setting page 0, and possibly a few more pages after it, no-access. If a mutator tries to access a field through a null pointer, it will attempt to read or write the no-access page. Since fielding a null pointer dereference exception is generally not required to be fast, this application can be a good trade-off. In the rare case of an access that has a large offset, the compiler can emit an explicit check. If the object layout places headers or other fields at negative offsets from the object pointer, the technique still works provided that one or more pages with very high addresses are set no-access. Most operating systems reserve the high addresses for their own use anyway.
The other common use for a no-access page is as a guard page. For example, the sequential store buffer technique for recording new remembered set entries consists of three steps: ensure there is room in the buffer; write the new element to the buffer; and increment the buffer pointer. The check for room, and the call to the buffer overflow handler routine, can be removed if the system places a no-access guard page immediately after the buffer. Since write barriers can be frequent and their code can be emitted in many places, the guard page technique can speed up mutators and keep their code smaller.
Some systems apply the same idea to detecting stack or heap overflow by placing a guard page at the end of the stack (heap). To detect stack overflow, it is best if a procedure’s prologue touches the most remote location of the new stack frame it desires to build. That way the trap happens at a well defined place in the code. The handler can grow the stack by reallocating it elsewhere, or add a new stack segment, and then restart the mutator with an adjusted stack and frame pointer. Likewise when using sequential allocation the allocator can touch the most remote word of the desired new object and cause a trap if it falls into the guard page that marks the end of the sequential allocation area.
In either case, if the new stack frame or object is so large that its most remote word might lie beyond the guard page, the system needs to use an explicit check. But such large stack frames and objects are rare in many systems, and in any case a large object will take more time to initialise and use, which amortises the cost of the explicit check.
No-access pages can also help in supporting a large logical address space in a smaller virtual address space. An example is the Texas persistent object store [Singhal et al, 1992]. Using the strategy for persistence (maintaining a heap beyond a single program execution) goes beyond our scope, but the mechanism is suitable for the non-persistent case as well. In this approach the system works in terms of pages, of the same size as virtual memory pages or some power-of-two multiple of that. The system maintains a table that indicates where each logical page is: either or both of an address in (virtual) memory and a location in an explicitly managed swapping file on disk. A page can be in one of four states:
• Unallocated: Not yet used, empty.
• Resident: In memory and accessible; it may or may not have a disk copy saved yet.
• Non-resident: On disk and not accessible.
• Reserved: On disk and not accessible, but with specific virtual memory reserved.
Initially, a new page starts Resident and has a new logical address, not determined by its virtual memory address. As virtual memory fills, some pages may be evicted to disk, saved according to their logical address. Also, the system converts all pointers in the page to their long logical form, a process called unswizzling in the literature [Moss, 1992]. Thus the saved form of a page is typically larger than its in-memory form. Also, the system must be able to find all the pointers in a page accurately. After evicting a page, its state is Reserved, and the system sets the virtual memory it occupied to no-access. This guarantees that if the program follows a pointer to an evicted object, there will be a page trap, which alerts the system to fetch the page back.
How can the system free up the Reserved virtual space for re-use? It must determine that there are no longer any Resident pages referring to the Reserved page. It can help make this happen by evicting pages that refer to the Reserved page. At that point the page can become Non-resident and the system can reuse the space.
Notice that Resident pages refer to each other and to Reserved pages, but never directly to data in Non-resident pages.
Now consider what happens if the program accesses a Reserved page (and if there are evicted data that are reachable in the object graph, then there must be Reserved pages). The system looks up the page’s logical address and fetches it from disk. It then goes through the page’s pointers and replaces long logical addresses with short virtual addresses (called pointer swizzling). For referents on pages that are Resident or Reserved, this consists of just a table lookup. If the referent is itself on a Non-resident page, then the system must reserve virtual address space for that page, and then replace the long address with a pointer to the newly Reserved page. Acquiring virtual address space for these newly Reserved pages may require evicting other pages so that some page(s) can be made Nonresident and their virtual address space recycled.
Just as an operating system virtual memory manager needs good page replacement policies, so the Texas approach needs a policy, though it can reasonably borrow from the vast store of virtual memory management algorithms.
How does the scheme work in the presence of garbage collection? It is clear that a full heap garbage collection of a heap larger than the virtual address space is probably going to involve significant performance penalties. Collection of persistent stores has its own literature and lies beyond our scope. However, we can say that partitioned schemes can help and techniques like Mature Object Space [Hudson and Moss, 1992] can offer completeness.
Related techniques include the Bookmarking collector [Hertz et al, 2005; Bond and McKinley, 2008]. However, the purpose of bookmarking is more to avoid thrashing real memory — it does not extend the logical address space beyond the physical. Rather it summarises the outgoing pointers of pages evicted by the operating system so that the collector can avoid touching evicted pages and thus remain within the working set, at a possible loss of precision similar to that occasioned by remembered sets and generational collection: the collector may trace from pointers in dead objects of evicted pages.
Other things being equal, larger heap sizes generally result in higher mutator throughput and lower collection cost. In some cases, a smaller heap size may improve mutator throughput by improving mutator locality by reducing cache or translation lookaside buffer misses. However, too big a heap may lead to a working set larger than can be accommodated in real memory, resulting in thrashing, particularly when the collector is active. Therefore, choosing an appropriate heap size often involves aiming to keep a program’s real memory footprint small enough. Knowing how small is small enough typically involves the run-time system and the operating system. We now review a number of schemes that automatic memory managers have used to adjust heap size. Alternative approaches to adjusting the size of the heap include choosing which pages to page out, as in the Bookmarking collector [Hertz et al, 2005; Hertz, 2006], and having the collector save rarely accessed objects to disk [Bond and McKinley, 2008].
Alonso and Appel [1990] devised a scheme where an ‘advice server’ tracks virtual memory usage using information available from ordinary system calls, vmstat in particular. After each full collection (the Appel collector for SML is generational), the collector reports its minimal space need, how much space more than that it is currently using for the heap, how long it has been since the last full collection and how much mutator and collector CPU time it has expended since the last collection. The advice server determines an additional amount of space that appears safe for the process to use, and the process adjusts its heap size accordingly. The aim is to maximise throughput of the managed processes without causing other processes to thrash either.
In contrast to Alonso and Appel, Brecht et al [2001, 2006] control the growth in heap size for Java applications without reference to operating system paging information. Rather, for a system with a given amount of real memory — they considered 64 and 128 megabytes — they give a series of increasing thresholds, T1 to Tk, stated as fractions of the real memory of the system. At any given time, a process uses a heap size of Ti for some i. If collecting at size Ti yields less than Ti+1 – Ti fraction of the space reclaimed, the system increases the threshold from Ti to Ti+1. They considered the Boehm-Demers-Weiser collector [Boehm and Weiser, 1988], which cannot shrink its heap, so their approach deals only with heap growth. The thresholds must be determined empirically, and the approach further assumes that the program in question is the only program of interest running on the system.
Cooper et al [1992] present an approach that aims for a specified working set size for an Appel-style SML collector running under the Mach operating system. They adjust the nursery size to try to stay within the working set size, and they also do two things specific to Mach. One is that they use a large sparse address space and avoid the need to copy tospace to lower addresses to avoid hitting the end of the address space. This has little to do with heap sizing, but does reduce collector time. The second thing specific to Mach is having the collector inform the Mach pager that evacuated fromspace pages can be discarded and need not be paged out, and if referenced again, such pages can be offered back to the application with arbitrary contents — the allocator will zero them as necessary. Cooper et al obtain a four-fold improvement in elapsed time for a small benchmark suite, with about half of the improvement coming from the heap size adjustment. However, the target working set size must still be determined by the user.
Yang et al [2004] modify a stock Unix kernel to add a system call whereby an application can obtain advice as to how much it may increase its working set size without thrashing, or how much to decrease it to avoid thrashing. They modify garbage collectors of several kinds to adjust their heap size using this information. They demonstrate the importance of adaptive heap sizing in obtaining the best performance as memory usage by other processes changes. They introduce the notion of the footprint of a program, which is the number of pages it needs in memory to avoid increasing the running time by more than a specified fraction t, set to five or ten percent. For a garbage collected program, the footprint depends on the heap size, and for copying collectors, also on the survival rate from full collections, that is, the live size. However, an observation they make, not unlike Alonso and Appel, is that the key relationship is between how the footprint changes for a given change in heap size. In particular, the relationship is linear, with the ratio determined by the particular collection algorithm. The ratio is 1 for mark-sweep based collectors, while it is 2 for copying collectors.
Grzegorczyk et al [2007] consider the relative helpfulness of several pieces of information related to paging that can be obtained from a standard Unix kernel. Specifically they look at page outs, the number of pages written to the swap area by the kernel swapping daemon, page faults, the number of pages missing when referenced that had to be fetched from disk, and allocation stalls, the number of times the process had to wait when trying to obtain a fresh page. These counts are all related to the particular executing process in that page outs have to do with the pages of that process, and page faults and allocation stalls occur because of actions of the process. Of these three possible indicators that a system is under so much memory load that shrinking the heap might be wise, they find that the number of allocation stalls is the best indicator to use. When a collection sees no allocation stalls, it will grow the heap by an amount originally set to 2% of the user-specified heap size; values between 2% and 5% gave similar results. If a collection experiences allocation stalls, the collector shrinks the nursery so that the total heap space, including the reserve into which the nursery is copied, fits within the space used the last time that there were no allocation stalls. This leaves the nursery cut by up to 50%. In the absence of memory pressure, the scheme performs similar to a non-adjusting baseline, while in the presence of memory pressure, it performs close to the non-pressure case while the baseline system degrades substantially.
The schemes we have discussed so far concern adjusting individual processes’ use of memory dynamically, perhaps in response to general use of memory within a system at any given time. If, on the other hand, the set of programs to be run is known in advance and does not vary, the approach of Hertz et al [2009] aims to indicate the best heap size to give to each program. In this scheme ‘best’ means ‘gives the least overall execution time’, which can also be stated as ‘give the highest overall throughput’. At run time, their Poor Richard’s Memory Manager has each process observe its recent page fault counts and resident set size. If the number of page faults observed in one time increment is greater than the number observed in the previous increment by more than a threshold amount, the collector triggers a full collection, in order to reduce the working set size. Likewise it triggers a full collection if the resident set size decreases. The resulting system appears to size competing processes’ heaps well to achieve the best throughput.
The dynamic heap sizing mechanism proposed by Zhang et al [2006] is similar in spirit to that of Hertz et al [2009], but has the program itself check the number of page faults at each collection and adjust the target heap size itself, rather than building the mechanism into the collector. Unlike the other mechanisms we have discussed, they assume that the user has somehow identified the phases of the program and inserted code to consider forcing collection at phase changes. They showed that dynamic adaptive heap sizing can substantially improve performance over any single fixed heap size.
The allocation interface presents a number of questions that the implementer must answer. Some answers may be dictated by the language semantics or by the level of concurrency in the environment (can objects ‘leak’ from their allocating thread?). Others may be at the discretion of the implementer and the decisions may be made in order to improve performance or the robustness of the run-time system.
We need to consider what requirements are made of allocation and initialisation. Is the language run-time’s job simply to allocate some space of sufficient size, must some header fields be initialised before the object can be usable or must initialising values for all the newly allocated object’s fields be provided? What are the alignment requirements for this object? Should the run-time distinguish between different kinds of objects, such as arrays and other objects? Is it beneficial to treat objects that may contain pointers from those that do not? Such a distinction may help to improve tracing since pointer-free objects do not need to be scanned. Avoiding scanning such objects is known to be particularly beneficial for conservative collectors.
Often we will want to consider carefully how much of the allocation code sequence can be inlined. Typically, we might inline a fast path in which an object can be allocated with the least work but not the other slower paths which might involve obtaining space from a lower-level allocator or invoking the collector. However, too much inlining can explode the size of the code and negate the benefit hoped for. Similarly, it might be desirable to dedicate a register to a particular purpose, such as the bump-pointer for sequential allocation. However, doing so may place too much pressure on the register allocator on a register-poor platform.
Depending on the language supported, for safety or for debugging, the run-time may zero memory. Space could be zeroed as objects are allocated but bulk zeroing with a well-optimised library routine is likely to be more efficient. Should memory be zeroed shortly before it is used (for best cache performance) or immediately when it is freed, which may help with debugging (though here writing a special value might be more useful)?
Collectors need to find pointers in order to determine reachability. Should the run-time provide a precise or a conservative estimate to the collector? Or might it provide a conservative estimate of the pointers in program threads and a more precise estimate of pointer locations in the heap? Conservative pointer finding can ease aspects of an implementation, but risks space leaks and may lead to worse performance than type-accurate collection. Finding pointers in the stack, especially if it contains a mixture of frame types (optimised and unoptimised subroutines, native code frames, bridging frames), can be challenging to implement type-accurately. On the other hand, scanning stacks for pointers constrains the choice of collection algorithm as objects directly reachable from stacks cannot be moved.
Systems generally provide stack maps to determine from a return address the function within which the address lies. Polymorphic functions and language constructs such as Java’s jsr bytecode complicate their use. The implementer must also decide when stack maps should be generated and when they can be used. Should the maps be generated in advance or should we defer generating until the collector needs one, thereby saving space? Is a map only valid at certain safe-points? Stack maps can be large: how can they be compressed, especially if they must be valid at every instruction? Stack scanning also raises the question of whether the stack should be scanned in its entirety, atomically, or incrementally. Incremental stack scanning is more complex but offers two benefits. First, it can bound the amount of work done in an increment (which may be important for realtime collectors). Second, by noting the portion of the stack that has not changed since the last time it was scanned, we can reduce the amount of work that the collector has to do.
Language semantics and compiler optimisations raise further questions. How should interior and derived pointers be handled? Language may allow access to objects from outside the managed environment, typically from code written in C or C++, and every language needs to interact with the operating system for input/output. The run-time must ensure that objects are not reclaimed while they are being used by external code and that external code can find these objects. Typically, this may involve pinning such objects or providing access to them through handles.
Some systems may allow a garbage collection at any point. However it is usually simpler to restrict where collection can happen to specific GC-safe points. Typically these include allocation, backward branches, and function entry and return. There are alternative ways to cause a thread to suspend at a GC-point. One way is to have threads poll by checking a flag that indicates that a collection has been requested. An alternative is to patch the code of a running thread to roll it forward to the next GC-point. The handshake between collector and mutator thread can be achieved by having threads check a thread-local variable, by setting a processor condition code in the saved thread state of a suspended thread, by hijacking return address or through operating system signals.
Several classes of garbage collection algorithm require ‘interesting’ pointers to be detected as mutators run. This opens up a wide range of design policies and implementations for the detection and recording of these pointers. As barrier actions are very common, it is essential to minimise any overhead they incur. Barriers may be short sequences of code inserted by the compiler before pointer loads or stores, or they may be provided through operating system support, such as page protection traps. As always, there are trade-offs to be considered. In this case, the trade-offs are between the cost to the mutator and the cost to the collector, between precision of recording and speed of a barrier. In general, it is better to favour adding overhead to relatively infrequent collector actions (such as discovering roots) than to very frequent mutator actions (such as heap stores). Adding a write barrier can increase the instruction count for a pointer write by a factor of two or more, though some of this cost may be masked by cache access times.
How accurately should pointer writes be recorded? Unconditional logging may impose less overhead on the mutator than filtering out uninteresting pointers but the implementation of the remembered set is key to this decision. How much filtering should be inline? Careful tuning is essential here. At what granularity is the location of the pointer to be recorded? Should we record the field overwritten, the object or the card or page on which it resides? Should we allow the remembered set to contain duplicate entries? Should arrays and non-arrays be treated in the same way?
What data structures should be used to record the locations of interesting pointers: hash tables, sequential store buffers, cards or a combination of these? How does this choice vary the overheads between the mutator and the collector? Data structures may overflow: how can this be handled safely and efficiently? Card tables offer an imprecise recording mechanism. At collection time they must be scanned to find dirty cards and hence objects that may contain interesting pointers. This raises three performance questions. What size should a card be? Card tables are often sparse: how can we speed up the search for dirty cards? Should a two-level card table be used? Can we summarise the state of a card, for example if it contains only one modified field or object? Once a dirty card is found, the collector needs to find the first object on that card, but that object may start on an earlier card. We need a crossing map that decodes how objects span cards. How does card marking interact with multiprocessor cache coherency protocols? If two processors repeatedly write to different objects on the same card, both will want exclusive access to the card’s cache line. Is this likely to be a problem in practice?
In systems run with virtual memory, it is important that garbage collected applications fit within available real memory. Unlike non-managed programs, garbage collected ones can adjust their heap size so as to fit better within available memory. What events and counts does the particular operating system provide that a collector might use to adjust heap size appropriately? Which of these events or counts are most effective? What is a good heap growth policy, and an appropriate one for shrinking, if shrinking is possible? How can multiple collected processes cooperate so as to offer good throughput for all?
In summary, many of the details raised here are subtle but both design choices and implementation details have substantial effect on performance. In later chapters, we shall see how the solutions discussed here can be used by garbage collection algorithms.
1In principle a Java program can catch the exception and try nulling some pointers and restarting a computation, but we are not aware of that strategy in real programs. Besides, Java’s soft references are an arguably better way to do the same thing.
2In either case it allows interior pointers, but in the more restrictive case it requires that any reachable object have a reachable pointer that is not interior. Thus in that configuration it ignores interior pointers when marking.
3This is a property of the representational approach, not of the language: in using this form of tagging the designer made a choice to represent integers (floats, and so on) as tagged pointers to their full (untagged) values.
4Bartlett [1989b] takes this approach for a Scheme implementation done by translating to C, and Cheadle et al [2000] take this approach in Non-Stop Haskell.
5Tarditi uses the term ‘call site’ where we use ‘GC-point’.
6Excepting the possibility of checking for adequate thread-private free space before a sequence of allocations.