So far we have seen that mark-sweep has comparatively cheap collection costs but may suffer from fragmentation. Given that garbage collection should account for only a small proportion of overall execution time in any well configured system, it is essential that overheads on the mutator are kept to a minimum and, in particular, that allocation is fast, since mutator costs dominate those of the collector. Mark-compact collectors eliminate fragmentation and support very fast, ‘bump a pointer’ allocation (see Chapter 7) but require multiple passes over live objects, and significantly increase collection times. In this chapter, we discuss a third style of tracing garbage collection, semispace copying [Fenichel and Yochelson, 1969; Cheney, 1970]. Copying compacts the heap, thus allowing fast allocation, yet requires only a single pass over the live objects in the heap. Its chief disadvantage is that it reduces the size of the available heap by half.
4.1 Semispace copying collection
Basic copying collectors divide the heap into two, equally sized semispaces, called fromspace and tospace. For simplicity, Algorithm 4.1 assumes that the heap is one contiguous region of memory, but this is not essential. New objects are allocated in tospace by incrementing the value of a free pointer if there is sufficient room.1 Otherwise, the role of the two semispaces is flipped (line 2 in Algorithm 4.2) before the collector copies all live objects from what is now the fromspace to the tospace. This collector simply picks out — evacuating or scavenging — live objects from the old semispace. At the end of the collection, all live objects will have been placed in a dense prefix of tospace. The collector simply abandons fromspace (and the objects it contains) until the next collection. In practice, however, many collectors will zero that space for safety during the initialisation of the next collection cycle (see Chapter 11 where we discuss the interface with the run-time system).
After initialisation, semispace copying collectors populate their work list by copying the root objects into tospace (line 4). Copied but not yet scanned objects are grey. Each pointer field of a grey object will hold either null or a reference to a fromspace object. The copying scan traces each grey field, updating it to point to the tospace replica of its target. When the trace visits a fromspace object, forward checks whether it has been evacuated (forwarded) yet. If not, the object is copied now to the location in tospace to which free points, and the free pointer is incremented by the size of the object (as for allocation). It is essential that collectors preserve the topology of live objects in the tospace copy of the heap. This is achieved by storing the address of each tospace object as a forwarding address in its old, fromspace replica when the object is copied (line 34). The forward routine, tracing from a tospace field, uses this forwarding address to update the field, regardless of whether the copy was made in this tracing step or a previous one (line 22). Collection is complete when all tospace objects have been scanned.
Algorithm 4.1: Semispace copying garbage collection: initialisation and allocation. For simplicity this assumes that the heap is a single contiguous region.
1 createSemispaces():
2 tospace ← HeapStart
3 extent ← (HeapEnd — HeapStart) / 2 | /* size of a semispace */ |
4 top ← fromspace ← HeapStart + extent
5 free ← tospace
6
7 atomic allocate(size):
8 result ← free
9 newfree ← result + size
10 if newfree > top
11 return null | /* signal |
12 free ← newfree
13 return result
Unlike most mark-compact collectors, semispace copying does not require any extra space in object headers. Any slot in a fromspace object can be used for the forwarding address (at least, in stop-the-world implementations), since that copy of the object is not used after the collection. This makes copying collection suitable even for header-less objects.
Like all tracing collectors, semispace copying needs a work list of objects to process. The work list can be implemented in different ways, leading to different orders of traversing the object graph and different space requirements. Fenichel and Yochelson [1969] implemented the work list as a simple auxiliary stack, just as the mark-sweep collectors described in Chapter 2 did. Copying is complete when the stack is empty.
The elegant Cheney scanning algorithm Cheney [1970] uses the grey objects in tospace as a first-in, first-out queue. It requires no additional storage other than a single pointer, scan, which points to the next unscanned object. When the semispaces are flipped, both the free and scan pointers are set to point to (the start of) tospace (see initialise in Algorithm 4.3). After the root objects are copied, the work list — the set of grey objects — comprises precisely those (copied but unscanned) objects between scan and free. This invariant is maintained throughout the collection. The scan pointer is advanced as tospace fields are scanned and updated (line 9). Collection is complete when the work list is empty: when the scan pointer catches up with the free pointer. Thus, the actions of this implementation are very simple. To determine termination, isEmpty does no more than compare the scan and free pointers; remove just returns the scan pointer; and no action is required to add work to the work list.
Algorithm 4.2: Semispace copying garbage collection
1 atomic collect() :
2 flip()
3 initialise(worklist) | /* empty */ |
4 for each fld in Roots | /* copy the roots */ |
5 process (fld)
6 while not isEmpty(worklist) | /* copy transitive closure */ |
7 ref ← remove(worklist)
8 scan(ref)
9
10 flip(): | /* switch semispaces */ |
11 fromspace, tospace ← tospace, fromspace
12 top ← tospace + extent
13 free ← tospace
14
15 scan(ref):
16 for each fld in Pointers (ref)
17 process (fld)
18
19 process(fld): | /* update field with reference to tospace replica */ |
20 fromRef ← *fld
21 if fromRef ≠ null
22 *fld ← forward(fromRef) | /* update with tospace reference */ |
23
24 forward(fromRef):
25 toRef ← forwardingAddress (fromRef)
26 if toRef = null | /* not copied (not marked) */ |
27 toRef ← copy(fromRef)
28 return toRef
29
30 copy(fromRef): | /* copy object and return forwarding address */ |
31 toRef ← free
32 free ← free + size(fromRef)
33 move (fromRef, toRef)
34 forwardingAddress(fromRef) ← toRef | /* mark */ |
35 add(worklist, toRef)
36 return toRef
Algorithm 4.3: Copying with Cheney’s work list
1 initialise(worklist):
2 scan ← free
3
4 isEmpty(worklist):
5 return scan = free
6
7 remove(worklist):
8 ref ← scan
9 scan ← scan + size(scan)
10 return ref
11
12 add(worklist, ref):
13 /* nop */
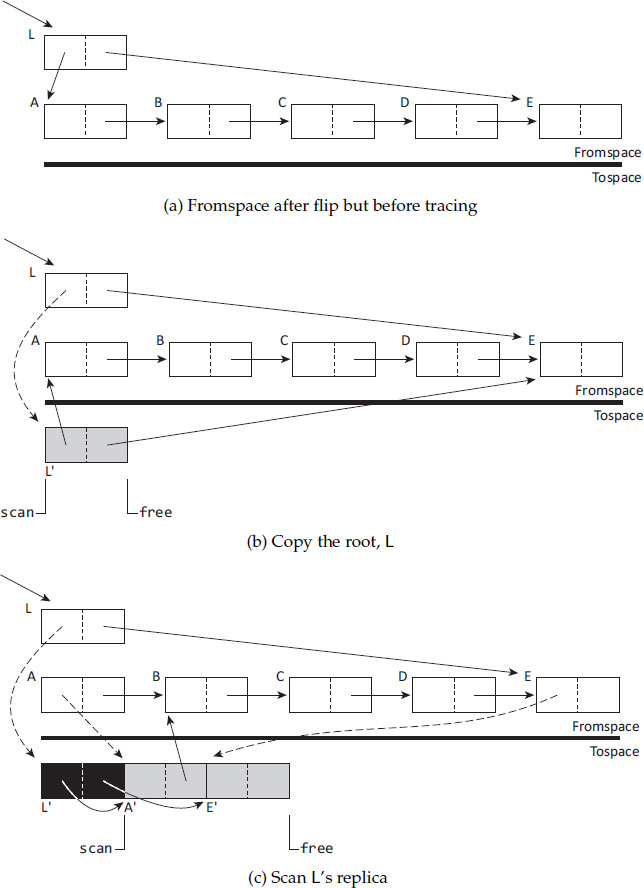
Figure 4.1 shows an example of how a Cheney scan would copy L, a linked list structure with pointers to the head and tail of the list. Figure 4.1a shows fromspace before the collection starts. At the start of the collection, the roles of the semispaces are flipped and L, which we assume is directly reachable from the roots, is copied to tospace (advancing the free pointer) and a forwarding reference to the new location L′ is written into L (for instance, over the first field). The scan pointer points to the first object in tospace (Figure 4.1b). The collector is now ready to start copying the transitive closure of the roots. The scan pointer points to the first object to process. L′ holds references to A and E in fromspace, so these objects are evacuated to the location pointed at by free in tospace (advancing free), the references in L′ are updated to point to the new locations A′ and E′ (Figure 4.1c), and scan is advanced to the next grey object. Note that the collector is finished with L′ so it is conceptually black, whereas the next objects to scan, A′ and E′, are grey. This process is repeated for each tospace object until the scan and free pointers meet (Figure 4.1f). Observe that, in Figure 4.1e, D′ holds a reference to E, which has already been copied. The referring field in D′ is therefore updated with the forwarding address stored in E, thereby preserving the shape of the graph. As with other tracing algorithms, copying garbage collection can cope with all shapes of graphs, including cyclic data structures, preserving sharing properly.
4.2 Traversal order and locality
Mutator and collector locality can have a significant impact on program performance. As we saw in the previous chapter, the collector can harm the mutator’s locality and hence its performance if it moves objects to arbitrary new locations without regard for either pointer relationships or the original allocation order [Abuaiadh et al, 2004]. However, there is a performance trade-off between locality benefits for the mutator, and for the collector and the frequency of collections. Compare mark-sweep and copying collection. Mark-sweep collectors have twice as much usable heap space available as do copying collectors, and hence will perform half as many collections, all other things being equal. Consequently, we might expect that mark-sweep collection offer better overall performance. Blackburn et al [2004a] found that this was indeed the case for collection in tight heaps, where he used a segregated-fits allocator for the non-moving collector. Conversely, in large heaps the locality benefits to the mutator of sequential allocation outweighed the space efficiency of mark-sweep collection, leading to better miss rates at all levels of the cache hierarchy. This was particularly true for newly allocated objects which tend to experience higher mutation rates than older objects [Blackburn and McKinley, 2003].
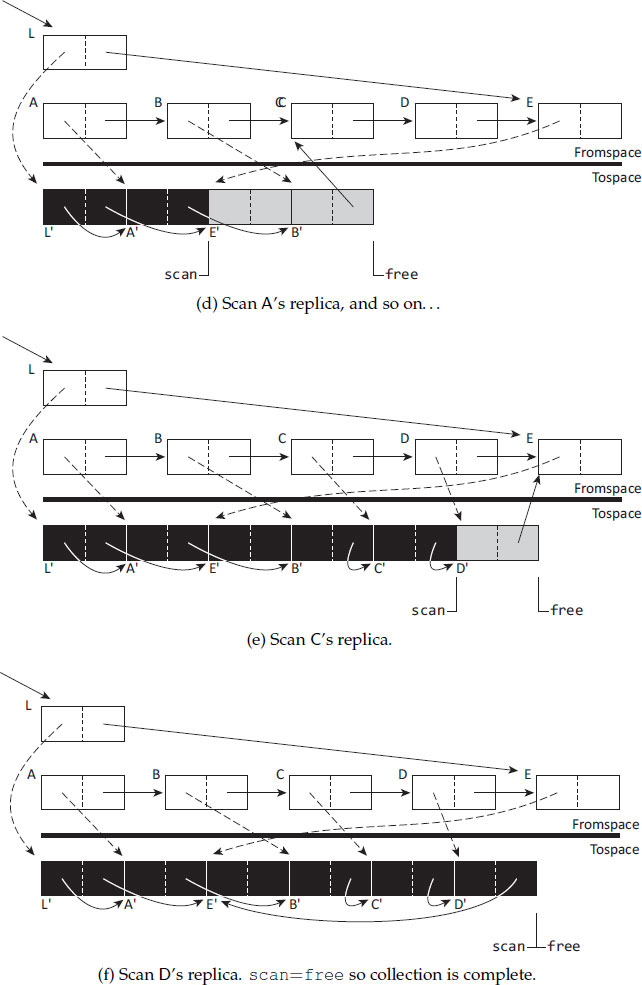
Figure 4.1: Copying garbage collection: an example
Figure 4.2: Copying a tree with different traversal orders. Each row shows how a traversal order lays out objects in tospace, assuming that three objects can be placed on a page (indicated by the thick borders). For online object reordering, prime numbered (bold italic) fields are considered to be hot.
The Blackburn et al [2004a] study copied objects depth-first. In contrast, Cheney’s copying collector traverses the graph breadth-first. Although this is implemented by a linear scan of — and hence predictable access to — the work list of grey tospace objects, breadth-first copying adversely affects mutator locality because it tends to separate parents and children. The table in Figure 4.2b compares the effect of different traversal orders on object layout, given the tree in Figure 4.2a. Each row shows where different tracing orders would place objects in tospace. If we examine row 2, we see that breadth-first traversal places only objects 2 and 3 near their parent. In this section we look more closely at traversal order and its consequences for locality.
White [1980] suggested long ago that the garbage collector could be used to improve the performance of the mutator. Both copying and compacting garbage collectors move objects, thus potentially affecting the mutators’ locality patterns. Sliding is generally considered to be best order for mark-compact algorithms since it preserves the order of layout of objects established by the allocator. This is a safe, conservative policy, but can we do better? Mark-compact algorithms condense the heap in place, either by moving objects into holes (arbitrary order compactors) or by sliding live data (overwriting only garbage or objects that have already been moved), and thus have no opportunity for more locality-aware reorganisation. However, any collector that evacuates live objects to a fresh region of the heap without destroying the original data can rearrange their layout in order to improve the performance of the mutator.
Unfortunately there are two reasons why we cannot find an optimal layout of objects, that minimises the number of cache misses suffered by the program. First of all, the collector cannot know what the pattern of future accesses to objects will be. But worse, Petrank and Rawitz [2002] show that the placement problem is NP-complete: even given a perfect knowledge of future accesses, there is no efficient algorithm to compute an optimal placement. The only solution is to use heuristics. One possibility is to use past behaviour as a predictor of future behaviour. Some researchers have used either profiling, on the assumption that programs behave similarly for different inputs [Calder et al, 1998], or online sampling, assuming that behaviour remains unchanged from one period to the next [Chilimbi et al, 1999]. Another heuristic is to preserve allocation order, as sliding compaction does. A third strategy is to try to place children close to one of their parents, since the only way to access a child is by loading a reference from one of its parents. Cheney’s algorithm uses breadth-first traversal, but its unfortunate consequence is that it separates related data, tending to co-locate distant cousins rather than parents and children. Depth-first traversal (row one), on the other hand, tends to place children closer to their parents.
Algorithm 4.4: Approximately depth-first copying [Moon, 1984] (we assume that objects do not span pages)
1 initialise(worklist):
2 scan ← free
3 partialScan ← free
4
5 isEmpty(worklist): | /* as per Cheney */ |
6 return scan = free
7
8 remove(worklist) :
9 if (partialScan < free)
10 ref ← partialScan | /* prefer secondary scan */ |
11 partialScan ← partialScan + size(partialScan)
12 else
13 ref ← scan | /* primary scan */ |
14 scan ← scan + size(scan)
15 return ref
16
17 add(worklist, ref): | /* secondary scan on the most recently allocated page */ |
18 partialScan ← max(partialScan, startOfPage (ref))
Early studies of the locality benefits of different copying orders focused on trying to minimise page faults: the goal was to place related items on the same page. Stamos found that simulations of Smalltalk systems suggested that depth-first ordering gave a modest improvement over breadth-first ordering but worse paging behaviour than the original object creation order [Stamos, 1982; Blau, 1983; Stamos, 1984]. However, Wilson et al [1991] argue that these simulations ignore the topology of real Lisp and Smalltalk programs which tended to create wide but shallow trees, rooted in hash tables, designed to spread their keys in order to avoid clashes.
If we are prepared to pay the cost of an auxiliary last-in, first-out marking stack, then the Fenichel and Yochelson algorithm leads to a depth-first traversal. However, it is possible to obtain a pseudo-depth-first traversal without paying the space costs that come from using a stack. Moon [1984] modified Cheney’s algorithm to make it ‘approximately depth-first’. He added a second, partialScan pointer in addition to the primary scan pointer (see Figure 4.3). Whenever an object is copied, Moon’s algorithm starts a secondary scan from the last page of tospace that has not been completely scanned. Once the last tospace page has been scanned, the primary scan continues from the first incompletely scanned page (Algorithm 4.4). In effect, the work list is implemented as a pair of Cheney queues. The advantage of this hierarchical decomposition scheme is that it is more effective than pure breadth-first search at depositing parents on the same page as their children. The hierarchical decomposition line of Figure 4.2b shows how this algorithm would copy the tree, assuming a page size of three objects.
Figure 4.3: Moon’s approximately depth-first copying. Each block represents a page. As usual, scanned fields are black, and copied but not yet scanned ones are grey. Free space is shown in white.
Figure 4.4: A FIFO prefetch buffer (discussed in Chapter 2) does not improve locality with copying as distant cousins (C, Y, Z), rather than parents and children, tend to be placed together.
The disadvantage of Moon’s algorithm is that objects may be scanned twice since he records only a pair of scan pointers, thus forgetting blocks between scan and free that have already been partially scanned; indeed, Wilson et al [1991] suggest that around 30% may be rescanned. They modified this algorithm to provide each page with its own scan and free pointers, making the work list now a list of partially scanned blocks to complete. This means that the primary scan does not have to revisit objects on pages already processed by a secondary scan.
When we discussed how to improve the marking loop of a mark-sweep collector in Section 2.6, we mentioned that Cher et al [2004] argued that using a stack to guide tracing leads to a depth-first traversal of the graph but cache lines are fetched breadth-first. A natural question to ask is can we combine stack-based, depth-first copying with the first-in, first-out prefetch queue suggested by Cher et al [2004]? Unfortunately it seems not, because although first-in, first-out helps the copying loop avoid cache miss stalls, it separates parents from children since it visits an object to follow its references only when it is removed from the queue, not from the stack.2 Imagine that a string object S is popped from the stack. Desirably, S should be placed adjacent to its associated character array C in tospace, as the depth-first algorithm would do. Using the first-in, first-out queue, after S is popped from the stack, it is added to the queue. Suppose that the queue is full, so the oldest entry X is removed, copied and its references Y and Z pushed on the stack, as illustrated in Figure 4.4. Unfortunately, Y and Z will be removed from the queue and copied after S but before C.
Algorithm 4.5: Online object reordering
1 atomic collect():
2 flip()
3 initialise(hotList, coldList)
4 for each fld in Roots
5 adviceProcess(fld)
6 repeat
7 while not isEmpty(hotList)
8 adviceScan(remove(hotList))
9 while not isEmpty(coldList)
10 adviceProcess(remove(coldList))
11 until isEmpty(hotList)
12
13 initialise(hotList, coldList):
14 hotList ← empty
15 coldList ← empty
16
17 adviceProcess(fld):
18 fromRef ← *fld
19 if fromRef ≠ null
20 *fld ← forward(fromRef)
21
22 adviceScan(obj):
23 for each fld in Pointers(obj)
24 if isHot(fld)
25 adviceProcess(fld)
26 else
27 add(coldList, fld)
The reorganisations above are static: the algorithms pay no attention to the behaviour of individual applications. However, it is clear that the benefits of layout reordering schemes depend on the behaviour of the mutator. Lam et al [1992] found that both algorithms were sensitive to the mix and shape of program data structures, giving disappointing performance for structures that were not tree-like. Siegwart and Hirzel [2006] also observed that a parallel hierarchical decomposition collector led to benefits for some benchmarks but little improvement overall for others. Huang et al [2004] address this by dynamically profiling the application and trying to copy ‘hot’ fields of objects alongside their parent. Their online object reordering scheme and its effect are shown in Algorithm 4.5 and the last row of Figure 4.2b. The main scanning loop of their algorithm (line 6) processes all hot fields in its work lists before any cold fields. Piggybacking on the method sampling mechanism of an adaptive dynamic compiler allows these fields to be identified comparatively cheaply (Huang et al report less than 2% of total execution time). Their implementation also accommodates changes of behaviour in different program phases by allowing the ‘heat’ of fields to decay and be resampled. They find that the performance of their system matches or improves that of static reorderings such as breadth-first.
Chen et al [2006] and Chilimbi and Larus [1998] proactively invoke the collector to improve locality in a generational collector. Their mechanism is expensive so is not always on. Instead, they use changes in allocation rates as their primary trigger to collection in order to improve locality; changes in data translation lookaside buffer (TLB) or Level 2 cache miss rate are used as a secondary trigger. They record object accesses in a fixed-size, circular buffer (they argue that profiling at the node level rather than the field level leads to overheads less than 5%, since most nodes in object-oriented programs are smaller than 32 bytes). An expensive (but aggressively optimised) read barrier3 operates during bursty sampling phases to identify hot objects as the mutators load references to them. Their collector copies hot objects in two phases. First, contemporaneously accessed objects are copied to a temporary buffer. Then, to improve paging, the collector appends hot objects to this buffer, using hierarchical decomposition [Wilson et al, 1991]. The original locations of copied objects are marked free, and the rearranged group of objects is moved from the temporary buffer to one end of the heap. The scheme aims to improve both cache performance and paging behaviour: the benefit of combining both optimisations was found to be greater than the sum of either applied on its own, and gave an average improvement in execution time for a range of large C# applications. Although it is possible that some garbage objects may be preserved, in practice the volume is very small.
Other authors have also suggested custom, static reordering by object type [Wilson et al, 1991; Lam et al, 1992], particularly for system data structures. By allowing class authors to specify the order in which fields are copied, Novark et al [2006] reduce the cache miss rate significantly for certain data structures. Shuf et al [2002] use off-line profiling to identify prolific types. The allocator is modified so that, when a parent is created, adjacent space is left for its children, thus both improving locality and encouraging clustering of objects with similar lifetimes. This approach may address to some extent the problem identified on page 51 of combining a first-in, first-out prefetch queue with depth-first copying.
Copying collection offers two immediately attractive advantages over non-moving collectors like mark-sweep: fast allocation and the elimination of fragmentation (other than to satisfy alignment requirements). Simple copying collectors are also easier to implement than mark-sweep or mark-compact collectors. The trade-off is that copying collection uses twice as much virtual memory as other collectors in order to match their frequency of collections.
Allocation in a compacted heap is fast because it is simple. In the common case, it simply requires a test against a heap or block limit and that a free pointer be incremented. If a block structured rather than a contiguous heap is used, occasionally the test will fail and a new block must be acquired. The slow path frequency will depend on the ratio of the average size of objects allocated and the block size. Sequential allocation also works well with multithreaded applications since each mutator can be given its own local allocation buffer in which to allocate without needing to synchronise with other threads. This arrangement is simpler and requires little metadata, in contrast with local allocation schemes for non-moving collectors where each thread might need its own size class data structures for segregated-fits allocation.
The code sequence for such a bump-a-pointer allocation is short but, even better, it is well behaved with respect to the cache as allocation advances linearly through the heap. Although the combination of sequential allocation, typically short object lifetimes and semispaces means that the next location to be allocated is likely to be the one least recently used, the prefetching abilities of modern processors are likely to hide the latency that might otherwise result. If this behaviour conflicts with the operating system’s least recently used (LRU) page eviction policy to the extent that paging becomes a problem, it is time to reconsider the configuration of the system. Either it requires more physical memory to run the application satisfactorily, or another collection policy — maybe one of the generational collectors we discuss in Chapter 9 — should be used.
Blackburn et al [2004a] found that although sequential allocation had an 11% advantage over free-list allocation in a micro-benchmark limit study, allocation itself accounted for less than 10% of overall running time in real applications. Thus, the difference in cost between bump-a-pointer allocation and free-list allocation may not be significant. However, allocation is only part of the picture for the mutator since the cost of creating a new object is likely to be dominated by its initialisation, certainly in systems that distinguish these actions. Furthermore, objects share similar life-cycles in many applications. The mutator creates some semantically related objects at around the same time, uses them, and finally tends to abandon them all at once. Here, compacted heaps offer good spatial locality, with related objects typically allocated on the same page and maybe in the same cache line if they are small. Such a layout is likely to lead to fewer cache misses than if related objects are allocated from different free-lists.
The immediate disadvantage of semispace copying is the need to maintain a second semispace, sometimes called a copy reserve. For a given memory budget and ignoring the data structures needed by the collector itself, semispace copying provides only half the heap space of that offered by other whole heap collectors. The consequence is that copying collectors will perform more garbage collection cycles than other collectors. Whether or not this translates into better or worse performance depends on trade-offs between the mutator and the collector, the characteristics of the application program and the volume of heap space available.
Simple asymptotic complexity analyses might prefer copying over mark-sweep collection. Let M be the total size of the heap, and L be the volume of live data. Semispace collectors must copy, scan and update pointers in live data. Mark-sweep collectors must similarly trace all the live objects but then sweep the whole heap. Jones [1996] defines the time complexities for copying and mark-sweep collection as, respectively:
The amount of memory reclaimed by each collector is:
Let r = L/M be the proportion of live memory, which we assume to be constant. The efficiency of an algorithm can be described by its mark/cons ratio, e, the amount of work done by the collector per unit allocated. The efficiency of these two algorithms is therefore:
Figure 4.5: Mark/cons ratios for mark-sweep and copying collection (lower is better).
The mark/cons ratio curves presented in Figure 4.5 show that copying collection can be made more efficient that mark-sweep collection, provided that the heap is large enough and r is small enough. However, such a simple analysis ignores several matters. Modern mark-sweep collectors are likely to use lazy sweeping, thus reducing the constant s and lowering mark-sweep’s mark/cons ratio. Complexity analyses need to be treated with some caution since they ignore implementation details, although Hertz and Berger [2005] confirm experimentally the general shape of the curves (for example, that the cost of mark-sweep collection is inversely proportional to the size of the heap). However, pragmatic details are important for real collectors. These are not captured by complexity analyses. One example is the locality benefit of sequential allocation [Blackburn et al, 2004a].
So, sequential allocation tends to lay out contemporaneously accessed objects contiguously, which helps to improve the mutator’s cache miss rate. But copying collection then reorders surviving objects in the heap. Although Cheney-style collectors need no auxiliary stack to guide the trace, their breadth-first traversal tends to separate parents and children. Hierarchical decomposition offers a compromise between paying the costs of a tracing stack and improving the layout of objects in the heap. However, although careful reordering has benefits for some programs, it often has negligible effects. Why is this? Most objects have short lifetimes and do not survive a collection. Moreover, many applications concentrate accesses, and especially writes, on these young objects [Blackburn and McKinley, 2003]. Collector traversal policies cannot affect the locality properties of objects that are never moved.
Printezis has also pointed out that whether parallel collector threads are used or not will influence the choice of copying mechanism. It may be simpler to do very fine-grained load-balancing by work stealing from per-thread stacks as opposed to using a Cheney queue.4 We discuss these issues in depth in Chapter 14.
The choice of a copying collector will depend in part on whether it is possible to move objects and the cost of doing so. In some environments objects cannot be moved. One reason is that lack of type accuracy means that it would not be safe to modify the slot holding a reference to a putative object. Another is that a reference to the object has been passed to unmanaged code (perhaps, as an argument in a system call) that does not expect the reference to change. Furthermore, the problem of pointer finding can often be simpler in a mark-sweep context than that of a moving collector. It suffices to find at least one reference to a live object with a non-moving collector. On the other hand, a moving collector must find and update all references to an evacuated object. As we will see in Chapter 17, this also makes the problem of concurrent moving collection much harder than concurrent non-moving collection since all the references to an object must appear to be updated atomically.
It is expensive to copy some objects. Although copying even a small object is likely to be more expensive than marking it, the cost and latency of doing so is often absorbed by the costs of chasing pointers and discovering type information. On the other hand, repeatedly copying large, pointer-free objects will lead to poor performance. One solution is simply not to copy them but instead devolve the management of large objects to a non-moving collector. Another is to copy them virtually but not physically. This can be done either by holding such objects on a linked list maintained by the collector, or by allocating large objects on their own virtual memory pages which can be remapped. We consider such techniques in Chapters 8 to 10.
1Note: our allocate and copy routines ignore issues of alignment and padding, and also the possibility that a copied object may have a different format, such as an explicit rather than an implicit hash code for Java objects.
2Tony Printezis, personal communication.
3We discuss barriers in Chapter 11.
4Tony Printezis, personal communication.